Introducción

Los sistemas térmicos generalmente involucran la transferencia de calor mediante la propagación de calor en diversos medios y se produce cuando existe el mismo material o cuando dos sistemas con diferentes temperaturas se ponen en contacto. Generalmente, estos sistemas se analizan en términos de resistencia y de capacitancia térmica considerando que no se presenten como elementos de parámetros concentrados. Por lo general, están distribuidos en todas las sustancias, por lo que, una hipótesis es simplificar el análisis considerando que un sistema térmico se representa mediante un modelo de parámetros concentrados, los cuales se caracterizan por una resistencia al flujo de calor y tienen una capacitancia térmica insignificante o aquellas sustancias que se caracterizan por una capacitancia térmica que tienen una resistencia insignificante al flujo de calor, respectivamente.

El calor fluye de una sustancia a otra mediante la conducción, la convección y la radiación, considerando estos lo principales medios de propagación de calor empleados para el control de sistemas termodinámicos. En lo que atañe al control de temperatura existen diversos estudios basados en sistemas térmicos que consideran el modelado de sistemas de calefacción mediante un mezclador, usando la resistencia y la capacitancia térmica, estos permiten el control de temperatura del líquido de entrada considerando la masa, la velocidad de flujo del líquido y la entrada de flujo de calor (^{Ogata, 2010}).

Entre los trabajos actuales más relevantes respecto al control de temperatura se tienen: Salcedo et al. (2018), donde los autores realizan el control predictivo generalizado de temperatura de clinkerización en un horno rotativo de cemento para construcciones, no obstante, esto está limitado a un área específica. En ^{Benítez et al. (2016)}, se presenta el control de temperatura bajo ganancias difusas de hornos para el recalentamiento de losas para la industria, éste se aplica en procesos industriales como fundición de metales. En Benítez et al. (2015) se presenta el control bajo un predictor de Smith, donde se controla la temperatura durante la formulación de medicamentos inyectables en reactores químicos. ^{Santos et al. (2018)}, presentan el control de temperatura de unos paneles solares. En ^{Villar et al. (2008)} se muestra el control de temperatura para reducir el consumo de energía basado en un controlador difuso que fomenta la sustentabilidad. Finalmente, en ^{Torres et al. (2017)} se presenta el modelado matemático y el control de temperatura para una planta térmica mediante un PID.

En lo que respecta a la ley de enfriamiento de Newton, que estudia la diferencia de temperaturas entre un cuerpo y su medio ambiente, no es demasiado grande, ya que el calor transferido en la unidad de tiempo hacia el cuerpo o desde el cuerpo por conducción, convección y radiación es aproximadamente proporcional a la diferencia de temperatura entre el cuerpo y el medio externo. En la literatura existen diversos trabajos aplicando la ley de enfriamiento de Newton y tienen como objetivo aproximar fenómenos termodinámicos de la vida cotidiana y de procesos, sin embargo, pocos estudian a detalle el modelo de la ley de enfriamiento de Newton para obtener un modelo derivado directamente de él para que sea aplicado en la teoría del control; entre los más relevantes se encuentran: ^{Mondol et al. (2018)} donde se presenta el modelado y se comparan las soluciones de la ecuación diferencial mediante el cálculo convencional y el cálculo fraccionario, considerando que el modelo propuesto con la derivada fraccionaria es más exacta que con la derivada continua. ^{Yan & Guo (2012)}, presentan la eficiencia y las limitantes en el uso de motores térmicos a máxima potencia usando la ley de enfriamiento de Newton considerando como variable la temperatura del motor. En los siguientes ejemplos se usa la ley de enfriamiento de Newton para resolver problemas reales, entre los que se encuentran ^{Boyles et al. (2019)} quienes realizan un análisis macro fisiológico para predecir los rangos actuales y futuros para mejorar la comprensión de la macro ecología endotérmica siguiendo el equilibrio térmico mediante la ley de enfriamiento de Newton. En ^{Wang et al. (2019)}, se considera un método de estudio e investigaciones experimentales del error de un termopar con perfil controlado de campo de temperatura, donde los valores de errores obtenidos son comparados con las estimaciones teóricas realizadas utilizando la ley de enfriamiento de Newton. En ^{Dilip & Pankaj (2007)}, se estudia el enfriamiento interno del pescado, en época de almacenamiento de hielo, basado en la ley de enfriamiento de Newton. Finalmente, en ^{Rezende & Bacigalupe (2015)} se estudia la termorregulación y la adaptación a la temperatura en las libélulas, donde se analiza si son capaces de mantener su temperatura corporal constante ante la temperatura del medio ambiente y se relaciona dicho efecto con la ley de enfriamiento de Newton.

Como se ha presentado, existen diversos trabajos de investigación donde se modela y se lleva a cabo el control de temperatura de diversos sistemas, sin embargo, en ninguno de ellos se presenta el modelado para obtener como resultado un modelo que permita aplicar directamente una estrategia de control. En lo que atañe a la ley de enfriamiento de Newton, los diversos trabajos han modelado y presentado trabajos que se basan en dicho estudio, sin embargo, en ninguno de los trabajos citados se ha presentado algún modelo derivado para el control de temperatura como un sistema térmico basado en la ley de enfriamiento de Newton.

La contribución de este artículo es la obtención de un modelo bajo la ley de enfriamiento de Newton. El modelo se da en términos del gradiente térmico del sistema y representa una función de transferencia, considerando la temperatura del sistema como salida y la temperatura exterior como entrada, donde se inserta la estrategia de control.

El modelo propuesto está en términos del gradiente térmico considerado como la propiedad o característica principal del sistema (^{Mondol et al., 2018}), es decir, pueden caracterizarse diversos modelos conociendo dicho parámetro. El modelo permite proponer y diseñar diferentes controladores para regular la temperatura, sin embargo, debido a que el sistema presentado es un sistema abierto existe la perdida de calor, por ende, se busca implementar un controlador que permitan obtener los objetivos de rendimiento deseados, como la minimización de la función de costo, emplear la menor energía de control y sintonizarlo de manera eficiente. Por lo tanto, se opta por un controlador óptimo capaz de satisfacer dichos requerimientos, cuyo problema clave consista en aplicar el controlador LQR, seleccionando a las matrices ponderadas Q y R correctas del índice de rendimiento, satisfaciendo la ecuación de Riccati. Además, se utiliza Matlab-Simulink, que implementa el diagrama de control y lleva a cabo la simulación del modelo propuesto. Los resultados de la simulación confirman que el controlador LQR puede reducir el error de estado estable, mejorar la respuesta y reducir los objetivos de rendimiento con poca energía.

Este trabajo se estructura como sigue, primero, en la Sección 2 se presenta el modelado de la ley de enfriamiento de Newton. En la Sección 3 se presenta el modelo propuesto y la aplicación de control a la ley de enfriamiento de Newton. En la sección 4 se presenta la discusión de los resultados de simulación para ilustrar los resultados del controlador LQR mediante dos líquidos diferentes. Finalmente, en la sección 5 se exponen las conclusiones.

Modelado de la ley de enfriamiento de Newton

La ley de enfriamiento de Newton considera que la velocidad a la que la temperatura de un cuerpo disminuye con el tiempo es proporcional a la diferencia de temperatura entre el cuerpo y sus alrededores. Matemáticamente, esto se representa como:

Donde:

T(t) = temperatura del cuerpo en un determinado tiempo t.

Tα = temperatura del medio ambiente.

α = gradiente térmico dentro del cuerpo de enfriamiento que se considera negativo, éste hace referencia a la dirección del flujo de calor, y en este caso, del cuerpo hacia su medio definido como:

h es el coeficiente de transferencia de calor, A es el área de contacto y C la capacidad térmica, esto es:

Donde Δt=Tt-Ta Además, q=CT se obtiene a partir de la cantidad de calor; derivando con respecto al tiempo t, se obtiene:

Sustituyendo (3) en (4), se tiene:

De (5) puede obtenerse:

Donde la constante de enfriamiento es determinada integrando la ecuación (1) de 0 a t, tomando la condición inicia T0=T0. Así,

La ecuación diferencial es llamada la ley de enfriamiento de Newton, que puede ser resuelta usando el cálculo convencional.

Resolviendo la ecuación (1) mediante la transformada de Laplace (^{Mondol et al., 2018}):

El desarrollo de (8) implica:

Reordenando los términos y considerando la condición inicial se obtiene:

Usando ahora la transformada inversa de Laplace, se obtiene la solución:

Una vez presentado el modelado de la ley de enfriamiento de Newton, a continuación, se presenta un modelo propuesto basado en una función de transferencia con base en (9), considerando las condiciones iniciales igual a cero.

Modelo propuesto y estrategia de control

En la teoría del control, las funciones de transferencia se usan comúnmente para describir las relaciones de entrada-salida de los componentes o sistemas que se pueden describir mediante ecuaciones diferenciales lineales invariantes en el tiempo. La función de transferencia según (^{Ogata, 2010}) se define como la relación de la transformada de Laplace de la salida y de la entrada, bajo el supuesto de que todas las condiciones iniciales son cero.

De esta manera, el modelo propuesto se basa en obtener una función de transferencia que represente a la ley de enfriamiento de Newton, considerando nulas las condiciones iniciales de (9). En este caso, la función de transferencia se define entre la temperatura del sistema en cualquier momento Tt,Tα(t) la temperatura del medio ambiente, α el gradiente térmico dentro del cuerpo de enfriamiento y se muestra:

Considerando que para el controlador la temperatura del medio ambiente Tα no será fija, es decir, se desea que el sistema sea capaz de llevar la temperatura de salida T(t) a una temperatura de referencia Tr(t) o regulable. Se realiza el siguiente cambio de variable Tα por u(t), es decir, se define como una función variable en el tiempo. En el dominio de Laplace es dada como U(s), así la ecuación (12) se define como:

Reordenando los términos es posible obtener la siguiente función de transferencia:

Donde U(s) se define como la señal de control, T(s) es la temperatura de salida del sistema, y considerando que el gradiente térmico α se encuentra en el cuerpo de enfriamiento:

Ahora, sustituyendo (15) en la ecuación (14) se define la función de transferencia mostrada en la Figura 1.

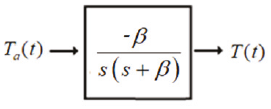
Figura 1 Función de transferencia para la ley de enfriamiento de Newton con condiciones iniciales en cero 

La función de transferencia para la ley de enfriamiento de Newton con condiciones iniciales en cero representa un modelo derivado de la ley de enfriamiento de Newton que muestra la relación entrada-salida entre la temperatura del cuerpo y la temperatura del medio ambiente, considerando como único parámetro el gradiente térmico que caracteriza al sistema según las características y las propiedades.

Partiendo de la función de transferencia representada en la Figura 1. En este artículo se plantea el control de temperatura de un cuerpo, el cual disminuye con el tiempo y es proporcional a la diferencia de temperatura entre el cuerpo y sus alrededores del ambiente dado por Tα(t) . Por lo tanto, el modelo parte de la función de transferencia dada por la Figura 1. De esta manera, el sistema depende del parámetro del gradiente térmico del líquido.

Las suposiciones anteriores permiten realizar un cambio de variable. En otras palabras, la temperatura del medio ambiente Tα(t) será controlada mediante un sistema de calefacción que permita llevar la temperatura de salida T(t) a una temperatura de referencia Tr(t) . De esta manera, es posible realizar un cambio de variable Tα(t) por u(T), quedando así la siguiente función de transferencia:

Donde u(s) representa la señal de control y T(s) es la temperatura de salida del sistema en el dominio de Laplace. Obteniendo la representación de (16) en dominio del tiempo:

Donde se define el error como et=Trt-T(t), dado como la diferencia entre la señal de referencia y señal de salida. Como Trt es constante, entonces e˙t=-T˙(t) y e¨t=-T¨(t). Así, la ecuación (17) en términos del error, la primera derivada y la segunda derivada del error, se muestra como:

Es decir, representado la ecuación diferencial (18) en un modelo en variables de estados, donde los estados se definen como x1t=e(t) y x2t=e˙(t) se obtiene:

Con base en el modelo propuesto (19), derivado de la ley de enfriamiento de Newton con condiciones iniciales cero, es posible proponer un controlador para que siga una temperatura de referencia.

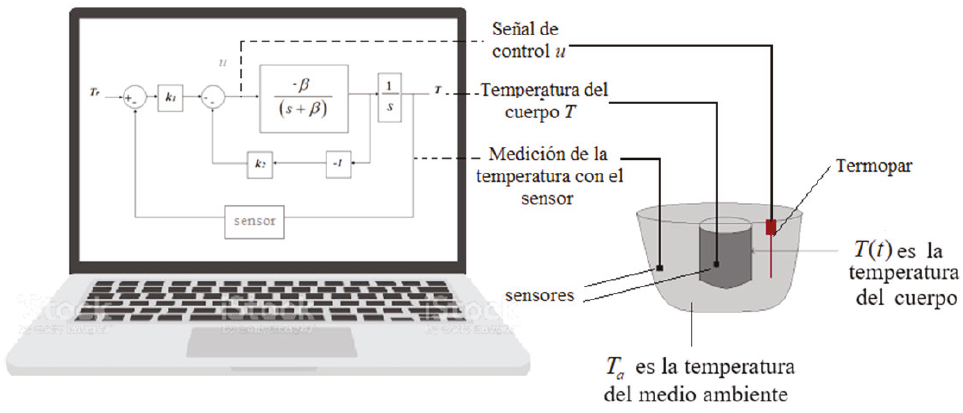
El sistema modelado es relativo a la Figura 2, donde se presenta un esquema general del prototipo que será implementado a futuro. Aquí el objetivo es controlar la temperatura del cuerpo mediante la temperatura del medio ambiente, es primordial considerar un sensor de temperatura que permita monitorear la temperatura de salida y en consecuente, permita controlar y ejercer una señal de control mediante el termopar. Es importante resaltar que se desea mantener constante la temperatura de salida, de manera que se puede implementar un controlador automático que ajuste el sistema de calefacción, reduciendo el error de estado estable y mejorando la respuesta, además que permita reducir los objetivos de rendimiento con la menor energía de control. Por tanto, se opta por un controlador LQR para realizar el control de la temperatura de salida con base en el modelo propuesto, reduciendo un índice de desempeño. Esto permitirá que haya la menor pérdida de energía en el sistema para el control de temperatura.

Figura 2 Diagrama esquemático para el esquema de control LQR para la ley de enfriamiento de Newton 

El controlador LQR es una técnica de control empleada para dispositivos activos utilizada para muchos ejemplos, incluido un motor de CC, es decir, ha sido probado en modelos de segundo orden (^{Qiang, 2014}). En el método LQR basado en un control óptimo busca ajustar las matrices de ponderación para minimizar el índice de desempeño J. Considerando el sistema lineal caracterizado por (19), donde X˙ es el vector de estado y u(T) es la acción de control. El índice de desempeño se define por (20) y (21):

Donde R es una matriz hermítica definida positiva o simétrica real, que es la matriz de ponderación de las variables de entrada u en la función de índice de rendimiento J. Q es la matriz simétrica real o hermítica definida positiva, que es la matriz de ponderación de las variables de estado X en J (^{Kemper et al., 2013}). Las matrices Q y R se denominan matrices de sintonización de control y estado; y determinan la importancia del error y del costo de esta energía, respectivamente.

El índice de control es un requisito entre la calidad del control y los costes de control (^{Teppa et al., 2015}; Fonseca et al., 2015). La calidad de control determina la primera parte de la expresión integrada. Se realiza ponderando la matriz Q y da forma a las variables de salida del estado. La segunda parte de la expresión integrada minimiza el consumo de energía de entrada y se realiza mediante la matriz R que forma las variables de entrada u. La matriz P se determinó a partir de la solución de (20):

La ecuación (22) a menudo se denomina ecuación de Riccati. Se puede programar y resolver fácilmente mediante métodos numéricos. El vector de retroalimentación óptimo K se muestra como la ecuación (23). La acción de control óptima para el control LQR es u(t) se obtiene como ecuación (24) para un controlador Proporcional Derivativo:

El esquema de control LQR se representa en la Figura 3.

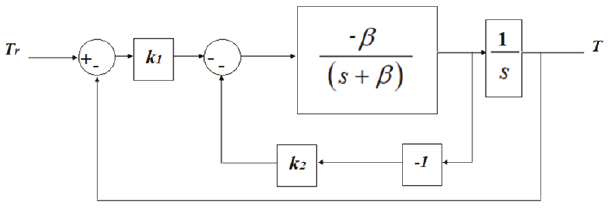
Figura 3 Diagrama de control LQR para la ley de enfriamiento de Newton con condiciones iniciales cero 

Donde Tr es la temperatura de referencia, T es la temperatura de salida, k1 y k2 se definen como las ganancias del controlador óptimo mostradas por el vector K=k1k2.

Este control óptimo se denomina regulador cuadrático lineal (LQR). El diseño de LQR significa diseñar el factor de ganancia de retroalimentación de estado K. Diseñar el controlador óptimo requiere que la función de índice de rendimiento cuadrático J debe establecerse. Obviamente, la tasa de retroalimentación de estado óptima se decide mediante las matrices de ponderación Q y R. Por lo tanto, la selección de matrices de ponderación Q y J juegan un papel importante en el correspondiente proceso de diseño óptimo del controlador. La elección de las matrices de ponderación no es fácil, y el método de prueba y error suele utilizarse para llegar a estas matrices y lograr una ganancia óptima. Para el problema de control de LQR, las matrices de peso Q y R en el índice de rendimiento tienen una gran influencia en los efectos de control.

Discusión y análisis de resultados

Para el análisis numérico y la validación de la estrategia de control propuesta, se consideran los gradientes térmicos de algunos líquidos, presentados en ^{Mondol et al. (2018)}, como son: el agua para un volumen de 300 ml β=0.109 y mercurio β=0.32. Estos parámetros del gradiente térmico son los correspondientes experimentos de temperatura medidos en grados Celsius (°C), estos son seleccionados debido a que ya se tienen estudios precedentes de ellos.

Las simulaciones y los resultados numéricos de este artículo se presentan en Matlab-Simulink. Se muestran simulaciones para tres líquidos con el desarrollo de controladores que validan la efectividad del controlador LQR propuesto. Las temperaturas de las simulaciones y los resultados numéricos se dan en °C. El periodo de muestreo de la simulación es de 0.010 s durante un tiempo de 500 s y se considera el método de solución de Runge-Kutta.

Simulación y resultados del controlador LQR para agua con volumen de 80 ml

Se presenta la primera simulación para el control de temperatura del modelo propuesto para agua con un volumen de 80 ml con un valor de β=0.109. En esta simulación se utiliza el comando de Matlab “lqr” para un sistema de tiempo continuo, la ley de retroalimentación de estado u = –KX minimiza la función de costo cuadrático.

Esta simulación para los resultados numéricos y para el controlador presentado, emplea las siguientes matrices:

A=010-0.109 (25)

B=00.109 (26)

Q=0.001000.1, R=0.001 (27)

El resultado para las matrices (25) y (26) para el controlador LQR y el uso de Matlab es:

K=19.9247 (28)

P=0.01090.00920.00920.0911 (29)

E=-0.0999-1.0909 (30)

Donde K es el vector de ganancias optimas, P es la matriz solución de la ecuación (22) y, E representa los polos en lazo cerrado del sistema para la matriz A–BK lo que implica que el sistema es estable. En la Figura 4 se muestra la respuesta del sistema, donde se presenta la señal de temperatura de referencia y la señal de salida de temperatura, respectivamente. Puede observarse que el controlador es capaz de controlar la temperatura debido a un bajo índice de desempeño.

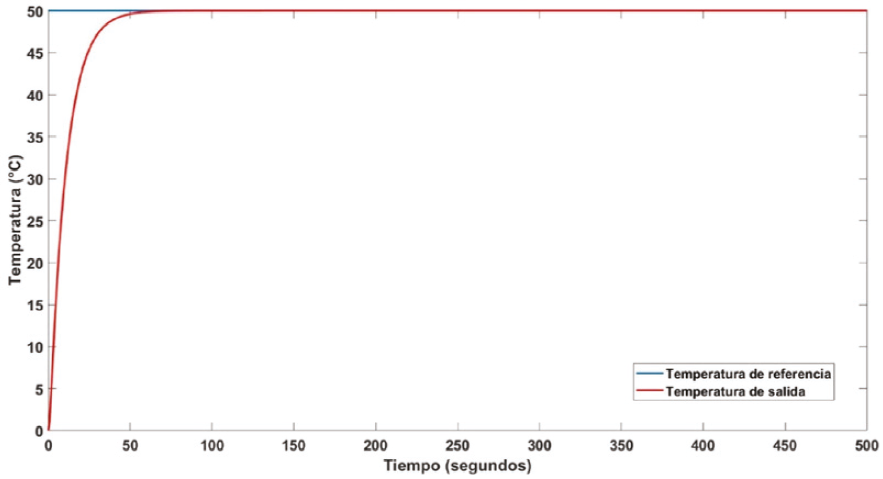
Figura 4 Señal de temperatura de salida y señal de temperatura de referencia usando el control LQR para el agua con un volumen de 80 mL 

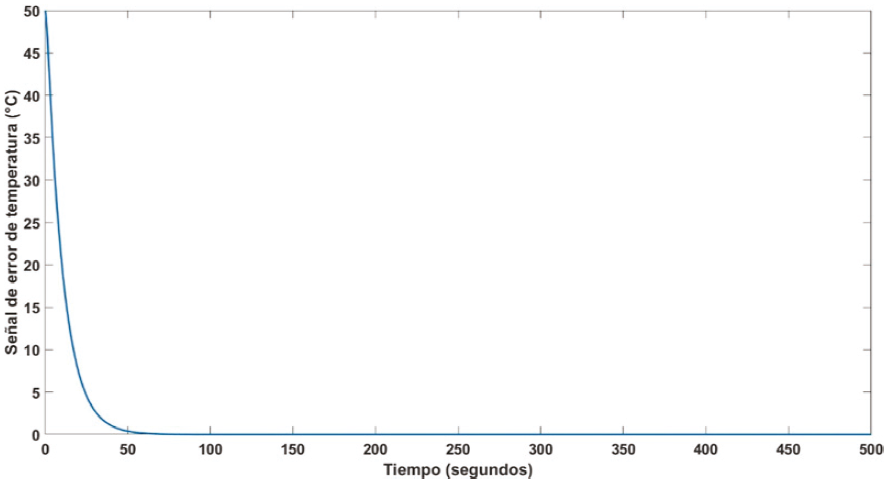
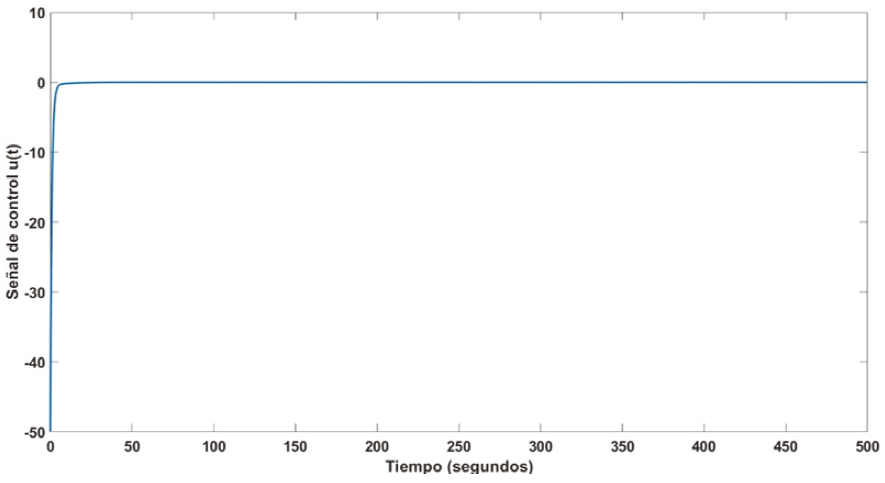
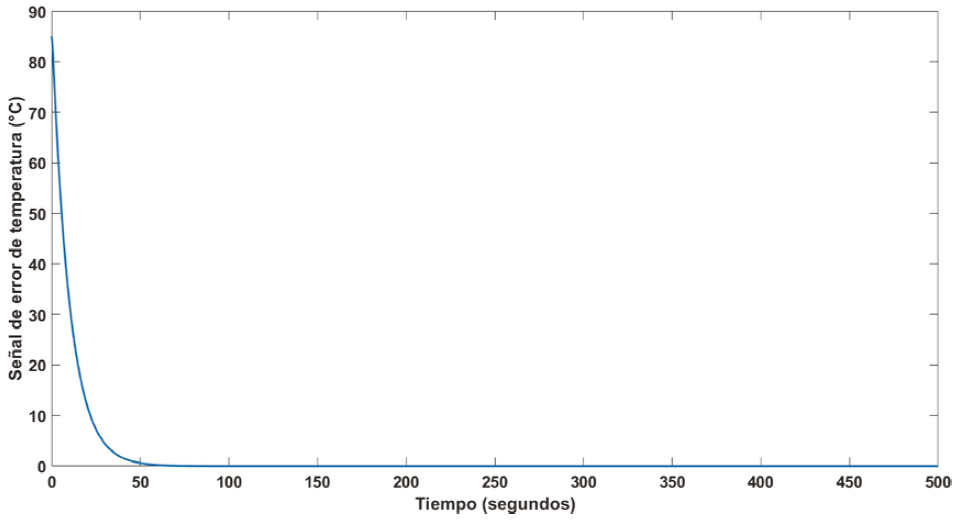
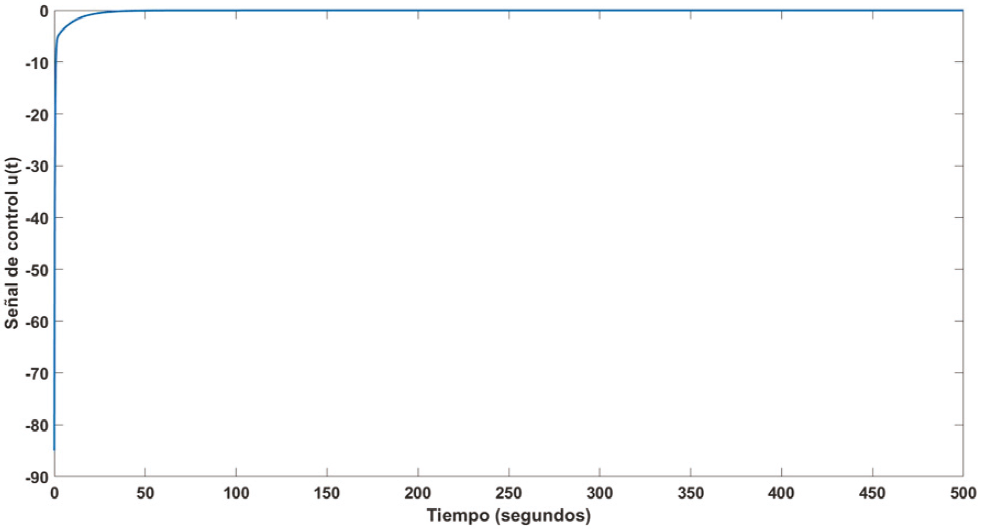
Es importante tener en cuenta que se requieren valores altos de los parámetros de ganancia para obtener un buen rendimiento, donde se puede minimizar la señal de error y reducir los objetivos de rendimiento con la menor energía de control. En la Figura 5 se muestra el error de temperatura. Mientras que, la señal de control correspondiente para la simulación se puede ver en la Figura 6. De manera similar se lleva a cabo la simulación numérica para el agua con un volumen de 80 mL considerando tres diferentes temperaturas como se muestra en la Figura 7.

Figura 5 Señal de error generada usando el control LQR para el agua con un volumen de 80 mL 

Figura 6 Señal de control generada usando el control LQR para el agua con un volumen de 80 mL 

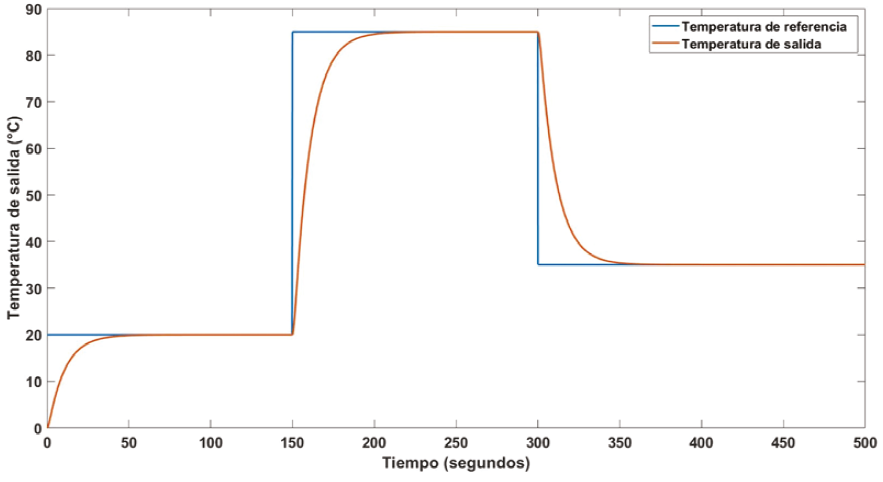
Figura 7 Señal con diferentes temperaturas de referencia y de salida usando el control LQR para el agua con un volumen de 80 mL 

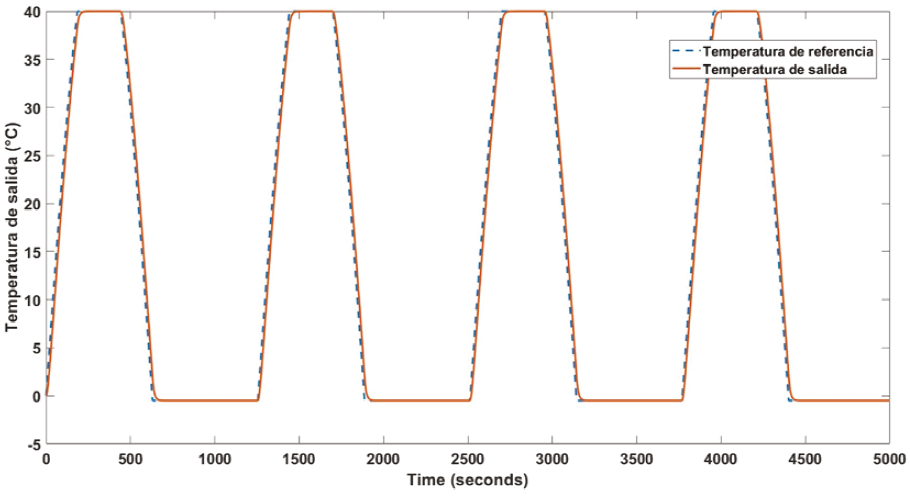
Finalmente, el modelo propuesto es evaluado bajo el seguimiento de trayectoria para la temperatura. En la Figura 8 se muestra la temperatura de salida para una señal senoidal recortada, por lo que el modelo propuesto puede emplearse para la regulación o el seguimiento de trayectoria para temperatura.

Figura 8 Señal de referencia y de salida para el seguimiento de trayectoria de temperatura usando el control LQR para el agua con un volumen de 80 mL 

Simulación y resultados del controlador LQR para mercurio

En la segunda simulación se presenta el control de temperatura del modelo propuesto para agua con un volumen de 80 mL con un valor de β = 0.32. En esta simulación se utiliza el comando de Matlab “lqr” para un sistema de tiempo continuo, la ley de retroalimentación de estado u = –KX minimiza la función de costo cuadrático.

Las matrices empleadas son las siguientes:

A=010-0.32 (31)

B=00.32 (32)

Q=0.001000.1, R=0.001 (33)

De manera similar al primer ejemplo, para este segundo se obtuvieron para el control LQR y las ecuaciones (31) y (32) los siguientes resultados:

K=19.3562 (34)

P=0.01040.00310.00310.0292 (35)

E=-0.0996-3.2144 (36)

Donde K es el vector de ganancias optimas, P es la matriz solución de la ecuación (22) y, E representa los polos en lazo cerrado del sistema para la matriz, A–BK lo que implica que el sistema es estable. En la Figura 9 se muestra la respuesta del sistema, donde se presenta la señal de temperatura de referencia y la señal de salida de temperatura para el mercurio, respectivamente. Puede observarse que el controlador es capaz de controlar la temperatura mediante un bajo índice de desempeño, mientras que en la Figura 10 se muestra la señal del error de temperatura. Es importante señalar que el sistema propuesto al controlador tiene una buena respuesta que minimiza la señal de error.

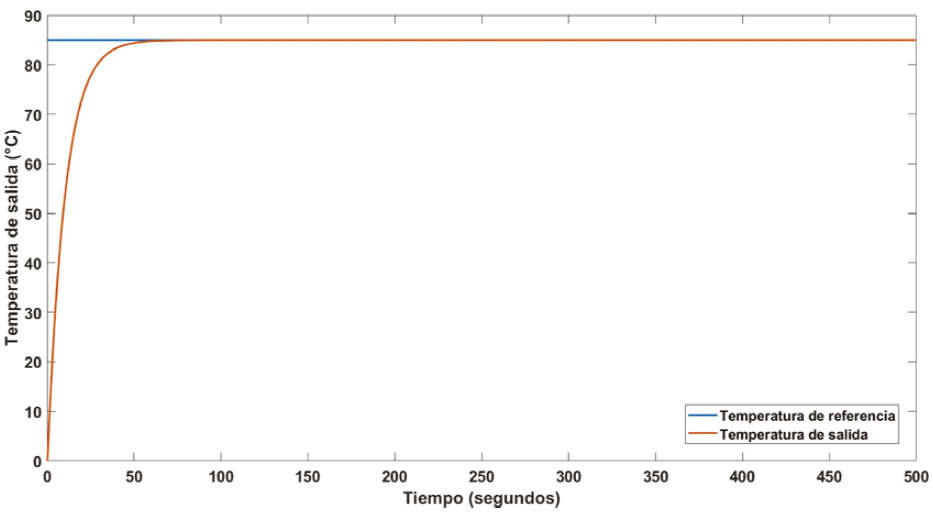
Figura 9 Señal de temperatura de salida y señal de temperatura de referencia usando el control LQR para el mercurio 

Figura 10 Señal de error generada usando el control LQR para el mercurio 

La Figura 11 marca la señal de control correspondiente para las simulaciones numéricas con mercurio.

Figura 11 Señal de control generada usando el control LQR para el mercurio 

Una vez que se han realizado las simulaciones y se han mostrado los resultados numéricos del controlador para dos líquidos diferentes, se muestra claramente que la eficiencia del controlador LQR para el modelo de control de temperatura con condiciones iniciales cero proporciona un buen rendimiento de las temperaturas de salida frente a una temperatura de referencia.

Conclusiones

Este artículo obtuvo un modelo representado mediante una función de transferencia derivado de la ley de enfriamiento de Newton. El modelo se da en términos del gradiente térmico del sistema y representa una función de transferencia considerando la temperatura del sistema como salida y la temperatura exterior como entrada, donde es insertada la estrategia de control.

Las simulaciones numéricas y los resultados presentados validan la efectividad del controlador LQR para temperatura. Las principales contribuciones de este documento son la propuesta de un modelo para la ley de enfriamiento de Newton con condiciones iniciales cero. El modelo propuesto por la ley de enfriamiento de Newton permitió implementar un controlador de temperatura basado en un control LQR con las condiciones de estabilidad necesarias, lo que no ha sido desarrollado en otras investigaciones que consideran el control de temperatura.

El trabajo futuro considera la propuesta de un modelo para la ley de enfriamiento de Newton con condiciones iniciales distintas de cero. Asimismo, la implementación de un prototipo físico que permite realizar el control de la temperatura mediante un sistema en tiempo real. Finalmente, el modelo presentado permite el desarrollo de otra clase de controladores.