Introducción
De manera preponderante, la porción centro-sur de la República Mexicana se localiza en la zona de influencia de los huracanes que se originan en los océanos Atlántico y Pacífico. Por otra parte, su porción norte la afectan los frentes fríos. Ambos fenómenos meteorológicos generan lluvias de gran magnitud, que producen crecientes o avenidas máximas, las cuales inundan extensas regiones y ponen en peligro a las obras hidráulicas (Aldama, 2000; Aldama et al., 2006).
Quizás la obra hidráulica más importante, por sus beneficios y peligrosidad de falla, sean los embalses de todo tipo. En relación con su dimensionamiento de seguridad hidrológica, desde hace dos décadas, sus Crecientes de Diseño se analizan como eventos multivariados, ya que las características que definen su hidrograma están correlacionadas. El enfoque más simple, el bivariado, está justificado por la escasa sensibilidad que tienen los embalses al lapso en que se llega al gasto pico del hidrograma (Aldama, 2000) y por la correlación que guardan tal gasto máximo con el volumen y el volumen con la duración total (Goel et al., 1998; Yue et al., 1999; Yue & Rasmussen, 2002).
Ramírez & Aldama (2000), Yue & Rasmussen (2002) y Volpi & Fiori (2012) destacan que el análisis de frecuencias bivariado conduce a una infinidad de combinaciones de gasto pico y volumen para una probabilidad de excedencia conjunta adoptada. Lo anterior implica que para un mismo periodo de retorno conjunto existen muchas crecientes o hidrogramas que producirán distintos efectos en el embalse que se diseña o revisa; adoptando lógicamente, el que genera las condiciones más críticas o severas en su vertedor y almacenamiento.
Los objetivos de este estudio fueron los cinco siguientes:
1) Exponer la distribución General de Valores Extremos bivariada (GVEb) y su método de ajuste por máxima verosimilitud.
2) Citar las ecuaciones de los periodos de retorno conjuntos.
3) Detallar la selección de los eventos de diseño críticos y la estimación de las probabilidades empíricas conjuntas.
4) Exponer la técnica de validación de la GVEb y de sus marginales.
5) Aplicar la teoría operativa al registro de 52 gastos pico y volúmenes anuales de las crecientes de entrada a la Presa Venustiano Carranza (Don Martín), del estado de Coahuila, México.
Teoría operativa
Distribución GVE bivariada (GVEb)
Emil Julius Gumbel estableció a inicios de los años sesenta el llamado modelo bivariado logístico, el cual acepta como distribuciones marginales las de valores extremos: Gumbel, General de Valores Extremos (GVE), Gumbel mixta y TCEV o de valores extremos de dos componentes (Escalante & Raynal, 1994; Ramírez & Aldama, 2000; Escalante & Reyes, 2004), su ecuación es:
Donde:
F(x) y F(y) = funciones de distribución de probabilidades (FDP) marginales de las variables aleatorias X y Y.
m = parámetro de asociación, el cual depende de la correlación entre las variables.
Si las marginales son distribuciones GVE o General de Valores Extremos (Hosking & Wallis, 1997; Rao & Hamed, 2000; Stedinger, 2017), sus expresiones son:
u, α y k son los parámetros de ubicación, escala y forma. Sustituyendo las ecuaciones 2 y 3 en la 1, se obtiene la FDP de la GVEb (Escalante & Raynal, 1994):
con
La distribución GVE representa tres modelos probabilísticos: si k < 0 la GVE tiene el tipo Fréchet, sin límite superior; caso aquí estudiado; si k = 0 se tiene el modelo Gumbel y cuando k > 0 se tiene la Weibull, con límite superior. La distribución GVE está definida por el conjunto {xi: [1 - k(xi - u)/α] > 0}, lo cual se indica con el signo + afuera del paréntesis.
Coles (2001) destaca que cualquier combinación de parámetros de ajuste que viola la condición anterior de positividad, implica que al menos uno de los puntos observados (xi), está más allá de los puntos finales de la distribución y entonces la función de verosimilitud es cero y su versión logarítmica -∞.
La solución inversa de las ecuaciones 2 y 3, permiten la estimación de predicciones (xp, yp) asociadas a una probabilidad de no excedencia p = F(x) ó p = F(y), son las siguientes:
En este estudio se ajustó la distribución GVE con tres métodos: Sextiles, momentos L y máxima verosimilitud, los cuales se pueden consultar respectivamente en: Campos (2006), Hosking & Wallis (1997) y Rao & Hamed (2000).
Restricciones de probabilidad
Las probabilidades de no excedencia univariadas y conjunta de la distribución GVEb, deben cumplir con la restricción siguiente (Escalante & Raynal, 1994; Ramírez & Aldama, 2000; Escalante, 2004):
Método de máxima verosimilitud
Para una muestra aleatoria (X1, X2, . . . , Xn) de observaciones independientes e idénticamente distribuidas (iid) que siguen una FDP denominada Fθ con parámetros de ajuste θ1, θ2, . . . ,θq. La probabilidad de obtener un valor Xi, será (Rao & Hamed, 2000; Coles, 2001; Meylan et al., 2012):
siendo, fθ(xi) la función de densidad de probabilidad. Como los datos son iid, la probabilidad de obtener los n valores Xi, será la probabilidad conjunta o función de verosimilitud, designada L del inglés likelihood; cuya ecuación es:
El método de máxima verosimilitud consiste en encontrar un vector
Lo anterior, es aceptable debido a que la función logarítmica es monotónica y entonces la función l(θ) alcanza su máximo en el mismo punto que la función L(θ).
l(θ) de la distribución GVEb
La función logarítmica de verosimilitud de la GVEb para el caso simple de variables aleatorias X, Y con igual amplitud de registro (n), ha sido expuesta por Escalante & Raynal (1994) y es la siguiente:
El algoritmo Complex
La maximización de la ecuación 11 para obtener los siete parámetros óptimos de ajuste
El número de variables de decisión y dependientes son siete
Periodos de retorno univariados
La probabilidad de un evento se define como el cociente del número de casos favorables (ncf) entre el número de casos posibles (ncp) a dicho evento y varía de cero a uno. Debido al manejo anual de las variables X, Y, la probabilidad de excedencia
En las expresiones anteriores, F(x) y F(y) se estiman con las ecuaciones 2 y 3.
Periodos de retorno conjuntos
El primer periodo de retorno conjunto del evento (X, Y) se define bajo la condición OR y la ecuación 14 de la manera siguiente (Goel et al., 1998; Yue, 2000b; Shiau, 2003):
F(x,y) es la probabilidad de no excedencia conjunta que se estima con la ecuación 4, previa estimación de sus parámetros de ajuste óptimos
El segundo periodo de retorno conjunto del evento (X, Y) está asociado al caso en que ambos límites son excedidos (X > x, Y > y) o condición AND, su ecuación es (Goel et al., 1998; Aldama, 2000; Ramírez & Aldama, 2000; Yue, 2000b y Shiau, 2003):
Aldama (2000) obtiene la expresión F’(x,y) de la probabilidad conjunta de excedencia mediante un razonamiento de probabilidades lógico y simple aplicado en el plano cartesiano. En cambio, Yue y Rasmussen (2002) recurren al plano cartesiano para definir numéricamente un evento bivariado (X, Y), que puede ocurrir en alguno de los cuatro cuadrantes.
Diversos autores (Yue, 2000b; Yue & Rasmussen, 2002; Shiau, 2003) han mostrado las gráficas de los dos periodos de retorno conjuntos y han discutido sus diferencias. En la Figura 1 se muestra la gráfica del periodo de retorno conjunto T’(Q,V), construida con los datos de la aplicación numérica que será expuesta.

Figura 1 Gráficas de los cuatro periodos de retorno conjunto T’(Q,V) de diseño, de las crecientes de entrada a la presa Venustiano Carranza (Don Martín), México
De acuerdo con Yue et al. (1999), Yue (2000b) y Yue & Rasmussen (2002) existe un tercer tipo de periodo de retorno conjunto, que tiene aplicación en la práctica hidrológica y que se define para un evento X dado que Y ≤ y o para un evento Y dado que X ≤ x y por ello, se designan condicionales. Para tales eventos, sus distribuciones de probabilidad condicional se definen de manera simple, con estas ecuaciones:
Sustituyendo las expresiones anteriores en la ecuación 14, se obtienen las fórmulas del periodo de retorno conjunto condicional:
Eventos críticos del T’(x,y)
Volpi y Fiori (2012) destacan que la gráfica del periodo de retorno conjunto de tipo AND, mostrada como Figura 1, presenta una severa inconsistencia al contener, en un contexto bivariado, umbrales críticos univariados. Debido a lo anterior, tal gráfica se considera integrada por dos porciones, las dos designadas simples (naive part) y la correcta (proper part). Las partes rectas son las colas o rectas asíntotas a la parte curva. La probabilidad de ocurrencia de un evento o pareja de Q y V, es variable en la parte curva y decrece a lo largo de la parte recta, aunque todos los valores definen el mismo periodo de retorno conjunto. En resumen, las parejas de valores de las rectas asíntotas tienen probabilidades de ocurrencia bajas y por ello no deben ser incluidos en los análisis de búsqueda de las crecientes (Q y V) críticas o severas.
Test de Wald-Wolfowitz
Esta prueba no paramétrica ha sido utilizada por Bobée & Ashkar (1991), Rao & Hamed (2000) y Meylan et al. (2012) para probar independencia y estacionariedad en registros de gastos máximos anuales (Xi). Permite verificar su aleatoriedad, cuando su estadístico U no excede de 1.96, en una prueba con nivel de significancia de 5 %.
Estimación de probabilidades empíricas
Las probabilidades de no excedencia empíricas univariadas y bivariadas se estimaron con base en la fórmula de Cunnane, que de acuerdo con Stedinger (2017) conduce a probabilidades de no excedencia (p) aproximadamente insesgadas, su expresión es:
siendo i el número del dato cuando se ordenan de menor a mayor y n su número total.
Para la estimación de las probabilidades empíricas bivariadas se siguió el mismo principio que aplica para la ecuación 20 (Yue et al., 1999; Yue, 2000b; Yue & Rasmussen, 2002), por ello se trabajó en el plano bidimensional, con los datos ordenados en forma progresiva; los gastos pico (Q) en los renglones y los volúmenes (V) en las columnas. El plano formado es un cuadrado de n por n casillas, con n casillas en su diagonal principal, cuando el número de orden del renglón es igual al de la columna. Después cada pareja de datos anuales (Q y V) se localiza en el plano bidimensional y la casilla definida por la intersección del renglón y columna se identifica con el número i que corresponde al año histórico dibujado.
Cuando las n parejas de datos están dibujadas, se busca el año 1 y se define un área rectangular o cuadrada de valores menores de Q y de V, cuyo conteo de casillas numeradas dentro, es NM1 o combinaciones de Q y V menores. Calculados los n valores de NMi, se aplica la ecuación 20 para calcular la probabilidad empírica conjunta:
Validación de la distribución GVEb
Esta es la etapa más importante del proceso de ajuste de la GVEb, pues en ella se verifica que tal modelo reproduzca fielmente las probabilidades conjuntas observadas (ecuación 21). Yue (2000a) indica que la forma más simple de representar las probabilidades conjuntas empíricas y teóricas, consiste en llevar al eje de las abscisas la primera y al eje de las ordenadas la segunda; lógicamente cada pareja de datos define un punto que coincide o se aleja de la recta a 45º.
Yue (2000b) y Yue & Rasmussen (2002) aplican el test de Kolmogorov-Smirnov con un nivel de significancia (α) de 5 % para aceptar o rechazar la diferencia máxima absoluta (dma) entre las probabilidades conjuntas. Para evaluar la estadística (Dn) del test, se utilizó la expresión que exponen Meylan et al. (2012), para α = 5 % es:
n es el número de datos. Si la dma es menor que Dn se acepta la GVEb.
Crecientes de entrada a la Presa Venustiano Carranza, México
Aldama et al. (2006) exponen los 52 gastos máximos y sus volúmenes de las crecientes anuales que entran a la Presa Venustiano Carranza (Don Martín), en el estado de Coahuila, México. Su área de cuenca es de 31034 km2. Tales datos se muestran en la Tabla 1.
Tabla 1 Gastos pico, volúmenes y sus números de orden bivariados de las crecientes que ingresaron a la Presa Venustiano Carranza, México (Aldama et al., 2006)
| Año |
Q (m3/s) |
V (Mm3) |
NMi | Año |
Q (m3/s) |
V (Mm3) |
NMi |
|---|---|---|---|---|---|---|---|
| 1930 | 241.0 | 38.76 | 19 | 1956 | 68.6 | 13.75 | 3 |
| 1931 | 89.2 | 53.59 | 8 | 1957 | 451.2 | 83.73 | 36 |
| 1932 | 1071.2 | 403.78 | 49 | 1958 | 1342.1 | 529.11 | 51 |
| 1933 | 203.2 | 62.10 | 21 | 1959 | 521.6 | 94.18 | 38 |
| 1934 | 90.7 | 11.48 | 3 | 1960 | 99.5 | 33.31 | 10 |
| 1935 | 431.2 | 75.40 | 34 | 1961 | 569.4 | 161.03 | 42 |
| 1936 | 62.0 | 64.75 | 4 | 1962 | 92.8 | 12.03 | 4 |
| 1937 | 138.3 | 19.64 | 11 | 1963 | 340.8 | 33.13 | 15 |
| 1938 | 166.3 | 35.01 | 17 | 1964 | 586.4 | 156.79 | 42 |
| 1939 | 134.2 | 16.99 | 9 | 1965 | 214.6 | 38.78 | 19 |
| 1940 | 182.1 | 21.18 | 12 | 1966 | 76.8 | 19.12 | 4 |
| 1941 | 252.1 | 43.43 | 21 | 1967 | 425.6 | 215.79 | 38 |
| 1942 | 339.7 | 63.62 | 28 | 1968 | 119.6 | 33.24 | 11 |
| 1943 | 284.8 | 35.02 | 19 | 1969 | 50.9 | 25.81 | 3 |
| 1944 | 655.9 | 269.58 | 46 | 1970 | 511.3 | 246.39 | 42 |
| 1945 | 146.7 | 28.04 | 13 | 1971 | 4320.7 | 983.02 | 52 |
| 1946 | 243.4 | 93.00 | 27 | 1972 | 214.2 | 129.87 | 25 |
| 1947 | 339.4 | 63.61 | 27 | 1973 | 449.2 | 65.18 | 33 |
| 1948 | 238.4 | 99.71 | 27 | 1974 | 756.5 | 244.05 | 46 |
| 1949 | 97.7 | 55.93 | 11 | 1975 | 751.6 | 169.43 | 44 |
| 1950 | 280.2 | 71.81 | 28 | 1976 | 614.3 | 466.05 | 46 |
| 1954 | 115.5 | 34.09 | 12 | 1995 | 80.6 | 13.48 | 3 |
| 1952 | 114.7 | 14.87 | 7 | 1996 | 47.6 | 4.69 | 2 |
| 1953 | 238.4 | 99.71 | 27 | 1997 | 87.4 | 15.96 | 5 |
| 1954 | 367.0 | 39.17 | 23 | 1998 | 29.5 | 3.75 | 1 |
| 1955 | 213.5 | 56.00 | 21 | 1999 | 85.0 | 64.22 | 7 |
Resultados y su discusión
Verificación de la aleatoriedad
A los registros de gasto pico y volumen anual de la Tabla 1 se les aplicó el test de Wald-Wolfowitz, para probar su independencia y estacionariedad. Se encontró que ambas series son aleatorias, con U = 0.726 y U = 1.054.
Ajuste de la distribución GVE
A los registros de la Tabla 1, se les ajustaron distribuciones GVE con los métodos de sextiles, momentos L y máxima verosimilitud. En la Tabla 2 se muestran los estadísticos básicos y los valores de los parámetros de ajuste de cada distribución GVE.
Tabla 2 Parámetros estadísticos y de ajuste de la distribución GVE en los registros de gasto pico y volumen anuales de entrada a la Presa Venustiano Carranza, México
| Parámetros estadísticos | Datos (ma*) |
Parámetros de ajuste | ||||||
|---|---|---|---|---|---|---|---|---|
| Media | Mediana | Cv | Cs | Ck | Ubicación | Escala | Forma | |
| 377.8 | 226.5 | 1.636 | 5.372 | 36.063 | Q (sx) | 167.2507 | 124.9967 | -0.5404 |
| Q (mL) | 160.2071 | 137.6962 | -0.5178 | |||||
| Q (mv) | 174.8915 | 148.3761 | -0.4974 | |||||
| 110.1 | 55.9 | 1.525 | 3.457 | 17.364 | V (sx) | 7.9797 | 3.3311 | -0.5354 |
| V (mL) | 39.6841 | 41.6717 | -0.5449 | |||||
| V (mv) | 46.8705 | 47.0951 | -0.5120 | |||||
* método de ajuste: (sx) sextiles, (mL) momentos L y (mv) máxima verosimilitud
Búsqueda de los parámetros óptimos de la GVEB
Debido a la gran similitud que mostraron los parámetros de ajuste de la distribución GVE en la Tabla 2, con los tres métodos aplicados para ambos registros, se decidió adoptar a los valores inferiores, iniciales y superiores de cada variable de decisión, con base en tales resultados; quedando así: u1 (160,167,175), α1 (125,138,148), k1 (-0.50,-0.52,-0.54), u2 (38,40,49), α2 (42,43,47) y k2 (-0.512,-0.535,-0.545). Además, se definieron cinco intervalos para el parámetro de asociación (m) y se adoptó como inicial el valor medio, tales límites fueron: 1.0 a 1.5, 1.5 a 2.0, 2.0 a 2.5, 2.5 a 3.0 y 3.0 a 3.5. En la Tabla 3 se muestran los resultados principales de las cinco corridas numéricas del algoritmo Complex. Los valores de la última columna se estimaron como se detalla en seguida.
Tabla 3 Resultados óptimos del algoritmo Complex durante la maximización de la ecuación 11, con las crecientes de entrada a la Presa Venustiano Carranza, México
| FO inicial |
FO final |
Núm. Iter. |
Parámetros de ajuste |
m inic. m final |
rxy dma |
||
|---|---|---|---|---|---|---|---|
| u1, u2 | α1, α2 | k1, k2 | |||||
| 549.8 | 537.8 | 141 | 162.540 | 125.003 | -0.500 | 1.25 | 0.9872 |
| 46.894 | 42.006 | -0.512 | 1.50 | 0.1637 | |||
| 538.7 | 527.2 | 163 | 160.167 | 125.000 | -0.500 | 1.75 | 0.9924 |
| 43.458 | 42.002 | -0.512 | 2.00 | 0.1164 | |||
| 528.7 | 517.8 | 121 | 160.000 | 125.002 | -0.500 | 2.25 | 0.9952 |
| 39.713 | 42.001 | -0.512 | 2.50 | 0.0802 | |||
| 519.9 | 509.6 | 116 | 163.902 | 125.003 | -0.500 | 2.75 | 0.9933 |
| 44.067 | 42.000 | -0.512 | 3.00 | 0.1116 | |||
| 512.2 | 502.3 | 97 | 161.897 | 125.001 | -0.500 | 3.25 | 0.9959 |
| 38.000 | 42.000 | -0.512 | 3.50 | 0.0658 | |||
Con base en los parámetros de ajuste óptimos, expuestos en las columnas 4 a 7 de la Tabla 3, se estimaron con la ecuación 4 las probabilidades de no excedencia conjunta teórica F(x,y), utilizando los datos xi, yi de la Tabla 1. Con base en la ecuación 21 y su procedimiento gráfico descrito, se calcularon las llamadas probabilidades de no excedencia empíricas bivariadas Fe(x,y), contra las cuales se contrastan los valores de la F(x,y).
La mejor correspondencia o similitud entre ambas probabilidades conjuntas Fe(x,y) y F(x,y), se obtuvo para la quinta aplicación numérica del algoritmo Complex, con un valor del coeficiente de correlación (rxy) de 0.9959 y diferencias máximas positiva y negativa de 0.0630 y -0.0658, que se indican sombreadas en la Tabla 4.
Tabla 4 Probabilidades de no excedencia conjuntas y sus diferencias para una parte de las crecientes anuales de entrada a la Presa Venustiano Carranza, México
| Núm. |
Fe (x,y) empírica |
F(x,y) teórica |
Diferencias | Núm. |
Fe (x,y) empírica |
F(x,y) teórica |
Diferencias |
|---|---|---|---|---|---|---|---|
| 1 | 0.3563 | 0.3593 | -0.0030 | 30 | 0.7203 | 0.6922 | 0.0281 |
| 5 | 0.0498 | 0.0817 | -0.0319 | 35 | 0.7969 | 0.8245 | -0.0276 |
| 10 | 0.1648 | 0.1464 | 0.0184 | 38 | 0.7203 | 0.7861 | -0.0658 |
| 15 | 0.8736 | 0.8875 | -0.0139 | 44 | 0.6245 | 0.5615 | 0.0630 |
| 20 | 0.2031 | 0.1609 | 0.0422 | 49 | 0.0307 | 0.0223 | 0.0084 |
| 25 | 0.4330 | 0.3763 | 0.0567 | 52 | 0.1264 | 0.1234 | 0.0030 |
Validación del modelo probabilístico
En la Figura 2 se han dibujado ambas probabilidades de no excedencia conjuntas (empíricas y teóricas de la Tabla 4 completa), observándose un buen balance entre diferencias positivas (24) y negativas (28). También se indican en un círculo las diferencias máximas negativa (pareja 38) y positiva (pareja 44). El valor del estadístico del test de Kolmogorov-Smirnov es 0.1883 (ecuación 22), por lo cual, la distribución GVEb es aceptada como modelo probabilístico conjunto de los datos de la Tabla 1, ya que dma = 0.0658 < Dn = 0.1883.

Figura 2 Contraste gráfico de probabilidades conjuntas del gasto pico y volúmenes de las crecientes anuales de entrada a la Presa Venustiano Carranza, México
Ratificación de las marginales
Primeramente, los gastos pico y volúmenes de la Tabla 1 se ordenaron de menor a mayor. Después, se calcularon sus probabilidades de no excedencia teóricas con las ecuaciones 2 y 3 utilizando los parámetros de ajuste óptimos de la Tabla 3 para la quinta corrida del algoritmo Complex. Las probabilidades de no excedencia empíricas de ambas series (Q y V) se estimaron con la ecuación 20.
En las Figuras 3 y 4 se muestra el contraste gráfico de probabilidades para cada serie ordenada. Las diferencias máximas entre probabilidades empíricas y teóricas de los gastos pico y volúmenes fueron 0.0912 y -0.0674; la primera ocurrió en el dato ordenado número 14 y la segunda en el 3, como se muestra en la Tabla 5. Como ambas diferencias absolutas son menores que Dn = 0.1883 (ecuación 22), se acepta que los registros de Q y V de la Tabla 1 tienen las marginales GVE definidas con el algoritmo Complex.
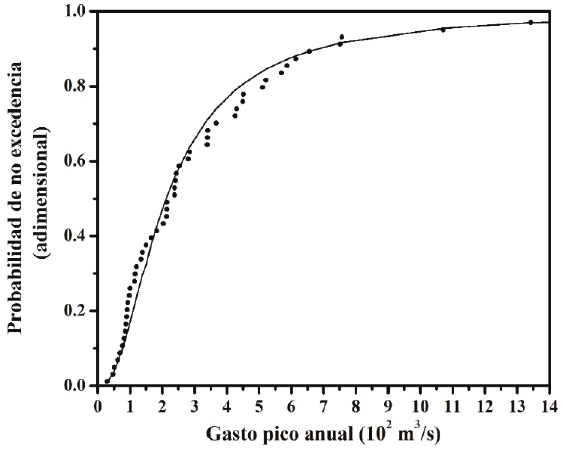
Figura 3 Distribución marginal GVE del gasto pico anual de las crecientes anuales de entrada a la Presa Venustiano Carranza, México
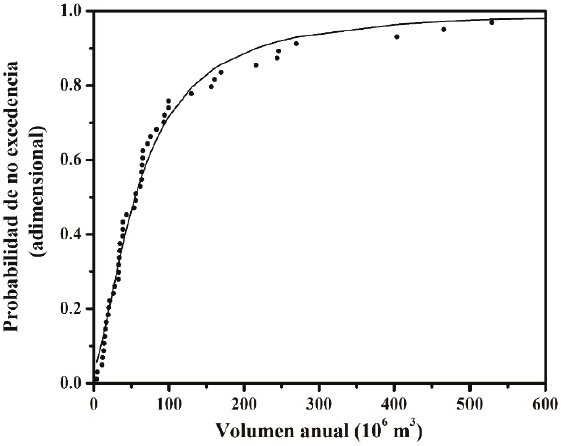
Figura 4 Distribución marginal GVE del volumen anual de las crecientes anuales de entrada a la Presa Venustiano Carranza, México
Tabla 5 Probabilidades empíricas (Fe) y teóricas en las distribuciones marginales GVE y sus diferencias para una parte de las crecientes anuales de entrada a la Presa Venustiano Carranza, México
| Núm. | Q | V | Fe | F(Q) | F(V) | Dif Q | Dif V |
|---|---|---|---|---|---|---|---|
| 1 | 29.5 | 3.75 | 0.0115 | 0.0109 | 0.0565 | 0.0006 | -0.0450 |
| 3 | 50.9 | 11.48 | 0.0498 | 0.0394 | 0.1172 | 0.0104 | -0.0674 |
| 10 | 89.2 | 19.12 | 0.1839 | 0.1370 | 0.1889 | 0.0470 | -0.0050 |
| 14 | 99.5 | 28.04 | 0.2605 | 0.1693 | 0.2759 | 0.0912 | -0.0154 |
| 20 | 146.7 | 35.02 | 0.3755 | 0.3216 | 0.3413 | 0.0536 | 0.0342 |
| 30 | 243.4 | 63.62 | 0.5670 | 0.5662 | 0.5554 | 0.0008 | 0.0117 |
| 40 | 449.2 | 99.71 | 0.7586 | 0.8053 | 0.7158 | -0.0467 | 0.0428 |
| 52 | 4320.7 | 983.02 | 0.9885 | 0.9968 | 0.9928 | -0.0083 | -0.0043 |
Verificación de las restricciones de probabilidad
Antes de proceder a estimar los periodos de retorno conjuntos de diseño T’(Q,V), es conveniente verificar la ecuación 7, que establece las restricciones de la probabilidad conjunta. Lo anterior se muestra en la Tabla 6 para un número reducido de parejas de datos históricos.
Tabla 6 Verificación de las restricciones de probabilidad conjunta de una parte de las crecientes anuales de entrada a la Presa Venustiano Carranza, México
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| Núm. | Q | V | F(x)∙F(y) | F(x,y) | F(x) | F(y) |
| 1 | 241.0 | 38.76 | 0.2103 | 0.3593 | 0.5615 | 0.3745 |
| 15 | 655.9 | 269.58 | 0.8305 | 0.8875 | 0.8932 | 0.9297 |
| 30 | 521.6 | 94.18 | 0.5891 | 0.6922 | 0.8452 | 0.6970 |
| 45 | 756.5 | 244.05 | 0.8406 | 0.8996 | 0.9161 | 0.9176 |
| 52 | 85.0 | 64.22 | 0.0694 | 0.1234 | 0.1242 | 0.5589 |
Se observa en la Tabla 6 y en su versión completa, que el valor de la columna 5 es siempre mayor que el de la 4 y menor que el más pequeño de las columnas 6 ó 7. Por lo cual, se cumple con la restricción que impone la ecuación 7.
Predicciones univariadas y periodos de retorno conjuntos de diseño
Aplicando en las ecuaciones 5 y 6 los seis parámetros de ajuste óptimos de la quinta corrida del algoritmo Complex, mostrados en la Tabla 3, se obtuvieron las predicciones mostradas en la Tabla 7.
Tabla 7 Predicciones univariadas calculadas con la distribución GVE en las crecientes anuales de entrada a la Presa Venustiano Carranza, México
| Datos | Periodos de retorno univariados, en años | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 5 | 10 | 25 | 50 | 100 | 250 | 500 | |
| Q (m3/s) | 212 | 441 | 682 | 1149 | 1671 | 2406 | 3861 | 5499 |
| V (Mm3) | 55 | 133 | 216 | 378 | 561 | 821 | 1340 | 1931 |
En esta aplicación numérica, las predicciones univariadas y los periodos de retorno conjuntos de diseño, fueron establecidos con apego estricto a sus ocurrencias reales. Por lo anterior, los datos de Q y V de la Tabla 1, se ordenaron de menor a mayor, para detectar sus valores extremos o dispersos (outliers); es decir, los que se apartan de manera notable de la tendencia general. Para el gasto pico se definió uno de 4320.7 m3/s y para el volumen se obtuvieron dos: uno de 529.11 y otro de 983.02 Mm3.
Debido a la amplitud del registro conjunto, de 52 años, las primeras predicciones por revisar de la Tabla 7 son del periodo de retorno de 50 años, cuyos valores de 1671 m3/s y 561 Mm3 se consideran acordes con los datos extremos observados. Para los periodos de retorno mayores, resultan aceptables, como máximo, las de 500 años, cuya predicción de gasto pico de 5499 m3/s puede aceptarse factible de ocurrir; en cambio, la del volumen es casi del doble del máximo observado. Por lo anterior, los periodos de retorno conjuntos de diseño serán los cuatro siguientes: 50, 100, 250 y 500 años.
Eventos de diseño obtenidos con regresión
El diagrama de dispersión de las 52 parejas de datos originales (Tabla 1) mostró una nube de puntos con tendencia lineal con un coeficiente de correlación lineal (rxy) de 0.9188 La ecuación de regresión lineal que la representa es la siguiente (Campos, 2003):
De la Tabla 7 se obtienen las predicciones siguientes para el gasto pico (Q) y los cuatro periodos de retorno conjuntos de diseño: 1671, 2406, 3861 y 5499 m3/s. Con base en la ecuación 23 se definen los volúmenes anuales (V) siguientes: 433, 617, 980 y 1389 Mm3, para los eventos de diseño buscados. Estas cuatro parejas de valores de Q y V se han dibujado en la Figura 1 y se indican con la letra “r”.
Eventos de diseño condicionales tipo T(Q|V)
Están definidos por las ecuaciones 18 y 19, cuya aplicación emplea las expresiones 2 a 4. Para los cuatro periodos de retorno conjuntos de diseño definidos, se obtienen de la Tabla 7 los siguientes cuatro gastos pico: 1671, 2406, 3861 y 5499 m3/s. Adoptando tales gastos como valores condicionantes (X ≤ x), se procedió por tanteos del volumen (y) a estimar, con la ecuación 19, el periodo de retorno condicional que debe igualar al del gasto pico. Los volúmenes estimados fueron: 386, 571, 940 y 1360 Mm3. Estas cuatro parejas de valores de Q y V se han dibujado en la Figura 1 y se indican con la letra “c”.
Gráficas del periodo de retorno conjunto T’(Q,V)
Los periodos de retorno conjuntos de tipo AND se estiman con base en la ecuación 15. Para cada periodo de retorno conjunto de diseño se seleccionan arbitrariamente volúmenes y gastos pico, para obtener sus probabilidades de no excedencia marginales (ecuaciones 2 y 3) y conjunta (ecuación 4). En la Tabla 8 se muestran algunos resultados para definir las cuatro gráficas de la Figura 1.
Tabla 8 Parejas de gasto pico y volumen anual utilizadas para definir las gráficas del periodo de retorno conjunto (Figura 1), con el modelo bivariado GVE, en las crecientes de entrada a la Presa Venustiano Carranza, México
| T’(Q,V)50 años | T’(Q,V)100 años | T’(Q,V)250 años | T’(Q,V)500 años | ||||
|---|---|---|---|---|---|---|---|
| Vol. Mm3 | Q m3/s | Vol. Mm3 | Q m3/s | Vol. Mm3 | Q m3/s | Vol. Mm3 | Q m3/s |
| 0 | 1671 | 0 | 2406 | 0 | 3861 | 0 | 5499 |
| 200 | 1668 | 300 | 2402 | 600 | 3847 | 500 | 5498 |
| 300 | 1655 | 500 | 2366 | 700 | 3833 | 800 | 5487 |
| 350 | 1638 | 550 | 2343 | 800 | 3808 | 900 | 5478 |
| 400 | 1608 | 600 | 2307 | 900 | 3764 | 1000 | 5463 |
| 450 | 1551 | 650 | 2252 | 1000 | 3692 | 1100 | 5441 |
| 475 | 1505 | 700 | 2163 | 1100 | 3566 | 1200 | 5410 |
| 500 | 1435 | 725 | 2097 | 1150 | 3468 | 1300 | 5365 |
| 510 | 1397 | 750 | 2006 | 1200 | 3328 | 1400 | 5299 |
| 520 | 1349 | 760 | 1958 | 1225 | 3234 | 1500 | 5204 |
| 530 | 1287 | 770 | 1901 | 1250 | 3113 | 1550 | 5140 |
| 540 | 1200 | 780 | 1831 | 1260 | 3054 | 1600 | 5062 |
| 545 | 1140 | 790 | 1742 | 1270 | 2987 | 1650 | 4965 |
| 550 | 1061 | 800 | 1620 | 1280 | 2907 | 1700 | 4840 |
| 555 | 940 | 805 | 1537 | 1290 | 2816 | 1725 | 4765 |
| 560 | 653 | 810 | 1427 | 1300 | 2708 | 1750 | 4677 |
| 561 | 0 | 815 | 1260 | 1310 | 2569 | 1775 | 4574 |
| 818 | 1087 | 1320 | 2381 | 1800 | 4451 | ||
| 821 | 0 | 1330 | 2087 | 1825 | 4301 | ||
| 1335 | 1833 | 1850 | 4108 | ||||
| 1340 | 0 | 1875 | 3847 | ||||
| 1900 | 3447 | ||||||
| 1920 | 2824 | ||||||
| 1931 | 0 | ||||||
En la Figura 1 o en la Tabla 8 se pueden seleccionar infinitas parejas de Q y V, que satisfacen el periodo de retorno conjunto de diseño y que definen como subgrupo de parejas críticas las que están dentro de la porción curva de cada gráfica de T’(Q,V), fuera de las rectas asíntotas (Volpi & Fiori, 2012).
Las combinaciones de gasto pico y volumen que tienen el mismo periodo de retorno conjunto, establecen crecientes o hidrogramas que producirán diferentes efectos en el embalse que se diseña o revisa; adoptando por seguridad, el que genera las condiciones más críticas, severas o desfavorables. Lo anterior, está incorporando en el diseño hidrológico las características físicas del vertedor y almacenamiento o vaso del embalse en proyecto o bajo revisión. Para formar cada hidrograma de diseño, existen métodos teóricos y empíricos (Aldama, 2000; Ramírez & Aldama, 2000).
Conclusiones
Se expuso la aplicación de la distribución GVE bivariada (GVEb), en el análisis de frecuencias conjunto de los 52 gastos pico (Q) y volúmenes (V) anuales de las crecientes de entrada a la Presa Venustiano Carranza (Don Martín), Coahuila, México. El ajuste de la GVEb incluye ocho etapas, que fueron descritas y que abarcan desde la prueba de aleatoriedad de los datos, hasta la estimación de los periodos de retorno conjuntos de tipo AND. La etapa más importante es la validación de la GVEb, que implica el contraste entre las probabilidades empíricas y teóricas conjuntas (Figura 2).
En el análisis de frecuencias conjunto (Figura 1) se definen decenas de parejas críticas de Q y V, para formar los hidrogramas de diseño, que producirán diferentes efectos en el embalse que se dimensiona o revisa. Se adopta por seguridad, el que genera las condiciones más severas. De esta manera se están incorporando en el diseño hidrológico las características físicas del embalse (lago y vertedor) bajo estudio.
La GVEb es adecuada para procesar de manera conjunta registros de Q y V de crecientes anuales, que presentan valores extremos dispersos (outliers), pero que no están integrados por poblaciones mixtas. Por lo anterior, la GVEb permite procesar crecientes de cuencas medianas y grandes, de zonas o regiones con mecanismos meteorológicos únicos de formación de las crecientes.











 nueva página del texto (beta)
nueva página del texto (beta)



