Introducción
Medir la capacidad de un proceso es una técnica relevante para la mejora continua de los productos en la manufactura industrial. Así el análisis estadístico de los datos nos permite construir índices de capacidad para cuantificar la proporción definida por los límites de tolerancia y la variación.
El concepto de variación indica que no existen dos productos o características que sean exactamente iguales, debido a la existencia de fuentes de variabilidad. Desde el punto de vista de requerimientos mínimos, el asunto de la variación a menudo es simplificado, ya que las partes dentro de las tolerancias de especificación son aceptables, partes fuera de especificaciones son no aceptables (AIAG, 2005).
Kane (1986) menciona que la capacidad del proceso puede definirse como la habilidad de combinar materiales, métodos, personal, maquinaria, equipo y mediciones para elaborar un producto que cumpla de forma consistente las expectativas del cliente. Los índices de capacidad del proceso (PCI) fueron desarrollados para proveer un lenguaje comprensivo para cuantificar el desempeño del proceso, son funciones adimensionales de los parámetros del proceso (voz del proceso) y las especificaciones (voz del cliente).
Para determinar si un proceso es capaz, es necesario conocer la distribución a la que se ajustan los datos generados por este. En la literatura estadística se construyen índices de capacidad en dos direcciones, uno bajo el supuesto que la distribución de probabilidad es normal, la otra cuando no se cumple este supuesto. En este caso de estudio veremos que los datos del proceso de división de Rollos EVA no se ajustaron a una distribución de probabilidad normal. A continuación, expondremos algunas líneas de investigación realizadas en la literatura estadística en la construcción de índices de capacidad en este contexto.
Por ejemplo, Hosseinifard et al. (2014) llevaron a cabo un estudio de simulación para comparar el desempeño de diferentes métodos para PCI’s en el proceso de filtrado de leucocitos en la sangre. Tang (1999) presentó un estudio comparativo y una revisión de literatura relacionada al cálculo de índices de capacidad del proceso para datos no-normales.
Sommerville & Montgomery (1996) analizaron el cálculo de índices de capacidad del proceso con distribuciones alternativas a la normal, mediante las distribuciones t, Gamma, Lognormal y Weibull, y con estas realizaron pruebas de bondad de ajuste.
Otro enfoque para el análisis de PPIs para datos con distribución no-normal se obtiene mediante las transformaciones de datos, bajo el supuesto de normalidad con los datos y especificaciones transformados. Los métodos más utilizados para la transformación de datos son las de Box-Cox y de Johnson.
Un tercer enfoque de transformación de datos es la de Clements, el cual es uno de los métodos más populares dada su facilidad de cálculo y aplicación.
Dentro del planteamiento de las transformaciones, Yang et al. (2010) presentaron un estudio comparativo sobre la eficiencia de las transformaciones Box-Cox y Johnson para el cálculo de PCI’s en datos no normales. Hosseinfard et al. (2009) evaluaron la eficiencia del uso de la raíz cuadrada en un estudio de simulación con datos Weibull, Gamma y Beta. Yeo y Johnson (2000) propusieron una nueva familia de transformaciones para normalizar datos.
Algunos enfoques alternativos para el análisis de PCI´s para datos no-normales son el uso de las redes neuronales (Abbasi, 2009), transformaciones para la reducción del sesgo en la distribución de la muestra (Abbasi et al., 2011). Ding (2004) presentó un método para transformación de datos basado en sus primeros cuatro momentos (media, desviación estándar, sesgo y curtosis) con el objetivo de caracterizar las propiedades de la distribución de datos mediante una ecuación derivada del ajuste por mínimos cuadrados.
Liu & Chen (2006) propusieron el uso de la distribución Burr XII para el cálculo de PCI’s en procesos no-normales. Parchami et al. (2014) utilizaron PCI’s basados en mediciones difusas. Wang et al. (2016) introdujeron un método simplificado de interpolación inversa y otro basado en interpolación por spline cúbico para simplificación del cálculo de PCI’s con una simulación de distribuciones Gamma, Lognormal y Weibull.
En este trabajo se realiza una aplicación de las pruebas de bondad de ajuste, transformaciones Box-Cox y Johnson y el método de Clements en una mejora del proceso de división de rollos de EVA, debido a que los datos no tienen una distribución normal. Se aplicaron las siguientes métricas: el índice de desempeño del proceso (Pp), índice de desempeño del proceso para la especificación superior (Ppu), índice de desempeño del proceso para la especificación inferior (Ppi) e índices de desempeño del proceso basado en la variación del proceso a lo largo del conjunto de datos (Ppk) para evaluar la variación del proceso contra los límites de especificación y verificar si existe mejora significativa al implementar un rodillo especial en la máquina, con la finalidad de reducir la variación en el proceso de dividido de los rollos.
Los resultados mostraron una mejora significativa del proceso con la implementación del rodillo, con el cual se pudo controlar adecuadamente la variación en el grosor del material a lo largo de los rollos de EVA. Los índices de desempeño del proceso incrementaron en todos los casos, debido a la reducción en la variabilidad. Se encontró, además, que los datos que presentan distribuciones tipo leptocúrticas muestran restricciones al momento de ajustar a una distribución teórica o al transformar los datos, ya que el requisito es que estos se ajusten a una distribución normal. El método de Clements permitió definir el punto de comparación para los índices de desempeño más confiables en el proceso.
La estructura del artículo es la siguiente: inicialmente, se analizan los índices clásicos de desempeño del proceso y se presenta una propuesta para el procedimiento de análisis de índices de desempeño en presencia de datos no normales. Enseguida, se definen los métodos para las pruebas de bondad de ajuste, transformaciones de Box- Cox y Johnson y el método de Clements. En la metodología se explica el procedimiento de muestreo y análisis del proceso de división de rollos de EVA, con base en la información de la voz del cliente. En la sección de resultados se muestran los índices y estadísticos obtenidos, comparando la eficiencia de cada uno de los métodos y su relación con el proceso. Finalmente se presentan las conclusiones y hallazgos del estudio en relación con el proceso y la eficiencia de los métodos utilizados.
Esta investigación es relevante para mejorar la calidad del proceso de elaboración de rollos EVA, debido a que el material producido es esencial en la manufactura de productos para el calzado, tales como las plantillas y otros componentes de calzado. La variación en el grosor de los rollos es una característica crítica de la calidad, ya que los productos generados a partir de los rollos de EVA deben mantener uniformidad a lo largo y ancho del mismo, como ejemplo, en aplicaciones de conformado de plantillas puede existir variación excesiva del material en zonas específicas del producto, generando disconformes que deberán desecharse, incurriendo en costos por mala calidad.
Análisis de capacidad del proceso e índices de desempeño
En el análisis de capacidad del proceso (PCA), la variación del proceso se define por la desviación estándar. La desviación estándar generalmente es desconocida y debe estimarse en el proceso. La desviación estándar puede utilizarse en la evaluación de PCI’s que se relacionan a la variabilidad de corto o largo plazo.
La variación de largo plazo se puede relacionar a causas comunes tales como la variación de parte a parte o variaciones en las máquinas. La variación debida a causas especiales se considera como variación a largo plazo, que puede relacionarse a variaciones de lote a lote, operario a operario, día a día o entre turnos. En el PCA, los PCI’s tanto de corto como de largo plazo se calculan y no se consideran de forma separada.
Los índices de corto plazo se estiman con la desviación estándar con base en la variación dentro de cada subgrupo de datos, se define el índice de habilidad del proceso a corto plazo (Cp), el índice de habilidad del proceso a corto plazo para la especificación superior (Cpu), el índice de habilidad del proceso para la especificación inferior (Cpi), el índice de habilidad del proceso con base en la variación dentro de los subgrupos (Cpk), y el índice de Taguchi (Cpm), que toma en cuenta la variación del proceso y la distancia entre el valor Target y la media del proceso. El muestreo generalmente se realiza por subgrupos racionales y se relaciona a gráficos de control por variables. Por otro lado, los índices de desempeño del proceso Pp, Ppu, Ppi y Ppk se calculan utilizando la desviación estándar de largo plazo mostrada en la Ecuación (1). En las Ecuaciones (2) a (5) se ilustran los índices de desempeño del proceso.
El desempeño del proceso se define como una característica en un proceso donde puede aún no estar demostrado que está bajo control estadístico. Una revisión del estado del arte sobre PPI’s puede consultarse en Kotz y Johnson (2002).
Donde
Alternativas y planteamiento para el análisis en el caso de no normalidad
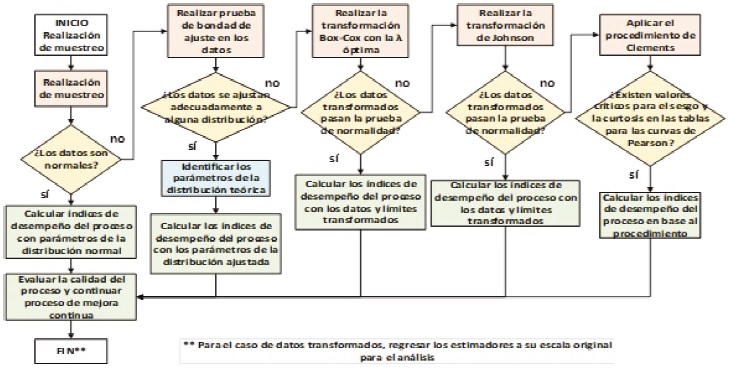
El procedimiento propuesto para el análisis se muestra en la Figura 1.
Para estudiar la capacidad del proceso se realizaron 100 observaciones mediante un muestreo en cada uno de los tres grosores, con base en la recomendación del tamaño muestral mínimo para estudios de desempeño del proceso en el manual SPC de la AIAG (2015), las lecturas se obtuvieron antes y después de la implementación del rodillo en la máquina. Inicialmente debe verificarse si se cumple la normalidad mediante una prueba de hipótesis para verificación de normalidad mediante pruebas de bondad de ajuste (Anderson-Darling, Kolgomorov Smirnov, Ji-Cuadrada, etc.) y el uso del gráfico de probabilidad normal. En caso de no existir ajuste adecuado pasar a las pruebas de bondad de ajuste con distribuciones teóricas conocidas, en caso de existir alguna trabajar con los parámetros de la distribución.
En caso de no obtener ajuste a otra distribución se aplica la transformación de Box-Cox, los datos transformados deberían pasar la prueba de normalidad, en caso de no obtener ajuste se pasa al método de transformación de Johnson, nuevamente se verifica si existe normalidad en los datos transformados.
En caso de no obtener un buen resultado en los métodos anteriores, pasar al procedimiento de Clements que se define más adelante y realizar el cálculo de los índices de desempeño en el proceso. El procedimiento propuesto es robusto y genera alternativas para el analista en presencia de datos no-normales.
Prueba de bondad de ajuste
Una de las cuestiones más importantes que se presentan en el muestreo es conocer si los datos observados siguen una distribución de probabilidad particular. No existen opciones estadísticas o paramétricas que se puedan aplicar hasta que se identifiquen las distribuciones de densidad de probabilidad mediante la prueba de bondad de ajuste (Ramachandran & Tsokos, 2015). Existen métodos analíticos y gráficos para determinar qué tan bueno es el ajuste de los datos a una distribución particular, en esta investigación se trabaja con la prueba de Anderson-Darling.
La prueba de bondad de ajuste de Anderson-Darling se utiliza para determinar si un conjunto dado de datos procede de una población que sigue una distribución de probabilidad específica. Sea
H0: Los datos dados siguen una distribución de probabilidad específica.
Contra:
Hα: Los datos dados no siguen la distribución de probabilidad específica.
El estadístico de prueba de Anderson-Darling para probar las hipótesis anteriores está dado por:
es el tamaño de la muestra aleatoria, Yi son los datos ordenados y F es la distribución de probabilidad especifica que estamos probando. Para un nivel de significancia dado α, la hipótesis se rechaza si el valor de prueba del estadístico A es mayor que el valor crítico Aα, esto es, si A> Aα. Así, se rechaza la hipótesis nula en favor de la hipótesis alternativa; la distribución de probabilidad especificada no se ajusta a la distribución de los datos de la población. El Aα se obtiene de las tablas de Anderson-Darling para un α dado.
Método de transformación Box-Cox
Box & Cox (1964) propusieron una familia de transformaciones de potencia sobre la repuesta necesariamente positiva Y. La transformación Box-Cox se indica en la Ecuación (6).
El parámetro λ puede estimarse mediante la estimación de máxima verosimilitud Lmax como se muestra en la Ecuación (7).
Para toda λ,J(λ,Y) es evaluada en la Ecuación (8):
Así la Ecuación. (9) se obtiene como sigue:
Para un valor determinado de λ, σ2 se estima con el uso de S(λ) como la suma residual de cuadrados de Y(λ). La estimación de σ2 se indica en la Ecuación (10).
Cuando el valor óptimo de λ es obtenido, los límites de especificación son transformados en variables normales para todos los valores de la característica de calidad Y. Los PCI’s pueden calcularse desde la media y desviación estándar de los datos transformados.
Método de transformación de Johnson
Johnson Norman L. (1949) propuso un sistema de transformaciones para transformar datos no-normales a una forma normal. El sistema de Johnson integra una familia de 3 curvas: SB: acotado, SL: Log normal y SU: no acotado. Farnum Nicholas (1996) ha proporcionado una descripción sobre el uso de las curvas de Johnson. El sistema de Johnson para las tres curvas que transforman los datos a una distribución z se expresa como:
Donde Y es el valor transformado, x es la variable a transformar, γ es el parámetro de forma 1, η es el parámetro de forma 2, ε es el parámetro de localización, λ es el parámetro de escala. Se han formulado reglas de decisión para la selección de las curvas SU, SB y SL en la transformación de los datos, el enfoque preferido es la transformación de los datos de forma recursiva mediante varios valores de parámetros y tipos de curvas. La transformación que dé un resultado más cercano a la Normal es la seleccionada.
Método de Clements
Clements John A. (1989) documentó el uso de colas estandarizadas utilizando los cuantiles 0.00135 y 0.99865 y las medianas estandarizadas (cuantil 0.50) para la familia de curvas de Pearson. El análisis de datos no-normales puede realizarse por el modelado de los datos con un miembro apropiado de las curvas de distribución de Pearson, las cuales fueron formuladas por Karl Pearson en 1893.
Las observaciones de datos son analizadas y se determina la medida de su sesgo (tendencia del pico a sesgarse a la derecha o izquierda) y la curtosis (naturaleza de pico o plana). Se selecciona una curva de Pearson adecuada que coincida con el sesgo y curtosis calculados. Un estimado del área bajo la curva de Pearson más allá de los límites de especificación ayudará a evaluar la capacidad del proceso bajo estudio.
El procedimiento de Clements está basado en los valores muestrales de sesgo (Eq. (14)) y curtosis (Eq. (15)) partiendo de los momentos 1, 2 y 3. Nota: consultar en Montgomery (2019). Sean:
El procedimiento se puede resumir de la siguiente forma: Obtener una muestra, calcular los valores de
Metodología
La metodología de análisis propuesta se resume en los siguientes pasos:
Realizar pruebas de normalidad y calcular los índices de desempeño propuestos.
Realizar pruebas de bondad de ajuste para verificar la adecuación de los datos con distribuciones alternativas.
Realizar la transformación de Box- Cox y probar la normalidad, calcular los índices de desempeño.
Realizar la transformación de Johnson y probar normalidad, calcular los índices de desempeño.
Aplicar el método de Clements y analizar los índices de desempeño.
Para esta investigación se realizaron todos los estudios con la finalidad de evaluar un comparativo, dado que los datos presentaron un comportamiento no-normal notorio.
Caso de análisis
El caso de análisis trata sobre el proceso de división de rollos de EVA (Figura 2), uno de los principales defectos que se generan en este proceso es la alta variabilidad en el grosor de los materiales, lo cual puede generar quejas o devoluciones por parte del cliente, ya que el cliente busca aprovechar en el mayor grado posible el área del material.
En el análisis del proceso se observó que una causa de la variación en el grosor del material se da por la falta de control en el material al momento de ingresar al área de corte en la que se realiza el corte del material por medio de una cuchilla giratoria. Con la finalidad de reducir la variación del grosor del material se diseñó un rodillo especial que sujeta el material al momento de ingresar al corte con la cuchilla, con el objetivo de estabilizar el material. En la Figura 3 se muestra el rodillo ya adaptado en la máquina de división.
Se realizó un muestreo del proceso de división antes y después de la implementación del rodillo, el muestreo se realizó por subgrupos de tamaño 10 al inicio de la división de 10 rollos para cada uno de los siguientes calibres 1.5 mm con límites (1.2, 1.8 mm), 2.5 mm con límites (2.2, 2.8 mm) y 3.0 mm con límites (2.7, 3. 0 mm), que son los rollos más solicitados por los clientes, el proceso se realizó en el transcurso de un mes. El muestreo se realizó de esta forma con base en los principios del control estadístico de procesos, realizando las muestras en espacios de tiempo considerables que permitan detectar causas especiales de variación.
El proceso de muestreo se repitió después de instalar el rodillo especial, las mediciones se llevaron a cabo con un medidor de espesores de garganta profunda en diferentes lugares del material dividido, los datos se muestran en la tabla del ANEXO 1 y los análisis se hicieron con apoyo del software MINITAB y RStudio.
Resultados y discusión
Los gráficos de capacidad del proceso y de probabilidad normal para los datos originales antes del cambio se muestran en la Figura 4 y los datos después del cambio en la Figura 5. En estas figuras es evidente el comportamiento no normal en los datos, lo cual se comprobó al realizar las pruebas de bondad de ajuste en las que se obtuvieron valores superiores a 2.5018 que es el valor crítico para la prueba de Anderson-Darling. Con base en lo anterior se rechazó el ajuste de los datos de las 6 muestras con la distribución normal.
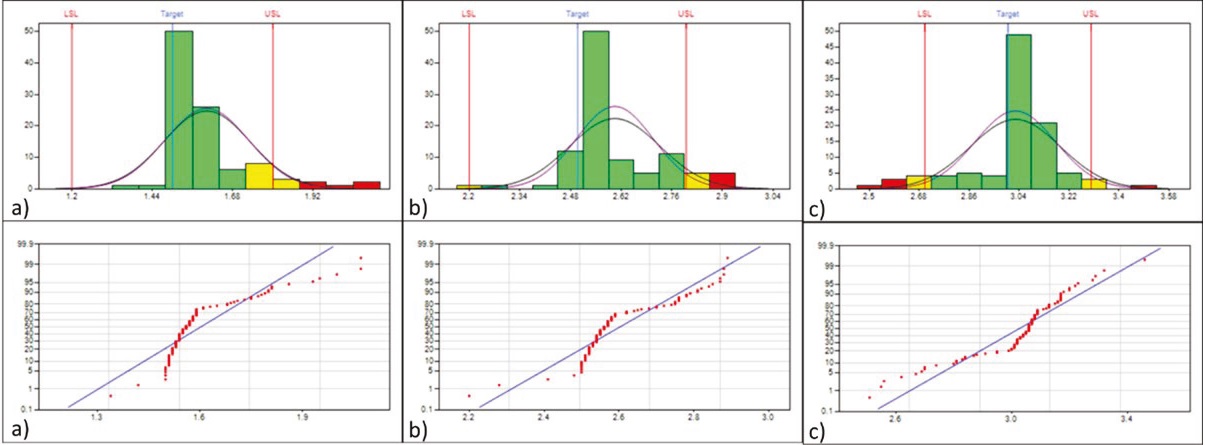
Figura 4 Gráficos de capacidad y de probabilidad normal para grosores: a) 1.5, b) 2.5 y c) 3.0 antes de implementación del rodillo para los datos originales

Figura 5 Gráficos de capacidad y de probabilidad normal para grosores: a) 1.5, b) 2.5 y c) 3.0 después de implementación del rodillo para los datos originales
Aplicando la prueba de Anderson-Darling con otras distribuciones se observó un buen ajuste con la distribución Cauchy en las muestras para los grosores 3.0 antes del cambio y las de 1.5, 2.5 y 3.0 después del cambio con valores de Anderson-Darling de 0.996, 2.099, 1.847 y 1.449, respectivamente, pero la prueba falló para las muestras en los grosores 1.5 y 2.5 antes del cambio con valores de Anderson-Darling de 5.161 y 6.379, respectivamente. Se procede al análisis de los datos originales y las transformaciones Box-Cox y el método de Clements. Las medidas estadísticas e índices de desempeño del proceso por la transformación de Box-Cox se muestran en la Tabla 1.
Tabla 1 Medidas estadísticas e índices de desempeño del proceso método Box-Cox
| Medición o índice estadístico |
Grosor de los rollos mm | |||||
| 1.5 BC | 2.5 BC | 3.0 BC | 1.5 AC | 2.5 AC | 3.0 AC | |
| Lambda | -5 | -2.43 | 5 | -0.99 | -5 | -5 |
| Prueba AD | FALLÓ | FALLÓ | FALLÓ | FALLÓ | FALLÓ | FALLÓ |
| A^2 | 4.0568 | 4.5837 | 3.1154 | 4.8746 | 1.0644 | 3.7262 |
| Valor p | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0082 | 0.0000 |
| LSE | 0.05292215 | 0.08192303 | 391.353930 | 0.55883065 | 0.00581045 | 0.00255523 |
| Target | 0.13168724 | 0.10789611 | 243.000000 | 0.66937525 | 0.01024000 | 0.00411523 |
| LIE | 0.40187757 | 0.14720172 | 143.489070 | 0.83485407 | 0.01940379 | 0.00696917 |
| Promedio (X-Bar) | 0.102 | 0.099 | 260.854 | 0.641 | 0.009 | 0.004 |
| Desviación Est. | 0.030772 | 0.009601 | 56.943813 | 0.032295 | 0.000870 | 0.000336 |
| Sesgo | -0.045 | 0.417 | -0.083 | 0.594 | -0.546 | -0.352 |
| Curtosis | 2.857 | 3.112 | 1.984 | 8.043 | 0.464 | 4.633 |
| Pp | 1.890 | 0.954 | 0.653 | 1.389 | 2.764 | 2.019 |
| Ppu | 0.530 | 0.493 | 0.687 | 0.830 | 1.363 | 1.144 |
| Ppl | 3.250 | 1.416 | 0.618 | 1.948 | 4.165 | 2.895 |
| Ppk | 0.530 | 0.493 | 0.618 | 0.830 | 1.363 | 1.144 |
| PPM < LSL | 55855.13 | 69536.82 | 31871.30 | 6384.20 | 21.64 | 300.43 |
| PPM > USL | 0.00 | 10.85 | 19629.07 | 0.00 | 0.00 | 0.00 |
| PPM | 55855.13 | 69547.67 | 51500.37 | 6384.20 | 21.64 | 300.43 |
La primera observación en el método de Box-Cox es que los datos transformados no se ajustaron a la distribución normal en ninguno de los grosores de rollo (Figura 6 y 7), por lo que los índices estimados no son confiables. Se observa que los índices de desempeño mejoran después de la implementación del rodillo debido a que se reduce la variación en el proceso. La Tabla 2 muestra las medidas estadísticas e índices de desempeño por el método de Johnson.

Figura 6 Gráficos de capacidad y de probabilidad normal para grosores: a) 1.5, b) 2.5 y c) 3.0 antes de implementación del rodillo por transformación de Box-Cox

Figura 7 Gráficos de capacidad y de probabilidad normal para grosores: a) 1.5, b) 2.5 y c) 3.0 después de implementación del rodillo por transformación de Box-Cox
Tabla 2 Medidas estadísticas e índices de desempeño del proceso método de Johnson
| Medición o índice estadístico |
Grosor de los rollos mm | |||||
| 1.5 BC | 2.5 BC | 3.0 BC | 1.5 AC | 2.5 AC | 3.0 AC | |
| Prueba AD | FALLÓ | FALLÓ | FALLÓ | FALLÓ | FALLÓ | FALLÓ |
| A^2 | 4.8272 | 4.5975 | 4.6371 | 4.9608 | 0.8648 | 5.0360 |
| Valor p | 0.0000 | 0.0000 | 1.4199E-11 | 0.0000 | 0.0255 | 0.0000 |
| LSE | 1.58031719 | 1.55877409 | 1.96562259 | 2.9989218 | 4.16585743 | 4.27487843 |
| Target | -1.27401447 | -1.00779213 | -0.06303554 | -1.41558533 | -1.31548184 | -1.41856128 |
| LIE | N/A | -5.33626249 | -1.96348997 | -8.34502839 | N/A | N/A |
| Promedio (X-Bar) | -2.1905E-1 | -1.1170E-1 | 0.126801 | -2.9782E-1 | 0.239433 | -1.7406E-1 |
| Desviación Est. | 1.204730 | 1.152890 | 1.053781 | 1.334899 | 1.115235 | 1.642306 |
| Sesgo | -0.273 | -0.653 | -0.935 | -0.722 | 0.179 | -1.121 |
| Curtosis | 5.313 | 4.151 | 1.919 | 8.730 | 0.041 | 5.245 |
| Pp | N/A | 0.997 | 0.621 | 1.416 | N/A | N/A |
| Ppu | 0.498 | 0.483 | 0.582 | 0.823 | 1.174 | 0.903 |
| Ppl | N/A | 1.511 | 0.661 | 2.009 | N/A | N/A |
| Ppk | 0.498 | 0.483 | 0.582 | 0.823 | 1.174 | 0.903 |
| PPM < LSL | N/A | 2.93 | 23649.70 | 0.00 | N/A | N/A |
| PPM > USL | 67642.03 | 73676.06 | 40494.64 | 6762.22 | 215.19 | 3374.73 |
| PPM | 67642.03 | 73678.99 | 64144.34 | 6762.22 | 215.19 | 3374.73 |
El método de curvas de Johnson permitió transformaciones de valor P < 0.05 y que no pasan la prueba de hipótesis para normalidad, como se observa en los gráficos de capacidad y de probabilidad normal en las Figuras 8 y 9. Los resultados obtenidos para los índices de desempeño del proceso son cercanos a los obtenidos por la transformación Box-Cox. En la Tabla 3 se muestran los estadísticos e índices de desempeño por el método de Clements.
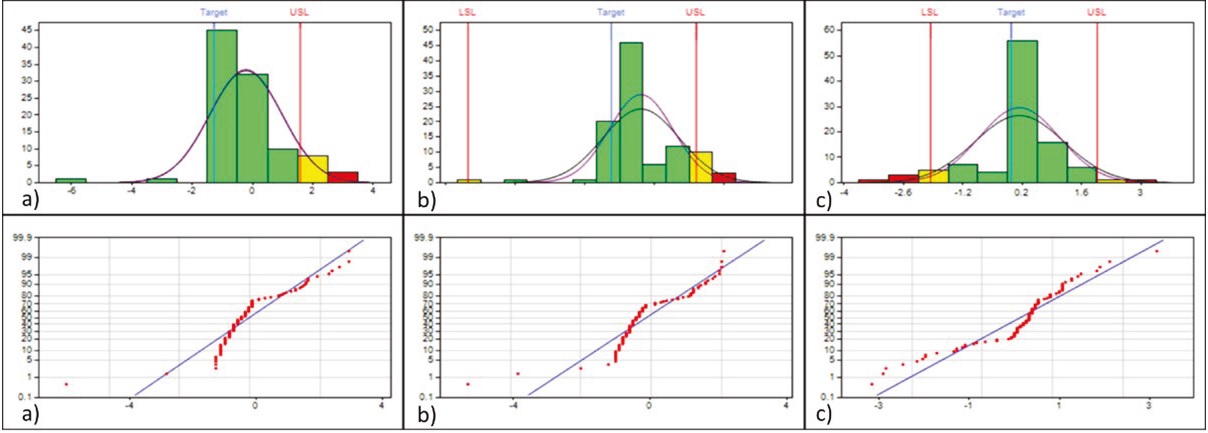
Figura 8 Gráficos de capacidad y normal para grosores: a) 1.5, b) 2.5 y c) 3.0 antes de implementación de rodillo por el método de transformación de Johnson

Figura 9 Gráficos de capacidad y normal para grosores: a) 1.5, b) 2.5 y c) 3.0 antes de la implementación de rodillo por el método de transformación de Johnson
Tabla 3 Medidas estadísticas e índices de desempeño del proceso método de Clements
| Medición o índice estadístico |
Grosor de los rollos mm | |||||
| 1.5 BC | 2.5 BC | 3.0 BC | 1.5 AC | 2.5 AC | 3.0 AC | |
| Promedio (X-Bar) | 1.6026 | 2.6024 | 3.0266 | 1.5705 | 2.5588 | 3.0509 |
| Desviación Est. | 0.128885 | 0.124966 | 0.162532 | 0.082074 | 0.047827 | 0.062346 |
| Sesgo | 1.812 | 0.439 | -1.078 | 0.581 | 0.921 | 1.618 |
| Curtosis | 3.517 | 0.875 | 1.976 | 4.640 | 1.280 | 8.631 |
| Percentil 50 | 1.5524 | 2.5948 | 3.0536 | 1.5665 | 2.5516 | 3.0416 |
| Percentil 99.865 | 2.2180 | 3.0896 | 3.3195 | 1.9534 | 2.7615 | 3.3989 |
| Percentil 0.135 | 1.4957 | 2.2550 | 2.2891 | 1.3038 | 2.4698 | 2.9090 |
| Pp | 0.831 | 0.719 | 0.582 | 0.924 | 2.057 | 1.225 |
| Ppl | 6.210 | 1.162 | 0.462 | 1.395 | 4.298 | 2.576 |
| Ppu | 0.372 | 0.415 | 0.927 | 0.604 | 1.183 | 0.723 |
| Ppk | 0.372 | 0.415 | 0.462 | 0.604 | 1.183 | 0.723 |
| PPM | 132230 | 106576 | 82879 | 34993.7 | 193.389 | 15041.4 |
El método de Clements arrojó resultados para las mediciones de antes y después de la implementación del rodillo en los 3 grosores, se considera que estos son los estimadores más confiables del estudio, ya que los datos se adaptaron de forma correcta a los valores de sesgo y curtosis disponibles en las distribuciones de Pearson. Los gráficos de capacidad y de probabilidad normal se muestran en las Figuras 10 y 11.
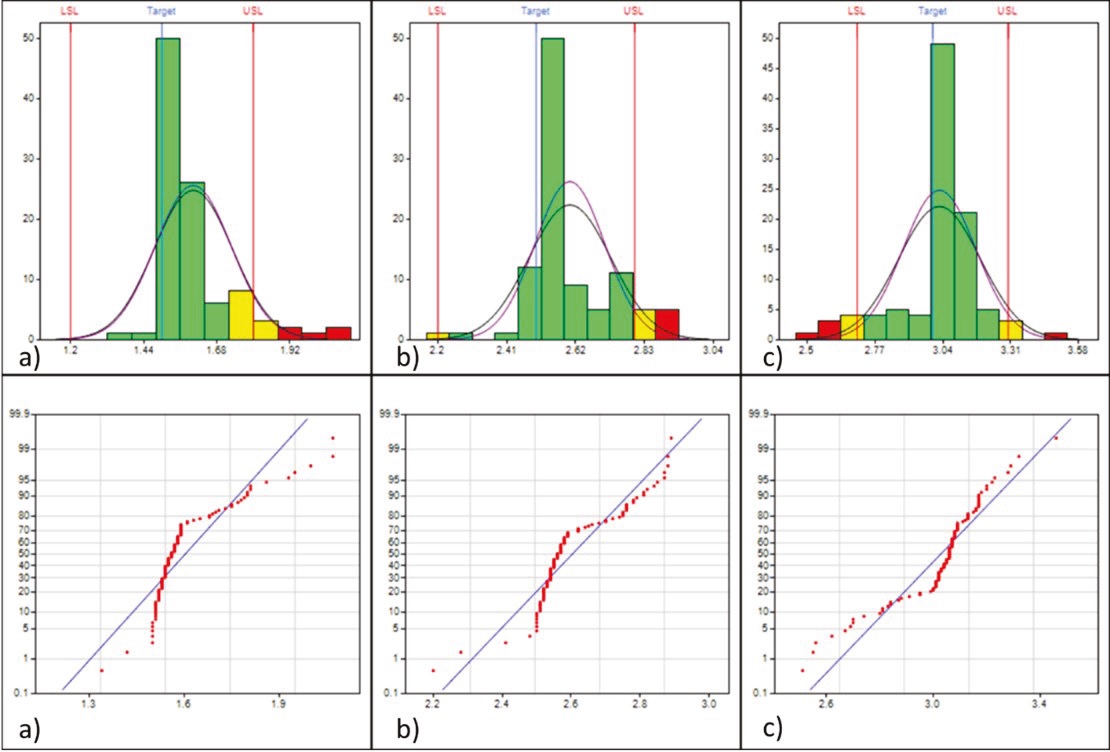
Figura 10 Gráficos de capacidad y normal para grosores: a) 1.5, b) 2.5 y c) 3.0 antes de implementación de rodillo por el método de Clements

Figura 11 Gráficos de capacidad y normal para grosores: a) 1.5, b) 2.5 y c) 3.0 después de implementación de rodillo por el método de Clements
Los resultados indican una variación notoria en comparación con los de las transformaciones de Box-Cox y Johnson, además de que las transformaciones por dichos métodos no se ajustaron adecuadamente a la distribución normal. Los estimados por el método de Clements muestran una mejoría después del cambio en los indicadores de desempeño del proceso, debido a la reducción de la variación en los rollos.
En la Tabla 4 se muestra un resumen comparativo de los hallazgos en esta investigación. Se observa que el único de los métodos que presentó confiabilidad es el método de Clements, ya que en el caso de la distribución normal y las transformaciones de Box-Cox y Johnson no presentan un ajuste adecuado de los datos a la distribución normal al aplicar la prueba de bondad de ajuste de Anderson-Darling.
Tabla 4 Resumen comparativo de los métodos utilizados
| Tipo de datos | Distribución para ajustar |
¿Ajuste de los datos? |
Criterio | Observaciones | ||
| Normal | Normal | NO | Anderson- Darling | Los índices obtenidos no son confiables, ya que no existe un buen ajuste de los datos originales | ||
| Box-Cox | Normal | NO | Anderson- Darling | Los índices obtenidos no son confiables, ya que no existe un buen ajuste de los datos transformados | ||
| Jhonson | Normal | NO | Anderson- Darling | Los índices obtenidos no son confiables, ya que no existe un buen ajuste de los datos transformados | ||
| Clements | Curvas de Pearson | SI | Valores de sesgo y curtosis/cuantiles | Los índices obtenidos son confiables, ya que los datos de sesgo y curtosis para los datos se ajustan adecuadamente a valores disponibles para las curvas de la familia de Pearson | ||
| Índices de desempeño del proceso para los datos |
Grosor 1.5 antes del cambio |
Grosor 2.5 antes del cambio |
Grosor 3.0 antes del cambio |
Grosor 1.5 después del cambio |
Grosor 2.5 después del cambio |
Grosor 3.0 después del cambio |
| Pp | 0.831 | 0.719 | 0.582 | 0.924 | 2.057 | 1.225 |
| Ppl | 6.21 | 1.162 | 0.462 | 1.395 | 4.298 | 2.576 |
| Ppu | 0.372 | 0.415 | 0.927 | 0.604 | 1.183 | 0.723 |
| Ppk | 0.372 | 0.415 | 0.462 | 0.604 | 1.183 | 0.723 |
| PPM | 132230 | 106576 | 82879 | 34993.7 | 193.389 | 15041.4 |
El método de Clements permitió un buen ajuste a curvas de la familia de Pearson mediante el criterio del sesgo y curtosis, por lo que los índices obtenidos son los adecuados para el estudio del proceso. Se observa una mejora significativa en el desempeño del proceso en los muestreos después de implementar el rodillo en la máquina, esto se logró con la reducción de la variación del grosor de los rollos a lo largo del área, demostrándose la mejora en el proceso por medio de la implementación del dispositivo.
Conclusiones
El supuesto de normalidad para los datos en el cálculo de los PPI’s presenta un reto importante para el analista, debido a que en la práctica es común la presencia de datos con comportamiento no normal, que son difíciles de transformar o ajustar a otras distribuciones.
En el caso de estudio se notó que los datos analizados se distribuyen con formas leptocúrticas, lo que impide el ajuste a otras distribuciones y reduce la eficiencia de la transformación. Las transformaciones de Box-Cox y de Johnson no originaron una transformación que normalizara los datos, por lo que se puede deducir que dichos métodos tienen capacidad limitada y no funcionan bien en todos los casos.
El método de Clements muestra buena flexibilidad para el análisis de los datos debido a la cantidad de combinaciones para sesgo y curtosis que se puedan dar en la familia de distribuciones de Pearson, obteniéndose ajustes adecuados de los datos. Como observación adicional, se pueden presentar dificultades para valores de sesgo o curtosis que no estén disponibles en las tablas.
La implementación del rodillo mostró buena eficiencia en el proceso, ya que se incrementaron los PPI’s de desempeño del proceso y se redujeron de forma notoria las partes por millón estimadas, por lo que la implementación del rodillo mejoró la estabilidad en el proceso y redujo la variación de los espesores a lo largo del área del rodillo en los tres grosores analizados.
Un factor que puede influir en la aparición de este tipo de distribuciones es el uso de aparatos con poca discriminación, lo cual puede generar observaciones modales con muchas repeticiones, resultando en una curtosis muy elevada. Se recomienda el uso de un aparato con buena resolución y discriminación para las mediciones, verificando previamente la confiabilidad del sistema de medición por métodos de MSA.
El alcance de esta investigación se limitó a una propuesta general para el análisis de desempeño de procesos en la presencia de datos no normales para su aplicación en la ingeniería; así como la mejora de un proceso productivo de amplio alcance y con impacto en la industria manufacturera de calzado de los pueblos del rincón y del bajío en el Estado de Guanajuato, México. En futuras investigaciones se abordará el uso y comparativo de índices de desempeño no normales alternativos mediante estrategias de ajuste en la función de distribución acumulada como alternativa de análisis en la mejora de procesos.











 nueva página del texto (beta)
nueva página del texto (beta)