Introduction
Container terminals are intermodal logistics nodes in a port logistics chain, where containers are temporarily stored to manage the time differences between inland and maritime transportation. The staking of containers on ideal locations within the yard is a crucial decision to improve posterior loading and retrieval operations, which affects the productivity of the container terminal. Accordingly, containers storage space allocation is a complex decision-making problem faced by container terminals worldwide (Expósito et al., 2012).
According to (Zhang et al., 2014a) to place a newly arriving container onto a stack, three decisions need to be made:
1. Allocate block-bays to vessels
2. Allocate arriving containers (of the same group) to block-bays
3.To assign a stack location within the bay to each individual arriving container
The first two decisions are usually referred to as the storage space allocation problem (SSAP), and the third decision is called the container staking problem (CSP). In the SSAP the number of block-bays to be allotted to a group of containers destined to each vessel is determined, usually considering the optimization of travel distances or yard resources utilization and productivity. On the other hand, the CSP is related to the specific location of individual containers. Where the decision to be made consists on determining the ideal location for each arriving container. This ideal location identifies the block, bay, row, and tier where the container must be stacked to improve subsequent pick-up or delivering activities, through heuristic algorithms like random, vertical, or sequential staking. This situation turns the storage space allocation problem into a tactical decision, and the specific storage location of arriving containers a real-time decision, for which it is difficult to establish a global optimization procedure to solve (Chen & Lu, 2012).
In the literature, the management of inbound and outbound containers flows have been treated differently, mainly because their retrieval times show different behaviors. In this study, we focus on the storage space allocation problem of outbound containers in the container yard. We aim to determine ideal storage locations for homogeneous groups of outbound containers using a novel approach that combines a clustering algorithm with a bi-objective optimization model. We decide to focus our research on outbound containers for two reasons. First, the container terminal, which provides us with the data to test our solution approach through a case study, is mainly export-oriented, with a ratio of 65 % of export containers against 35 % of imports. Second, the stacking position of outbound containers is an important decision that affects the uploading sequence of containers and, consequently, the throughput of the vessels.
Literature review
In the container’s terminal literature, the storage space allocation problem has received considerable attention. (Carlo et al., 2014) classify the current research into five classes:
1. Assignment of individual containers (Chen & Lu, 2012).
2. Assignment of containers by groups (Huang & Ren, 2011).
3. Comparison of storage rules (Ku et al., 2010).
4. Housekeeping (Cordeau et al., 2007).
5. Storage space assignment in relation to other yard decisions (Chang et al., 2019).
In order to solve these referred problems, several state-of-the-art methods have been proposed, including exact approaches (Kim & Park, 2003), simulation models (Dekker et al., 2006), intelligent approaches (Petering, 2015), analytical approaches (Maldonado et al., 2019), and hybrid approaches (Ozcan & Eliiyi, 2017). These methods have been implemented into hierarchical (Zhang et al., 2003) or integrated (Hu et al., 2014) solution frameworks.
Some of these methods have demonstrated to be better options than others regarding the operational characteristics and scenarios faced by the container terminals. Such scenarios may be characterized by a combination of the following features:
1. Static or dynamic time periods (Yang & Kim, 2006).
2. Consideration of uncertainty factors (Liu et al., 2017).
3. Tactical, operational or real-time decisions.
4. The type of container (inbound, outbound or transshipment).
Accordingly, the container terminals operators must analyze their current and further scenarios in order to assess which strategy gives the best storage plan for them.
Recently, (Maldonado et al., 2019) describes an approach that combines a data analytics predictive method with a heuristic algorithm to solve the inbound containers stacking problem. The predictive data analytics phase, predicts dwell times (using the random forest method), in a second stage yard bays are assigned to the arriving containers, finally, in a third stage, the predicted dwell times are used to feed three heuristic algorithms aiming to locate inbound containers in the yard while minimizing rehandles. Chang et al. (2019) consider the problem of simultaneously solve the storage space allocation and handling operation problems for outbound containers. An interactive algorithm using a heuristic procedure to determine the location of containers in a first stage, and a genetic algorithm to obtain a staking sequence in a second stage. Zheng et al. (2019) propose an algorithm for choosing ideal locations for outbound containers while optimizing the relocation sequences during retrieval operations. Hu et al. (2019) study the joint vehicle dispatching and SSAP in automated container terminals, proposing a mixed-integer linear programming model and a metaheuristic algorithm to minimize vehicles operating cost. Zhou et al. (2020) study the impact of container reshuffling on storage space allocation decisions, showing that ignoring reshuffling activities during planning causes losses to container terminals.
Compared with existing literature, this paper presents a double contribution. On one hand, it proposes a new methodological framework that combines operations research and data mining techniques to solve a storage space assignment problem for outbound containers. On the other hand, it analyzes the impact of three factors on four performance metrics used to evaluate the quality and quantity of alternative solutions to the problem of allocation of storage space for outbound containers. Most of the storage space allocation models published in literature pursue a single objective to determine which block-bays are allocated to each vessel, while the decision to assign individual containers relies on a heuristic algorithm. However, in our approach, we group containers into clusters of similar loading characteristics to assign them to block-bays, then in a second stage, we solve a bi-objective optimization problem to determine a set of alternative solutions where to allocate these groups of similar containers in the yard. We perform a computational campaign in order to appraise the impact of three factors on four performance metrics of the Pareto front.
In the next section, this paper defines in more detail the problem under investigation and our contribution. After describing the proposed methodology, and presenting an experimental design study, this paper describes the application of the proposed approach on the Altamira Container Terminal located in Mexico. Finally, some concluding remarks are reported.
Background and problem description
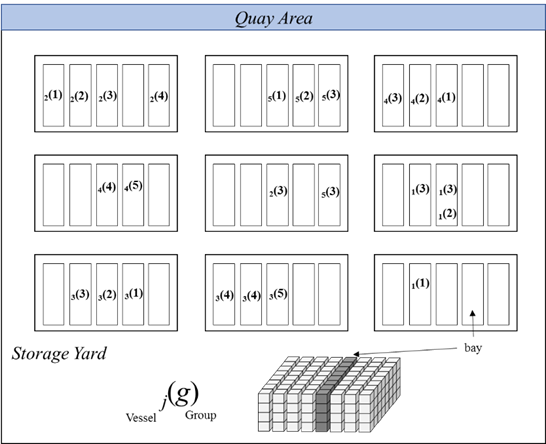
Container terminals are areas where containers are temporarily stored while waiting for maritime or land transportation. The storage yard consists of several areas perpendicular or parallel to the berth called blocks. Each block is composed of several bays that represent the length of the block, several rows which represent its width and by some tiers which represent its height (Figure 1).
The storage space allocation problem aims to find solutions to improve posterior loading and retrieval operations while optimizing a given objective function. Solving this problem is a complicated task. Commonly, container terminals handle three different types of containers: inbound, outbound, and transshipment containers.
For the management of outbound containers, whenever a vessel is scheduled to arrive at a terminal, the container terminal determines the block-bays from the export blocks, where the containers destined to a vessel, will be temporary stored. To make this decision the container terminal considers the rough storage plan provided by the shipping line and applies predefined segregation criteria such as the shipping line route, vessel, destination port, weight and type of containers.
Several days before the arrival of a vessel, the reception of outbound containers begins. During the reception of an outbound container, the external truck arrives at the terminal gate (usually within the time window of the appointment system). The gate operator, considering mainly the congestion in the yard and the previous assignment of container groups of a vessel to blocks, assigns to the arriving container a specific location within the yard. When the external truck arrives at the corresponding block, a yard crane takes the container and place it into a specific coordinate defined by the triplet (bay, row, and tier). Most of the container terminals use rubber tire gantry (RTG) cranes as yard cranes. Usually, terminal operators assign one RTG to each export block; however, during the loading process, two RTG may be assigned to an export block. During the vessel loading operations, outbound containers are retrieved from the corresponding block by an RTG and loaded into an internal truck, which transports the container to the corresponding quay crane.
Let us consider the following assumptions to define our problem accurately:
1. The container terminal has previous knowledge of the number and characteristics of outbound containers to be loaded onto each vessel scheduled to arrive.
2. These characteristics allow to group the outbound containers into clusters of similar loading characteristics.
3. The number of blocks and bays available to storage outbound containers are known, as well as their storage capacities.
4. Terminal operators follow a wide range of accepted heuristic principles for space planning and congestion management obtained from experience.
These principles aim to obtain an efficient loading sequence (Kim & Park, 2003). The first rule (the nearest location principle) aims to assign bay-yards to a vessel closest to their berthing position. The second rule (the concentrated location principle) aims to locate close together containers of the same group in order to load them consecutively. The third rule (the least congestion principle) aims to distribute the containers of the same vessel over several blocks in order to avoid interference between yard cranes during the loading operations. Finally, the fourth rule (the least relocation principle) aims to minimize the relocations of containers during the loading operations.
From the perspective of analytics, the challenging problems we try to solve are:
Methodological approach
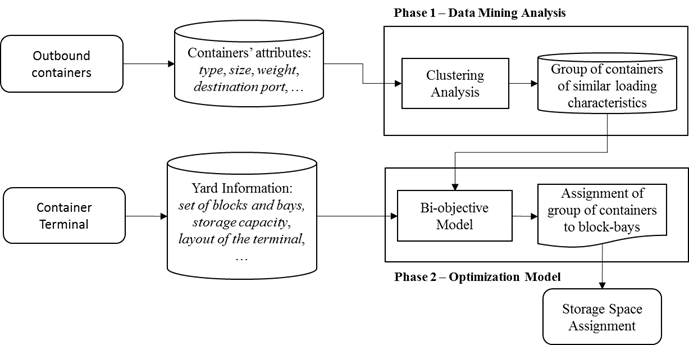
To address the problem depicted above, this paper proposes a two-phase hierarchical approach that combines a clustering technique and an operational research model. Figure 2 details the proposed approach. The first phase groups outbound containers of each vessel into clusters of similar loading characteristics (in order to load them consecutively). The resulting groups are the input to the bi-objective storage space assignment model, which determines the ideal assignment of groups of containers to block-bays as output.
Clustering outbound containers
Clustering is the process of grouping physical or abstract objects into classes of similar objects. Thus, given a set of records (outbound containers), an unsupervised learning algorithm organizes them into clusters (groups, classes) considering similarity metrics or probability density models (Xu & Wunsch, 2005).
Clustering of outbound containers is performed following the KDD process proposed by Fayyad et al. (1996): data selection, preprocessing, transformation, data mining, evaluation, and knowledge extraction; and the steps of the cluster analysis procedure (Xu & Wunsch, 2005): feature selection, clustering algorithm design or selection, cluster validation, and interpretation of results.
The features used to group container into clusters of similar loading characteristics are those usually used to segregate containers into the yard: shipping line route, vessel, size and type of container, destination port, and weight. What follows feature selection is a clustering method acting on the set of the chosen features. In our solution procedure, the Two-Step Hierarchical Agglomerative Clustering method is used to group outbound containers with similar operational loading conditions. Clusters are validated using the similarity matrix.
Storage space assignment model
In this section, a bi-objective model for the assignment of outbound containers to block-bays, considering a single period planning horizon, is proposed. Our formulation is used to determine the ideal allocation of groups of outbound containers to block-bays. The objective function is twofold: on the one hand, to minimize the distance between bay position in the yard and the berth (nearest location principle), and on the other to balance the workload in the yard to avoid interference between yard cranes during the ship operation (least congestion principle). The aim is to locate containers of the same group close together in order to load them consecutively (concentrated location principle). The model uses a vicinity matrix to represent the neighbor structure between different block-bays (see Figure 3).
To formulate the bi-objective storage space assignment model, let us consider the following assumptions, index, parameters, and decision variables.
Assumptions:
1. Containers destined to be loaded to each vessel have been previously grouped into clusters.
2. The number of containers to arrive during the planning horizon are known.
3. The containers are assumed to be of one-same size.
4. The inbound containers and outbound containers are not stacked in the same block.
5. There are enough yard crane resources to move the outbound containers in the yard.
6. The berth allocation of vessels is known.
7. All containers arriving to the yard are stored in a bay until they are loaded onto a departing vessel.
Indices and Sets:
K The set of blocks designated for storing outbound containers in the yard, K = {k1, k2, …, k|K|}.
B The set of bays available for storing outbound containers, B = {b1, b2, …, b|B|}.
Bk The sub-set of bays that belong to block k, Bk ⊆ B, B = Ukk=1Bk
J The set of vessels under consideration in the planning horizon, J = {j1, j2, …, j|J|}.
Rb Subset of bays that are neighbors of bay b. This is obtained from a R(B×B) vicinity matrix that takes the value 1 if bays b and b’ are adjacent in a way that trucks must use the same path to travel between them.
Parameters:
Djg Number of containers destined to vessel j, grouped in cluster g, which are expected to arrive during the planning horizon.
Nj Total number of containers destined to be loaded on vessel j, Nj = Σg=1njDjg ∀j ∈ J.
nj Number of clusters into which containers of vessel j are grouped.
Cb Storage capacity of bay b.
dbj Travel distance of yard vehicle from yard bay b to the berthing location of vessel j.
γ Maximum occupancy percentage for each bay; 0 ≤ γ ≤ 1.
Vb0 Number of containers in yard bay b at the beginning of the planning horizon.
Decision Variables:
xjgb Number of containers destined to vessel j, grouped in cluster g, that will be stored in bay b during the planning horizon.
δjgb 1 if containers destined to vessel j, grouped in cluster g, are staked in yard bay b, 0 otherwise.
Wmax Maximum workload in blocks during
the planning horizon; Wmax =
Wmin Minimum workload in blocks during
the planning horizon; Wmin =
The mathematical model is given by:
Subject to:
The objective function is twofold: in equation
(1) the objective function minimizes the travel distances between the
yard position of containers and the berthing positions of vessels; in equation (2) the objective function
minimizes the disparity of containers stacked among the block during the planning
horizon. Constraint (3) is a demand
satisfaction constraint; it states that all containers from vessel
j must be stored in a yard bay location. Constraints (4) is a capacity constraint; it states
that the total number of containers assigned to each block cannot exceed their
storage capacity. Constraint (5) is a
logical constraint used to related variables. Constraints (6) and (7) compute the workload in yard blocks
(Wk), where
Solution Approach. In order to solve the above model, the ε-constraint method is used. This methodology consists of the minimization of the primary objective function (in our case distance traveled) considering the second objective function (i.e., imbalance of workload) as an additional constraint on the model, using the appropriate bounds. By imposing gradually decreasing bounds εi on the secondary objective function, a sample of Pareto optimal solutions (i.e., Pareto frontier) can be found.
Performance Metrics. Storage space is a critical resource in container terminals. Thus, the main objectives of space allocation decisions for outbound containers are to utilize space efficiently and make loading operations more efficient. When a problem is formulated as a bi-objective optimization problem, the solution's performance assessment is less straightforward than when formulated as a single-objective optimization problem. It is mainly because, in bi-objective optimization (where there is conflicting nature of the objectives), two goals are searched during iterations of the algorithms:
1. Convergence to the Pareto-optimal set and
2. Maintenance of diversity in solutions of the Pareto-optimal set (Deb, 2001; Chambari et al., 2012).
Thus, two types of metrics are required: two performance metrics to assess the set of solutions approximating the Pareto-optimal front, and two performance metrics to assess the quality of each non-dominated solution in the Pareto frontier (Table 1).
Table 1: Performance metrics to assess the quality of the solutions
| Metrics for Pareto optimal front | Metrics for non-dominated solutions |
|---|---|
| P1 Number of Pareto Solution: This metric is used for showing the number of Pareto optimal solutions that are obtained | M1 Traveled distance: Average distance traveled by internal trucks, during the loading operation, when carrying the containers from its position in the bays, and the berthing position of vessels |
| P2 Mean ideal
distance: It is used for measuring the closeness
between Pareto solution and an ideal point (0,0). This metric is
formulated as [38]: |
M2 Imbalance: Deviation of workload between the blocks |
Experimental framework
This section describes the experimental framework used to analyze the impact of the main factors involved in the storage space allocation problem, for which there is an empirical conjecture affecting the performance metrics defined above. As issued here, a sensitivity analysis on the performance metrics, when varying the factors under consideration, is performed. Three experimental factors have been considered (see Table 2). Factor A refers to the capacity of the container terminal; it is used to see how storage space decisions are affected when the storage capacity is close to critical congestion. Factors B and C are related to the clustering results; we aim to analyze how storage space decisions are affected by the solution of the first phase of our proposed approach.
Table 2: Factors levels considered
| Factor | Factor level 1 (low) | Factor level 2 (high) |
|---|---|---|
| A- Capacity of the storage yard | 20 % over demand | 60 % over demand |
| B- Number of clusters per vessel | nj = 3 | nj = 6 |
| C- Balance in clusters | Unbalanced | Balanced |
Each one of the 23 factor level combinations represents a sample scenario. For each scenario, ten sample instances were created and solved to find their Pareto frontier. Considering that for each frontier, 22 points are computed in order to compute the metrics, (8)(10)(22) = 1760 linear programming models were solved. All experimental results have been generated and analyzed using a laptop Intel Core i7 2.4 GHz with 16 GB of RAM. We used CPLEX to solve the optimization models and MINITAB to carry out the statistical analysis.
Table 3 summarizes the results of our experimental campaign. These have been analyzed to gain insights into the storage space assignment of the outbound containers process. Figure 4 shows the main effect plots.
Table 3: Summarizing results for each instance set
| Set | Factor | Metrics for Pareto front | Metrics for non-dominated solutions | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | P1 | P2 | M1 | M2 | |||||
| Min | Max | Δ | Min | Max | Δ | ||||||
| 1 | 1 | 1 | 1 | 17 | 415.69 | 380.72 | 398.15 | 17.44 | 88.00 | 226.00 | 138.00 |
| 2 | 1 | 1 | 2 | 18 | 415.44 | 381.12 | 400.48 | 19.36 | 85.00 | 226.00 | 141.00 |
| 3 | 1 | 2 | 1 | 22 | 404.86 | 369.90 | 378.95 | 9.05 | 84.00 | 226.00 | 142.00 |
| 4 | 1 | 2 | 2 | 22 | 404.88 | 373.33 | 383.88 | 10.56 | 84.00 | 209.00 | 125.00 |
| 5 | 2 | 1 | 1 | 22 | 387.55 | 358.53 | 381.38 | 22.85 | 35.00 | 205.00 | 170.00 |
| 6 | 2 | 1 | 2 | 22 | 378.25 | 358.37 | 379.97 | 21.60 | 35.00 | 150.00 | 115.00 |
| 7 | 2 | 2 | 1 | 22 | 376.41 | 357.85 | 373.95 | 16.10 | 35.00 | 150.00 | 115.00 |
| 8 | 2 | 2 | 2 | 22 | 377.15 | 357.90 | 376.03 | 18.13 | 35.00 | 150.00 | 115.00 |
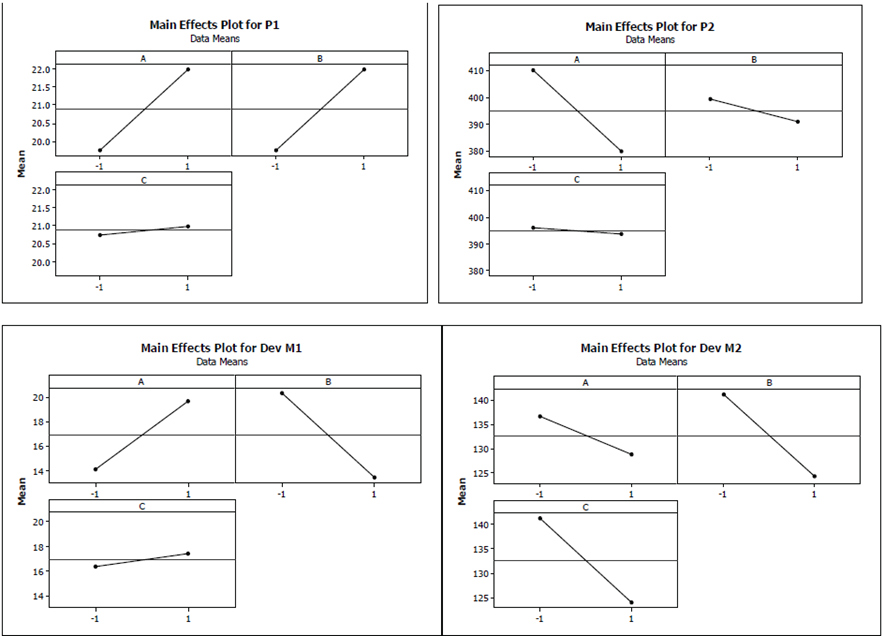
Results demonstrate that Factor B (number of clusters per vessel) and Factor A (capacity of the storage yard) are significant for metric M1 (mean travel distance). Factor A explains 36.94 % of the observed variability in mean travel distance, while Factor B explains 55.97 %. However, any factor is significant for metric M2 (imbalance). Regarding the metrics for Pareto optimal front, Factors A and B, as well as the interaction between both show a significant influence metric P1 (number of non-dominated solutions); each factor and their interaction explain 32.79 % of the observed variability. Factors A and B have a positive influence, while the interaction a negative influence. For metric P2 (average distance from the ideal point), only Factor A shows a significant negative influence, explaining 90.42 % of the observed variability.
Case study
In this section, a case study in a Mexican Container Terminal, located in Altamira (ATP, Altamira Terminal Portuaria), is carried out aiming to evaluate the performance of the proposed approach. The port of Altamira is located in the Gulf of Mexico. Altamira is the second largest Mexican port in the Gulf of Mexico, moving, on average, more than 600,000 containers per year, and connecting to over 20 major ports worldwide. ATP is the biggest container terminals operating in the port of Altamira, and was the focus of this case study, providing the raw data.
Current Situation
The ATP terminal moves on average 1,400 outbound containers per week. The arrival of outbound containers begins from 3 to 4 days before the arrival of the vessel. Thus, the planning horizon for storage space decisions is four days. The current stacking policy of the ATP corresponds to a semi-random assignment, in which export (outbound) containers are stacked in one of the predefined block-bays, according to their departure vessel. Export containers are sent to the less congested block where storage space has been assigned for the corresponding vessel. This strategy causes many reallocations when containers are retrieved to be loaded onto their corresponding vessels. The proposed approach is motivated by the need to improve this situation.
The dataset provided by the container terminal contains the historical records of the outbound containers that were handled during the last four months of 2017. The dataset includes the following variables: container ID, type of container (tank, flat, reefer, general propose), weight, time and date of arrival, destination port, shipping line route, vessel, and ID of the location where the containers were staked prior the arrival of the vessel. Additionally, further meetings were performed in order to gather information regarding:
1. The expected occupancy percentage of bays.
2. The bays designated to each vessel.
3. Segregation criteria, and
4. The layout and roads within the terminal in order to compute a travel distance matrix and vicinity matrix.
The original dataset contains 38,585 records of outbound containers. After filtering out missing values, inconsistencies, and outliers, 38,082 observations remained.
We choose an ordinary week from these historical records, in order to take a real instance and analyze the behavior of the ATP when managing outbound containers (see details in Table 4). In this instance, 1,405 outbound containers arrive during the planning horizon. The current decision method of the terminal results in an average travel distance of 405.82 meters per container during the loading operations, and an imbalance of 317 containers among the blocks. Table 5 shows the detailed distribution of containers among the blocks.
Table 4: Current situation instance
| Feature | Value |
|---|---|
| Planning horizon | 1 week |
| Number of vessels | 4 |
| Number of outbound containers (total) | 1,405 |
| Number of export blocks | 8 |
| Number of bays (used) | 128 |
| Stacking capacity (available) | 3,072 |
| Average traveled distance (M1) | 405.82 mts |
| Imbalance (M2) | 317 cnt |
Note: Week 24, γ =0.8, rows = 6. and tiers = 5
Table 5: Distribution of workload in current situation
| Block | Vessel | Σ | Utilization | |||
|---|---|---|---|---|---|---|
| j1 | j2 | j3 | j4 | |||
| Block 1 | 44 | 31 | 37 | 32 | 144 | 0.38 |
| Block 2 | 55 | 43 | 43 | 80 | 221 | 0.58 |
| Block 3 | 28 | 5 | 20 | 12 | 65 | 0.17 |
| Block 4 | 42 | 34 | 33 | 65 | 174 | 0.45 |
| Block 5 | 84 | 34 | 67 | 52 | 237 | 0.62 |
| Block 6 | 112 | 39 | 61 | 31 | 243 | 0.63 |
| Block 7 | 102 | 45 | 90 | 82 | 319 | 0.83 |
| Block 8 | 1 | 0 | 1 | 0 | 2 | 0.01 |
| Σ | 468 | 231 | 352 | 354 | ||
Clustering results
A cluster analysis was performed as described above. This provides analytical support in having clusters internally homogeneous and heterogeneous among them. The main reason for group containers with similar loading characteristics into clusters is to distribute them close together within the yard. Table 6 shows the clustering results for each vessel. The silhouette value (ξ) helps to assess the goodness of a classification. It measures the average distance from each object to the other objects belonging in the same cluster it is assigned to, as well as the average distance from the other clusters. The values range from -1 to +1. A good acceptable average silhouette value should be above +0.4.
Table 6: Classification results
| Vessel ID | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Nj | Avg. Predictor importance | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ξ | nj | ξ | nj | ξ | nj | ξ | nj | A | B | C | D | ||
| Vessel 1 | 0.52 | 188 | 0.57 | 134 | 0.69 | 146 | --- | --- | 468 | 0.96 | 0.87 | 0.55 | 0.47 |
| Vessel 2 | 0.65 | 76 | 0.58 | 63 | 0.43 | 92 | --- | --- | 231 | 0.92 | 0.74 | 0.68 | 0.38 |
| Vessel 3 | 0.58 | 106 | 0.65 | 108 | 0.33 | 138 | --- | --- | 352 | 0.89 | 0.86 | 0.63 | 0.48 |
| Vessel 4 | 0.62 | 100 | 0.58 | 101 | 0.61 | 71 | 0.81 | 82 | 354 | 0.90 | 0.64 | 0.41 | 0.34 |
Note: A - Shipping line route, B - Destination port, C - Weight, D - Type of container. ξ - Silhouette value
Storage space assignment results
According to the clustering results, 13 clusters were required to homogeneously group the 1,405 outbound containers, which will be uploaded to four vessels. From each cluster, we identify the information related to parameters Djg, Nj, and nj. Capacity parameters (Cb and γ) were obtained during personal meetings with the terminal manager. Finally, the travel distances and the vicinity matrix were obtained from the layout of the terminal. Some data were modified in order to preserve container terminal confidentiality without losing validity.
Figure 5 shows the set of Pareto optimal solutions for the case study. It should be noted that the current solution (405.82, 317) is far away from Pareto Frontier. A more in-depth analysis reveals that the current solution is 514.96 distant from Ideal Point (0,0). Through the ε-constraint method, we found 22 non-dominated solutions. The average distance from the Pareto front to the Ideal Point is 400.01, and the distance between extreme non-dominated solutions is 140.46. The average travel distance per container during the loading operations in the Pareto front ranges from 368.30 to 379.63 m, while the imbalance of containers among blocks ranges from 75 to 215 containers.
In comparison with current practice, the confidence interval for the mean (α = 0.05) of improvement in Imbalance range from 153.12 to 191.52; while the confidence interval for distance ranges from 33.75 to 36.38; outperforming the current practices of this port terminal. Table 7 shows the distribution of workload among blocks for one of the non-dominated solutions.
Table 7: Distribution of workload in an alternative optimal solution
| Block | Vessel | Σ | Utilization (%) | |||
|---|---|---|---|---|---|---|
| j1 | j2 | j3 | j4 | |||
| Block 1 | 63 | 41 | 52 | 43 | 199 | 0.52 |
| Block 2 | 45 | 32 | 32 | 90 | 199 | 0.52 |
| Block 3 | 109 | 7 | 58 | 26 | 200 | 0.52 |
| Block 4 | 46 | 38 | 37 | 79 | 200 | 0.52 |
| Block 5 | 51 | 0 | 81 | 67 | 199 | 0.52 |
| Block 6 | 61 | 41 | 65 | 32 | 199 | 0.52 |
| Block 7 | 90 | 71 | 22 | 17 | 200 | 0.52 |
| Block 8 | 3 | 1 | 5 | 0 | 9 | 0.02 |
| Σ | 468 | 231 | 352 | 354 | ||
Conclusions and further research
This paper proposes a novel methodology to solve the storage space assignment problem of outbound containers. The methodology combines a clustering approach and a bi-objective optimization model. In the first stage, our proposed methodology, groups containers into clusters of similar loading characteristics. In a second stage, a bi-objective formulation is proposed in order to find a frontier of alternative solutions for the allocation of containers within the yard.
Since we obtain a set of solutions approximating the Pareto optimal front in every instance, two types of metrics were computed; two performance metrics to assess the set of alternative solutions, and two performance metrics to assess the quality each non-dominated solution in the Pareto front. Results from an experimental design study demonstrate that the number of alternative solutions increases as the capacity of the storage yard increase; while the distribution of containers within the clusters is not significant for any performance metric. Results in the case study demonstrate that our approach outperforms current practice at ATP.
As further research, we propose to combine the storage space allocation of containers with the design of a double-truck appointment system for inbound and outbound containers. Furthermore, the analysis of the flows of transshipment containers through data analytics would be useful to derive appropriate optimization models and algorithms for stacking decisions.











 nova página do texto(beta)
nova página do texto(beta)