Introducción
Un sistema eléctrico de potencia está constituido por las etapas de generación, transmisión, distribución y consumo de la energía eléctrica. En la operación de un sistema eléctrico se debe garantizar el nivel de voltaje y el suministro de potencia activa contratados por parte de los usuarios, principalmente del sector industrial. No obstante, para tener una buena regulación de voltaje en los puntos de consumo de una red eléctrica, es necesario compensar con potencia reactiva por parte del usuario industrial, esto con el fin de mejorar el factor de potencia y, en consecuencia, optimizar la infraestructura de transmisión y distribución de la energía eléctrica al disminuir los niveles de corriente. La compensación de la potencia reactiva en instalaciones industriales se realiza comúnmente por medio de bancos de capacitores, generalmente conmutando diversos valores de capacitancia con la activación y desactivación de contactores. Algunas empresas con altos consumos de energía eléctrica optan por instalar motores síncronos sobreexcitados que operan en condiciones de vacío, para entregar potencia reactiva a la red y así mejorar el factor de potencia (Tabatabaei et al., 2017).
La compensación de la potencia reactiva para mejorar la regulación de voltaje en diversos puntos de un sistema eléctrico puede también realizarse con sistemas de control robusto y continuo, implementados en los compensadores estáticos de Var’s y en sistemas flexibles de transmisión en CA (FACTS, del inglés, Flexible AC Transmission Systems), entre otros dispositivos. Estos dispositivos incorporan sistemas de control que se aplican a convertidores de estado sólido que utilizan diodos, tiristores, IGBT’s, etcétera. Por su parte, mediante los compensadores de potencia reactiva de estado sólido basados en tiristores, la compensación de VAr’s es continua en un sistema eléctrico de potencia (Gyugyi, 1988). También en Arulampalam et al. (2003) se aborda la aplicación del compensador síncrono estático (STATCOM, del inglés, Static Synchronous Compensator), con almacenamiento de energía para compensación de potencia activa y reactiva, regulación del voltaje y mitigación de perturbaciones en el sistema eléctrico. En lo descrito anteriormente, queda expuesto que para lograr regulación de voltaje, corrección del factor de potencia, mitigación de perturbaciones, entre otros aspectos, se requiere de un dispositivo que provea de potencia reactiva al sistema eléctrico. En este sentido, este trabajo de investigación se enfoca en el diseño y control robusto de un STATCOM, como medio para el suministro de potencia reactiva a un sistema eléctrico de potencia.
El STATCOM se conecta en paralelo a la red eléctrica para intercambiar potencia reactiva mediante el ajuste de la magnitud y fase del voltaje de salida del convertidor electrónico del compensador. Se han reportado trabajos con diferentes métodos para compensar la potencia reactiva. En Garcia & Garcia (2000) se presenta un sistema de control para un STATCOM basado en modulación de ancho de pulso (PWM), en donde el modelo del sistema en lazo cerrado en tiempo discreto asegura el control desacoplado de la potencia activa y reactiva; no obstante, solo se considera el desempeño continuo, mientras la inyección de armónicos no se analiza. En Singh et al. (2014) se emplea un STATCOM trifásico que regula el voltaje de un generador de inducción autoexcitado (SEIG, del inglés, Self-Excited Induction Generator), sin embargo, la regulación de potencia reactiva para la operación del generador y el consumo de la energía no demuestra un desempeño apropiado debido a que se utiliza un controlador PI no robusto. En Seo et al. (2009) se presenta un sistema de generación fotovoltaico con compensación de potencia reactiva y de armónicos en corriente, a través de un inversor PWM usado como STATCOM, aunque se puede apreciar el error en estado estacionario en la compensación de potencia reactiva. En Wang et al. (2019) se analiza en detalle el principio del método de desacoplamiento (ADRC, por sus siglas en inglés Active Disturbance Rejection Control) aplicado al STATCOM con filtro LCL. La capacidad del ADRC para estimar y compensar las perturbaciones mejora la robustez del STATCOM, sin embargo, no se presentan resultados experimentales para comprobar la robustez y desempeño del controlador ADRC.
La principal aportación del presente trabajo consiste en describir paso a paso la metodología de diseño de un sistema de control robusto aplicado a un compensador estático de VAr’s, conocido como STATCOM, para regular la potencia reactiva que se entrega a un sistema eléctrico de potencia ante la presencia de perturbaciones externas. Se originaron perturbaciones al alimentar un motor de inducción trifásico, el cual es sometido a cambios súbitos en el par de carga. Además, se caracteriza un filtro LCL utilizado para reducir el contenido armónico de las corrientes, en donde se ajustan los valores del capacitor y de la resistencia de amortiguamiento por medio de un análisis paramétrico en frecuencia, para obtener la mejor respuesta dinámica del filtro. La metodología de diseño y control propuesto para el STATCOM se valida experimentalmente en un prototipo de laboratorio.
Modelo del compensador estático de VAr’s
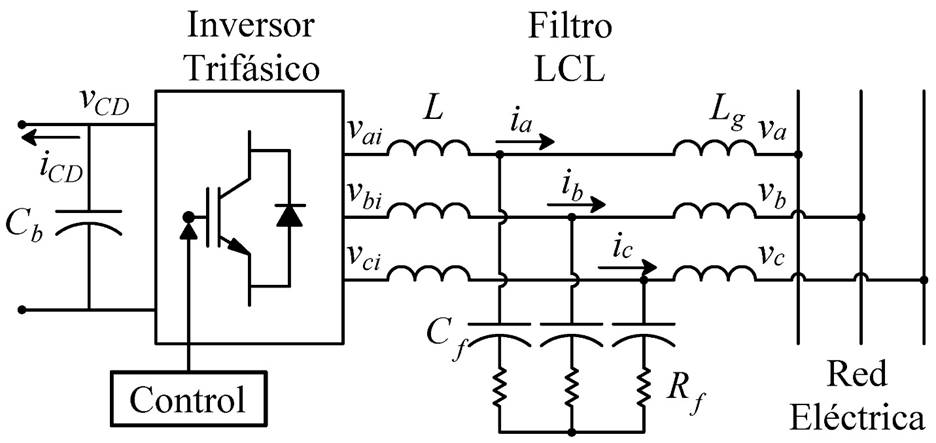
El compensador estático de potencia reactiva STATCOM se caracteriza por regular la potencia reactiva en un valor predeterminado y entregarla a la red eléctrica. En este trabajo se propone un STATCOM compuesto por la red eléctrica, un filtro LCL conectado en estrella, un inversor trifásico tipo puente, el bus de CD y un banco de capacitores, como se muestra en la Figura 1.
El STATCOM se conecta en paralelo para intercambiar potencia reactiva con la red eléctrica. La cantidad y dirección de la potencia reactiva intercambiada se puede controlar ajustando la amplitud y fase del voltaje trifásico de salida del convertidor, |vabci|. Si |vabci| es mayor que la magnitud del voltaje trifásico de la red eléctrica |vabc|, el STATCOM entrega potencia reactiva a la red. En caso contrario, si |vabci| es menor que |vabc|, el STATCOM almacena potencia reactiva de la red. En caso de que ambos voltajes tengan la misma magnitud no hay transferencia de potencia reactiva.
El modelado del compensador estático de potencia reactiva, se basa en:
a) El equilibrio de potencia activa de entrada y salida del sistema, omitiendo las pérdidas del inversor y del filtro.
b) La diferencia de voltajes en terminales de las inductancias de acoplamiento del filtro LCL en cada una de las fases, en donde se omite el capacitor para reducir el orden del sistema.
Por lo que el modelo trifásico del compensador estático de VAr’s, tiene la siguiente representación:
Donde:
vabc e iabc = |
vectores de voltaje y corriente en la red eléctrica, respectivamente |
T = |
operación de transpuesta |
vabci = |
vector de voltaje en terminales del inversor |
Cb = |
capacitor del bus de CD |
Req y Leq = |
equivalente en serie de las resistencias e inductancias de las dos bobinas del filtro LCL, respectivamente, sin considerar el capacitor |
El primer término del sistema (1) corresponde al cálculo de la potencia trifásica instantánea en la red eléctrica, a través del producto escalar de los vectores de voltaje y corriente.
Con la finalidad de establecer un modelo de un sistema conectado a la red eléctrica más sencillo, es práctica común transformar las variables eléctricas del sistema trifásico abc al sistema dq0, mediante la transformación de Park. El modelo resultante en dq0 es de orden reducido y con parámetros constantes. Al definir la transformación de Park se toma como referencia la posición del eje d respecto a la fase a del sistema trifásico, ver Figura 2, y tiene la siguiente representación:
donde θe es el ángulo comprendido entre el eje d y el eje de la fase a (θe = ωet cuando el marco de referencia gira a la frecuencia de la red eléctrica).
La componente en el eje directo fd resulta del producto del primer renglón de la matriz de transformación y el vector de una señal del sistema trifásico, obteniéndose:
aplicando la identidad del producto de dos funciones coseno a diferente frecuencia y reduciendo términos, se obtiene:
donde la componente de la señal eléctrica en el eje directo fd corresponde a la amplitud de la señal por fase Fm y es una señal de directa, sin frecuencia. Por otro lado, la componente en el eje en cuadratura fq resulta del producto del segundo renglón de la matriz de transformación y el vector de una señal del sistema trifásico, obteniéndose:
aplicando la identidad del producto de una función seno con una función coseno a diferente frecuencia y reduciendo términos, resulta:
donde la componente de la señal eléctrica en el eje en cuadratura fq se anula al referir el eje d con el eje de la fase a.
Al aplicar la transformación de Park (2) al modelo trifásico del compensador estático de VAr’s (1) representado en espacio de estados, resulta:
realizando las operaciones indicadas en (7), se obtiene el modelo del compensador estático de VAr’s en el sistema dq0, como sigue:
El compensador estático de VAr’s no tiene habilitada ninguna línea de neutro y no existe conexión alguna al sistema de tierras, por lo que no se presentan señales de secuencia cero. Por tal motivo, se reduce el orden del modelo del compensador (8), mismo que se representa de aquí en adelante únicamente en el marco dq, con la siguiente representación:
el modelo (9) es no lineal y está desacoplado, por lo que se puede controlar cada una de las corrientes id e iq con su correspondiente entrada de control vdi y vqi; además, el modelo tiene dos entradas de control, por lo tanto, se pueden seleccionar dos variables de salida a controlar.
Diseño del filtro LCL
El filtro LCL mostrado en la Figura 1, se utiliza como interfaz en la interconexión de un sistema con inversor trifásico y la red eléctrica. El filtro LCL se caracteriza por agregar dinámica al sistema que se interconecta con la red eléctrica, además de reducir la distorsión armónica en las corrientes producidas por la operación del inversor, en donde los IGBT’s conmutan a alta frecuencia mediante la técnica de modulación por ancho de pulso en el espacio vectorial (SVPWM). Los valores de los parámetros del filtro LCL se establecen de acuerdo con el flujo de potencia activa nominal en el sistema, el voltaje entre líneas de la red eléctrica y la frecuencia de conmutación de los IGBT’s. Para determinar el valor de la inductancia del filtro LCL, lado del inversor, se considera al voltaje de la red eléctrica como un cortocircuito para altas frecuencias y se utiliza la siguiente función de transferencia de primer orden a la frecuencia de conmutación (Liserre et al., 2005):
donde vi (hsw) es el armónico del voltaje del inversor como entrada e ig (hsw) es el armónico de la corriente de salida del inversor, ambas señales a la frecuencia de conmutación (ωsw). Al proponer un nivel de atenuación de corriente de 0.02 en la función de transferencia (10) con una frecuencia de conmutación de ωsw = 2π (3300 Hz), y resolviendo para la inductancia lado del inversor se obtiene, L = 3 mH. Es importante tomar en cuenta que la inductancia total del filtro LCL no debe exceder el valor de 0.1 p.u., y con esto, limitar la caída de voltaje durante la operación (Liserre et al., 2005).
Para definir el valor de la inductancia del lado de la red, se considera la configuración del filtro LCL sin la resistencia, y se aplica la siguiente expresión en su cálculo (Reznik et al., 2014):
donde ka es la relación entre la corriente inyectada a la red eléctrica ig (hsw) y la corriente generada por el inversor ii (hsw), es decir, la atenuación en corrientes a la frecuencia de conmutación, cuyo valor puede seleccionarse en un 20 % (Liserre et al., 2005 y Reznik et al., 2014); para definir un valor inicial del capacitor Cf, se necesita calcular la impedancia base Zb y la capacitancia base Cb (Liserre et al., 2005 y Reznik et al., 2014), las cuales se definen por:
Donde:
VLL = |
voltaje de línea a línea de la red eléctrica |
Pb = |
potencia activa nominal del sistema |
ωe = |
frecuencia de la red eléctrica de 377 rad/s |
En el prototipo del presente proyecto se consideró VLL = 220 V y Pb = 1.5 kW; al aplicar (12), la impedancia base resulta Zb = 32.26 Ω y la capacitancia base resulta de Cb = 82.23 μF.
Considerando una atenuación de ka = 0.02, una frecuencia de conmutación ω sw = 2π (3300 Hz) de los IGBT’s y un valor inicial del capacitor de Cf = 4.1 μF usando Cf = 0.05Cb, cuya estimación considera una variación del factor de potencia en un 5 % (Liserre et al., 2005 y Reznik et al., 2014), al aplicar (11) se obtiene el valor de inductancia lado de la red Lg = 3.4 mH.
A partir del valor inicial de capacitancia de Cf = 4.1 μF, se procede a realizar un análisis paramétrico en frecuencia para seleccionar la ubicación de la frecuencia en resonancia, la cual se calcula mediante la siguiente expresión:
se recomienda que la frecuencia de resonancia ωres esté ubicada a la izquierda de la parte media del rango de frecuencias, el cual tiene como límite inferior el valor de 10 veces la frecuencia de la red eléctrica ωe y como límite superior la frecuencia de conmutación ωsw de los IGBT’s (Liserre et al., 2005 y Reznik et al., 2014). Mediante un análisis en frecuencia con el diagrama de Bode se proponen varios valores de capacitancia Cf cercanos al valor inicial, y se verifica el efecto de resonancia para cada valor, utilizando la siguiente función de transferencia del filtro LCL:
al realizar el análisis en frecuencia en el rango de 1 kHz a 5 kHz y utilizando la función de transferencia del filtro LCL (14) con tres valores de capacitancia: 4.5, 6.0 y 7.5 μF, se seleccionó el valor de 7.5 μF, el cual tiene una menor frecuencia de resonancia de 1.46 kHz, ver Figura 3.
Finalmente, un valor inicial de la resistencia Rf, utilizada para amortiguar las corrientes a la frecuencia de resonancia, se calcula como una tercera parte de la impedancia del capacitor mediante la siguiente relación (Liserre et al., 2005 y Reznik et al., 2014):
posteriormente, el valor inicial de la resistencia Rf se ajusta mediante un análisis paramétrico aplicado al filtro LCL completo utilizando la siguiente función de transferencia:
del análisis en frecuencia de (16) y utilizando el diagrama de Bode, se selecciona el valor de resistencia que presenta la mejor respuesta, es decir, donde se presente una respuesta suave de la ganancia sin sobreimpulso. El valor inicial de la resistencia de amortiguamiento Rf se calculó en 6.2 Ω utilizando (15); al realizar el análisis en frecuencia en el rango de 1 kHz a 5 kHz utilizando la función de transferencia del filtro LCL completo (16) con dos valores de resistencia: 6 y 10 Ω, se seleccionó el valor de 10 Ω, valor con el cual el filtro tiene una mejor respuesta dinámica en frecuencia con una amortiguación de 0.03 de la corriente a la frecuencia de resonancia de 1.46 kHz, como se muestra en la Figura 4.
Con el proceso de caracterización del filtro LCL se obtuvieron los siguientes valores: inductancia lado del convertidor L =3 mH, inductancia lado de la red Lg =3.4 mH, capacitor del filtro Cf =7.5 μF y la resistencia de amortiguamiento Rf =10 Ω.
Diseño del controlador del STATCOM
El modelo del compensador estático de VAr’s (9) es de tercer orden y están desacopladas las dos entradas de control vdi y vqi, por lo tanto, es posible seleccionar dos salidas a controlar: el valor de potencia reactiva por entregar a la red eléctrica y el voltaje en el bus de CD. Como primer paso se define la variable de estado ε1 como la señal de error de regulación de voltaje:
en donde se propone que su dinámica sea estable y que converja de forma exponencial aplicando la técnica de linealización por control a bloques, para obtener:
para proponer un control mediante corrientes en el eje d, se resuelve id en (18) para obtener la corriente de referencia de la siguiente forma:
Como segundo paso, se define la variable de error en corrientes en el eje d, como:
cuya dinámica tiene la siguiente forma:
donde el termino de perturbación queda definido por:
los términos que incluyen la primera y segunda derivada del voltaje de referencia v̇ref y v̈ref no son incluidos en la perturbación ρ2, debido a que se está resolviendo el problema de regulación de voltaje en el bus de CD, y por lo tanto son nulos.
Como último paso, se define la tercera variable de estado como el error de regulación en la potencia reactiva:
donde la potencia reactiva se define por:
la dinámica de la nueva variable toma la forma:
donde el termino de perturbación es:
Sustituyendo (20) en (18) y reagrupando con (21) y (25), se obtiene un sistema equivalente del modelo del compensador estático de potencia reactiva (9) en el marco dq con variables de error de regulación, con la siguiente representación:
Este sistema equivalente es no lineal y de tercer orden, y se caracteriza por estar desacoplado respecto a las entradas de control vdi y vqi. Por lo tanto, para regular la potencia reactiva y el voltaje del bus de CD, se definen las variables de deslizamiento sd = ε2 y sq = ε3, las cuales son el argumento de la ley de control super-twisting, que tiene la siguiente representación:
donde λk y αk son las ganancias de la ley de control, sk es la superficie de deslizamiento que es forzada por la ley de control hacia cero, sign(sk) es una función que define el signo de las ganancias, lo cual proporciona robustez a la acción de control, y uk es una componente integral del controlador. Al estabilizar y forzar la superficie sq hacia cero en tiempo finito con la ley de control, se logra directamente la regulación de la potencia reactiva; así mismo, al forzar la superficie sd hacia cero en tiempo finito, se logra un movimiento estable y asintótico hacia cero del error de regulación de voltaje del bus de CD, mediante el control de las corrientes en el eje d.
Para garantizar estabilidad en el sistema de regulación de potencia reactiva y voltaje del bus de CD (27) del compensador estático de VAr’s, las ganancias de la ley de control super-twisting λd y αd deben cumplir con las siguientes restricciones:
donde la norma de la perturbación incluida en la segunda ecuación del sistema (27) se define como |ρ2| = δd|sd|1/2, para δd > 0, el resto de los parámetros son definidos en el modelo (1). Mientras que las ganancias de control λq y αq deben cumplir con las siguientes restricciones:
donde la norma de la perturbación incluida en la tercera ecuación del sistema (27) se define como |ρ3| = δq |sq |1/2, para δq > 0, el resto de los parámetros son definidos en el modelo (1). Estas desigualdades en los ejes d y q, que definen las ganancias de la ley de control super-twisting, se establecen de acuerdo con el procedimiento definido en Morfín et al. (2018), siguiendo el análisis de estabilidad de un sistema en lazo cerrado con el algoritmo super-twisting establecido en Dávila et al. (2009), cuando la entrada de control tiene coeficiente unitario. Por lo que en las desigualdades propuestas (29) y (30) se incluyeron los coeficientes de vdi y vqi definidos en el sistema (27).
Acondicionamiento de las señales de control
Una técnica de acondicionamiento de las señales de control vdi y vqi del sistema (27) es la modulación de ancho de pulso en el espacio vectorial (SVPWM), la cual es muy empleada en inversores trifásicos para generar los pulsos de activación de los IGBT’s y de esta manera modular el nivel de voltaje requerido para realizar la acción de control del STATCOM.
La fuente de voltaje trifásico generado por las conmutaciones en el inversor tipo puente queda definida por Rivera et al. (2009):
donde VCD es el voltaje del bus de CD y s1, s2 y s3, es el estado de encendido o apagado de los IGBT’s de la parte superior del convertidor. Mientras que el estado de los de los IGBT’s de la parte inferior del puente se definen con el complemento, mediante las siguientes relaciones:
El vector de voltajes de fase vabc se transforma al sistema αβ estacionario aplicando la transformación de Park (2) con θe = 0, de la siguiente forma:
Sustituyendo (31) en (33) se define el vector de voltajes en terminales del inversor en αβ en función de los estados de encendido y apagado de los IGBT’s, con la siguiente representación:
La representación polar de los voltajes vα y vβ se determina mediante las siguientes relaciones:
El vector resultante (35) en forma polar es de magnitud 2/3VCD y tiene la característica de girar a la velocidad de la frecuencia de la red eléctrica. Como son tres interruptores que se presentan en la parte superior del inversor tipo puente, se presentan 8 combinaciones de bits, donde dos de ellas 000 y 111 mandan voltaje nulo. Tomando como referencia a la fase a, un ciclo de voltajes trifásico queda definido por las siguientes combinaciones de bits: 101 100 110 010 011 001 aplicando la transformación (31). Al aplicar la transformación (34) a las seis combinaciones de bits, los voltajes resultantes en αβ en forma polar son: 2/3VCD ∠300°, 2/3VCD ∠0°, 2/3VCD ∠60°, 2/3VCD ∠120°, 2/3VCD ∠180°, 2/3VCD ∠240°, los cuales definen 6 sectores en un ciclo, estos se representan con un hexágono (Rivera et al., 2009). Sin perder generalidad, se puede analizar el sector I que abarca 60° e inicia en el eje x, y está definido por las combinaciones de bits 100 y 110 de los pasos P2 y P3. Las proyecciones de u sobre los pasos P2 y P3 se determinan aplicando la ley de senos, y toman la forma:
en donde las magnitudes de v2 y v3 cumplen con las siguientes relaciones de proporción, respectivamente:
en donde Tp es el periodo de muestreo. Sustituyendo (36) en (37) y resolviendo para los tiempos de activación T1 y T2 quedan definidos por (Rivera et al., 2009):
Como las señales de control vdi y vqi en (27) están en el sistema dq, estas deben transformarse al sistema αβ mediante la siguiente trasformación:
para proceder con el acondicionamiento de las señales de control aplicando la técnica SVPWM.
Resultados
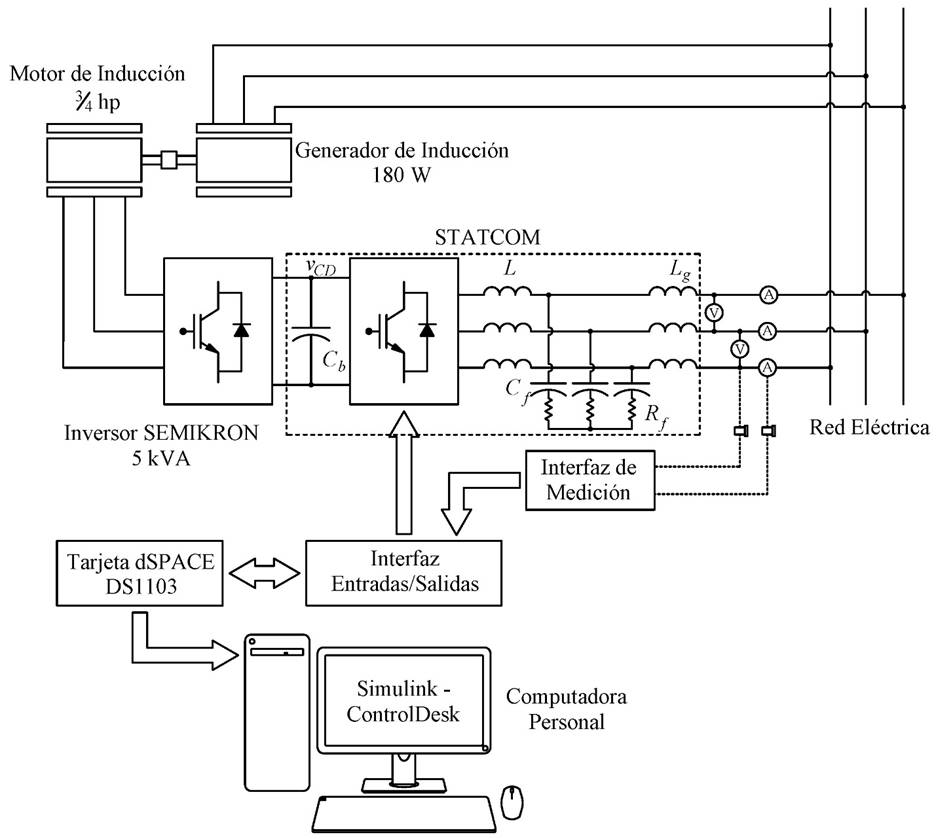
El compensador de potencia reactiva (STATCOM) propuesto, regula con robustez la potencia reactiva que se entrega a un sistema eléctrico de potencia y regula en forma robusta el nivel de voltaje del bus de CD en el inversor trifásico. El STATCOM básicamente está constituido por un inversor trifásico tipo puente, un filtro LCL conectado entre la alimentación trifásica y el inversor, un banco de capacitores conectado en el bus de CD del inversor, como se muestra en la Figura 5. La implementación del sistema STATCOM se realiza con el hardware descrito anteriormente y con el kit DS1103 de dSPACE compuesto por una tarjeta de control y adquisición de datos, una interfaz de entradas/salidas y el software ControlDesk utilizado para visualizar las señales y sintonizar las ganancias del controlador (Figura 5). El programa base del sistema de control del STATCOM se configura en Simulink/MATLAB, con un tiempo de muestreo (paso de solución) de 150 μs, y se compila en la tarjeta de control dSPACE DS1103, las entradas de control se acondicionan con la técnica de modulación de ancho de pulso en el espacio vectorial (SVPWM) para generar los pulsos que activan los IGBT’s del inversor.
El voltaje del sistema de alimentación trifásico es de 220 V de línea a línea, la potencia nominal del sistema es de 1.5 kW, el voltaje del bus de CD de 270 V, el banco de capacitores es de 4200 μF, el motor de inducción es de 3/4 hp. Se sensan dos voltajes de línea a línea y las corrientes en las tres fases de la red eléctrica, además de sensar el voltaje del bus de CD y la corriente en CD entre los dos inversores; estas señales sensadas son utilizadas en el sistema de control del STATCOM. El flujo de potencia activa se realiza mediante un segundo inversor trifásico tipo puente conectado al bus de CD y que alimenta a un motor de inducción jaula de ardilla, marca Baldor M3112 de 3/4 de hp, el cual se acopla mecánicamente con un generador de inducción, marca Lab-Volt 8231-03, para establecer los cambios del par de carga del motor.
La robustez del sistema de control se corrobora ante la presencia de perturbaciones externas que se originan al variar el flujo de potencia activa que alimenta, mediante un inversor conectado al bus de CD, a un motor de inducción con control de velocidad que impulsa a un generador de inducción que se conecta directamente con la red eléctrica. A través del seguimiento de un tren de pulsos arriba de la velocidad de sincronismo, se presentan cambios súbitos en la velocidad de deslizamiento del motor y, en consecuencia, se presentan también cambios súbitos en el par de la carga y en el flujo de potencia activa.
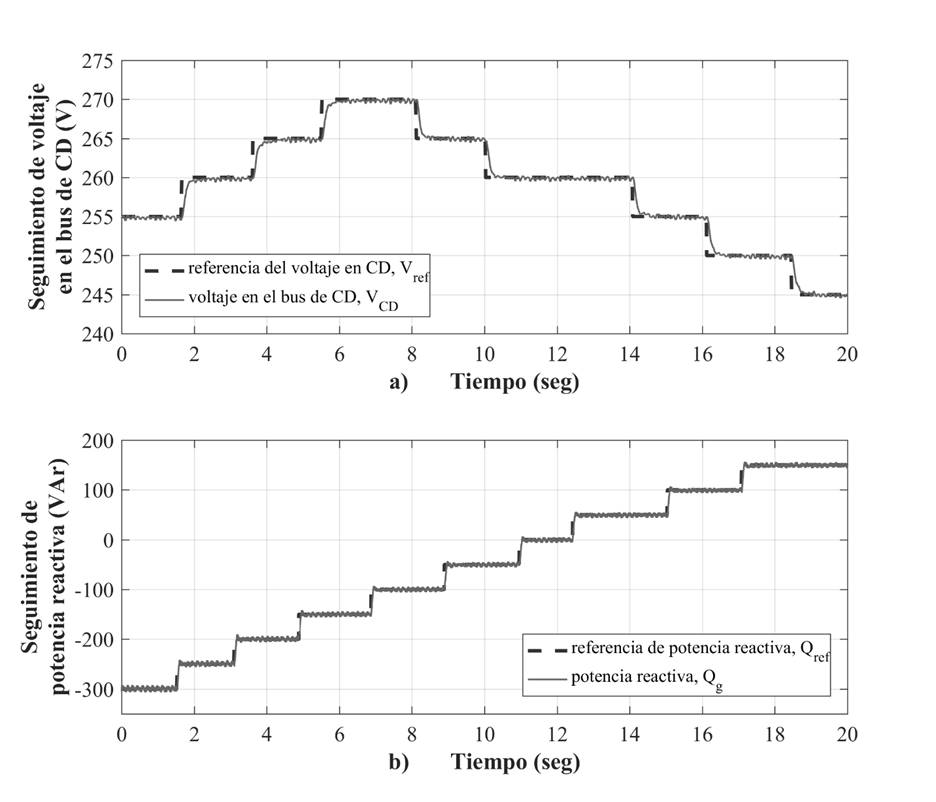
En la Figura 6 se muestran los resultados de la prueba de robustez del STATCOM. En la Figura 6a se muestra el desempeño robusto de la regulación de voltaje del bus de CD del STATCOM, en donde el voltaje de referencia varia de 255 V a 270 V en escalones de 5 V, para posteriormente reducirlo en pasos de 5 V hasta 245 V. La respuesta dinámica del voltaje del bus de CD ante los cambios en escalón del voltaje de referencia no presenta sobreimpulso y tiene un tiempo de restablecimiento promedio de 0.3 s al subir el escalón, y de 0.25 s al bajar el escalón. En cuanto a la regulación de la potencia reactiva, esta se varió a partir de -300 VAr’s en pasos de 50 VAr’s hasta 150 VAr’s, pasando de factor de potencia en adelanto a factor de potencia en atraso, como se muestra en la Figura 6b. La robustez en la regulación de la potencia reactiva se evalúa de acuerdo con su respuesta dinámica ante los cambios en escalón de la potencia de referencia, en donde se presenta un sobreimpulso de 15 % con un tiempo de restablecimiento de 0.15 s.
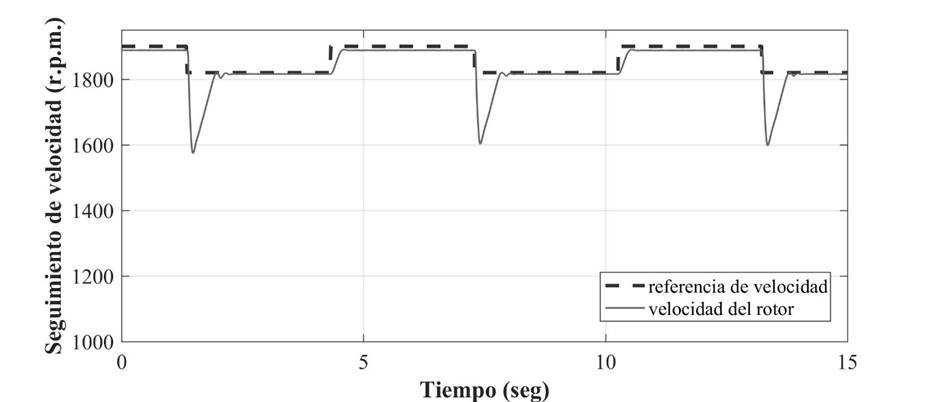
En la Figura 7 se muestra el desempeño del sistema de control del STATCOM en presencia de perturbaciones externas, las cuales son originadas por cambios súbitos en escalón de la potencia activa, al cambiar las condiciones de carga de un motor de inducción. Las perturbaciones externas se originan debido al seguimiento de un tren de pulsos de velocidad de 1820 a 1900 r.p.m. (Figura 8) por parte de un motor de inducción que está acoplado mecánicamente con un generador de inducción, el cual se conecta directamente a la red eléctrica. Con el seguimiento del tren de pulsos por parte del motor, se originan cambios súbitos en la velocidad de deslizamiento y, en consecuencia, se presentan cambios súbitos en el par de carga (par electromagnético del generador) y en el flujo de potencia activa que se entrega a la red eléctrica. A la velocidad de 1820 r.p.m. se presenta el flujo mínimo de potencia activa, mientras que a la velocidad de 1900 r.p.m. se presenta el flujo máximo de potencia.
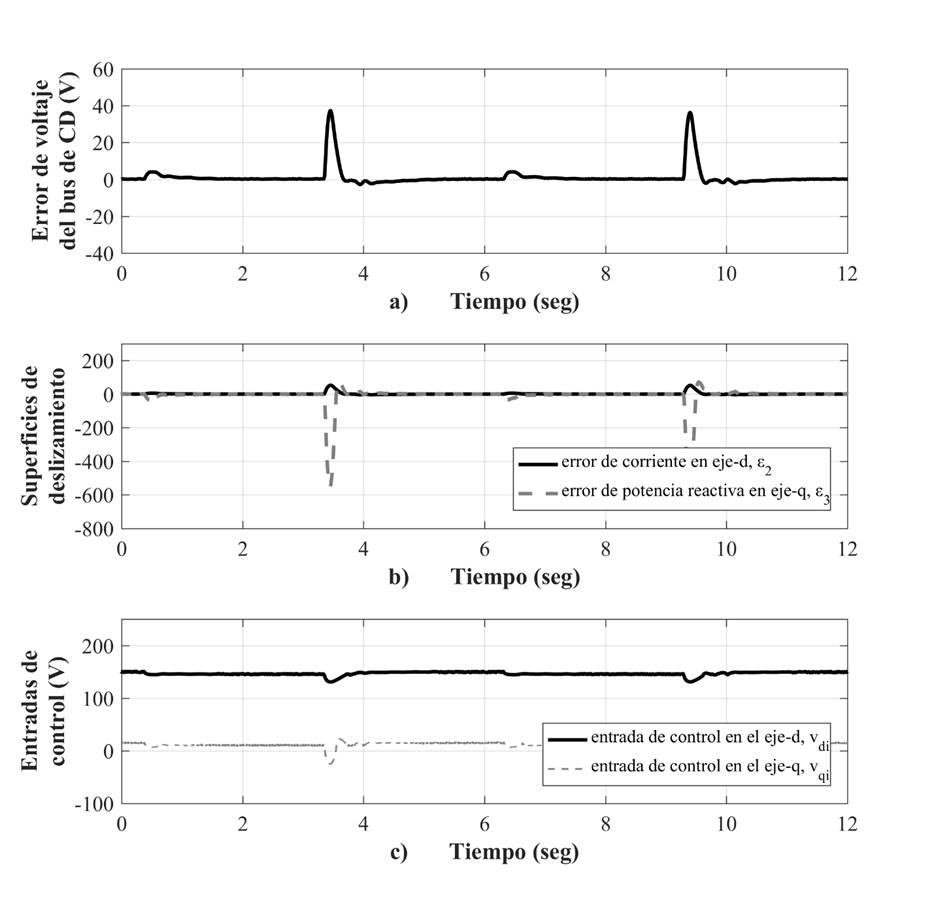
En la Figura 7a se muestran los cambios en el factor de potencia de 0.42 a 0.78 debido a los cambios en la potencia activa, puesto que la potencia reactiva se mantiene regulada en 300 VAr’s, como puede observarse en la Figura 7b, en donde se presenta un sobre impulso de potencia reactiva de 183 % con una duración de 0.35 s, cuando la potencia activa baja, y un sobre impulso de 181 % con una duración de 0.4 s, cuando la potencia activa sube. En la Figura 7c se muestra la robustez en la regulación de voltaje del bus de CD en 270 V, en donde se presenta un sobreimpulso hacia abajo de 13 % con una duración de 0.32 s, cuando se presentan cambios en la potencia activa.
En la Figura 9 se muestran las acciones de control vd y vq del STATCOM. La ley de control super-twisting (20) en el eje d, vd, con un valor de 150 V (Figura 9c) obliga a que se desvanezca la superficie de deslizamiento s2 a cero en tiempo finito cuando se presenta una perturbación (Figura 9b), logrando un movimiento asintótico hacia cero del error de voltaje del bus de CD (Figura 9a). Por otro lado, la acción de control en el eje q, vq, aplicando el algoritmo super-twisting, con un valor de 10 V (Figura 9c), forza directamente el movimiento hacia cero de la superficie s3 (Figura 9a), logrando directamente la regulación de la potencia reactiva en 300 VAr’s que se entregan a la red eléctrica.
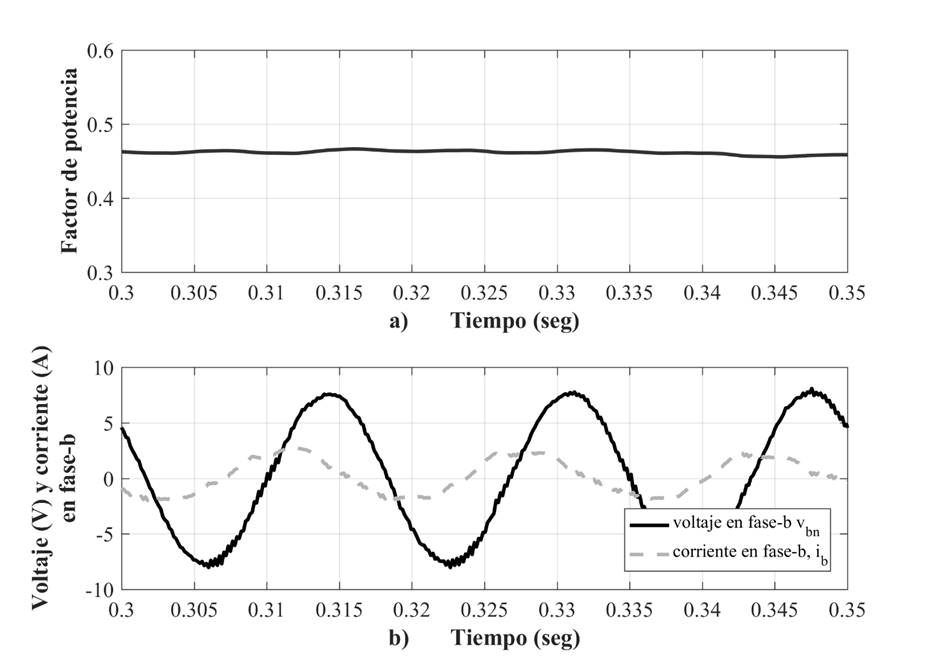
En la Figura 10 se muestra el factor de potencia en adelanto del STATCOM, en donde la corriente tiene un adelanto de 64.67° respecto al voltaje, ambos de la fase b, estableciendo un factor de potencia de 0.46, como consecuencia de los 300 VAr’s que se entregan a la red eléctrica y del flujo de potencia activa que alimenta al motor de inducción. En la Figura 11 se muestran las corrientes y los voltajes de línea a línea vab y vcb, en la red eléctrica, señales que son sensadas para la operación del sistema de control del STATCOM.
En la Figura 12 se muestra el desempeño del acondicionamiento de las señales de control vdi y vqi, utilizando la técnica de modulación de ancho de pulso en el espacio vectorial. En la Figura 12a se muestran los sectores que va abarcando el vector de voltaje resultante que gira a la frecuencia de la red eléctrica, conforme a la secuencia de combinaciones de bits para la activación de los IGBT’s descritos en la Sección IV. En la Figura 12b se muestra el índice de modulación del inversor trifásico tipo puente de 0.76, el cual corresponde a la relación del tiempo de activación T1 de un transistor con el tiempo de muestreo Tp.
Conclusiones
En este trabajo se diseña e implementa experimentalmente el sistema de control para un STATCOM, que tiene como objetivos: regular la potencia reactiva que se entrega a un sistema eléctrico de potencia y el voltaje del bus de CD en forma robusta ante la presencia de perturbaciones externas. Se originaron perturbaciones externas al variar el flujo de potencia activa que alimenta a un motor de inducción con control de seguimiento de velocidad y cambios súbitos en el par de carga. Adicionalmente, se plantea un procedimiento para la caracterización de los parámetros del filtro LCL que se utiliza para reducir el contenido de armónicos en las corrientes. En dicho proceso se ajustan los valores del capacitor y de la resistencia de amortiguamiento del filtro mediante un análisis paramétrico en frecuencia, cuyo resultado se presenta en un diagrama de Bode, con lo que se obtuvo una respuesta suave y sin sobreimpulso en la atenuación de las corrientes a altas frecuencias. Finalmente, mediante resultados experimentales se muestra la efectividad y el desempeño robusto del sistema de control de potencia reactiva del STATCOM ante la presencia de perturbaciones externas. El STATCOM propuesto será utilizado en un trabajo futuro para la corrección del factor de potencia y mejora en la regulación de voltaje de un sistema eléctrico, en donde la generación de energía eléctrica se equilibre con el consumo aplicando compensadores de potencia activa y reactiva. Para lograr esto, es necesario se involucre un administrador de energía, quien define los valores preestablecidos de potencias activa y reactiva en los compensadores al monitorear estas potencias en los puntos de consumo.











 nova página do texto(beta)
nova página do texto(beta)