Introducción
Clasificación de problemas y métodos para elegir la mejor decisión
Los problemas de decisión pueden clasificarse como deterministas o probabilistas. En ambos casos, es posible tener un objetivo o varios. Enseguida se comentan los métodos para obtener la mejor decisión en cada uno de estos casos.
Problemas deterministas con un solo objetivo
Los métodos para alcanzar la decisión óptima en esta situación son: el valor presente neto, la relación beneficio costo, la relación efectividad costo, la tasa interna de retorno y el período de recuperación. En los tres primeros se utiliza una tasa de descuento, en el cuarto se calcula la tasa de rendimiento y en el quinto no se emplea ninguna tasa.
En el sector académico se ha utilizado mucho el criterio del valor presente neto, el cual establece que si es positivo debe aceptarse como rentable un proyecto. Con este criterio es posible determinar, entre varios, el mejor, pero no sirve para priorizarlos.
En el sector público, normalmente se usan las relaciones beneficio costo y efectividad costo. En la primera los beneficios son monetarios y tanto ellos como los costos se actualizan a valor presente. Un proyecto es rentable cuando la relación es mayor que uno. Con este criterio es posible priorizar los proyectos, mientras mayor es la relación es mejor el proyecto. La relación efectividad costo se utiliza cuando no es posible determinar monetariamente los beneficios.
En el sector empresarial se han empleado como criterios de decisión la tasa interna de retorno y el período de recuperación. La tasa interna de retorno es la tasa de descuento que hace que el valor presente neto del proyecto sea igual a cero. Los proyectos son rentables cuando su valor es mayor que la tasa de descuento de la empresa. En general, no es fácil calcular la tasa interna de retorno, por ello se usa mucho el otro criterio, el período de recuperación. Este período es el tiempo en que se recobra la inversión sin actualizar ni los ingresos ni los costos. Mientras menor sea ese período es mejor el proyecto. El cálculo de este criterio es muy sencillo, pero su desventaja consiste en que no considera lo que sucede después de reembolsada la inversión, por lo que pueden quedar excluidos proyectos muy rentables.
Problemas deterministas con varios objetivos
En este caso han proliferado los métodos multicriterio, donde cada autor clama que su método es el mejor, ya que generalmente, conducen a resultados diferentes. Son fáciles de utilizar, incluso muchos de ellos están automatizados, lo cual ha hecho que su aplicación sea muy amplia en problemas reales (Hajkowiczs & Collins, 2007; Cinelli et al., 2014; Balali et al., 2014; De Brito & Evers, 2016). Su principal inconveniente es que puede cambiar la solución óptima al introducir en el análisis una alternativa que no es la mejor.
Un método alternativo que no presenta dicho inconveniente combina el análisis de dominancia con las permutas compensatorias de objetivos (Hammond et al., 2000).
Problemas probabilistas con un solo objetivo
Estos problemas se han analizado con la Teoría de decisiones bayesianas de los pioneros Raiffa (1968) y Schlaifer (1969) de la Universidad de Harvard, quienes consideran problemas con varias etapas para determinar la estrategia óptima que contemple las mejores decisiones, dependiendo de los eventos que vayan ocurriendo. Un libro más reciente sobre este tema es el de Jordaun (2005).
Problemas probabilistas con varios objetivos
En este caso, cuando no se conocen las distribuciones de probabilidad se dice que hay problemas con incertidumbre y, cuando son conocidas, son problemas de riesgo. También puede haber una sola etapa o varias.
Algunos métodos para analizar decisiones en problemas con incertidumbre, eventos discretos y una etapa son: criterio de Laplace, de max-min, de max-max y de lamentos. Estos métodos son sencillos y por ello se han aplicado mucho a problemas reales, no obstante que Raiffa (1968) los describe y muestra claramente que no es conveniente su uso. Posteriormente De Neufville (1990) vuelve a describirlos agregando el criterio de índices ponderados, mostrando de nuevo por qué pueden conducir a decisiones erróneas. El uso de las hojas de cálculo en computadoras los ha hecho muy populares. En vez de usarlos es mejor determinar las funciones de probabilidad y usar el método de la función utilidad con atributos múltiples de Keeney-Raiffa.
Este método puede consultarse en Keeney & Raiffa (1976) o en Acosta (1996).
En cuanto a sus aplicaciones el caso del Aeropuerto de la Ciudad de México es clásico: Fue la primera aplicación importante de dicho enfoque y ha sido publicado extensivamente en Drake et al. (1972) y De Neufville & Marks (1976). El autor de este artículo participó en el estudio dirigido por el M. en I. Jauffred-Mercado Francisco Javier en la entonces Secretaría de Obras Públicas de México, contando con la asesoría de Richard de Neufville, Howard Raiffa y Ralph Keeney.
Algunas aplicaciones adicionales han sido para elegir materiales (Field & De Neufville, 1988); la evaluación sustentable de obras de infraestructura (Gervásio & Da Silva, 2012); elegir un procedimiento para recomendar una liga en Internet (Bai et al., 2017); seleccionar un sistema de protección ante huracanes (Acosta, 2013); asignar tripulación y autobuses en un sistema público de transporte (Sacgut et al., 2017).
Ahora bien, en ingeniería pueden darse problemas como la elección del sitio donde debe construirse una carretera, una presa, un puente o un aeropuerto, donde deben tomarse en consideración además de los aspectos técnicos otros factores como la afectación a la sociedad o al ambiente por las obras que se van a realizar. Las resultantes de tomar decisiones erróneas son de tal magnitud que es fructífero utilizar un método eficiente para analizar sus consecuencias.
Finalidad del algoritmo que se presenta
El enfoque Keeney-Raiffa no es sencillo porque requiere del cálculo de distribuciones conjuntas de probabilidad de diferentes variables y la determinación de funciones utilidad de esas mismas variables. Posiblemente esa dificultad ha conducido a que existan pocas aplicaciones.
Para obviar dicha dificultad elaboramos el algoritmo que presentamos para el caso de decisiones con incertidumbre, o sea, cuando no se conocen las distribuciones de probabilidad y se sugiere utilizar la función densidad uniforme (Acosta, 2019). En este artículo se amplía la aplicación de ese algoritmo al considerar decisiones con riesgo, es decir, cuando ya se conocen las distribuciones de probabilidad. Como dichas distribuciones pueden ser muy variadas, dependiendo del contexto del problema que se esté analizando, se eligieron solamente dos: la distribución triangular y la normal, para mostrar el procedimiento que puede seguir un analista cuando tenga una distribución diferente (Humphreys et al., 2015).
En las tres primeras partes del algoritmo se hace una transformación de las variables aleatorias en deterministas. En la cuarta parte, con dichas variables deterministas se realizan las iteraciones que alternan un análisis de dominancia con las permutas compensatorias (Hammond et al., 2000) hasta que quede solo una de ellas, la cual constituye la solución. El algoritmo siempre converge al resultado óptimo y el número máximo de iteraciones que se requieren es el total de objetivos. Por otra parte, como no está automatizado e interactúan el analista con el decisor no es relevante la duración del procedimiento.
Metodología
Utilidad esperada con varios objetivos
Para comparar las decisiones se calcula la utilidad esperada para cada una de ellas y se elige la decisión que tenga la utilidad más grande.
La utilidad esperada de una decisión con varios objetivos es la integral del producto de la distribución conjunta de las medidas de efectividad de los objetivos por la utilidad conjunta de los mismos.
Luego, cuando se tiene un solo objetivo, la utilidad esperada de una decisión es la integral del producto de la distribución de la medida de efectividad de ese objetivo por la utilidad de esa medida de efectividad.
Equivalente bajo certeza
Se define como Equivalente Bajo Certeza de una decisión aquella cantidad cuya utilidad es igual a la utilidad esperada de esa decisión.
En cuanto se conocen los Equivalentes Bajo Certeza (EBC) pueden usarse en lugar de las situaciones probabilistas. Enseguida se presenta su cálculo para las distribuciones normal y triangular, ambas para variables continuas.
Distribución normal
Preferencias crecientes y aversión constante al riesgo
Para calcular el equivalente bajo certeza se requiere la función utilidad que representa la estructura de preferencia del decisor y la función densidad de probabilidad. La función utilidad se obtiene de la Tabla 1. Esta tabla fue elaborada a partir del libro de Keeney y Raiffa (1976). En ella se presentan las funciones utilidad que corresponden a los comportamientos de aversión constante, neutralidad y propensión constante cuando dichas funciones son monotónicas crecientes, es decir, cuando valores mayores se prefieren más y cuando son monotónicas decrecientes, cuando valores mayores se prefieren menos.
Tabla 1: Función utilidad u(x), con c > 0
| Monotónica creciente | Monotónica decreciente | |
|---|---|---|
| Aversión constante | -e-cx | -ecx |
| Neutralidad | x | -x |
| Propensión constante | ecx | e-cx |
Si el decisor tiene aversión constante al riesgo y sus preferencias son monotónicas crecientes, de la Tabla 1 su función utilidad es:
donde c es un parámetro positivo.
Cuando la función densidad de probabilidad es normal se tiene:
En esta función, x es la variable aleatoria con media m y desviación estándar σ.
Ahora bien, por definición el decisor es indiferente entre el Equivalente Bajo Certeza (EBC) y la lotería (L) asociada. Si es indiferente entre ellos, quiere decir que la utilidad que el percibe de EBC y L debe ser la misma, es decir:
La utilidad de una lotería se considera como la utilidad esperada de sus consecuencias x, luego:
Sustituyendo u(x) y f(x) en la ecuación anterior se obtiene:
Sacando las constantes de la integral queda:
Utilizaremos una nueva variable y, definida como:
Despejando a x:
Derivando la ecuación (3) respecto a x se obtiene:
Sustituyendo (3), (4) y (5) en (2):
Completando el binomio al cuadrado en el exponente y sacando las constantes fuera de la integral la ecuación queda:
Se define una variable nueva:
Derivando se obtiene:
Sustituyendo (7) y (8) en (6):
Se conoce que la función
Sustituyendo (10) en (9) queda:
Puesto que
Ya que existe indiferencia entre la lotería L y su equivalente bajo certeza EBC, sus utilidades deben ser iguales, es decir, (11) debe ser igual a (12)
Si se multiplican por -1 ambos lados de la ecuación anterior y se calcula, también en ambos lados, el logaritmo natural, se tiene
Despejando EBC, nos da
Preferencias crecientes y propensión constante al riesgo
En este caso, de la Tabla 2,
Tabla 2: Equivalentes bajo certeza, EBC, cuando la distribución es normal
| u(x) es monotónica creciente | u(x) es monotónica decreciente | |
|---|---|---|
| Aversión constante | m-cσ2/2 | m+cσ2/2 |
| Neutralidad | m | m |
| Propensión constante | m+cσ2/2 | m-cσ2/2 |
Haciendo los cálculos del caso anterior usando la nueva u(x) se obtiene:
Preferencias crecientes y neutralidad al riesgo
Para el caso de neutralidad al riesgo usando la Tabla 2 se conoce que u(x)=x.
De manera que
La media de una función densidad de probabilidad es la esperanza de la variable,
luego
Por lo anterior
Puesto que
Preferencias decrecientes y aversión constante al riesgo
En este caso, de la Tabla 2,
Haciendo los cálculos que se hicieron cuando las preferencias eran crecientes y usando la nueva u(x) se obtiene:
Preferencias decrecientes y propensión constante al riesgo
En este caso, de la Tabla 2,
Haciendo los cálculos que se hicieron cuando las preferencias eran crecientes y usando la nueva u(x) se obtiene:
Preferencias decrecientes y neutralidad al riesgo
Con preferencias decrecientes y neutralidad al riesgo, usando la Tabla 2,
De manera que:
Igualando (15) y (16) queda
Los resultados anteriores se presentan en la Tabla 2.
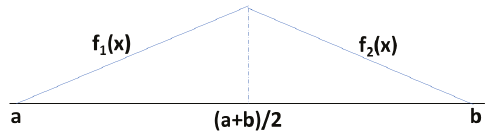
Distribución triangular
En la Figura 1 se muestra la función densidad de probabilidad triangular empleada donde:
cuando los valores de la medida de efectividad x están entre a y a+b/2; y cero cuando están fuera de ese rango.
Y
Para obtener los equivalentes bajo certeza usando esta distribución triangular se hizo un desarrollo semejante al caso de la distribución normal. Los resultados se presentan en la Tabla 3.
Tabla 3: Equivalentes bajo certeza, EBC, con función densidad de probabilidad triangular
| u(x) es monotónica creciente | u(x) es monotónica decreciente | |
|---|---|---|
| Aversión constante | (-1/c)Ln(4(e-ca + e-cb - 2 e-c(a+b)/2 )/(c2(b - a)2)) | (1/c)Ln(4(eca + ecb -2ec(a+b)/2 )/(c2(b - a)2)) |
| Neutralidad | (b + a)/2 | (b + a)/2 |
| Propensión constante | (1/c)Ln(4(eca + ecb -2ec(a+b)/2 )/(c2(b - a)2)) | (-1/c)Ln(4(e-ca + e-cb - 2 e-c(a+b)/2 )/(c2(b - a)2)) |
Distribución uniforme
El Equivalente bajo certeza para la distribución uniforme lo calculamos en nuestro primer artículo (Acosta, 2019) aquí simplemente lo copiamos en la Tabla 4.
Tabla 4: Equivalentes bajo certeza, EBC, con distribución uniforme
| u(x) es monotónica creciente | u(x) es monotónica decreciente | |
|---|---|---|
| Aversión constante | (-1/c)Ln((e-cb - e-ca )/(c(a - b)) | (1/c)Ln((ecb - eca )/(c(b - a)) |
| Neutralidad | (b + a)/2 | (b + a)/2 |
| Propensión constante | (1/c)Ln((ecb - eca )/(c(b - a)) | (-1/c)Ln((e-cb - e-ca )/(c(a - b)) |
Función utilidad para un solo objetivo
Esta función u(x) representa el comportamiento del decisor y está en función del parámetro c.
Para determinar el valor de dicho parámetro se establece el rango de valores de
la variable x. Sea este
Si la función utilidad de x fuera monotónica creciente en
preferencias, como por ejemplo en ganancias, donde mientras más grande es la
ganancia la preferimos más, pueden darse tres casos al comparar
EBCL con la esperanza de la lotería,
Para el primer caso, donde
La ecuación anterior tiene solamente como incógnita el valor de c > 0. Al resolverla se obtiene dicho valor.
En el segundo caso u(x)=x, por lo que no existe el parámetro c.
En el tercer caso,
Si la función utilidad de x fuera monotónica decreciente en
preferencias, como por ejemplo en costos, donde mientras mayor sea el costo lo
preferimos menos, también pueden darse tres casos al comparar
EBCL con la esperanza de la lotería,
Para el primer caso, aversión al riesgo, donde
En el segundo caso, neutralidad al riesgo, u(x)=-x, por lo que no existe el parámetro c.
En el tercer caso, propensión al riesgo,
Tabla 5: Ecuaciones para determinar el parámetro c > 0
| u(x) es monotónica creciente | u(x) es monotónica decreciente | |
|---|---|---|
| Aversión constante |
|
|
| Neutralidad | No hay parámetro c | No hay parámetro c |
| Propensión constante |
|
|
Vemos en la tabla que cuando existe aversión o propensión se tiene una ecuación con una sola incógnita. Esta ecuación permite obtener el valor de c por ensayo y error. Una de sus raíces es cero, pero este valor no es útil porque recordemos que c debe ser mayor que cero.
Finalmente, se muestra el algoritmo modificado, ilustrando su uso mediante dos ejemplos hipotéticos, el primero donde se encuentran las mejores inversiones para cada uno de tres inversionistas y el segundo, donde se determina la mejor localización de un aeropuerto.
Algoritmo para analizar decisiones con objetivos múltiples, riesgo e incertidumbre
Parte uno. Definición de objetivos y medidas de efectividad:
Paso 1-1. Defina el horizonte de planeación, así como los objetivos.
Paso 1-2. Para cada objetivo, determine la o las medidas de efectividad que permitirán conocer su logro.
Paso 1-3. Establezca para todas las medidas de efectividad si son monotónicas crecientes o decrecientes.
Parte dos. Estipulación de alternativas y parámetros:
Paso 2-1. Estipule las alternativas.
Paso 2-2. Para cada alternativa precise el límite inferior (a) y el límite superior (b) de cada medida de efectividad.
Paso 2-3. Para cada medida de efectividad calcule a* como el menor de todos los límites a; y b* como el mayor de los límites b.
Paso 2-4. Para cada medida de efectividad forme la lotería cuyas consecuencias son a* y b*, con probabilidades de 0.5 cada una. Pídale al decisor su equivalente bajo certeza (EBC) de cada una de esas loterías. Calcule el valor esperado (VE) de la lotería. Si la medida de efectividad es monotónica creciente y VE > EBC entonces se tiene un comportamiento de aversión al riesgo; si VE = EBC, el comportamiento es de neutralidad al riesgo; y si VE < EBC es de propensión al riesgo. Si la medida de efectividad es monotónica decreciente y VE > EBC entonces se tiene propensión al riesgo; si VE = EBC, neutralidad al riesgo; y si VE < EBC aversión al riesgo. Conociendo lo anterior determine, para cada medida de efectividad, su u(x) en la Tabla 1.
Paso 2-5. Para cada medida de efectividad con aversión o propensión al riesgo formule la ecuación u(EBC) = 0.5u(a*) + 0.5u(b*), la cual es una ecuación con una sola incógnita, el parámetro c. Resuelva dicha ecuación (para determinar la ecuación, consulte la Tabla 5).
Paso 2-6. Si la distribución es uniforme o triangular vaya al Paso
3-1; si es normal, antes de continuar con el Paso 3-1 calcule
Parte tres. Cálculo numérico de los equivalentes bajo certeza:
Paso 3-1. Para cada alternativa y para cada medida de efectividad compute el valor numérico del equivalente bajo certeza (EBC) utilizando las fórmulas de las Tablas: 2 para distribución normal, 3 para distribución triangular y 4 para distribución uniforme. Presente los resultados en una tabla donde los renglones sean las alternativas y las columnas las medidas de efectividad.
Parte cuatro. Selección de la mejor alternativa:
Paso 4-1. Encuentre y elimine las alternativas dominadas. La alternativa A domina a la B cuando A es mejor que B en algunas medidas de efectividad y en todas los demás es igual que B.
Paso 4-2. ¿Queda solo una alternativa? en caso afirmativo, esa alternativa es la mejor opción y termina el algoritmo. Si no es así habrá que continuar con el Paso 4-3.
Paso 4-3. Haga permutas compensatorias para eliminar una medida de efectividad. Cuando se haya eliminado esa medida de efectividad regrese al Paso 4-1.
Enseguida se presentan los ejemplos que ilustran la aplicación del algoritmo.
Ejemplos hipotéticos
Análisis de inversiones
Se tienen tres inversionistas, Daniel, Delia y Pedro. Existen seis inversiones que deberá jerarquizar cada inversionista.
Los rendimientos de las inversiones son aleatorios con distribuciones normales. En la Tabla 6 se presentan los rangos de las inversiones con sus rendimientos correspondientes, en Valor Presente Neto (VPN), en miles de pesos.
Tabla 6: Rango de variación del VPN de la inversión más sus rendimientos, en miles de pesos
| Inversión | a =Límite inferior | b =Límite superior |
|---|---|---|
| A | 70,000 | 90,000 |
| B | 80,000 | 120,000 |
| C | 75,000 | 115,000 |
| D | 85,000 | 95,000 |
| E | 75,000 | 90,000 |
| F | 90,000 | 110,000 |
Posteriormente se aplicará el algoritmo propuesto.
Paso 1-1. Se ha establecido un horizonte de planeación de diez años. El objetivo es maximizar el Valor Presente Neto de la inversión más sus rendimientos.
Paso 1-2. La medida de efectividad es el Valor Presente Neto en miles de pesos.
Paso 1-3. Como mientras mayor es el Valor Presente Neto lo preferimos más, dicha medida de efectividad es monotónica creciente.
Paso 2-1. Las inversiones alternativas son: A, B, C, D, E y F.
Paso 2-2. Ambos límites, inferior (a) y superior (b), de cada alternativa están en la Tabla 6.
Paso 2-3. En dicha tabla puede observarse que el mínimo de los
límites inferiores,
Paso 2-4. Con esos valores mínimo y máximo se forma la lotería L asignándoles una probabilidad de 0.5 a cada uno de ellos, como se muestra en la Figura 2.
Ahora se le pide a Daniel que nos diga la mínima cantidad que estaría dispuesto a aceptar a cambio de la lotería L
Daniel contestó que 90,000 pesos sería lo mínimo que estaría dispuesto a aceptar
a cambio de dicha lotería, por lo que su equivalente bajo certeza,
Calculando el valor esperado de la lotería L, VE, se obtiene:
Como
Ahora se le pide a Delia, que especifique lo mínimo que estaría dispuesta a
aceptar a cambio de la misma lotería L. Su respuesta fue de 105,000 pesos, por
lo que su equivalente bajo certeza,
Como
Finalmente, se le hace a Pedro la misma pregunta que a Daniel y a Delia. Su
respuesta fue 95,000. Entonces
Paso 2-5. Ya que la función utilidad es monotónica creciente, la ecuación a resolver para Daniel en la Tabla 5 es:
Sustituyendo en ella los valores de EBCL,
Que es una ecuación con una sola incógnita. Su solución es c = 0.00001644.
Como Delia tiene propensión al riesgo y puesto que su función utilidad continúa siendo monotónica creciente, la ecuación a resolver de la Tabla 1 es:
Sustituyendo en ella los valores de EBCL,
Que es una ecuación con una sola incógnita. Su solución es c = 0.00003611.
En cuanto a Pedro, por tener un comportamiento de neutralidad al riesgo su función utilidad no tiene ningún parámetro c.
Paso 2-6. Ahora se obtendrán los valores de m y
σ de cada inversión usando las ecuaciones
Estos valores se muestran en la Tabla 7.
Tabla 7: Valores de m y σ en miles de pesos
| Inversión | a | b | m | σ |
|---|---|---|---|---|
| A | 70,000 | 90,000 | 80,000 | 2,778 |
| B | 80,000 | 120,000 | 100,000 | 5,556 |
| C | 75,000 | 115,000 | 95,000 | 5,556 |
| D | 85,000 | 95,000 | 90,000 | 1,389 |
| E | 75,000 | 90,000 | 82,500 | 2,083 |
| F | 90,000 | 110,000 | 100,000 | 2,778 |
Paso 3-1. Como la distribución es normal se usa la Tabla 2 que contiene las expresiones que permiten calcular los equivalentes bajo certeza de los tres inversionistas. Esas expresiones son:
Los valores numéricos se muestran en la Tabla 8.
Tabla 8: Equivalentes bajo certeza, en VPN y miles de pesos
| Inversión | EBCDaniel | EBCDelia | EBCPedro |
|---|---|---|---|
| A | 79,937 | 80,139 | 80,000 |
| B | 99,746 | 100,557 | 100,000 |
| C | 94,746 | 95,557 | 95,000 |
| D | 89,984 | 90,035 | 90,000 |
| E | 82,464 | 82,578 | 82,500 |
| F | 99,937 | 100,139 | 100,000 |
Paso 4-1. En el caso de Daniel la inversión F domina a las demás. Para Delia la inversión B domina a las otras. Y para Pedro las inversiones B y F dominan a las restantes.
Paso 4-2. Para Daniel su mejor opción es la inversión F; para Delia su mejor opción es la B; y para Pedro como B y F tienen el mismo VPN, ambas constituyen su mejor opción.
Elección del mejor sitio para situar un aeropuerto
En este ejemplo se ha supuesto que todas las opciones disponibles proveen la capacidad adecuada para satisfacer las demandas de aviones; también que todas las alternativas ofrecen la misma seguridad del sistema; así como que tienen los mismos efectos por la contaminación de ruido debido al tránsito aéreo.
Se aplicarán los pasos del Algoritmo.
Paso 1-1. El horizonte de planeación es de 30 años y se cuenta con los tres objetivos siguientes:
Minimizar los costos totales de construcción y mantenimiento.
Minimizar la perturbación social causada por la provisión de nuevas instalaciones aeroportuarias.
Minimizar el tiempo de acceso al aeropuerto.
Paso 1-2. Las medidas de efectividad respectivas para esos tres objetivos son:
ME1. Costo total a valor presente en millones de pesos.
ME2. Número de personas desplazadas de sus hogares o lugares de trabajo por el desarrollo del aeropuerto.
ME3. Tiempo de acceso a y desde el aeropuerto en minutos ponderados por el número de viajeros en cada zona de la ciudad analizada.
Paso 1-3. Las tres medidas de efectividad son monotónicas decrecientes.
Paso 2-1. Se ha determinado técnicamente que existen dos sitios posibles para construir el aeropuerto, el sitio U y el V. Considerando que se pueden construir instalaciones para alojar vuelos comerciales internacionales, comerciales nacionales, generales y militares se han determinado las alternativas que se muestran en la Tabla 9, donde cada alternativa contempla las acciones para ambos sitios. En dicha tabla no están otras combinaciones por considerarse técnicamente inviables.
Tabla 9: Alternativas de construcción del aeropuerto
| Alternativas | Sitio U | Sitio V |
|---|---|---|
| A | Internacional, nacional, general y militar | No se construye nada |
| B | Nacional, general y militar | Internacional |
| C | Internacional | Nacional, general y militar |
| D | Nacional y militar | Internacional y general |
| E | Internacional y general | Nacional y militar |
| F | No se construye nada | Internacional, nacional, general y militar |
Paso 2-2. En el Paso 1-2 se establecieron las tres medidas de efectividad siguientes: ME1. Costo total a valor presente en millones de pesos; ME2. Número de personas desplazadas de sus hogares o lugares de trabajo por el desarrollo del aeropuerto; y ME3. Tiempo de acceso a y desde el aeropuerto en minutos ponderados por el número de viajeros en cada zona de la ciudad considerada.
Al analizar el comportamiento de dichas medidas de efectividad se encontró que las tres son variables aleatorias con distribución normal. En la Tabla 10 se presentan los límites (a, inferior y b, superior) de cada medida de efectividad para cada alternativa.
Tabla 10: Límites de las medidas de efectividad
| Alternativas | ME1 | ME2 | ME3 | |||
|---|---|---|---|---|---|---|
| a | b | a | b | a | b | |
| A | 500 | 3000 | 2500 | 10000 | 70 | 90 |
| B | 2000 | 4000 | 100000 | 250000 | 12 | 15 |
| C | 1100 | 3400 | 41500 | 106000 | 47 | 60 |
| D | 1400 | 3600 | 61000 | 154000 | 35 | 45 |
| E | 1325 | 3550 | 56125 | 142000 | 38 | 49 |
| F | 1175 | 3450 | 46375 | 118000 | 44 | 56 |
Paso 2-3. En dicha tabla puede observarse que para la medida de
efectividad 1, el mínimo de los límites inferiores,
Paso 2-4. Para la medida de efectividad 1, costo total en
millones de pesos, se formó la lotería
Se le preguntó al decisor lo máximo que estaría dispuesto a pagar para no tener
que jugar dicha lotería. Su contestación fue 3,200. Por lo anterior EBC = 3,200
se calculó el valor esperado de dicha lotería VE = 0.5(500) + 0.5(4000) =2,250.
Como EBC > VE y la preferencia es monotónica decreciente, entonces para esta
medida de efectividad el decisor tiene aversión al riesgo y su función utilidad
es
Para la medida de efectividad 2, número de personas desplazadas, se formó la
lotería
Finalmente, para la medida de efectividad 3, tiempo de acceso en minutos, se
formó la lotería
Paso 2-5. Para la medida de efectividad 1, la ecuación para
determinar el valor de c es
Para la medida de efectividad 3, la ecuación para determinar el valor de c es
Paso 2-6. Como las tres medidas de efectividad son normales se calculó su media y su desviación estándar para cada una de las alternativas. Los resultados están en la Tabla 11.
Tabla 11: Media y desviación estándar
| Alternativas | ME1 | ME2 | ME3 | |||
|---|---|---|---|---|---|---|
| m | σ | m | σ | m | σ | |
| A | 1750 | 347.22 | 6250 | 1041.67 | 80 | 2.78 |
| B | 3000 | 277.78 | 175000 | 20833.33 | 13.5 | .42 |
| C | 2250 | 319.44 | 73750 | 8958.33 | 53.5 | 1.81 |
| D | 2500 | 305.56 | 107500 | 12916.67 | 40 | 1.39 |
| E | 2437.5 | 309.03 | 99062.5 | 11927.08 | 43.5 | 1.53 |
| F | 2312.5 | 315.97 | 82187.5 | 9947.2 | 50 | 1.67 |
Paso 3-1. Ya que el decisor tiene un comportamiento de aversión
constante al riesgo en las medidas de efectividad 1 y 3, y de neutralidad en la
medida 2; las tres funciones utilidad son monotónicas decrecientes y la
distribución de probabilidad de las tres medidas es la normal, entonces usando
la Tabla 2 se obtiene que
Tabla 12: Equivalentes bajo certeza, EBC, para cada medida de efectividad
| Alternativas | ME1 | ME2 | ME3 |
|---|---|---|---|
| A | 1798 | 6250 | 80 |
| B | 3030 | 175000 | 14 |
| C | 2290 | 73750 | 54 |
| D | 2537 | 107500 | 40 |
| E | 2475 | 99063 | 44 |
| F | 2351 | 82188 | 50 |
Paso 4-1. Ninguna alternativa domina a otra, por lo que continuamos con el Paso 4-2.
Paso 4-2. Hay seis alternativas por lo que seguimos al Paso 4-3.
Paso 4-3. Mediante permutas compensatorias todas las alternativas tendrán un tiempo de acceso igual a 14 minutos. El decisor consideró que para ello en la alternativa A estaría dispuesto a incrementar el costo en 660 millones; en la C en 400 millones; en la D en 260 millones; en la E en 300 millones; y en la F en 360 millones. Aplicando lo anterior es posible eliminar la medida de efectividad 3 y los nuevos valores de EBC se muestran en la Tabla 13.
Tabla 13: Equivalentes bajo certeza, EBC
| Alternativas | ME1 | ME2 |
|---|---|---|
| A | 1798+660=2458 | 6250 |
| B | 3030 | 175000 |
| C | 2290+400=2690 | 73750 |
| D | 2537+260=2797 | 107500 |
| E | 2475+300=2775 | 99063 |
| F | 2351+360=2711 | 82188 |
Paso 4-4. Ahora la alternativa A domina a las demás, por lo que se eliminan.
Paso 4-5. Como solo resta la alternativa A, ella es la solución.
Conclusiones
Se complementó el algoritmo desarrollado originalmente (Acosta, 2019) para considerar además de la situación con incertidumbre con distribuciones de probabilidad uniformes, la situación bajo riesgo. Se contemplaron las distribuciones de probabilidad normales y triangulares al realizar el cálculo de los equivalentes bajo certeza para esas distribuciones, con lo que se expandió el rango de aplicación de dicho algoritmo. Asimismo se presentó la determinación del parámetro “c”, que se encuentra en las funciones de utilidad que representan el comportamiento del decisor cuando tiene aversión o propensión al riesgo. Finalmente, se ilustró el uso del algoritmo modificado mediante dos ejemplos hipotéticos.
En el primer ejemplo se encontraron las mejores inversiones para cada uno de los tres inversionistas considerados. Como cada uno de ellos tenía un comportamiento al riesgo diferente no existe alguna razón para que sus mejores decisiones coincidan. Las mejores decisiones para una compañía pequeña, que no puede afrontar mucho riesgo, son diferentes a las de compañías más grandes, con mayores recursos. En el segundo ejemplo, se determinó la mejor localización de un aeropuerto. En ambos estuvo implícito el uso del principio de “dividir y conquistar” puesto que se le pidió al decisor que tomara decisiones en problemas hipotéticos simples, usando sus respuestas para llegar a la solución del problema original, obviamente más complejo que los anteriores.
Este algoritmo es útil cuando existe un solo decisor, una sola etapa y las distribuciones de probabilidad son la normal, la triangular o la uniforme. Si en el problema que se estuviese analizando las distribuciones fuesen diferentes, este artículo presenta el procedimiento para que el analista pueda determinar los valores de los equivalentes bajo certeza requeridos. De igual forma, es conveniente señalar que proporciona la solución óptima, pero no permite priorizar las diferentes opciones.











 text new page (beta)
text new page (beta)