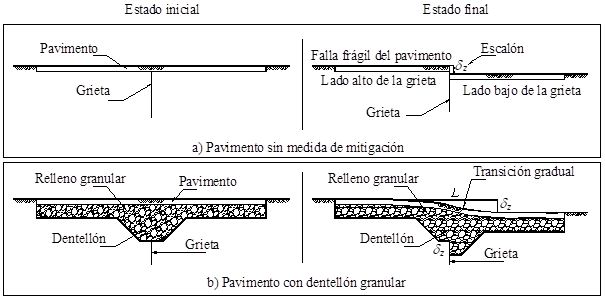Introducción

Desde hace varios decenios, se han observado grietas en el suelo de la Ciudad de México, principalmente en las alcaldías de Iztapalapa, Tláhuac, Xochimilco y Milpa Alta. Estas grietas inducen daños en las edificaciones, servicios públicos y vialidades que ponen en riesgo el bienestar de los pobladores, además de requerir costos de mantenimiento importantes.

Una grieta se puede iniciar a consecuencia de cualquier condición que genere esfuerzos de tensión importantes en el suelo (^{Auvinet, 2010}; ^{Auvinet et al., 2013a}, ^2013b, ²⁰¹⁷, ²⁰¹⁸). Ciertos mecanismos como el fracturamiento hidráulico facilitan la generación y propagación de las grietas. Sin embargo, las grietas más importantes y destructivas son causadas por los asentamientos diferenciales asociados al hundimiento regional debido a la extracción de agua en el subsuelo del valle de México. El fenómeno de agrietamiento se ha agravado a raíz de los sismos de septiembre de 2017 y se han observado algunos escalones que rebasan 1 m de altura. Las grietas se vuelven más problemáticas cuando se erosionan y ensanchan, por lo que es preferible sellarlas inmediatamente para restablecer la continuidad del terreno.

Las grietas por hundimiento regional se caracterizan por presentar escalones con la parte baja hacia la zona de mayor asentamiento (Figura 1) y en la práctica son muy difíciles de controlar (^{Auvinet, 2017}).

Figura 1: Grieta con escalón en una vialidad de la Ciudad de México 

Para reducir los daños a las edificaciones, servicios públicos y vialidades se debe tomar en cuenta la presencia de las grietas en el diseño. Para muros y bardas ha resultado útil el uso de juntas que permiten el paso libre de la grieta. Sin embargo, estas medidas de mitigación de daños se han implementado en forma empírica y no se han realizado estudios orientados al diseño de estas soluciones. Las medidas de mitigación de los daños ocasionados por la propagación de las grietas deben basarse en soluciones estructurales y geotécnicas robustas. Entre estas últimas se encuentran las basadas en la disipación del escalón en la superficie del terreno para mitigar daños en calles y vialidades. Las soluciones presentadas en este trabajo están exclusivamente relacionadas con el problema del escalón en la superficie del terreno. Las soluciones propuestas se evalúan mediante análisis numéricos basados en el enfoque de medios discontinuos (método de elementos discretos) que se comparan con los que se pueden realizar aplicando la mecánica de los medios continuos (método de elementos finitos).

Solución propuesta

Se ha observado que un material continuo en la superficie del terreno, como el pavimento de las vialidades, presenta una falla frágil en presencia de hundimientos diferenciales (Figura 1 y 2a), provocando un escalón abrupto. El concepto principal en la solución propuesta es sustituir superficialmente el terreno natural por material granular, como arena o grava sin finos, que no transmita tensiones y cuyos granos se reacomoden ante el movimiento de la grieta (Figura 2b).

Figura 2: Comportamiento hipotético de un dentellón para el control de hundimientos diferenciales 

Más adelante, esta solución se evalúa por medio de simulaciones numéricas con modelos de elementos discretos y modelos numéricos tradicionales con elementos finitos. En los análisis, se considera la existencia de una grieta en una vialidad y se agrega un dentellón en la parte superior de la grieta.

La geometría propuesta para el modelo de análisis se presenta en la Figura 3. Las dimensiones horizontales del modelo son suficientes para permitir el libre desarrollo de los asentamientos. La simulación de la formación de un escalón en la grieta consiste en imponer un desplazamiento vertical δ _z a la mitad del lado derecho del modelo y en restringir el desplazamiento del lado izquierdo. Se consideran desplazamientos verticales δ _z en la grieta de 0.1, 0.2 y 0.3 m.

Figura 3: Modelo con dentellón de arena 

Modelado con enfoque de medios discontinuos

El método de elementos discretos (^{Cundall y Strack, 1979}), DEM por sus siglas en inglés, permite simular la interacción mecánica entre un conjunto de partículas independientes, de acuerdo con un modelo reológico de contacto. En el caso de las arenas, las fuerzas de interacción en los contactos entre granos se rigen por la fricción en su superficie. Las partículas se representan por discos o esferas rígidos, con una densidad ρ= 2600 kg/m³ y un coeficiente de fricción μ = 0.7 (equivalente a un ángulo de fricción interparticular ϕμ = 35 °). Se realizan simulaciones bidimensionales (2D) y tridimensionales (3D).

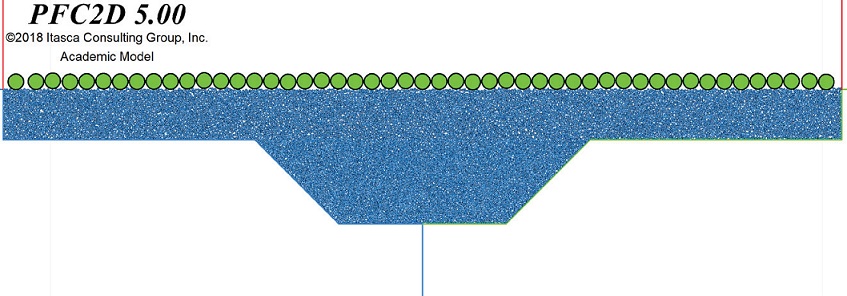
Para simular el problema de interés, se seleccionan las partículas de acuerdo con una granulometría relativamente uniforme (Coeficiente de uniformidad Cu=2), se depositan por gravedad y se deja que la muestra alcance el equilibrio. Se nivela la superficie y se colocan las partículas que representan el pavimento (Figura 4). Posteriormente, para simular un incremento en el escalón de la grieta, el lado derecho del modelo se desplaza hacia abajo hasta un valor δ _z dado. La velocidad del desplazamiento es muy baja para evitar efectos de inercia.

Figura 4: Modelo DEM 2D con dentellón de arena 

Por prueba y error se determinó que los taludes apropiados del dentellón son de 1:1. El ancho de la base puede ser el mínimo permitido por la herramienta de excavación. Es conveniente que el dentellón se encuentre centrado horizontalmente sobre la grieta.

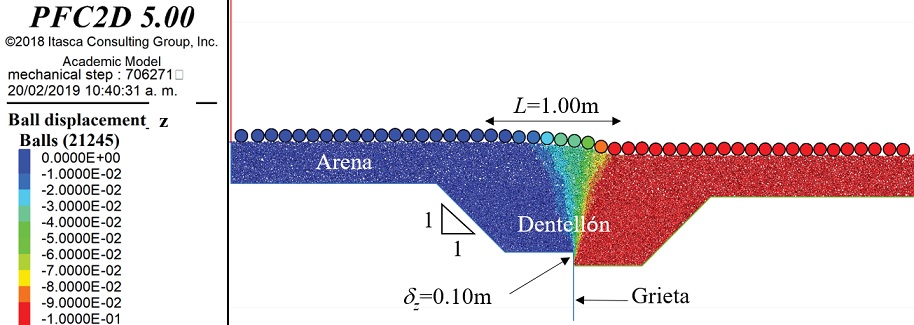
En la Figura 5 se presentan los desplazamientos verticales de las partículas. Se observa que en el ápice de la grieta se presenta un escalón, pero que en la superficie se tiene una pendiente suave como se suponía en la Figura 2b. Esto es resultado de los movimientos individuales de las partículas de la arena.

Figura 5: Desplazamientos verticales para δ_z = 0.10 m. Modelo DEM 2D con dentellón de arena 

Se observa también que, en la mayor parte del modelo, las partículas conservan sus posiciones relativas. En el lado alto de la grieta, las partículas permanecen estáticas (δ_z = 0) y en el lado bajo casi todas las partículas bajan junto con la frontera móvil que las subyace (δ _z = 0.1 m).

Los desplazamientos verticales diferenciales ocurren en la zona cercana a la grieta. La Figura 5 muestra que la longitud horizontal L, en la que se distribuyen los desplazamientos diferenciales verticales crece verticalmente. La forma en “V” de los colores de igual desplazamiento vertical indica que entre más profunda se encuentre la grieta (mayor espesor del dentellón granular), será menor la deformación unitaria δ_z /L en la superficie del terreno.

Considerando un dentellón granular de 0.5 m de profundidad y para un escalón en la grieta δ_z = 0.1 m, en el ápice de esta L = 0, mientras que, en la superficie del modelo, L = 1.00 m. Por tanto, la deformación unitaria δ_z /L es infinita en la grieta, pero en la superficie del modelo es 0.10. Para estos cálculos se desprecian desplazamientos diferenciales verticales menores que 0.001 m.

Se probaron diferentes posiciones de la grieta en la base del dentellón y diferentes valores del coeficiente de fricción interparticular en el intervalo μ∊ (0.5, 0.7). En todos los casos, la superficie del modelo resulta aproximadamente la misma. Por lo anterior, se concluye que la reducción de las deformaciones unitarias está controlada principalmente por la profundidad del dentellón.

Tomando en cuenta que, en tres dimensiones los granos tienen un grado de libertad adicional, se pueden esperar resultados más realistas a partir de simulaciones 3D. La Figura 6 presenta el estado inicial de un modelo de análisis tridimensional.

Figura 6: Modelo DEM 3D con dentellón granular 

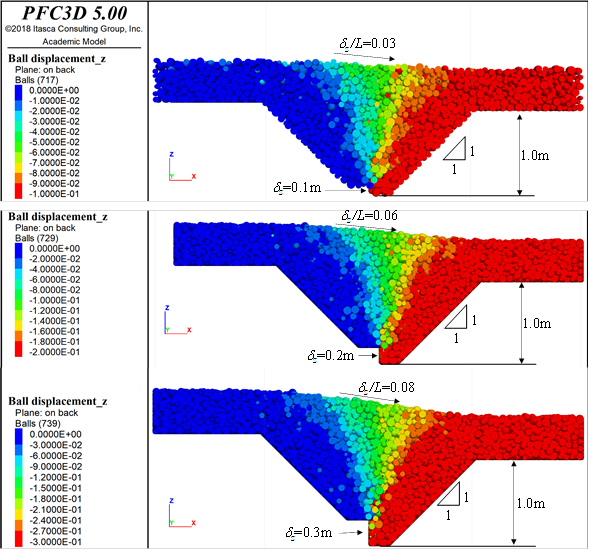
Repitiendo con el modelo 3D el caso con δ _z = 0.10 m (Figura 7), se obtiene L = 1.70 m en la superficie y por tanto δ _z /L=0.06. El resultado es por tanto más favorable que en el caso bidimensional. Esto se puede comprender si se toma en cuenta que, en arreglos regulares de discos de igual diámetro la porosidad puede variar 12.2 % (de 9.3 a 21.5 %), mientras que en esferas de igual tamaño la porosidad puede variar 21.7 % (de 25.9 a 47.6 %), es decir, hay mayor libertad de movimientos de los granos en tres dimensiones que en dos.

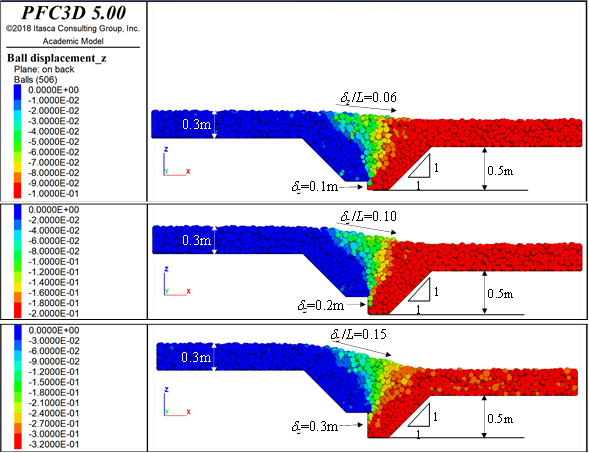
Figura 7: Desplazamientos verticales para distintos valores de δ_z. Cortes longitudinales en el modelo DEM 3D con dentellón de 0.5 m de profundidad 

Para desplazamientos verticales de la grieta δ _z = 0.2 m y δ _z = 0.3 m, en la superficie del modelo se obtienen δ _z /L = 0.10 y δ _z /L = 0.15, respectivamente. En la Figura 7 se puede observar que, al aumentar la altura del escalón en la grieta, la longitud de la superficie inclinada permanece aproximadamente constante.

Se observa que los desplazamientos verticales diferenciales se propagan más hacia el lado alto de la grieta. Esto se debe a que las partículas del lado bajo siguen invariablemente el movimiento de la frontera inferior, pero las partículas del lado alto quedan apoyadas parcialmente en la frontera fija y parcialmente en las partículas del lado bajo que presentan un movimiento descendiente.

Una vez rebasado el valor de δ _z /L admisible (0.15 en rampas para vehículos de acuerdo con CDMX, 2017), será necesario realizar trabajos de mantenimiento consistentes en retirar el pavimento de la vialidad, nivelar la superficie y volver a colocar el revestimiento.

Dependiendo de la velocidad de incremento del escalón en una grieta y de la importancia de la vialidad, en la práctica se puede adoptar una profundidad diferente del dentellón granular. Por ejemplo, en la Figura 8 se presentan los desplazamientos verticales para un dentellón de 1 m de profundidad, donde se observa que se obtienen deformaciones unitarias tolerables incluso para un escalón de 0.3 m.

Figura 8: Desplazamientos verticales para distintos valores de δ_z. Cortes longitudinales en el modelo DEM 3D con dentellón de 1.0 m de profundidad 

Modelado con enfoque de medios continuos

Para el análisis con elementos finitos se considera un modelo constitutivo elasto-plástico de tipo Mohr-Coulomb. Se acepta un peso volumétrico de ρ = 20 kN/m³, con parámetros elásticos: E = 18000 kPa y υ = 0.35, y parámetros plásticos: ϕ=25° y c=0. Para comparar la efectividad de la solución propuesta (Caja disipadora de deformaciones unitarias), se analiza la distribución de los asentamientos diferenciales en la superficie del terreno para cada uno de los tres desplazamientos propuestos (δ _z =0.1 m, 0.2 m y 0.3 m).

Después de un análisis paramétrico para diferentes valores del ángulo de fricción interna (ϕ), se concluyó que el análisis de la caja de arena mediante medios continuos, se puede modelar mejor al considerar el caso extremo en el que el ángulo de fricción interna es nulo (ϕ =0). Así, el criterio de Mohr-Coulomb se reduce al de Tresca (^{Jones, 2009}) de máximo esfuerzo cortante τ_máx. Con base en las condiciones de frontera del modelo numérico, los desplazamientos impuestos inducen un desconfinamiento en el material y generan un esfuerzo cortante en la línea de la grieta. Este comportamiento puede representarse por un estado de esfuerzos de extensión, como lo mostró ^{Biarez (1961)}. Para el análisis con elemento finito, y de acuerdo con el criterio de Tresca, se requiere establecer un flujo plástico (relación esfuerzo-deformación) con un esfuerzo de fluencia σ_y (esfuerzo límite elástico), interpretado como una resistencia al esfuerzo cortante τ _máx cuya magnitud dependerá del desplazamiento impuesto δ _z . El criterio de Tresca evita involucrar parámetros como ϕ y φ que, para el estudio de la caja de arena con medios continuos, pueden conducir a resultados irreales.

De los resultados de los análisis, se graficaron los desplazamientos verticales en la superficie de la caja para las tres condiciones de frontera (δ _z = 0.1, 0.2 y 0.3 m) y para las dos profundidades del dentellón (0.50 m y 1.00 m). Las Figuras 9 y 10, muestran los resultados de la influencia de la profundidad del dentellón sobre la distancia horizontal L en la superficie en la que se distribuyen los asentamientos diferenciales. Por ejemplo, cuando se tiene un desplazamiento δ _z = 0.1 m, la deformación unitaria en la superficie es δ _z /L = 0.06 y δ _z /L = 0.03, para 0.5 m y 1.0 m de profundidad del dentellón, respectivamente. Se observa que los asentamientos diferenciales superficiales se distribuyen en una longitud de 1.6 m para el dentellón de 0.5 m de profundidad, mientras que para el de 1.0 m la longitud es de 3.0 m. A mayor profundidad de la caja de arena, es menor δ _z /L en la superficie. Por lo tanto, la eficiencia de la caja es una función de la profundidad de la misma. Asimismo, se observa que las distancias horizontales L donde se disipa el asentamiento, son similares con las obtenidas con los análisis de elemento discreto, las cuales son de 1.70 m y 3.60 m para para 0.5 m y 1.0 m de profundidad del dentellón.

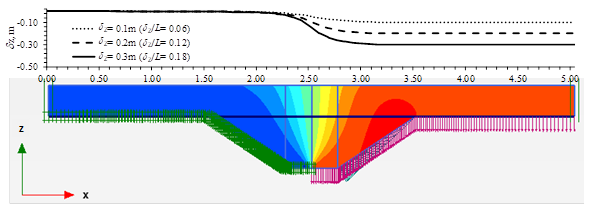
Figura 9: Asentamientos en la superficie para desplazamientos verticales impuestos de δ_z =0.10, 0.20 y 0.30 m. Dentellón de 0.50 m de profundidad 

Figura 10: Asentamientos en la superficie de la caja de arena para desplazamientos verticales impuestos de δ_z =0.10, 0.20 y 0.30 m. Dentellón de 1.0 m de profundidad 

Conclusiones y recomendaciones

Para mitigar los problemas en las vialidades asociados a grietas con escalón, se propone la colocación de un dentellón granular en la superficie del suelo. Esta idea se sustenta en que los materiales granulares, como la arena, no transmiten tensiones y sus partículas constitutivas pueden cambiar sus posiciones relativas dentro del medio adaptándose a los movimientos externos.

Se considera que, de los métodos utilizados, el de elementos discretos es el más apropiado para analizar el problema, ya que toma en cuenta explícitamente la naturaleza discontinua de los medios granulares. Se observó que las simulaciones bidimensionales conducen a diseños conservadores. Los modelos bidimensionales facilitan los cálculos, pero subestiman de manera considerable los beneficios del relleno granular. De los resultados de los análisis se exponen los siguientes puntos importantes respecto a la caja disipadora de deformaciones unitarias:

El modelado de la caja de arena es un problema de partículas independientes que se rige por un mecanismo de trabazón entre partículas. Con los medios continuos es difícil representar el comportamiento de los medios granulares al involucrar el ángulo de fricción φ y el ángulo de dilatancia φ. Sin embargo, el criterio de Tresca, que considera φ=0, facilita el modelado del comportamiento de la caja de arena. El análisis confirma que la profundidad del dentellón influye en la magnitud de longitud horizontal donde se distribuyen los asentamientos.