Introducción
En la actualidad, los sistemas de levitación magnética se utilizan en diversas aplicaciones, tales como; trenes de pasajeros de alta velocidad, rodamientos sin fricción, aislamiento de vibraciones, cojinetes magnéticos, entre otras (Qin et al., 2014; Amrhein et al., 2016; Barahona et al., 2010). En lo que se refiere al ámbito académico, existen diversos prototipos considerados como bancos de pruebas para la implementación de diferentes algoritmos de control (Morales, 2011). Uno de los más populares consiste en una esfera metálica inmersa en un campo magnético vertical creado por un electroimán, en dicho sistema, se controla la posición de la esfera mediante la manipulación del flujo magnético de la bobina (Qin et al., 2014; Lilienkamp, 2004). Algunos otros prototipos que han sido desarrollados con actuadores electromagnéticos, se pueden encontrar en trabajos como: el presentado en (Moriano & Naranjo, 2012), en el cual se plantea un sistema bola-viga con un actuador electromagnético ubicado en un extremo del prototipo, en dicho sistema el centro de masa se encuentra desplazado del punto de apoyo de la viga y funciona por atracción magnética, además se implementan dos algoritmos de control, un controlador no lineal de ganancias programadas y uno basado en modos deslizantes. Por su parte, Lin et al. (2005), proponen un sistema bola-viga con dos actuadores de suspensión magnética ubicados en cada uno de los extremos, implementan un controlador backstepping, garantizando estabilidad asintótica global. El sistema de levitación propuesto en este trabajo se conforma de una viga con libertad para rotar, la cual se estabiliza mediante un electroimán colocado en uno de los extremos. El objetivo principal de control en el sistema es mantener la viga en una posición deseada. Existen en la literatura diversos trabajos que abordan el problema de regulación y seguimiento de trayectoria en sistemas de levitación magnética, como el propuesto por (Lindlau & Knospe, 2002), en el cual se controla una viga mediante la manipulación de dos electroimanes ubicados en los extremos, para ello se emplea una linealización por realimentación.
Hu et al. (2005) proponen un algoritmo de control no lineal basado en un diseño sistemático con entradas y estados restringidos, obteniendo una región de atracción mayor en comparación con otras técnicas lineales. En Rodríguez et al. (2000) se usa el método de pasividad para resolver el problema de estabilización del sistema. Otro trabajo interesante es la propuesta de Lee et al. (2003) que solucionan el problema de control de este sistema mediante dos actuadores magnéticos utilizando control por modos deslizantes. Por otra parte, en (Cruz et al., 2017) se presenta el modelado de un sistema de levitación magnética de un grado de libertad, así como el procedimiento de diseño del actuador electromagnético. En dicho prototipo, se implementó un algoritmo de control PI para la regulación de la posición de la viga.
En este artículo, se desarrolla un controlador PI difuso para regulación y seguimiento de trayectoria en un sistema de levitación magnética de un grado de libertad controlado mediante repulsión magnética, debido a que puede utilizarse tanto en situaciones que involucran sistemas altamente complejos cuyo comportamiento no se comprende bien y donde se requiere una solución aproximada pero rápida (Ross, 2010).
El controlador PI convencional es muy robusto y se desempeña bien en las condiciones de trabajo normales, puede abordar diversos tipos de perturbaciones, pero requiere un ajuste adecuado para cada punto de operación. Por ello, su tolerancia a las variaciones de los parámetros se ve gravemente afectada (Pal & Mudi 2008). A diferencia de un control PI clásico, un PI-Difuso presenta características no lineales con ganancias kp y kj variables (Zheng et al., 2009; Tang et al., 2001; Genc et al., 2009), es decir; los parámetros del controlador PI se ajustan automáticamente para un amplio rango ganancias y también para un cambio amplio en las condiciones de operación (Precup & Hellendoorn, 2011), lo cual le permite un mejor desempeño en sistemas no lineales, variantes en el tiempo o incluso, con un modelo matemático desconocido (Amrhein et al., 2016; Barahona et al., 2010).
Para este caso, el sistema presenta una dinámica no lineal, así como el efecto de histéresis en el actuador electromagnético, además de la presencia de perturbaciones exógenas y dinámicas no modeladas, lo cual hace viable la implementación de un control PI-Difuso. En particular, un controlador PI-Difuso se puede encontrar en aplicaciones como; control de presión de aire de suministro para el sistema de calefacción, ventilación y aire acondicionado (Pal & Mudi, 2008), control de velocidad de un motor de reluctancia conmutada (Kavitha & Umamaheswari, 2014), control de la temperatura deseada en una máquina de rodillo de tapa de prensa utilizada en el proceso de laminación de té negro (Bambang et al., 2001), entre otras.
Por otra parte, se describe la implementación del esquema de control en un sistema de cómputo embebido para verificar su funcionamiento, permitiendo que el sistema sea utilizado como banco de pruebas para la implementación de diferentes estrategias de control.
El trabajo se organiza de la siguiente manera: La sección siguiente describe el modelo matemático de la dinámica del sistema, así como el planteamiento del problema a solucionar. La sección tres presenta la metodología utilizada para el diseño del controlador PI-Difuso. En la siguiente sección, se presentan los resultados experimentales obtenidos durante la implementación del controlador para tareas de regulación y seguimiento de trayectoria. Finalmente, las conclusiones obtenidas.
Modelo matemático
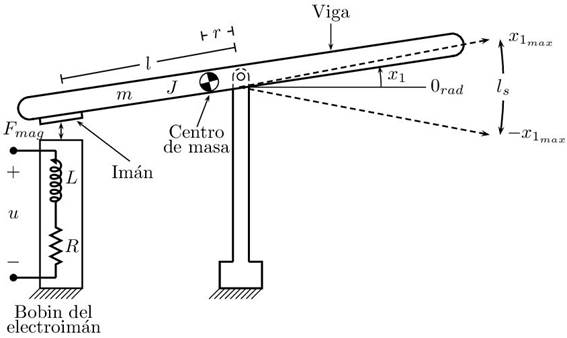
El sistema de levitación magnética mostrado en la Figura 1, consiste en una viga con libertad para rotar, en donde este movimiento se afecta por efecto gravitacional y la entrada de control proveniente de la fuerza magnética producida por un electroimán (Cruz et al., 2017).
El modelo matemático se define mediante el enfoque de Euler-Lagrange, donde la dinámica del movimiento de la viga es:
donde los parámetros:
J y m= |
momento de inercia y masa de la viga |
θ = |
ángulo de la viga con la horizontal |
˙θ = |
velocidad angular |
g = |
aceleración debida a la gravedad |
r = |
distancia radial del centro de masa de la viga al centro de rotación. |
La fuerza F creada por el electroimán está dada por la siguiente expresión:
donde:
l = |
distancia entre el pivote y el centro del imán permanente |
i = |
corriente que circula en la bobina del electroimán |
Ce= |
constante de proporcionalidad de la fuerza electromagnética. |
Por otra parte, aplicando la ley de voltajes de Kirchhoff se obtiene la ecuación (3), la cual modela la dinámica de la corriente.
L y R representan la inductancia y la resistencia del subsistema electromagnético, respectivamente, y u es la entrada de control, la cual se aplica al sistema electromagnético.
Definiendo las siguientes variables de estado:
Después algunas manipulaciones algebraicas, el sistema descrito en (1), (2) y (3) se puede representar en función de las variables de estado definidas en (4), quedando:
En este caso, se asume que la variable de salida es la posición angular de la viga, x1 (Figura 1).
Formulación del problema
El objetivo primordial es estabilizar el sistema alrededor del punto de equilibrio, a través de una estrategia de control difuso, suponiendo que la viga se encuentra inicialmente en la región ls = (-x1max; x1max) con x1max fijo en los valores de operación.
En otras palabras, la intención es llevar la viga a la posición deseada x1. Por otra parte, como un problema adicional se pretende que, dada una trayectoria de referencia suave del ángulo de la viga, se tenga un error de seguimiento cercano a una vecindad del origen después de tiempo establecido.
Diseño del controlador PI difuso
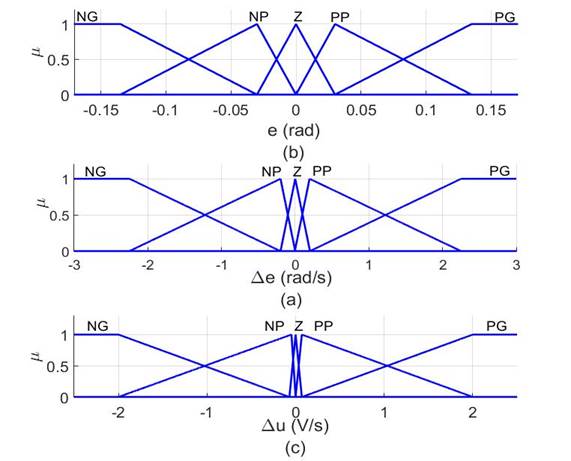
Para el proceso de fuzzificación, tanto para las entradas como para la salida, se utilizaron funciones de pertenencia triangulares y trapezoidales con el universo de discurso definido de la siguiente manera:
donde e= x1-x*1 y Δe= ˙x1-˙x*1, aquí es x*1 la posición deseada de la viga.
Es importante notar que los valores del universo de discurso (6) se obtuvieron mediante la linealización del modelo descrito en (5) y la obtención de la función de transferencia en lazo cerrado con un control tipo PI, el cual se sintonizó mediante el método de oscilaciones sostenidas de Ziegler- Nichols. Posteriormente, se procedió a la observación de los valores correspondientes de e, Δe y la entrada de control u. (Cruz et al., 2017). La Figura 2 muestra las funciones de pertenencia utilizadas para las variables de entrada y salida.
Para este caso, las etiquetas utilizadas para los conjuntos difusos son: negativo grande (NG), negativo pequeño (NP), cero (Z), positivo pequeño (PP) y positivo grande (PG). Los rangos de las etiquetas se definen en la siguiente Tabla 1.
Tabla 1: Rangos de los conjuntos difusos
| NG | NP | Z | PP | PG | |
| e | [-0.27, -0.03] | [-0.135, 0] | [-0.03, 0.03] | [0, 0.135] | [0.03, 0.27] |
| Δe | [-4.5 , 0.2] | [-2.25, 0 ] | [-0.2,0.2] | [-0.00578,2.25] | [-0.2,4.5] |
| ∆u | [-3.25,-0.07] | [-2,0] | [-0.07,0.07] | [0,2] | [0.07,3.25] |
Mecanismo de inferencia
El mecanismo de inferencia es el encargado de involucrar o referirse a la base de reglas de modo que se disparen las reglas apropiadas. Debido a su facilidad de implementación, se utiliza el modelo inferencia de Mamdani y el método max-min (Amjad et al., 2010).
Base de reglas difusas
La base de reglas difusa utilizada en el diseño se muestra en la Tabla 2, las cuales se proponen a partir de la metodología sugerida en Lee (1990) y Chen y Pham, (2001).
Tabla 2: Matriz de reglas difusas (FAM)
| Δe | e | NG | NP | Z | PP | PG |
| NG | NG | NG | NG | NP | Z | |
| NP | NG | NP | NP | Z | PP | |
| Z | NG | NP | Z | PP | PG | |
| PP | NP | Z | PP | PP | PG | |
| PG | Z | PP | PG | PG | PG |
Las reglas de la Tabla 2 tienen el formato:
permitiendo obtener 25 reglas que relacionan los estados del proceso y la variable de control. Además, definiendo α1=(e AND ∆e) se tendrá la siguiente relación μα1= μe ∧ μΔe=min{μe, μΔe} (Zhang y Chen, 2006).
Por otra parte, para proporcionarle a la señal de control u, un valor de pertenencia μu de tal forma que esté cambiando con μe y μΔe, se considera que μu= μe x μΔe. Por tal motivo, cada regla tiene un valor de pertenencia correspondiente para la lógica de implicación dada por z=µ(x→u)=min{1,1+μu-μe y μx}. Finalmente, se obtiene la señal de control de cada regla en forma ponderada definida por: z x μu x u.
Recordando que un controlador PI se expresa como:
donde k l es la ganancia integral.
Entonces, diferenciando (7) con respecto al tiempo, se tiene:
Expresando (8) en forma discreta se obtiene lo siguiente:
Por tanto, la expresión (9) representa un controlador tipo PI difuso (Ponce, 2010), el cual a partir del error y el cambio de error puede obtener el cambio de la señal de control, que puede integrarse para determinar la señal de control que emplea la FAM mostrada en la Tabla 2, evitando la dificultad de formular reglas dependientes del error integral, ya que; este puede tener un amplio universo de discurso, donde no es conveniente su empleo (Reznik, 1997).
La Figura 3 muestra el diagrama de bloques del sistema de control, donde k l la ganancia del error y kp la ganancia del cambio de error.
Defuzzificación
La técnica de defuzzificación utilizada es el enfoque de centro de gravedad (área), debido a que proporcionó el menor error cuadrático integral. La expresión utilizada para la defuzzificación está dada por
donde:
Factor de escalamiento
Para esta etapa, se sintonizó el controlador utilizando factores de escala de entrada y salida para mejorar el rendimiento del sistema. El factor de escala de salida fue necesario para garantizar que la entrada de control u tenga un valor suficiente para mover la viga y, en consecuencia, mantenerla en la posición deseada. Los valores de escala que se utilizaron se presentan en la Tabla 3.
En la Figura 4 se muestra un ejemplo de la aplicación de las funciones de membresía mostradas en la Figura 2 y la FAM descrita en la Tabla 2. Para dicho ejemplo se considera el caso cuando e=0.0148 y ∆e=-0.016.
El caso descrito anteriormente (Figura 4) presenta dos posibles soluciones que se pueden expresar en formato IF-THEN.
Es decir, la acción de control debe pertenecer a los conjuntos difusos cero (Z) y positivo pequeño (PP). Así, aplicando el método de defuzzificacion mencionado anteriormente, se tiene una acción de control Δu pi = 0.6, la cual se encuentra en un rango que abarca dichos conjuntos.
La Figura 5 muestra la superficie de control generada por la base de reglas establecidas en la Tabla 2.
Resultados experimentales
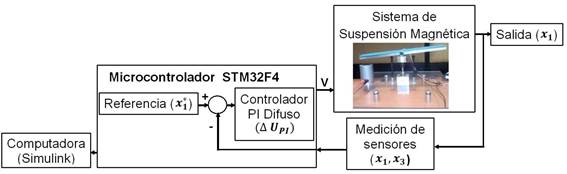
En esta sección presentamos los resultados cuando se aplica la estrategia de control en un prototipo experimental desarrollado en el Laboratorio de Robótica Avanzada de la UPIITA-IPN (Cruz et al., 2017). Como primer aspecto, se presenta una descripción del entorno experimental y posteriormente, se muestra el comportamiento en tiempo real del sistema físico en las tareas de regulación y seguimiento de trayectoria.
Entorno experimental
Los experimentos se realizaron utilizando una plataforma experimental, cuyo diagrama se muestra en la Figura 5, dicha plataforma está compuesta por una viga de aluminio que tiene colocada en un extremo un imán de neodimio para lograr la interacción entre campos magnéticos, cuenta con un sensor de corriente y una Unidad de Medición Inercial (IMU, por sus siglas en inglés), para medir la corriente de la bobina (x3) y la posición angular de la viga (x1), respectivamente. Adicionalmente, tiene una tarjeta Discovery STM32F4 que se emplea como tarjeta de adquisición de datos, además de realizar el cálculo y envío de la señal de control al sistema mediante la técnica de PWM.
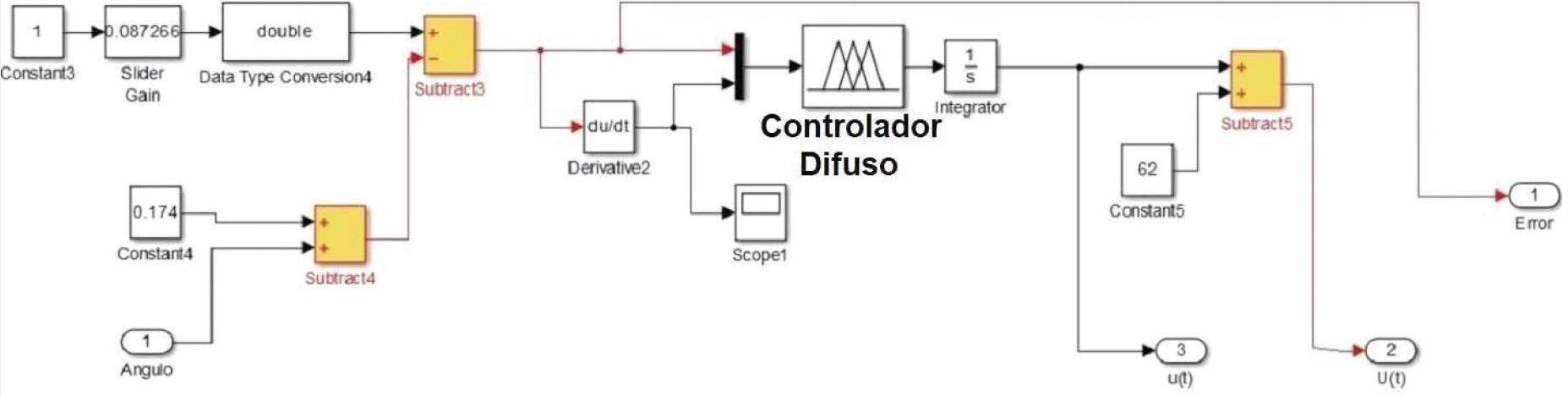
La implementación del algoritmo de control en la tarjeta se realizó con el software MATLAB-Simulink, empleando el Simulink Waijung Blockset de la compañía Aimaigin, desarrollado para las tarjetas embebidas Discovery. En la Figura 6 se muestra el programa almacenado en el sistema cómputo embebido para ejecutar las tareas de adquisición de datos, cálculo de la ley de control y el envío de la señal de control al sistema físico. Por otra parte, en la Figura 7 se presenta la descripción del algoritmo de control propuesto, en donde se puede observar que el algoritmo cuenta con una prealimentación de 62 %, en el valor de u , con la finalidad de proporcionar el valor que se requiere para mantener la viga en su punto de equilibrio. Permitiendo que la acción del control PI difuso se encargue de compensar las desviaciones que se pudiesen presentar en el sistema. Lo anterior, parte de la idea de emplear variables de desviación (Smith et al., 1991), definidas como:
Donde:
x1 (t) y ˉx1 = |
valor dinámico y estado estacionario del ángulo de la viga, respectivamente. |
uPI(t) y ˉuPI = |
valor dinámico y estacionario de la acción de control. |
Finalmente, en lo que concierne a la acción de control, esta se encuentra en términos de porcentaje y mantiene la relación 1 %UPI= 0.12 V (Figura 8).
Control para regulación de la posición
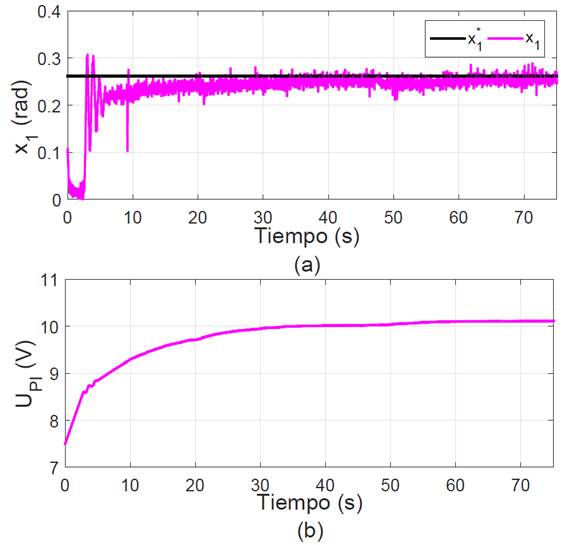
Como primer experimento se propone llevar la posición angular de la viga al valor de x*1=π12rad, empleando el controlador PI-Difuso, considerando que la condición inicial del sistema es x1 (0)=0 rad. La Figura 9 muestra el comportamiento de la posición y la acción de control, observando que el sistema tarda cerca de 20 s en alcanzar la posición deseada de manera suave (Figura 9a). En lo que concierne a la acción de control, se muestra que alcanza un valor constante de 10 V, que equivale a la energía requerida para mantener al sistema en el punto de equilibrio deseado (Figura 9b).
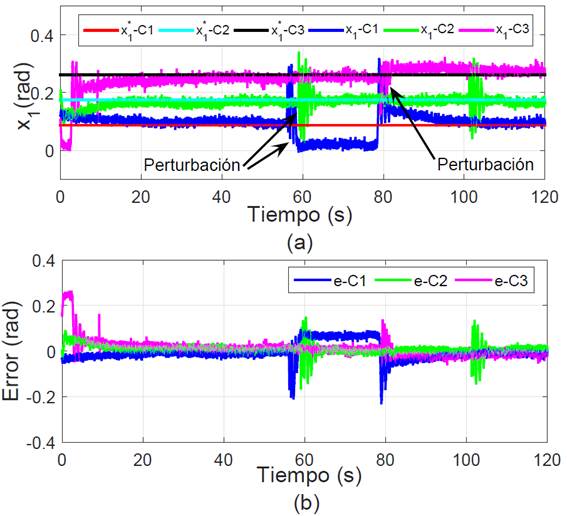
Como segundo experimento, se propone llevar a cabo las tareas de regulación de la posición angular de la viga (x1) en presencia de perturbaciones externas, para este fin se plantean los siguientes tres casos:
Considerando las misma del controlador del experimento anterior.
En la Figura 10a se observa el comportamiento del sistema en presencia de perturbaciones, como primer paso, para cada caso se alcanza el valor deseado (π/36, π/18 o π/12) alrededor de los 20 s. Posteriormente, se aplica una perturbación externa, observando que el sistema logra permanecer alrededor del equilibrio x*1. En otras palabras, el controlador propuesto garantiza la convergencia del error a un valor cercano a cero en tiempo finito, sin importar la presencia de perturbaciones en el sistema (Figura 10b).
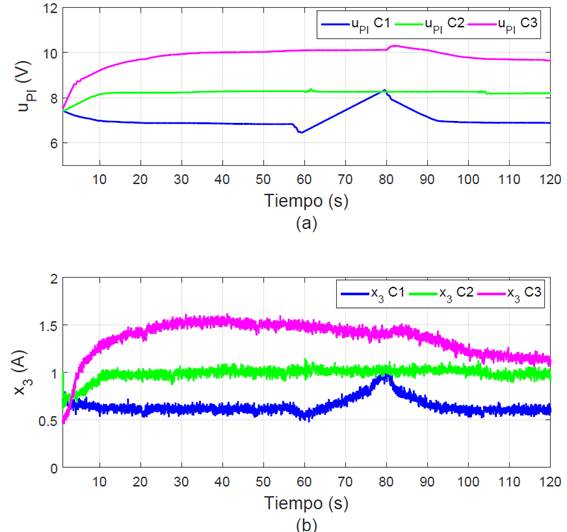
En la Figura 11 se muestra el comportamiento de la señal de control U pi y el valor de corriente que circula por la bobina x3, las cuales, tienden a un valor estacionario conforme el error tiende a cero, que equivale a los valores necesarios para mantener la viga en equilibrio.
Control para seguimiento de trayectoria
En la sección anterior se mostró la capacidad del controlador PI difuso de mantener a la viga en un valor deseado. A continuación, se muestran los resultados obtenidos al realizar un seguimiento de trayectoria. Para este fin, se propone una trayectoria de referencia tipo polinomio de Bézier de grado ocho, la cual comienza en π/36 y alcanza un valor de π/12 rad en un intervalo comprendido entre 20 y 50 s. Además, la condición inicial del sistema es x1(0) = π/12 rad
Las Figura 12 muestra la posición y el error obtenido durante el seguimiento de trayectoria, mostrando la capacidad del controlador para llevar de la posición inicial (x1(0) = π/12 rad) a la posición final de (x1(f) = π/12 rad) después de 50 s. Lo anterior, se observa en la Figura 12b, donde se muestra que el error se encuentra cercano a cero durante la evolución del tiempo. Cabe mencionar, que el error cuadrático medio obtenido por el controlador es igual 0.0018 rad.
Finalmente, la Figura 13 describe el comportamiento de las variables Upi y x3 durante el experimento. En el caso de la señal de control, el voltaje promedio empleado fue de 8.8892 V y la corriente que circula por la bobina oscila entre 1.8 A, siendo estos los valores necesarios para mantener al sistema en el valor deseado.
Conclusiones
El algoritmo de control propuesto permite realizar maniobras de regulación y seguimiento de trayectoria en x1. A pesar de la presencia de perturbaciones, los objetivos de control se alcanzan en un tiempo menor a 20s. Los resultados experimentales se hicieron considerando diferentes referencias (constantes y una trayectoria suave) a fin de controlar el sistema de levitación magnética de un grado de libertad. Así, se demuestra de forma experimental la capacidad de este tipo de controladores para trabajar con sistemas no lineales.
El sistema de levitación magnética funciona bajo principio de repulsión electromagnética a diferencia de varios sistemas que trabajan con atracción electromagnética (Lilienkamp, 2004; Amrhein et al., 2016; Qin et al., 2014; Lin et al., 2005), que lo hace interesante para aplicaciones de diversos algoritmos de control, ya que presenta histéresis en el electroimán, singularidades en el sistema e imantación del mismo. Se debe resaltar que el sistema presenta sobretiros pequeños durante el período transitorio, el cual es lento debido a la dinámica del actuador, después de 20 s, se obtiene un error en estado estacionario que converge a un valor cercano a cero de forma suave, este comportamiento se mantiene hasta entrar a una región de operación que acota al error en un rango de ± 0.02, garantizando la estabilidad del sistema.
Los resultados obtenidos corroboran la correcta caracterización y selección de los universos de discurso de e y Δe, Δuip así como las reglas implementadas. Finalmente, la metodología propuesta en este trabajo, permite cumplir con los objetivos de control planteados para un rango de -5 a 10 radianes, mediante su implementación en un sistema de procesamiento embebido, evitando la necesidad de contar con un equipo de procesamiento de mayores capacidades, permitiendo que el sistema se emplee como banco de pruebas para verificar el funcionamiento de diversas estrategias de control.











 nueva página del texto (beta)
nueva página del texto (beta)