Introducción
En años recientes, los estudios de demanda del servicio aéreo han incrementado el interés de las aerolíneas, aeropuertos, gobiernos e investigadores, dado que estos viajes son un papel clave del transporte, conforme avanza el proceso de globalización. El servicio aéreo es una herramienta indispensable para la integración nacional, el turismo, la creación de negocios y el comercio nacional e internacional de mercancías, por lo que, es un factor determinante de la competitividad y el desarrollo. En el caso de las aerolíneas, el análisis y pronóstico de la demanda del servicio es esencial para el manejo de sus flotas. Para los aeropuertos, la evaluación actual y futura de la demanda es un elemento fundamental para sus planes de inversión y ampliación de instalaciones. Mientras que, para los gobiernos, los pronósticos de esta demanda son imprescindibles para el diseño de políticas públicas que impulsen el desarrollo económico. Por su parte, los investigadores han desarrollado estudios de la demanda del servicio aéreo, sin embargo, la mayoría de estos trabajos se han centrado en países desarrollados, particularmente en Estados Unidos, el Reino Unido, España y Australia, y muy pocos casos en otros países (Valdes, 2015). En particular, este documento se centra en el caso de México y utiliza información del grado de marginación de las localidades del país y de las áreas de influencia de los aeropuertos mexicanos.
Algunos estudios previos han establecido que existe alguna relación entre las condiciones socioeconómicas de las ciudades y el volumen de pasajeros transportados en los aeropuertos de dichos sitios (Lakew, 2015); y en estudios aplicados en el ámbito mundial se ha encontrado que hay una correlación entre los flujos de pasajeros transportados y la actividad económica de las distintas áreas geográficas (Profillidis et al., 2015). Por último, se ha sugerido determinar la correlación entre las áreas de influencia de los aeropuertos, los grados de marginación que comprenden y su actividad aérea, con objeto de generar un modelo para predecir los flujos de pasajeros (Herrera et al., 2014).
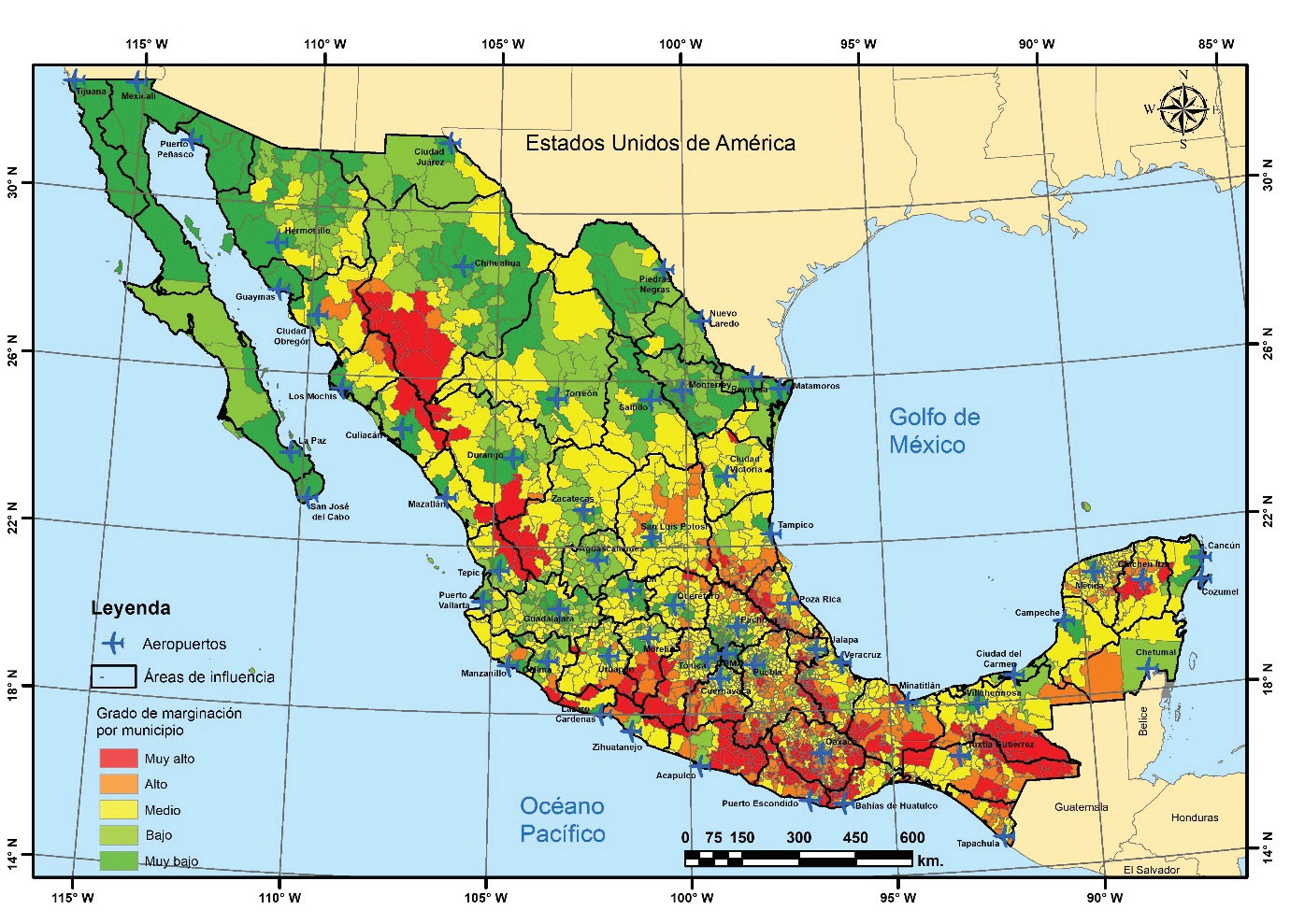
El índice de marginación es una medida-resumen que permite diferenciar al país según el impacto global de las carencias que padece la población, por lo que contribuye a identificar las disparidades territoriales. Para cuantificar la intensidad global de la marginación (índice) se utilizan nueve indicadores que miden la intensidad de exclusión. Este índice permite agrupar las áreas de interés en cinco conjuntos claramente diferenciados, de acuerdo con la síntesis de las nueve formas de exclusión social. Mediante un método estadístico se divide el recorrido del índice de marginación en cinco intervalos, mediante cuatro puntos de corte. De esta manera, se establecen los grados de marginación: muy bajo, bajo, medio, alto y muy alto, según el intervalo en que se ubique el valor de su índice (CONAPO, 2011).
Dado que la marginación es una medida integrada de las carencias de la población, su magnitud y distribución pueden servir para estimar el potencial de la actividad aérea. Una población con muy alta marginación difícilmente podrá acceder a este servicio, por el contrario, una marginación muy baja se puede relacionar con la población que puede acceder a este servicio regularmente.
El objetivo general de este trabajo es establecer un modelo de demanda de la actividad aérea en México. Para ello, se consideró que esta actividad depende de ciertas características de los aeropuertos, en particular de su ubicación, la cual define su área de influencia y del grado de marginación de la población en dicha zona.
Desarrollo
Inicialmente, se determinaron las áreas de influencia de los aeropuertos, diferenciando a sus dos servicios, el nacional y el internacional. En los dos casos, se utilizó el método de accesibilidad espacial (isócronas de recorrido). Posteriormente, se determinó para cada zona de influencia la población asociada con sus diferentes grados de marginación. Por último, mediante un análisis estadístico, se determinaron los modelos matemáticos que ofrecieron las mejores correlaciones entre la población por grado de marginación y los pasajeros atendidos en cada área de influencia.
Método de accesibilidad espacial o de isócronas de recorrido
Cada usuario antes de seleccionar su vuelo, debe decidir cuál aeropuerto es el más conveniente. Se considera que los usuarios eligen el aeropuerto en función del tiempo que les toma llegar hasta él, y eligen aquel que les ofrece el menor tiempo de acceso.
Mediante el método de accesibilidad espacial se delimitó el área de influencia de los aeropuertos. Este método considera que el espacio terrestre no es isotrópico, dado que existen diferencias de impedancia en el terreno, derivadas de la topografía y de las distintas vías de comunicación entre los aeropuertos y sus destinos.
El método de accesibilidad espacial (González, 2007) incorpora modelos digitales de elevación, así como las características geométricas y velocidades de desplazamiento en la infraestructura carretera. Como resultado de estas consideraciones se obtienen isócronas de recorrido, es decir, líneas que muestran el mismo tiempo de desplazamiento de uno o varios objetivos de interés.
La accesibilidad se calcula a partir de una superficie de fricción, que consta de una cuadrícula bidimensional (formato raster), donde cada celda de la cuadrícula representa la impedancia existente en el terreno para el óptimo desplazamiento en esa celda. El formato raster es una forma de tratamiento y representación de los elementos espaciales mediante la disposición de “n” número de celdas o píxeles en forma de matriz numérica. Los elementos de impedancia considerados para este estudio fueron los índices de velocidad de desplazamiento, según el tipo de carretera; la pendiente del terreno; y la modalidad de transporte utilizado (vehículo automotor y/o recorrido pedestre). Dichos elementos condicionantes quedaron plasmados como el valor de impedancia en cada celda o píxel. De esta forma, cada celda de la superficie de fricción representa el tiempo de viaje o desplazamiento en ella.
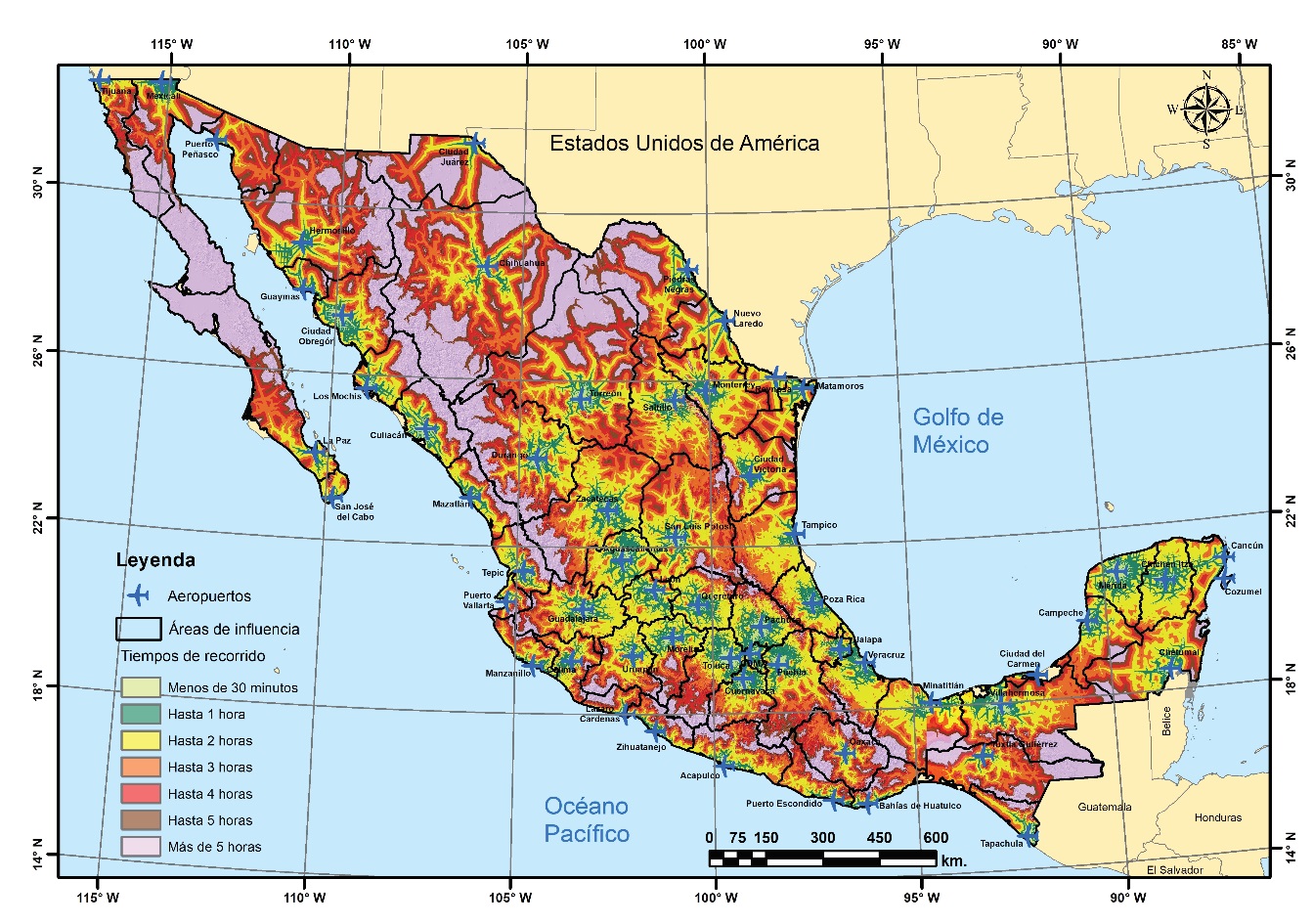
En las Figuras 1 y 2, se muestra una capa raster de isócronas de recorrido (junto con un modelo digital de terreno), tomando como objetivo a cada uno de los aeropuertos mexicanos. La primera figura corresponde al caso de los servicios nacionales y la segunda al de internacionales.
Fuente: Elaboración propia con base en la metodología de accesibilidad espacial
Figura 1: Isócronas de recorrido y áreas de influencia de los aeropuertos mexicanos en servicio nacional

Fuente: Elaboración propia con base en la metodología de accesibilidad espacial
Figura 2: Isócronas de recorrido y áreas de influencia de los aeropuertos mexicanos en servicio internacional
En estas imágenes; con color verde claro se muestra aquel perímetro que se encuentra a menos de treinta minutos de desplazamiento; con color verde oscuro el área indica hasta una hora de desplazamiento; el área con color amarillo representa hasta dos horas de desplazamiento; enseguida los colores naranja, rojo-coral y café, representan desplazamientos de hasta tres, cuatro y cinco horas, respectivamente; pasando dicha área, con color lila se representa todo aquel territorio que necesita más de cinco horas para su acceso.
De esta forma, las áreas de influencia resultantes mediante el método de accesibilidad espacial, para los dos tipos de servicios, nacional e internacional, están delimitadas mediante líneas negras en las Figuras 1 y 2. Se debe señalar que este método supone que los aeropuertos de interés cumplen con las demandas de los usuarios, es decir, que ofrecen las instalaciones, equipos y servicios demandados (por ejemplo, destinos, tarifas, frecuencias de vuelo, terminales de pasajeros, y servicios de migración); en caso contrario, los usuarios se desplazarían hacia el aeropuerto más cercano que sí los ofrezca.
En todos estos mapas se utilizó una proyección cónica conforme de Lambert (CCL) y datum WGS84. Las capas de información utilizadas en la elaboración de estos mapas fueron: para la ubicación de los aeropuertos (SENEAM, 2018); y para la estimación de las áreas de influencia (INEGI, 2018a), (INEGI, 2018b) e (IMT/SCT, 2010).
Posteriormente, se incorporaron a las áreas de influencia estimadas, los distintos grados de marginación por localidad para 2010, Figuras 3 y 4 (CONAPO, 2011). De esta forma, se estimó para cada área de influencia, la distribución correspondiente de los cinco grados de marginación.
Fuente: Elaboración propia con base en la metodología establecida en este inciso
Figura 3: Grados de marginación dentro de las áreas de influencia de los aeropuertos mexicanos en servicio nacional

Fuente: Elaboración propia con base en la metodología establecida en este inciso
Figura 4: Grados de marginación dentro de las áreas de influencia de los aeropuertos mexicanos en servicio internacional
Los resultados de la aplicación de esta metodología se presentan en las Tablas 1 y 2. Observe que en la última columna de estas tablas se incluyó la cantidad de pasajeros que atendió cada aeropuerto anualmente durante 2010 (DGAC, 2010).
Tabla 1: Distribución de la población por grado de marginación dentro de cada área de influencia de los aeropuertos en servicio nacional durante 2010 y pasajeros atendidos anualmente
| Aeropuerto | Población por grado de marginación | Población | Pasajeros | |||||
| Muy alto | Alto | Medio | Bajo | Muy bajo | total | atendidos | ||
| 1 | Acapulco | 257.761 | 863.846 | 74.181 | 860.922 | 402 | 2.057.112 | 555.477 |
| 2 | Aguascalientes | 2.526 | 171.355 | 211.892 | 684.623 | 779.686 | 1.850.082 | 220.458 |
| 3 | Bahías de Huatulco | 39.864 | 204.426 | 159.680 | 128.982 | 4.249 | 537.201 | 307.011 |
| 4 | Campeche | 2.170 | 142.910 | 104.793 | 12.202 | 222.127 | 484.202 | 97.129 |
| 5 | Cancún | 2.820 | 55.999 | 37.311 | 809.460 | 710 | 906.300 | 3.414.580 |
| 6 | Chetumal | 2.060 | 126.350 | 54.901 | 68 | 151.517 | 334.896 | 85.657 |
| 7 | Chichen Itzá | 12.307 | 332.306 | 52.516 | 1.789 | 192 | 399.110 | 14 |
| 8 | Chihuahua | 88.721 | 107.642 | 78.147 | 226.951 | 1.404.841 | 1.906.302 | 782.018 |
| 9 | Ciudad del Carmen | 231 | 33.434 | 1.097 | 192.304 | 19 | 227.085 | 229.815 |
| 10 | Ciudad Juárez | 100 | 3.174 | 26.417 | 42.228 | 1.462.421 | 1.534.340 | 622.130 |
| 11 | Ciudad Obregón | 7.353 | 131.982 | 51.820 | 175.295 | 452.383 | 818.833 | 204.188 |
| 12 | Ciudad Victoria | 2.127 | 59.524 | 74.860 | 79.894 | 308.580 | 524.985 | 46.982 |
| 13 | Colima | 8.253 | 77.770 | 181.698 | 326.217 | 267.454 | 861.392 | 37.930 |
| 14 | Cozumel | 15 | 1.863 | 19 | 77.245 | 88 | 79.230 | 3.509 |
| 15 | Cuernavaca | 65.765 | 630.343 | 340.943 | 859.740 | 588.250 | 2.485.041 | 7.982 |
| 16 | Culiacán | 17.008 | 168.527 | 132.699 | 169.725 | 774.065 | 1.262.024 | 1.077.305 |
| 17 | Del Bajío | 13.838 | 570.467 | 453.460 | 1.835.810 | 659.940 | 3.533.515 | 503.228 |
| 18 | Durango | 32.000 | 76.966 | 133.633 | 245.894 | 561.562 | 1.050.055 | 140.100 |
| 19 | Guadalajara | 4.922 | 219.248 | 462.767 | 2.368.749 | 3.114.130 | 6.169.816 | 4.850.640 |
| 20 | Guaymas | 696 | 7.991 | 11.472 | 4.238 | 158.063 | 182.460 | 204 |
| 21 | Hermosillo | 1.449 | 54.763 | 19.837 | 75.142 | 1.072.504 | 1.223.695 | 1.119.676 |
| 22 | Jalapa | 29.191 | 621.182 | 277.051 | 194.347 | 450.952 | 1.572.723 | 9.132 |
| 23 | La Paz | 1.408 | 25.143 | 14.205 | 90.369 | 241.192 | 372.317 | 472.598 |
| 24 | Lázaro Cárdenas | 7.230 | 21.093 | 88.729 | 13.669 | 79.200 | 209.921 | 15.145 |
| 25 | Los Mochis | 11.699 | 155.763 | 213.208 | 206.377 | 345.189 | 932.236 | 221.978 |
| 26 | Manzanillo | 3.362 | 60.448 | 78.821 | 71.283 | 131.755 | 345.669 | 66.790 |
| 27 | Matamoros | 2.482 | 22.686 | 29.444 | 112.226 | 450.570 | 617.408 | 45.862 |
| 28 | Mazatlán | 9.257 | 78.983 | 68.565 | 139.525 | 381.872 | 678.202 | 392.844 |
| 29 | Mérida | 2.640 | 557.381 | 98.248 | 186.635 | 778.793 | 1.623.697 | 1.038.577 |
| 30 | Mexicali | 276 | 21.951 | 33.133 | 171.319 | 903.765 | 1.130.444 | 442.267 |
| 31 | México | 684 | 169.072 | 841.933 | 1.663.172 | 8.081.078 | 10.755.939 | 15.311.056 |
| 32 | Minatitlán | 74.698 | 880.953 | 516.915 | 503.393 | 42.973 | 2.018.932 | 114.173 |
| 33 | Monterrey | 1.264 | 29.512 | 40.309 | 160.075 | 4.270.174 | 4.501.334 | 4.623.651 |
| 34 | Morelia | 21.976 | 675.864 | 430.693 | 400.057 | 683.357 | 2.211.947 | 231.595 |
| 35 | Nuevo Laredo | 61 | 3.509 | 1.230 | 29.914 | 414.436 | 449.150 | 89.177 |
| 36 | Oaxaca | 77.154 | 835.103 | 234.181 | 394.290 | 53.026 | 1.593.754 | 395.612 |
| 37 | Pachuca | 50.994 | 790.841 | 714.001 | 1.288.003 | 5.282.640 | 8.126.479 | 463 |
| 38 | Piedras Negras | 237 | 6.181 | 7.334 | 82.844 | 479.262 | 575.858 | 779 |
| 39 | Poza Rica | 112.208 | 1.166.226 | 407.103 | 371.711 | 27.188 | 2.084.436 | 90.571 |
| 40 | Puebla | 199.002 | 2.248.965 | 1.145.822 | 1.054.856 | 1.663.076 | 6.311.721 | 286.370 |
| 41 | Puerto Escondido | 91.244 | 439.963 | 52.082 | 627 | 498 | 584.414 | 47.746 |
| 42 | Puerto Peñasco | 162 | 12.879 | 9.897 | 70.695 | 65.874 | 159.507 | 3.649 |
| 43 | Puerto Vallarta | 393 | 11.731 | 52.330 | 116.038 | 267.187 | 447.679 | 717.630 |
| 44 | Querétaro | 25.224 | 977.129 | 489.350 | 658.327 | 1.292.388 | 3.442.418 | 59.947 |
| 45 | Reynosa | 476 | 7.959 | 23.319 | 128.720 | 591.970 | 752.444 | 188.694 |
| 46 | Saltillo | 2.067 | 70.712 | 44.038 | 27.315 | 1.122.310 | 1.266.442 | 58.499 |
| 47 | San José del Cabo | 976 | 50.237 | 23.094 | 82.172 | 84.480 | 240.959 | 721.150 |
| 48 | San Luis Potosí | 28.101 | 653.836 | 221.703 | 216.837 | 1.058.357 | 2.178.834 | 131.870 |
| 49 | Tampico | 60.805 | 780.255 | 312.313 | 537.753 | 583.557 | 2.274.683 | 396.639 |
| 50 | Tapachula | 36.276 | 560.800 | 145.494 | 219.373 | 1.462 | 963.405 | 181.682 |
| 51 | Tepic | 18.900 | 65.573 | 164.575 | 149.480 | 394.302 | 792.830 | 26.278 |
| 52 | Tijuana | 5.928 | 100.656 | 128.382 | 173.665 | 1.794.878 | 2.203.509 | 3.537.093 |
| 53 | Toluca | 74.171 | 2.096.859 | 671.670 | 1.284.767 | 3.874.370 | 8.001.837 | 2.063.135 |
| 54 | Torreón | 1.899 | 50.673 | 144.148 | 371.717 | 1.028.021 | 1.596.458 | 281.261 |
| 55 | Tuxtla Gutiérrez | 267.839 | 1.461.823 | 511.237 | 542.613 | 6.854 | 2.790.366 | 631.412 |
| 56 | Uruapan | 25.287 | 571.938 | 460.564 | 629.873 | 9.525 | 1.697.187 | 92.405 |
| 57 | Veracruz | 219.012 | 1.041.906 | 337.313 | 657.284 | 889.998 | 3.145.513 | 811.897 |
| 58 | Villahermosa | 239.137 | 1.404.252 | 508.942 | 554.467 | 555.694 | 3.262.492 | 709.496 |
| 59 | Zacatecas | 37.361 | 197.847 | 263.161 | 369.192 | 385.718 | 1.253.279 | 181.097 |
| 60 | Zihuatanejo | 14.867 | 102.371 | 128.074 | 6.850 | 9.258 | 261.420 | 283.745 |
Fuente: Elaboración propia con base en la metodología presentada en este inciso
Tabla 2: Distribución de la población por grado de marginación dentro de cada área de influencia de los aeropuertos en servicio internacional durante 2010 y pasajeros atendidos anualmente
| Aeropuerto | Población por grado de marginación | Población | Pasajeros | |||||
| Muy alto | Alto | Medio | Bajo | Muy bajo | total | atendidos | ||
| 1 | Acapulco | 281.494 | 1.070.334 | 105.121 | 861.549 | 444 | 2.318.942 | 139.275 |
| 2 | Aguascalientes | 2.519 | 168.434 | 211.662 | 684.412 | 779.686 | 1.846.713 | 60.146 |
| 3 | Bahías de Huatulco | 80.286 | 421.286 | 196.022 | 128.982 | 4.574 | 831.150 | 60.286 |
| 4 | Cancún | 12.251 | 251.500 | 144.005 | 809.524 | 152.320 | 1.369.600 | 8.461.921 |
| 5 | Chihuahua | 90.073 | 112.355 | 104.223 | 269.129 | 2.789.854 | 3.365.634 | 53.559 |
| 6 | Ciudad del Carmen | 231 | 33.273 | 1.097 | 192.321 | 19 | 226.941 | 20.596 |
| 7 | Ciudad Victoria | 2.105 | 60.770 | 76.844 | 81.510 | 308.613 | 529.842 | 31 |
| 8 | Cozumel | 15 | 1.863 | 19 | 77.245 | 88 | 79.230 | 365.794 |
| 9 | Culiacán | 28.308 | 323.345 | 345.158 | 375.295 | 1.119.254 | 2.191.360 | 706 |
| 10 | Del Bajío | 14.445 | 587.630 | 469.560 | 1.835.810 | 659.940 | 3.567.385 | 318.735 |
| 11 | Durango | 31.657 | 76.529 | 133.480 | 245.894 | 561.532 | 1.049.092 | 12.804 |
| 12 | Guadalajara | 17.547 | 439.267 | 703.037 | 2.894.977 | 3.119.818 | 7.174.646 | 1.996.639 |
| 13 | Guaymas | 7.398 | 138.842 | 63.472 | 179.743 | 610.446 | 999.901 | 6.920 |
| 14 | Hermosillo | 1.665 | 68.273 | 30.693 | 146.484 | 1.215.786 | 1.462.901 | 72.110 |
| 15 | La Paz | 352 | 7.647 | 4.695 | 8.423 | 223.204 | 244.321 | 20.484 |
| 16 | Loreto | 1.056 | 18.276 | 9.942 | 82.905 | 33.594 | 145.773 | 26.138 |
| 17 | Manzanillo | 14.835 | 117.709 | 286.557 | 134.657 | 477.379 | 1.031.137 | 74.459 |
| 18 | Mazatlán | 15.415 | 109.062 | 157.340 | 183.625 | 381.895 | 847.337 | 338.688 |
| 19 | Mérida | 7.832 | 919.682 | 173.866 | 200.594 | 1.001.012 | 2.302.986 | 86.642 |
| 20 | México | 42.819 | 854.196 | 1.602.525 | 3.077.571 | 12.895.474 | 18.472.585 | 8.363.164 |
| 21 | Minatitlán | 75.811 | 874.312 | 514.652 | 503.393 | 42.973 | 2.011.141 | 46 |
| 22 | Monterrey | 1.339 | 35.281 | 45.441 | 198.001 | 4.554.269 | 4.834.331 | 644.119 |
| 23 | Morelia | 39.032 | 1.073.603 | 704.781 | 821.407 | 688.255 | 3.327.078 | 173.736 |
| 24 | Oaxaca | 102.869 | 858.515 | 230.670 | 394.290 | 53.199 | 1.639.543 | 20.519 |
| 25 | Puebla | 258.327 | 2.929.885 | 1.338.163 | 1.222.023 | 1.663.589 | 7.411.987 | 31.102 |
| 26 | Puerto Vallarta | 9.966 | 41.439 | 120.395 | 180.401 | 661.435 | 1.013.636 | 1.869.873 |
| 27 | Querétaro | 27.619 | 1.075.998 | 525.201 | 722.137 | 1.292.561 | 3.643.516 | 39.316 |
| 28 | Reynosa | 2.944 | 28.582 | 49.603 | 239.374 | 1.067.070 | 1.387.573 | 38 |
| 29 | Saltillo | 2.312 | 76.274 | 48.340 | 101.754 | 1.707.350 | 1.936.030 | 16.296 |
| 30 | San José del Cabo | 976 | 50.237 | 23.094 | 82.172 | 84.490 | 240.969 | 1.904.503 |
| 31 | San Luis Potosí | 28.322 | 661.481 | 223.518 | 216.837 | 1.058.357 | 2.188.515 | 66.932 |
| 32 | Tampico | 102.508 | 1.454.040 | 438.043 | 846.508 | 609.382 | 3.450.481 | 27.500 |
| 33 | Tijuana | 6.204 | 121.827 | 161.083 | 344.025 | 2.683.027 | 3.316.166 | 21.330 |
| 34 | Toluca | 120.486 | 2.449.336 | 873.406 | 1.863.332 | 4.930.279 | 10.236.839 | 88.997 |
| 35 | Torreón | 1.969 | 51.369 | 144.558 | 372.066 | 1.028.051 | 1.598.013 | 44.607 |
| 36 | Tuxtla Gutiérrez | 316.997 | 2.071.869 | 665.591 | 762.381 | 8.316 | 3.825.154 | 5.219 |
| 37 | Veracruz | 284.115 | 1.724.072 | 758.066 | 838.058 | 1.342.170 | 4.946.481 | 34.922 |
| 38 | Villahermosa | 228.179 | 1.408.870 | 532.243 | 554.091 | 555.701 | 3.279.084 | 30.273 |
| 39 | Zacatecas | 40.030 | 200.675 | 265.270 | 369.558 | 385.718 | 1.261.251 | 71.719 |
| 40 | Zihuatanejo | 15.626 | 103.203 | 115.318 | 6.850 | 9.258 | 250.255 | 186.673 |
Fuente: Elaboración propia con base en la metodología presentada en este inciso
Además, el método de isócronas de recorrido estimó que 66.5 % de la población total tiene acceso al servicio aéreo doméstico en un rango de tiempo de una hora. Este valor sube a 89.6, 95, 97 y 98 % para los rangos de hasta dos, tres, cuatro y cinco horas, respectivamente. Para el servicio internacional los porcentajes respectivos desde una hasta cinco horas son: 55.6, 81.7, 90.6, 96 y 98 %.
Análisis estadístico de los pasajeros atendidos y de los diferentes grados de marginación
En este inciso se realizaron análisis estadísticos de regresión lineal simple y múltiple de los pasajeros atendidos y de la población de los cinco distintos grados de marginación, establecidos en el inciso anterior. Además, se determinaron las estadísticas de las regresiones, se detectaron los datos atípicos, se realizaron pruebas de hipótesis junto con sus análisis de varianza y se establecieron los coeficientes estandarizados de la mejor correlación entre las variables explicativas.
Pasajeros en vuelos nacionales considerando todos los grados de marginación
Inicialmente se consideró que la población con los distintos grados de marginación dentro del área de influencia de cada aeropuerto, eran variables determinantes de la cantidad de pasajeros aéreos atendidos (PASAJEROS). Bajo este supuesto, la relación más simple y directa se obtiene mediante la siguiente ecuación:
Esta ecuación se determinó mediante el método de regresión lineal múltiple.
Coeficiente de correlación múltiple = 0.8229
Coeficiente de determinación R2 = 0.6772
R2 ajustado = 0.6473
Se observa que existe una correlación múltiple entre las variables explicativas (la población con los distintos grados de marginación) y la variable explicada (pasajeros) correspondiente a 0.8229, y que el modelo descrito explica 64.73 % de la variabilidad entre los datos, de acuerdo con el coeficiente de determinación R2 ajustado, dado que se está aplicando una técnica de regresión lineal múltiple y tomando en cuenta el número de variables incluidas en el modelo.
Sin embargo, es necesario hacer pruebas de hipótesis sobre los coeficientes encontrados, para determinar si explican la variable con un nivel de significancia aceptable. En este caso β0 es la intersección de la recta de regresión.
Para validar el modelo de regresión se analizó si la variabilidad de PASAJEROS, atribuida al efecto del conjunto de las variables predictoras es lo suficientemente grande, con relación a la variabilidad no explicada o residual. Para este propósito, se utilizó el estadístico F de Fisher. La probabilidad (Pr) asociada al resultado de aplicar esta prueba indica el grado de certidumbre con el que la parte explicativa del modelo y el residual coinciden. Si dicha probabilidad es pequeña (sí es menor que α = 0.05), se concluiría que la parte explicativa supera en cantidad suficiente a la no explicada, por lo que las variables explicativas se considerarían significativas en su conjunto.
Hipótesis alternativa, H1: Existe i = 1,…,5 tal que βi ≠ 0
Para estas hipótesis se utilizó la prueba t, el resultado de aplicar esta prueba puede ser encontrado en el análisis de regresión como el valor p de las betas, si este es menor a 0.05, el coeficiente βi es significativo, como se observa a continuación Pr > |t| (Tabla 3).
Tabla 3: Parámetros de la regresión
| Fuente | Valor | Error estándar | t | Pr > |t| |
| Intersección | -83674.818 | 231585.135 | -0.361 | 0.719 |
| MUY_ALTO | 7.276 | 3.986 | 1.825 | 0.073 |
| ALTO | -2.092 | 0.776 | -2.697 | 0.009 |
| MEDIO | 1.162 | 1.709 | 0.680 | 0.499 |
| BAJO | 0.676 | 0.537 | 1.260 | 0.213 |
| MUY_BAJO | 1.092 | 0.164 | 6.651 | < 0.0001 |
Fuente: Elaboración propia
valor p de β0 = 0.719 > 0.05, luego, el valor de la intersección encontrada no es significativamente aceptable, así, no se rechaza la hipótesis nula; β0 = 0
valor p de β1 = 0.073 > 0.05, luego, no se rechaza la hipótesis nula; β1 = 0
valor p de β2 = 0.009 < 0.05, luego, el valor encontrado para β2 es significativamente aceptable, así, se acepta la hipótesis alternativa; β2 ≠ 0, β2 =-2.092
valor p de β3 = 0.499 > 0.05, luego, el valor encontrado para β3 no es significativamente aceptable, así, no se rechaza la hipótesis nula; β3 = 0
valor p de β4 = 0.213 > 0.05, luego, no se rechaza la hipótesis nula; β4 = 0
valor p de β5 < 0.0001 < 0.05, luego, el valor encontrado para β5 es significativamente aceptable, así, se acepta la hipótesis alternativa; β5 ≠ 0, β5 = 1.092
Luego, se corre nuevamente el modelo de regresión, pero únicamente con las variables MUY_BAJO y ALTO, con la constante de intersección igual a cero (Tabla 4).
Tabla 4: Parámetros de la regresión
| Fuente | Valor | Error estándar | t | Pr > |t| |
| Intersección | 56093.31 | 232110.98 | 0.24166 | 0.8099 |
| ALTO | -0.7253 | 0.3444 | -2.10568 | 0.0396 |
| MUY_BAJO | 1.2342 | 0.1237 | 9.97359 | < 0.0001 |
Fuente: Elaboración propia
Así, la ecuación (1) se modifica como:
Es conveniente notar los signos que acompañan a las variables MUY_BAJO y ALTO. Ya que el primero tiene signo positivo, lo que significa que contribuye de forma directa a la variable PASAJEROS. Por el contrario, la variable ALTO presenta un signo negativo, así que su contribución es opuesta a la anterior, es decir, a mayor magnitud de población con grado de marginación ALTO, se espera una menor demanda de PASAJEROS y viceversa. A continuación, se depurarán los datos para mejorar el modelo.
Pasajeros en vuelos nacionales, excluyendo datos atípicos y considerando todos los grados de marginación
Para determinar los datos atípicos se realizó un análisis de residuales. Un residual ri es la diferencia entre el valor observado Yi y el valor estimado por la línea de regresión Ŷi, es decir:
El residual puede ser considerado como el error aleatorio ei observado.
En la Figura 5 se presentan los residuales estandarizados para los distintos aeropuertos (observaciones) con objeto de detectar datos discrepantes. Al utilizar los residuales estandarizados, un dato más allá de 2 o -2 es considerado atípico. Por lo tanto, las observaciones 5 (aeropuerto de Cancún), 31 (aeropuerto de México) y 37 (aeropuerto de Pachuca) son atípicas.

Fuente: Elaboración propia
Figura 5: Residuales estandarizados para determinar datos atípicos en el servicio nacional
A continuación, se realizó el análisis de regresión múltiple, pero sin los datos discrepantes, con lo que se obtuvo la siguiente ecuación:
Con un R2 ajustado de 0.647411.
Por otra parte, para establecer estimaciones adecuadas de los coeficientes de las ecuaciones se requiere que las variables explicativas no presenten correlaciones altas entre sí. Se dice que los coeficientes de la ecuación múltiple son coeficientes de correlación parcial por lo que, en caso de existir gran colinealidad entre los predictores (variables independientes), las estimaciones de regresión lineal hechas para cada regresora diferirán considerablemente respecto a los resultados obtenidos, lo cual nos interesa ampliamente en nuestro caso. En la Tabla 5 se presentan los coeficientes de correlaciones, observe que se han subrayado los más altos, que corresponden a ALTO y MEDIO (0.779) y después a MUY_ALTO y ALTO (0.748).
Tabla 5: Coeficientes de correlaciones
| MUY_ALTO | ALTO | MEDIO | BAJO | MUY_BAJO | PASAJEROS | |
| MUY_ALTO | 1 | 0.748 | 0.469 | 0.258 | -0.057 | -0.086 |
| ALTO | 0.748 | 1 | 0.779 | 0.449 | 0.145 | -0.054 |
| MEDIO | 0.469 | 0.779 | 1 | 0.721 | 0.516 | 0.326 |
| BAJO | 0.258 | 0.449 | 0.721 | 1 | 0.571 | 0.486 |
| MUY_BAJO | -0.057 | 0.145 | 0.516 | 0.571 | 1 | 0.780 |
| PASAJEROS | -0.086 | -0.054 | 0.326 | 0.486 | 0.780 | 1 |
Fuente: Elaboración propia
Ya que las variables utilizadas dadas su significancia estadística son MUY_BAJO y ALTO, los altos grados de correlación mencionados no son de importancia.
Pasajeros en vuelos nacionales con base en el grado de marginación MUY_BAJO
En este inciso, se realiza una regresión lineal simple, considerando al número de pasajeros como la variable dependiente y a la población con el grado de marginación MUY_BAJO como la variable independiente, sin considerar los datos atípicos.
Se busca una relación que explique de la mejor forma posible a los datos mediante una ecuación de la forma:
De acuerdo con el análisis de regresión se estimaron los coeficientes β0 y β1, estableciéndose la siguiente relación:
Coeficiente de correlación múltiple = 0.7983
Coeficiente de determinación R2 = 0.6372
R2 ajustado = 0.6307
Así, la ecuación (4) es útil para modelar 63.72 % de los datos, en donde PASAJEROS es la variable dependiente de MUY_BAJO (variable independiente). Por otra parte, es necesario realizar una prueba de hipótesis para determinar si el valor verdadero de las betas es distinto de cero y así definir si el coeficiente estimado explica a la variable con un nivel de significancia aceptable. En este caso β0 es la intersección de la recta de regresión y β1 es la razón estimada entre la variable dependiente (PASAJEROS) y la independiente (MUY_BAJO) (Tabla 6).
Tabla 6: Parámetros de la regresión
| Fuente | Valor | Error estándar | t | Pr > |t| |
| Intersección | 55901.714 | 99729.378 | -0.561 | 0.577 |
| MUY_BAJO | 0.902 | 0.092 | 9.831 | < 0.0001 |
Fuente: Elaboración propia
De acuerdo con el análisis de varianza:
valor p de β0 = 0.577 > 0.05, no se rechaza la hipótesis nula; β0 = 0
valor p de β1 < 0.0001 < 0.05, luego, se acepta la hipótesis alternativa; β1 ≠ 0, β1 = 0.902
Por lo que la ecuación lineal presentada arriba (4), es válida.
Pasajeros en vuelos nacionales para los otros cuatro grados de marginación
Similarmente, como en el caso anterior aplicando un análisis de regresión lineal simple, se estimaron las ecuaciones para los grados de marginación BAJO, MEDIO, ALTO y MUY_ALTO en forma individual, sin embargo, se obtuvieron valores de R2 muy bajos. Por lo que las regresiones lineales con grado de marginación BAJO (R2 = 0.179), MEDIO (R2 = 0.0112), ALTO (R2 = 0.001) y MUY_ALTO (R2 = 0.00022), no explican individualmente de manera significativa a la variable PASAJEROS mediante un análisis de regresión simple.
Por lo anterior, se trataron de ajustar en cada caso los datos con una ecuación polinómica, de grado 2, 3, 4 y 5. Sin embargo, en todos los casos se obtuvieron valores de R2 con un valor casi igual a cero, y no hubo variables con valor p significativo. Por lo que, la mejor opción para describir la variable PASAJEROS con una sola variable solo se presentó en el caso del grado de marginación MUY_BAJO (inciso anterior).
Pasajeros en vuelos nacionales, con base en los grados de marginación MUY_BAJO, BAJO, MUY_ALTO y ALTO
En este caso:
Con un R2 ajustado igual a 64.74 %.
De acuerdo con la ecuación (5), por cada unidad que aumenta la variable ALTO (a mayor población con grado de marginación), disminuye -0.2964 la variable PASAJEROS, es decir, mientras mayor sea la población con grado de marginación alto, disminuye la demanda de pasajeros en el aeropuerto. También, se observa que por cada unidad que aumenta MUY_BAJO, aumenta 0.9411 PASAJEROS.
A continuación, se estiman los coeficientes estandarizados del análisis anterior de regresión múltiple (Tabla 7).
Tabla 7: Parámetros de la regresión (coeficientes estandarizados)
| Fuente | Valor | Error estándar | t | Pr > |t| |
| MUY_ALTO | 0.320 | 0.114 | 2.799 | 0.007 |
| ALTO | -0.500 | 0.123 | -4.066 | 0.000 |
| BAJO | 0.211 | 0.091 | 2.309 | 0.025 |
| MUY_BAJO | 0.828 | 0.084 | 9.844 | < 0.0001 |
Fuente: Elaboración propia
La ventaja de estos coeficientes, sobre los no estandarizados, es la posibilidad de poder evaluar y comparar el poder explicativo de cada predictor en la ecuación, al ser directamente comparables. Como el coeficiente βi es solo una tasa de cambio, esta se mide en las unidades de la relación: Unidades de la variable dependiente / Unidades de la variable explicativa. Para estimar una variable estandarizada, al valor individual de dicha variable se le debe restar el valor de su media, y dividir esa diferencia entre su desviación estándar. En la regresión de Y y X, se definen como:
Donde:
Yi* , Xi* = |
Variables estandarizadas |
ˉY = |
Media muestral de Y |
ˉX= |
Media muestral de X |
SY = |
Desviación estándar muestral de Y |
SX = |
Desviación estándar muestral de X |
Los coeficientes estandarizados establecen una escala única (en desviaciones típicas respecto al cero) sobre la que se miden las diferentes variables y, por lo tanto, constituyen la base para conocer comparativamente en cuántos puntos modifica la variable Y por cuenta de cada variable regresora. Transformando la ecuación a su forma estandarizada, los coeficientes son ahora directamente comparables.
Así, sí se mantienen constantes a ALTO, BAJO y MUY_BAJO, un aumento igual a una desviación estándar en MUY_ALTO ocasiona, en promedio, un aumento de 0.320 desviación estándar en PASAJEROS. Aplicando un análisis análogo para el resto de las variables, se observa que la variable con el mayor impacto en PASAJEROS es la variable MUY_BAJO. Sí se mantienen constantes MUY_ALTO, ALTO y BAJO, un aumento de una desviación estándar en la variable MUY_BAJO ocasiona, en promedio, un aumento de 0.828 desviación estándar en la variable PASAJEROS.
Pasajeros en vuelos internacionales considerando todos los grados de marginación
Se realizó un análisis similar al aplicado para los vuelos nacionales (sección anterior). En particular, con base en el análisis de los residuos estandarizados se encontró solo un valor atípico (+ 5.019), que correspondió al aeropuerto de Cancún. Posteriormente, al depurar el modelo mediante un análisis de regresión múltiple que consideró a todos los grados de marginación, pero que excluyó al valor discrepante, se determinó que tres de las cinco variables son significativas. Las variables a considerar entonces son ALTO, MEDIO y MUY_BAJO, por lo que se realizó nuevamente el modelo de regresión, pero únicamente con estas tres variables, sin el valor discrepante y con la constante de intersección igual a cero (ecuación 7).
Se obtuvo un R2 ajustado igual a 75.64 %.
En este caso, al estimar los coeficientes estandarizados, para hacerlos directamente comparables se obtuvo la relación (8).
Por otra parte, se realizó un análisis de regresión lineal simple para cada variable explicativa en forma individual. Para el grado de marginación MUY_BAJO se encontró:
Con R2 igual a 67.41 %.
Sin embargo, para el resto de las variables se estimaron valores de R2 muy bajos. Por lo que, las regresiones lineales con grado de marginación BAJO (R2 = 0.3844), MEDIO (R2 = 0.2815), ALTO (R2 = 0.000233) y MUY_ALTO (R2 = 0.0104), no explican de manera significativa a la variable PASAJEROS en el análisis de regresión simple.
Discusión y análisis de resultados
Para delimitar las áreas de influencia, mediante los modelos de accesibilidad espacial, se requirió de una gran capacidad de cómputo para su ejecución. Se utilizó una máquina virtual con cuatro procesadores de ocho núcleos cada uno y memoria RAM mayor a 128 GB, el tiempo de ejecución de cada modelo (doméstico e internacional) fue de aproximadamente cuatro horas.
Se observó que, dentro del intervalo de dos horas, la mayor parte de la población tiene acceso al servicio aéreo doméstico e internacional, 89.6 % y 81.7 % de la población total, respectivamente.
Se detectó que el número de pasajeros atendidos anualmente en algunos aeropuertos es mayor que la población total dentro de sus respectivas áreas de influencia. En el caso del servicio nacional esto se presentó en los aeropuertos de la Ciudad de México, Cancún, Tijuana, San José del Cabo, Puerto Vallarta, Monterrey, La Paz, Zihuatanejo y Ciudad del Carmen; y en el internacional solo en Cancún, San José del Cabo, Puerto Vallarta y Cozumel.
En el caso del servicio nacional, los datos atípicos correspondieron a los aeropuertos de la Ciudad de México, Cancún y Pachuca, con un residual estandarizado positivo para los dos primeros (+ 3.744 y + 2.336, respectivamente) y negativo para el tercero (- 4.746). Esto significa que en el caso del Aeropuerto Internacional de la Ciudad de México (AICM) y Cancún los valores reales de pasajeros atendidos son mayores que los que estimó el modelo inicial, en cambio, para el aeropuerto de Pachuca sucede lo contrario. En otras palabras, el AICM y el aeropuerto de Cancún están atendiendo más pasajeros de los que explica la población incluida dentro de su área de influencia, considerando sus distintos grados de marginación. Se debe recordar que uno de los supuestos para delimitar el área de influencia de cada aeropuerto fue que todos los aeropuertos ofrecían los mismos servicios, sin embargo, esto no sucede en todos los casos. De hecho, el AICM es el principal centro concentrador y distribuidor (hub) de pasajeros domésticos (Tabla 1), debido a que ofrece mayor conectividad que cualquier otro aeropuerto nacional, aunque con menor importancia en este sentido el aeropuerto de Cancún también destaca en conectividad. Esto explicaría por qué estos dos aeropuertos atienden más pasajeros que lo que estima el modelo inicial. En el caso de Pachuca con un residual estandarizado negativo, el modelo inicial indica que de acuerdo con la población comprendida dentro de su área de influencia y considerando sus distintos grados de marginación, debería atender más pasajeros. La explicación de por qué no atiende un mayor número de pasajeros, como debería, tiene que ver con su falta de conectividad aérea, la cual, a su vez, se relaciona con su cercanía al principal hub nacional (el AICM), y a que, además debe competir con los aeropuertos aledaños de Toluca, Puebla e incluso Querétaro.
En el caso del servicio internacional solo se presentó un valor atípico (+ 5.019), que correspondió al aeropuerto de Cancún. El residual estandarizado indica que el valor real de los pasajeros atendidos en este aeropuerto, es mayor que lo estimado por el modelo inicial. La explicación en este caso tiene dos vertientes, la primera se debe a que este aeropuerto es el principal hub internacional, superando incluso al AICM (Tabla 2), por lo que tiene gran conectividad con el extranjero y, de esta forma, atiende pasajeros de otras áreas de influencia de aeropuertos con menor conectividad internacional. La segunda explicación, tiene que ver con el hecho de que, al tratarse de vuelos internacionales, hay un componente de la demanda que no proviene de la zona de influencia del aeropuerto dentro del territorio nacional, sino del extranjero; y ese componente no está considerado dentro del modelo, el cual únicamente considera los grados de marginación dentro de las aéreas de influencia en México, pero no los de los aeropuertos de origen o destino en el extranjero.
En el análisis de regresión lineal simple se encontró que las mejores relaciones para explicar a la variable dependiente PASAJEROS, corresponden a la variable independiente MUY_BAJO, tanto para el servicio nacional como para el internacional.
Por otra parte, con base en la regresión lineal múltiple en el servicio nacional la mejor estimación para la variable PASAJEROS se obtuvo con las variables ALTO y MUY_BAJO; y de acuerdo con la evaluación de los coeficientes estandarizados, la variable que tuvo mayor relevancia para los pasajeros atendidos fue MUY_BAJO. En cambio, en el servicio internacional la mejor estimación se obtuvo con base en las variables ALTO, MEDIO y MUY_BAJO; y de acuerdo con los coeficientes estandarizados, la variable que tuvo mayor impacto fue MEDIO.
Conclusiones
Esta es la primera vez que se estima un modelo de demanda para todos los aeropuertos nacionales considerando la accesibilidad espacial y el grado de marginación de la población, anteriormente, solo se habían desarrollado modelos regionales.
Los modelos para determinar la demanda de pasajeros para cada aeropuerto en función de la población clasificada, de acuerdo con su grado de marginación, quedaron definidos por las ecuaciones 5 y 7, para los servicios domésticos e internacionales, respectivamente. Sin embargo, se debe tener presente que en algunos aeropuertos otras características no consideradas pueden modificar las estimaciones, lo que abre las posibilidades de mejora para estudios futuros. Aún con todo, los modelos obtenidos brindan una aproximación para estimar la demanda de pasajeros, el modelo para el servicio nacional explica un 64.74 % de la variabilidad de los datos y 75.64 % en el servicio internacional.
En el servicio nacional, de acuerdo con su ubicación y características de población, el aeropuerto de Pachuca presenta potencial para incrementar sus servicios. De esta forma, atendería la demanda potencial que tiene y que es atendida en otros aeropuertos cercanos. Para ello, se debe incentivar la utilización de sus servicios, por ejemplo, incrementando su conectividad aeroportuaria.











 nueva página del texto (beta)
nueva página del texto (beta)




