Introducción
La energía geotérmica es un tipo de energía renovable y abundante que solo se puede utilizar de acuerdo con las características térmicas de la misma (Ramazankhani et al., 2016). Por ejemplo, la energía geotérmica de alta temperatura (T > 150 °C) se utiliza principalmente para la producción de electricidad mediante plantas “single flash”o “doble flash”, mientras que la energía geotérmica de media temperatura (100 - 150 °C) y de baja temperatura (T < 100 °C) se utiliza para la producción de electricidad mediante máquinas ORC y para diversos usos directos (Kanoglu et al., 2010). Adicionalmente, dentro de los principales usos de la energía geotérmica también se pueden distinguir varias categorías que incluyen, la producción de frío mediante tecnologías de refrigeración activadas térmicamente y el secado de productos frescos mediante procesos de deshidratación (Kanoglu et al., 2016). Esta variedad de usos, hace posible la integración de sistemas de conversión de energía más eficientes, como el denominado uso en cascada geotérmica. La utilización en cascada utiliza el recurso geotérmico para producir varios productos simultáneamente y es una forma eficiente de aprovechar la energía geotérmica disponible tras haber sido utilizada previamente, beneficiándose en diferentes usos de menor requerimiento de temperatura. Normalmente, tras la producción eléctrica, el fluido aún caliente puede aprovecharse para otros usos con menores requerimientos de temperatura, como lo son: la refrigeración y la deshidratación (Rubio et al., 2015).
Alrededor del mundo se pueden encontrar algunas aplicaciones prácticas. Por ejemplo, el desarrollo en cascada construido en Canby, California, que consiste de una planta ORC de 50 kW, invernaderos, calefacción de distrito y acuicultura (Lund et al., 2006 y Merrick, 2013). En Reno, Nevada, se reporta otra instalación conformada por una planta de potencia y un sistema de deshidratación de cebolla y ajo (Gordon, 2004). En Chena (Alaska) se ha implementado la energía geotérmica en cascada para mantener la temperatura de un museo de hielo y la temperatura de una piscina (Erickson et al., 2005). Otros sistemas similares se pueden encontrar en Islandia, como es el caso de la planta de ciclo Kalina en Husavik, donde el calor residual se emplea en usos directos; y la planta Svartsengi instalada en la península de Reykjanes, donde el calor residual se utiliza en la famosa “Laguna Azul” (Eliasson et al., 2003 y Thorolfsson, 2005). Desde el punto de vista teórico también se encuentran propuestas más complejas de uso en cascada. Nevton et al., (2012), han presentado un concepto innovador con uso híbrido de energía solar y energía geotérmica, mediante lo que denominan multi-centros de servicios que incluyen spa, gimnasio y piscinas termales, así como invernaderos y agricultura. Estos sistemas reflejan los esfuerzos internacionales para mostrar la aplicación práctica de la utilización en cascada. Sin embargo, los métodos de diseño, síntesis y evaluación del desempeño energético no son reportados, y únicamente se presentan algunos datos técnicos de operación.
Dado que la viabilidad de la utilización en cascada se ha presentado en diversas aplicaciones prácticas, estos sistemas se están estudiando desde diferentes perspectivas para determinar las mejores condiciones energéticas para su implementación. En este sentido, el análisis exergético ha demostrado ser una poderosa herramienta para identificar y ubicar la magnitud y las causas de las ineficiencias termodinámicas en los sistemas térmicos (Torchia et al., 2010 y Marín et al., 2009). Luo et al., (2016), han analizado diferentes regímenes de temperatura para la integración en cascada del agua geotérmica residual, incorporando varios criterios para la evaluación y selección con base en un proceso analítico jerárquico. En el estudio se identifica el esquema de temperaturas óptimas del sistema que mejoran la eficiencia energética, exergética y presenta viabilidad económica. Arslan et al., (2010), han estudiado diversos conceptos de utilización en cascada de la energía geotérmica, usando métodos de exergía y costo de ciclo de vida para obtener un estudio de pre-factibilidad. Alzaharani et al. (2013), han propuesto y analizado termodinámicamente un sistema en cascada compuesto por un ciclo de Rankine, un electrolizador y un sistema de recuperación de calor, mostrando la factibilidad de la propuesta. Ratlamwala et al. (2012), han propuesto y analizado un sistema integrado para producción de electricidad, calefacción, refrigeración y producción de agua caliente. En el estudio reportado se lleva a cabo una evaluación del desempeño termodinámico, evaluando las eficiencias energéticas y exergéticas, identificando los parámetros de operación para diversas temperaturas del fluido geotérmico. En el mismo sentido, Fu et al. (2013), presentan una evaluación del ciclo de Kalina (KC) activado mediante energía geotérmica y acoplado a procesos en campos petroleros. En la investigación establecen un modelo matemático del KC y una optimización mediante el análisis de las eficiencias exergéticas.
Como puede apreciarse, los métodos convencionales basados en exergía se han aplicado durante las últimas décadas para mejorar la eficiencia energética o para reducir el consumo de energía en plantas geotérmicas de potencia. Sin embargo, en la revisión de la literatura no se identifican trabajos o investigación relacionados con el análisis exergético convencional de plantas de poligeneración operando en cascada geotérmica. El presente estudio ha sido motivado por lo expuesto anteriormente y pretende llenar este vacío en la literatura. El alcance de este trabajo radica en determinar el desempeño exergético al que aspira una planta de poligeneración operando bajo diferentes criterios de eficiencia. El objetivo principal es aplicar el análisis exergético convencional para determinar el desempeño exergético de la planta de poligeneración e identificar los componentes con mayor destrucción de exergía operando en condiciones reales, inevitables e ideales.
Descripción de la planta de poligeneración en cascada
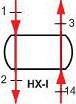
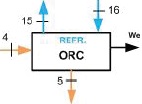
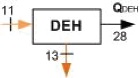
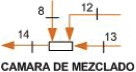
La planta de poligeneración está integrada por tres componentes principales; un ciclo ORC, una máquina de absorción (TAR) y un deshidratador (DEH). La planta se activa mediante un recurso geotérmico a una temperatura de 120 °C a razón de 8.42 kg/s. Mediante este recurso y por integración apropiada de los componentes mencionados anteriormente, la planta tiene la capacidad de producir en condiciones de diseño (condiciones que se denominaran reales para los efectos del presente estudio), 40 kWe mediante el ORC, 50 toneladas de refrigeración (a 5°C) mediante la TAR y destinar 30 kWt para operar el DEH. Una particularidad del sistema es que de las 50 TR producidas por la TAR, 25 TR son utilizadas para mantener el condensador del ORC a una temperatura más estable y 25 TR son empleadas para la conservación de producto fresco. En el sistema existen dos circuitos principales: uno de aporte térmico denominado circuito caliente y otro de rechazo de calor; el primero está formado por las corrientes 3-14 y el segundo por las corrientes 17-21, respectivamente. Más detalles de los equipos que conforman la planta y las corrientes que los unen se pueden ver en la Figura 1.
Análisis termodinámico
El análisis del sistema se efectuará utilizando la primera y segunda leyes de la termodinámica y la definición del Fuel-Product aplicada a cada componente del sistema, denominado genéricamente como componente (kth), y finalmente obtener la exergía destruida.
Consideraciones para el modelado
Las principales suposiciones para el análisis de la planta geotérmica en cascada son las siguientes:
El sistema opera en condiciones de estado estacionario y los cambios en energía cinética y potencial son despreciados.
El fluido de aporte térmico se tratará como agua caliente en la fase de líquido incompresible.
La variación de temperatura en el fluido de trabajo ocasionado por las válvulas y equipo de bombeo se desprecia.
El calor especifico del agua se asume constante con un valor de 4.19 kJ/kg K.
La diferencia de temperaturas del agua caliente entre la entrada y la salida del ORC, TAR y DEH se mantiene con un valor constante de 10 °C para los casos real, inevitable e ideal, (Ambriz et al., 2017).
El análisis exergético convencional requiere establecer unas condiciones denominadas reales, inevitables e ideales. Por esta razón, primeramente es necesario desarrollar y resolver el modelo termodinámico del sistema bajo condiciones reales para obtener el flujo másico requerido por cada componente. Una vez determinados estos flujos de masa, deben permanecer constantes para el análisis del sistema y tener una misma base comparativa. De esta forma, es posible observar las prestaciones energéticas y exergéticas del sistema cuando opera a diferentes condiciones. La Tabla 1 muestra la definición de parámetros reales, ideales e inevitables para el análisis de cada componente del sistema (HX-I y HX-II son las designaciones abreviadas para los intercambiadores de calor de la Figura 1).
Tabla 1: Consideraciones real, ideal e inevitable
| Componente | Parámetro | Real | Inevitable | Ideal |
|---|---|---|---|---|
| HX-I |
|
45% | 49.5% | 89.89% |
| ORC |
|
8% | 8.8% | 22.85% |
| TAR |
|
0.68 | 0.748 | 1.45 |
| DEH |
|
75% | 82.5% | 89% |
| HX-II |
|
35% | 38.5% | 43% |
Es necesario mencionar que las condiciones reales han sido obtenidas de las fichas técnicas de cada componente de la planta, y para el caso de las condiciones inevitables se ha supuesto un incremento en los parámetros de rendimiento de 10%, respecto de las condiciones reales. Para las condiciones ideales se ha utilizado la eficiencia de Carnot para el caso del ciclo ORC, el COP máximo teórico para el caso de la TAR y, para el caso de los intercambiadores de calor se ha utilizado la máxima efectividad posible, la cual ocurre cuando no se presenta destrucción de exergía dentro del componente (Moran, 2006).
Análisis exergético convencional
Las ecuaciones básicas necesarias para llevar a cabo el análisis exergético convencional para cada componente kth del sistema (HX-I, ORC, TAR, DEH, Cámara de mezclado, HX-II, Torre de refrigeración y Cámara de conservación) se presentan en las Ecuaciones (1) a (3). Estas expresiones están escritas utilizando la terminología Fuel-Product. A partir de estas ecuaciones se puede determinar el balance exergético de cada componente y del sistema global, (Morosuk et al., 2013).
Donde
|
= la tasa de exergía del Fuel, la exergía del producto y la exergía interna destruida en el componente kth |
tot |
= cantidad total del sistema global |
|
= pérdida de exergía total del sistema |
Las expresiones (4)-(6), necesarias para el análisis, representan respectivamente, la eficiencia exergética, la relación de destrucción de exergía y la relación de destrucción de exergía del componente, respecto a la destrucción de exergía total del sistema, (Galindo et al., 2016).
A nivel de componentes, los flujos de exergía están asociados con el combustible o el producto en cada componente. Por lo tanto, la pérdida de exergía (exergía destruida debido a la irreversibilidad dentro de un sistema) en el componente kth está relacionada con la transferencia de energía térmica a temperatura ambiente. La pérdida de exergía es la transferencia de exergía del sistema al entorno. Teniendo en cuenta los límites del análisis de componentes fijados a temperatura ambiente, la pérdida de exergía es cero y las ineficiencias termodinámicas consisten sólo en destrucción de exergía (Kelly et al., 2009). Los balances de energía, parámetros termodinámicos de eficiencia y balances de exergía para la planta geotérmica en cascada se presentan en las Tablas 2-4.
Tabla 3: Parámetros termodinámicos de eficiencia
| Componente kth | Parámetro de eficiencia |
|---|---|
| HX-I |
|
| ORC |
|
| TAR |
|
| HX-II |
|
Tabla 4: Ecuaciones del balance de exergía
| Componente kth del ciclo | Balance de exergía | *También para el balance de exergía con Eq. (2) | |
|---|---|---|---|
| Fuel | Producto | ||
| HX-I |
|
|
|
| ORC |
|
|
|
| TAR |
|
|
|
| DEH |
|
|
|
| Cámara de Mezclado |
|
|
|
| HX-II |
|
|
|
| Torre de Refrigeración |
|
|
|
| Cámara de Conservación |
|
|
|
Resultados y discusión
Las ecuaciones fueron codificadas y resueltas en el software EES utilizando los datos de la Tabla 1, así como las suposiciones establecidas. En primer lugar, se resolvió el caso correspondiente a las condiciones de diseño (o reales para propósitos de este trabajo), posteriormente se resolvió el caso para las condiciones ideales y finalmente para las condiciones inevitables, obteniendo de esta manera, las prestaciones energéticas del sistema y de cada uno de los componentes asociados. En primer lugar la Tabla 5 muestra la potencia, la capacidad de enfriamiento de la TAR, el calor de deshidratación y la eficiencia energética del sistema global para todos los casos analizados. Puede verse que la eficiencia del sistema en condiciones reales es la menor (30.78%), debido a que los equipos que conforman la planta operando bajo estas condiciones alcanzan una menor eficiencia. La eficiencia de la planta en condiciones inevitables es de 33.96%, mientras que la eficiencia máxima teórica es de 65.72%.
Tabla 5: Productos y rendimiento para condiciones ideales, inevitables y reales
| Parámetro | Real | Inevitable | Ideal |
|---|---|---|---|
|
|
40 | 44 | 114.2 |
|
|
500 | 500 | 500 |
|
|
175.8 | 193.4 | 375 |
|
|
258.6 | 258.6 | 258.6 |
|
|
30 | 33 | 35.6 |
|
|
30.78 | 33.96 | 65.72 |
Los principales parámetros que comprueban este comportamiento son la eficiencia y los flujos másicos. Los flujos másicos se han obtenido con el sistema (planta de poligeneración) operando bajo condiciones reales y esta misma distribución de flujos se ha considerado fija para los principales componentes cuando el sistema opera bajo condiciones inevitables e ideales. Por esta razón, el calor de activación del ciclo ORC y la TAR (500 kW, 258.6 kW) se mantienen constantes para los tres casos, cambiando únicamente la magnitud de los productos debido a los cambios en los parámetros de eficiencia y conversión de energía (Tabla 5). Finalmente, la producción de potencia eléctrica (W e,ORC ), producción de frio (Q FRIO,TAR ) y calor útil (Q DEH ), quedan limitados a los valores obtenidos del sistema operando bajo las condiciones de operación inevitables (44 kW, 193.4 kW, 33 kW). Se espera que mediante futuras mejoras en el diseño y manufactura de los componentes, se puedan reducir las irreversibilidades y mejorar los valores obtenidos. Sin embargo, hay que considerar que los valores máximos corresponden al caso ideal sin presencia de irreversibilidades/ y establecen los valores límite que podrían alcanzarse. En este estudio estos valores son 114.2 kW para la potencia eléctrica, 375 kW de capacidad de enfriamiento y 35.6 kW térmicos para deshidratación.
Otra ventaja del análisis exergético convencional es que permite detectar en magnitud cuáles son los equipos del sistema que destruyen una mayor cantidad de energía disponible. La Tabla 6, muestra resultados para el análisis exergético convencional cuando el sistema opera bajo condiciones reales. En este sentido las tecnologías que destruyen una mayor cantidad de exergía es el HX-I (44.05 kW), el ORC (44 kW) y la TAR (21.85 kW). El resto de los equipos tienen una destrucción de exergía inferior comparada con el resto de componentes. La eficiencia exergética de la planta operando bajo condiciones reales alcanza un valor de 26.97%, para un producto total de 47.17 kW y una exergía del Fuel de 174.9 kW.
Tabla 6: Resultados del análisis exergético convencional, condiciones reales
| Componente |
|
|
|
ε (%) | yk (%) |
|
|---|---|---|---|---|---|---|
| HX-I | 174.9 | 130.9 | 44.05 | 74.81 | 25.19 | 34.49 |
| ORC | 88.05 | 40 | 44 | 45.43 | 49.96 | 34.44 |
| TAR | 37.19 | 10.32 | 21.85 | 27.74 | 58.75 | 17.1 |
| DEH | 4.739 | 3.159 | 1.58 | 66.66 | 33.34 | 1.273 |
| Cámara de mezclado | 88.64 | 87.76 | 0.8725 | 99.02 | 0.9844 | 0.683 |
| HX-II | 5.158 | 0.2449 | 4.913 | 4.748 | 95.25 | 3.847 |
| Torre de refrigeración | 9.327 | 0 | 9.327 | 0 | 100 | 7.302 |
| Cámara de conservación | 5.158 | 4.01 | 1.148 | 77.75 | 22.25 | 0.898 |
| Total planta poligeneración | 174.9 | 47.17 | 127.7 | 26.97 | 73.03 | 100 |
La Tabla 7 muestra los resultados de la planta operando bajo condiciones inevitables. Bajo estas condiciones de análisis, los componentes que destruyen una mayor cantidad de exergía son el ORC (45.35 kW), el HX-I (38.59 kW) y la TAR (23.74 kW), respectivamente. Por otro lado, el ORC es el que destruye una mayor cantidad de exergía comparado con el caso real donde el HX-I es el que destruye una mayor cantidad de exergía. Esto se atribuye a que la efectividad del HX-I juega un papel importante, es decir, a mayor efectividad menor destrucción de exergía. Otro factor se atribuye a la influencia que tienen los componentes externos del sistema sobre el componente. Adicionalmente, el producto total de la planta operando bajo condiciones inevitables es de 52.04 kW, la destrucción de exergía total de 122.9 kW con una eficiencia exergética de 29.75% y la exergía del Fuel de 174.9 kW. Tanto el producto del sistema como la eficiencia exergética global son mayores para el caso inevitable comparado con el caso real, lo que resulta también en una menor destrucción de exergía.
Tabla 7: Resultados del análisis exergético convencional, condiciones inevitables
| Componente | Ė F (kW) | Ė P (kW) | Ė D (kW) | (%) | y k (%) | y* k (%) |
|---|---|---|---|---|---|---|
| HX-I | 174.9 | 139.3 | 35.59 | 79.65 | 20.35 | 29.64 |
| ORC | 93.2 | 44 | 45.35 | 57.21 | 48.66 | 36.91 |
| TAR | 40.06 | 11.1 | 23.74 | 27.7 | 59.25 | 19.32 |
| DEH | 5.21 | 3.875 | 1.335 | 74.38 | 25.62 | 1.087 |
| Cámara de mezclado | 106.5 | 105.7 | 0.8495 | 99.2 | 0.7974 | 0.691 |
| HX-II | 5.548 | 0.307 | 5.241 | 5.535 | 94.47 | 4.226 |
| Torre de refrigeración | 9.382 | 0 | 9.382 | 0 | 100 | 7.636 |
| Cámara de conservación | 5.548 | 4.164 | 1.384 | 75.05 | 24.95 | 1.127 |
| Total planta poligeneración | 174.9 | 52.04 | 122.9 | 29.75 | 70.4 | 100 |
La Tabla 8 muestra resultados del análisis exergético de la planta operando bajo condiciones ideales. En este caso se observa una gran diferencia en el producto del sistema (E P =127.7 kW), una mayor eficiencia exergética (73%) y una menor destrucción de exergía del sistema (47.22 kW). Para este caso, la destrucción de exergía de los equipos principales es cercana a cero, debido a que operan bajo su máxima eficiencia teórica. Sin embargo, se puede ver que la torre de enfriamiento tiene la mayor destrucción de exergía, lo que se atribuye a la disipación del calor de la planta al medio ambiente. Para todos los casos, real, ideal e inevitable, la exergía del Fuel se ha mantenido constante (174.9 kW), ya que se ha mantenido fija la temperatura de 120 °C y el flujo de 8.42 kg/s proveniente del pozo geotérmico, y de esta forma tener una misma base comparativa. En otras palabras, el recurso geotérmico para todos los casos analizados permanece con la misma magnitud.
Tabla 8: Resultados del análisis exergético convencional, condiciones ideales
| Componente | Ė F (kW) | Ė P (kW) | Ė D (kW) | (%) | y k (%) | y* k (%) |
|---|---|---|---|---|---|---|
| HX-I | 174.9 | 174.8 | 0.06646 | 99.96 | 0.038 | 0.1408 |
| ORC | 114.8 | 114.7 | 0.3814 | 99.51 | 0.332 | 0.807 |
| TAR | 52.1 | 20.88 | 23.88 | 40.09 | 45.85 | 50.58 |
| DEH | 7.179 | 5.983 | 1.196 | 83.35 | 16.65 | 2.532 |
| Cámara de mezclado | 204.7 | 204 | 0.7571 | 99.63 | 0.3698 | 1.604 |
| HX-II | 10.44 | 2.114 | 8.329 | 20.24 | 79.76 | 17.64 |
| Torre de refrigeración | 9.62 | 0 | 9.62 | 0 | 100 | 20.32 |
| Cámara de conservación | 10.44 | 7.458 | 2.985 | 71.42 | 28.58 | 6.321 |
| Total planta poligeneración | 174.9 | 127.7 | 47.22 | 73 | 27 | 100 |
Como es de apreciarse en las Tablas 6, 7 y 8, a medida que se incrementan el valor de los parámetros de eficiencia de las diferentes componentes, se incrementan también los productos a nivel sistema global y también a nivel componente. Del mismo modo, se reduce la destrucción de exergía global del sistema operando bajo condiciones inevitables e ideales, respecto del sistema operando bajo condiciones reales. En otras palabras, la planta geotérmica en cascada destruye 127.7 kW operando bajo condiciones reales, 122.9 kW operando bajo condiciones inevitables y 47.22 kW operando bajo condiciones ideales. Un resultado curioso y a la vez importante, es que aunque el sistema global refleja una menor destrucción de exergía, cuando opera con estándares de eficiencias más altos, los componentes pueden destruir una mayor cantidad de exergía por la forma en que se interconectan.
Un ejemplo de ello se presenta en las Tablas 6 y 7, donde en condiciones reales el equipo que destruye una mayor cantidad de exergía es el HX-I, mientras que el equipo operando bajo condiciones inevitables con mayor destrucción de exergía es el ORC. También como puede observarse los componentes ORC, TAR, HX-II, Torre de refrigeración y Cámara de conservación destruyen una mayor cantidad de exergía operando bajo condiciones inevitables, respecto de los valores de destrucciones de exergía obtenidos bajo condiciones reales. De entrada, esto puede parecer ilógico, pero sobre la situación es posible debido a las interconexiones de un componente con los demás componentes. Es decir, puede ser posible porque al operar cada tecnología con parámetros de eficiencia más elevados puede tener un producto mayor y en este caso de operación del sistema en cascada, un producto de una componente anterior es el Fuel del siguiente componente. Por esta razón, al operar una tecnología con una eficiencia mayor produce un mayor producto, lo que representa un mayor Fuel para la activación de la tecnología posterior, y a su vez, le representará una mayor destrucción de exergía aunque también tenga mayor producción del producto. Esto puede apreciarse claramente en el ORC que de manera real tiene un Fuel de 88.05 kW, un Producto de 40 kW y destruye en exergía 44 kW, mientras que de manera inevitable este mismo componente opera con un Fuel de 93.2 kW, un producto de 44 kW y alcanza una destrucción de exergía 45.35 kW. Finalmente, el equipo menos afectado por la interconexión con las demás tecnologías es el HX-I donde de manera inevitable la tecnología destruye en exergía 35.59 kW, mientras que de manera real tiene una destrucción de exergía de 44.05 kW. Esta tecnología es la menos influenciada por la interconexión con el resto de las tecnologías, debido a que es la tecnología con la que se inicia el ciclo en cascada.
Conclusiones
El análisis exergético convencional de la planta en cascada con fines de producción de electricidad, enfriamiento y calor útil para deshidratación, ha resultado ser un análisis muy importante para conocer las prestaciones máximas teóricas del sistema global, así como de sus componentes principales y auxiliares. Mediante el análisis exergético convencional se ha detectado en magnitud el componente que destruye una mayor cantidad de exergía del sistema. Este componente, para el sistema modelado bajo condiciones reales, ha resultado ser el intercambiador de calor HX-I. En este mismo sentido, pero respecto al sistema global, se ha detectado que al mejorar las condiciones de operación de los componentes que conforman el sistema global se tiene una menor destrucción de exergía del sistema en conjunto, pero no así de las componentes individuales.
La importancia del modelado del análisis exergético convencional de la planta operando bajo condiciones reales, ideales e inevitables, radica en comparar los resultados obtenidos bajo diferentes condiciones. Es decir, el sistema global operando bajo condiciones reales arroja el peor comportamiento exergético de la planta. Sin embargo, al compararlo frente a los resultados de las condiciones inevitables, que son las condiciones máximas tecnológicas que se pueden alcanzar, se puede apreciar hasta dónde existen posibilidades para mejorar las tecnologías para que la planta alcance un mayor desempeño exergético. En el análisis realizado, cuando el sistema opera bajo condiciones reales, puede producir 47.17 kW y alcanzar una eficiencia exergética de 26.97%, mientras que si la planta opera bajo condiciones inevitables puede producir hasta 52.04 kW y alcanzar una eficiencia exergética de hasta 29.75%. Es decir, si se realizan mejoras en las condiciones de operación y los componentes de la planta, el sistema, operando bajo condiciones reales, alcanzaría los productos del sistema como si operara en condiciones inevitables. Finalmente, si se realizaran mejoras tecnológicas en las tecnologías, el sistema real podría aspirar a obtener los productos y las eficiencias del sistema global acercándose a las condiciones ideales.











 nueva página del texto (beta)
nueva página del texto (beta)