Introducción
Los generadores de humedad suministran flujos de aire con humedad conocida y controlada, los cuales tienen aplicaciones a nivel industrial y en laboratorios de calibración. En particular, son de interés en institutos de metrología donde se usan como patrones de referencia para la calibración de higrómetros, o para suministrar muestras de humedad que permiten la caracterización de otros sistemas, como los higrómetros gravimétricos.
Los generadores termodinámicos de humedad tienen algunas ventajas respecto a otros métodos de generación, ya que tienen como base un método primario, requieren tiempos cortos de estabilización, pueden alcanzar alta estabilidad y proveen muestras de aire que no afectan el funcionamiento de los medidores utilizados.
Entre los métodos de generación de humedad más comunes se encuentran los métodos químicos, los tubos de permeación y los generadores termodinámicos, donde los últimos son los que tienen mayor uso en aplicaciones metrológicas.
Los generadores de humedad basados en principios termodinámicos son métodos primarios, ya que las magnitudes involucradas son independientes de la humedad generada y son susceptibles de medirse con alta exactitud (Quinn, 1997). Los generadores más conocidos son: el generador de dos presiones, el generador de dos temperaturas y el generador de flujo dividido.
Los fundamentos teóricos sobre los que se basa este tipo de generadores, incluyen la ley de conservación de la masa, las leyes generales de los gases y las relaciones de aire seco con vapor de agua. Los modelos desarrollados con estos principios describen satisfactoriamente las condiciones de humedad del aire en condiciones de equilibrio (y en estado estacionario), lo que simplifica su análisis. Cuando se requiere realizar un análisis en estado transitorio del proceso de saturación, o de las condiciones en que se alcanza el equilibrio, aunado a lo anterior, se debe tomar en cuenta la ley de conservación de cantidad de movimiento y la ley conservación de energía (Cengel y Boles, 2005; Carpentier, 2005; Carpentier et al., 2006). El caso transitorio no se analiza aquí porque está fuera del alcance de este trabajo.
Uno de los modelos termodinámicos más completos para calcular la humedad, cuando se mezclan flujos de aire (seco y húmedo), es descrito por Lovell-Smith (2009), quien derivó el modelo usando fracciones molares para expresar la humedad en el aire. El modelo derivado aquí se realizó con base en la definición de razón de masas.
Modelos similares se dan por Takahashi y Kitano (1998); Carpentier (2005) y Meyer et al. (2008). En los modelos revisados, no se encontró una evaluación completa de las magnitudes de influencia, que es necesaria para optimizar el sistema de generación de humedad, porque permite seleccionar aquellas magnitudes que requieren un buen control para reducir la incertidumbre de la muestra generada.
En este trabajo se describen los pasos generales para derivar el modelo de un generador híbrido, a partir del cual se hace una evaluación exhaustiva y se realiza un análisis de las magnitudes que intervienen. En la evaluación se determinan las condiciones óptimas para desarrollar un generador susceptible de aplicarse en un intervalo amplio de humedad.
Derivación de modelo de generación
Considere un volumen de control que tiene dos entradas y una salida. En una entrada se suministra aire seco y en la otra aire saturado con vapor de agua, cuyos flujos se mezclan en una cámara de prueba (volumen de control). En la salida, el aire se libera al ambiente, como se muestra en la Figura 1.
Supóngase que el aire seco se encuentra a la presión (Pd), temperatura (td), flujo másico (fd) y humedad (rd), y el aire saturado tiene (PS, tS, fw, rw), respectivamente. La humedad (r) es la masa del vapor de agua por unidad de masa del aire seco.
Si se considera que los flujos se mantienen estables y que el volumen de control no está en movimiento, la energía cinética y la energía potencial no contribuirán en el balance total (Carpentier et al., 2006). Entonces, la ecuación de balance de flujo másico en el volumen de control (Figura 1) está dado por la ecuación (1).
Es decir, el flujo que entra (fd+ fw) es igual al flujo que sale (fc).
En consecuencia, el balance de masa de vapor de agua está dado por la ecuación (2).
La cual establece que la suma de la humedad de los flujos de aire entrantes es igual a la humedad del aire que sale (fc rc).
Al combinar las ecuaciones (1) y (2), rc se escribe como
Por otro lado, la razón de masas (r) de una muestra de aire se puede escribir en términos de la temperatura de punto de rocío (tdp) mediante la ecuación
donde
Mv |
= masa molecular del vapor de agua |
Ma |
= masa molecular del aire seco |
P |
= presión total de la muestra de aire |
e(tdp ) |
= presión parcial de vapor de agua a la temperatura de punto de rocío tdp |
Por simplicidad, en la ecuación (4) no se incluyó el factor de corrección que toma en cuenta las desviaciones del vapor de agua respecto a un gas ideal. No obstante lo anterior, la inclusión del factor de corrección no cambia la forma matemática del modelo derivado.
Al realizar la sustitución de (4) en (3) para cada uno de los flujos de aire, la presión de vapor de agua en la cámara de prueba se puede escribir como (ver ecuación 5).
La ecuación (5) describe el modelo general para calcular la temperatura de punto de rocío de la mezcla de aire, bajo la consideración de que el aire seco contiene trazas de humedad.
De la ecuación (5) se pueden derivar las magnitudes que se usan comúnmente para expresar la humedad de una muestra de gas.
Generador híbrido de humedad
Si se considera que la muestra de aire seco no contiene trazas de agua (es decir, e(tda)= 0), entonces la ecuación (5) se puede escribir como
Con la suposición de que e(tda)=0, el modelo no depende de la presión del aire seco.
La solución de la ecuación (6) para tdp permite obtener la temperatura de punto de rocío, mientras que la humedad relativa se calcula con la ecuación (7)
Donde e(tc) es la presión de vapor a la temperatura de la cámara (tc).
A partir de las ecuaciones (6) y (7) y con algunas simplificaciones, se pueden obtener los modelos que se conocen ampliamente, como son el generador de dos presiones (2P), el generador de dos temperaturas (2T) y el generador de flujo dividido.
La ecuación de la presión de vapor de agua utilizada en este trabajo fue propuesta por Hardy (1998).
En la evaluación que se realiza a continuación, no se toma en cuenta el factor de corrección que considera que el vapor no es un gas ideal, el cual tiene efectos en presiones altas.
Evaluación del modelo
Análisis del modelo de generador híbrido
En el análisis de las ecuaciones (6) y (7) se hacen las siguientes consideraciones:
Se considera que Pc no cambia durante el proceso de generación; por lo tanto, esta magnitud se considera constante en todo el análisis.
La temperatura tc no interviene en el cálculo de tdp, ya que la temperatura de punto de rocío es independiente de la temperatura en la cámara; por lo tanto, su análisis se restringe a la evaluación de su efecto en HR.
La temperatura de punto de rocío en la cámara depende de Ps, ts y fw. En el caso de la humedad relativa, se requiere además controlar la temperatura tc en la cámara de prueba.
Un análisis preliminar de las ecuaciones (6) y (7) permite observar que cuando el flujo de aire seco (fd) se reduce a cero, se obtiene el modelo de un generador de dos presiones.
Adicionalmente, si se considera que las presiones en el saturador y en la cámara son iguales (Ps=Pc), entonces se obtiene el modelo de generación de dos temperaturas (o del generador de una sola presión). Este modelo opera satisfactoriamente para bajas concentraciones de humedad (HR<8%, tdp <-40 °C) pero tiene limitaciones para altas concentraciones de humedad, ya que a temperaturas mayores al ambiente, se presentan problemas de condensación en la cámara de prueba.
Al imponer las restricciones en presión (Ps=Pc) y en temperatura (ts=tc), se obtiene el modelo del generador de flujo dividido. En este modelo la humedad se controla básicamente con los flujos de aire seco y aire saturado de vapor de agua, aunque tiene dependencia con la temperatura. El modelo se puede simplificar aún más para evitar la dependencia con la temperatura, sin embargo, este opera satisfactoriamente para temperaturas menores que 25 °C.
La variación de una magnitud (manteniendo fijas las otras) limita el intervalo de generación de humedad, ya que, por ejemplo, no es práctico generar vapor saturado de agua a muy altas presiones (mayores que 2 MPa) o incrementar el flujo de aire seco (o húmedo) de manera ilimitada. Por lo anterior, es conveniente contar con un sistema que permita medir y controlar la mayoría de las magnitudes involucradas en el proceso.
Con el propósito de extender el análisis del modelo del generador híbrido, se evalúa el efecto de combinar dos magnitudes simultáneamente, es decir, HR =f(x,y) y tdp=g(x,y) mientras se mantienen fijas las otras magnitudes. Al combinar las 6 magnitudes (Ps, Pc, ts, tc, fw, fd) en pares, se encuentra que existen 15 combinaciones diferentes, cuyo número se reduce a 10 si se considera que la presión en la cámara prueba se mantiene constante y se reduce a 6 combinaciones cuando se desea conocer tdp.
Evaluación de las magnitudes de entrada para generar humedad relativa
Las condiciones de base para la evaluación del modelo de generación de HR son: Ps=Pc=101.325 kPa, fw=fd=1 g/min, ts=tc=22 °C. A partir de estos valores se realizarán variaciones de las diferentes magnitudes.
En el análisis que se presenta a continuación, se realizarán variaciones simultáneas de dos magnitudes seleccionadas, mientras las restantes se mantienen constantes en las condiciones según las condiciones de base.
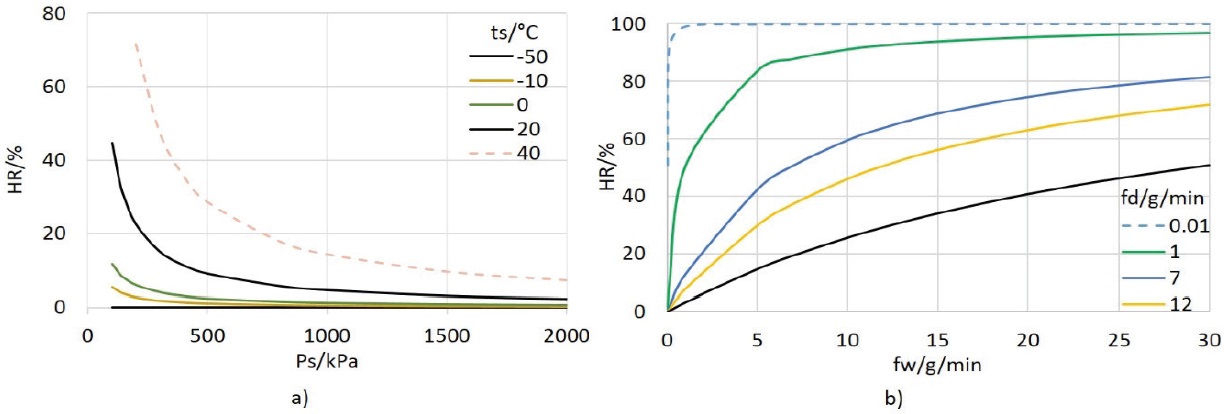
HR(Ps,ts): El primer caso que se analiza es la variación simultánea de la presión (Ps) y la temperatura en el saturador (ts), cuyo comportamiento se muestra en la Figura 2a.
Según se observa en la Figura 2a, el incremento en ts aumenta la humedad relativa, mientras que el incremento en Ps reduce la humedad relativa. Por lo anterior, a presiones altas y temperaturas bajas en el saturador se espera obtener muestras con humedad relativa baja. Por ejemplo, al evaluar la ecuación (7) para Ps=2 MPa y ts=-50 °C, se obtiene una humedad relativa de aproximadamente 0.01%. Si en el sistema solo se puede variar la presión, para alcanzar una humedad relativa de 0.06% se requiere una presión Ps de aproximadamente 90 MPa, el cual es tan elevado que complica su materialización.
Cuando se requiere incrementar la humedad relativa mediante variaciones de Ps y ts, se observa que se requiere disminuir Ps hasta aproximadamente la presión atmosférica y aumentar la temperatura en el saturador. Mediante esta combinación se pueden alcanzar valores cercanos a 100%HR. Por ejemplo, si Ps=130 kPa y ts=37.8 °C, entonces HR=99.2%.
En resumen, con un control adecuado de Ps y ts, es posible generar la escala de 0% a 100% en humedad relativa, sin complicaciones experimentales.
HR(fd, fw): La variación simultánea de los flujos de aire seco (fd) y aire saturado con vapor de agua (fw), permite obtener un amplio intervalo de humedad relativa.
En la Figura 2b se muestra el efecto de cambiar el flujo de aire seco (fd) y el flujo de aire saturado con vapor de agua (fw). El análisis individual del efecto de cada flujo es simple: al incrementar el flujo de aire seco se reduce HR, mientras que si se incrementa el flujo de aire saturado, HR se incrementa. La variación simultánea de ambos flujos permite cubrir el intervalo de 0% a 100% sin necesidad de hacer variaciones de flujo en las regiones de valores extremos, ya que es conveniente considerar valores que en la práctica se puedan controlar. Por ejemplo, el control de flujo a un nivel de 0.01 g/min está en el límite de control. Adicionalmente, al variar solo un flujo, por ejemplo el aire seco, y al fijar el aire saturado a 1 g/min, se encuentra que se requiere incrementar el flujo de aire seco a valores mayores de 30 g/min para obtener valores bajos de HR, lo cual tiene complicaciones en el diseño.
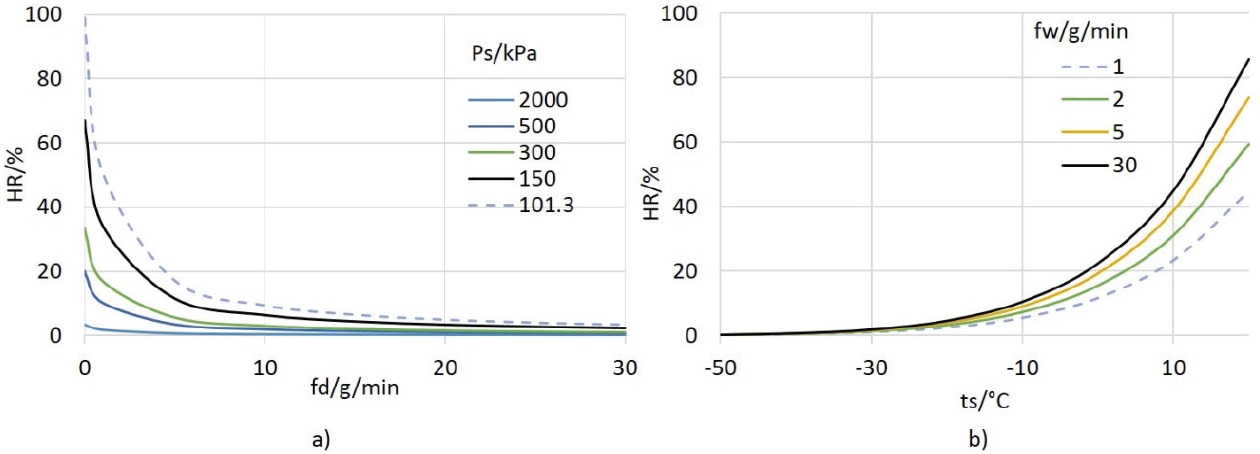
HR(Ps,fd): La variación individual de Ps y fd se presentó en casos anteriores, por lo cual el análisis de la Figura 3a se restringe al efecto combinado.
Se observa que para obtener valores altos de humedad relativa se requiere reducir tanto la presión Ps como el flujo de aire seco. Los valores bajos de HR se obtienen al incrementar la presión y el flujo de aire seco; de hecho se observa que es suficiente aumentar la presión a valores moderados (1 MPa) y fd=20 g/min para alcanzar un valor de HR=0.5%. El sistema controlado con estas dos magnitudes tiene limitaciones para obtener valores elevados de HR. Por ejemplo, si se reduce la presión Ps hasta la presión atmosférica y el flujo a fd=0.1 g/min, se obtiene aproximadamente 91%HR; es decir, se requiere reducir considerablemente el valor de fd para aumentar HR, lo cual es poco práctico.
HR(ts,fw): El efecto de variar simultáneamente ts y fw se presenta en la Figura 3b.
Se observa que para generar valores altos de HR, se requiere aumentar ambas magnitudes. Además, el sistema es más sensible a cambios de temperatura que a cambios de flujo; es decir, pequeños cambios de temperatura generan cambios grandes de HR. Por ejemplo, con ts=28.5 °C y fw=2 g/min generan 99.4%HR, mientras que con ts=22 °C y fw=80 g/min se alcanza 99%HR, aproximadamente.
Los valores bajos de HR se obtienen al reducir los valores de ambas magnitudes. Por ejemplo, para generar 3.6%HR se requiere ts=-15 °C y fw=0.5 g/min, cuyas condiciones se pueden obtener experimentalmente.
HR(Ps,fw): El efecto de combinar las magnitudes Ps, y fw se muestra en la Figura 4a. Los valores elevados de HR se obtienen al aumentar fw y disminuir Ps; los valores de HR disminuyen si se incrementa Ps y disminuye fw.
El coeficiente de sensibilidad de fw es mayor en el intervalo de 0 g/min a 5 g/min, mientras que la máxima sensibilidad de Ps se presenta en el intervalo de 101.325 kPa a 500 kPa.
Según se observa en la Figura 4a, con estas magnitudes se pueden generar valores desde 0% a 100% HR, aproximadamente.
HR(fd,ts): Los cambios en HR por cambios en la temperatura del saturador (ts) y en el flujo de aire seco (fd), se presentan en la Figura 4b.
Se observa que la humedad relativa se incrementa al disminuir el flujo de aire seco y aumentar la temperatura del saturador. Por ejemplo, de la ecuación (7) se encuentra que para ts=40.3 °C y un flujo de fd= 2 g/min se obtiene HR=99.5%; es decir, no se requieren condiciones extremas en las magnitudes involucradas para generar valores elevados de humedad relativa.
Según se observa en la Figura 4b, la combinación de estas magnitudes también da buenos resultados para generar valores bajos de HR; por ejemplo, una temperatura de ts=10 °C y un flujo de fd=20 g/min permite alcanzar un valor de HR=2.2%, que es útil en muchas aplicaciones.
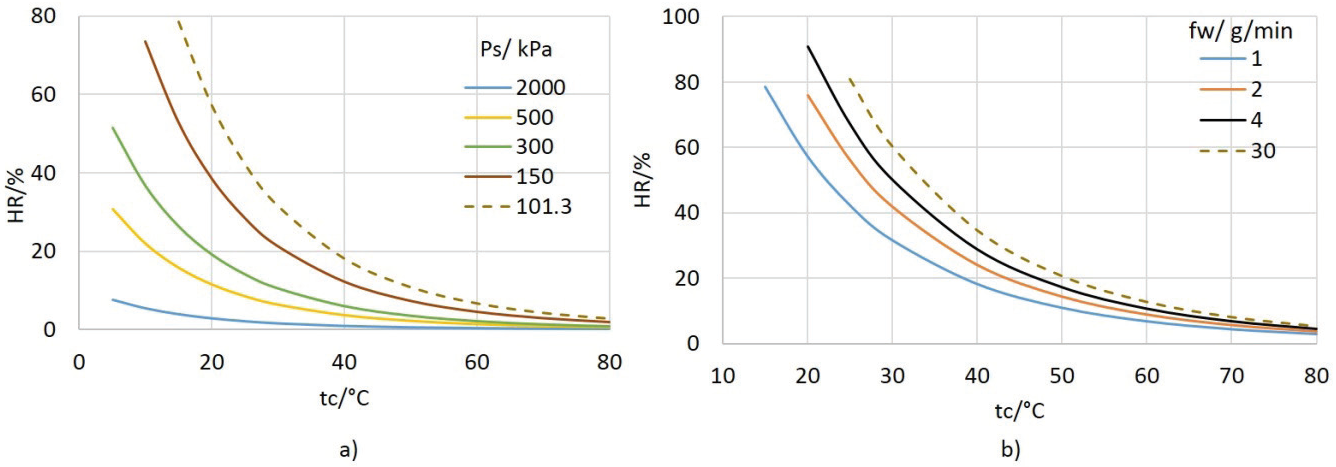
HR(tc,Ps): En la Figura 5a se muestra el intervalo de HR generado por cambiar (tc, Ps) simultáneamente.
De acuerdo con la Figura 5a, valores altos de humedad se obtienen con presiones cercanas a la presión atmosférica y temperaturas menores que la temperatura ambiente. Por ejemplo, cuando Ps=101.325 kPa y tc=11.0 °C, se obtiene HR= 98.7%.
Por otro lado, HR se reduce al aumentar tanto la temperatura de la cámara como la presión del saturador. Para Ps=1000.0 kPa y tc=40 °C se obtiene un valor de HR= 1.8%. En ambos casos, los valores de las magnitudes de control para cubrir el intervalo de aproximadamente 0% a 100% se alcanzan experimentalmente sin complicaciones.
HR(tc, fw): En la Figura 5b se presenta el efecto en la humedad relativa al combinar el flujo de aire húmedo fw y la temperatura de la cámara de prueba tc.
Se observa que para aumentar HR se requiere reducir la temperatura de la cámara y aumentar el flujo de aire húmedo. Por el contrario, HR se reduce al aumentar tc o reducir el flujo de aire húmedo; por ejempo con fw=10 g/min, y tc=20.5 °C se obtiene HR=99.9%; mientras que con tc=50 °C y fw=0.1 g/min se obtiene HR=2.0%.
HR(tc, fd): Al hacer variaciones simultáneas del flujo de aire seco y la temperatura de la cámara de prueba, se observa que la disminución de ambas magnitudes incrementa la humedad relativa en la cámara; mientras que en el caso contrario disminuye la humedad relativa (Figura 6a).
El modelo es más sensible para valores bajos de flujo fd (0 g/min a 5 g/min) y de temperatura tc (0 °C a 5 °C).
HR(ts,tc): La variación simultánea de ts y tc (cuando son las únicas magnitudes de control) da lugar al generador de dos temperaturas, el cual opera adecuadamente a bajas concentraciones de humedad. En la Figura 6b se presenta el comportamiento de la humedad relativa ante variaciones de ts y tc.
En la Figura 6b se observa que para valores de ts bajos y tc altos se obtienen valores bajos de HR; mientras que en el caso contrario, HR se incrementa. Por ejemplo, para ts=-40 °C y tc=40 °C, se puede generar un valor de HR≈0.1%, mientras que para ts= 22 °C y tc=12 °C, se obtiene HR≈95.5%.
De acuerdo con los casos revisados, se mostraron diez combinaciones de pares de magnitudes que se pueden seleccionar para el desarrollo de un sistema de generación de humedad relativa, algunos de los cuales pueden tener menos complicaciones.
La selección de las magnitudes para el desarrollo de un sistema de generación depende de los equipos y diseños disponibles para su materialización.
Evaluación de las magnitudes de entrada para generar temperatura de punto de rocío
Las condiciones de base utilizadas para realizar la evaluación del generador de temperatura de punto de rocío son: Ps=Pc=101.325 kPa, fw=fd=1 g/min, ts=22 °C.
En la evaluación del modelo se considera que la presión y la temperatura en la cámara se mantienen constantes, por lo cual ellas no se incluirán en el análisis.
El cálculo de la temperatura de punto de rocío (tdp) se obtiene aplicando el método de Newton-Raphson, ya que tdp no se encuentra de manera explícita en la ecuación (6).
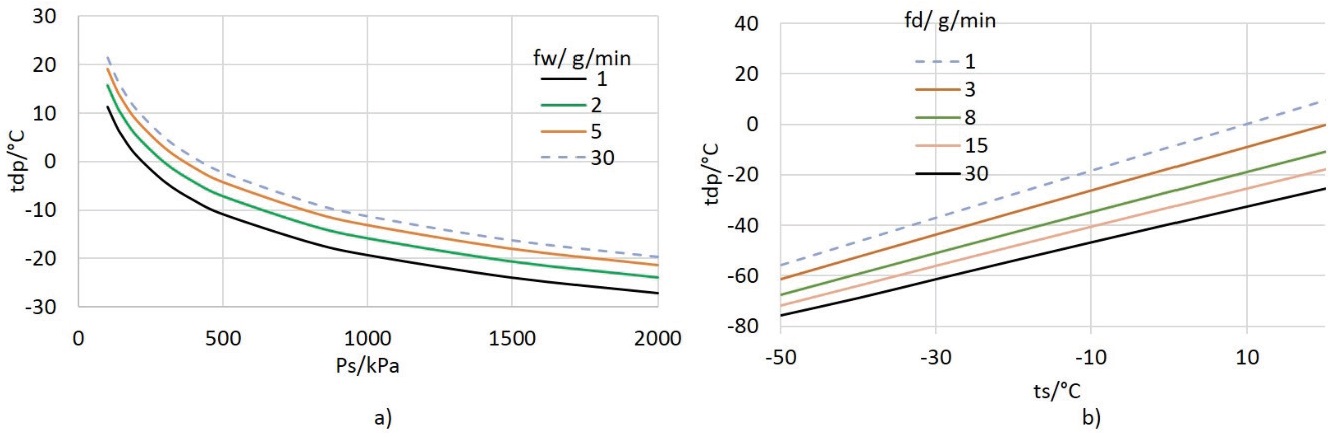
tdp(ts, Ps): El primer caso que se analiza considera la variación simultánea de la temperatura (ts) y la presión (Ps) en el saturador.
Como se observa en la Figura 7a, la temperatura de punto de rocío generada en la cámara de prueba disminuye cuando la presión en el saturador aumenta, lo cual se debe a la diferencia de presión entre ambas (Ps y Pc); es decir, en el saturador la temperatura (ts) es igual a la temperatura de punto de rocío, luego al expandir el aire a una presión menor, tdp cambia poco si la caída de presión es pequeña, pero si la caída de presión es alta, para condensar el agua se requiere una temperatura menor, por lo tanto tdp disminuye considerablemente.
El cambio que se presenta en tdp, debido al cambio de presión desde aproximadamente 100 kPa a 2000 kPa, es alrededor de 40 °C.
Adicionalmente, en la Figura 7a se observa que la temperatura de punto de rocío en la cámara de prueba disminuye al reducir la temperatura del saturador (y viceversa), ya que la temperatura de punto de rocío solo depende de la presión, la cual en este caso, se mantiene constante. Ante esto se espera que la temperatura del saturador sea igual a la temperatura de punto de rocío. Los casos que se grafican en la Figura 7a toman en cuenta que existe una mezcla de aire seco y vapor de agua, cuyos flujos corresponden a las condiciones establecidas inicialmente.
El alcance de tdp se puede ampliar considerablemente al combinar Ps y ts; por ejemplo, para alcanzar temperaturas de punto de rocío bajas se puede incrementar la presión y reducir la temperatura del saturador; en el caso contrario se reduce la presión y se incrementa la temperatura del saturador.
tdp(fd, fw): Al mezclar el flujo de aire seco (fd) con el flujo de aire húmedo (fw), mientras se mantienen fijas las otras magnitudes, se obtiene el generador de flujo dividido, con el cual se puede tener un intervalo amplio de temperatura de punto de rocío. En la Figura 7b se muestra el efecto al cambiar los flujos de manera individual, así como el comportamiento al hacer variaciones simultáneas de ambas magnitudes.
En la Figura 7b se muestra el comportamiento de la temperatura de punto de rocío al mezclar los flujos de aire seco y aire húmedo. El intervalo de flujo en el que se realizó la mezcla fue de 0 g/min a 30 g/min, lo que permite generar valores de temperatura de punto de rocío desde aproximadamente -65 °C a 20 °C. No obstante, que al combinar los flujos de aire se puede obtener un intervalo de temperatura de punto de rocío amplio, en los extremos del intervalo generado se tienen complicaciones experimentales en los equipos, en el diseño del saturador y en la cámara de prueba.
tdp(Ps, fd): Como se describió anteriormente, el incremento en Ps reduce la temperatura de punto de rocío, al igual que el incremento en el flujo de aire seco (fd).
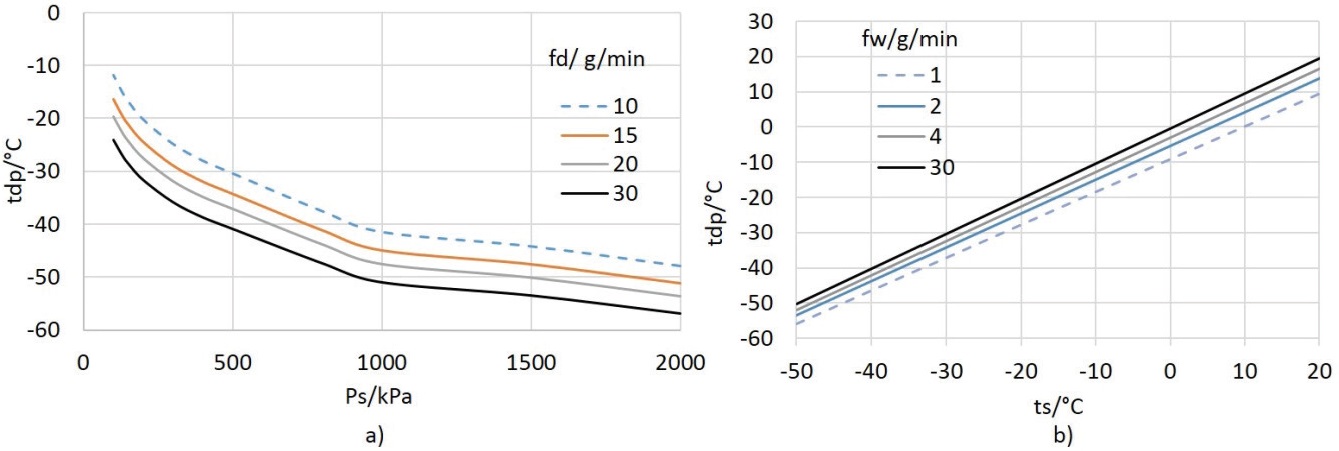
Al incrementar simultáneamente Ps y fd se encuentra que, a una presión Ps=2000 kPa y fd=30 g/min, se puede alcanzar una temperatura de punto de rocío de aproximadamente -57 °C (Figura 8a), mientras que al reducir ambos valores (Ps=101.325 kPa, md=0.01 g/min) se puede obtener un valor de tdp de aproximadamente 22 °C, el cual corresponde a la temperatura del saturador.
tdp(ts, fw): El valor de tdp varía en la dirección de cambio de ts, así como de fw. Por lo tanto, el valor más alto de td se obtiene con los valores más altos de ts y fw. En este caso, si ts=80 °C y fw=30 g/min, se obtiene un valor de tdp≈80 °C, mientras que el valor más bajo es tdp≈-56 °C cuando ts=-50 °C y fw=1 g/min. En la Figura 8b se muestra el efecto de combinar ts y fw tanto de manera individual como de manera combinada.
tdp(Ps, fw): La combinación de Ps y fw en el saturador da como resultado valores altos de tdp cuando se reduce Ps (hasta un valor muy cercano al de la la presión atmosférica) y se incrementa fw (hasta fw=30 g/min, el valor razonablemente medido en un saturador), en cuyo caso se obtiene un valor de aproximadamente tdp≈21. 5 °C. Los valores menores de tdp se obtienen al incrementar la presión Ps y reducir el flujo de aire húmedo; en este caso el valor más bajo de tdp≈-27 °C se obtiene al considerar Ps=2000 kPa y fw=1 g/min. En la Figura 9a se muestra el efecto de cambiar de manera individual o combinada Ps y fw.
tdp(ts, fd): La variación simultánea de ts y fd permite obtener un amplio intervalo de temperatura de punto de rocío; por ejemplo, para obtener valores altos de tdp se requiere reducir el valor de fd e incrementar el valor de ts, mientras que los valores más bajos se obtienen al incrementar fd y reducir ts (Figura 9b). Con variaciones razonables de ambas magnitudes se pueden generar valores de temperatura de punto de rocío desde -75 °C hasta 65 °C.
Otros casos
Como se describió anteriormente, la temperatura de punto de rocío es independiente de la temperatura en la cámara, por lo que no es conveniente analizar aquí los casos de combinar (tc, Ps), (fw,tc), (fd, tc) y (ts, tc), ya que estos son casos particulares de los que se analizaron anteriormente.
De manera resumida, en los casos analizados se encontró que al variar a una de las magnitudes, mientras se fijan las restantes, resulta instrumentalmente más complicado cubrir un intervalo amplio de humedad (HR o tdp) que al combinar dos o más magnitudes. La consecuencia de considerar muchas variables de influencia es el incremento en la incertidumbre esperada.
Conclusiones
En este trabajo se derivó un modelo híbrido para generación de humedad relativa y temperatura de punto de rocío, el cual, mediante algunas simplificaciones, permite obtener los modelos del Generador de Dos Presiones, del Generador de Dos temperaturas y del Generador de Flujo de Dividido, los cuales son ampliamente conocidos.
A diferencia de otros modelos, el modelo descrito se derivó usando la razón de masas por peso y tiene la ventaja de ser muy versátil en su materialización, ya que las magnitudes a controlar se pueden seleccionar de acuerdo con la instrumentación disponible.
Adicionalmente, como resultado de la evaluación, se encontró que existen al menos 15 combinaciones de dos magnitudes que permiten generar intervalos amplios de humedad relativa (0% a 99%), y al menos 10 combinaciones para generar distintos valores de temperatura de punto de rocío (desde trazas de humedad hasta aproximadamente 100 °C en punto de rocío).
La selección de las magnitudes que se pueden utilizar para el desarrollo de un generador, depende de la disponibilidad de los instrumentos requeridos, del diseño de las partes involucradas, del intervalo de humedad a generar y de la incertidumbre esperada del generador.











 text new page (beta)
text new page (beta)