Modelado empírico simple del rompimiento de presas pequeñas de tierra (hidrograma de salidas)

 

Simple Empirical Modeling of Small Earth-Dam Break (Outflow Hydrograph)

 

Campos-Aranda Daniel Francisco

 

Facultad de Ingeniería, Universidad Autónoma de San Luis Potosí. Correo: campos_aranda@hotmail.com

 

Información del artículo: recibido: enero de 2012.
Aceptado: febrero de 2013

 

Resumen

Se exponen varias ideas generales respecto al rompimiento de presas con cortina de tierra. En seguida, se presenta con detalle el establecimiento de las dos ecuaciones diferenciales que rigen su proceso de falla, las cuales constituyen un modelo empírico, ya que su coeficiente de erosividad debe ser calibrado. Se expone únicamente la solución analítica de tales ecuaciones, para brecha de falla rectangular y erosión no lineal, por ser la más simple. Se describe brevemente el calibrado del modelo y el análisis de sensibilidad de sus parámetros. Antes de iniciar la aplicación numérica del modelo a 97 presas pequeñas con cortina de tierra del país, se citan varias fórmulas empíricas que resumen la experiencia mundial y que permiten estimar el ancho promedio de la brecha, la duración de la falla y el gasto máximo de descarga. El modelo expuesto es simple, está físicamente basado y su aplicación a cualquier presa pequeña del país requiere únicamente como datos básicos, la altura de la cortina y el volumen de agua almacenado antes de la falla; permite estimar el hidrograma de salidas debido al rompimiento de la cortina por desbordamiento.

Descriptores: desbordamiento, proceso erosivo, brecha de falla, modelos analíticos, estudios de seguridad de presas.

 

Abstract

In this work several general ideas about the earth-dam break are exposed. The two differential equations that govern the failure process are presented, constituting thus an empirical model, since the erosivity coefficient must be calibrated. For its simplicity, only the analytical solution for the case of rectangular breach of failure and nonlinear erosion is exposed. The calibration of the model and the analysis of the sensitivity of its parameters are described briefly. The empirical formulas that summarize the world-wide experience to estimate the average width of the breach, the time failure and the maximum outflow are cited. The model was applied to 97 small dams with earth embankment of the country. The results allow concluding that the exposed model is simple and physically based, and that its application to any small dam in the country only requires as input data: the embankment height and the stored volume of water before the failure. The model allows an estimate of the outflow hydrograph due to the dam breaking by overtopping flow.

Keywords: overtopping, erosive process, breach failure, analytical models, dam safety studies.

 

Introducción

Las presas son las obras de infraestructura hidráulica más importantes y también son numerosas. Son construidas para favorecer el desarrollo económico e involucran grandes inversiones de recursos financieros, naturales y humanos. Las presas están constituidas básicamente por tres estructuras: (1) la cortina, que es la obra que obstruye el flujo del río, represándolo y formando un lago artificial en lo que se llama el vaso o embalse de la presa; (2) el vertedor u obra de excedencias, diseñado para dar paso seguro a los escurrimientos excedentes o crecientes que llegan al embalse cuando éste está lleno, evitando que se derramen sobre la cortina con posibilidad de dañarla y (3) la obra de toma, la cual permite las extracciones controladas, ya sean éstas para abastecimiento de agua potable, riego o generación de energía hidroeléctrica.

De los diversos tipos de cortinas que pueden construirse, las de materiales térreos son las más comunes, en sus diferentes versiones, según su tamaño. Cuando son pequeñas, por lo general, son homogéneas y cuando son grandes lo común es que lleven corazón impermeable de arcilla, respaldos de otros materiales granulares y protecciones de enrocamiento. Desafortunadamente, son las cortinas de tierra las más susceptibles a fallar que las de otros tipos. La causa de falla normalmente está asociada al desbordamiento y la formación de una brecha en el cuerpo de la cortina, o bien, al flujo de agua y erosión consecuente cercana al desplante de la cortina, lo que origina tubificación, y a la postre, una brecha por colapso de tal cavidad (Singh, 1996).

En general, la falla o rompimiento de una presa resulta en un gran desastre, cuyas consecuencias abarcan pérdida de vidas humanas y daños a todas las construcciones de aguas abajo de una manera severa. La falla de una cortina, implica la liberación súbita del agua almacenada en su vaso, generándose una creciente de enormes proporciones comparada con las naturales, la cual amenaza todo lo que existe aguas abajo de la presa, incluyendo otros embalses (Arganis et al., 2009; Fuentes et al., 2010). Debido al mecanismo de la falla, son dos los factores más importantes que intensifican tal proceso y sus consecuencias, la altura de la cortina y el volumen de agua almacenado en el vaso.

La modelación de la falla de una cortina de tierra por desbordamiento, causa más común, es de vital importancia para el desarrollo de programas de seguridad y riesgo asociados a cada presa y su entorno de aguas abajo (Campos, 1993). En este trabajo se describe con detalle y aplica el modelo de Singh y Scarlatos (1988), el cual permite estimar de una manera simple el hidrograma de salidas de una presa pequeña de tierra debido a su falla o rompimiento por desbordamiento, lo que origina una brecha rectangular. El modelo requiere como datos, únicamente la altura de su cortina y su volumen almacenado, por lo cual es aplicable en cualquier presa pequeña del país. En las 97 presas procesadas, la altura de cortina varió de 10 a 34 metros y su capacidad de conservación fluctuó de 1.0 a 30.0 Mm³ (millones de metros cúbicos).

 

Desarrollo

Rompimiento de presas de tierra (ecuaciones del proceso)

La falla de una cortina de tierra es un fenómeno dependiente del tiempo, que involucra la interacción del agua y los materiales térreos, los cuales no son homogéneos, ya sea porque existen diversos tipos o porque no tienen el mismo grado de compactación. En resumen, el proceso es dinámico y complicado, estando regido por la hidrodinámica, la mecánica del transporte de sedimentos y los aspectos relativos a la geotecnia; todo ello define la formación de la brecha y la falla subsecuente de la cortina (Singh, 1996).

Conceptualmente, la formación de la brecha en una cortina de tierra puede ser considerada un fenómeno de dos fases, en la interacción del agua y el sedimento, producto de la erosión. El agua que desborda por la cortina es la fuerza que erosiona y forma la brecha, cuyo aumento permite un mayor flujo de agua con el consecuente incremento en la erosión. El proceso continúa hasta que el agua del vaso es liberada o hasta que la cortina resiste la erosión. Entonces las ecuaciones que rigen el proceso son la fórmula que describe el abatimiento del agua en el vaso y otra que define la relación entre la erosión y las características del flujo. La primera fórmula es (Singh y Scarlatos, 1988; Singh, 1996):

en donde, A_s(H) es la superficie libre del agua en el vaso de la presa función de H, que es la elevación del agua referida a un cierto nivel, que comúnmente es el nivel del mar; I, Q_b y Q son los gastos, el que entra al embalse, el que sale por la brecha y el que se descarga por encima de la cortina, el vertedor y obra de toma. La ecuación anterior se puede simplificar notablemente si se considera que la diferencia entre I y Q es mucho menor que la magnitud de Q_b y por lo tanto se elimina; esta consideración implica que el vaciado del vaso se ha iniciado. Si además se considera que A_s es independiente de H, es decir, que el vaso es prismático y que el gasto Q_b corresponde al de un vertedor de cresta ancha, la ecuación 1 se reduce a

siendo ahora, v la velocidad del flujo en la brecha, cuya área es A_b. Esta velocidad es igual a

en la cual, α₁ es un coeficiente empírico que Singh y Scarlatos (1988) y Singh (1996) adoptan igual a 1.50 m^1/2/s para tomar en cuenta la convergencia del flujo, ya que en vertedores de cresta ancha es del orden de 1.70; Z es la elevación del fondo de la brecha, referida a un cierto nivel. Finalmente la expresión 2 se transforma en

que es una ecuación diferencial ordinaria de primer orden con dos variables desconocidas, H y Z. La ecuación adicional necesaria se obtiene estableciendo a la erosión como una función potencial de la velocidad del flujo, esto es (Singh y Scarlatos, 1988; Singh, 1996):

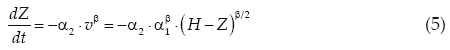
en donde α₂ y β son coeficientes empíricos. La expresión anterior es muy simple, pero está basada físicamente, ya que la erosión es directamente proporcional al esfuerzo cortante que origina la velocidad del flujo. La hidráulica del transporte de sedimentos en ríos ha establecido que su magnitud es función de la velocidad media del flujo a la potencia 4, 5 ó 6, de manera que cabría esperar que el exponente β tuviera un valor similar; sin embargo, Singh y Scarlatos (1988) y Singh (1996) encontraron que ciertas soluciones analíticas exactas sólo son factibles con valores de β enteros menores que dos. Estos autores consideran que tal discrepancia se absorbe o incorpora durante la calibración del coeficiente de erosividad (α₂). Por lo anterior, el modelo descrito por las ecuaciones 4 y 5 es empírico, ya que implica el calibrado del coeficiente α₂.

Si la forma de la brecha es conocida, entonces A_b puede ser fácilmente estimada y el sistema de ecuaciones 4 y 5 se puede resolver con respecto a H y Z, aceptando erosión lineal (β = 1) o no lineal (β ≠ 1) y proporcionado las siguientes condiciones iniciales H = H₀ y Z = Z₀ en t = 0.

 

Solución analítica para brecha rectangular con erosión no lineal

Singh y Scarlatos (1988) analizan tres formas de brecha, la rectangular, la triangular y la trapezoidal; lógicamente, las soluciones analíticas al sistema de ecuaciones 4 y 5 más sencillas corresponden a la forma rectangular y de éstas, al enfoque de erosión no lineal. Tomando en cuenta que estos autores, encuentran que las cuatro soluciones relativas a las brechas rectangular y triangular conducen a resultados bastante similares, únicamente se expone la solución analítica cuya formulación algebraica es la más simple.

Considerando una brecha rectangular de ancho constante b, la cual crece exclusivamente en la dirección vertical, es decir que se erosiona en su piso, su área será

Combinando la ecuación 4 con la 6 y dividiendo entre la 5, se obtiene (Singh y Scarlatos, 1988; Singh, 1996):

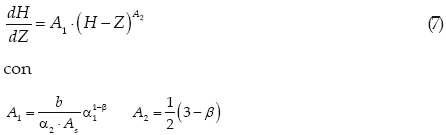
las soluciones de la ecuación 7 sólo son alcanzables cuando β = 2 y son las siguientes:

el resultado de esta ecuación, que está en función de la carga hidráulica, se utiliza en la expresión siguiente para obtener la nueva elevación del fondo de la brecha, conforme transcurre el tiempo t.

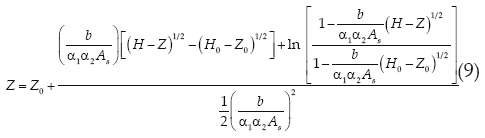
Finalmente, cuando el proceso de erosión se ha completado, es decir que Z = 0, la ecuación 4 se reduce a

cuya solución es (Singh y Scarlatos, 1988; Singh, 1996):

en la cual, H_t es la carga hidráulica en el instante t en que la erosión terminó (Z = 0). La ecuación 11 establece el vaciado del agua del vaso a través de la brecha rectangular formada. Lógicamente, la fórmula que permite evaluar el gasto descargado por la brecha en cada instante analizado es:

El modelo del rompimiento de presas pequeñas de tierra con una brecha rectangular, definido por las ecuaciones 8, 9, 11 y 12, es empírico y válido exclusivamente donde la diferencia entre el gasto que entra a la presa (I) y el que sale de ella (Q) es pequeña comparada con la descarga a través de la brecha (Q_b) y donde la función A_s(H) no varía sustancialmente. Su desventaja principal se centra en la necesidad de adoptar un coeficiente α₂ y por ello, se requiere buscar relacionarlo con algunas características físico-químicas de los suelos utilizados en la construcción de cortinas de tierra; ya que desafortunadamente, el conocimiento sobre la erosión en ríos no es aplicable al mecanismo del rompimiento de presas de tierra (Singh y Scarlatos, 1988; Singh, 1996).

 

Calibración del coeficiente de erosividad (α₂)

Singh y Scarlatos (1988) recopilaron información mundial de 52 casos de fallas de presas, para establecer relaciones geométricas promedio con la forma y tamaño de la brecha. De tal recopilación, 19 casos que cuentan con más datos y de éstos, los autores citados seleccionaron 14 para realizar el calibrado del coeficiente α₂. Se encontró que la media aritmética y la mediana de los coeficientes α₂ calibrados fue 0.000725 s/m, magnitud que deberá ser utilizada como valor inicial en la modelación del rompimiento de presas pequeñas de tierra. El coeficiente α₂ varía entre 0.00015 y 0.00210 s/m como valores extremos calibrados.

 

Análisis de sensibilidad del modelo en la Presa Teton, Idaho

Varios modelos del rompimiento de presas han sido contrastados con los datos disponibles de la falla de la Presa Teton, en el río del mismo nombre en el estado de Idaho, USA, ocurrida el 5 de junio de 1976, cuyo gasto máximo de descarga fue de 68,500 m³/s. Para esta aplicación del modelo (ecuaciones 8, 9, 11 y 12), Singh y Scarlatos (1988) y Singh (1996), definieron los valores mostrados para el ensayo 1 (tabla 1), cuyo intervalo de tiempo de los análisis fue de 60 segundos.

A partir de los resultados de la tabla 1 se establece que en el modelo el gasto máximo de descarga (Q_max) se incrementa o disminuye, conforme se asignen valores mayores o menores a α₂, b o A_s. Afortunadamente, el modelo es insensible a la carga hidráulica inicial (H₀ - Z₀), pero resulta altamente dependiente del valor de α₂, como se observa en los ensayos 3 y 4. El ensayo 2 demuestra que cuando α₁ disminuye también lo hace le gasto máximo y se retrasa su ocurrencia.

 

Estimación de los parámetros del modelo

Buscando dejar sólo al coeficiente α₂ como parámetro predictivo del modelo, habrá que realizar estimaciones confiables del ancho promedio de la brecha (b) y de la superficie representativa del embalse (A_s). Para b se puede utilizar la fórmula propuesta por Froehlich (2008), obtenida al procesar 69 casos de fallas de presas, ésta es

en la cual, b está en metros, k₀ es adimensional y vale 1.30 para fallas debidas a desbordamiento y 1.00 para los otros tipos, tubificación por ejemplo; V es el volumen de agua almacenado arriba del fondo de la brecha, en m³ y que por lo tanto define el hidrograma de salidas y H_b altura de la brecha, en m.

En presas pequeñas de tierra que fallan por desbordamiento y cuyo fondo de la brecha llega al cauce, H_b corresponde a la altura de la cortina (Hc), es decir, la diferencia entre la elevación de la corona de la cortina y el nivel del cauce; para el volumen V se puede adoptar el doble de la capacidad de conservación (Cc), considerando que en promedio del nivel de la cresta del vertedor de excedencias, al nivel de la corona existe un almacenamiento similar a Cc (Wetmore y Fread, 1984). Lógicamente, cuando la falla es por erosión en el cuerpo de la cortina y la consecuente tubificación, V es igual a la Cc.

Froehlich (2008) también presentó, con base en 23 casos, la expresión para la estimación del tiempo que tarda en desarrollarse la brecha trapecial o tiempo de falla (T_f) en segundos, ésta es

Una estimación que puede ayudar en la selección del coeficiente α₂, es la del gasto máximo descargado por la brecha, el cual según MacDonald y Langridge (1984) es función del factor de formación de la brecha (V⋅H_b), con las dos expresiones siguientes expuestas por Wahl (2004), ya que estos autores presentaron sus resultados en un gráfico logarítmico

La primera ecuación corresponde a la mayoría de los casos observados de presas de tierra y la segunda a la curva envolvente de valores extremos registrados.

 

Aplicación numérica en 97 presas pequeñas de tierra

En el libro Presas Construidas en México (SRH, 1976), se tienen catalogadas por orden cronológico de construcción 1,007 presas, cuya capacidad es mayor de medio millón de m³ y altura de cortina superior a 5 metros, construidas desde la época de la Colonia hasta finales de 1974. De estas presas, sólo se presentan 382 láminas con fotografía de la presa e información sobre capacidades y datos generales de cortina, vertedor y obra de toma. Para la aplicación numérica, se adoptó una altura mínima de cortina (Hc) de 10 metros y una capacidad de conservación (Cc) mínima de un millón de m³ (1.00 Mm³); este almacenamiento corresponde a la suma de la capacidad para sedimentos y la útil. Con tales restricciones se tienen 112 presas con cortina de tierra, pero sólo 97 con lámina conteniendo más información.

En las láminas citadas, se presenta el llamado "sobrealmacenamiento" que corresponde al volumen retenido por el funcionamiento libre del vertedor al presentarse la creciente máxima. Este dato hidrológico, toma en cuenta de manera implícita el crecimiento del vaso hasta el llamado NAME o nivel de aguas máximas extraordinarias y por ello se utilizó para estimar el volumen almacenando hasta un nivel mayor al de la corona de la cortina (V), de la manera siguiente; se aceptó que entre el NAME y el nivel de desbordamiento existe un volumen igual a 150% del sobrealmacenamiento (S_almac), por lo tanto

Esta aproximación se puede evitar al disponer de las curvas elevaciones-áreas-capacidades del vaso de la presa bajo estudio y obtener la capacidad (V) para una cota igual a la elevación de la corona de la cortina más una carga de 50 cm durante el desbordamiento en cortinas sin protección de enrocamiento o pasto, o bien, de un metro en cortinas con tal protección. El recubrimiento con roca está recomendado en zonas áridas y semiáridas; en cambio, el de pasto puede ser una opción económica en zonas húmedas.

En las 97 presas de esta aplicación numérica, se considera probable su falla sólo por desbordamiento (k₀ = 1.30 en la ecuación 13), ya que debido a su antigüedad es muy probable que su azolvamiento o aterramiento sea significativo, con lo cual disminuye la carga hidráulica y se sellan los caminos posibles al flujo del agua, limitándose así el proceso de tubificación.

Por otra parte, debido a que la información que presenta la lámina de cada presa para la altura de cortina, corresponde a la diferencia entre su corona y el nivel más bajo de la cimentación, se corrigió tal dato, restándole la profundidad de la trinchera para obtener la diferencia entre nivel de desplante y la corona o altura de cortina (Hc). En la aplicación del modelo definido por las ecuaciones 8, 9, 11 y 12, se adoptaron las consideraciones siguientes: (1) H₀ = Hc, Z₀ = Hc - 1, α₂ = 0.000725 s/m y Δt = 60 segundos; (2) b se estima con la ecuación 13 y (3) el área A_s del vaso se consideró igual al cociente entre el volumen almacenado (V) y la altura de la presa (H₀). Los resultados se presentan en las dos últimas columnas de la tabla 2, conjuntamente con los datos generales de cada presa y las estimaciones de las ecuaciones 13 a 16. Al final de la tabla 2 se detalla cómo se estimó cada valor consignado en sus columnas 7 a 16; en la columna 2 se indica el número de orden cronológico de construcción según catálogo SRH (1976), mismo que corresponde al de cada lámina de la presa.

 

Análisis de los resultados de la aplicación numérica

En presas con cortinas altas (>15 m.) y volumen de almacenamiento reducido, los tiempos estimados al pico resultan de unos pocos minutos, siendo entonces recomendable realizar la aplicación del modelo con intervalos de tiempo menores de un minuto, quizás de 10 ó 15 segundos, para mejorar la exactitud de los resultados. Este es el caso de las presas números: 19, 27, 33, 43, 63, 71, 90, 92 y 96.

En general, se observa que las estimaciones del gasto máximo obtenidas con el modelo, columna 15 de la tabla 2, son coincidentes con los órdenes de magnitud que establecen las ecuaciones 15 y 16. Lo anterior es sumamente importante, pues implica que el modelo reproduce la experiencia mundial de las fallas ocurridas en presas con cortinas de tierra; permitiendo además obtener el hidrograma de salidas, como se ilustra en las figuras 1 y 2 para una presa pequeña y otra grande.

Respecto a los límites de aplicación del modelo, conviene destacar que la reproducción aceptable que hace del hidrograma de salidas de la falla en la presa Teton, implica que puede ser aplicable a cortinas y almacenamientos de hasta 90 metros y 308 Mm³, respectivamente, que fueron las características físicas de esta presa (300 ft y 250,000 acre-ft).

 

Conclusiones

El modelo expuesto (ecuaciones 8, 9, 11 y 12), relativo al rompimiento gradual de cortinas de tierra por desbordamiento según una falla rectangular, está físicamente basado y su aplicación a cualquier presa del país requiere únicamente como datos, la altura de su cortina y el volumen almacenado al nivel máximo antes de la falla.

La aplicación del modelo, utilizando estimaciones del ancho promedio de la brecha de falla (b), del área media del vaso (A_s) y un coeficiente de erosividad (α₂) de 0.000725 s/m, conduce, en las 97 aplicaciones numéricas realizadas a presas pequeñas del país con cortinas de tierra, a valores del gasto máximo descargado que se apegan a la experiencia mundial de este tipo de fallas.

La sencillez del modelo y el hecho de sólo requerir dos datos físicos de la presa, lo vuelven aplicable a cualquier presa pequeña del país, en la cual se desea estimar el hidrograma de salidas debido al rompimiento de su cortina por desbordamiento. Lo anterior como requisito básico para la formulación de cualquier plan de riesgo y emergencia y la elaboración de los planos de zonas inundables y áreas de peligro, ya que es imposible garantizar un riesgo nulo en relación con la falla de una presa.

 

Referencias

Arganiz M., E. Bladé J., Dolz M. Sánchez O.A. Fuentes V.F. y De Luna F.. Simulación de la ruptura de la cortina de la presa La Parota, Guerrero, México, usando un algoritmo de alta resolución. Ingeniería Hidráulica en México, volumen XXIV (número 3), julio-septiembre de 2009: 101-106.         [ Links ]

Campos-Aranda D.F. Propuesta de criterios para la elaboración de estudios hidrológicos (Segunda parte). Ingeniería Hidráulica en México, volumen VIII (números 2 y 3), mayo-diciembre de 1993: 17-28.         [ Links ]

Froehlich D.C. Embankment Dam Breach Parameters and Their Uncertainties. Journal of Hydraulic Engineering, volumen 134 (número 12), diciembre de 2008: 1708-1721.         [ Links ]

Fuentes-Mariles O.A., Arganiz-Juárez, M.L., De Luna-Cruz F., Franco V. Estimación numérica del hidrograma de salida de una presa debido a su ruptura. Ingeniería. Investigación y Tecnología, volumen XI (número 3), julio-septiembre de 2010: 267-276.         [ Links ]

MacDonald T.C. y Langridge-Monopolis J. Breaching Characteristics of Dam Failures. Journal of Hydraulics Engineering, volumen 110 (número 5), mayo de 1984: 567-586.         [ Links ]

Secretaría de Recursos Hidráulicos (SRH). Presas Construidas en México, Dirección de Proyectos de Irrigación y Control de Ríos, México, D F, 1976.         [ Links ]

Singh V.P. Dam Breach Modeling Technology, Chapter 5, Empirical Models: Dimensional Analytical Solutions, pp. 101-121, Kluwer Academic Publishers. Dordrecht, The Netherlands, 1996, 242 p.         [ Links ]

Singh V.P. y Scarlatos P.D. Analysis of Gradual Earth-Dam Failure. Journal of Hydraulics Engineering, volumen 114 (número 1), enero de 1988: 21-42.         [ Links ]

Wahl T.L. Uncertainty of Predictions of Embankment Dam Breach Parameters. Journal of Hydraulics Engineering, volumen 130 (número 5), mayo de 2004: 389-397.         [ Links ]

Wetmore J.N. y Fread D.L. The NWS Simplified Dam Break Flood Forecasting Model. Program Documentation and User's Guide with Example Problem, Maryland, USA, Office of Hydrology, National Weather Service, Silver Spring, 1984, 38 p.         [ Links ]

 

Semblanza del autor

Daniel Francisco Campos-Aranda. Obtuvo el título de ingeniero civil en diciembre de 1972, en la entonces Escuela de Ingeniería de la UASLP. Durante el primer semestre de 1977, realizó en Madrid, España un diplomado en hidrología general y aplicada. Posteriormente, durante 1980-1981 llevó a cabo estudios de maestría en ingeniería en la especialidad de hidráulica, en la División de Estudios de Posgrado de la Facultad de Ingeniería de la UNAM. En esta misma institución, inició (1984) y concluyó (1987) el doctorado en ingeniería con especialidad en aprovechamientos hidráulicos. Ha publicado artículos principalmente en revistas mexicanas de excelencia: 40 en Tecnología y Ciencias del Agua (antes Ingeniería Hidráulica en México), 14 en Agrociencia y 12 en Ingeniería. Investigación y Tecnología. Fue investigador nacional (nivel I) desde el 1° de julio de 1991 hasta el 31 de diciembre de 2007. Actualmente es profesor jubilado de la UASLP, desde el 1° de febrero del 2003. En noviembre de 1989 obtuvo la medalla Gabino Barreda de la UNAM y en 2008 le fue otorgado el Premio Nacional "Francisco Torres H." de la AMH, a la práctica profesional de la Hidráulica.