Aplicación inversa del método de Krylov para obtener una matriz de orden tres

 

Inverse Application of Krylov's Method to Obtain an Order–Three Matrix

 

Cortés–Rosas J.J.¹, Arganis–Juárez M.L.²

 

¹ Departamento de Ciencias Aplicadas Facultad de Ingeniería Universidad Nacional Autónoma de México. Correo: ma_an_di@yahoo.com.mx

² Instituto de Ingeniería Coordinación de Hidráulica Universidad Nacional Autónoma de México. Correo: MArganisJ@iingen.unam.mx

 

Información del artículo: recibido: septiembre de 2009.
Aceptado: marzo de 2011.

 

Abstract

En este artículo se presenta un procedimiento para obtener una matriz cuadrada A de orden tres a partir de su ecuación característica, utilizando el método de Krylov, que tradicionalmente realiza el procedimiento contrario. Los elementos de la matriz A finalmente son encontrados a partir de resolver un sistema de ecuaciones no lineales.

Descriptores: ecuación característica, matriz cuadrada, método de Krylov, sistema de ecuaciones no lineales, Cayley–Hamilton, Solver.

 

Abstract

In this article a procedure is presented to obtain a square order–three matrix A given its characteristic equation, by means of Krylov's method, that traditionally performs the opposite problem. Finally, the elements of matrix A are found by solving a nonlinear equation system.

Keywords: characteristic equation, square matrix, Krylov's method, non–linear equation system, Cayley–Hamilton, Solver.

 

Introducción

La determinación de la ecuación característica y de los valores característicos de una matriz cuadrada A es un problema con numerosas aplicaciones en la ingeniería, sobre todo si los modelos matemáticos son ecuaciones diferenciales; ejemplo de ello son las determinaciones de las frecuencias naturales de oscilación de un sistema hidráulico, cuyo modelo matemático es un sistema de ecuaciones lineales (figura 1). Otro problema que se resuelve es la determinación de la mayor frecuencia natural real de oscilación de sistemas masa resorte con o sin amortiguamiento (figuras 2 y 3), (Torres y Czitrom, 1980).

El método directo del cálculo del determinante de A–λI (Solar y Speziale, 2001) resulta muy laborioso cuando la matriz A es de orden mayor que 3 y la matriz no es del tipo porosa o diagonal. El método de Krylov (Torres et al., 1980, Luthe et al, 1984, Iriarte, 1990) es un procedimiento numérico que evita el problema del cálculo del determinante, pero tiene la particularidad de que debe seleccionarse un valor adecuado de un vector auxiliar .

Se puede afirmar que toda matriz cuadrada n tiene una sola ecuación característica, pero no se puede decir que dada una ecuación característica existe una sola matriz cuadrada que le da origen; lo anterior se puede ilustrar de manera relativamente sencilla en el caso de matrices de orden dos, por ejemplo, las matrices:

tienen como ecuación característica a:

λ² – 5λ + 4 = 0

Encontrar matrices con ecuaciones características iguales se vuelve un problema elaborado a medida que se incrementa el orden de la matriz.

Existen procedimientos del álgebra lineal para estimar distintas matrices A con la misma ecuación característica, pero con la particularidad de que se toma como base una matriz con una forma en particular (muchos ceros o unos entre sus elementos) tal es el caso del llamado método de la matriz compañera (Chen, 1970, Marcus et al., 1964) que considera una matriz porosa A de la forma:

Donde b₁...b_n–2, b_n–1, b_n son los coeficientes de la ecuación característica con la forma dada en la ecuación 3.

La transpuesta de la matriz A tiene la misma ecuación característica.

Adicionalmente se pude encontrar una matriz similar a la matriz A, cuya ecuación característica se conoce. Dicho concepto toma en cuenta el producto de matrices, la igualdad de matrices, así como la definición de matriz inversa, al considerar que la matriz similar C se puede calcular como (Chen, 1970, Marcus et al., 1964):

donde B es una matriz no singular que se puede proponer.

En estos métodos debe conocerse previamente la matriz A, cuya ecuación característica es conocida. Si se propone una matriz B, los elementos de C se pueden calcular con un sistema de ecuaciones lineales.

El método de Givens (Givens, 1954, Scheid, 1968) y su modificación a partir del reordenamiento de las operaciones de transformación hecha por Johansen (1961) para disminuir tiempos de cálculo, resuelve el problema de obtener los valores característicos de una matriz simétrica A, transformándola en una forma tridiagonal con ayuda de una secuencia de matrices rotadas. Pero de nueva cuenta se parte de conocer la matriz A.

Si el método de Krylov se utiliza a la inversa para abordar el problema de la obtención de la matriz A, conocida la ecuación característica, se presentan requerimientos de métodos numéricos adicionales para el caso de matrices de órdenes superiores a dos, en este caso, la resolución de sistemas de ecuaciones no lineales. En este artículo se presenta la determinación de una matriz cuadrada A de orden 3, a partir de que se conoce su ecuación característica.

 

Metodología

Método de Krylov

Este método permite obtener la ecuación característica de una matriz cuadrada A, sea:

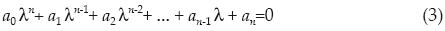
la ecuación característica de un matriz cuadrada A de orden n.

Si la matriz es de orden n, la ecuación característica es de grado n y por lo tanto a₀ ≠ 0. Definiendo los coeficientes b_i:

Sustituyendo en (1):

Aplicando el teorema de Cayley–Hamilton que establece que: "Toda matriz cuadrada A satisface su ecuación característica expresada como una ecuación matricial".

En la ecuación anterior se suman matrices de n × n y las incógnitas son los coeficientes b_i. Para sumar vectores y no matrices el método propone posmultiplicar por un vector compatible con A, diferente de cero y normalizado:

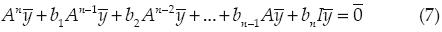
El vector debe seleccionarse adecuadamente de manera que al final se logre obtener un sistema de ecuaciones lineales compatible determinado, cuyas incógnitas son los coeficientes b_i. Algunas propuestas para este vector son aquellos que tengan un uno entre sus elementos y los restantes sean cero, o bien, el vector de sólo unos.

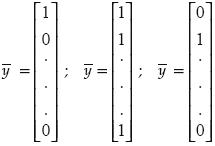
El sistema de ecuaciones lineales dado por la ecuación 4 se resuelve y los coeficientes b_i obtenidos se sustituyen en la ecuación 5 obteniendo con ello la ecuación característica buscada.

 

Solver© en ambiente Excel para resolver sistemas de ecuaciones no lineales

La herramienta Microsoft Excel Solver© utiliza el código de optimización no lineal (GRG2) desarrollado por la Universidad Leon Lasdon de Austin (Texas) y la Universidad Allan Waren (Cleveland ).

Los problemas lineales y enteros utilizan el método más simple con límites en las variables y el método de ramificación y límite, implantado por John Watson y Dan Fylstra de Frontline Systems, Inc. (Microsoft Office Excel, 2003).

El procedimiento para su empleo consiste en generar una hoja en Excel en la que se indican las celdas incógnitas y las ecuaciones que las relacionan (puede ser una ecuación o todo un sistema de ecuaciones lineales o no lineales); se indica en otra celda la función objetivo que puede maximizarse, minimizarse o buscar los valores de las incógnitas que la hacen cero. También se pueden añadir ecuaciones de restricción al problema.

Dentro de Excel al invocar a la herramienta Solver© se indican las celdas incógnitas, a las que se les asignan valores iniciales dados por el usuario como primera aproximación; se debe proporcionar también la celda que contiene la función a optimizar y el algoritmo encuentra una solución al problema.

 

Método de Krylov a la inversa

El método de Krylov se puede aplicar para determinar una matriz cuadrada de orden n, si se conoce su ecuación característica de grado n. Los pasos a seguir en este caso son:

1) Proponer un vector auxiliar , compatible con A diferente de cero y normalizado.

2) Se propone la forma de la matriz A; según el orden se determinarán n × n elementos.

3) Se aplica el Teorema de Cayley–Hamilton, con la forma de la ecuación 5, lo anterior implica hacer los productos correspondientes de la matriz por el vector columna y los coeficientes de la ecuación característica conocida.

4) Se resuelve el sistema de ecuaciones no lineales resultante, obteniendo los elementos de la matriz A.

 

Aplicación

Se plantea el siguiente problema:

La ecuación característica de la matriz cuadrada A está dada por: λ³–9λ²+18λ–6=0.

a) Use el método de Krylov para obtener a la matriz A. Proponga el vector auxiliar para resolver el problema.

b) Con la matriz A obtenida en el inciso a), compruebe la ecuación característica usando el método directo.

Para resolverlo se propuso un vector auxiliar = [100]^T y la matriz incógnita con

elementos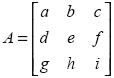

Se aplicó el método de Krylov a partir de la ecuación (7), por lo que se determinó:

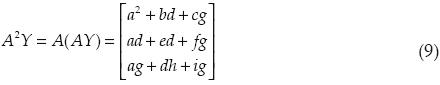
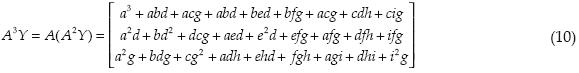
Sustituyendo en la ecuación (7):

Se obtiene el sistema de ecuaciones no lineales:

Es un sistema de tres ecuaciones con nueve incógnitas, es indeterminado y tendrían que fijarse 6 incógnitas para resolverlo; un camino para agregar ecuaciones al sistema es proponer otros dos vectores auxiliares y compatibles con A, diferentes de cero y normalizados. Otro camino es fijar seis de las incógnitas y resolver para las tres restantes, y encontrar una de las múltiples soluciones del sistema.

En este artículo se presenta el segundo caso, en donde se propone por sencillez que la matriz A sea una matriz diagonal, es decir, proponiendo como ceros los elementos b, c, f, d, g, h, el sistema de ecuaciones se reduce a

De nueva cuenta se tendría una ecuación y tres incógnitas: a, e, i, y tiene la forma de la ecuación característica original.

 

Resultados

Si se encuentran todas las raíces del polinomio usando la herramienta Solver y buscando los valores de A que hacen cero a la función, se determina una raíz del polinomio y las otras dos se encuentran con la fórmula general para resolver ecuaciones de segundo grado. Finalmente las tres raíces encontradas son:

a₁₌0.415774508387036; a₂=6.28994506 y a₃=2.29428043

y se podrían obtener seis matrices A diagonales, que tienen la ecuación característica indicada, quedando condicionados los valores de los elementos e, i, como sigue:

Las matrices A₁ a la A₆ tienen el mismo valor del determinante A – λI y por lo tanto, la misma ecuación característica:

λ³ – 9λ² + 18λ–6 = 0

Se puede aseverar entonces, que dada una ecuación característica puede provenir de más de una matriz cuadrada A.

 

Conclusiones

La determinación de una matriz cuadrada de orden superior a dos a partir de conocer su ecuación característica se vuelve un problema con requerimientos algebraicos y de algoritmos numéricos para resolver sistemas de ecuaciones que pueden ser no lineales, debido a que en este caso la matriz buscada no es única.

Se aplicó el método de Krylov a la inversa en la búsqueda de una matriz cuadrada, cuya ecuación característica es conocida y con la propuesta de un vector columna auxiliar Y; al aplicar el procedimiento se obtuvo un sistema de ecuaciones no lineales indeterminado por lo que se fijaron algunas incógnitas con la propuesta por simplicidad de que A fuera una matriz diagonal; con este planteamiento se determinó que existe más de una matriz A con la ecuación característica buscada, en este caso, se encontraron seis matrices A diagonales que tienen la ecuación característica buscada.

Adicionalmente se determinó la herramienta Solver© que permite resolver un sistema de ecuaciones no lineales, en este caso particular el sistema se redujo a una ecuación tipo polinomial de tercer grado.

Se pudo concluir que la aplicación del método de Krylov a la inversa permite la obtención de matrices cuadradas, conocida su ecuación característica y la forma de la matriz que se desea encontrar dependerá de la interpretación física o matemática del problema analizado.

 

Referencias

Chapra S., Canale. Métodos numéricos para ingenieros, México, Mc Graw Hill, 2000, pp. 982.         [ Links ]

Chen C.T. Introduction To Linear Systems Theory, New York, Holt, Rinehart And Wiston Inc., 1970.         [ Links ]

Givens W. Numerical Computation of the Characteristic Values of a Real Symmetric Matrix. Oak Ridge National Laboratory. Report No. ONRL 1574, 1954.         [ Links ]

Iriarte V.B.R. Métodos numéricos, México, Facultad de Ingeniería, UNAM, Trillas, 1990, pp. 269.         [ Links ]

Johansen D.E. Modified Givens Method for the Eigenvalue Evaluation of Large Matrices. Journal of the ACM (JACM), 8(3):331–335. July 1961 [en línea]. Disponible en: http://portal.acm.org/citation.cfm?id=321077        [ Links ]

Luthe R., Olivera A., Schutz F. Métodos numéricos, México, Limusa, 1984, pp. 443.         [ Links ]

Marcus M., Minc H. A Survey of Matrix Theory and Matrix Inequalities, Prindle, Boston, MA, Weber & Smith, Inc., 1964.         [ Links ]

Microsoft Office Excel. Temas de ayuda del Software Excel versión 2003.         [ Links ]

Scheid F. Numerical Analysis. Schaum's Outline Series. London, McGraw–Hill, 1968.         [ Links ]

Solar G.E., Speziale De G.L. Apuntes de álgebra lineal, México, Limusa–Noriega Editores, Facultad de Ingeniería, UNAM, 2001, pp. 291–866.         [ Links ]

Torres F.J.A., Czitrom De G.V. Métodos para la solución de problemas con computadora digital. México. Impresiones y Servicios de Ingeniería, SA de CV, 1980, pp. 579.         [ Links ]

 

Semblanza de los autores

Jesús Javier Cortés–Rosas. Es ingeniero mecánico electricista egresado de la Facultad de Ingeniería de la UNAM y maestro en administración por la Facultad de Contaduría y Administración, con diplomado en planeación y administración de recursos humanos y en desarrollo humano. Tiene todos los créditos de la maestría en administración de organizaciones. Es profesor de carrera de la Facultad de Ingeniería en el área de matemáticas aplicadas. Actualmente es jefe del Departamento de Matemáticas Avanzadas, Análisis Numérico y Dibujo. Fue jefe de servicio de campo en Equipos de Construcción e Industria, SA de CV de la División Bienes de Capital del Grupo ICA y fue auditor técnico externo, entre otros cargos.

Maritza Liliana Arganis–Juárez. Egresada de la Facultad de Ingeniería, con maestría y doctorado por la misma institución. Actualmente es investigadora asociada de la Coordinación de Hidráulica del Instituto de Ingeniería y profesora de asignatura definitiva de análisis numérico y de cinemática y dinámica, asignaturas que imparte en la Facultad de Ingeniería de la UNAM en el Departamento de Ciencias Aplicadas. En 1993, inició su colaboración con la UNAM como profesora de física en la Escuela Nacional Preparatoria. Actualmente realiza investigaciones en el área de aprovechamientos hidráulicos e hidrología, incluyendo el cómputo evolutivo aplicado a la hidrología y a la hidráulica.