Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.13 no.1 Ciudad de México ene./mar. 2012
Efecto de la textura superficial en el desempeño a fricción de cojinetes de empuje
Effect of the Surface Texture on Friction Thrust Bearing Performance
Suárez–Bustamante F.A.1, Toro–Botero F.M.2, Vélez–Restrepo J.M.3
1 Grupo de Tribología y Superficies (GTS) Ciencia y Tecnología de Materiales (CTM) Universidad Nacional de Colombia, Sede Medellín Correo: alexandersb@gmail.com
2 Posgrado en Aprovechamiento de Recursos Hidráulicos Universidad Nacional de Colombia–Sede Medellín Correo: fmtoro@unalmed.edu.co
3 Grupo de Tribología y Superficies (GTS) Ciencia y Tecnología de Materiales (CTM) Universidad Nacional de Colombia–Sede Medellín Correo: jmvelez@unalmed.edu.co
Información del artículo: recibido: agosto de 2010.
Reevaluado: noviembre de 2010.
Aceptado: febrero de 2011.
Resumen
En este trabajo se presenta un modelo teórico que establece relaciones entre las condiciones de operación de un cojinete de empuje, su micro–topografía acondicionada y el coeficiente de fricción, cuando opera en condiciones de Lubricación Hidrodinámica (HL). Entre los resultados más sobresalientes obtenidos en una exploración efectuada con el modelo están: la construcción de un mapa donde se caracteriza el desempeño de estos componentes y la obtención de algunas relaciones entre diversos grupos adimensionales, los cuales muestran que es factible ampliar el régimen de lubricación hidrodinámica de este tipo de cojinetes mediante el acondicionamiento artificial de sus superficies.
Descriptores: tribología, cojinetes, lubricación, superficies texturizadas, fricción.
Abstract
This paper shows a theoretical model which stablishes relations among the operational conditions of a thrust bearing, its conditioned microtopography and the friction coeficient when it works under Hydrodynamic Lubrication conditions. Among the most outstanding results obtained from an exploration made with the model are: building of a map where the performance of these components is characterized and the obtention of some relations among several adimentional groups that show the possiblility to enhance the hydrodynamic lubrication regime for this sort of bearings by artificial conditioning of their surfaces.
Keywords: tribology, sliding bearings, lubrication, textured surfaces, friction.
Introducción
La búsqueda de alternativas que permitan controlar las fuerzas de fricción inherentes al funcionamiento de dispositivos mecánicos, se ha constituido como un aliciente para promover el desarrollo de nuevas tecnologías y modelos físicos que permitan adquirir un conocimiento más profundo de los mecanismos asociados a estos fenómenos de disipación (Pettersson, 2005; Jane et al., 2005).
Desde hace varios años, la ingeniería de superficies se ha enfocado en el diseño y la fabricación de superficies que permitan reducir la fricción (Anno et al., 1968). Gran parte de estos trabajos han sido aplicados inicialmente en la industria automotriz y en el conformado de materiales; sin embargo, el abanico de aplicaciones directas es mucho más amplio, al igual que los beneficios económicos y ambientales (Ronen et al., 2001; Kligerman et al., 2002; Brizmer et al, 2003; Etsion et al., 2004 y Kovalchenco et al., 2005).
Todo esto motivó la realización de este trabajo, el cual busca presentar un modelo teórico que establece relaciones entre las condiciones de operación de un cojinete de empuje, su micro–topografía acondicionada y su coeficiente de fricción, cuando éste opera en condiciones de Lubricación Hidrodinámica (HL). Este tipo de cojinete es un elemento de uso frecuente en diversas aplicaciones mecánicas.
Sistema de estudio
El sistema tribológico de estudio consta de un cojinete de empuje (elemento de soporte plano y de longitud infinita), su contracuerpo y un lubricante líquido (figura 1a). El cojinete posee una textura acondicionada, caracterizada por surcos trapezoidales orientados transversalmente a la dirección de deslizamiento para la cual fue concebido. Además, se supone constituido por un material rígido y homogéneo, posee n surcos separados entre sí por una distancia l, y su ancho total es L. Las dimensiones de su textura correponden a la escala de las rugosidades (micrométrica), y se desprecia el efecto de las ondulaciones. El elemento a soportar por el cojinete se considera como un sólido también rígido y homogéneo, sin textura alguna en su superficie y con rugosidad despreciable. Finalmente, el lubricante considerado se comporta como un fluido newtoniano; siendo caracterizado por su viscosidad dinámica μ, la cual se asume constante para las diferentes condiciones de operación del sistema. Este supuesto, también es empleado por otros investigadores (Anno et al., 1968; Ronen et al., 2001).
Las condiciones de operación impuestas al sistema se caracterizaron mediante la velocidad de deslizamiento U, la carga normal total por unidad de longitud PT y el paralelismo existente entre las superfiecies nominales de los elementos texturizado y soportado. Según los resultados predichos por la ecuación de Reynolds (Ronen et al, 2001; Schlichting, 1979):

en ausencia de texturizado, situación en la cual las superficies serían paralelas y no existiría una macro–cuña convergente, este sistema tribológico no podría formar una película lubricante capaz de sustentar carga alguna en condiciones dinámicas. Adicionalmente, se asumió una condición de estado estable para el sistema de estudio. De acuerdo con ésta, U y PT , permanecen constantes en el tiempo y el sistema se encuentra trabajando en un régimen de lubricación hidrodinámica. Finalmente, las presiones a la entrada PO y a la salida del elemento texturizado PS se supusieron nulas.
Con estas condiciones, el sistema de interés se redujo al estudio de la celda unitaria mostrada en la figura 1b, la cual está constituida por uno de los n micro–cojinetes que conforman el elemento texturizado. Por consiguiente, PT = nP, donde P es la carga sustentada por un micro–cojinete. De manera similar, la fuerza total de fricción ejercida por el fluido sobre el elemento texturizado sería igual a FfT = nFj. Sin embargo, los coeficientes de fricción promedio del sistema y de un micro–cojinete serían iguales,  T = f.
T = f.
El micro–cojinete de estudio posee cuatro etapas (MC4E), una convergente (C) y una divergente (D) separadas entre sí por un par de regiones planas (P). Cada etapa está caracterizada por una "fracción espacial" & que normaliza su tamaño con respecto a la longitud total del micro–cojinete,

Por lo tanto, los parámetros microtopográficos c, s, d, e y Δe, mostrados en la figura 2 pueden expresarse en función de ζi.
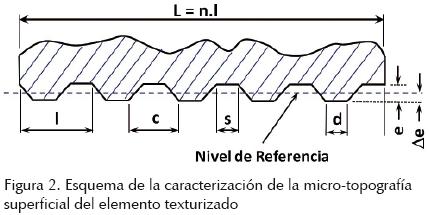
Caracterización de la textura superficial del cojinete
La rugosidad superficial asociada a los micro–cojinetes puede representarse como la suma de dos componentes para sus diferentes parámetros descriptores (bien sea Ra, Rq, Rz, Ry o Rsm, entre otros); es decir,

donde RACOND es la componente asociada a la geometría del texturizado ideal y RDESV hace referencia a las desviaciones de éste encontradas en la realidad sobre los elementos texturizados. Al despreciar el efecto de RDESV, es posible hacer una caracterización micro–topográfica de las superficies empleando parámetros de rugosidad normalizados relacionados con las alturas de las asperezas (como RaN, RqN y RzN, entre otros) y/o con su distribución espacial (como por ejemplo RSmN). Estos parámetros normalizados son adimensionales, de manera que,

donde e es la altura de las mesetas medida desde el fondo de los surcos (figura 2).
El plano de referencia para medir la rugosidad se definió con base en el criterio de mínimos cuadrados aplicado a la micro–topografía de la superficie del cojinete (figura 2).
La ubicación de este plano está dada por Ae y se relaciona con e de la siguiente manera,

donde D = c/l = 1 – ζ2 es la densidad de superficie texturizada y β = s/c = ζ4/D es la razón entre el ancho del fondo de los surcos y su ancho efectivo (Suárez, 2008). Ambos parámetros varían en el intervalo [0;1], y pueden describirse a su vez en términos de ζi. De esta manera, las versiones normalizadas (adimensionales) de los parámetros de rugosidad adquieren las formas,

donde Φ es una función de las fracciones espaciales ζi. El súbíndice x hace referencia a las letras usualmente empleadas para designar los parámetros de regusidad; por ejemplo,  = RaN representa la rugosidad media aritmética normalizada. Para el caso de RaN y RqN, esta expresión adopta respectivamente las formas,
= RaN representa la rugosidad media aritmética normalizada. Para el caso de RaN y RqN, esta expresión adopta respectivamente las formas,


Como tambien es importante describir la distribución espacial de los patrones, se seleccionó para esto al parámetro Rsm (espaciamento promedio entre los patrones), el cual, en términos de la geometría de los micro–cojinetes queda definido como,

dado que,

Descripción del modelo
Con base en la geometría alcanzada por la película lubricante en su condición estable (figura 1), se establecieron las siguientes relaciones entre h1, h2 y e,


es el parámetro de la película lubricante asociado a la primera etapa del cojinete y está definido por la relación entre el espesor de la película fluida a la entrada h1, y su espesor a la salida h2 (figura 1b).
Para que se satisfaga la condición de un movimiento lento (Schlichting, 1979), es decir,  e <<1 se debe cumplir que,
e <<1 se debe cumplir que,

Al aplicar la ecuación de conservación de masa a la película lubricante se establecieron las siguientes relaciones adimensionales entre las condiciones de operación (condensadas en el parámetro de lubricación H = μU/P), el coeficiente de fricción promedio f, y los descriptores de la geometría de los micro–elementos fluidos y de la superficie del elemento texturizado.
Relaciones que consideran a H:



Relaciones que consideran a f:



Relaciones que consideran a Ff:

Esta última relación permite obtener curvas del tipo Stribeck–McKee para el tribo–sistema. Haciendo uso de la ecuación 11 se transforma en:

Para los grupos de ecuaciones presentados (ecuaciones 14 – 21), T(α,ζi) y Λ(α,ζi) son dos funciones adimensionales que combinan los aspectos geométricos de la película lubricante y de la textura del cojinete y dan cuenta del comportamiento exhibido por el sistema tribológico de estudio. Estas funciones se han construido con base en el parámetro de la película lubricante a y las fracciones espaciales asociadas al texturizado ζi.
De acuerdo con las ecuaciones 14 a 21, si se caracteriza apropiadamente la superficie de un elemento con este tipo de textura y se controlan adecuadamente las condiciones de operación, se puede estimar el parámetro de la película lubricante α y por ende, su espesor mínimo, h2. Comparaciones entre el valor así deducido de h2 y su valor medido, ayudarían a validar el modelo presentado en este trabajo y a evaluar su aplicabilidad en condiciones extremas impuestas al sistema.
Resultados en aplicaciones de micro–cojinetes de tres etapas
El modelo desarrollado se empleó inicialmente para estudiar sistemas compuestos por micro–cojinetes de tres etapas (MC3E), ζ4 = 0. Para los microcojinetes de hasta 3 etapas, las funciones T(α,ζi) y Λ(α,ζi) mostradas en las ecuaciones 14 a 21, adquieren las formas:


donde


Con el objetivo de determinar los intervalos de las fracciones espaciales ζi donde es posible obtener el efecto de sustentación y maximizarlo, se realizó una exploración del comportamiento conjunto de las ecuaciones 14 a 25. Dicha exploración se dividió en tres fases, las cuales se describen a continuación.
Una primera aproximación fue realizada con el diseño muestral presentado en la figura 3, que permite hacer una evaluación rápida de la consistencia del modelo en situaciones límite (condiciones de los tipos ζi = 1 y ζj≠i= 0, y ζ1 = ζ3) e identificar posibles zonas de interés dentro del dominio de trabajo.

La figura 4 muestra los resultados iniciales de esta exploración, separándolos por tipos de micro–cojinetes: Divergente–Plano–Convergente (DPC, 0 < α <1) y Convergente–Plano–Divergente (CPD, α > 1). A diferencia de los CPD, los DPC presentan un comportamiento muy sensible a pequeñas variaciones del parámetro a. Sin embargo, en estos últimos, se pueden alcanzar valores más altos del producto (h2/l)2/H.
En ambos tipos de micro–cojinetes, existen algunas combinaciones de parámetros ζi, para las cuales se logra el efecto de sustentación. De éstas, las que permiten la sustentación para α > 1, no la permiten para 0 < a < 1, y viceversa. Además existen combinaciones que generan un efecto nulo de sustentación (sin ser negativo). En estos casos particulares, los surcos o asperezas son simétricos (ζ1 = ζ3) o simplemente, no se forman regiones convergentes y/o divergentes en ninguna porción del micro–cojinete, es decir, cuando la superficie del cojinete es totalmente plana y paralela a la del elemento soportado (ζ2 = 1 o α = 1  ζ1, ζ3 ≠ 0).
ζ1, ζ3 ≠ 0).
Según la figura 4b, existen configuraciones de Micro–Cojinetes de 2 Etapas (MC2E) donde el factor (h2 / l)2 / H es mayor que el alcanzable con una configuración de micro–cuñas 100% convergentes (Configuración A). Estos MC2E son del tipo Convergente–Plano (CP) como el de la configuración D, por ejemplo. A su vez, nótese que la configuración A es mejor que las asociadas a algunos MC2E como lo son aquellos del tipo Convergente–Divergente CD, en los cuales, ζ2 = ζ4 = 0 (ver gráficas de configuraciones F e I). De todo esto se concluye que, el efecto del achatamiento de las asperezas (configuraciones D y G por ejemplo, comparadas con la configuración A), representado por la zona intermedia de magnitud ζ2, induce cambios representativos en el desempeño de estos elementos, los cuales son benéficos sólo en algunos casos.
El trabajo con micro–cojinetes del tipo DPC bien podría ser prometedor desde el punto de vista de grandes valores del grupo (h2 / l)2 / H y bajos valores para el grupo f ·(h2/1), con respecto a los valores máximos y mínimos obtenibles en micro–cojinetes del tipo CPD. Sin embargo, existe un inconveniente: la alta sensibilidad del comportamiento de los DPC a pequeñas variaciones de α dificulta el control de su operación para garantizar el comportamiento deseado en aplicaciones específicas; por esta razón, las siguientes fases exploratorias se enfocan sólo en micro–cojinetes CPD.
La segunda fase de la exploración se centró en la búsqueda de configuraciones ζi para α > 1 , cuyas curvas (h2 / l)2 / H fuesen superiores a la que caracteriza a la configuración ζ1 = 1 . Se encontró que es factible incrementar hasta en un 20% la capacidad de carga de un sistema empleando configuraciones diferentes a la de referencia (ζ1 = 1) y adicionalmente, se hizo un importante hallazgo que permitió simplificar la tercera fase de la exploración. De las curvas obtenidas en función de a para diferentes combinaciones de los parámetros se observó que éstas tienden a no cortarse, siendo más o menos "paralelas en algunos casos"; esto permitió alejar la atención de la variable α para el desarrollo de esta última fase exploratoria, facilitando la caracterización del grupo (h2 / l)2/ H mediante el uso de ζi solamente (Suárez, 2008).
Finalmente, en la tercera fase se fijó a en 2,2 (valor cercano al máximo del grupo adimensional (h2 / l)2 / H en todas las configuraciones estudiadas) y se construyó el mapa mostrado en la figura 5. En éste se caracteriza el desempeño de todos los posibles micro–cojinetes compuestos hasta por 3 etapas con α >1 . De acuerdo con el mapa, no todas las configuraciones permiten alcanzar el efecto de sustentación de carga y, sólo un pequeño grupo de configuraciones permite igualar y/o superar el valor (h2 / l)2 / H = 0,16 asociado a la configuración tomada como refererencia. Dado que las configuraciones que poseen las mejores capacidades de soporte de carga, poseen a su vez los menores coeficentes de fricción, este mapa también revela información del desempeño a fricción de los microcojinetes.
Conclusiones
Para los micro–cojinetes considerados en este trabajo, se encontró que la geometría de los surcos y su separación influyen significativamente en el coeficiente de fricción promedio de estos tribo–sistemas y en su capacidad de soporte de carga. De esta manera, resulta evidente la importancia que tiene tanto la micro–topografía de la superficies como las condiciones de operación en el desempeño tribológico de estos sistemas, y por ende, este aspecto debe tenerse en cuenta durante el diseño y la fabricación de elementos texturizados destinados a aplicaciones similares a las modeladas.
La relación Ra / RSm constituye una variable importante para definir el comportamiento de los cojinetes estudiados. Ésta aporta información más relevante de la que puede aportar un simple parámetro descriptor de las alturas de las asperezas como Ra o Rq.
El modelo desarrollado se aplica a varias escalas de trabajo. La capacidad de soporte de carga disminuye con la longitud total de los micro–cojinetes, es nula para el caso en el que ésta es cero. El parámetro RSm, y más específicamente sus límites máximo y mínimo permisibles en una aplicación dada, condicionan fuertemente la magnitud de la carga máxima a soportar. Desde el punto de vista de la fricción, ésta varía inversamente con la relación RSm / Ra para cojinetes con los mismos parámetros ζi.
Finalmente, los resultados de la exploración realizada muestran que, en general, es factible ampliar el régimen de lubricación hidrodinámica de este tipo de cojinetes mediante el acondicionamiento adecuado de su superficie. Esto permite disminuir el coeficiente de fricción promedio del sistema e incrementar su capacidad de soporte de carga, o equivalentemente, aumentar la capacidad del sistema para operar a velocidades más bajas, aún manteniéndose en un régimen hidrodinámico.
Agradecimientos
Los autores de este trabajo agradecen a la Universidad Nacional de Colombia, Facultad de Minas (Sede Medellín) por su colaboración en el desarrollo de este trabajo.
Referencias
Pettersson U. Surfaces Designed for High and Low Friction. Thesis (Doctor of Philosophy). Uppsala Universitet. 2005. 44 p. [ Links ]
Jane–Wang Q., Dong Z. Virtual Texturing: Modelling the Performance of Lubricated Contacts of Engineered Surfaces. Transactions of the ASME, 127:722–728. 2005. [ Links ]
Anno J.N., Walowit J.A., Allen C.M. Microasperity Lubrication. Journal of Lubrication Technology, pp. 351–357, April 1968. [ Links ]
Ronen A., Etsion I., Kligerman Y. Friction–Reducing Surface–Texturing in Reciprocating Automotive Components. Tribology Transactions, 44(3):359–366. 2001. [ Links ]
Kligerman Y., Etsion I. Experimental Investigation of Laser Surface Texturing for Reciprocating Automotive Components. Tribology Transactions, 45(4):444–449. 2002. [ Links ]
Brizmer V., Kligerman Y., Etsion I. A Laser Surface Textured Parallel Trhust Bearing. Tribology Transactions, 46(3):397–406. 2003. [ Links ]
Etsion I., Halperin G., Brizmer V., Kligerman Y. Experimental Investigation of Laser Surface Textured Parallel Thrust Bearings. Tribology Letters, 17(2):295–300. August 2004. [ Links ]
Kovalchenko A., Ajayi O., Erdemir A., Fenske G., Etsion I. The Effect of Laser Surface Texturing on Transitions in Lubrication Regimes During Unidirectional Sliding Contact. Elsevier. Tribology International, 38:219–225. 2005. [ Links ]
Schlichting H. Boundary Layer Theory, McGaw–Hill, Inc, USA, 1979, pp.116–123. [ Links ]
Suárez F.A. Efecto de la textura superficial en el desempeño a fricción de un cojinete plano de deslizamiento. Tesis (Maestría). Universidad Nacional de Colombia, Medellín. 2008. 124 p. [ Links ]
Semblanza de los autores
Fabio Alexander Suárez–Bustamante. Realizó sus estudios de ingeniería mecánica en la Facultad de Minas de la Universidad Nacional de Colombia (UN), donde obtuvo grado de honor por su trabajo en el área de tribología sobre el análisis del modelo de desgaste propuesto por Archard. Realizó su maestría en la misma universidad graduándose en el año 2008. Sus principales temas de interés incluyen desgaste por deslizamiento en seco, diseño de superficies de ingeniería, lubricación hidrodinámica y mecánica del contacto. Actualmente dicta cursos de tratamientos térmicos a materiales metálicos y propiedades mecánicas en la UN, es miembro activo del grupo de Tribología y Superficies y del grupo de Tecnología de Materiales de esa Universidad.
Francisco Mauricio Toro–Botero. Estudió ingeniería civil en la Facultad de Minas de la Universidad Nacional de Colombia (UN). Realizó sus estudios de maestría y doctorado en la Universidad de Mississipi (EU) en el área de hidrociencias e ingeniería. Durante el desarrollo de su doctorado se destacó como el mejor estudiante de la Facultad de Ingeniería (Universidad de Mississippi, 1992). Desde 2010 se desempeña como profesor titular de la Universidad Nacional de Colombia (Sede Medellín, Facultad de Minas) donde ha dictado numerosos cursos en pregrado y posgrado relacionados con manejo de calidad de aguas (modelamiento), turbulencia, hidráulica transitoria, simulación hidrodinámica, hidráulica fluvial y métodos numéricos, entre otros.
Juan Manuel Vélez–Restrepo. Ingeniero mecánico de la Universidad Nacional de Colombia (Facultad de Minas, Medellín). Realizó sus estudios de maestría y doctorado (1997) en la Universidad de Sao Pablo, Brazil. Desde 1985 es profesor de la Universidad Nacional de Colombia (UN), donde ha dictado cursos de ciencia de materiales e ingeniería, transformaciones de fases y tribología entre otros. Ha sido director del Departamento de Ingeniería de Materiales (2003); director de investigación de la Facultad de Minas (2002–2003), decano de la misma en el periodo 2006–2010. Coordinador del grupo de investigación en Ciencia y Tecnología de Materiales y director del Proyecto Leonardo da Vinci, que promueve la alfabetización científica y tecnológica, así como la innovación en el aprendizaje.














