Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Ingeniería, investigación y tecnología
versão On-line ISSN 2594-0732versão impressa ISSN 1405-7743
Ing. invest. y tecnol. vol.13 no.1 Ciudad de México Jan./Mar. 2012
Analogía para derivar un teorema extendido de Pitágoras para "N" dimensiones
Analogy to Derive an Extended Pythagorean Theorem to "N" Dimensions
Acosta–Robledo J.U.
División de Ingeniería Mecánica e Industrial, Facultad de Ingeniería, Universidad Nacional Autónoma de México. Correo: julises@gmail.com
Información del artículo: recibido: marzo de 2010.
Aceptado: febrero de 2011.
Resumen
Este artículo demuestra que es posible extender el teorema de Pitágoras a "N" dimensiones. Esta demostración se basa principalmente en el álgebra lineal, sobre todo en el producto vectorial en "N" dimensiones.
Descriptores: teorema de Pitágoras, álgebra lineal, análisis vectorial, geometría Analítica, espacios vectoriales, matemáticas.
Abstract
This article demonstrates that it is possible to extend the Pythagorean Theorem to "N" dimensions. This demonstration is mainly done based on linear algebra, especially in the vector product of "N" dimensions.
Keywords: Pythagorean Theorem, linear algebra, vector analysis, analytic geometry, vector spaces, mathematics.
Introducción
Uno de los teoremas más importantes de la geometría, si no es que el más importante, es el teorema de Pitágoras. Este teorema es un legado ancestral que ha podido perdurar hasta nuestros días. Pitágoras nació en la isla griega de Sarrios, alrededor del año 582 a.C. y murió alrededor del 507 a.C. Fue hijo de un mercader fenicio establecido en Sarros, estudió con Percenidas, Anaxi– H2 = X2 + Y ' mander y probablemente con Tales. Viajó a Grecia y a Fenicia, estudiando tres años en Sidón, Tiro y Babilonia. Posteriormente viajó a Egipto haciendo escala en Haifa y visitando templos en el Monte Carmel. Estudió 22 años en Egipto y permaneció 13 en Babilonia al caer cautivo en su regreso a Samos. Cuando llegó a su ciudad natal, Polycrates le impidió continuar sus estudios, así que viajó a Crotona, al sur de Italia y fundó su comunidad iniciática dedicada al estudio de la filosofía, las matemáticas y las ciencias de la naturaleza. Se dice que en esta comunidad podían participar tanto hombres como mujeres.
Al final, el movimiento pitagórico progresó, se propagó e influyó en todos los campos de la sociedad de aquella época. La comunidad pitagórica llegó a su fin por la oposición de ciertos núcleos de la oligarquía Crotona. No se sabe si Pitágoras murió en la destrucción de su comunidad, pero se sabe que Filolao, uno de sus discípulos, sobrevivió. Este se hizo dueño de gran parte de la documentación de la comunidad. Posteriormente la viuda de Filolao le vendió a Platón esta documentación, con lo cual este filósofo se convirtió en uno de los herederos de Pitágoras.
Actualmente mucha de la sabiduría pitagórica se ha perdido en el tiempo, y aún así ha sido la base de gran parte de la ciencia y la tecnología moderna. Nuestro deber como herederos de los grandes maestros es honrarlos, aprovechando y desarrollando su legado para el bienestar de la humanidad.
Este artículo pretende honrar a Pitágoras y a mis maestros al desarrollar una generalización del teorema de Pitágoras para "N" dimensiones.
Anteriormente se han realizado trabajos en donde se expone que este teorema se puede generalizar a tres y cuatro dimensiones (Murray, 2003). Este artículo va a seguir los mismos pasos, pero se hará uso de una gran herramienta legado de mis maestros: el álgebra vectorial. Principalmente, la base es el producto cruz de "N" dimensiones expuesto por Murray (2004).
La teoría básica es relativamente simple. El teorema de Pitágoras originalmente expone que: ''El cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma del cuadrado de sus otros dos lados''.
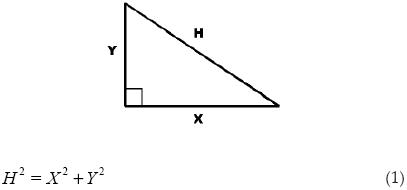
Ahora supongamos que cada uno de los lados del triángulo es un vector.
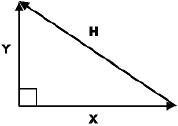
Si es así, los vectores  y
y  se definen de la siguiente manera:
se definen de la siguiente manera:
 = [X 0],
= [X 0],  = [0 Y]
= [0 Y]
El vector  sería la resta de los vectores
sería la resta de los vectores  y
y  :
:
 = [–X Y]
= [–X Y]
Hasta ahora no se ha visto nada nuevo ni espectacular, pero en este momento empezaremos a mostrar paulatinamente los secretos de este artículo. El paso siguiente no parece muy impresionante en dos dimensiones, pero su gran potencial se incrementa conforme las dimensiones aumentan.
Ahora se obtendrá un vector perpendicular a cada vector del triángulo, por medio del producto vectorial en dos dimensiones como lo propone Murray (2003). Este vector en dos dimensiones es de la misma longitud que el vector original, lo que cambia en más dimensiones, pero el vector sigue siendo proporcional.
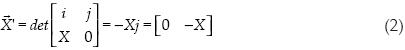
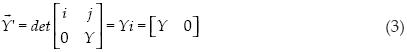
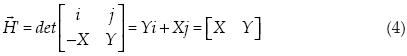
Ahora sólo resta obtener la magnitud al cuadrado de cada uno de estos últimos vectores. Esto se facilita al obtener el producto de cada vector consigo mismo.
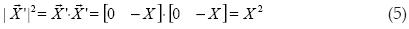
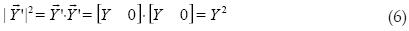
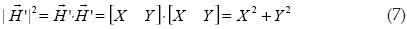
Como  ,
,  y
y  son de la misma magnitud que
son de la misma magnitud que  ,
,  y
y  respectivamente, llegamos a la conclusión que ya sabíamos: ''La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa''.
respectivamente, llegamos a la conclusión que ya sabíamos: ''La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa''.
Aquí lo interesante es que este procedimiento es aplicable desde dos hasta "N" dimensiones. Y con ello podemos generalizar el teorema de Pitágoras.
Desarrollo
Teorema de Pitágoras en tres dimensiones
El teorema de Pitágoras en su forma original es aplicable a dos dimensiones, cuando se aplica a tres dimensiones el teorema se redefine de la siguiente manera: ''El cuadrado del área del plano que se forma por un plano cortado por los planos XY, YZ y ZX es igual a la suma del cuadrado de cada una de las áreas que se forman por estos tres últimos planos delimitadas por el primer plano''.
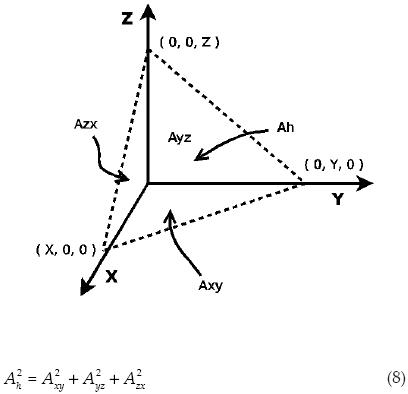
Demostración
Para desrrollar la demostración utilizamos el cálculo del área de cada superficie por medio del producto vectorial. El producto vectorial entre dos vectores da como resultado un vector cuyo módulo es el doble del área del triángulo definido por esos vectores. Como lo que nos interesa es el área al cuadrado, la obtenemos dividiendo el vector entre dos y obteniendo el producto punto consigo mismo:


Visto lo anterior, el procedimiento que se va a utilizar para la demostración es el cálculo del área al cuadrado de la superficie delimitada por los planos XY, YZ y ZX. Posteriormente, calcularemos el área de las superficies al cuadrado en los planos XY, YZ y ZX, y veremos si la suma de estas últimas áreas al cuadrado es igual al área del la primera superficie.
Cálculo del área al cuadrado de la primera superficie
Para el cálculo del área al cuadrado de esta superficie primero necesitamos obtener dos vectores que definan esta área. Para hacerlo se toma como eje el punto de corte del plano con el eje X, y se le restan los puntos de corte del plano en los ejes Y y Z, con lo cual se obtienen los dos vectores buscados:

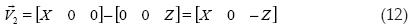
Ya con estos vectores procedemos a obtener el producto cruz:
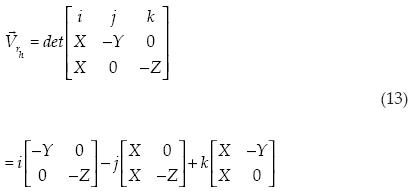

Para obtener el área al cuadrado, dividimos el vector entre dos y obtenemos el producto punto consigo mismo.

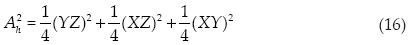
Obtención del área al cuadrado de la superficie en el plano XY
Para el cálculo del área en este plano se hace lo mismo que en el plano anterior, con la única diferencia de que los vectores que definen esta superficie se encuentran sobre los ejes X y Y, y su magnitud está definida por los puntos de corte de estos ejes con el plano que genera la primera superficie.
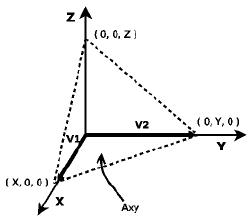
Procedemos al cálculo del producto cruz:
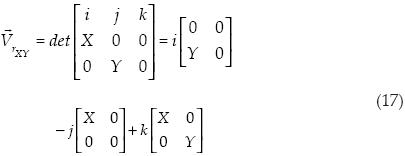

Después obtenemos el área al cuadrado:


Se puede ver claramente que la ecuación (20) es igual al último término de la ecuación (16).
Obtención del área al cuadrado de la superficie en el plano YZ
Aquí se realiza el mismo procedimiento que para la superficie anterior, pero en este caso los vectores van a estar sobre los ejes Y y Z.
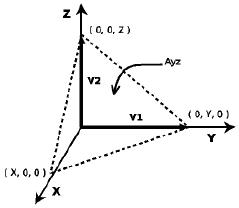
Cálculo del producto cruz:
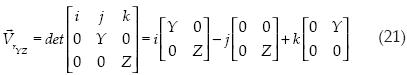

Procedemos a obtener el área al cuadrado:


Se puede ver claramente que la ecuación (24) es igual al primer término de la ecuación (16).
Obtención del área al cuadrado de la superficie en el plano ZX
Aquí se realiza el mismo procedimiento que para la superficies anteriores, pero en este caso los vectores van a estar sobre los ejes Z y X.
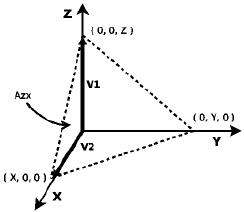
Cálculo del producto cruz:
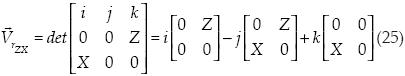

Procedemos a obtener el área al cuadrado:


Se puede ver claramente que la ecuación (28) es igual al término restante de la ecuación (16).
Resultado
Con las ecuaciones (16), (20), (24) y (28) de las subsecciones anteriores podemos concluir que la siguiente ecuación es cierta para tres dimensiones:

Teorema de Pitágoras en cuatro dimensiones
El caso tetradimensional del teorema de Pitágoras es igual al caso en dos dimensiones. La única diferencia es que en vez de manejar supeficies determinadas por dos vectores, se utilizan volúmenes determinados por tres vectores.
Para este caso, vamos a suponer un plano en un espacio de cuatro dimensiones que corta a los ejes ortogonales X, Y, Z y A. Estos últimos ejes son los ejes de referencia en este espacio de cuatro dimensiones, igual que los ejes X, Y y Z en tres dimensiones.
Demostración
Para la demostración de este caso se sigue el mismo procedimiento que se realizó para tres dimensiones, con la variante de que los volúmenes están definidos por tres vectores y por lo tanto, los productos cruz se hacen con tres vectores. Otra variante es que en lugar de dividir el vector resultante entre dos, se divide entre seis.


Cálculo del cuadrado del primer volumen
Para el cálculo del cuadrado de este volumen primero necesitamos obtener tres vectores que lo definan. Para hacer esto tomamos como eje al punto de corte del plano con el eje X y se restan los puntos de corte del plano en los ejes Y, Z y A, con lo cual se obtienen los vectores buscados:
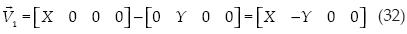
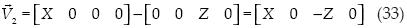
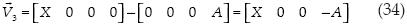
Ya con estos vectores se procede a obtener el producto cruz:
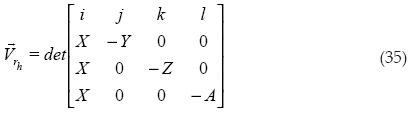
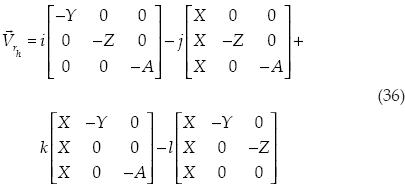
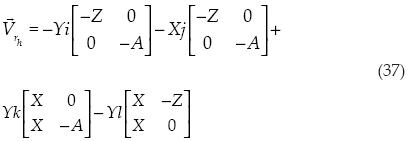
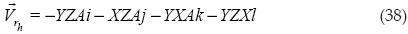
Para obtener el volumen al cuadrado, se divide el vector entre seis y se obtiene el producto punto consigo mismo.

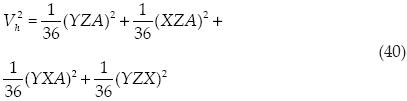
Obtención del cuadrado del volumen XYZ
Para el cálculo de este volumen se hace lo mismo que en el paso anterior, con la única diferencia que los vectores que definen este volumen se encuentran sobre los ejes X, Y y Z, y su magnitud está definida por los puntos de corte en estos ejes con el plano que genera la primera superficie.
Procedemos al cálculo del producto cruz:
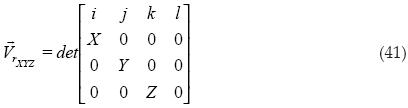
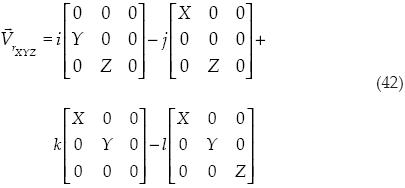

Después se obtiene el volumen al cuadrado:
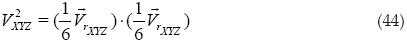

Podemos ver claramente que la ecuación (45) es igual al último término de la ecuación (40).
Obtención del cuadrado del volumen YZA
Aquí se realiza el mismo procedimiento que para el volumen anterior, pero en este caso los vectores van a estar sobre los ejes Y, Z y A. Cálculo del producto cruz:
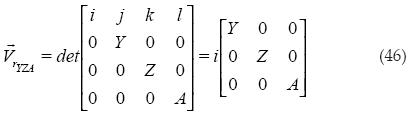

Procedemos a obtener el volumen al cuadrado:
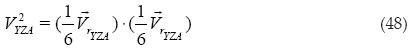

Se puede ver claramente que la ecuación (49) es igual al primer término de la ecuación (40).
Obtención del cuadrado del volumen ZAX
Aquí se realiza el mismo procedimiento que para el volumen anterior, pero en este caso los vectores van a estar sobre los ejes Z, A y X.
Cálculo del producto cruz:
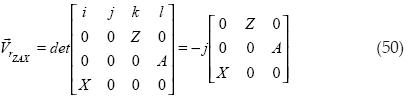

Procedemos a obtener el volumen al cuadrado:


Podemos ver claramente que la ecuación (53) es igual al segundo término de la ecuación (40).
Obtención del cuadrado del volumen AXY
Aquí se realiza el mismo procedimiento que para los volúmenes anteriores, pero los vectores van a estar sobre los ejes A, X y Y.
Cálculo del producto cruz:
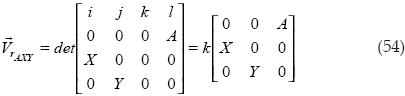

Procedemos a obtener el volumen al cuadrado:
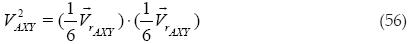

Se puede ver claramente que la ecuación (57) es igual al tercer término de la ecuación (40).
Resultado
Con lo anterior, queda demostrado que el teorema de Pitágoras es válido para cuatro dimensiones.
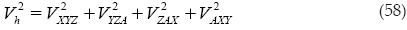
Teorema de Pitágoras para "N" dimensiones
El teorema de Pitágoras se puede generalizar a N dimensiones siguiendo la misma lógica que para cuatro dimensiones. Siendo, en este caso, los volúmenes de dimensión N–1.
Demostración
Para esta demostración se realizará un procedimiento similar al de tres y cuatro dimensiones, con la variante de que se va a trabajar en "N" dimensiones y con los volúmenes definidos por N –1 vectores y por lo tanto, los productos cruz se hacen con N –1 vectores. Otra variante es que en lugar de dividir el vector resultante entre dos o seis, se divide entre (N –1)!
Para facilitar el procedimiento algebraico se sustituye N por n +1 en los cálculos de esta sección (por lo tanto, la demostración se va a hacer para N –1 dimensiones).

Los vectores de posición que definen los puntos de corte de la superficie con cada uno de los ejes en nuestro espacio vectorial son los siguientes:
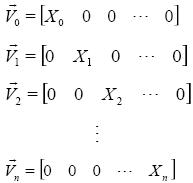
Cálculo del cuadrado del primer volumen
Para el cálculo del cuadrado del primer volumen se realiza el mismo procedimiento que para las dimensiones 3 y 4.
Primero se obtiene el producto vectorial de los vectores que definen el volumen.
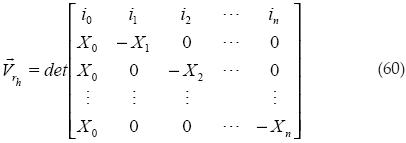
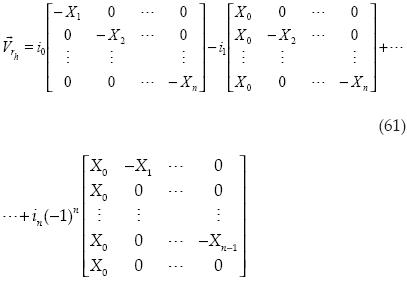
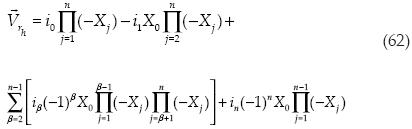
Luego se obtiene el volumen al cuadrado:

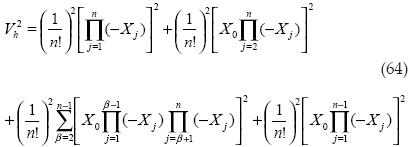
Obtención del cuadrado del primer volumen (β = n)
Desde este punto vamos a utilizar a β como el índice que indica qué columna de la matriz de vectores va tener únicamente ceros.
Aquí vamos a obtener el primer volumen formado por los n–1 primeros vectores que indican los puntos de corte de la superficie con los ejes.
Primero obtenemos el producto cruz de los primeros n–1 vectores.
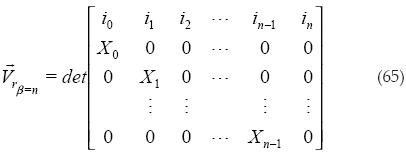

Luego se obtiene el volumen al cuadrado:


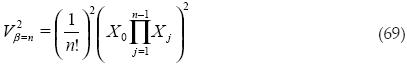
En este caso podemos ver que la ecuación (69) es similar al último elemento de la ecuación (64), sólo variando en el signo de los valores de los elementos internos de la sumatoria. Esta variación sólo hace que el término en la ecuación (64) que se encuentre en los paréntesis pueda ser positivo o negativo, pero al estar elevado al cuadrado, prácticamente la ecuación (69) es igual al último término de la ecuación (64) (para valores que no contengan componente imaginaria).
Obtención de los volúmenes 2 al antepenúltimo (1<β<n)
Obtenemos el producto cruz:
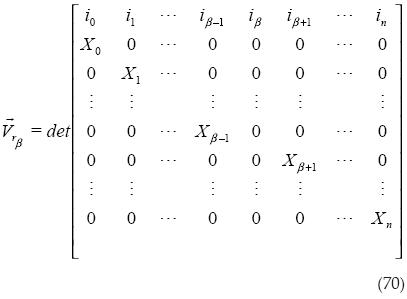

Procedemos a obtener el volumen al cuadrado:

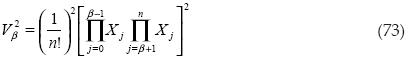
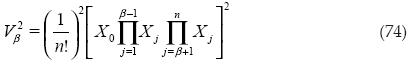
Si se suman los volúmenes al cuadrado desde el segundo hasta el antepenúltimo, queda lo siguiente:
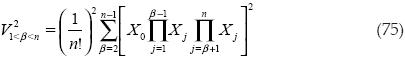
En este caso podemos ver que la ecuación (75) es igual al tercer término de la ecuación (64) para valores que no contengan componente imaginaria.
Obtención del cuadrado del penúltimo volumen (β = 1)
Obtenemos el producto cruz:
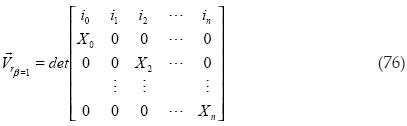

Se obtiene el volumen al cuadrado:

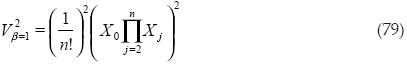
En este caso podemos ver que la ecuación (79) es igual al segundo término de la ecuación (64) para valores que no contengan componente imaginaria.
Obtención del cuadrado del último volumen (β = 0)
Se obtiene el producto cruz:
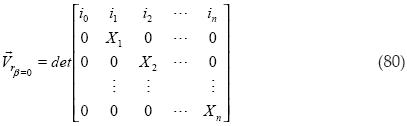

Procedemos a obtener el volumen al cuadrado:
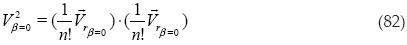

En este caso se obesrva que la ecuación (83) es igual al primer término de la ecuación (64) para valores que no contengan componente imaginaria.
Resultado
Con lo anterior se demuestra que el teorema de Pitágoras es válido para N dimensiones (N–1), siempre y cuando, los puntos de corte en los ejes de la dimensión propuesta, no contengan componente imaginaria.

Conclusiones
Podemos decir que el teorema de Pitágoras es generalizable a "N" dimensiones de la siguiente manera:
"Siendo un espacio de N dimensiones, se puede decir que el cuadrado del volumen de dimensión N–1 generado por el corte de un plano N–dimensional sobre los N ejes ortogonales, es igual a la suma de los cuadrados de los volúmenes de dimensión N–1 que resultan de las combinaciones de los N vectores de posición que definen los puntos de corte de los ejes con dicho plano, tomados de N–1 en N–1."
Es necesario aclarar que lo anterior es verdad, siempre y cuando los cortes con los ejes no contengan componentes imaginarias.
Agradecimientos
Agradezco a mis padres, a mis ancestros, a mis maestros, a mis grandes maestros y a los grandes maestros. Espero honrarlos a todos ellos con este trabajo y seguirlos honrando en el futuro.
Referencias
Murray–Lasso M.A. Sobre el producto cruz en espacios vectoriales N–dimensionales. Ingeniería Investigación y Tecnología. 1:27—47. 2004. [ Links ]
Murray–Lasso M.A. Sobre la aplicación de la analogía para derivar un teorema extendido de Pitágoras para el tetraedro. Educación matemática. 15(1):129–153. 2003. [ Links ]
Bibliografía sugerida
Klein F. Elementary Mathematics from an Advanced Standpoint, 3a ed., New York, Courier Dover Publications, 2004, 244 p. [ Links ]
Richter S. Pitágoras [en línea] 2010 [fecha de consulta 1o de marzo 2010]. Disponible en: <http://www.mastermason.com/fmisrael/pitagoras.html> [ Links ]
Semblanza del autor
Jesús Ulises Acosta–Robledo. Es ingeniero civil egresado de la Facultad de Ingeniería de la Universidad Nacional Autónoma de México. Es estudiante de la maestría en planeación en la misma universidad. Ha sido instructor de varios cursos de software libre y programación por parte de la División de Ingenierías Civil y Geomática de la Facultad de Ingeniería de la UNAM y por parte de varios clubes estudiantiles de la misma Facultad. Ha trabajado como administrador de cómputo en la UNAM y realizado varios desarrollos para la iniciativa privada, principalmente, sistemas sobre software libre.














