Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Ingeniería, investigación y tecnología
versão On-line ISSN 2594-0732versão impressa ISSN 1405-7743
Ing. invest. y tecnol. vol.13 no.1 Ciudad de México Jan./Mar. 2012
Análisis y diseño de un sistema de generación eléctrica termosolar con concentrador de disco parabólico y motor Stirling de 2.7 kW enfriado por aire
Analysis and Design of a Dish/Stirling System for Solar Electric Generation with a 2.7 kW Air-Cooled Engine
Beltrán-Chacón R.1, Velázquez-Limón N.2 y Sauceda-Carvajal D.3
1 Centro de Estudio de las Energías Renovables, Instituto de Ingeniería, Universidad Autónoma de Baja California. Correo: rbeltran1@uabc.edu.mx
2 Centro de Estudio de las Energías Renovables, Instituto de Ingeniería, Universidad Autónoma de Baja California. Correo: nicolas.velazquez@uabc.edu.mx
3 Universidad Politécnica de Baja California. Correo: dsaucedac@upbc.edu.mx
Información del artículo: recibido: febrero de 2009.
Reevaluado: septiembre de 2010.
Aceptado: febrero de 2011.
Resumen
Este trabajo presenta un modelado matemático, la simulación y diseño de un sistema de generación eléctrica termosolar de disco parabólico con motor Stirling de 2.7 kW enfriado directamente por aire. El modelo utilizado para el concentrador, la cavidad y el motor Stirling, fueron validados satisfactoriamente con datos experimentales. Con base en un estudio paramétrico se realizó el dimensionamiento de los componentes del motor. El estudio realizado muestra que conforme se incrementa la capacidad del sistema, la eficiencia global se ve limitada por la potencia requerida por el ventilador, dado que el diseño del enfriador necesita retirar mayores cantidades de calor aumentando el flujo de aire, sin afectar las condiciones internas del proceso (flujo másico del gas de trabajo y dimensiones internas del mismo). El sistema fue optimizado obteniendo una eficiencia global de conversión de energía solar a eléctrica de 26.7%. Este estudio muestra que el uso de un motor Stirling enfriado directamente por aire es potencialmente atractivo para la generación de energía eléctrica en bajas capacidades.
Descriptores: motor Stirling, solar, modelo, simulación, diseño, enfriado por aire.
Abstract
This paper presents a mathematical modeling, simulation and design of a solar power system of a parabolic dish with an air-cooled Stirling engine of 2.7 kW. The model used for the solar concentrator, the cavity and the Stirling engine were successfully validated against experimental data. Based on a parametric study, the design of the components of the engine is carried out. The study shows that as system capacity increases, the overall efficiency is limited by the power required by the fan, since the design of the cooler needs greater amounts of heat removal by increasing the air flow without affecting the internal conditions of the process (mass flow of working gas and internal dimensions of the same). The system was optimized and achieves an overall efficiency of solar to electric energy conversion of 26.7%. This study shows that the use of an air-cooled Stirling engine is potentially attractive for power generation at low capacities.
Keywords: Stirling engine, solar, model, simulation, design, air cooled.
Código de clasificación: 221302.
Introducción
El continuo incremento en la demanda de energía eléctrica y la contaminación asociada a los modos de producción convencionales han demandado el desarrollo de tecnologías sustentables que permitan aprovechar las energías renovables, dentro de las cuales la energía solar es la más abundante. Actualmente existen distintas tecnologías para convertir la energía solar en energía eléctrica, destacando entre ellas el disco/Stirling por su máxima eficiencia (Parlak et al, 2009; Reza et al, 2008; Thombare et al, 2008).
El motor Stirling fue inventado por Robert Stirling en 1816 y aunque su aplicación llegó a ser popular, fue remplazado por el motor de combustión interna y el motor eléctrico (Sentf, 1993). Recientemente, la necesidad de aprovechar las energías renovables para obtener un desarrollo sustentable ha despertado un renovado interés en el desarrollo de tecnología Stirling; sin embargo, no se han encontrado trabajos sobre motores enfriados directamente por aire para la generación de energía eléctrica de baja capacidad (Kongtragool, 2003). Por tal motivo, el objetivo de este trabajo es proporcionar una metodología para el diseño y optimización de sistemas disco/Stirling y evaluar el potencial del enfriamiento directo por aire en las unidades de baja capacidad. Para ello, se muestra el modelo matemático, la simulación y un estudio paramétrico que permite establecer el punto de diseño de los principales componentes de un sistema para una capacidad de 2.7 kW eléctricos. El modelo desarrollado a diferencia de otros trabajos es sensible a la variación de la irradiancia solar, la temperatura ambiente, la velocidad del viento y la orientación del receptor solar. El rendimiento teórico del sistema propuesto, permite sugerir su aplicación para la generación de energía eléctrica en bajas capacidades bajo el concepto de generación distribuida, satisfaciendo los requerimientos de los sectores residencial, comercial y agrícola, así como de los usuarios alejados de la red eléctrica.
Descripción del sistema disco/Stirling
En la figura 1 se muestra esquemáticamente un sistema de generación eléctrica termosolar de disco/Stirling que se compone por un concentrador solar, un receptor, el motor Stirling y un generador eléctrico. El absorbedor se coloca dentro de una cavidad para disminuir las pérdidas térmicas por convección y radiación hacia el ambiente. El motor utiliza helio como fluido de trabajo y tiene dos pistones de simple acción en acoplamiento tipo alfa, un regenerador de mallas metálicas y un disipador de calor compacto enfriado por aire directamente del tipo de tubos con aleta ondulada. Una de las ventajas de utilizar enfriamiento directo, es que elimina el circuito de tuberías, la bomba de agua y el intercambiador agua/aire utilizados en el enfriamiento indirecto convencional, reduciendo el costo y complejidad del sistema.

Metodología
El modelo matemático desarrollado para el sistema de generación eléctrica termosolar de disco parabólico con motor Stirling enfriado por aire, se resuelve de acuerdo al algoritmo mostrado en la figura 2. En el planteamiento de dicho modelo se considera que los procesos se realizan en estado estacionario y que las variables operativas tienen valores instantáneos. El algoritmo de solución utiliza procedimientos iterativos (regla falsa) para las variables de flujo másico del aire de enfriamiento, la temperatura de la superficie externa del absorbedor y enfriador, así como para la temperatura del gas en el absorbedor y enfriador. Como apoyo al diagrama del algoritmo de solución, a continuación se muestran las principales ecuaciones del modelo matemático de cada uno de los componentes del sistema.
Concentrador solar
Para predecir el comportamiento de un concentrador de disco parabólico, el modelo utiliza los errores típicos reportados por Stine y Harrigan (1983), dentro de los cuales se encuentra el error de la estructura, el sistema de seguimiento (sensor y mecanismo), la posición del receptor y la reflectividad especular de la superficie, entre otros.
Las principales variables del concentrador son el ancho de la imagen solar en la zona focal (w) y el factor de intercepción (cp) (Stine y Harrigan, 1983):

El factor de intercepción, definido como:

Receptor de cavidad
El receptor del sistema está compuesto por dos elementos, una cavidad que limita las pérdidas térmicas hacia los alrededores y dentro de ella un absorbedor de tubos donde se calienta el gas de trabajo del motor. El análisis de la cavidad considera las pérdidas térmicas por convección natural y la debida al viento, la radiación reflejada y emitida, y la conducción de calor a través del aislante. Suponiendo que la distribución de la irradiancia es uniforme y que las propiedades ópticas y térmicas de la cavidad y absorbedor permanecen constantes, el flujo de calor que es transferido al motor (Qen,mot) se calcula mediante:

El flujo de calor hacia el receptor (Qen,rec) considerando el área de apertura no sombreada del concentrador solar (Aconcentrador)

La irradiancia reflejada fuera de la cavidad se calcula con (Duffie, 2006):

Las pérdidas térmicas por conducción a través del aislante se disipan posteriormente por convección en el exterior de la cavidad y se obtienen mediante:

El cálculo de las pérdidas por convección desde el interior del receptor, se realiza mediante la correlación propuesta por Stine y McDonald (1989), que también se utilizó en otros estudios (Nepveu, 2008; Sendhil, 2007):

donde b se define como:
b = 0.982 (Dap/Drec) +1.12
Para calcular las pérdidas térmicas por convección desde el interior del receptor debidas a la velocidad del viento, se utiliza el modelo propuesto por Ma (1993), donde el coeficiente de convección se obtiene de:

La radiación emitida fuera del receptor a través de la apertura de la cavidad está dada por:

El flujo de calor absorbido por el absorbedor es conducido hacia el interior de los tubos y se calcula mediante:

Una vez conocida la temperatura de la superficie interna de los tubos del absorbedor, es posible calcular el flujo de calor suministrado al motor y simular el comportamiento termodinámico utilizando el modelo de segundo orden propuesto por Martini (1983).
Motor Stirling
El análisis fluido-dinámico y de transferencia de calor en el interior del motor Stirling se realiza suponiendo un flujo estacionario equivalente al flujo no estacionario promedio, y la potencia ideal producida se calcula asumiendo que:
1. El espacio que ocupa el gas de trabajo dentro del motor está dividido en tres secciones y cada sección tiene una temperatura isotérmica uniforme.
2. La variación del volumen del gas de trabajo es sinusoidal y la ley del gas ideal aplica.
3. No hay diferencia de presión entre las secciones que ocupa el gas.
4. La transferencia de calor y las pérdidas fluido-dinámicas en las conexiones entre los intercambiadores son despreciables.
5. La expansión y compresión del gas de trabajo es isotérmica y la transferencia del gas a través del regenerador es a volumen constante.
La potencia del motor se define como la diferencia entre la potencia ideal calculada y la sumatoria de las pérdidas térmicas, fluido-dinámicas y mecánicas del motor. Las pérdidas consideradas por el modelo son:
1. Conducción de calor a través de la cara del pistón, la pared del cilindro de expansión, y de la pared y matriz del regenerador hacia el enfriador.
2. Emisión de radiación desde la cara del pistón hacia el cárter.
3. Fricción mecánica del motor y fricción fluido-dinámica del gas de trabajo.
4. Ineficiencia térmica y oscilación de la temperatura de la matriz del regenerador.
El método propuesto por Martini (1983) considera que las pérdidas por fricción mecánica del motor son equivalentes a 20% de la potencia ideal. El modelo matemático fue validado por Chen y Griffin (1983), quienes reportaron que corrigiendo el factor de fricción del gas por un factor de 2.9, se reduce el porcentaje de error a sólo ±10% en el cálculo de la potencia y eficiencia. Dicha corrección se implementó corroborando la mejora en la predicción del valor experimental cerca del punto de diseño.
Considerando un flujo estacionario, la temperatura del gas en el interior del absorbedor se calcula mediante:
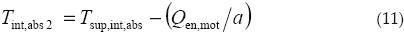
donde a se define como:
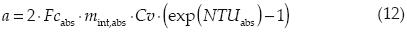
Enfriador
El calor removido del motor Stirling se realizó por medio de un enfriador compacto y de alta eficiencia. Para calcular el número de Nusselt y el coeficiente de fricción (f) en la superficie externa del enfriador (aire de enfriamiento) se utilizó la correlación propuesta por Wang y otros (1997):

El factor de fricción para el cálculo de la caída de presión externa está dado por:
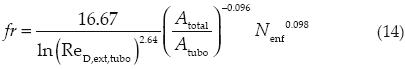
La eficiencia de superficie se define como:

Considerando un flujo estacionario, la temperatura del gas en el interior del enfriador se calcula mediante:

donde b se define como:

El flujo de calor removido por el enfriador (Qenf):

Generador eléctrico
El generador propuesto es del tipo de inducción y se acopla directamente al motor. La eficiencia asociada a estos generadores varía entre 96 y 97% (Hau, 2006) y se supone que permanece constante.
La energía eléctrica útil se define como la diferencia entre energía eléctrica producida y la potencia requerida por el ventilador del enfriador:

Resultados y discusión
El dimensionamiento y análisis operativo del sistema se realiza por medio de un estudio paramétrico donde se establecen los puntos de diseño para cada una de las variables que permiten obtener una máxima eficiencia y capacidad.
Validación de los modelos matemáticos
Con la finalidad de validar el simulador desarrollado, se realizó una comparación entre los resultados experimentales reportados en la literatura contra los resultados obtenidos mediante la simulación, para las mismas geometrías y condiciones de operación. Los parámetros comparados fueron el factor de intercepción y las pérdidas por convección en la cavidad, así como el flujo de calor suministrado y la potencia producida por el motor Stirling.
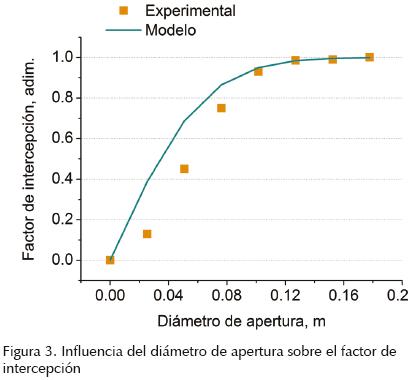
La comparación del factor de intercepción obtenido con el simulador contra los valores experimentales para el concentrador WGA-500 (Diver, 2001) se presenta en la figura 3, obteniendo un excelente acercamiento para valores por encima de 0.95; por debajo de este valor el modelo sobreestima dicho factor. Sin embargo, no resulta de gran interés diseñar sistemas con factores de intercepción menores a 0.95. En la figura 4, se muestra la comparación de las pérdidas térmicas en el receptor de cavidad obtenidas con el simulador contra las reportadas por Ma (1993), los resultados obtenidos presentan un error promedio de ±7.2% para las pérdidas por convección y un error promedio de ±0.5% para la emisión de radiación.

Para validar el flujo de calor suministrado y la potencia producida por el motor, en la figura 5 se muestra la comparación hecha para el motor GPU-3 (Martini, 1983, Timoumi et al., 2008), donde el flujo de calor suministrado resultó con un error promedio de 5.7% y un error máximo de 9.6%. La potencia producida a una presión de operación de 6.89 MPa, resultó con un error mínimo de -8.2%, y un máximo de -17.7%, cuando la presión de operación es 1.72 MPa. Con esta comparación se observa que el modelo propuesto tiene una buena representatividad del comportamiento del concentrador y el receptor de cavidad, mientras que para el motor, la estimación del flujo de calor suministrado resulta aceptable dentro del rango explorado; sin embargo, la potencia del motor tiene mejor ajuste conforme aumenta la presión y disminuyen las revoluciones.
Estudio paramétrico
Discusión de resultados del receptor
Una de las principales variables que influye sobre el comportamiento térmico del receptor es el diámetro interno de los tubos del absorbedor, como se muestra en la figura 6, donde al aumentar dicho diámetro se incrementa el área transferencia de calor y disminuye el coeficiente de convección en el interior de los tubos del absorbedor, dando como resultado un mínimo en la temperatura del absorbedor y en las pérdidas térmicas, presentando un punto de máxima eficiencia del receptor cuando el diámetro es 0.22 cm. Sin embargo, con un diámetro de 0.26 cm, la eficiencia combinada alcanza un máximo, por tal razón se selecciona este diámetro como punto de diseño. La influencia del número de tubos sobre la eficiencia y capacidad del receptor manteniendo el área del absorbedor constante, resultó despreciable.

En la figura 7 se muestra que al aumentar el diámetro de apertura de la cavidad se incrementa la cantidad de irradiancia interceptada, así como la temperatura del absorbedor. Bajo estas condiciones un diámetro de apertura mayor a 8.4 cm provoca mayores pérdidas térmicas, en comparación con el aumento de la irradiancia interceptada, presentándose un punto de máxima potencia producida por el motor.

Discusión de resultados del enfriador
En la figura 8 se observa que al aumentar el diámetro de los tubos del enfriador manteniendo fija el área frontal del banco de tubos, se reduce el área de flujo para el aire de enfriamiento, lo que incrementa la caída de presión y el coeficiente externo de transferencia de calor por convección. Bajo estas condiciones la potencia eléctrica útil comienza a disminuir de manera considerable para diámetros mayores que 0.28 cm, debido al aumento de la potencia requerida por el ventilador. Por otra parte, los puntos de máxima potencia para el motor y para la energía eléctrica útil están ligeramente próximos, esto indica que la transferencia de calor por convección en el interior de los tubos no es una etapa limitante para el logro de altas potencias y eficiencias.

En la figura 9 se observa cómo la potencia eléctrica útil alcanza un valor máximo antes de que la potencia producida por el motor llegue a su mayor capacidad. Esto sucede debido a que al aumentar el número de columnas del enfriador, la altura del banco de tubos se reduce, lo que aumenta la velocidad del aire de enfriamiento, la caída de presión y en consecuencia la potencia requerida por el ventilador. De igual manera, al aumentar el número de columnas, se incrementa el coeficiente de convección externo y la capacidad de enfriamiento del motor, reduciendo la temperatura y trabajo de compresión, lo que resulta en una mayor potencia neta del motor. El punto de diseño se elige para la máxima potencia eléctrica.
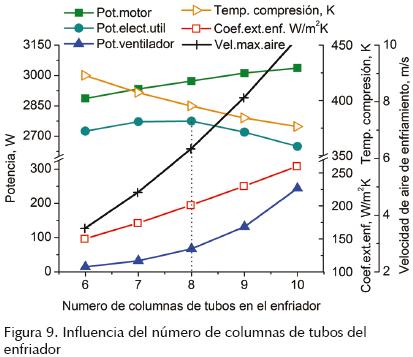
La potencia requerida por el ventilador es uno de los principales factores que limitan la obtención de una mayor eficiencia global. No obstante, el sistema diseñado para una capacidad de 2.7 kW enfriado por aire logra una eficiencia aceptable.
Comportamiento del sistema
En la figura 10 se observa que al aumentar la irradiancia solar el sistema incrementa su capacidad y eficiencia, no obstante, la temperatura de la superficie del absorbedor se eleva en una forma considerable. En la figura 11 se muestra que al aumentar la velocidad del motor, la temperatura del absorbedor disminuye, lo que provoca un aumento de la eficiencia de la cavidad debido a la disminución de las pérdidas térmicas. La eficiencia combinada del sistema presenta un valor máximo de 32%, no obstante, a pesar de tener una menor eficiencia se selecciona el punto correspondiente a una temperatura de 957 K, debido a que la temperatura de operación es menos severa, evitando utilizar materiales costosos y manteniendo una eficiencia aceptable del sistema.
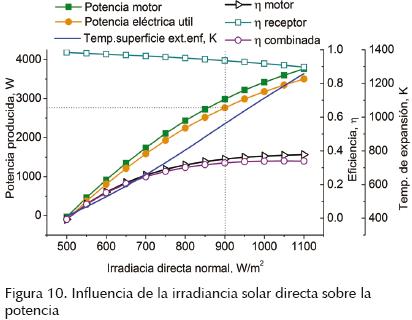

Con los resultados anteriores se muestra la factibilidad teórica del sistema de generación eléctrica termosolar de disco parabólico y motor Stirling de baja capacidad enfriado por aire.
En la tabla 1 se observa el valor de los parámetros óptimos y condiciones de operación encontrados a través del estudio paramétrico.
Conclusiones
Se desarrolló un modelo matemático para la simulación y diseño de un sistema de generación eléctrica termosolar disco/Stirling de 2.7 kW enfriado directamente por aire.
El simulador desarrollado es sencillo y fácil de utilizar como herramienta de diseño y optimización. Los resultados obtenidos por el simulador fueron comparados contra datos experimentales mostrando buena concordancia. El diseño del receptor tiene una gran influencia sobre el flujo de calor y la temperatura que se suministra al motor, por lo que debe especificarse tomando en cuenta su orientación y geometría. Se encontró que el diseño del enfriador tiene una gran influencia sobre la potencia y eficiencia del sistema, debido a que su máxima capacidad está limitada por la potencia requerida por el ventilador. Se diseñó un motor Stirling enfriado directamente por aire, con una eficiencia de 35%. El sistema de generación eléctrica optimizado produce 2.7 kW a una eficiencia global (solar a eléctrica) de 27.6% y una irradiancia de 900 W/m2. Estos resultados indican que un sistema de disco/Stirling de baja capacidad enfriado por aire es potencialmente atractivo para la producción de energía eléctrica bajo el concepto de generación distribuida.
Nomenclatura

Agradecimientos
Los autores extienden su agradecimiento a CONACYT por su apoyo a través del proyecto con clave CONAVI-200901-127156 y la beca otorgada para los estudios de doctorado. De igual manera, agradece a François Nepveu las consultas y material bibliográfico proporcionados.
Referencias
Chen N.C., Griffin F.P. A Review of Stirling Engine Mathematical Model, Oak Ridge National Laboratory, pp. 9, 1983. [ Links ]
Diver R.B., Andraka C.E., Scott R.K., Goldberg V., Thomas G. The Advanced Dish Development System Project, en: Proceedings of Solar Forum 2001, Solar Energy, The Power to Choose (2001, Washington, DC), p. 6. [ Links ]
Duffie J.A. y Beckman W.A. Solar Engineering of Thermal Processes, 3a. ed., John Wiley & Sons, 2006. [ Links ]
Hau E. Wind Turbines, Fundamentals, Technologies, Application, Economics, 2a. ed., Reino Unido, Springer, 2006, p. 326. [ Links ]
Kongtragool B., Wongwises S. A Review of Solar-Powered Stirling Engines and Low Temperature Differential Stirling Engines. Renewable and Sustainable Energy Reviews (7):131-154, 2003. [ Links ]
Ma-R.Y. Wind Effects on Convective Heat Loss From a Cavity Receiver for a Parabolic Concentrating Solar Collector, Department of Mechanical Engineering, California State Polytechnic University, 1993. [ Links ]
Martini W.R. Stirling Engine Design Manual, National Aeronautics and Space Administration, Lewis research center, 2a. ed., 1983, DOE/NASA/3194-1 NASA CR-168088. [ Links ]
Nepveu F., Ferriere A., Bataille F. Thermal Model of a Dish/Stirling Systems. Solar Energy, (83):81-89, 2009. [ Links ]
Parlak N., Wagner A., Elsner M., Soyhan H.S. Thermodynamic Analysis of a Gamma Type Stirling Engine in Non-Ideal Adiabatic Conditions. Renewable Energy, (34):266-273. 2009. [ Links ]
Reza A.T., Zomorodiana A., Akbar A.G. Simulation, Construction and Testing of a Two-Cylinder Solar Stirling Engine Powered by a Flat-Plate Solar Collector without Regenerator. Renewable Energy, (33):77-87, 2008. [ Links ]
Sendhil N.K., Reddy K.S. Numerical Investigation of Natural Convection Heat Loss in Modified Cavity Receiver for Fuzzy Local Solar Dish Concentrator. Solar Energy, (81):846-855, 2007. [ Links ]
Senft J.R. Ringborn Stirling Engines, 1a. ed., New York, Oxford University Press, 1993. [ Links ]
Stine W.B., McDonald C.G. Cavity Receiver Convective Heat Loss, en: International Solar Energy Society, Solar World Congress (1989, Kobe, Japon). [ Links ]
Stine W.B., Raymond W.H. Solar Energy Fundamentals and Design with Computer Applications, New York, Wiley-Interscience, 1985. [ Links ]
Thombare D.G., Verma S.K. Technological Development in the Stirling Cycle Engines. Renewable and Sustainable Energy Reviews, (12):1-38. 2008. [ Links ]
Timoumi Y., Iskander T., Sassi B.N. Design and Performance Optimization of GPU-3 Stirling Engines. Energy, 33:1100-1114, 2008. [ Links ]
Urieli I. Y Berchowitz D. Stirling Cycle Analysis, Adam Hilger, Bristol, 1984. [ Links ]
Wang C.C., Fu W.L., Chang C.T. Heat Transfer and Friction Characteristics of Typical Wavy Fin-and-Tube Heat Exchangers. Experimental Thermal and Fluid Science, (14):174-186, 1997. [ Links ]
Semblanza de los autores
Ricardo Beltran-Chacón. Es ingeniero mecánico por la Facultad de ingeniería de la Universidad Autónoma de Baja California. Actualmente es candidato a doctor en el programa MyDCI de la misma universidad y su trabajo se dirige hacia el desarrollo de tecnologías sustentables para la generación de energía eléctrica, principalmente a través de sistemas con motor Stirling, activados térmicamente mediante energía solar.
Nicolás Velázquez-Limón. Es ingeniero industrial químico por el Instituto Tecnológico de Los Mochis, maestro en ciencias de ingeniería química por el Instituto Tecnológico de Celaya y doctor en ingeniería química por la Facultad de Química y Centro de Investigación en Energía de la UNAM. Es investigador y jefe del Centro de Estudios de las Energías Renovables del Instituto de Ingeniería de la UABC. Sus investigaciones se dirigen al desarrollo de tecnologías sustentables aprovechando las energías renovables, enfocándose principalmente a la aplicación de la energía solar térmica y sistemas avanzados de enfriamiento termosolar en los sectores residencial, comercial e industrial.
Daniel Sauceda-Carvajal. Es ingeniero mecánico por el Instituto Tecnológico de Mexicali. Actualmente es candidato a doctor en el programa MyDCI del Instituto de Ingeniería de la UABC. Sus áreas de interés son el desarrollo de ciclos de enfriamiento avanzados, así como el estudio e integración de colectores solares de mediana y alta concentración para su aplicación en la conservación de alimentos y acondicionamiento de espacios.














