Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.12 no.4 Ciudad de México oct./dic. 2011
Elemento acústico de tres nodos para interacción fluido estructura basado en un principio variacional parametrizado
Three Nodes Acoustic Element for Fluid–Structure Interaction Based on a Parameterized Variational Principle
Correa S.1 y Militello C.2
1 Departamento de Ingeniería de Diseño de Producto Universidad EAFIT, Medellín, Colombia. E–mail: scorrea5@eafit.edu.co
2 Departamento de Física Fundamental Experimental, Electrónica y Sistemas Universidad de La Laguna Campus de Anchieta,Tenerife, España E–mail: carmelomilitello@gmail.com
Información del artículo: recibido: septiembre de 2009.
Aceptado: noviembre de 2010.
Resumen
Este artículo presenta una formulación en elementos finitos basada en un principio variacional parametrizado para resolver problemas planos de interacción fluido–estructura, utilizando los desplazamientos como variable de estado para formular el sólido y el fluido. La formulación no presenta modos espúreos de circulación, los cuales son comunes a las formulaciones en desplazamientos. Asimismo el parámetro de penalización no es aleatorio ya que se determina de acuerdo con un criterio energético. Por último la formulación no es sensible a la definición de la dirección normal en el contorno de la interfase sólido–fluido.
Descriptores: elementos finitos, interacción fluido–estructura, elemento lineal, formulación en desplazamientos, modos espúreos, método de penalización.
Abstract
This article presents a finite element formulation based on a parameterized variational principle for solving plane problems of fluid–structure interaction using the displacements as state variable for both solid and fluid media. The circular spurious modes, typical of displacement formulations are avoided. The penalty parameter is not random because it is selected according to energy criterion. Finally the formulation is not sensible to the definition of the normal direction in the fluid–structure interface.
Keywords: finite elements, fluid–structure interaction, linear element, displacement based formulation, spurious modes, penalty method.
Introducción
Varias formulaciones se han desarrollado con el objeto de simular un fluido acústico en problemas de interacción fluido estructura, diferenciándose básicamente por la naturaleza de las variables de campo que emplean para la discretización en elementos finitos. Entre otras, tenemos la formulación en desplazamiento (Hamdi et al, 1978; Belytschko et al, 1976 y 1980), la formulación en desplazamiento (velocidad) potencial y presión (Morand et al., 1979; Everstine, 1981; Olson et al., 1985; Felippa et al, 1990a) y la de desplazamiento, presión y momento de vorticidad (Bathe et al., 1995; Wang et al., 1997).
La formulación en desplazamientos es preferida por muchos investigadores, ya que los elementos acústicos pueden acoplarse directamente con elementos estructurales. La desventaja de esta formulación es que presenta modos rotacionales espúreos a frecuencias diferentes de cero (Hamdi et al., 1978; Olson et al., 1985). El método de penalidad en las rotaciones (Hamdi et al., 1978), arroja buenos resultados para elementos cuadriláteros de 8 nodos. Los resultados obtenidos con el elemento de bajo orden dependen del valor de penalidad utilizado. Olson (1985) y posteriormente Bathe (1995) concluyen que el elemento en desplazamientos de Hamdi (1978) no puede resolver varios problemas típicos de interacción fluido–estructura, debido entre otras, a las restricciones de irrotacionalidad e incompresibilidad.
Otros elementos en desplazamientos se basan en polinomios de Raviart–Thomas que no presentan modos espúreos de rotación (Bermúdez et al., 1994). La utilización de desplazamientos normales en la mitad de los lados no son atractivos para programas generales de elementos finitos. Además la continuidad en los desplazamientos de la interfase se impone en forma integral, condensándose los grados de libertad en la mitad del lado.
Otros autores utilizan una matriz de masa proyectada en combinación con integración reducida en un punto para la matriz de rigidez (Wang et al., 1997). Después se presentó un elemento (Kim et al., 1997) que combina la penalización a las rotaciones (Hamdi et al., 1978) con la matriz de masa proyectada e integración reducida (Chen et al., 1990). De nuevo, el factor de penalización a las rotaciones queda indeterminado, debiendo seleccionarlo el usuario.
Los elementos en desplazamiento, presión y momento de vorticidad (Bathe et al, 1995; Wang et al., 1997) son de difícil implementación en programas convencionales de elementos finitos, salvo que puedan condensarse los campos de presión y vorticidad a nivel elemental. Los resultados son satisfactorios para elementos cuadriláteros de 12 nodos, con 9 grados de libertad en desplazamientos, 3 grados de libertad en presiones y 3 grados de libertad en momento de vorticidad. Los elementos de bajo orden presentan modos checker board. Una limitación añadida es que se obtienen modos singulares no físicos, lo que impide estudiar problemas de propagación, ya que deben eliminarse con anterioridad. Los experimentos numéricos muestran que también es sensible a la definición de la dirección normal al contorno.
Ninguna de estas formulaciones en desplazamientos presenta una expresión cerrada para los factores de penalización. La extensión de las mismas a dominios 3D, en algunos casos, no es trivial.
En el presente trabajo mostraremos cómo la formulación de la energía de un fluido acústico puede ajustarse exactamente a la formulación de un Principio Variacional Parametrizado (PVP) (Felippa et al., 1990b) y que las recetas aplicables a los mismos en elasticidad lineal pueden aplicarse en este caso. Desarrollaremos un elemento triangular plano de 3 nodos y veremos que el mismo puede considerarse un elemento de alto rendimiento (high performance) (Felippa et al., 1990b). El elemento presenta un coeficiente de estabilización que emana en forma natural del PVP, asegurando la convergencia a las ecuaciones diferenciales que gobiernan el problema. Se desarrolla una forma cerrada para el coeficiente de estabilización (factor de penalización) que depende del tamaño del elemento. Se desarrollan varios ejemplos para verificar la calidad del elemento, la efectividad del coeficiente de estabilización y la sensibilidad de los resultados a la definición de las normales al contorno.
Ecuaciones básicas
Se considera que el fluido es no viscoso, isentrópico y las vibraciones son de tan baja amplitud que no modifican apreciablemente la densidad del mismo. La energía elástica acumulada en el volumen del fluido acústico es
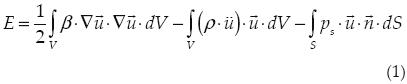
Donde β es el módulo de compresibilidad,  es el campo de desplazamientos, ρ es la densidad del fluido, ps es la presión impuesta en el contorno y
es el campo de desplazamientos, ρ es la densidad del fluido, ps es la presión impuesta en el contorno y  es el vector normal a la superficie donde se impone la presión.
es el vector normal a la superficie donde se impone la presión.
Se busca la estacionalidad de la energía respecto a una variación arbitraria del campo de desplazamientos, obteniendo
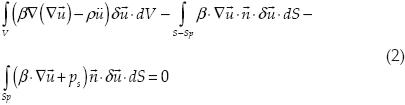
Dado que el fluido es no viscoso, sólo la componente normal esta impuesta y debe ser igual al desplazamiento del sólido.

Algunas formulaciones son especialmente sensibles a la imposición en forma discreta de esta condición de contorno.
Formulación del elemento basado en el PVP
El elemento posee tres nodos con dos grados de libertad por nodo, esto es, los desplazamientos ui y vi, para cada nodo i, paralelos al sistema de coordenadas global. Se supone un campo básico de desplazamientos lineal
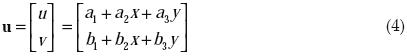
La deformación o cambio de volumen es constante

La propuesta es obtener la deformación de alto orden a partir de un campo de desplazamientos que se active cuando el campo intente rotar. Se prueba con el siguiente campo de desplazamientos
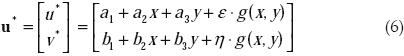
Para g(x,y) se propone

Deseamos, en principio, que nuestro campo sea irrotacional, luego
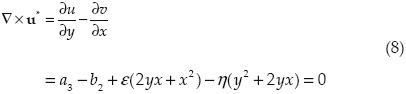
Los coeficientes ε,η son los encargados de mantener la irrotacionalidad del fluido, ya que tomarán valores diferentes de cero en cuanto el fluido intente rotar.
La ecuación (8) no produce suficientes condiciones para evaluar los coeficientes ε,η, por tanto se propone la siguiente condición integral
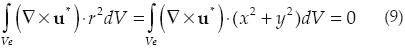
Se puede satisfacer esta condición si se pide
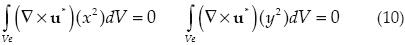
con lo que se obtiene
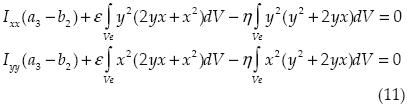
donde
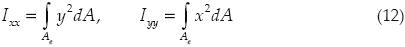
Las constantes ε,η pueden obtenerse de (11) como
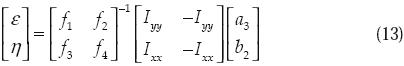
donde
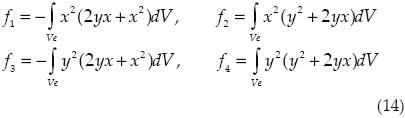
Abreviando
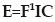
Las funciones g(x,y) se eligen de forma que aseguren que la matriz F sea invertible para todas las geometrías.
Finalmente, se obtiene una expresión matricial para E en función de los desplazamientos nodales
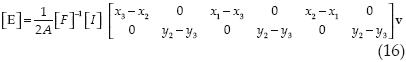
Abreviando,

donde A es el área del triangulo y vT= [u1 v1 u2 v2 u3 v3].
Se intenta así obtener una deformación de alto orden por cambio de volumen que agrega energía al fluido en respuesta a un campo de desplazamientos rotacional.
Esta primera aproximación a la deformación de alto orden la expresamos
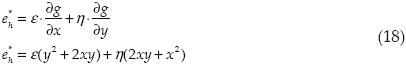
Partiendo de esta aproximación debemos buscar una expresión para la deformación de alto orden que satisfaga las condiciones del Principio Variacional Parametrizado (Felippa et al., 1995):
La deformación de alto orden debe quedar en función de los desplazamientos nodales en el contorno del elemento, es decir

El campo de deformaciones de alto orden debe cancelarse ante un campo de desplazamientos nodales consistente con un desplazamiento rígido o un campo de deformación constante, vrc, luego

La matriz AQ es arbitraria, pero debe cumplir la condición de no generar deformaciones medias, es decir:

Satisfaciendo dichas condiciones, la deformación de alto orden se expresa como

donde la matriz A es de la forma
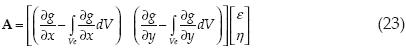
Se obtienen así las matrices A y Q necesarias para definir la matriz de rigidez elemental como

donde Kh es la matriz de rigidez de alto orden, definida como

El valor de α es arbitrario, mientras que produzca matrices elementales definidas positivas, y puede variar de elemento a elemento sin comprometer la convergencia.
Debemos entender que en este contexto definimos como convergencia la capacidad del elemento de copiar un estado de presión constante ( ∇ · u = constante ).
Por último, la matriz básica se obtiene como:

donde Bb es la matriz que calcula el campo de deformación constante a partir de los desplazamientos nodales.
Factor de estabilización de energía
Proponemos como criterio para calcular el factor de estabilización de energía la relación entre la energía producida por un campo de desplazamientos irrotacional asociado con Kb y la energía producida por un campo de desplazamientos rotacional asociado con Kh. Un campo irrotacional pertenece al espacio nulo de Kh y un campo rotacional al espacio nulo de Kb.
Ante un campo de desplazamientos rotacional, la matriz de rigidez de alto orden deberá aportar energía suficiente, al menos del mismo orden que la matriz de rigidez básica ante un campo irrotacional de la misma longitud de onda espacial.
Proponemos una malla de control de dimensiones l × l, como se muestra en la figura 1.
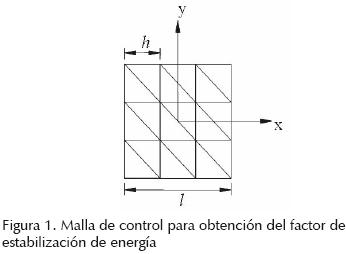
Se supone que el número mínimo de elementos necesarios para capturar una semionda es tres, es decir

El campo de desplazamientos irrotacional propuesto es

El campo de desplazamientos rotacional propuesto es
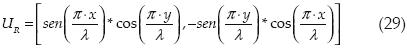
Ambos campos tienen su origen en el centro de la malla de control.
Estimando los autovalores producidos por ambos campos mediante el cociente de Rayleigh (Bathe, 1982):

Igualando ambas expresiones y despejando a:

Nótese que el coeficiente propuesto depende de consideraciones geométricas y no del material.
La variación de α en función del tamaño del elemento h se ajusta a la ecuación

Para la formulación de Hamdi (1978), este elemento produce un factor a constante que no depende del tamaño del elemento. Por ello, la matriz Kh de la presente formulación no es la misma que se obtiene con dicho elemento.
Para una malla no estructurada se toma como dimensión característica h de un triángulo cualquiera el diámetro de un círculo inscrito en el mismo.
La obtención de una forma cerrada explícita de este factor de estabilización, en función de las dimensiones del elemento constituye una de las principales ventajas con que cuenta la formulación basada en el PVP sobre las demás formulaciones.
Problemas de verificación
Primero debemos destacar que el elemento desarrollado no resuelve el problema del comportamiento límite incompresible. Por eso abordaremos como problema de verificación la interacción fluido–estructura en el problema del pistón rígido inclinado vibrando en el interior de una cavidad cerrada de paredes rígidas, tal y como se aprecia en la figura 2.
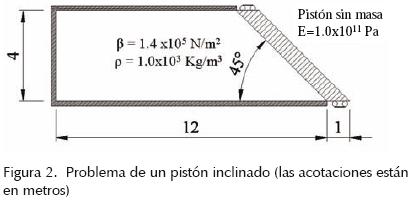
En las paredes rígidas se impone que el desplazamiento normal a las mismas es nulo. En el pistón inclinado se impone, mediante multiplicadores de Lagrange (Felippa et al., 1995), que el desplazamiento del elemento estructural y del fluido normal a la superficie de contacto es el mismo (condición de impenetrabilidad).
Se analizan la convergencia al refinar la malla, el efecto de una malla no uniforme y el efecto del error en la definición de las normales al contorno de interacción fluido–estructura.
Análisis de convergencia y mallas no uniformes
El análisis con malla no uniforme tiene como objetivo valorar la eficiencia en la formulación desarrollada para evaluar el factor de estabilización de energía. Los problemas resueltos con formulaciones similares (Hamdi et al, 1978; Bathe et al, 1995; Wang et al, 1997) presentan mallas estructuradas y uniformes, y aunque una de ellas (Bathe et al., 1995) prueba la satisfacción del test de la parcela (Taylor et al., 1986), no se menciona la relación entre el tamaño del elemento y el valor de penalización (en este caso, al momento de vorticidad) seleccionado.
En nuestra formulación, el factor de estabilización de energía es dependiente del tamaño del elemento y afecta a la matriz de alto orden elemento a elemento, con lo que, una malla distorsionada no afecta la convergencia, tal como se aprecia más adelante.
La figura 3 muestra las mallas utilizadas para verificar la convergencia, los efectos de mallas no uniformes y la variación en la dirección de la normal al contorno.
La tabla 1 presenta los resultados de las primeras cuatro frecuencias de vibración y su comparativa con la solución obtenida mediante la formulación u–Ø (Olson et al., 1995). Cabe anotar que para la malla no uniforme se ha impuesto una malla más gruesa en la interfase sólido–fluido, lo que supone una condición más desfavorable para la convergencia.
Para el tercer y cuarto modos, las frecuencias están muy cercanas y es posible que el solucionador pueda darnos los dos autovalores básicos o una combinación lineal de los mismos. En la figura 4 vemos los modos que se obtienen para la malla uniforme de 339 elementos. Las presiones mostradas se obtienen calculando la presión en el centro del elemento y obteniendo un promedio en los nodos de todos los elementos que contribuyen al mismo.
En la figura 5 vemos los autovectores obtenidos para el cuarto modo con las cuatro mallas. Vemos que para la malla no uniforme se obtiene la combinación lineal de ambos modos a la frecuencia correcta.
Efecto de la variación de la normal al contorno
La selección de la dirección normal adecuada a la malla es un problema ya discutido por Bathe (1995) y posteriormente por Wang (1997), se observa que dicha formulación es sensible a esta variación a menos que se corrija numéricamente la dirección. Nosotros verificamos el efecto de la variación en la dirección normal sobre nuestra formulación, sin realizar ningún tipo de corrección. Suponemos una variación aleatoria ± 5° en la dirección del vector normal al contorno, en los nodos ubicados en la interfase entre estructura y fluido. El efecto sobre los resultados en frecuencia pueden observarse en la tabla 2. La degradación del modo 4 para las distintas mallas puede verse en la figura 6. Puede notarse la insensibilidad del elemento a este tipo de perturbación.
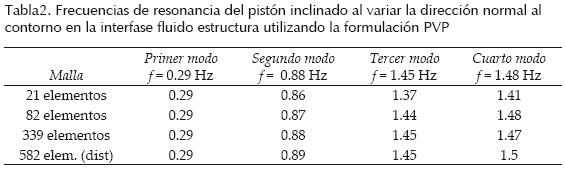
Conclusiones
Hemos desarrollado un elemento acústico triangular plano basado en desplazamientos. La matriz de alto orden se genera de tal forma que se desarrolla energía de cambio de volumen ante la aparición de un campo rotacional. Debido a que utilizamos un PVP de un solo parámetro podemos utilizar éste para estabilizar la formulación y evitar la aparición de modos rotacionales espúreos. El parámetro se obtiene en forma explícita y resulta una función sencilla del tamaño del elemento, independizando al usuario de su elección. El elemento desarrollado es estable y converge a la solución correcta. Por otro lado se muestra poco sensible a la definición de la normal en el contorno. La generalización a elementos tridimensionales es directa como se mostrará en un próximo trabajo.
Referencias
Bathe K.J. Finite Element Procedures in Engineering Analysis, Nueva Jersey, Prentice Hall, 1982, pp. 255–256. [ Links ]
Bathe J.K. et al. A Mixed Displacement–Based Finite Element Formulation for Acoustic Fluid–Structure Interaction. Computers & Structures, (56):225–237, 1995, ISSN:0045–7949. [ Links ]
Belytschko T.B., Kennedy J.M. A Fluid–Structure Finite Element Method for the Analysis of Reactor Safety Problems. Nuclear engineering Design, (38):71–81, 1976, ISSN:0029–5493. [ Links ]
Belytschko T.B. Fluid–Structure Interaction. Computer & Structures, (12):459–469, 1980, ISSN:0045–7949. [ Links ]
Bermúdez A., Rodríguez R. Finite Element Computation of the Vibration Modes of a Fluid–Soil System. Computer Methods in Applied Mechanics and Engineering, (119):355–370, 1994, ISSN:0045–7825. [ Links ]
Chen H.C., Taylor R.L. Vibration Analysis of Fluid–Solid Systems Using a Finite Element Displacement Formulation. Int. J. Num. Meth. Engng, (29):683–698, 1990, ISSN:0029–5981. [ Links ]
Everstine G.C. A Symmetric Potential Formulation for Fluid–Structure Interaction. Journal of Sound and Vibration, (79):157–160, 1981, ISSN:0022–460X. [ Links ]
Felippa C.A., Haugen B., Militello C. From the Individual Element Test to Finite Element Templates: Evolution of the Patch Test. Int. J. Num. Meth. Engng., (38):199–229, 1995, ISSN:0029–5981. [ Links ]
Felippa C.A., Ohayon R. Mixed Variational Formulation of Finite Element Analysis of Acoustoelastic/slosh Fluid–Structure Interaction. Journal of Fluids and Structures, (4):35–57, 1990a, ISSN:0889–9746. [ Links ]
Felippa C.A., Militello C. Variational Formulation of High Performance Finite Elements: Parameterized Variational Principles. Computers & Structures, (36):1–11, 1990b, ISSN:0045–7949. [ Links ]
Hamdi M.A. et al. A Displacement Method for the Analysis of Vibrations of Coupled Fluid–Structure Systems. Int. J. Num. Meth. Engng, (13):139–150, 1978, ISSN:0029–5981. [ Links ]
Kim Y.S., Yung C.B. A Spurious Free Four–Node Displacement–Based Fluid Element for Fluid–Structure Interaction Analysis. Engineering Structures, 19(8):665–678, 1997, ISSN:0141–0296. [ Links ]
Morand H., Ohayon R. Substructure Variational Analysis of the Vibrations of Coupled Fluid–Structure Systems. Finite Element Results. Int. J. Num. Meth. Engng., (14):741–755, 1979, ISSN:0029–5981. [ Links ]
Olson L.G., Bathe K.J. Analysis of Fluid–Structure Interactions. A Direct Symmetric Coupled Formulation Based on the Fluid Velocity Potencial. Computers & Structures, (21):21–32, 1985, ISSN:0045–7949. [ Links ]
Olson L.G., Bathe K.J. A Study of Displacement–Based Fluid Finite Elements for Calculating Frequencies of Fluid and Fluid–Structure Systems. Nuclear Engineering and Design, (76):137–151, 1983, ISSN:0029–5493. [ Links ]
Taylor R.L. et al. The Patch Test. A Condition for Assesing f.e.m Convergence. Int. J. Num. Meth. Engng., (22):39–62, 1986, ISSN:0029–5981. [ Links ]
Wang X., Bathe K.J. Displacement/Pressure Based Finite Element Formulations for Acoustic Fluid–Structure Interactions. Int. J. Num. Meth. Engng, (40):2011–2017, 1997, ISSN:0029–5981. [ Links ]
Semblanza de los autores
Santiago Correa. Es ingeniero mecánico por la Universidad EAFIT en Medellín, Colombia y doctor en ingeniería mecánica por la Universidad Politécnica de Madrid. Su trabajo doctoral se centró en el desarrollo de formulaciones en elementos finitos para el problema de la interacción fluido acústico–estructura. Actualmente es profesor asociado de la Universidad EAFIT en el Departamento de Ingeniería de Diseño de Producto.
Carmelo Militello. Es ingeniero mecánico por la Universidad de Rosario en Argentina y maestro en ciencias y doctor en Aerospace Engineering Science por la Universidad de Colorado en Boulder. Desarrolló, junto con el profesor Carlos Felippa un marco generalizado para los principios variacionales de la mecánica, conocido como Principio Variacional Parametrizado. Adicionalmente formuló los elementos ANDES. Actualmente es catedrático de la Universidad de La Laguna.














