Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.12 no.4 Ciudad de México oct./dic. 2011
Modelación del envejecimiento de los pavimentos asfálticos con la metodología de la superficie de respuesta
Pavement Aging Model by Response Surface Modeling
Chávez–Valencia L.E.1, Hernández–Barriga C.2 y Manzano–Ramírez A.3
1 Departamento de Ingeniería Civil. División de Ingenierías Universidad de Guanajuato E–mail: lechavez@ugto.mx.
2 Departamento de Diseño División de Arquitectura, Arte y Diseño Universidad de Guanajuato E–mail: c.hernandez@ugto.mx
3 Centro de investigaciones y de estudios avanzados del IPN Unidad Querétaro E–mail: amanzano@qro.cinvestav.mx
Información del artículo: recibido: mayo de 2008.
Aceptado: enero de 2011.
Resumen
En la presente investigación se realizó la modelación del envejecimiento de una carpeta asfáltica por medio de la Metodología de Superficie de Respuesta (MSR). Se elaboraron muestras cilíndricas tipo Marshall, que fueron colocadas en un horno bajo las condiciones de tiempo y temperatura establecidos por las condiciones ambientales de la región geográfica donde se construyen pavimentos asfálticos con el AC–20 de la Refinería Ing. Antonio M. Amor, los cuales fueron codificados en la MSR, con esto se determinaron los modelos que predicen el cambio de la estabilidad Marshall (ΔL) y del flujo (ΔF), así como la volatilización del material (VM). Además, se extrajeron muestras cilíndricas de una carpeta asfáltica piloto para determinar el error de modelación, observando que el material volatilizado predicho por el modelo VM fue muy cercano al real, no así para los modelos de ΔLy ΔF, posiblemente asociado a los factores ambientales que no fueron considerados al inicio de la investigación.
Descriptores: deterioro, envejecimiento, pavimento asfáltico, MSR, modelación y asfaltos.
Abstract
In this work, surface course aging was modeled by Response Surface Methodology (RSM). The Marshall specimens were placed in a conventional oven for time and temperature conditions established on the basis of the environment factors of the region where the surface course is constructed by AC–20 from the Ing. Antonio M. Amor refinery. Volatilized material (VM), load resistance increment (ΔL) and flow resistance increment (ΔF) models were developed by the RSM. Cylindrical specimens with real aging were extracted from the surface course pilot to evaluate the error of the models. The VM model was adequate, in contrast (ΔL) and (ΔF) models were almost adequate with an error of 20 %, that was associated with the other environmental factors, which were not considered at the beginning of the research.
Keywords: wear, aging, surface course, RSM, pavement modeling.
Introducción
El envejecimiento del cemento asfáltico es considerado una causa del deterioro de la superficie de los pavimentos flexibles, que se presenta como desprendimientos del agregado pétreo en general o la pérdida de la capa de rodadura en particular (Reunión del Consejo de Directores de Carreteras de Iberia e Iberoamérica, 2002). El fenómeno del envejecimiento de cemento asfáltico tiene décadas de investigación, en las cuales se han propuesto una gran variedad de relaciones matemáticas simples basadas esencialmente en los resultados de los laboratorios. Además, se han establecido relaciones entre el tiempo de servicio de la carpeta asfáltica y el desempeño de la misma, mediante la representación grafica de los resultados de campo (Bell, 1989).
La mayoría de los modelos matemáticos o análogos propuestos por los investigadores son limitados, ya que corresponden a ecuaciones generadas en condiciones locales, para sistemas específicos que no son aplicables en otras geografías o cuando algún elemento del sistema cambia, por ejemplo, la calidad del cemento asfáltico. Lo anterior, nos remite a buscar técnicas de modelación que sean asertivas en el momento de generar los resultados.
La modelación es la representación simplificada de un fenómeno de la naturaleza que nos interesa conocer con mayor profundidad de la que la misma nos permite, pero que a la vez incluye las variables necesarias para que las conclusiones desprendidas sean válidas para el sistema real. La modelación puede ser física, analógica, administrativa, matemática, así como la abstracta o de simulación que es la que nos ocupa.
A su vez, los modelos de simulación se pueden clasificar como: determinísticos, estocásticos (probabilísticos), estáticos, dinámicos, discretos y continuos. Las aplicaciones prácticas de los modelos de simulación son: predicción, entrenamiento, juegos, investigación y toma de decisiones. Las características deseables de un modelo son: confiabilidad, sencillez, bajo costo de desarrollo y operación, manejabilidad, de fácil entendimiento y una relación costo/beneficio positiva (Azarang, 1996).
Los modelos de simulación determinísticos se caracterizan por ser una técnica de resolución de problemas, como un cambio en conjunto de las variables con el tiempo. Los modelos son una aproximación al sistema real y en ningún momento optimizan el proceso o los sistemas. De lo anterior, resulta la necesidad de repetir múltiples ejecuciones de la simulación, consecuentemente, su uso en una investigación debe planificarse como una serie de experimentos que conduzcan a interpretaciones significativas de las relaciones de interés. Los experimentos pueden ser tan complejos que requieren el uso de técnicas estadísticas de diseño de experimentos.
Para generar el modelo de simulación se consideraron los siguientes pasos (Bratly, 1987):
1. Definición del sistema,
2. Elección del método de modelación,
3. Variables,
4. Recolección y análisis de datos,
5. Codificación del modelo, y
6. Validación del modelo.
La elección del método de modelación es el paso siguiente al análisis del sistema. Dicha elección resulta un proceso complejo, ya que las herramientas analíticas de resolución son escasas y en ocasiones la elegida no es la apropiada. Por lo que, para esta investigación se empleó la metodología de superficie de respuesta (MSR). Esta metodología de modelación es un acercamiento holístico que permite postular la forma de la función objetivo, actualizar y limitar los valores de los parámetros, así como explorar la región cercana al óptimo estimado.
La MSR es una herramienta empleada en la investigación científica y desarrollo tecnológico, que combina el uso de los diseños experimentales, técnicas de modelación del análisis de regresión y técnicas matemáticas de optimización (Castaño, 2003).
Desarrollo
Definición del sistema
El pavimento flexible o asfáltico es el sistema real, el cual está formado por varias capas constructivas, siendo la carpeta asfáltica o superficie de rodamiento la que se encuentra directamente expuesta al medio ambiente y consecuentemente presenta envejecimiento. El envejecimiento se ha asociado a factores ambientales: radiación térmica, tiempo de radiación, temperatura ambiente, rayos UV, ozono, oxígeno, evapotranspiración, precipitación y humedad relativa (Yoder et al., 1975).
El ozono, oxígeno y los rayos UV son factores que existen, pero no varían, los demás factores ambientales tienen interdependencia: la humedad relativa, es un indicador de la evapotranspiración y precipitación, y depende de la temperatura. La variación de la temperatura del día a la noche es función de la radiación térmica del sol y del tiempo de radiación.
Entonces, los factores importantes que describen las condiciones ambientales a las que está sujeto el pavimento asfáltico son: la temperatura (T en grados Celsius) y la humedad relativa (H en porcentaje), ya que todos los demás están relacionados con estos dos. Si continuamos suponiendo que la carpeta asfáltica fue construida con materiales y procedimiento especificados, ésta tendrá una impermeabilidad mínima establecida por la SCT de 95 a 100%, por lo que la humedad relativa no tiene influencia en el envejecimiento. Se concluye que, de todos los factores ambientales, sólo la temperatura tiene una influencia marcada en el envejecimiento, lo cual coincide con los resultados de las investigaciones actuales (Bell, 1989).
Se supone que los demás factores tienen una influencia mínima y pueden presentar un error sistemático, para aceptar o rechazar esta suposición se tomaron muestras del campo previamente caracterizadas y se compararon los resultados de las propiedades evaluadas con las predichas por el modelo, la diferencia, que se espera sea muy pequeña, corresponde a la influencia de los factores ambientales que fueron considerados con una influencia despreciable en el envejecimiento del pavimento asfáltico.
Si consideramos al envejecimiento del asfalto en dos etapas: a corto plazo (cuando se elabora la mezcla) y a largo plazo (representativo del servicio), las unidades experimentales ya presentan el envejecimiento a corto plazo y sólo resta analizar el envejecimiento a largo plazo (t en días) que sucede en el campo y se simuló con un intemperismo acelerado en un horno convencional de circulación forzada.
Por lo anterior, se determinaron 2 factores de experimentación, la temperatura (T) y el tiempo (t), sus niveles de aplicación se determinaron de acuerdo con las zonas climáticas. Para el factor temperatura, la zona geográfica de modelación corresponde a los lugares donde se construyen los pavimentos asfálticos con el cemento asfáltico AC–20 de la refinería Ing. Antonio M. Amor de la ciudad de Salamanca, Gto., en la cual se presentan tres tipos de clima: Cálido Húmedo–Lluvioso en verano con 30°C de temperatura máxima promedio anual (TMPA), Templado Húmedo–Lluvioso en verano con 25°C de TMPA y Estepario–Lluvioso en verano con 20°C de TMPA. Para el factor tiempo (t) las mejores condiciones de experimentación se establecen conforme se realiza la modelación por medio de la MSR.
Elección de método de modelación
La MSR es un método que consiste en tres pasos (Montgomery, 2001), el primero llamado Prediseño, un diseño factorial 22 se implementó para generar un modelo lineal que es necesario para el segundo paso, llamado Ascenso por la trayectoria de mayor pendiente, donde una línea recta trazada de manera tangente al modelo lineal es la auxiliar para encontrar el máximo o mínimo de la propiedad monitoreada. El tercer paso, llamado Caracterización de la superficie de respuesta, se propuso un diseño factorial 32 para generar un modelo de segundo orden.
Variables
Las propiedades de la mezcla asfáltica que se emplearon como funciones de salida fueron ΔL (cambio en la estabilidad Marshall de la muestra colocada en el horno y el patrón de referencia según ASTM D 5581), ΔF (cambio en el flujo de la muestra colocada en el horno y el patrón de referencia según ASTM D 5581) y VM (cambio en la gravedad específica de la muestra colocada en el horno y el patrón de referencia según ASTM D 1188).
Recolección, análisis de datos y codificación del modelo
Prediseño
En este paso la temperatura se consideró como la variable independiente que causa la volatilización del cemento asfáltico. La metodología recomienda plantear un diseño experimental que pueda generar un modelo lineal, por lo que se implementó un diseño experimental factorial 22 para verificar la selección adecuada de los factores y sus niveles. De acuerdo con las temperaturas de la zona geográfica, se propusieron 20 y 30°C como el nivel bajo y alto del factor temperatura, respectivamente, después 2 y 4 días como el nivel bajo y alto del factor tiempo, respectivamente. Si t, denota la variable independiente tiempo y T, la variable independiente temperatura, entonces las variables codificadas se pueden calcular con las ecuaciones siguientes:


El diseño factorial 22 fue empleado para recolectar los datos de ΔL, ΔF y VM, por medio de cuatro corridas (condiciones t y T para la prueba), aumentado en 5 puntos centrales para evaluar el error experimental y verificar el ajuste adecuado del modelo lineal (Montgomery, 2001). Se elaboraron treinta y tres especímenes cilíndricos con el contenido óptimo de cemento asfáltico de acuerdo a la norma ASTM D 5581, se conservaron 6 como muestras de referencia y el resto de ellos fueron colocados en un horno convencional en grupos de 3 (réplicas) según las condiciones de prueba para t y T, mostradas en la tabla 1. Después de terminar el intemperismo acelerado, los especímenes fueron enfriados a temperatura ambiente y se determinaron ΔL, ΔF y VM correspondientes.
Se observa que el material volatilizado (VM) no presentó cambio, porque los días de prueba fueron pocos. Siguiendo el procedimiento de resolución de experimentos factoriales de dos niveles (algoritmo de Yates), los datos experimentales fueron ajustados por mínimos cuadrados a un modelo lineal con la ayuda de software comercial. Dicho software fue empleado para ajustar los datos y generar el análisis de varianza del modelo que verifica su ajuste. Las tablas 2 y 3 muestran el análisis de varianza de los modelos lineales.
Para verificar si el modelo ΔL es adecuado, se emplean los resultados de la tabla 2 como sigue: si usamos α (probabilidad de error) = 0.05, el valor crítico del valor F (prueba de estadística) es F0.05, 2, 22 = 3.05. Entonces para el valor F = 397.22>3.05 de la fuente de variación Modelo, se observa que t y T tienen efecto sobre el modelo de ΔL. El valor P, 9.4E–09 (probabilidad del valor F) para Modelo es cero. En contraste, el valor F para la fuente de variación Interacción y para Cuadrático están muy cercanos a cero, se observa que (t)(T) – interacción, y t2, T2 – cuadráticos, no tienen efecto en el modelo de ΔL. Los valores P para Interacción y Cuadrático están muy cercanos a uno. Como el efecto de Interacción y Cuadrático no son significantes y el valor F del modelo es significante, entonces el modelo lineal (modelo de primer orden) es adecuado para modelar los resultados del cambio en la resistencia a la carga (ΔL). Se emplearon los resultados de la tabla 3 para verificar si el modelo ΔF es adecuado, como sigue: si usamos a = 0.05 el valor critico de F es F0.05, 2, 22 = 3.05. Entonces el Valor F para Modelo es 647.3782 > 3.05, se observa que t y T tienen efecto sobre el modelo de ΔF. El valor P = 9.6742E–11 para Modelo es cero. En contraste el valor F para la fuente de variación Interacción no es cero (15.5481), entonces, es significante y el valor F para la fuente de variación Cuadrático están muy cerca de cero, por lo que, no es significante, además la interacción (t)(T), tiene efecto sobre el modelo ΔF, aun cuando los términos cuadráticos no tienen efecto y el Modelo es significante, los términos de interacción tienen el efecto suficiente para considerar el modelo lineal no adecuado, quizás un modelo de segundo orden podría tener un ajuste mejor, pero como en este paso de la metodología no es el objetivo, no se realizó. Por lo que el modelo lineal de ΔL fue el único adecuado. En la tabla 4, se presenta la estimación de los efectos de los términos del modelo, obtenidos con el uso de un programa comercial.
El valor P del término T igual a 0.00 y el valor P del término t igual a 0.00 indican que los coeficientes de regresión son significantes, en contraste, el valor P del término (t)(T) igual a 1.00 indica que este coeficiente de regresión no es significante, para α = 0.05 con 95% de intervalo de confianza (Box, 1987). Entonces el modelo lineal es:

Donde ΔL es el modelo que describe el efecto de las variables t y T sobre el cambio de la estabilidad Marshall en kilogramos y se observa que dicho efecto no existe para los términos de interacción y cuadráticos, entonces t y T podrían ser los principales factores causantes de la volatilización.
Ascenso por la trayectoria de mayor pendiente
En este paso se trazó una línea tangente al modelo, con la cual podemos encontrar la respuesta máxima del cambio en las propiedades (ΔL, ΔF y VM) que se están determinando a los especímenes cilíndricos. De los coeficientes de las variables codificadas de la tabla 4, se puede observar que si establecemos el punto de origen en las coordenadas X1 = 0 y X2 = 0 y considerando un desplazamiento de 4.333 unidades en la dirección X1 y de 2.1666 en la dirección X2 se da una pendiente de ascenso de 0.5. Se decidió utilizar un paso de ascenso para la variable T de 15°C. Para cada uno de los pasos se elaboraron tres especímenes cilíndricos con el contenido óptimo de cemento asfáltico de acuerdo con la norma ASTM D 5581, para las condiciones de tiempo y temperatura mostrados en la tabla 5 y para 6 especímenes de referencia.
Los especímenes cilíndricos fueron retirados del horno, se dejaron enfriar a temperatura ambiente y se les determinó su estabilidad Marshall, se calculó ΔL y se observó su comportamiento hasta que se notó un cambio. Los resultados se presentan en la tabla 5, donde se observa un valor máximo en el cambio de ΔL en el cuarto paso y todos los demás valores son menores o fueron destruidos por el calor. El valor óptimo se encuentra en X1 = 4 y X2 = 2, para variables codificadas que son t = 42 días y T = 93°C para variables independientes. Al igual que el prediseño, las variables t y T parecen ser las variables que tienen más influencia en el cambio de propiedades del material.
Caracterización de la superficie de respuesta
Se propuso un diseño factorial de tres niveles (32) para los dos factores (t y T). Como el valor óptimo de ΔL se observó para t = 42 días y T = 93°C, entonces se propusieron los niveles de los factores en valores cercanos a éstos para tener una buena descripción de la superficie del modelo y en consecuencia, un mejor ajuste. Los valores para los niveles de la temperatura propuestos son 60, 80 y 100°C para el nivel bajo, medio y alto, respectivamente. Para los niveles de tiempo son 24, 36 y 48 días para el nivel bajo, medio y alto, respectivamente, lo que da un total de nueve corridas con seis réplicas y nueve especímenes cilíndricos como referencia, sumando un total de 54 especímenes cilíndricos elaborados con el contenido óptimo de cemento asfáltico, según la norma ASTM D5581 y colocados en un horno convencional, de acuerdo con las condiciones mostradas en la tabla 6.
Las muestras se retiraron del horno después de su tratamiento térmico, se dejaron enfriar a temperatura ambiente y se les determinó la estabilidad Marshall (Lf), el flujo (Ff) y la gravedad específica (GEf), con los datos de las muestras de referencia se calculó ΔL, ΔF y VM. Los resultados se resumen en la tabla 6.
Siguiendo el método de resolución para diseños de tres niveles y con la ayuda de un programa comercial, los datos de la tabla 6 se ajustaron a un modelo de segundo orden y se realizó el análisis de varianza. Los términos del modelo se separaron en principales y de interacción. Se determinaron los valores P para cada grupo como se muestran en la tabla 7. El valor P del grupo de los términos principales (T, T2, t, t2) están más cercanos al cero que los términos de interacción (Tt, Tt2, T2t, T2t2), debido a que los coeficientes principales contribuyen más significativamente (Walpole, 1998) y para tener un modelo con los términos necesarios para un uso práctico, se seleccionaron sólo los coeficientes principales. Los datos de la tabla 6 se volvieron a ajustar por mínimos cuadrados con la ayuda de un programa comercial y se realizó el análisis de varianza para comprobar si el modelo es el adecuado, los resultados se muestran en las tablas 8 y 9, respectivamente.
De la tabla 9, se verificó lo adecuado de los modelos ΔL, ΔF, VM como sigue (Box, 2000): usando α= 0.05, el valor crítico de F es F0.05, 4, 45 = 2.55. Los valores F son iguales a 608.46, 494.80 y 880.51 para el factor T de los modelos ΔL, ΔF y VM, respectivamente, y los valores F iguales a 43.74, 82.11 y 1072.35 para el factor t de los modelos ΔL, ΔF, VM, respectivamente son mayores que 2.55, entonces los factores T y t son significantes, además los valores F de error de ajustes son más pequeños que los de los factores T y t, entonces el error de ajuste es no significante para el modelo.
Los modelos de ΔL, ΔF y VM son los siguientes de acuerdo con los coeficientes de regresión de la tabla 8, donde T es la temperatura ambiente en °C y t es el tiempo de envejecimiento en meses:



Validación del modelo
Para conocer los coeficientes P de regresión de estos modelos para la zona geográfica de modelación, se extrajeron especímenes cilíndricos (corazones) de la carpeta asfáltica en servicio, de acuerdo con la norma ASTM D 5361. Se tomaron tres corazones de la carpeta asfáltica con 0, 12, 24, 36, 48 y 60 meses de envejecimiento real, mientras que en los modelos se sustituyó el valor de la temperatura promedio de 20°C y los tiempos 0, 12, 24, 36,48 y 60 meses. El promedio de los resultados del cambio en la estabilidad Marshall, flujo y el material volátil, así como la comparación en el valor predicho y el real se muestran en las figuras 1, 2 y 3, respectivamente.

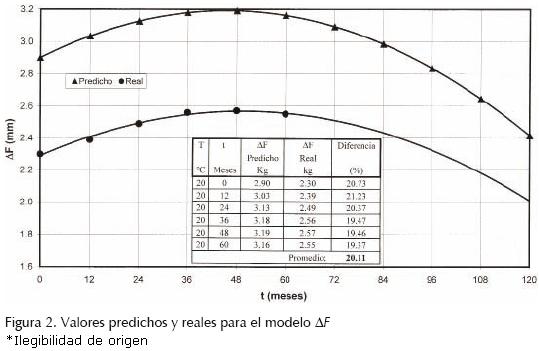
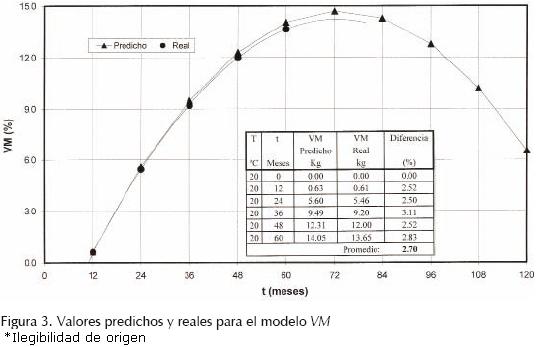
La diferencia entre el valor predicho y el real para ΔL y ΔF son 18% y 20%, respectivamente, y dichas diferencias pueden estar relacionadas con las deficiencias en la construcción, el exceso de tránsito y posiblemente con los factores climáticos que no fueron considerados al inicio de la investigación. Por el contrario, la diferencia entre el valor predicho y el real del modelo VM es 3% lo que indica que el procedimiento de envejecimiento simulado implementado en esta investigación es representativo de las condiciones reales y que la temperatura y el tiempo son los factores ambientales que tienen la mayor influencia sobre la cantidad de material que se volatiliza en la carpeta asfáltica en servicio. El error de modelación de VM de 3% está asociado a variaciones no controladas de la extracción de las muestras de campo, al igual que a las propiedades iníciales de la mezcla asfáltica colocada en la carpeta asfáltica y a la diferencia en el proceso constructivo de los tramos monitoreados.
Conclusiones
La metodología de superficie de respuesta se empleó para la generación de modelos de simulación del tipo determinístico en varias ramas del conocimiento y en la de materiales de construcción ha demostrado ser asertiva en los resultados que dichos modelos predicen.
Los modelos de las propiedades mecánicas desarrollados en esta investigación presentaron errores de predicción que podrían estar asociados al TDPA, a la carga por eje equivalente y a los demás factores ambientales omitidos en el planteamiento de la modelación, por lo que se deben considerar para que estas diferencias sean menores.
Como el modelo para VM presentó una diferencia o error de modelación de 3%, entonces el procedimiento de simulación del envejecimiento empleado en esta investigación es representativo de las condiciones de tiempo y temperatura reales, y la temperatura es el factor ambiental que tiene mayor efecto sobre la cantidad de material que se volatiliza en la mezcla asfáltica.
Agradecimientos
Los autores agradecen al Consejo Nacional de Ciencia y Tecnología por el apoyo recibido mediante el proyecto 58425 del mismo tema de investigación, así como a la Universidad de Guanajuato por el apoyo financiero a través del proyecto 44/07.
Referencias
Azarang–Esfandiari M. Simulación y análisis de modelos estocásticos, 1ª edición, McGraw–Hill, México, 1996, p. 2. [ Links ]
Bell C. Aging of Asphalt–Aggregate Systems, 1ª edición,Transportation Research Bureau Press. EUA, 1989, p. 120. [ Links ]
Box G. Empirical Model–Building and Response Surfaces, 1ª edición, John Wiley & Sons, EUA, 1987, pp. 55–68. [ Links ]
Box G.E. Statistics for Experimenters. An Introduction to Design, Data Analysis and Model Building, 1ª edición, John Wiley & Sons, EUA, 2000,pp. 69–78. [ Links ]
Bratly P. A Guide to Simulation, 2ª edición, Springer–Verlag, EUA, 1987, pp. 35–55, 67. [ Links ]
Castaño–Tostado E. Experimentos: estrategias y análisis en ciencia y tecnología, 1ª edición, México, S y G editores, 2003, p. 295. [ Links ]
Montgomery D. Response Surface Methodology,1ª edición, John Wiley & Sons, EUA, 1995, pp. 24–35. [ Links ]
Montgomery D. Design and Analysis of Experimenters, 2ª edición, John Wiley & Sons, EUA, 2001, pp. 23–150. [ Links ]
Reunión del Consejo de Directores de Carreteras de Iberia e Iberoamérica. (No.11, 2002, México). Catalogo de deterioro de pavimentos flexibles, México, 2002, p. 6. [ Links ]
Yoder, Witczak. Principles of Pavement Design, 2ª edición, John Wiley & Sons, Nueva York, 1975, pp. 24–27. [ Links ]
Walpole R. Probability and Statistic for Engineers and Scientists, 1ªedición, Prentice–Hall, EUA, 1998, pp. 3–12. [ Links ]
Semblanza de los autores
Luis Elias Chávez–Valencia. Ingeniero civil egresado de la Universidad Michoacana de San Nicolás de Hidalgo, en donde realizó estudios de maestría en ciencias de los materiales. Egresó del doctorado en ciencias con especialidad en materiales del CINVESTAV, Unidad Querétaro. Actualmente se desempeña como profesor de tiempo completo en el Departamento de Ingeniería Civil de la Universidad de Guanajuato.
Claudia Hernández–Barriga. Arquitecta egresada de la Universidad Michoacana de San Nicolás de Hidalgo en donde realizó los estudios de maestría en arquitectura. Obtuvo el doctorado en arquitectura por la Universidad Nacional Autónoma de México. Actualmente se desempeña como profesora de tiempo parcial en el Departamento de Diseño de la Universidad de Guanajuato.
Alejandro Manzano–Ramírez. Es ingeniero químico metalurgista por la Universidad Nacional Autónoma de México. Obtuvo su doctorado en ciencias por la Sheffield University, Inglaterra. Actualmente se desempeña como investigador titular (CINVESTAV 3C), en el laboratorio de investigación en materiales del CINVESTAV–IPN, Unidad Querétaro. Es SNI nivel II.














