Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.11 no.2 Ciudad de México abr./jun. 2010
Metodología para el modelado del comportamiento mecánico de hueso esponjoso a partir de sus microestructuras
Mechanical Modelling of Cancellous Bone from their Microstructure
Ramírez–Díaz E.I.1, Ortiz–Prado A.2, Schouwenaars–Franssens R.3 y Ruiz–Cervantes O.4
1 Unidad de Investigación y Asistencia Técnica en Materiales (UDIATEM). Facultad de Ingeniería, Universidad Nacional Autónoma de México. E–mail: edgarisaac10@yahoo.com.mx
2 Unidad de Investigación y Asistencia Técnica en Materiales (UDIATEM). Facultad de Ingeniería, Universidad Nacional Autónoma de México. E–mail: armandoo@unam.mx
3 Unidad de Investigación y Asistencia Técnica en Materiales (UDIATEM). Facultad de Ingeniería, Universidad Nacional Autónoma de México. E–mail: raf_schouwenaars@yahoo.com
4 Unidad de Investigación y Asistencia Técnica en Materiales (UDIATEM). Facultad de Ingeniería, Universidad Nacional Autónoma de México. E–mail: ocervantes@hotmail.com
Recibido: octubre de 2007
Reevaluado: abril de 2009
Aceptado: septiembre de 2009
Resumen
En este trabajo se establece una metodología para generar modelos bidimensionales de hueso esponjoso, que son analizados mediante paquetería de elemento finito.Los modelos están enfocados a representar la arquitectura trabecular mediante celdasde Voronoi, a partir de las coordenadas de los centros de los poros de la estructura ósea observados en imágenes generadas mediante microscopía óptica. Buscando similitud geométrica, se asignó un mayor espesor en la zona de unión de las trabéculas, ya que se ha comprobado que esta consideración lleva a resultados más aproximados a los experimentales. Para nutrir el modelo se realizaron pruebas de compresión a probetas de hueso trabecular, tomando los valores de deformación máxima y esfuerzo máximo para determinar la rigidez del tejido. Mediante el análisis de imágenes de probetas deformadas, se estableció que el momento del colapso de la estructura trabecularse da por la sucesión de fallas enlas trabéculas individuales y se determinó un valor crítico de aproximadamente un 36% de las trabéculas. Finalmente, se determinó mediante análisis por elemento finito, que la rigidez del tejido esponjoso es de 323[MPa], y a partir de este valor se evaluó la variación de la resistencia en función de la densidad y la arquitectura trabecular.
Descriptores : estructuras de Voronoi, caracterización mecánica de hueso, hueso trabecular.
Abstract
In this paper is established a spongy bone bidimensional models methodology for its analysis by finite element software. The models are focused to represent the bone trabecular structure by Voronoi cells, using the coordinates of the porous center, contained within the bone structure, obtained by optical microscope images. Looking for a better geometrical similarity, it was assigned a thicker transversal area in the trabecula union zone, because has been reported that this factor gives a better approximation to experimental results. To feed the finite element models, compression test has been done to trabecular specimens, taking the maximum strain and maximum stress, to obtain the elastic modulus. By means of strained specimen images analysis, it has been established the structure collapse moment. It was when the 36% of total trabeculae failed. Finally it was obtained a tissue Young modulus of 323 [MPa] and with this value, the resistance variation in function of density and trabecular architecture.
Keywords: Bone mechanical modeling, voronoi structures, bone mechanical characterization, trabecular bone.
Introducción
Tejido esponjoso
El tejido óseo se puede clasificar en dos tipos principalmente; el hueso esponjoso y el cortical.
El hueso cortical es una masa sólida con canales únicamente microscópicos. Aproximadamente el 80% de la masa esquelética de un ser humano adulto es hueso cortical, el cual se forma como una pared exterior de los huesos y sus funciones principales son de soporte y protección.
El 20% restante pertenece al hueso esponjoso, también conocido como poroso o trabecular (figura 1), que está compuesto de una red interconectada de placas y barras que reciben el nombre de trabéculas, que a su vez, están compuestas de cristales de hidroxiapatita dentro de una matriz de fibras de colágeno.

A densidades bajas, las celdas forman una red abierta de barras, conforme la densidad relativa aumenta más material se acumula en las paredes de las celdas y la estructura se transforma en una red más cerrada de placas.
El hueso esponjoso se encuentra principalmente cerca de las terminales de los huesos largos y en los cuerpos vertebrales. En los huesos largos, distribuye las cargas mecánicas desde las superficies articulares hasta el hueso cortical, mientras que en las vértebras es el constituyente principal que absorbe la carga (Cowin, 2001).
La densidad, arquitectura y función del hueso en una posición localizada dependen de la magnitud de las cargas a las que está sometido.
El comportamiento mecánico de los materiales celulares como el hueso trabecular depende de tres parámetros principalmente, el tipo de estructura que forman las celdas, la fracción volumétrica de sólido y las propiedades del material de la pared de la celda. La razón primordial para su modelado es debido a que si bien la resistencia del hueso depende primordialmente del hueso cortical, las fracturas más frecuentes que no tienen que ver con un impacto que supera la resistencia del hueso, están asociadas a regiones donde se presenta una alta concentración de hueso trabecular.
Modelos de hueso esponjoso
La respuesta mecánica de los sólidos celulares ha sido modelada mediante la representación de la estructura celular en distintas formas. Los modelos iniciales desarrollados para análisis estructural de una celda unitaria como un hexágono en dos dimensiones y un dodecaedro (poliedro 12 caras) o tetracaidecaedro (poliedro de 14 caras) en 3 dimensiones.
Beaupré y Hayes en 1985, supusieron una estructura cúbica conteniendo una cavidad esférica, donde el diámetro es mayor que la longitud de la celda, por lo que los huecos se encuentran interconectados y dependiendo del diámetro el material que queda en la estructura toma la forma de barras o de placas perforadas (figura 2).

Gibson y Ashby (1997), suponen celdas equiaxiales donde a bajas densidades las celdas son una red de barras mientras que a altas densidades su estructura es en forma de platos perforados, donde las celdas se encuentran desfasadas, lo que permite flexión de las paredes.
Según Gibson (1985), existen cuatro estructuras básicas de hueso esponjoso: la asimétrica, celda abierta y con estructura de barras (figura 3a); la asimétrica, celda cerrada con estructura de placas (figura 3b); la columnar, celda abierta con estructura de barras (figura 3c); y la columnar, celda cerrada con estructura de placas (figura 3d).

Las geometrías escogidas para los modelos son simples y altamente idealizadas y solo en algunos casos, toman en cuenta propiedades geométricas como la aniso–tropía en el hueso esponjoso. En los modelos se usan argumentos dimensionales, que no dependen de la geometría exacta del modelo, lo que provoca que los resultados numéricos difieran de la realidad, pero si reproducen los mecanismos de deformación.
Kim y Al–Hassani (2002) presentan un modelo analítico de celda unitaria que considera un aumento en su sección cerca de las zonas de unión, con el cual predicen las propiedades del hueso esponjoso. En éste se demuestra la importancia de aumentar el espesor cerca de las zonas de unión en las celdas, para mejorar la exactitud al momento de calcular las propiedades mecánicas (figura 4).
Todos los modelos hasta ahora presentados, se basan en celdas unitarias para el estudio del comportamiento del hueso trabecular, en 1997 Silva y Gibson plantean un modelo bidimensional de elemento finito para simular el hueso trabecular de una vértebra, usando el concepto de celdas de Voronoi (figura 5). Este diagrama es ampliamente utilizado en construcciones geométricas que definen cómo el espacio de dos o tres dimensiones puede ser dividido en celdas y que a diferencia de los modelos anteriores considera la orientación de las trabéculas.

Desarrollo experimental
Caracterización mecánica de hueso esponjoso
Se obtuvieron 10 probetas cilíndricas con una relación longitud–diámetro de 2:1. Lo anterior con la ayuda de un sacabocados, con el cual se extrajo una probeta de cada cabeza del fémur. Posteriormente, se ajustó la muestra a sus dimensiones finales mediante una cortadora de disco de diamante para obtener un corte más fino en las superficies planas de la probeta y dejar una longitud final de 2cm.
Las muestras fueron lavadas con agua y jabón, sin el uso de sosa o algún elemento desengrasante, debido a los daños que pueda ocasionar en la misma y posteriormente se realizó un lavado ultrasónico para eliminar médula y grasa, ya que la limpieza con aire a presión puede dañar la estructura. El almacenamiento de las muestras se realizó en solución isotónica de cloruro de Sodio Abbott (Cloruro de Sodio al 0.9%), procediendo a su refrigeración por un periodo de 8 días a una temperatura aproximada de 10 ° C.
La determinación de las propiedades mecánicas se realizó mediante ensayos de compresión, esto en una máquina de ensayos universales electromecánica Instron equipada con celda de carga de 5KN, buscando con esto una mayor exactitud en los resultados. Finalmente, se probaron las muestras húmedas a una velocidad de 0.05 mm/s.
Las curvas esfuerzo–deformación obtenidas de las pruebas de compresión, presentan el comportamiento típico para sólidos celulares, que se caracteriza por presentar tres regiones perfectamente identificadas (figura 6):
1. Régimen elástico lineal, correspondiente a la flexión en las trabéculas o la deformación de las paredes;
2. Esfuerzo meseta (plateau), correspondiente al colapso progresivo de la celda por pandeo elástico, cedencia plástica o fractura frágil dependiendo de la naturaleza del material de las trabéculas;
3. Densificación, correspondiente al colapso de las celdas a través del material y de la carga subsecuente de los bordes y de las caras de las celdas, unas sobre otras (Ramirez et al., 2007).
El análisis de las curvas se realizó únicamente en la región elástica, obteniéndose los resultados que se presentan en la tabla 1.

El módulo obtenido de la tabla anterior se conoce como módulo aparente E*, y es el módulo de elasticidad asociado a la estructura (trabéculas y poros) considerándola como un continuo, pero para el modelo no puede ser utilizado, ya que éste último considera la porosidad en su geometría.
Por lo anterior, los valores que se utilizarán para la obtención de la rigidez del hueso serán los de deformación y esfuerzo máximo promedio.
La deformación máxima promedio fue utilizada dentro del modelo mediante un desplazamiento a compresión, con un módulo de elasticidad de 1 [GPa], este último posteriormente fue ajustado con la finalidad de obtener sobre la imagen el esfuerzo máximo experimental de 5.5 [MPa], teniendo en cuenta que a este esfuerzo, la estructura colapsa.
Análisis microestructural del hueso esponjoso
A la par de la caracterización mecánica se llevó a cabo la obtención de imágenes microestructurales de hueso esponjoso con la finalidad de tener las estructuras de partida para los modelos y obtener sus dimensiones características.
Para llevar a cabo la caracterización microestructural se obtuvieron tres muestras cilíndricas de hueso esponjoso mediante la metodología utilizada para la caracterización mecánica.
Para la adquisición de imágenes de la estructura trabecular, se optó por usar la cortadora de diamante y dividir en dos la probeta cilíndrica, de donde se obtuvo el área de observación para tres diferentes muestras (figura 7). De lo anterior, se obtuvieron imágenes a 100X mediante el microscopio óptico, tomando toda la superficie de cada una de las probetas, de tal forma que se pudiera reconstruir mediante Corel Draw®, el área transversal de cada muestra (figuras 8–10).


Para la medición de espesores trabéculares se dividió cada una de las imágenes en tres regiones del mismo tamaño, debido a la clara diferencia en el espesor trabecular a lo largo de la altura de la probeta. Se llevaron a cabo 10 mediciones en cada una de las zonas, obteniendo para cada una de éstas el valor de L (espesor trabecular en la zona de unión con las demás trabéculas) y el valor de l (espesor mínimo en la zona central de la trabécula) mostrado en la figura 11 y colocando los valores promedio en la tabla 2.
Para el caso de la probeta 1 y 2 es evidente la variación de espesor a lo largo de la altura de la sección transversal de la probeta, en particular, en la zona denominada como "abajo" donde los valores promedio de "l" y "L" son mayores en comparación con las otras dos zonas. Por lo que para los modelos de estas probetas se determinará el valor promedio del espesor medido entre la región de arriba y en medio y éste será asignado a 2/3 de la estructura, mientras que para el tercio restante se utilizarán los valores de la región de abajo. Para el modelo de la probeta 3 simplemente se utilizarán los valores promedio de las tres regiones tanto para l como L.
Modelado de la arquitectura trabecular
Para la generación de los modelos a partir de las microestructuras de hueso trabecular se utilizaron las celdas de Voronoi como herramienta para discretizar el espacio.
Un diagrama de Voronoi es construido a partir de un grupo de puntos de nucleación, que pueden estar espaciados regularmente o sin orden. El diagrama es generado mediante la construcción de bisectores perpendiculares para cada par de puntos adyacentes.
Las celdas resultantes son aquellas que son formadas simultáneamente desde los puntos de nucleación y crecen a una velocidad uniforme hasta que se conectan con las celdas adyacentes.
De esta manera en el diagrama de Voronoi, las paredes de las celdas se encuentran vinculadas a todos los puntos en el espacio que están cercanos a un solo punto de nucleación.
Para los diagramas de hueso trabecular, los puntos de nucleación no tienen ningún significado físico, son simplemente entidades de construcción que permiten crear los diagramas de un modo repetitivo.
A partir de las imágenes (8–10), se obtuvieron las coordenadas de los centros de cada uno de los poros de la arquitectura trabecular, mediante los cuales se construyeron los modelos de celdas de Voronoi con ayuda de Mathematica® (figuras 12–14).

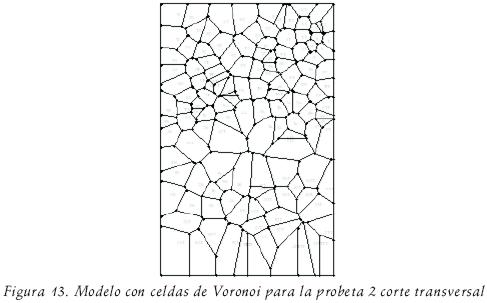

Las estructuras generadas por celdas de Voronoi presentan similitudes con las estructuras originales, en el caso de las figuras 12 y 13 se observa una distribución homogénea de los poros en la región de arriba. Por otro lado, en la figura 14 se observa la orientación preferencial que tienen las celdas que van desde la esquina inferior izquierda hasta la esquina superior derecha, al igual que en la imagen de la cual se partió, pero en la esquina inferior derecha se obtuvo una estructura que no presenta la orientación preferencial que si se observa la imagen de partida.
A partir de las estructuras de Voronoi generadas mediante paquetería, se transfirieron los datos a Abaqus® para analizar éstas mediante elemento finito.
A cada una de las barras de la estructura de Voronoi se le asignó la geometría trabecular que se observa en la figura 15.

Buscando que la estructura se asemeje en mayor medida a la geometría que se observa en las imágenes y tomando en consideración lo reportado por Kim y Al–Has–sani, ya que éstos indican que se obtiene una mejor aproximación al comportamiento si se considera el en–grosamiento en las zonas de unión de las trabéculas.
El modelo de la trabécula individual consta de 2 circunferencias de radios iguales a la mitad del espesor medido en las regiones más gruesas (L/2), mientras que la sección media tiene como espesor el valor medio evaluado en el centro de las trabéculas (l) (figura 15).
Las estructuras generadas en la paquetería quedan como se muestran en las Figuras 16–18, de las cuales se determinó mediante la paquetería el área que ocupa el sólido, se dividió entre el área total que ocuparía si no tuviera porosidades con lo que se obtuvo la fracción de área para cada una de éstas.
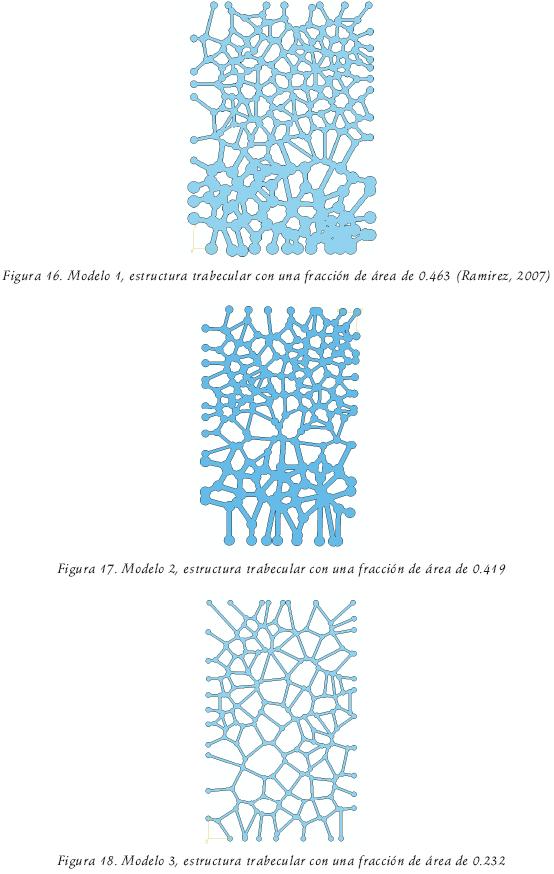
Evolución de la arquitectura trabecular durante la deformación
Con la finalidad de establecer un criterio para determinar el momento en que la estructura trabecular colapsa, es decir, cuando llega a su esfuerzo máximo, se llevó a cabo el análisis de la evolución de la arquitectura del hueso esponjoso durante la deformación.
Las pruebas consistieron en tomar distintas muestras de hueso esponjoso y someterlas a compresión, de tal manera que cada una fue sometida a un distinto porcentaje de deformación, desde 2% hasta 6% (2, 3,4, 5 y 6%). En las pruebas experimentales se observó que la deformación correspondiente al esfuerzo máximo es del orden del 5.5% y es por esto que el valor de deformación máxima que se tomó fue del 6%. Todo este análisis se encuentra en el rango elástico de las curvas esfuerzo–deformación, por lo que se puede esperar que después de la deformación exista una recuperación total de la muestra, lo cual implicaría que al tomar las imágenes no existiera ninguna evidencia de las solicitaciones a las que estuvo sometida. Sin embargo, y dado que no se trata de un continuo sino de una estructura, se tiene que algunas de las trabéculas fallan a deformaciones menores a la máxima, en consecuencia, lo que se midió es el daño causado en las trabéculas durante la deformación, es decir, el número de trabéculas rotas.
Para llevar a cabo el análisis cuantitativo, las piezas deformadas fueron llevadas al microscopio óptico y de nuevo se reprodujeron por completo las imágenes de las probetas, pero para este estudio únicamente es de interés el resultado asociado a la estructura que fue sometida a un 6% de deformación, ya que es la relacionada con el colapso de la estructura.
Se midió la cantidad de trabéculas faltantes por unidad de área, considerando como trabéculas faltantes todas aquellas trabéculas incompletas, o donde parece que en un momento dado estaba la presencia de alguna. La realidad es que estas trabéculas no desaparecen durante la deformación, simplemente se fracturan y quedan dispersas.
En la figura 19 se observa la muestra con un 6% de deformación, en la cual se contaron aproximadamente 235 trabéculas faltantes, en un área analizada de 96.81 [mm2]. Se contó que la cantidad total de trabéculas es de 652, por lo que es necesario que aproximadamente el 36% de las trabéculas fallen para que se presente el colapso de la estructura.

Resultados
De lo observado microestructuralmente tanto en las muestras que fueron sometidas a pruebas de compresión, como en las que se realizó el análisis de la evolución de falla, la estructura que aparece de forma más común es la que generó el tercer modelo; aun cuando de las estructuras seleccionadas para modelar, dos tienen una variación en el espesor de las trabéculas a lo largo de su altura, lo que genera que tengan una mayor densidad.
Por lo antes mencionado, la rigidez del hueso trabecular fue determinada para el tercer modelo, asignándole un desplazamiento vertical en la superficie superior que corresponde al 5.5 % de deformación, mientras que la superficie inferior fue empotrada.
Se consideró el comportamiento como elástico asignando un módulo de Young de 1 GPa y una relación de Poisson de 0.3, con esto se observó el nivel de esfuerzos presente en la estructura, se ajustó la escala de colores para que el 36% de las trabéculas quedaran fuera de rango y con esto determinar el factor por el que hay que multiplicar el módulo de elasticidad para obtener el valor de esfuerzo máximo de 5.5 [MPa] sobre la estructura. Para ésta última se determinó un módulo de 323 MPa (figura 20). Este dato se encuentra en los valores reportados por la literatura, dado que para vértebras de cerdo se encontraron valores entre 610 [MPa] hasta 1550[MPa], para fémur de cabra valores entre 234 hasta 770 [MPa], para fémur de humano desde 190 hasta 1610 [MPa] (Yuehuei et al., 2000).
Cabe mencionar que se malló con elementos triangulares lineales, para el modelo 1 se tuvieron 21540 elementos; para el modelo 2, 13347 elementos y para el modelo 3, 13029 elementos. Además, se consideró auto–contacto sin fricción, ya que durante la deformación se puede presentar que unas trabéculas empiecen a interactuar con otras.
Asignando la rigidez de 323 [MPa] a las tres estructuras, considerando que esta propiedad depende principalmente del nivel de mineralización y obteniendo la variación en la resistencia para cada estructura.
En las figuras 21 y 22 se observa el nivel de esfuerzos en las estructuras 1 y 2 para un módulo de elasticidad de 323 [MPa], donde para la estructura 1 se encuentra que la resistencia máxima aumenta de 5.5 [MPa] hasta 10 [MPa], mientras que para la estructura 2 se obtiene un valor de 9.4 [MPa], lo cual comprueba que si bien la rigidez del material de los tres modelos es la misma, la rigidez de cada una de las estructuras difiere, y para los casos analizados en particular, se tiene que la estructura con una densidad relativa mayor, presenta una mayor rigidez y una mayor resistencia.
Pero hay que mencionar que para evaluar el efecto de la arquitectura trabecular en la resistencia se necesitan hacer estos modelos paramétricos y compararlos para el caso en que tengan exactamente la misma densidad.
Adicionalmente para cada una de las estructuras se graficó la sumatoria de las fuerzas de reacción en la superficie del modelo contra el desplazamiento vertical de la muestra, lo que arrojó los resultados que se presentan en la figura 23.

En la gráfica (figura 23) se observa que tanto para el modelo 2 como para el modelo 3, se presenta un comportamiento lineal como era de esperarse, ya que el comportamiento asignado a las trabéculas es elástico, pero en el modelo 1 la linealidad se pierde a partir de los últimos 3 datos graficados, situación que coincide con el momento en el cual empiezan a interactuar algunas trabéculas y la condición de auto–contacto se activa, lo que provoca una disminución en la fuerza de reacción, ya que se consideró una condición sin fricción.
Por otro lado, se observa que la estructura con menor densidad es la que presenta una menor resistencia y que la que tiene mayor densidad (modelo 1) si no fuera por el efecto que tiene la condición de auto–contacto hubiera presentado la mayor resistencia. Analizando la evolución de la falla en el modelo 3, se presenta un comportamiento similar al que se observó en las estructuras inspeccionadas en el microscopio, en las cuales a deformaciones del orden del 2% ya se presenta que en algunas zonas localizadas de las trabéculas, ya se supere el esfuerzo máximo de 5.5 [MPa], lo que se puede ver como puntos de inicio de grietas. A deformaciones mayores del orden del 4%, se observa que estas áreas aumentan y aparecen nuevos puntos de inicio de grietas (figura 24).

Conclusiones
Cabe mencionar que si bien se llevaron a cabo algunos análisis a las estructuras obtenidas, el objetivo de esta etapa del proyecto es el de establecer una metodología para el modelado de la estructura trabecular del hueso, condición que se consiguió desde el punto de vista de similitud geométrica y al tomar en cuenta los factores mas importantes para el comportamiento mecánico de los sólidos celulares.
El método de celdas de Voronoi es una técnica geométrica que permite reproducir de una forma relativamente simple una estructura celular como la del hueso trabecular. Este modelo a diferencia de aquellos que consideran únicamente una celda unitaria, tiene la ventaja que se pueden tomar en cuenta los tres factores determinantes de cualquier sólido celular; las propiedades del tejido, la arquitectura trabecular y la densidad o fracción volumétrica, este último punto se puede desarrollar variando el espesor mínimo de las trabéculas.
En la secuencia de imágenes obtenida durante la deformación de la arquitectura, se observó que la falla de las trabéculas se presenta desde deformaciones muy por debajo del valor máximo obtenido experimentalmente. Por otra parte, no es hasta que una cierta cantidad de trabéculas fallan cuando se da el colapso de la estructura.
Con los datos obtenidos experimentalmente se determinó la rigidez del tejido óseo mediante la paquetería de elemento finito y se obtuvo un módulo de elasticidad de 323 [MPa] para la tercera estructura, esto permitió a su vez observar la variación en la resistencia de las estructuras trabeculares analizadas. El nivel de esfuerzos en las estructuras 1 y 2 para un módulo de elasticidad del tejido óseo de 323 [MPa], es de 10 [MPa] y de 9.4 [MPa], respectivamente, mientras que para la estructura 3 fue de 5.5 [MPa], lo cual comprueba que si bien la rigidez del material de los tres modelos es la misma, la rigidez de cada una de las estructuras difiere, finalmente para los casos analizados, en particular, se tiene que a mayor densidad relativa mayor resistencia.
Si bien para estos primeros modelos se omitieron ciertos factores de relevancia como el comportamiento anisotrópico del hueso, así como la fricción que existiría en el momento en que entran en contacto las trabéculas; son cuestiones con las que actualmente ya se están trabajando para generar modelos con un comportamiento más aproximado a la realidad. Adicionalmente a lo anterior, también ya existen avances en la optimación de la generación de geometrías, tanto en tiempo como en similitud geométrica, las cuales se presentarán en trabajos posteriores.
Agradecimientos
Se agradece el apoyo en las diferentes etapas del presente estudio a los ingenieros Víctor Hugo Jacobo, Efraín Ramos, Roberto Cisneros, Ignacio Cueva, Jorge Romero y al biólogo Germán Álvarez. Por otra parte, se reconoce el apoyo económico brindado por la Dirección de Asuntos del Personal Académico de la UNAM, esto a través de los proyectos PAPIIT Micromecánica de hueso 2 IN113209 y PAPIME Laboratorio de biomateriales PE 104109.
Referencias
An Y. y Draughn R. Mechanical Testing of Bone and the Bone–Iimplant Interface. USA. CRC press. 2000. [ Links ]
Beaupré G. y Hayes W. Finite Element Analysis for a Three Dimensional Open–Celled Model for Trabecular Bone. J. Biomech. 1985. [ Links ]
Cowin S. Bone Mechanics Handbook. 2ª edición. USA. CRC. 2001. [ Links ]
Gibson L. The Mechanical Behavior of Cancellous Bone. J. of Biomechanics, 5:317–328. 1985. [ Links ]
Gibson L. y Ashby M. Cellular Solids: Structure and Properties. 2da edición. 1997. [ Links ]
Gibson y Lorna. Biomechanics of Cellular Solids. J. Biomech. Massachusetts. 2004. [ Links ]
Kim H., Al–Hassani S. A Morphological Model of Vertebral Trabecular Bone. Journal Biomechs. 35:1101–1114. South Korea, 2002. [ Links ]
Narváez M. Propuesta para el análisis de las propiedades mecánicas del hueso esponjoso vertebral. Tesis (Licenciatura en ingeniería). México DF. Universidad Nacional Autónoma de México. 2004. [ Links ]
Ramírez E., Ortiz A., Schouwenaars R., Ruiz O. Modelado de hueso trabecular mediante paquetería de elemento finito basándose en estructuras de Voronoi. Revista de la Sociedad Mexicana de Ingeniería Mecánica, 2(5). Septiembre 2007. [ Links ]
Silva M. y Gibson L. Modeling the Mechanical Behavior of Vertebral Trabecular Bone: Effects of Age–Related Changes in Microstructure. Bone, 21(2). 1997. [ Links ]
Semblanzas de los autores
Edgar Isaac Ramírez–Díaz. Estudió la licenciatura en la Facultad de Ingeniería de la Universidad Nacional Autónoma de México (UNAM), obteniendo el título de ingeniero mecánico en el 2004. Pertenece a la Unidad de Investigación y Asistencia Técnica en Materiales desde 2003, colaborando en proyectos académicos y para la industria, primordialmente en el área de análisis de falla, modelado por elemento finito, optimización de procesos de conformado. Estudió el posgrado en el Instituto de Investigaciones en Materiales en la misma Universidad, obteniendo el grado de maestro en ciencia e ingeniería de materiales en el 2007. Es profesor asociado "C", T.C. en la Facultad de Ingeniería de la UNAM desde el 2004, donde ha impartido ciencia de materiales II, metalurgia física, laboratorio de ciencia de materiales II, laboratorio de modelado de procesos de manufactura y proyecto de ingeniería. Ha publicado un artículo en congreso internacional, 13 artículos en congresos nacionales y 2 artículos en revistas y ha dirigido 7 tesis a nivel licenciatura con 8 alumnos titulados.
Armando Ortiz–Prado. Se graduó como ingeniero mecánico electricista (Ingeniería mecánica) por la Facultad de Ingeniería de la Universidad Nacional Autónoma de México (UNAM) en 1980. Posteriormente, obtuvo la maestría y el doctorado en ingeniería mecánica. Es profesor desde hace 29 años, impartiendo cátedra principalmente en las áreas de procesos de manufactura y ciencia de materiales. Es profesor titular "C" de tiempo completo definitivo y tutor doctoral de los posgrados de ciencia e ingeniería de materiales y de ingeniería. Sus líneas de investigación son modelado de procesos de conformado mecánico, análisis de falla, comportamiento mecánico de biomateriales y corrosión en equipo electrónico. Ha desarrollado proyectos y estudios para diferentes empresas privadas y entidades gubernamentales, orientados éstos al desarrollo y mejora de métodos de manufactura, desarrollo de materiales, corrosión y análisis de falla; lo cual se traduce en más de 50 estudios y asesorías para la industria, 12 proyectos de investigación y desarrollo tecnológico. A la fecha, suma más de 90 tesis de licenciatura. Su experiencia se ha transmitido a través de 7 textos para licenciatura en las áreas de manufactura, materiales y corrosión. Asimismo, su productividad incluye más de 15 artículos en congresos internacionales, más de 80 artículos en congresos nacionales y más de 20 artículos en revistas arbitradas. Fue galardonado por la UNAM con la Distinción Universidad Nacional para Jóvenes Académicos (Docencia en ciencias exactas) en 1989. Su productividad académica y científica ha sido reconocida por la UNAM, a través del otorgamiento del nivel D del PRIDE y por el CONACYT con el nombramiento de Investigador Nacional Nivel I.
Rafael Schouwenaars–Franssens. Obtuvo el grado de maestro en ingeniería de minas en la Universidad de Lovaina, Bélgica y el doctorado en ingeniería mecánica en la FI–UNAM. Ocupa el nivel I en el sistema nacional de investigadores. Durante cuatro años estaba activo como investigador, trabajando proyectos industriales relacionados con la textura cristalográfica en aceros en el Departamento de Metalurgía e Ingeniería de Materiales de la misma universidad. Su trabajo en México lo inició como experto en microscopía electrónica dentro de la Unidad de Investigación y Asistencia Tecnológica en Materiales (UDIATEM). Posteriormente combinó estas actividades con una carrera de profesor en la Facultad de Ingeniería. En el ámbito tecnológico se dedica al análisis de falla y la optimización de procesos en la industria metal–mecánica, con un enfoque especial hacia las aleaciones tribológicas dúctiles. Ha realizado estudios científicos enfocados a las propiedades mecánicas de materiales complejos, los cuales se han publicado en 25 artículos internacionales, 7 en revista nacional y 37 que se han presentados en 30 congresos tanto internacionales como nacionales. Es árbitro de varias revistas tanto nacionales como internacionales y miembro del comité científico de dos series de congresos internacionales de primer nivel.
Osvaldo Ruiz–Cervantes. Realizó sus estudios de licenciatura en la Facultad de Ingeniería de la UNAM, obteniendo el título de ingeniero mecánico en el 2004. Pertenece a la Unidad de Investigación y Asistencia Técnica en Materiales desde 2005, desempeñándose como ingeniero de proyectos en las áreas de simulaciones numéricas, procesos de conformado mecánico y caracterización de hueso trabecular. Actualmente realiza trámites para obtener el grado de maestro en ciencias e ingeniería en el Posgrado del Instituto de Investigaciones en Materiales, teniendo como asesor al Dr. Armando Ortiz Prado. Imparte las materias de Modelado de Procesos de Manufactura e Ingeniería de Materiales en la Facultad de Ingeniería de la Universidad Nacional Autónoma de México.















