Sensibilidad paramétrica de modelos de circuitos equivalentes de orden superior de turbogeneradores

 

Parameter Sensitivity of High–Order Equivalent Circuit Models Of Turbine Generator

 

I. López–García¹, R. Escarela–Pérez², T. Niewierowicz–Swiecicka³ y E. Campero–Littlewood⁴

 

¹ Universidad Autónoma Metropolitana–Azcapotzalco. México. E–mail: irvinlopez@yahoo.com

² Universidad Autónoma Metropolitana–Azcapotzalco. México. E–mail: r.escarela@ieee.org

³ Instituto Politécnico Nacional U.P. Adolfo López Mateos. México. E–mail: tniewi@ipn.mx

⁴ Universidad Autónoma Metropolitana–Azcapotzalco. México. E–mail: ecl@correo.azc.uam.mx

 

Recibido: enero de 2008
Aceptado: enero de 2009

 

Resumen

En este trabajo se presentan los resultados del análisis de sensibilidad paramétrica realizado a modelos de circuitos equivalentes de orden superior de un turbogenerador (150 MVA, 120 MW, 13.8 kV y 50 Hz). La representación del generador síncrono se hace en el espacio de estados, utilizando la teoría de dos ejes (d y q). El objetivo del estudio de sensibilidad es evaluar el impacto que tiene cada uno de los parámetros en la respuesta transitoria de los modelos analizados –circuitos equivalentes desde una hasta cinco ramas de amortiguamiento en el eje d y de una a cuatro ramas en el eje q–. En este trabajo el concepto de sensibilidad paramétrica se formula en términos generales, planteando la función de sensibilidad a partir de condiciones de cortocircuito en las terminales del generador. Los resultados se presentan señalando el nivel de importancia de cada parámetro en el comportamiento del modelo. Los algoritmos utilizados fueron diseñados en MATLAB®. Así, este estudio permite inferir aspectos electromagnéticos de los generadores síncronos de rotor sólido que no han sido previamente estudiados. La metodología de sensibilidad que se presenta en este trabajo también se puede aplicar a otros sistemas físicos.

Descriptores: sistemas eléctricos de potencia, generador síncrono, circuitos equivalentes, sistemas dinámicos, función de sensibilidad, ecuación desensibilidad.

 

Abstract

This work shows the results of a parametric sensitivity analysis applied to a state–space representation of high–order two–axis equivalent circuits (ECs) of a turbo generator (150 MVA, 120 MW, 13.8 kV y 50 Hz). The main purpose of this study is to evaluate each parameter impact on the transient response of the analyzed two–axis models –d–axis ECs with one to five damper branches and q–axis ECs from one to four damper branches–. The parametric sensitivity concept is formulated in a general context and the sensibility function is established from the generator response to a short circuit condition. Results ponder the importance played by each parameter in the model behavior. The algorithms were design within MATLAB^® environment. The study gives way to conclusions on electromagnetic aspects of solid rotor synchronous generators that have not been previously studied. The methodology presented here can be applied to any other physical system.

Keywords: Electric power systems, synchronous generators, two–axis equivalent–circuits, dynamic systems, sensibility function and sensibility equation.

 

Introducción

La creciente demanda de energía eléctrica y la búsqueda de una mayor rentabilidad de los Sistemas Eléctricos de Potencia (SEP) hacen necesario disponer de modelos que simulen de manera precisa el comportamiento de sus elementos. Un elemento de gran importancia en los SEP es el generador síncrono (GS) y por lo tanto, resulta importante disponer de modelos que sean precisos, y a la vez prácticos, en la interconexión con los demás elementos del sistema.

En la literatura clásica (Grainger et al., 1996, Kundur, 1994 y Anderson et al., 2003) se describen modelos sencillos consistentes en una fuente de voltaje en serie con una reactancia "aparente". Estos modelos son prácticos y simples, pero no simulan de manera precisa el comportamiento transitorio del generador. Por otra parte, hay modelos obtenidos con el Método del Elemento Finito (MEF) (Arjona, 2004, Escarela et al., 1998), que simulan de manera muy cercana el comportamiento real del GS. Estos modelos son muy útiles en el análisis individual de generadores y en la validación de otros modelos, pero no son prácticos para el análisis de redes con gran cantidad de generadores.

Los modelos que utilizan circuitos equivalentes (CE) en dos ejes (d y q) (Adkins et al., 1975, Kundur, 1994) ofrecen un balance adecuado entre precisión e interconectividad con el resto del SEP. La precisión de estos modelos puede graduarse en función del número de ramas que se utilicen en cada eje para simular el comportamiento de los circuitos de amortiguamiento.

Para modelar al GS mediante CE en dos ejes, es necesario identificar los parámetros (resistencias e inductancias) que los conforman. Una de las técnicas más utilizadas para la obtención de estos parámetros, y que además se ha convertido en estándar, es mediante el análisis de la respuesta a la frecuencia de los devanados del generador en reposo (Standstill Frequency Response, SSFR) (IEEE Std. 115–1995).

En este trabajo se hace un análisis de sensibilidad paramétrica para estudiar el impacto de cada uno de los parámetros en la precisión del modelo. Esto permite evaluar el modelo y conocer cuáles parámetros son determinantes en la simulación que se logra del sistema dinámico. El estudio se lleva a cabo utilizando el modelo de un turbogenerador, cuyos parámetros fueron identificados en (Niewierowicz et al., 2003) y del cual se cuenta con resultados (validados experimentalmente) de una simulación de una condición transitoria obtenida con el MEF (Escarela et al., 1998 y 2004).

En primer término, se plantean los conceptos más importantes de la teoría de sensibilidad (Frank, 1978, Khalil, 2002). En seguida se presenta el modelado de GS mediante la teoría de los dos ejes (Adkins et al., 1975, Kundur, 1994). El modelo del GS se plantea utilizando ecuaciones de estado definidas a partir de las ecuaciones de voltaje de los devanados de los ejes d y q.

Para el análisis que se hace del sistema, se define una Función de Sensibilidad (FS) (López, 2005) mediante la cual se determina la sensibilidad del modelo a cambios del valor de cada uno de los parámetros. En este trabajo, se utiliza como FS a las corrientes obtenidas de la solución del sistema dinámico para una condición de cortocircuito en las terminales del GS, que operaba en vacío. La sensibilidad del modelo a cambios de cada uno de sus parámetros, o lo que es lo mismo, la importancia de cada uno de sus parámetros se cuantifica a partir de las variaciones de esta función.

En la sección de resultados se presenta la sensibilidad paramétrica en la condición transitoria descrita. Esto se lleva a cabo para modelos del eje d con hasta cinco ramas de amortiguamiento y del eje q con hasta cuatro ramas. Así se obtienen conclusiones reveladoras al respecto de la importancia de la presencia de cada uno de los parámetros de los modelos.

 

Conceptos básicos de la teoría de sensibilidad

El modelado de sistemas mediante variables de estado es una práctica común. De la teoría de ecuaciones diferenciales ordinarias es sabido que sus coeficientes tienen repercusión en su solución, y que el modelo nunca se puede considerar exacto. Por tal razón, la certidumbre del modelo requiere normalmente de un estudio de sensibilidad paramétrica.

El estudio de sensibilidad paramétrica investiga de manera sistemática la importancia que los parámetros tienen en el modelo (Frank, 1978, Khalil, 2002). La idea principal de esta metodología es ver al modelo como un sistema, donde, a partir de alguna entrada, se define como salida a una función caracterizada por los parámetros del modelo.

Un sistema cualquiera puede ser representado por la relación de su estrada y salida (explícita o implícita), donde su proceso dinámico puede ser alterado por su entrada o por cambios en sus parámetros (Frank, 1978). En la figura 1 se muestran los puertos de entrada de estas cantidades en el sistema.

Para el objetivo de este estudio las condiciones de entrada del sistema se suponen constantes y la dinámica del sistema se representa mediante un modelo de variables de estado

donde:

x ⁿ son los estados del sistema.

α ^P son los parámetros del modelo.

t [t₀,t₁ ] es el intervalo de tiempo para la solución.

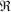En la ecuación (1) se supone que f (t,x,α) es continua en (t,x,α) para todo (t,x,α) [t₀,t₁] × ⁿ × 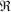^P. Si se fija α₀ como el valor nominal de α, lo que se obtiene es la ecuación para la condición nomina

que se supone que tiene solución única (t, α₀) sobre [t₀,t₁]. De acuerdo con el teorema de continuidad de soluciones en términos de los estados iniciales y parámetros (Khalil, 2002), para toda a suficientemente cercano a α₀, esto es, para la norma α–α₀suficientemente pequeña, la ecuación de estados

tiene solución única sobre [t₀,t₁], esto es, cercana a la solución nominal x(t, α₀). Si f es continua y diferenciable con respecto a x, y α , entonces se asegura que la solución x(t, α) es diferenciable para valores de α cercanos a α₀ (Frank, 1978, Khalil, 2002). Por lo tanto, si x_α(t, α) es la derivada parcial de la solución x(t, a) con respecto a y se deriva con respecto a t, x_a(t,a) satisface la siguiente ecuación diferencial

donde:

Para α suficientemente cercanas a α₀, las matrices A(t,α) y B(t,α) están definidas en[t₀,t₁]. Así, x_α(t, α) está definida en el mismo intervalo de tiempo.

Si se define a s(t)= x_α(t, α₀), se puede plantear la Ecuación de Sensibilidad (ES)

donde su solución única es la FS.

Como la FS proviene de una estimación de primer orden del efecto de la variación en los parámetros en la solución, esta condición puede ser usada para aproximar la solución cuando α es lo suficientemente cercano al valor nominal α₀. Esto se hace mediante la aplicación de series de Taylor a la solución nominal x_α(t, α₀) y despreciando los términos de alto orden. La ecuación de aproximación queda (Frank, 1978, Khalil, 2002)

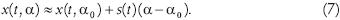
En la ecuación (7) resulta suficiente con conocer la solución nominal del sistema y la FS para aproximar la solución de todos los valores de α en una pequeña región centrada en α₀.

En muchos casos prácticos la solución de las ecuaciones diferenciales se obtiene numéricamente (Frank, 1978, Khalil, 2002).

 

Modelado en dos ejes del generador síncrono

El modelo que representa al generador se desarrolló bajo la Teoría de los dos ejes (Adkins et al., 1975, Kundur, 1994). En la figura 2 se muestran los devanados equivalentes d y q que reproducen la fuerza magnetomotriz del estator de la máquina real, el devanado f que corresponde al campo y los devanados kd y lq que, en este caso, por tratarse de un turbogenerador con rotor sólido, representan el efecto de amortiguamiento debido a la presencia de las corrientes de remolino en el rotor (Adkins et al., 1975, Kundur, 1994). El número de circuitos de amortiguamiento cambia para cada uno de los modelos analizados.

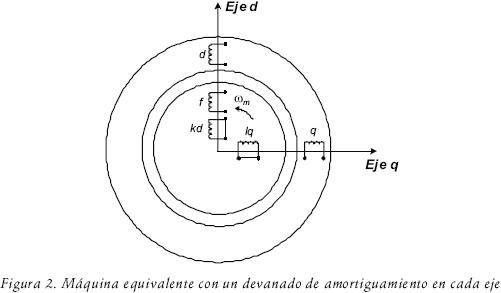
La construcción de los CE se plantea a partir de los enlazamientos de flujo magnético entre todos los devanados de cada eje de la máquina equivalente (figura 2), que son representados por inductancias, tal y como se muestra en la figura 3.

Los enlazamientos entre el devanado de campo y los de amortiguamiento son representados por las inductancias conocidas como de Canay (1969 y 1993), quien al igual que el estándar IEEE Std. 115–1995, señala la necesidad de incluirlas.

Las ecuaciones de voltaje de los devanados de estator (d y q), campo (f) y amortiguamiento (kd y lq) de la máquina equivalente en dos ejes (figura 2) se plantean matricialmente de la siguiente manera (Kamwa et al., 1997, López, 2005)

donde los vectores i, u 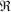^3+kd+lq son los estados y las entradas, respectivamente; las matrices R, L y G 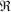^{((3+kd+lq)× (3+kd+lq))} son matrices de parámetros del modelo correspondiente, para k, l lN . ω_me es la velocidad mecánica en pu. Las matrices R y L contienen, respectivamente, las resistencias e inductancias de todos los devanados del modelo y la matriz G contiene las inductancias involucradas en la inducción de voltaje por velocidad (Adkins et al., 1975, Kundur, 1994).

Los vectores y matrices en (8) se escriben por conveniencia de manera explícita y se definen de la siguiente manera

donde:

 

Los subíndices d y q corresponden a la designación de los ejes directo y cuadratura. Los ceros en u son los voltajes de las trayectorias cerradas de las corrientes parásitas en el rotor (devanados de amortiguamiento).

De la manipulación de las ecuaciones (8), con las corrientes como variables de estado se obtiene

donde A, B 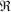^{((3+kd+lq)× (3+kd+lq))} y están definidas de la siguiente manera

 

Función de sensibilidad

Para el estudio de la sensibilidad paramétrica de un sistema dinámico debe asegurarse que tiene solución única y que se conoce la FS. En general, en los problemas prácticos, este análisis se complica si se intenta resolver la ecuación (6) para obtener la FS. La opción más viable es plantear un método aproximado tal como se expresa en la ecuación (7).

Para este trabajo, se parte del conocimiento de que el sistema (16) tiene solución única (López, 2005), y la FS se establece a partir de la dinámica de las corrientes i_d, i_q e i_f para una condición de cortocircuito en las terminales del GS. Estas corrientes son las que se utilizan en (López, 2005) para validar los modelos del GS. Entonces la FS queda expresada por

donde FS corresponde a la suma de las magnitudes de las corrientes producto de la solución de (16) para cada intervalo de tiempo t_k a lo largo de m particiones. El subíndice nom se refiere a que son las corrientes que se obtienen con los parámetros (nominales) identificados por Niewierowicz et al. (2003). Estos parámetros fueron identificados con una precisión de ±1×10^–6.

Una vez definida la FS y usando el concepto de sensibilidad relativa dada en (Frank, 1978), junto con la aproximación de (7), se pueden obtener los valores de las corrientes para cambios en cada uno de los parámetros del modelo utilizando la expresión

donde: P_j es el valor nominal del parámetro, cuyo impacto está siendo evaluado; ΔP_j es el cambio impuesto en su valor y ΔSF es la diferencia entre las curvas que describen las corrientes de cortocircuito

donde i_{cc_mod}(t_k) es la curva de cortocircuito obtenida de (16) con un cambio en el valor de P_j, mientras los valores de los demás parámetros del modelo se mantienen constantes. La variación de los parámetros para el análisis de sensibilidad se fijó en 1×10^–6, que corresponde a la precisión lograda en el proceso de identificación realizado por Niewierowicz et al. (2003).

La figura 4, muestra de forma esquemática, la cuantificación que la ecuación (20) hace de la diferencia entre las curvas de cortocircuito nominales (curva 1) y la obtenida para el cambio del valor de un parámetro (curva 2).

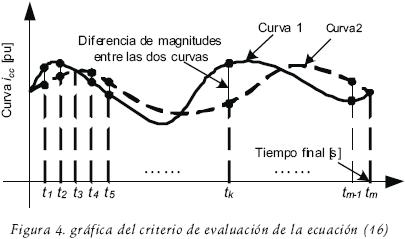
Las corrientes de cortocircuito se obtienen de la solución del sistema de ecuaciones de estado (16) mediante la función ode45 de MATLAB^® (Using matlab 6.0, 2000) basada en el método de Runge–Kutta de cuarto y quinto orden.

 

Resultados

Se analizaron los modelos de una a cinco ramas de amortiguamiento en el eje d y de una a cuatro en el eje q. En la figura 5 aparece la nomenclatura para cada parámetro.

Los parámetros del CE del eje d, cuyos valores se hicieron variar para el análisis de sensibilidad, son las inductancias diferenciales de dispersión (L_1kf, L_2kf, L_3kf, L_4kf, L_5kf), la inductancia de dispersión del devanado de campo (L_f), y las inductancias de dispersión y resistencias de los devanados de amortiguamiento (L_{1 d}, L_2d, L_3d, L_4d, L_5d, R_1d, R_2d, R_3d, R_4d y R_5d). Para el caso del eje q se incluyen las inductancias de dispersión y resistencias de las ramas de devanados amortiguamiento (L_1q, L_2q, L_3q, L_4q, R_1q, R_2q, R_3q, R_4q).

En las tablas 1 a 9,(2,3,4,5,6,7,8) aparecen los resultados obtenidos de la evaluación de la sensibilidad paramétrica. En la primera columna aparece el parámetro que impactó de manera más importante la respuesta del modelo de CE correspondiente (eje d o q), conforme se avanza a las siguientes columnas se va reduciendo la importancia del parámetro en la respuesta del modelo. Los parámetros que no aparecen en las tablas es porque su impacto en la respuesta del modelo fue prácticamente nulo (López, 2005).

Los resultados de la sensibilidad para los CE del eje d se presentan en las tablas 1, 2, 3, 4 y 5.

En estas tablas, puede observarse el nivel de importancia de cada parámetro en la respuesta del modelo del GS. Resulta interesante observar que las inductancias diferenciales aparecen entre los parámetros de alto nivel de impacto en el modelo. Por ejemplo, en los modelos de una hasta cuatro ramas de amortiguamiento, el parámetro de mayor importancia es precisamente la inductancia diferencia L_1kf.

Lo anterior coincide con las conclusiones del trabajo de Canay (1969 y 1993) y del estándar IEEE (Std 1110–2002) en donde no se ha dado una justificación sistematizada para explicar la importancia de cada parámetro. Sin embargo, es interesante ver que el orden de importancia de los parámetros es diferente en todos los modelos, es decir, los parámetros no tienen el mismo patrón de importancia.

Un resultado interesante es que el parámetro L_f sólo aparece como importante en dos modelos (una y dos ramas de amortiguamiento).

En las tablas 6 a 9 (7,8) se presentan el orden de importancia de los parámetros del CE en el eje q con hasta cuatro ramas de amortiguamiento.

Los resultados para los tres modelos del eje q, reportados en la tablas 7, 8 y 9, comparten la misma característica detectada en las tablas correspondientes al eje d con relación a las diferencias de los patrones de importancia de los parámetros en los CE de los diferentes modelos. Los parámetros tampoco tienen el mismo patrón de importancia dentro del mismo modelo para las tres corrientes analizadas.

 

Conclusiones

Las inductancias diferenciales de dispersión juegan un papel importante en la sensibilidad de los modelos para los CE en el eje d. Este es un resultado que coincide con las conclusiones del trabajo de Canay (1993), donde el análisis se llevó a cabo cualitativamente al inspeccionar/analizar oscilogramas de corrientes.

De manera más específica se pueden hacer conclusiones al respecto del nivel de importancia de algunos parámetros.

Por ejemplo, para los circuitos del eje d las inductancias diferenciales de dispersión más alejadas del devanado de campo aparecen como las más importantes.

También se encontró que, los órdenes de importancia que resultan para las resistencias e inductancias de dispersión de los devanados amortiguadores, y la inductancia de dispersión del devanado de campo, son distintos para todos los modelos e inclusive para la corriente considerada dentro del mismo modelo. Sólo existe correspondencia en el patrón de importancia cuando se comparan las corrientes i_d e i_f en los modelos para una y dos ramas de amortiguamiento en el eje d y para una rama en el eje q.

Las diferencias encontradas en los patrones de importancia de los parámetros en los modelos estudiados, permiten concluir que resulta necesario realizar otros estudios de sensibilidad paramétrica para tener mayor información de la importancia que los parámetros (resistencia e inductancias) tienen en los modelos del GS utilizados en otras condiciones de operación. Así, los resultados obtenidos muestran la necesidad de profundizar en el análisis de las diferencias encontradas en los órdenes de importancia. De la misma manera, resulta conveniente explorar las posibilidades de eliminar los parámetros que resultaron con un nivel de importancia casi nulo.

 

Referencias

Adkins B., Harley R.G. The General Theory of Alternating Current Machines. London. Chapman and Hall. 1975. Pp. 58–97.        [ Links ]

Anderson P.M., Fouad A.A. Power System Control and Stabilility. Second edition. New York. John Wiley. 2003.        [ Links ]

Arjona–L M.A. Parameter Calculation of a Turbogenerador During an Open–Circuit Transient Excitation. IEEE Transactions on Energy Conversion, 19(1):46–52. March 2004.        [ Links ]

Canay I.M. Causes of Discrepancies of Calculation of Rotor Quantities and Exact Equivalent Diagrams of the Synchronous Machine. IEEE Transactions on Power Apparatus and Systems, 88(7):1114–1120. July 1969.        [ Links ]

Canay I.M. Modelling of Alternating–Current Machines Having Multiple Rotor Circuits. IEEE Transactions on Energy Conversion, 8(2):280–296. June 1993.        [ Links ]

Escarela–Perez R., Macdonald D.C. A Novel Finite–Element Computation of Two–Axis Parameters of Solid Rotor Generators for Use in Power Systems. IEEE Transactions on Energy Conversion, 13(1):49–54. March 1998.        [ Links ]

Escarela–Perez R., Arjona M., Melgoza M., Campero E., Aviles C. A Comprehensive Finite Element Model of a Turbine–Generator Infinite–Busbar System. International Journal of Finite Elements in Analysis and Design (Elsevier Science Ltd.), 40(5–6):485–509. 2004.        [ Links ]

Frank–Paul M. Introduction to System Sensitivity Theory. New York. Academic Press. 1978. Pp.314.        [ Links ]

Grainger J., Stevenson W.D Jr. Análisis de sistemas de potencia. Mc Graw Hill. 1996.        [ Links ]

IEEE Std. 115–1995. IEEE Guide: Test Procedures for Synchronous Machines.        [ Links ]

IEEE Std. 1110–2002. IEEE Guide for Synchronous Generator Modeling Practices and Applications in Power System Stability Analyses. Pp. 10–15.        [ Links ]

Khalil H.K. Nonlinear Systems. Third edition. Prentice–Hall. 2002. Pp. 99–102.        [ Links ]

Kamwa I., Wankeve R., Dai–Do X., General Approaches to Efficient d–q Simulation and Model Translation for Synchronous Machines: a Recap. Electric Power Systems Research 8Elsevier Ltd),42(3):173–180. 1997.        [ Links ]

Kundur P. Power System Stability and Control. Mc Graw Hill. 1994. Pp. 67–92, 169–191.        [ Links ]

López–García I. Estudio estructural y de sensibilidad paramétrica de circuitos equivalentes en dos ejes para un turbogenerador. Tesis (Maestría). México. Sección de Estudios de Posgrado e Investigación del Instituto Politécnico Nacional, Unidad Zacatenco. Mayo de 2005.        [ Links ]

Niewierowicz T., Escarela–Perez R., Campero–Littlewood E. Hybrid Genetic Algorithm for the Identification of High–Order Synchronous Machine Two–Axis Equivalent Circuits. International Journal of Computers and Electrical Engineering (Pergamon, Elsevier Science Ltd), 29(4):505–522.2003.        [ Links ]

The Mathworks, Inc. Using matlab version 6.0. November 2000. (COPYRIGH|T 1984–2000 by The MathWorks, Inc).        [ Links ]

 

Semblanza de los autores

Irvin López–García. Obtuvo el grado de ingeniero electricista en la UAM–Azcapotzalco en 2002, la maestría en la ESIME del Instituto Politécnico Nacional, Zacatenco en 2005. Actualmente estudia el doctorado en la Facultad de Ingeniería de la UNAM en el área de control. Está interesado en el modelado, análisis y control de máquinas eléctricas.

Rafael Escarela–Pérez. En 1992, obtuvo el grado de ingeniero electricista por la UAM–Azcapotzalco. En 1996, el doctorado en el Imperial Collage de la Universidad de Londres. En 1996, ingresó como profesor de tiempo completo en la UAM–Azcapotzalco, donde es profesor Titular "C" desde 2000. Es miembro del Sistema Nacional de Investigadores (Nivel II). Sus áreas de interés en investigación son el análisis numérico y experimental de máquinas eléctricas.

Tadeusz Niewierowicz–Swiecicka. Realizó la licenciatura y la maestría en ingeniería eléctrica en el Instituto Electrotécnico en Leningrado, USSR, en 1965. Obtuvo el grado de doctor en el Instituto Politécnico en Lodz, Polonia, en 1974. Es miembro del Sistema Nacional de Investigadores (Nivel I). Sus áreas de interés son el control óptimo y adaptable de procesos industriales y aplicación de computadoras en control y diseño técnico.

Eduardo Campero–Littlewood. En 1969 obtuvo el grado de ingeniero mecánico electricista por la Facultad de Ingeniería de la UNAM. Trabajó en la industria hasta 1975, año en el que inició sus estudios de maestría en el Imperial College de la Universidad de Londres. En 1977, ingresó como profesor de tiempo completo en la UAM–Azcapotzalco, en donde es profesor Titular "C" desde 1991. Sus principales áreas de interés en investigación son: máquinas eléctricas y uso eficiente de la energía.