Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.10 no.3 Ciudad de México jul./sep. 2009
Predicción numérica del tamaño y forma de una llama en un quemador elevado dentro de un flujo cruzado de aire
Numerical Prediction for the Size and Shape of a Flare in a Cross–Wind
W. Vicente y Rodríguez1, M. Salinas–Vázquez2, J.E. Barrios–Bonilla3 y E.R. Barrera–Avendaño4
1 Coordinación de Ingeniería de Procesos Industriales y Ambientales. Instituto de Ingeniería, Universidad Nacional Autónoma de México. E–mail: wvicenter@ii.unam.mx
2 Coordinación de Ingeniería de Procesos Industriales y Ambientales. Instituto de Ingeniería, Universidad Nacional Autónoma de México. E–mail: msalinasv@ii.unam.mx
3 Departamento de Termoenergía y Mejoramiento Ambiental Facultad de Ingeniería, Universidad Nacional Autónoma de México E–mail: besteban@servidor.unam.mx
4 Coordinación de Ingeniería de Procesos Industriales y Ambientales. Instituto de Ingeniería, Universidad Nacional Autónoma de México. E–mail: erikraymundo.barrera@halliburton.com
Recibido: abril de 2007
Aceptado: septiembre de 2008
Resumen
Un modelo de dinámica de fluidos computacional es utilizado para simular la combustión turbulenta en un quemador elevado dentro de un flujo cruzado de aire. La investigación está enfocada, principalmente, en el estudio de la influencia de la velocidad del flujo cruzado en parámetros aerodinámicos de la llama. La simulación del flujo es tridimensional y en coordenadas cartesianas. Para simular la combustión es usado un modelo de química rápida con un paso de reacción irreversible para formar CO2 y H2O. Un modelo de radiación es usado para identificar la trayectoria media de la llama. La configuración simulada consiste en una descarga de propano expuesta a una corriente de aire, la cual proporciona el oxigeno para que se lleve a cabo la combustión. La velocidad de este flujo cruzado se modifica desde 0.8 m/s hasta 12 m/s. Comparaciones con datos experimentales muestran que las predicciones, en términos de la longitud de llama y el ángulo de deflexión, se predicen adecuadamente.
Descriptores: Mecheros elevados, CFD, combustión, propano, radiación, flujo cruzado.
Abstract
A computational fluid–dynamics model is used to simulate the turbulent combustion in a flare exposed to a cross–wind. Our research is mostly focused on the cross flow velocity influence to flame aerodynamics. The flow simulation is performed as three dimensional along a Cartesian coordinates system. In order to simulate the combustion process, a fast–chemistry model with a 1–step global irreversible reaction to form CO2 and H2O is used. A radiation model is used to identify the mean flame trajectory. The simulated configuration consists in a propane discharge into an air stream, get ting oxygen supply from the cross–wind. The velocity of this cross–flow is increased from 0.8 m/s to 12 m/s. Comparative analysis of our predicted values with respect to available experimental results shows good agreement in terms of flame length as well as inclination angles.
Keywords: Flare, CFD, combustion, propane, radiation, flame, cross flow.
Introducción
Distintas ramas de la industria hacen uso de mecheros elevados para quemar gases que no se pueden recuperar, provenientes de la evaporación de combustibles en tanques de almacenamiento, o que son gases residuales provenientes de procesos petroquímicos o químicos.
Por razones de seguridad, estos gases son descargados a la atmósfera para evitar su acumulación, que eventualmente puede ser tóxica o explosiva. Sin embargo, el riesgo para el entorno puede ser igualmente grande. Por estas razones, los gases deben ser quemados antes de ser descargados al medio ambiente. Este proceso se cumple con el uso de los ya mencionados mecheros industriales.
La combustión de gases en estas circunstancias es estocástica, debido a las condiciones climatológicas a las que son expuestas las llamas producidas. Entre las principales contingencias está el viento cruzado, que puede ser la razón de la inestabilidad y enfriamiento de la llama. Estas últimas contingencias pueden ser causa de eventos indeseables que van desde la combustión incompleta hasta la extinción de la llama.
Por las circunstancias bajo las cuales estos gases son manejados, las llamas que se producen en estos mecheros son generalmente del tipo difusivas o premezcladas con bajas concentraciones de aire, en ambos casos, la estabilidad de la flama es importante.
La información publicada se concentra principal mente en experimentos de laboratorio (Brzutowski, 1976; Kalghatgi, 1983 y Majeski et al., 1999), debido a la dificultad que se presenta al tratar de medir en campo la calidad de las emisiones en estos mecheros, sometidos a condiciones climatológicas bajo las que funcionan normalmente y dificultando la recolección de muestras de los gases de combustión de manera realista. Por este motivo, los estudios se restringen, principalmente, al estudio de modelos a escala o a simulaciones numéricas de configuraciones sencillas (Castiñeira y Edgar, 2006). Siendo esta última alternativa el enfoque de este trabajo.
El objetivo de este trabajo se enfoca principalmente en la predicción de parámetros aerodinámicos de la llama en un flujo cruzado, tales como longitud y forma de la misma. La razón principal para estar interesados en estos parámetros es el diseño seguro y eficiente de los sitios de los quemadores, ya que excesivos niveles de radiación térmica de la llama hacia la superficie del suelo y la posibilidad de la llama de pegarse a la estructura del quemador son consideraciones importantes en el desarrollo de un diseño seguro del sistema.
Por lo anterior, se requiere establecer un método que permita predecir confiablemente la dependencia de tamaño y trayectoria de la llama a partir de variables como composición del gas combustible y su velocidad de descarga; así como la velocidad del flujo cruzado.
En este trabajo se simula una llama de propano en flujo cruzado, para la cual existen datos experimentales (Majeski et al., 1999). La simulación se hace mediante la alternativa de Ecuaciones Promediadas de Navier–Stokes (Reynolds o Favre Averaged Navier–Stokes Equa tions, RANS). El término de convección turbulenta, resultado del promediado de las ecuaciones, se representa mediante el modelo de turbulencia k–s (Launder y Spalding, 1972). La combustión se simula con un modelo de química rápida con un paso de reacción (Spalding, 1979). Debido a la diferencia de densidades, se incluye el término de las fuerzas de cuerpo gravitacionales. Para discretizar el dominio se utiliza una malla en coordenadas cartesianas en 3 dimensiones. La trayectoria media de la llama se define mediante un modelo de radiación. La solución de estas ecuaciones se lleva a cabo mediante un método de volúmenes finitos. Comparaciones entre predicciones y datos numéricos, muestran que la llama se predice adecuadamente.
Configuración experimental
El caso simulado es una llama turbulenta de propano expuesta a una corriente horizontal de aire, flujo cruzado, que se estudió experimentalmente por Majeski et al. (1999). La geometría considerada es un chorro vertical de combustible, liberado de un tubo de descarga y colocado en un flujo cruzado. El tubo circular tiene un diámetro exterior e interior de 24.7 y 22.1 mm, respectivamente, y una altura variable entre 25 y 78 cm. La altura variable del tubo es permitida para ser posicionado dentro de la velocidad uniforme del túnel sin que la capa límite del piso y del techo afecten la llama. La velocidad del propano es de 1 m/s y el rango de velocidades del flujo cruzado es de 0.8 m/s a 12.0 m/s. Un diagrama esquemático de la configuración experimental se presenta en la Figura 1. El experimento se realizó en un túnel de viento con una sección transversal de prueba de 1.2 m de alto por 2. 4 m de ancho. En un lado del túnel se tiene una ventana de vidrio (0.91m x 2.1m) para permitir una visualización de la llama aguas abajo de la salida del chorro.

La llama luminosa fue filmada por una video cámara para obtener imágenes instantáneas de la misma. De estas imágenes instantáneas, previo procesamiento, se sacaron imágenes medias, las cuales se utilizaron para determinar las características medias de la llama, que en este caso son: longitud y el ángulo de deflexión.
Modelo numérico
En esta sección se presentan los modelos y submodelos de la aerodinámica y combustión, así como los detalles numéricos que se utilizaron para simular la llama en un flujo cruzado. También se muestra el modelo de radiación que se utilizó para comparar las predicciones con los datos experimentales.
Aerodinámica
Para estudiar la aerodinámica tanto del flujo de la llama como del aire a su alrededor se necesitan resolver numéricamente las ecuaciones de transporte en su forma diferencial de la conservación de masa (ecuación de continuidad), de cantidad de movimiento (2ª ley de Newton) y de energía (Primera Ley de la Termodinámica). Aplicando promedios de Favre,  que se basan en tomar como función de peso a la densidad, se obtienen las ecuaciones de transporte antes mencionadas:
que se basan en tomar como función de peso a la densidad, se obtienen las ecuaciones de transporte antes mencionadas:


donde  y ρ son, respectivamente, la velocidad y la densidad media de la mezcla reactiva, p es la presión, g es la aceleración de la gravedad, h es la entalpia, µ la viscosidad molecular de la mezcla, y
y ρ son, respectivamente, la velocidad y la densidad media de la mezcla reactiva, p es la presión, g es la aceleración de la gravedad, h es la entalpia, µ la viscosidad molecular de la mezcla, y  es el tensor delta de Kronecker. Los términos con el número romano I, se refieren a los términos difusivos moleculares. Esto es, difusión debida a las propiedades del fluido. El flujo de calor se obtiene a partir de la ley de Fourier:
es el tensor delta de Kronecker. Los términos con el número romano I, se refieren a los términos difusivos moleculares. Esto es, difusión debida a las propiedades del fluido. El flujo de calor se obtiene a partir de la ley de Fourier:

donde k es la conductividad térmica del flujo. Los términos adicionales (ρνi''/h'',ρνi'' νi,") que involucran a las fluctuaciones de las variables, no son conocidos a priori y representa físicamente el transporte convectivo turbulento de energía y de cantidad de movimiento respectivamente. A partir de la aproximación de Boussinesq, que considera que estos términos pueden ser expresados en función de las derivadas de las variables pro mediadas y de una viscosidad turbulenta, que es función del flujo y no del fluido, estos términos se pueden conocer. El problema se simplifica simplemente en encontrar esta viscosidad turbulenta; para lo cual se requiere un modelo turbulencia que permita encontrarla y así cerrar el sistema de ecuaciones. En el presente trabajo se utilizó un modelo de turbulencia del tipo k–s (Launder y Spalding, 1972). Finalmente, en las ecuaciones de cantidad de movimiento es incluido el término fuente de fuerzas de cuerpo gravitacionales, dado que en el flujo se presentan cambios en la densidad. Los efectos de las pérdidas por radiación no son incluidos en la ecuación energía. Las ecuaciones de la aerodinámica son resueltas usando un método de volúmenes finitos, con un algoritmo del tipo SIMPLE (Patankar y Spalding, 1972) para resolver el acoplamiento presión–velocidad.
Modelo de combustión
La combustión de la llama se simula con un modelo de reacción química sencilla (Spalding, 1979), que postula que la combustión se produce mediante la reacción irreversible:
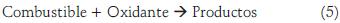
donde los productos que se forman son CO2 y H2O. Adicionalmente, el modelo supone: a) que la reacción química es infinitamente rápida, b) que los coeficientes de intercambio de masa son iguales para todas las especies y para la energía y c) que los reactantes no pueden existir en el mismo lugar y tiempo.
Una consecuencia de estas suposiciones es que con la fracción másica de combustible, Ycomb, y la de mezcla, f, permiten describir la composición de la mezcla reactante. La fracción de mezcla se define como la masa del material proveniente de la corriente del combustible, por unidad de masa de la mezcla, sin considerar si está quemada o no. Una expresión para f es (Spalding, 1979)

donde s es la relación aire y combustible de la mezcla reactiva y Yprod es la fracción másica de los productos. En llamas no premezcladas o difusivas (flujo de combustible y aire están separados), como la analizada en este trabajo, se usa la simplificación adicional que considera la reacción infinitamente rápida e ignora totalmente la tasa cinética de reacción. Si se usa esta aproximación, solamente se requiere conocer la fracción de mezcla para describir la composición de la mezcla de gases. Las relaciones entre la fracción de mezcla, f y la fracción másica de combustible, de oxidante y de productos son (Spalding, 1979):

donde Ycomb es la fracción másica del combustible, Yoxid es la fracción másica del oxidante, Yprod es la fracción másica de los productos (CO2 y H2O), f es la fracción de mezcla de la llama y festeq es la fracción de mezcla estequiométrica e igual a f=1(1+sesteq); donde sesteq , es la relación aire y combustible para proporciones estequiométricas.
La fracción de mezcla local, f, se conoce mediante la resolución de una ecuación del tipo:

donde  es la media del vector velocidad, p es la densidad media, Sc y σ, son los números de Schmidt laminar y turbulento, respectivamente, y µ y µ T es la viscosidad laminar y turbulenta, respectivamente. Para el cálculo de µT se usa el modelo de turbulencia k–ε (Launder y Spalding, 1972) usado en la aerodinámica.
es la media del vector velocidad, p es la densidad media, Sc y σ, son los números de Schmidt laminar y turbulento, respectivamente, y µ y µ T es la viscosidad laminar y turbulenta, respectivamente. Para el cálculo de µT se usa el modelo de turbulencia k–ε (Launder y Spalding, 1972) usado en la aerodinámica.
La fracción de mezcla es una propiedad conservativa, es decir, no reacciona, motivo por el cual la ecuación (10) está igualada a cero. Esta variable toma valores de 0 y 1 cuando el fluido es aire y combustible puros, respectivamente.
La densidad media de la mezcla se calcula como:

donde p es la presión media, Rc es la constante universal de los gases,  es la temperatura media de la mezcla,
es la temperatura media de la mezcla,  y Wα es la fracción másica media y peso molecular de las especies químicas α que componen la mezcla. La temperatura media se calcula como:
y Wα es la fracción másica media y peso molecular de las especies químicas α que componen la mezcla. La temperatura media se calcula como:

donde  es la entalpía media de la mezcla, H es el calor de combustión, y Cp es el calor específico a presión constante de la mezcla, que se calcula con el calor específico a presión constante de las especies individuales.
es la entalpía media de la mezcla, H es el calor de combustión, y Cp es el calor específico a presión constante de la mezcla, que se calcula con el calor específico a presión constante de las especies individuales.
Modelo de radiación
Los parámetros experimentales son obtenidos a partir de mediciones de luminosidad, que indican la presencia de la llama, por lo que la comparación con sus correspondientes parámetros numéricos puede resultar complicada, ya que el único parámetro que indica la presencia de la llama en los cálculos es la temperatura. Sin embargo, parte de los contornos de temperatura corresponden a gases calientes no visibles.
En este trabajo se propone calcular la presencia de la llama a partir de su energía radiante. El modelo que se usa en este trabajo calcula la radiación a partir de especies "luminosas" como el CO2 y H2O.
En este modelo de radiación se considera la hipótesis de llama ópticamente delgada (absorción del gas despreciable) y se desprecia el efecto de la dispersión. Por lo tanto, el flujo de calor por radiación se puede escribir como (Siegel y Howell, 1981; Chen et al., 1993):

donde σ es la constante de Stefan–Boltzmann (5.67x10–8 Wm–2K–4) y Kp es el coeficiente de absorción medio de Planck. El coeficiente Kp es (Chen et al., 1993):

donde Kp,CO2 y K p,H2O son los coeficientes de absorción del CO2 y H22O, que se pueden encontrar en Chen et al. (1993).
Detalles numéricos
La simulación de la llama se hace en tres dimensiones, usando mallas en coordenadas cartesianas para la discretización del sistema. Con fines de ahorro en memoria y tiempo de cálculo, el dominio de la simulación es la mitad del quemador en la sección transversal. El dominio de cálculo se discretiza con una malla de 165x90x190 en las direcciones x, y, y z, respectivamente. Un mayor número de celdas es usado ( 4000000) para verificar la independencia de las predicciones numéricas con el tamaño de malla.
4000000) para verificar la independencia de las predicciones numéricas con el tamaño de malla.
La discretización del término convectivo de las ecuaciones de transporte se hace con el esquema de discretización híbrido (Spalding, 1972). La velocidad de salida del combustible se coloca en 1 m/s y la velocidad del flujo cruzado vario desde 0.8 m/s has ta 12 m/s. En el flujo de combustible f=1.0 y en el flujo de aire f=0.0.
Resultados y discusiones
En esta sección se presentan comparaciones entre las predicciones y datos experimentales, en donde éstos están disponibles. Primero cualitativamente y después cuantitativamente, en términos de longitud y ángulo de deflexión de la llama. Estas cantidades se presentan en la figura 3.
Las simulaciones se enfocaron para un velocidad de salida del combustible de 1.0 m/s y para un rango de velocidades en el aire, flujo cruzado, de 0.8 a 12.0 m/s.
Al igual que lo estable ce Majeski et al. (1999), las formas de las llamas sugieren 3 distintos tipos de trayectorias. Estas 3 formas de trayectoria pueden ser observadas para velocidades en el flujo cruzado de 0.8 m/s, 2.0 m/s y 3.5 m/s. Estas trayectorias son mostradas en las figuras 2, 3, 4. La forma de las trayectorias es el resultado del equilibrio entre las fuerzas de flotación y cantidad de movimiento, tanto de la llama como del flujo cruzado. El aire que ingresa a la llama produce la combustión del propano y un intercambio en la cantidad de movimiento entre los 2 flujos. La combustión producida genera gases calientes, que tienen una menor densidad que la del aire del flujo cruzado, lo que resulta en una fuerza de flotación ascendente. Para que se genere la combustión del propano, éste debe de mezclarse con el aire en aproximadamente una relación de 1 a 17.
En velocidades de flujo cruzado bajas o en relaciones de velocidad Vj/V∞ mayores a 1.25 (donde Vj es la velocidad de salida de la descarga de propano y U∞ es la velocidad del flujo cruzado), la llama está completamente arriba del tubo de descarga del combustible con una cur vatura hacia arriba como resultado del dominio de las fuerzas de flotación sobre la cantidad de movimiento del flujo cruzado. Si la velocidad del aire se incrementa (es decir, Vj/V∞< 0.5) la trayectoria se curva hacia arriba y después tiende a ser paralela a la dirección del flujo cruzado, debido a que en este extremo de la llama las fuerzas de flotación no son lo suficientemente capaces para continuar con la tendencia hacia arriba. La base de esta llama es atrapada en la zona de la estela, que se localiza en la parte posterior del tubo de descarga. Las fuerzas de flotación de los gases productos de la combustión generados en la zona de recirculación van a producir que la trayectoria de la llama tienda hacia arriba, después de que los mismos salgan de esta zona. Si la velocidad del flujo cruzado se continúa incrementando (relaciones de velocidad Vj/V∞< 0.29), la región de recirculación atrapa más flujo de combustible, el cual es quemado en la misma zona. En estas condiciones, la cantidad de movimiento del flujo cruzado predomina sobre las fuerzas de flotación de la llama, que provoca que ésta permanezca prácticamente horizontal. En los tres distintos casos, las trayectorias simuladas de la llama (Figuras 2b, 3b, y 4b), presentan un comportamiento similar a su correspondiente parte experimental.
Para mostrar la acción de las fuerzas de flotación e inerciales que actúan en el fluido se grafica: Gr/Re2, donde Gr es el número de Grashof y Re es el número de Reynolds, en el centro de la llama para el caso de 2 m /s en el flujo cruzado de aire (figura 5). Este término adimensional es proporcional al cociente entre las fuerzas de flotación y las fuerzas inerciales que actúan en el fluido. El comportamiento mostrado en la figura 5 confirma lo anteriormente expuesto con relación a estas fuerzas presentes en la llama.
La longitud media de la llama como función de la relación de velocidades Vj/VK se muestra en la figura 6. Al aumentar la velocidad del flujo cruzado desde una condición próxima al reposo se produce un incremento en la longitud de la llama hasta llegar a un máximo en aproximadamente Vj/V∞  0.2.
0.2.

Después, si se continúa incrementando esta velocidad, la longitud de la llama disminuye. Este comportamiento se puede deber a que conforme se incrementa la velocidad del flujo cruzado, se generan, con mayor intensidad, 2 vórtices medios en el interior de la llama, los cuales introducen aire circundante de la parte posterior de la misma hacia su interior (Vicente et al., 2008). Parte de este aire arrastrado es utilizado en la combustión. Sin embargo, si la tasa de entrada de este aire es muy grande se puede producir un enfriamiento y/o extinción de la llama. Un a consecuencia de lo anterior es la disminución en tamaño de la llama. Las predicciones son mostradas en la misma figura 6, el comportamiento es simular al mostrado por los datos experimentales. Las diferencias se pueden deber, al estado no estacionario asociado a todo flujo turbulento, que la aproximación de ecuaciones promediadas no representa del todo bien. Adicionalmente, el fenómeno complejo de la combustión se está representando mediante un modelo sencillo de 1 paso de reacción. También, para el modelo de radiación, no es considerada la formación de hollín, que es el causante de la visibilidad de la llama.
En la figura 7 se presenta el ángulo de deflexión medio de la llama como función de la relación de velocidades Vj/V∞. Este ángulo es medido con respecto a la vertical como se muestra en la figura 3. Un incremento monótono en el ángulo de la llama se produce cuando se incrementa la velocidad en el flujo cruzado.

A diferencia de la figura 6, en esta gráfica no se presenta una transición brusca entre los casos en los cuales las llamas están por arriba del tubo de descarga y dentro de la zona de recirculación que se genera después del mismo. Comparaciones entre datos experimentales y predicciones muestran que este parámetro se predice adecuadamente.
Conclusiones
En este trabajo se ha simulado numéricamente la combustión de una llama de propano dentro de un flujo de aire cruzado, el cual representa la combustión de gases, cuyo aprovechamiento resultaría poco factible en un mechero elevado. El modelo utilizado se basa en un modelo de Dinámica de Fluidos Computacional. La combustión se representa mediante un modelo de química rápida de un paso de reacción. para comparar predicciones con datos de la llama obtenidos a partir de medidas luminosidad se usa un modelo de radiación.
El equilibrio entre las fuerzas de flotación y cantidad de movimiento producen, básicamente, 3 tipos de trayectorias en las llamas. En velocidades del flujo cruzado bajas, la llama es posicionada completamente arriba del tubo de salida del combustible y la llama se curva hacia arriba. Si se incrementa la velocidad del flujo cruzado, la zona de recirculación atrapa parte de la corriente del combustible, lo que produce que inicialmente la curvatura de la llama baje y después suba. Si se continúa con el incremento en la velocidad del aire, la trayectoria de la llama tiende a ser prácticamente horizontal y a disminuir de tamaño. La longitud de la llama alcanza un máximo en Vj/V∞ 0.2 y después disminuye. Este comportamiento se debe a la intensidad con la cual los vórtices ingresan el aire, el cual proporciona el oxígeno necesario para la combustión. Si la cantidad de aire que ingresa a la llama es muy grande, se puede causar enfriamiento y/o extinción de la misma, produciendo una disminución en su tamaño. Adicionalmente, a este efecto, la cantidad de movimiento del flujo cruzado torna la llama prácticamente horizontal.
0.2 y después disminuye. Este comportamiento se debe a la intensidad con la cual los vórtices ingresan el aire, el cual proporciona el oxígeno necesario para la combustión. Si la cantidad de aire que ingresa a la llama es muy grande, se puede causar enfriamiento y/o extinción de la misma, produciendo una disminución en su tamaño. Adicionalmente, a este efecto, la cantidad de movimiento del flujo cruzado torna la llama prácticamente horizontal.
Comparaciones con datos experimentales en términos de la longitud y ángulo de deflexión medios de la llama muestran que el flujo se predice adecuadamente.
Agradecimientos
Se agradece a la Dirección General de Asuntos del Personal Académico de la UNAM por el apoyo recibido a través del proyecto PAPIT–IN109106–3.
Referencias
Brzustowski T.A. Flaring in the Energy Industry. Progress in Energy and Combustion Science, 2:129–141. 1976. [ Links ]
Castiñeira D., Edgar T.F. CFD for Simulation of Steam–Assisted and Air–Assisted Flare Combustion Systems. Energy and Fuels, 20(3): 1044–1056. 2006. [ Links ]
Chen J.Y., Liu Y., Rogg B. CO–H2–N2/Air Diffusion Flames: Thermal Radiation and Transfer Effects. Lecture Notes in Physics, m15. Berlin. Springer–Verlag. 1993. [ Links ]
Kalghatgi G.T. The Visible Shape and Size of a Turbulent Hydrocarbon Jet Diffusion Flame in a Cross–Wind. Combustion and Flame, 52:91–106. 1983. [ Links ]
Launder B.E. and Spalding D.B. Lectures in Mathematical Models of Turbulence. Academic Press. 1972. [ Links ]
Majeski A.J., Wilson D.J., Kostiuk L. W. Size and Trajectory of a Flare in a Cross Flow. En: Combustion Canada, Alberta, May 1999, pp. 26–28. [ Links ]
Siegel R., Howell J.R. Thermal Radiation Heat Transfer. 2nd edition. Washington. McGraw–Hill. 1981. [ Links ]
Spalding D.B. Combustion and Mass Transfer. Pergamon Press. 1979. [ Links ]
Vicente W., Salinas M., Barrios E., Kostiuk L.W. Numerical Analysis of Mean Flame in a Flare in a Cross Flow. Fire Safety Journal, 2008. En revisión. [ Links ]
Bibliografía sugerida
Gollahalli S.R., Brzustows ki T.A., Sullivan H.F. Characteristics of a Turbulent Propane Diffusion Flame in a Cross–Wind. Transactions of the CSME, 3:205–214. 1975. [ Links ]
Patankar S.V., Spalding D. B. A Calculation Procedure for Heat, Mass and Momentum Transfer in Three Dimensional Parabolic Flows. Int. J. Heat and Mass Transfer, 15:1787–1806. 1972. [ Links ]
Spalding D. B. A Novel Finite–Difference Formulation for Differential Expressions Involving Both First and Second Derivatives. Int. Journal Num. Methods Engineering, 4:551. 1972. [ Links ]
Semblanza de los autores
William Vicente y Rodríguez. Se graduó como ingeniero mecánico electricista en 1991, y en 1994, de maestro en ingeniería energética por la Facultad de Ingeniería, UNAM. Obtuvo en el año 2000 el grado de doctor en mecánica de fluidos por la Universidad de Zaragoza, España. Actualmente es investigador titular "A" del Instituto de Ingeniería de la UNAM e investigador nacional nivel I. Sus áreas de trabajo son: Dinámica de fluidos computacional, combustión y turbulencia.
Martín Salinas–Vázquez. Se graduó como ingeniero mecánico electricista en 1994, y en 1996, obtuvo la maestría en ingeniería mecánica, ambas por la Facultad de Ingeniería, UNAM. Asimismo, en 1999 logró el doctorado en Mécanique des Fluides et Transfer por el Instituto Politécnico de Grenoble, Francia. Realizó un postdoctorado en el Centro Nacional de Estudios Espaciales (CNES), Francia. Actualmente es investigador titular del Instituto de Ingeniería de la UNAM e investigador nacional nivel I. Es profesor de diversas asignaturas en la licenciatura de ingeniería mecánica, área de termo fluidos, así como de las maestrías en energía e ingeniería mecánica en la UNAM.
José Esteban Barrios–Bonilla. Ingeniero en energía por la UAM. Maestro en ingeniería por la UNAM. Estancia de investigación por dos años en Lehigh University, Pensilvania EEUU. Tiene 29 años de experiencia en investigaciones relacionadas con la combustión y la contaminación atmosférica, así como en el Departamento de Energía de EEUU (DOE) para el uso racional de la energía. Desde 1990, es profesor titular en la Facultad de Ingeniería de la UNAM. Asimismo, fue investigador en el Instituto de Investigaciones Eléctricas y en el Energy Research Center, Lehigh Univer sity.
Erick Raymundo Barrera–Avendaño. Se graduó como ingeniero mecánico en 2007 por la Facultad de Ingeniería, UNAM. Actualmente trabaja para Halliburton, en donde desempeña funciones como ingeniero de campo en el área de Frac/Acid Services.














