Structural Reliability Analysis of Limit State Functions With Multiple Design Points Using Evolutionary Strategies

 

Análisis de confiabilidad estructural de funciones de estado límite con múltiples puntos de diseño usando estrategias evolutivas

 

F. Barranco–Cicilia¹, E. Castro–Prates de Lima² y L.V. Sudati–Sagrilo³

 

¹ Mexican Petroleum Institute, Research Program on Exploitation of Oil Fields in Deepwater, México DF. E–mail: fbarran@imp.mx

² COPPE–Federal University of Rio de Janeiro, Civil Engineering Department, Cidade Universitária, Centro de Tecnologia, Brazil. E–mail: edison@coc.ufrj.br

³ COPPE–Federal University of Rio de Janeiro, Civil Engineering Department, Cidade Universitária, Centro de Tecnologia, Brazil. E–mail: sagrilo@coc.ufrj.br

 

Recibido: abril de 2006
Reevaluado: febrero de 2007
Aceptado: agosto de 2008

 

Abstract

The complete identification of all relevant design points is of paramount importance for the reliability analysis of real structures. In this paper a methodology based on Evolutionary Strategies (ES) algorithm is proposed to perform structural reliability analysis of limit state functions with multiple design points. A multidimensional optimization method using ES is first used to obtain a preliminary mapping of the relevant design points (local maxima). The approximate coordinates of these points are employed as initial guesses in the HL–RF (Hasofer and Lind–Rackwitz and Fiessler) algorithm when the First Order Reliability Method (FORM) for series systems is used to evaluate the system probability of failure. These points are also employed as the central points when Monte Carlo Simulation with Importance Sampling (MCIS) method is employed in the structural reliability evaluation. Numerical applications show the feasibility and the robustness of the proposed methodology.

Keywords: System reliability analysis, multiple design points, evolutionary strategies, FORM, Monte Carlo simulation, importance sampling.

 

Resumen

La identificación de todos los puntos de diseño es de suma importancia en el análisis de confiabilidad de estructuras reales. En este artículo se propone una metodología basada en el algoritmo numérico de las Estrategias Evolutivas (ES) para llevar a cabo el análisis de confiabilidad estructural de funciones de estado límite con múltiples puntos de diseño. Inicialmente, un método de optimización multidimensional utilizando ES se aplica para obtener la posición aproximada de los puntos de diseño (máximos locales). Las coordenadas de estos puntos son utilizados como puntos de partida en el bien conocido algoritmo HL–RF (Hasofer y Lind – Rackwitz y Fiessler) para obtener la probabilidad de falla del sistema con el Método de confiabilidad de Primer Orden (FORM). Estos puntos también son utilizados como los centros para la evaluación de la probabilidad de falla a través del método de simulación numérica Monte Carlo con muestreo por importancia (MCIS). Diversas aplicaciones numéricas muestran la versatilidad y la precisión de la metodología propuesta.

Desciptores: Análisis de confiabilidad de sistemas, múltiples puntos de diseño, estrategias evolutivas, FORM, simulación Monte Carlo, muestreo por importancia.

 

Introduction

Randomness in loads, resistances and analytical models, causes the existence of a probability that structures do not meet the code standards used for their design. This probability is known as probability of failure (pf) and it can be evaluated mathematically through the next multiple integral:

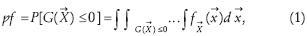
where is the joint Probability Density Function (PDF) of the n basic random variables X ={X₁X₂,...,X_n}^T in to the limit state function . The limit state function is defined in such way that =0 separates the failure ((<0) and safe (>0) domains.

Evaluation of equation (1) is not an easy task because it involves an n–fold integral over a complex domain. Various simulation–based and analytical methods have been proposed to deal with this problem. An approximation to pf can be obtained by analytical techniques such as First or Second Order Reliability Methods (FORM or SORM). The main idea of these methods is to move the reliability problem from the space of the basic random variables X to the space of standard normal statistically independent random variables using a suitable transformation , such as Rosemblatt or Nataf transformations (Melchers, 2001). In the space, equation (1) can be expressed as:

where is the marginal PDF of a standard normal random variable U_i.

In FORM an approximation to the probability of failure is obtained by making the failure surface =0 linear at the design point *. This is the point on the failure surface closest to the origin and with the highest probability (local maximum) in the failure domain of the standard normal space. The distance from the origin to the design point is the well–known reliability index p = *. Using the reliability index, pf is evaluated as:

where Φ(.) is the Cumulative Probability Function (CPF) of a standard normal random variable.

Generally, the FORM approximation gives a reasonable result for a limit state function with only one global design point. However, this is not the case when there are other local design points on the failure surface. A failure function with two design points is shown in figure 1. In this case, both design points have important contributions to the total system probability of failure and significant errors will be induced in it if one of them is missing. Unfortunately, the optimization algorithms used in connection with FORM, such as HL–RF approach, are only able to identify just one design point wit hout giving any further information about the possibility of remaining design points. Multiple design points are also found in structural series system problems where the global structural failure occurs when at least one of various limit states is violated (Melchers, 2001).

Monte Carlo simulation methods have also been largely employed to structural reliability analysis. In these methods N_S samples , i = 1,...N_S, are generated according with

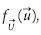
and then it is verified if the structure fails or not for each one of them. The pf is estimated as the number of failures divided by N_S. Since Monte Carlo method is basically a sampling process, the results are subjected to sampling error that decreases with the sample size. However, using procedures known as variance reduction techniques the error may be reduced wit hout increasing the sample size. One of such procedures with a high convergence rate is the Monte Carlo with Importance Sampling (MCIS) (Melchers, 2001). In MCIS, the regions of inte rest for the simulation process are those around the points in the failure domain having the largest values for

Over the last years some few research studies on procedures for searching multiple design points have been published. For instance, Der Kiureghian et al. (1998) presented an heuristic method, based on the HL–RF algorithm, for the systematic identification of multiple design points. In that method, each time that one design point is identified, the failure surface is de formed around this point through a bulge and the HL–RF method is reinitialized in order to search for another possible remaining design point. On the other hand, in the field of nonlinear optimization the so–called Genetic Algorithms have recently gained more attention to solve complicated problems (Michalewicz, 1992; Lagaros, 2002). One important aspect associated to these algorithms is that they are not gradient–based methods as, for instance, the HL–RF approach used in reliability analysis.

In this paper the Evolutionary Strategies (ES) algorithm, a class of Genetic Algorithm, is employed to develop a new search methodology that is able to identify the presence of multiple design points in structural reliability analysis. The proposed methodology is applied in connection with FORM and/or MCIS to evaluate the probability of failure. Two numerical applications are presented: the first one is a non–linear limit state function with two design points and the second one is a limit state function with a series system representing failure mechanisms for a plane frame. The results obtained show the robustness and accuracy of the proposed approach.

 

Reliability analysis of limit state functions with multiple design points

The proposed methodology to perform the reliability analysis of functions with multiple design points consists of the following main steps:

1. Mapping of the approximate position of the relevant design points (local maxima) on the integration domain through the ES algorithm;

2. Improving the precision of design points coordinates applying the HL–RF method for each local maximum point identified in Step 1 when FORM approach (for series systems) is chosen for the computing the probability of failure (an schematic representation is shown in figure 2); and/or

3. Using directly the points identified in Step 1 as the center points for the simulation process when the probability of failure is evaluated by MCIS.

 

Searching design points with evolutionary strategies

Finding the entire set of relevant design points (local maxima) is, in general, a very difficult problem to be solved by the classical gradient–based optimization methods. The so–called Genetic Algorithms (Michalewicz, 1992) and Simulated Annealing methods (Corana, 1987) are much more effective and reliable to do this task because they have the capability to step up and out off regions near local maxima. Among the several Genetic Algorithms presented in literature there is the Evolutionary Strategies (ES) approach (Lagaros, 2002; Greenwood, 1997). It is based on the principles of adaptive selection found in the natural world. Each generation (iteration of the algorithm) takes a population of individuals (potential solutions) and stochastically modifies the genetic material (problem parameters) to produce the new offspring.

For the application of the ES algorithm to structural reliability problems it is more convenient to extend the integration domain in equation (2) for all Rⁿ space, using the following indicator function:

Using equation (4), equation (2) can be re–written as:

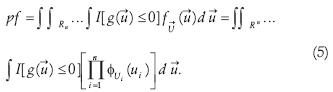
Due to the rotational symmetry and exponential decay of the PDF in the normal standard space, the design points have the highest likelihood among all points in the failure domain (figure 3). Hence, the problem of finding these points can be solved by maximizing the argument of the integral in equation (5) in the Rⁿ space. Thus, the design points' search process can be defined as the unrestricted optimization of the objective function

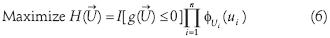
The optimization problem in equation (6) can be solved through a simple version of the ES algorithm (Barranco, 2002). This algorithm is based on a population consisting of a single individual submitted to only mutation operations during his life. Two real vectors represent each individual: one containing a point in the search space and other with the corresponding mutations . The latter corresponds to a joint statistically independent normal vector with each one of its components having zero mean and a standard deviation σ_i. The search algorithm is presented schematically in figure 3 and consists of the following steps:

1. Establish the lower and upper search limits, u_ai and u_bi for each random variable u_i.

2. Set the first inidividual of the population . This initial point can be made equal to = {0,0,... ,0 ]^T;

3. The objective function in equation (6), H_j , is evaluated for each individual . In this step, evaluation of the function is required and then, transformation of the variables must be performed;

4. The off spring of the individual is generated by applying the following mutation operator:

where is one artificially generated realization of the random mutation vector A first estimative of σ_i =(u_ai –u_bi )/6 can be assumed in order to extend the search fiield over all integration domain. During the subsequent simulations the standard deviations can be reduced in order to increase the numerical precision of the search algorithm;

5. The objective function is evaluated for the new population member This offspring member will be only accepted in replacement of his progenitor if it satisfies all the problem constraints, and produces a better result for the objective function, i.e., If these conditions are not satisfied, the off spring is eliminated and its progenitor continues as member of the population;

6. The algorithm continues through steps 3 and 4 until a given maximum number of simulations is reached.

The simulation–based procedure established in steps 1 to 6 above gives an approximation to just one design point. The algorithm is extended to find multiple design points by including constraints around the design points previously identified. Mathematically this is expressed by the updated optimization problem:

where U*_k are all k–design points previously identified,

is the distance between the current point and k–th design point, and R is a chosen radius of a hyper–sphere in the Rⁿ space.

In summary, after a design point has been found the remaining points are searched with the same algorithm now applied over the region of the Rⁿ space outside the union of the hyper–spheres centered at the design points previously identified. Limited experience suggests avalue in the range 1–3 units for R. Figure 4 shows the search space for a third design point, after and have been found. The algorithm is repeated until all the significant or a maximum specified number of design points in the integration domain have been found. The former condition is verified when the latest identified point falls far away from the failure surface, i.e., g(Uk*) > Δ, where Δ 0.5.

The algorithm presented above is easily adapted to consider series systems composed of M individual limit state functions , i=1,...M (Madsen et al., 1986). This is done by just changing the indicator function in equations (4) and (5) for, where it is equal to one if at least one of the individual failure functions satisfies the condition <0 and zero otherwise.

 

True design points using HL–RF method

Because the random nature of the search algorithm presented above, the precision of the results for the design points are dependent on the number of simulations. In order to increase the precision of the results wit hout increasing the number of simulations the well–known HL–RF method (Melchers, 2001; Madsen et al., 1986) can be used.

 

This method is an optimization algorithm used in connection with FORM and SORM in the reliability analysis of structural systems. The objective of the HL–RF method is to obtain the design point ^* by solving the following constrained optimization problem in the standard normal random variables space:

The gradient–based solution technique of equation (9) consists in the generation of a sequence of points , i = 1,2,3,... according to the rule (Zhang, 1994):

where is a search direction vector, is the gradient of the limit state function and λ is the size of the increment λ_i is selected such that the inequality between the merit function:

evaluated in two consecutive points is held. In the merit function, c is a parameter satisfying the condition

in each step. is considered as a design point ^*when the reliability index error Q in two consecutive iterations is less than or equal to anadequate tolerance margin, commonly in the order of 1 x 10^–4. In the present approach, each starting point in HL–RF technique is taken as one approximate design point identified by ES algorithm. The HL–RF is repeated as many times as the number of identified design points. The final set of design points is obtained by taking apart all repeated points, if they exist.

 

Evaluation of the probability of failure

FORM Approach

Under the FORM approach, the total failure probability associated to a series system or a single limit state function having multiple design points can be calculated through the unions and intersections of the failure domains associated to the hyper–planes tangent to each design point, as shown in figure 2. The probability of failure is evaluated with the following equation (Madsen et al., 1986):

where N_P is the number of elements of the system, β is the reliability index associated to the j–th design point, ρ_ji is the correlation coefficient between two hyper–planes, and Φ(.,.,ρ) is the standard bi–normal CPF. Due to the fact that the individual failure probabilities P_j are generally small, the third order terms P_jil in equation (11) can usually be neglected.

The standard bi–normal CPF can be calculated with the equation (Madsen et al., 1986)

where φ(.,.,z) is the standard bi–normal PDF.

Monte Carlo Simulation with Importance Sampling

Using Monte Carlo simulation with Importance Sampling (MCIS) technique for a structural reliability problem with multiple design points, the total probability of failure can be estimated by (Melchers, 2001)

where

is a new sampling PDF and ω_k is a weight factor. Numerically the integral in equation (13) can be estimated by

where N_S is total number of samples (simulations) generated artificially from the new sampling PDF. As shown by Melchers (2001), the k^th par cel of this function can be obtained by just shifting the peak of the joint PDF to the design point:

and the k–th weight factor is giving by

Standard formulae exist to evaluate the number of simulations N_s needed to achieve a desired level of confidence on the estimator given by equation (14), (Melchers, 2001). When compared to the crude Monte Carlo simulation approach the Importance Sampling technique greatly improves the convergence rate to achieve the failure probability, i.e., the number of simulation N_s is significantly reduced. It is important to notice that it is not necessary to employ the exact design points in equation (14 ) to take advantage of the MCIS technique. Then, the points identified by the ES algorithm described above can directly be used in connection with MCIS technique.

 

Numerical applications

The proposed methodology is applied initially to a case of bi–dimensional limit state function with multiple design points in order to illustrate some relevant aspects on convergence and precision of the proposed methodology. In the sequence, the reliability analysis of one plane frame structure having seven random variables is presented.

Example 1. Parabolic Limit State function

The parabolic limit state function considered in this example is given by,

where X₁ and X₂ are normal standard uncorrelated random variables with the characteristics presented in table 1. In this case, the original space and the standard normal space are the same. As pointed out by Der Kiureghian et al. (1998), this failure function has two design points.

In the Evolutionary Strategy search algorithm, the origin of the standard normal space was used as the first member of the population. After the first design point has been found, a hyper–sphere with ra dius equal to three units (R=3) was centered on it in order to constrain the search space for the next point and so on. To investigate the precision of the ES algorithm, the search for design points was carried out using different number of simulations, from 100 to 100000. The ES approximations to design points are shown in figure 5, while figure 6 presents the corresponding errors in the approximated reliability indexes with respect to the ones obtained with FORM.

Figures 5 and 6 show that the search algorithm based on ES is very efficient to identify multiple design points. For example, for 10,000 simula tions or more the error in reliability indexes obtained using only ES algorithm is less than 0.1% and with only 1000 simulations the error is no more than 0.25%. Figure 7 presents the mean number of iterations that the HL–RF method used to find the design points, considering the guesses obtained with ES algorithm as starting points. It is noticed that even with a small number of 100 simulations, the mapping obtained by the ES is enough for the HL–RF method to identify the correct design points. It is al so noticed that when the number of simulations increase the number of simulations in the HL–RF decreases, once the design points identified by the ES algorithm are very close to the correct ones as illustrated in figure 6.

Table 2 presents both the approximate design points obtained with ES (case of 10,000 simulations) and the ones using HL–RF method. The final design points are the same as those published by Der Kiereghian et al. (1998).

In table 3 the total probability of failure is evaluated using the FORM approximation, considering isolated and joint contribution of each design point. Table 3 also includes the result from MCIS approach using the approximate design points obtained with ES and the exact ones obtained trough numerical integration. The number of simulations for this latter approach has been calculated automatically in order to obtain a coefficient of variation (CoV) of 2.5% in the estimated probability of failure (Melchers, 2001).

It is observed that the system probability of failure computed by FORM taking into account only the contribution of the first design point presents an error of 39% and considering only the second point the error is around of 67%. However, when the contributions of both design points are considered the error is only of 6%. MCIS approach gives almost the exact probability of failure.

Example 2. Plane Frame Failure

This example considers the possibility of failure of the plane frame presented in figure 8 by means of plastic hinge mechanisms as investigated by Madsen et al. (1986). The failure function for this structure can be written by

which represents a series system of three failure mechanisms given by the following limit state functions

In equation (18) min[.] means the minimum value of [.]. The characteristics of the statistically independent random variables are presented in table 4. It is known from Madsen et al. (1986) that equation (1 8) presents three design points, each one corresponding to a limit state function presented in equation (1 9). In (Madsen et al., 1986) the design points are obtained, differently of the approach presented in this work, by separated reliability analyses for each limit state function

By setting the maximum number of simulations equal to only 100 and R=1, the approximated design points obtained by ES algorithm, and used as initial guesses for the HL–RF approach, are able to identify correctly the design points as shown in table 5. The results found for the probability of failure are compared with those from crude Monte Carlo simulation in table 6. As it can be observed the results obtained are in very good agreement.

As this problem is solved in R⁷ space, it is not easy to find with high precision the design points directly through ES algorithm. In order to achieve a high precision, the number of simulations must be in the order 10⁷–10⁸. However, using the ES algorithm in connection with HL–RF approach the number of simulations drops to the order of 10².

 

Conclusions

The complete identification of all design points is of paramount importance for the reliability analysis of real structures due to the serious errors that can be introduced in the failure probability evaluation if any of them is neglected. In this paper a new simple and practical algorithm based on Evolutionary Strategies (ES) is presented to cope with the problem of multiple design points. Firstly, the ES algorithm is used to map over the integration domain the approximate position of the relevant design points (local maxima). Secondly, the coordinates of these points are used as initial guesses in the HL–RF algorithm to increase the numerical precision of the relevant design points coordinates. Finally, the structural failure probability can be evaluated by FORM approach for series systems or by Monte Carlo Simulation with Importance Sampling (MCIS) method using the identified design points as the center of the simulation process regions.

Trough the numerical examples presented in this work the ES algorithm sho wed to be a simple, very ef fective and reliable methodology for the identification of multiple design points. Depending on the number of simulations this algorithm can even identify precisely the position of the design points. This de pends heavily on the di men sion of the integration space, i.e., the number of random variables considered. However, its main advantage is the possibility of performing a systematic mapping of the number and position of all relevant design points on the integration domain using only a small number of simulations (around 100). With this rough mapping, the HL–RF approach easily arrives at the design points with a required precision.

One important point in the reliability analysis of some real structures is that the limit state functions usually can not be expressed by means of analytical expressions and must be evaluated implicitly, for instance, through various finite element structural analyses. This aspect increases the computational costs of the analysis. To cope with this constraint an adaptive multidimensional interpolation approach, as presented by Barranco (2002) and Lima (1997), can be used to approximate analytically the true failure function. In this approach an initial set of interpolation points is successively up dated in the interpolation scheme to encompass the regions associated with the maximum likelihood points. The se points are quickly identified by the proposed search approach based on the approximate failure function.

 

References

Barranco–Cicilia F. Analysis of Systems with Multiple Design Points. DSc Qualification Seminar. Department of Civil Engineering, COPPE/UFRJ, 2002 (In Portuguese).        [ Links ]

Corana A, Marchesi M, Martini C, Ridella S. Minimizing Multimodal functions of Continuous Variables with the Simulated Annealing Algorithm. ACM Transactions on Mathematics Software, 13(3):262–280, 1987.        [ Links ]

Der–Kiureghian A, Dakessian T. Multiple Design Points in First and Second Order Reliability. Structural Safety, 20(1):37–49, 1998.        [ Links ]

Greenwood G.W. Chaotic Behavior in Evolution Strategies. Physica D, 109(3–4):201–241, 1997.        [ Links ]

Lagaros N.D., Papadrakakis M., Kokossalakis G., Structural Optimization Using Evolutionary Algorithms. Computers and Structures, 80(7–8): 571–589, 2002.        [ Links ]

Lima E.C.P. Structural Reliability Analysis by Unconstrained Optimization and Multimodal Monte Carlo Conditional Importance Sampling. In: Carneiro F.L.L., Ferrante A.J., Batista R.C. and Ebecken N.F.F., editors, 1997. International Offshore Engineering. Computational Mechanics Publications, Chichester.        [ Links ]

Madsen H.O., Krenk S., Lind N.S. Methods of Structural Safety. New Jersey. Prentice Hall. 1986.        [ Links ]

Melchers R.E., Structural Reliability Analysis and Prediction. 2^nd Edition. John Wiley. Chichester. 2001.        [ Links ]

Michalewicz Z. Genetic Algorithms+Data Structures = Evolution Programs. Heidelberg. Springer–Verlag. 1992.        [ Links ]

Zhang Y., Der–Kiureghian A. Two Improved algorithms for Reliability Analysis. In: Proc. of the 6^th IFIPWG 7.5 Working Conference on Reliability and Optimization of Structural Systems, Assisi, Italy, 1994.        [ Links ]

 

About the authors

Federico Barranco–Cicilia. Was graduated in Civil Engineering from the National Polytechnic Institute (Mexico) in 1992, he was granted a Master's Degree in Civil Engineering by the UNAM, in 1995, and a Doctor in Sciences degree by Federal University of Rio de Janeiro, with a thesis focused towards the technologies for hydrocarbon exploitation in deep waters. Dr. Barranco has published 6 technical articles in national congresses (Structural Engineering and Seismic Engineering), 8 in international congresses (OMAE, ISOPE and Rio Oil & Gas) and 2 in refereed international journals (ASCE and EE & SD). Since 1991, Dr Barranco works for the Mexican Petroleum Institute in the Research Program on Oil Field Exploitation in Deep Waters. Since1992, he has lectured diverse courses on Structural Engineering at the Technological University of Mexico and lately at the Postgraduate Division of the Faculty of Engineering of the UNAM. Currently, Dr. Barranco is member of the National System of Researchers of the Research Council in Mexico, CONACyT.

Luís Volnei Sudati–Sagrilo. Received degrees in Civil Engineering (1986) from Federal University of Santa Maria (Brazil), Master in Sciences (1989) and Doctor in Sciences (1994) both from COPPE–Federal University of Rio de Janeiro (Brazil). He worked as a Research Engineer at the Department of Civil Engineering of COPPE/UFRJ from 1988 to 2005. In 2006 he became a Full Professor at the same department. His main research and academic activities are related to structural reliability, nonlinear random dynamic analysis and offshore structures. He has co–authored more than 75 technical publications and taken part in more than 50 consulting activities for private and state–owned companies in Brazil. He has already super ised 10 M.Sc. and 3 D.Sc. thesis. Recently, he has been pointed as the head of the Laboratory of Analysis and Reliability of Offshore Structures at COPPE/UFRJ.

Edison Castro–Prates de Lima. Born in Rio de Janeiro, RJ, Brazil in 1947. Received his graduation Diploma (1970) from Civil Engineering Department of UFRGS (Federal University of Rio Grande do Sul). Received his M.Sc. degree (1972) and D.Sc. degree (1977) from Civil Engineering Department of UFRJ (Federal University of Rio de Janeiro). Professor at Civil Engineering Department of COPPE/UFRJ, having had the following positions: 1972–1977, Assistant Professor; 1977–1983, Adjoin Professor and Full Professor since 1983. Most of his academic and research activities have been developed in structural engineering, finite element methods, random dynamic analysis, structural reliability, offshore structures, numerical methods and software development. He is co–author of over 175 scientific and technical publications, has supervised over 20 M.Sc. and 15 D.Sc. thesis. He is a scientific and technical adviser for several private and State companies and has supervised over 250 consulting activities. He is also an ad–hoc adviser for CNPq, FINEP and FAPERJ.