Educación en ingeniería

 

Funciones distancia asimétricas y no positivas definidas Parte II: Modelado

 

Asymmetric and Non–Positive Definite Distance Functions Part II: Modeling

 

H. Sánchez–Larios¹ y S.T. Guillén–Burguete²

 

¹ Instituto de Ingeniería, Universidad Nacional Autónoma de México. E–mail: hsanchezl@ii.unam.mx

² Instituto de Ingeniería, Universidad Nacional Autónoma de México. E–mail: sguillenb@ii.unam.mx

 

Recibido: enero de 2006
Aceptado: febrero de 2007

 

Resumen

Las funciones distancia involucradas en problemas de investigación de operaciones tradicionalmente se han modelado usando combinaciones lineales positivas de métricas L_p . Por lo tanto, las funciones distancia resultantes son simétricas, uniformes y positivas definidas. A partir de una nueva definición de longitud de arco, proponemos un método para modelar funciones distancia generalizadas, que llamamos premétricas, las cuales pueden ser asimétricas, no uniformes y no positivas definidas. Demos tramos que toda función distancia que satisface la desigualdad del triángulo y cuya derivada direccional unilateral es continua, puede ser modelada como un problema de cálculo de varia ciones. La "longitud" de un arco d–geodésico C(a,b) que va desde a hasta b respecto de la premétrica d (la d–longitud) puede ser negativa, y por tanto la d–distancia desde a hasta b puede representar la mínima energía necesaria para mover un objeto móvil desde a hasta b. ilustramos nuestro método con dos ejemplos.

Descriptores: Funciones distancia, geodésicas, cálculo de variaciones, problema de localización de servicios.

 

Abstract

Traditionally the distance functions involved in problems of Operations Research have been modeled using positive linear combinations of metrics Lp. Thus, the resulting distance functions are symmetric, uniforms and positive definite. Starting from a new definition of arc length, we propose a method formo deling generalized distance functions, that we call premetrics, which can be asymmetric, non uniform, and non positive definite. We show that every distance function satisfying the triangle inequality and having a continuous one–sided directional derivative can be modeled as a problem of calculus of variations. The "length" of a d–geodesic arc C(a,b) from a to b with respect to the premetric d (the d–length) can be negative, and therefore the d–distance from a to b may represent the minimum energy needed to move a mobile object from a to b. We illustrate our method with two examples.

Keywords: Distance functions, geodesics, variational calculus, facility location problem.

 

Introducción

Las funciones distancia involucradas en problemas del mundo real frecuentemente son asimétricas, no uniformes y no positivas definidas. Por ejemplo, en el modelado de tráfico en horas pico, o del tráfico sobre una superficie no horizontal, se obtienen funciones distancia asimétricas y no uniformes. Un ejemplo que lleva a funciones distancia no positivas definidas es el movimiento de un robot con un sistema de recuperación de energía.

En la literatura actual el modelado de funciones distancia se ha enfocado exclusivamente al ajuste estadístico de parámetros de funcion estales como las normas Lp pesadas, o combinaciones lineales positivas de éstas. Las normas Lp pesadas y las combinaciones lineales positivas de éstas, conducen a funciones distancia simétricas, positivas definidas, y uniformes. Esto significa que la distancia de a a b es igual a la distancia de b a a, que la distancia entre cualesquiera dos puntos diferentes es estrictamente positiva, y que la distancia desde un punto hasta otro punto es invariante bajo traslaciones, respectivamente. Love et al. (1979), Berens et al. (1985) y Brimberg et al. (1993) obtuvieron funciones distancia a partir de las normas Lppesadas. Ward et al. (1980) y Brimberg et al. (1992) formularon funciones distancia a partir de combinaciones lineales positivas de normas L_p pesadas. Hodgson et al. (1987), Drezner et al. (1989) y Plastria (1992) obtuvieron funciones distancia asimétricas, pero uniformes y positivas definidas. Aplican sus funciones distancia a problemas de localización de servicios.

En este trabajo se propone una nueva forma de modelar funciones distancia, las cuales pueden ser asimétricas, no uniformes y no positivas negativas. Nuestras funciones distancia se pueden referir a costos de transporte, distancias de recorrido, tiempo de recorrido, energía gastada, etc.

Estas funciones distancia son úti les en muchos pro blemas de Investigación de Operaciones que requieren distancias en sus formulaciones, tales como problemas de transporte, problemas de localización de servicios, problema del agente viajero, etc.

 

Premétricas

Definimos la función distancia premétrica como una función binaria d: Rⁿ x Rⁿ R que cumple la propiedad de identidad (la distancia de un punto consigo mismo es cero, d(a, a) = 0 para toda a Rⁿ) y la desigualad del triángulo (para toda a, b, cRⁿ (a,b) < d(a , c) + d(c ,b)).

Recordar que una métrica es una función binaria que cumple la desigualdad del triángulo (a, b, cRⁿ, d(a,b) < d(a,c)+d(c,b)), no negatividad (a , bRⁿ, d(a,b) > 0 a ≠ b) y simetría ( a, bRⁿ, d(a,b) = d(b,a)).

De acuerdo con las propiedades que cumplen, las funciones distancia se pueden clasificar como sigue:

Una métrica débil es una premétrica no negativa, d(a,b) > 0 para todo a , bRⁿ. Una cuasimétrica es una métrica débil que satisface la condición de definitoreidad, para toda a , bRⁿ, d(a,b)= 0 a = b, es decir, una cuasimétrica es una premétrica estrictamente positiva (para toda a , bRⁿd(a,b)> 0 a ≠ b). Una pseudométrica es una métrica débil simétrica (para toda a , bRⁿ, d(a,b)= d(b,a)). Una métrica es una pseudometrica que satisface la propiedad de definitoreidad.

La longitud de un arco (ordenado) C(a,b) respecto de una premétrica d es la menor cota superior de la sumatoria

donde (a = x₀, x₁, x₂, .., x_k, x_k+1 = b) es una sucesión de puntos sobre C(a,b) que va de a a b. Si este límite existe y es finito, el arco se llama d–rectificable. Se de muestra (Sánchez et al., 2008) que si la derivada direccional unilateral de d, dada por

(Rockafellar, 1970) es continua, entonces la d–longitud de un arco C(a,b) d–rectificable está dada por

donde x: [a, b]Rⁿ es una representación paramétrica clase C¹ de C(a,b). Puesto que d cumple la propiedad de identidad, d(x,x) = 0 para todo xRⁿ, la derivada direccional unilateral F se puede escribir como

Un arco d–geodésico es un arco C(a,b) tal que la distancia desde a hasta b es un mínimo,

Por las propiedades de las integrales, la longitud de un arco formado por dos o más subarcos es igual a la suma de las longitu desde sus subarcos. Además, por la desigualdad del triángulo todo subarco de un arco d–geodésico es un arco d–geodésico.

Es inmediato que un arco C(a,b) es d–geodésico, si y sólo si, la restricción de d a C(a,b) cumple la igualdad del triángulo respecto del punto final b,

donde x: [a, b]Rⁿes una representación paramétrica de C(a,b).

Una d–geodésica es un arco con la propiedad de que sus subarcos suficientemente pequeños son arcos d–geodésicos, y que no está contenido propiamente en otro arco que cumple esta propiedad. Por tanto, un a d–geodésica no está contenida propiamente en otra d–geodésica. Además, en una d–geodésica cualquier triada de puntos suficientemente próximos están conectados por un arco d–geodésico. Observar que un subarco de una d–geodésica puede no ser un arco d–geodésico.

Una premétrica d es (geodésicamente) completa si para todos los puntos existe un arco d–geodésico que los une.

Toda premétrica completa con derivada direccional unilateral continua puede ser modelada mediante un problema de cálculo de variaciones. En términos forma les, se tiene el siguiente teorema:

Teorema 1

(Existencia de una función fundamental F₀ correspondiente a una premétrica d)

Para toda premétrica d: Rⁿ x Rⁿ R completa, cuya derivada direccional unilateral F: Rⁿ x RⁿR dada por (2) es continua, entonces existe al menos una función F₀: Rⁿx Rⁿ tal que

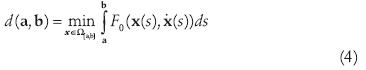
para toda a, bRⁿ.

En particular, la derivada direccional unilateral de d cumple (4), es decir,

para toda a, b Rⁿ, teniéndose que F(x, v) es una función homogénea positiva de grado en uno en x para todo vRⁿ, y es convexa en v para todo x Rⁿ.

Demostración

Se sabe que si una premétrica d: Rⁿ x Rⁿ R tiene una derivada direccional unilateral F: Rⁿ x Rⁿ R continua, entoncestodo arco C(a,b) clase C¹ es d–rectificable y su d–longitud está dada por (1). Puesto que d es completa, existe una d–geodésica clase C¹ de a a b que resuelve

que por definición de arco d–geodésico es igual a la distancia d(a, b). Por tanto F cumple (4). Resta probar qu e F(x, v) es una función homogénea positiva de grado uno en x para todo vRⁿ, y además convexa en v para todo xRⁿ, lo cual se prueba directamente:

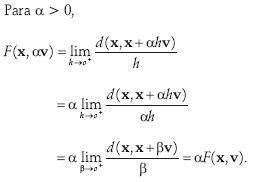
y por tanto F(x, v) es una función homogénea positiva de grado uno en x para todo vRⁿ.

De la ecuación (2) y por ser F(x, v) una función homogénea positiva de grado uno en x, para todo vRⁿ,

y por tanto F(x, v) es una función convexa en v para to do xRⁿ.

Q.E.D.

En la ecuación (4) la función F₀: Rⁿx Rⁿ R es una función dada a priori llamada función fundamental de d.

Teorema 2

(Premétrica definida a partir de una función fundamental)

Sea F₀: Rⁿx Rⁿ R una función homogénea positiva de grado uno con F₀(x, 0) = 0 para to do xRⁿ, y tal que cumple la siguiente condición de solubilidad: para cada par ordenado a , bRⁿexiste un camino x: [a, b]Rⁿ de a a b clase C¹ que resuelve el problema de cálculo de variaciones

Sea d: Rⁿ x Rⁿ R la función dada por (4). Entonces:

a) d es una premétrica sobre Rⁿ, la cual es completa si F₀ es la derivada direccional unilateral de d.

b) F₀ es la derivada direccional unilateral de d si y solamente si F₀(x, v) es convexa en v.

Demostración

La homogeneidad positiva de F₀ implica que to da transformación continua que preserva la orientación de un camino x: [a, b] Rⁿ que resuelve (4) es un camino que también resuelve (4), teniendo ambos caminos la misma imagen.

Por tanto, dados a y b, cada solución de (4) depende sólo del arco y no de la elección particular de su representación paramétrica. Entonces la función d dada por (4) está bien definida.

(a) Por las propiedades de las integrales, la función d dada por (4) cumple la propiedad de identidad y la desigualdad del triángulo, y por tanto d es una premétrica. Si F = F₀ , entonces para cada par ordenado de puntos a y b existe un arco C(a,b)que cumple d(a,b)= l_d C(a,b)), y por definición C(a,b)es un arco d–geodésico. Así que d es una premétrica completa.

(b) La homogeneidad positiva de F₀ implica que la convexidad de F₀ se reduce a

F₀ (x, v₁+v₂) < F_o(x,v₁) + F₀(x,v₂) para todo v₁, v₂Rⁿ. Por tanto, la convexidad de F₀ implica que la derivada direccional unilateral F de la función d da da por (4) es la propia función F₀:

La última igualdad se puede explicar como sigue. En el límite cuando h 0⁺, x(s) se puede considerar constante, y por tanto el integrando dF₀ (x(s), x(s)) sólo depende de x(s). Debido a la convexidad de F₀, la integral alcanza su valor mínimo si x(s) tiene la dirección de v en todos los puntos a lo largo del arco que va de x a x + vh. Por tanto, el integrando F₀(x(s),x(s)) permanece constante a lo largo del arco que va de x a x + vh y to ma el valor F₀(x, v). : Recíprocamente, supóngase que la función F₀ que define a d a través de (4) es igual a la derivada direccional unilateral de d, F = F₀. Por (a) d es una premétrica, es decir, d cumple la desigualdad del triángulo. Por la última afirmación del teorema 1, F₀ es una función convexa.

Q.E.D.

Obtención de las d–geodésicas

Bajo ciertas condiciones, el problema variacional (4) se resuelve mediante las ecuaciones de Euler Lagrange:

Las soluciones de (6) son las d–geodésicas asociadas a la premétrica d: RⁿxRⁿR, las cuales contienen los arcos d–mínimos que resuelven (4). La distancia d(a,b) se determina sustituyendo en el integrando de la ecuación (4) una d–geodésica que va de a a b.

Para el caso n = 2, las coordenadas de cada punto se denotan por (x, y), y (6) se escribe como

y en este caso, (4) se puede escribir como

Si F₀ se expresa en términos de una variable independiente, entonces (9) resulta

Para el problema (10) las ecuaciones de Euler Lagrange (7) y (8) vienen a ser

 

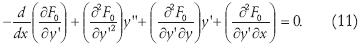
Geodésicas de una suma de premétricas

Es inmediato que cualquier suma de premétricas en Rⁿ es una premétrica en Rⁿ. El siguiente teorema indica que si un arco es una geodésica de varias premétricas en Rⁿ, entonces este arco es una geodésica de la suma de esas premétricas.

Teorema 3

(Geodésicas de una suma de premétricas)

Sean d₁ y d₂ dos premétricas sobre Rⁿ, y sea C una geodésica de d₁ y d₂. Entonces C es una geodésica de d₁+ d₂.

Demostración

Sea d una premétrica definida por,

d(a,b) = d₁(a,b) + d₂(a,b) para toda a , bRⁿ.

Si C es una geodésica de d₁ y d₂, es decir, d₁ y d₂ satisfacen (3), entonces la suma d = d₁ + d₂ también satisface (3), y por tanto C es una geodésica de d.

Q.E.D.

Corolario del teorema 3

Sea d_F una premétrica sobre Rⁿ y sea d_h la premétrica correspondiente a una función real valuada h: RⁿR. Entonces las geodésicas de d_F y las geodésicas de d = d_h + d_F son las mismas.

 

Premétrica asociada a una función real

Sea h: RⁿR una función real valuada. La función binaria d_h: Rⁿ x RⁿR definida por d_h(a,b) =h(b) – h(a) para toda a, bRⁿ, satisface la igualdad del triangulo,

d_h(a,b) = d_h(a,c) + d_h(c,b) para toda a, b, cRⁿ,

y también satisface la propiedad de identidad. Por tanto, d_h es una premétrica, denominada premétrica asociada a la función real h. Esta premétrica satisface la propiedad de antisimetría, d(a, b) = –d(b, a), para toda a , bRⁿ. Todos los arcos de a a b tienen la misma longitud respecto de la premétrica d_h(a,b), y por tanto, todos los arcos de a a b son arcos d_h–geodésicos. Esta premétrica es completa aún cuando d_h sea una función binaria discontinua.

Si la función h es diferenciable, entonces la derivada direccional unilateral de d_h es

donde es el gradiente de la función h y denota el producto punto. Entonces, la longitud con respecto a la premétrica d_h de cualquier arco x que va de a a b está dada por

para toda xΩ_[a,b], lo que confirma que todos los arcos de a a b tienen la misma longitud con respecto a la premétrica, d_h, h(b) – h(a).

 

Modelado de funciones distancia: modelado de premétricas sobre R² con interpretación física

En esta sección obtendremos la función fundamental F y su correspondiente premétrica d para el movimiento de un objeto deslizándose sobre una superficie rugosa. La fuerza externa aplicada a tal objeto debe vencer la gravedad y la fricción. El dominio de la función distancia (premétrica d) a considerar es el plano horizontal R², y la "longitud" de un arco que va de aR²a aR² está definida como la energía gastada a lo largo del arco debida a las fuerzas de gravedad y de fricción. Por tanto, la "distancia" de a a b es la mínima energía gastada para mover el objeto desde a hasta b.

El objeto se desliza "lentamente", de modo que las fuerzas inerciales son despreciables comparadas con las de la gravedad y la fricción.

Por el teorema 1, toda premétrica completa con derivada direccional unilateral continua se puede modelar a partir de una función fundamental F(x,v) homogénea positiva de grado uno y convexa en v, lo cual requerirá resolver el problema de cálculo de variaciones en (4). Recíprocamente, por el teorema 2, si F(x,v) es homogénea positiva de grado uno y convexa en v (y por tanto F es la derivada direccional unilateral de d) y además F cumple que para cada par ordenado de puntos a, b en R² existe un camino de a a b clase C¹ que resuelve el problema de cálculo de variaciones (5), entonces la premétricadada por (4) es una premétrica completa.

 

Un objeto deslizándose sobre una superficie rugosa bajo la influencia de la gravedad y fricción

En esta sección, la premétrica d tiene un significado físico. La "distancia" de a a b representa la energía mínima necesaria para deslizar un objeto de masa m sobre una superficie z=f (x, y) desde (a, f(a))R³ hasta (b, f(b))R³, donde a y b son las proyecciones del punto inicial y final, respectivamente, sobre el plano horizontal. El dominio de la premétrica d es el plano horizontal. Se supone que f: R²R es una función diferenciable. En general, el coeficiente de fricción µ es una función de la posición (x, y) y la dirección , pero por simplicidad µ se considera constante. La magnitud de la fuerza de gravedad es mg, y la magnitud de la fuerza de fricción es µmgcosθ, donde θ es al ángulo de inclinación del plano tangente a f en (x, y, f (x,y)) con respecto al plano horizontal, y g es la aceleración de la gravedad. Se considera que la velocidad es suficientemente pequeña como para que la fuerza de inerciasea despreciable con respecto a las fuerzas de gravedad y de fricción. La última consideración implica que los segmentos de recta son arcos d–geodésicos. Puesto que

entonces

Se supone que el objeto se mue ve desde (x, y, f (x,y)) hasta (x+Δx, y+Δy, f(x+Δx , y+Δy)) sobre la superficie, donde Δx y Δy son suficientemente pequeñas, de modo que: a) la proyección de la trayectoria sobre el plano horizontal es el segmento de recta que va desde (x,y) hasta (x + Δx, y + Δy); b) el objeto se desliza sobre el plano tangente a f en (x, y, f (x,y)). Por tanto,

Entonces el cuerpo se desliza sobre la superficie f a lo largo del segmento de recta que va desde (x, y, f(x,y)) hasta (x+Δx, y + Δy, f(x,y) + Δx ∂f / ∂x + Δy ∂f / ∂y). Este segmento está contenido en el plano tangente a f en (x, y, f(x,y)) y tiene una longitud euclidiana dada por

La cantidad de energía necesaria para vencer la fuerza de gravedad es

y la energía necesaria para vencer la fuerza de fricción es

Por simplicidad se considera mg = 1. Tomando en cuenta la ecuación (13), la energía total es

La función fundamental F(x,y,x,y) en este caso está dada por

donde Δs es la proyección de Δl sobre el plano horizontal. F(x,y,x,y) es el factor por el cual ds debe ser multiplicado para obtener la energía dW necesaria para mover el objeto una distancia ds sobre el plano horizontal. En el límite, la distancia ds corresponde a la distancia dl sobre la superficie f. Tomando en cuenta que=1, la función fundamental F viene a ser

La suma de los dos primeros términos del lado derecho de (14) es el gradiente de f. Por (12), la premétrica d_f asociada con la función f está dada por

d_f(a,b) = f(b) –f(a) para toda a, bR²,

la cual es una premétrica antisimétrica que puede ser calculada directamente de f.

El tercer término de la ecuación (14), que se denota por F_µ,

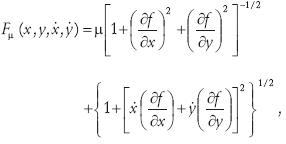
es una función convexa y homogénea positiva de primer grado en 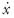y , y no depende explícitamente del parámetro s. Por la ecuación (9), la premétrica d_α asociada a F_α está dada por

Por el corolario del teorema 3, las geodésicas de d_α coinciden con las geodésicas de la premétrica d_f = d_f + d_α . Por tanto, la premétrica d_F asociada a la función fun da mental F₀ dada por (14) es

d_F(a,b) =d_f (a,b) + d_α(a,b) para toda a, a, bR²,

donde la premétrica d_f se calcula a partir de la función f y la premétrica d_αse calcula a partir de las correspondientes ecuaciones de Euler Lagrange.

Sustituyendo F_µ en la ecuación (10), y considerando que d_µ es una premétrica de R², se obtiene

donde dx es igual a 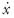ds y el camino x está dado por la función y(x). Esta premétrica se resuelve a través de la ecuación de Euler–Lagrange (11 ), donde la función F₀ se reemplaza por F_µ.

Se ilustra nuestro modelo con dos ejemplos. En el primero, la superficie f es un plano inclinado, y en el segundo, f es una semiesfera.

 

Ejemplo 1

Objeto que se desliza sobre un plano inclinado

En este caso, el objeto del desarrollo precedente se desliza sobre un plano rugoso con un ángulo de inclinación 0 con respecto al plano horizontal, 0 <θ<π/2 . El coeficiente de fricción µ se considera constante. Por comodidad se toma como eje x la intersección de ambos planos y como eje y la dirección en la cual aumenta la pendiente. Así, ∂f / ∂x = 0 y ∂f / ∂y = tanθ.

Puesto que =1, la expresión (14) se puede escribir como

Las geodésicas correspondientes a F_f = tanθ son todos los arcos en el plano horizontal. Las geodésicas de se obtienen resolviendo las ecuaciones de Euler Lagrange (11). Estas geodésicas son los segmentos de recta. Por tanto, por el corolario del teorema 3, las geodésicas correspondientes a la función fundamental F₀ dada por (15) son los segmentos de recta sobre el plano. Así, para un par de puntos dados (a, b) y (x, y), la geodésica de d_F0 que va de (a, b) a (x, y) es la recta que conecta estos dos puntos. Entonces,

donde l = ((x – a)² + (y – b)²)^1/2 es la distancia euclidiana entre los puntos (a, b) y (x, y), los cuales están en el plano horizontal. Sustituyendo en (15) e integrando a lo largo de la geodésica que va de (a, b) a (x, y), se obtiene la premétrica d_F0 correspondiente a la función fundamental F₀:

La premétrica obtenida en (16) es uniforme, pero es asimétrica debido al término antisimétrico (y – b) tanθ.

Si tan θ> µ, entonces (16) da distancias negativas: para x = a y b > y,

En este caso, la premétrica d_F0 es uniforme, y no satisface las condiciones de no negatividad y definitoreidad.

Notar que si (2) se aplica a la premétrica (16), se obtiene la derivada direccional unilateral F de d_F0 , la cual resulta igual a la función fundamental F₀ (15):

Ejemplo 2 Objeto que se desliza sobre una media esfera

Supóngase ahora que el objeto se desliza sobre una semiesfera rugosa. Primero se considera que el objeto no se encuentrabajo la influencia de la gravedad, la cual se incluye después. Sea una semiesfera de radio r, f(x, y) = (r² – x² – y²)^1/2, cuyo dominio es el disco abierto D dado por x² + y²< r². En este caso, el integrando en (10) se puede expresar como

F(x, y, y') = [1 + y' ² + (r² – x² – y²)^–1(x + y y')²]¹'^/2.

Sustituyendo esta última igualdad en la ecuación de Euler Lagrange (11), se obtienen las d–geodésicas sobre el disco abierto x² + y²< r². Estas d–geodésicas son las proyecciones de los grandes semicírculos en la semiesfera f(x, y) = (r² – x² – y²)^1/2 sobre el disco abierto D. Por tanto, la distancia de aR² bR²en el disco abierto D, es la longitud euclidiana del gran semicírculo que une (a, f(a)) y (b, f(b)) en la semiesfera. Sean a = (a₁, a₂) y b = (b₁, b₂) dos puntos en el disco abierto D. La distancia d_F de (a₁, a₂, (r²–a₁²–a₂²)^1/2) a (b₁ , b₂, (r²–b₁²–b₂²)^1/2) es la longitud euclidiana del gran semicírculo que conecta estos dos puntos en la semiesfera, r θ, donde

Por tanto, la premétrica d_F es

La premétrica (17) satisface las propiedades de las métricas, sin embargo, esta métrica no es uniforme: suponiendo r = l, d((0,0), (0,0.8))=0.93 ≠ d((0.5,0), (0.5,0.8)) = 1.003.

Para tomar en cuenta la gravedad, sea la premétrica dada por (12), d_h (a,b) = h(b) — h(a), la cual representa la energía potencial. Por tanto, la suma d_F + d_h es la premétrica d dada por

Por el corolario del teorema 3, las geodésicas en el disco abierto D correspondientes a la premétrica (18) y las geodésicas correspondientes a la premétrica (17) son las mismas.

Si h en (18) es una función no constante, entonces la premétrica d dada por (18) es asimétrica y puede ser no positiva definida y violar la propiedad de definitoreidad.

 

Conclusiones

El método propuesto permite modelar funciones distancia generalizadas, que llamamos premétricas, que cumplen la propiedad de identidad y la desigualdad del triángulo, pero a diferencia de las métricas Lp y sus combinaciones lineales positivas usadas tradicionalmente, pueden ser asimétricas, no uniformes y no positivas definidas. Por tanto, la "distancia" desde un punto hasta otro puede representar la mínima energía gastada, el mínimo costo, el mínimo tiempo de recorrido, etc. Nuestro método consiste en formular una función F(x, v), llamada función fundamental, la cual depende de dos parámetros, el punto x y la dirección v en ese punto. La distancia desde a hasta b es el mínimo de la integral de F sobre todos los arcos sua ves que van de a a b, por lo que se obtiene un problema de cálculo d e variaciones. Se demostró que esta integral representa la longitud de los arcos respecto de la premétrica d sólo si F(x, v) es convexa en v. Mediante dos ejemplos ilustramos el método propuesto; las funciones distancia obtenidas resultaron no simétricas, no positivas definidas, y no uniformes, las cuales no podrían modelarse mediante los métodos tradicionales de ajuste de parámetros de las métricas Lp.

 

Referencias

Berens W., Körling F. Estimating Road Distances by Mathematical Functions. European Journal of Operational Research, 21:54–56. 1985.         [ Links ]

Brimberg, J., Love R.F. A New Distance Function for Modeling Travel Distances in a Transportation Network. Transportation Science, 26(2): 129–137. 1992.         [ Links ]

Brimberg J., Love R.F. General Considerations on the Use of the Weighted Lp Normas an Empirical Distance Measure. Transportation Science 27(4):341– 349. 1993.         [ Links ]

Drezner Z., Wesolowsky G.O. The Asymmetric Distance Location Problem. Transportation Science, 23(3):201–207. 1989.         [ Links ]

Hodgson M.J., Wong R.T., Honsaker J. The P–Centroid Problem on an Inclined Plane. Operations Research, 35:221–233. 1987.         [ Links ]

Love R.F., Morris J.G. Mathematical Models of Road Travel Distances. Management Sciences 25:130–139. 1979.         [ Links ]

Plastria F. On Destination Optimality in Asymmetric Distance Fermat–Weber Problems. Annals of Operations Research, 40:355–369. 1992.         [ Links ]

Rockafellar T. Convex Analysis. Princeton University Press. 1970. Pp. 213.         [ Links ]

Sánchez L. y Guillén S. Funciones distancia asimétricas y no positivas definidas, (Primera parte). Revista de Ingeniería, Investigación y tecnología, 9(4):339–346. Octubre–diciembre, 2008. ISSN: 1405–7743.         [ Links ]

Ward J.E., Wendell R.E. A New Norm for Measuring Distance Which Yields Linear Loca tion Problems. Operations Research, 28:836–844. 1980.        [ Links ]

 

Semblanza de los autores

Hérica Sánchez–Larios. Realizó la maestría y el doctorado en ingeniería (Investigación de operaciones), ambos en la Facultad de Ingeniería de la UNAM. Trabajó en PEMEX, fue instructora de cursos sobre instrumentación de laboratorios en CONACYT y ha impartido clases en diversas universidades. Actualmente es investigadora del Instituto de Ingeniería de la UNAM y profesora en el Programa de Maestría y Doctorado en Ingeniería de la UNAM.

Servio Tulio Guillén–Burguete. Es egresado de la ESIME del IPN. Obtuvo la maestría en ingeniería de control y el doctorado en ingeniería (Investigación de operaciones), ambos en la Facultad de Ingeniería de la UNAM. Laboró en el Sistema de Transporte Colectivo Metro de la Ciudad de México. Es investigador del Instituto de Ingeniería de la UNAM y profesor en el Programa de Maestría y Doctorado en Ingeniería, así como en la Facultad de Ciencias de la UNAM.