Estudios e investigaciones recientes

 

Programación lineal con espacios covariante y contravariante. Una perspectiva física y matemática

 

Linear programming in covariant and contravariant manifolds. A physical and mathematical perspective

 

J.L. Urrutia–Galicia¹, J.C. Alcérreca–Huerta² y M.A. Ordaz–Alcántara³

 

¹ Instituto de Ingeniería, Mecánica Aplicada, Universidad Nacional Autónoma de México,

² Facultad de Ingeniería, Universidad Nacional Autónoma de México y

³ Facultad de Ciencias, Universidad Nacional Autónoma de México E–mail: jurg@pumas.iingen.unam.mx

 

Recibido: abril de 2006
Aceptado: noviembre de 2007

 

Resumen

En este artículo se presenta un método de optimización nuevo y diferente a los utilizados actualmente, como en el "Método Simplex". Se basa en el empleo de los espacios covariante y contravariante, ambos espacios biortogonales entre sí, lo que permite una visualización del problema de optimización tanto física como matemática. El resultado obtenido proporciona la mejor aproximación de acuerdo a los datos concentrados en las restricciones del problema, éstas últimas visualizados como vectores (como un espacio completo o incompleto) y no como rectas, planos o hiperplanos. Asimismo, con este nuevo método se puede cuantificar el error generado entre los vectores aproximación y el objetivo, lo que permite observar y medir la efectividad de la solución propuesta.

Descriptores: Métodos de optimización, espacio covariante (espacio de columnas) y contravariante (matriz inversa) –vs– método simplex, rotación de hiperplano, convergencia, solución exacta.

 

Abstract

In this paper a new optimization method is presented. The theoretical back ground is different to that used presently as in the case of the "Simplex Method". The presentation is based on the use of the covariant and contravariant spaces, both being biorthogonal spaces, al low a visualization of the optimization problem from a physical as well as mathematical points of view. The obtained result provides the best approximation according to the data provided in the constraints of the problem, which are visualized like vectors and not like straight lines, planes or hyperplanes. Also, in this new method the error generated between the approximation and the objective vectors can be measured, which allows to observe and prove the accuracy of the proposed solution.

Keywords: Optimization methods, covariant and contravariant spaces –vs– simplex method, hyperplane rotation, convergence, exact solution.

 

Introducción

Bien es sabido que dentro de los márgenes de cualquier problema práctico, lo que se busca es el mejor empleo de los recursos humanos, comerciales, laborales, tecnológicos, etc., de tal manera que se logre la distribución y uso más ventajoso de los mismos. Es por eso que surgen modelos que tratan de optimizar los recursos disponibles, ya sean maximizando ganancias o minimizando gastos o pérdidas.

Los problemas de optimización se presentan en múltiples disciplinas, teniendo en común una meta por alcanzar, sujeta a restricciones que influyen de manera directa limitando las posibles soluciones al problema de maximizar o minimizar el objetivo propuesto. Por ejemplo; en administración, un objetivo muy común es el de maximizar las ganancias, tomando en cuenta los límites impuestos por los tiempos de operación, costos de producción, capital disponible para la inversión, entre otros factores; a nivel industrial, los gastos de operación se encuentran sujetos a la eficiencia de la maquinaria, a los productos manufacturados o la llegada de materia prima.

Fue alrededor de la Segunda Guerra Mundial en que se iniciaron los primeros pasos hacia la búsqueda de modelos matemáticos que resolvieran los problemas de optimización, uno de estos modelos surge con el fin de resolver los problemas de asignación de recursos por parte de la fuerza aérea estadounidense. George B. Dantzig, miembro del proyecto SCOOP (Scientific Computation of Optimun Programs) de la fuerza aérea de E.U., fue quien diseñó el método simplex de solución en 1947, modelo que sigue siendo ampliamente utilizado hasta nuestros días (Fraleigh y Beauregard, 1989a).

El desarrollo de la programación lineal, es considerado por mucha gente como uno de los avances científicos más importantes de la segunda mitad del siglo XX. De hecho, una proporción importante de todo el cálculo científico que se lleva a cabo por computadoras se dedica al uso de la programación lineal y a técnicas íntimamente relacionadas, estimándose en un 25%, de acuerdo a un estudio de la IBM (Marrero et al, 2006).

Un modelo de programación lineal, como el método simplex o el que se desarrolla en este artículo empleando los espacios covariante y contravariante, tratan de proporcionar una vía eficiente para determinar una solución óptima para los problemas de maximización o minimización de un objetivo dadas determinadas restricciones.

 

Método Simplex

Análisis gráfico

El método simplex busca resolver problemas de programación lineal; dicho método, cuando posee dos variables de optimización es visto de manera gráfica como la traza de planos dados por las ecuaciones de las restricciones, generándose un polígono al graficar todas éstas. Al desplazar la traza del plano de la función objetivo hacia el polígono mencionado anteriormente, se obtiene una solución óptima en el primer punto en que ambos se intersectan.

Para mostrar lo anterior, se toma un ejemplo de Fraleigh y Beauregard (1989b), donde se propone el siguiente problema:

Ejemplo 1

Sea una compañía maderera que posee dos talleres de contrachapado, donde se producen los tres mismos tipos de tableros, hallar el número de días que debe operar cada taller durante un semestre para proporcionar de la manera más económica los tableros requeridos. La tabla 1 muestra la producción y costo diarios por taller.

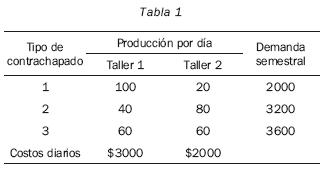
Con los datos contenidos en la tabla podemos determinar tanto la función objetivo como las restricciones que intervienen en el problema:

Minimizar C=3000x₁+2000x₂                     (1)

condicionado a las siguientes restricciones:

100x₁ +20x₂ > 2000

40x_± +80x₂ > 3200                           (2)

60x1 +60x₂ > 3600

y con x₁ > 0,x₂ > 0.

En la figura 1, se encuentra achurado el espacio solución limitado por las gráficas de las trazas de los planos de las restricciones; asimismo, con línea punteada, se encuentra graficada la pendiente de la función objetivo. Al desplazar la función objetivo hacia el polígono e intersectarse, como se muestra en la figura 2, se obtiene la solución óptima, que resulta ser x₁ = 10 y x₂ = 0.

Al sustituir los valores de x₁ y x₂ en la función objetivo de costo inicialmente planteada, se tiene que el costo mínimo de producción sería:

C= 3000(10) + 2000(50)

C = $130 000                           (3)

 

Algoritmo del método simplex

La forma analítica del método simplex funciona de manera similar al método gráfico, la diferencia radica en que para buscar la intersección entre el polígono y la traza de la función objetivo se recorren las aristas del polígono o poliedro generado por las restricciones, siendo los vértices o puntos esquina las soluciones factibles al problema, sin necesidad de probar todos los puntos esquina. Para iniciar el recorrido a lo largo del polígono o poliedro, es necesario añadir a las restricciones, representadas con igualdades o desigualdades como: variables de holgura, variables excedentes y variables artificiales, esto último con el motivo de convertir todas las desigualdades de las restricciones en igualdades, además de que con ello se genera un conjunto de variables básicas y otro de variables no básicas con lo que se puede empezar dicho recorrido.

Primeramente se comienza en cualquier punto esquina, para después moverse hacia cualquier otro adyacente, de manera que la función objetivo se incremente lo más rápidamente posible (Fraleigh y Beauregard, 1989c), para hacer lo anterior, una variable básica se hace no básica y viceversa, disponiendo del conjunto de variables no básicas generado al introducir las variables de holgura, excedentes y artificiales. Un óptimo se alcanza cuando el valor de la función es máximo y ninguna otra solución básica factible puede ser encontrada (Bhatti, 2000).

En caso de que se busque minimizar una función objetivo, cuyas restricciones sean de la forma Ax < b, con b > 0, se hace uso de la siguiente expresión:

[Mínimo de f (x)] =– [Máximo de – f (x)]            (4)

Empleando el problema mostrado anteriormente en el método gráfico, se ejemplifica de manera breve, la forma de resolución a través del algoritmo del método simplex.

Una vez que se han obtenido la función objetivo (1) y las restricciones del problema (2), se procede a convertir las desigualdades de las restricciones en igualdades por medio de la adición, en este caso, de variables excedentes y artificiales, por lo que se tiene:

100x₁ + 20x₂ –y₁ + q₁ =2000

40 x₁ + 80x₂ –y₂ + q₂ =3200                (5)

60 x₁ + 60x₂–y₃ + q₃ =3600

Dado que se desea minimizar la función objetivo C (1) es necesario utilizar la expresión mostrada en (4). Aún cuando las restricciones deban tener la forma Ax < b, la cuestión se ve resuelta tras la añadidura de las variables excedentes.

Las variables artificiales deberán tomar el valor cero para obtener una solución factible al problema original. Entonces el problema de minimizar C se transforma en un problema de maximizar P=–C, siendo la nueva función objetivo:

P = –3000x₁ – 2000x₂ – Mq₁ – Mq₂ – Mq₃                (6)

Donde M es un número muy grande, lo que permite que la función objetivo no se pueda optimizar sin que los qi tomen el valor cero, como se mencionó arriba.

Una vez modificadas las restricciones y la función objetivo, se elabora una tabla inicial donde se hallan concentradas todas las variables de las restricciones (5) y el objetivo.

Para la formación de la última fila de la tabla inicial, correspondiente al objetivo, se tiene que para una columna etiquetada con una variable x_i, se añade en la fila objetivo el negativo del producto de M por la suma de coeficientes que multiplican a x_i en las restricciones. En las columnas etiquetadas con y_i se añade M, mientras que en las etiquetadas con q_i se escriben ceros; en la última columna se tiene el negativo del producto de M por la suma de los términos independientes de las restricciones.

A continuación, mediante un tipo de reducción de Gauss–Jordan, las variables básicas se hacen no básicas y viceversa, hasta que se obtiene la solución óptima al no quedar registros negativos de la fila objetivo y si ninguna variable artificial es básica o si todas las variables artificiales básicas tienen valor cero, como se muestra en las tablas 2 a 4.(tabla 2, 3 y 4)

En la tabla 4, se encuentran los valores de x₁ = 10 y x₂ = 50, obteniéndose el máximo de P igual con –130000. Al emplear nuevamente la expresión señalada en (4), se tiene que el costo mínimo de producción es de $130000, solución que se obtuvo con el método gráfico.

No obstante, hay que destacar que aunque se satisficieron las restricciones del problema, se puede observar en la última columna de la tabla 4 que la variable excedente y₂ tiene un valor igual con 1200, indicativo de una sobreproducción del contrachapado 2 producido por ambos talleres y que, al comparársele con la demanda semestral del producto que es igual con 3200 representa el 37.5% de la ya mencionada demanda, por lo que sería recomendable encontrar una solución alternativa.

 

Método con espacios covariante y contravariante

Este método se basa principalmente en una visión física y matemática de los problemas, por lo que las soluciones encontradas responden a diversas situaciones planteadas en la realidad. Como se verá, las variables de holgura, excedentes y artificiales, que son introducidas en el método simplex, no representan absolutamente nada al utilizar el nuevo método, ya que no forman parte del problema original.

Urrutia (2003), mostró la metodología para invertir matrices rectangulares y para modificar óptimamente las restricciones (cuando esto es posible o mandatario), la cual tiene aplicación para la optimización de funciones dadas determinadas restricciones.

Con el motivo de hacer hincapié en el tratamiento físico que se hará al problema, las restricciones (2) del problema presentado, son escritas de la siguiente manera:

donde las ecuaciones de las restricciones son vistas como una combinación lineal de dos vectores en la que las variables de optimización x₁ y x₂ son escalares que multiplican a los vectores:

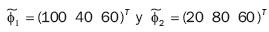
respectivamente, para obtener como objetivo

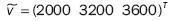
Por otra parte, el fin sigue siendo minimizar la función costo mostrada en (1):

C=3000x₁ +2000x₂

Las restricciones del problema, en este caso, son de la forma Ax > b; sin embargo, lo deseable en un problema de optimización es lograr la igualdad en las restricciones, es decir, que se obtenga la solución a Ax = b o en donde Ax – b resulta mínima. El método con espacios covariante y contravariante (de cálculo tensorial) busca cumplir con dicha igualdad, por lo tanto, al aplicar el método se sustituye el signo de desigualdad y se cambia por el de igualdad en miras de conseguir la mejor solución y de emplear sin dificultades la metodología para invertir matrices rectangulares. Para pasar de la desigualdad a la igualdad no es necesario añadir ningún tipo de variable como sucede en el método Simplex, sino que se busca resolver el problema con las variables presentes en el problema original. Así entonces, las restricciones de este problema se escriben como sigue:

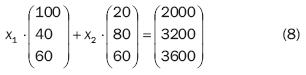
A continuación se agrupan los vectores y las variables de optimización como se muestra:

La matriz que agrupa a los vectores , (pertenecientes al espacio covariante) se le designará con el nombre de A; al conseguir la inversa por la izquierda de dicha matriz (A^–1) escrita en la forma estándar

se obtienen los vectores

que por conveniencia en la visualización de la matriz conformada por vectores es mejor escribir:

Al multiplicar (8) por los vectores (pertenecientes al espacio contravariante) servirán para hallar los valores de las variables de optimización:

al efectuar las operaciones señaladas en (12) y (13), se obtienen los valores de x₁= 14.285714 y x₂= 37.142857 que, al ser sustituidos primero en la ecuación (2) nos daría la siguiente producción:

En seguida se sustituyen x₁= 14.285714 y x₂= 37.142857 en la función costo (1) proporcionando el valor mínimo de costos de producción y el cual resulta ser menor al obtenido con el método simplex:

C = 3000(14.285714) + 2000(37.142857) C = $117142.86             (14)

Haciendo la consideración de que se trabajan 8 horas por día, los valores de x₁ y x₂ al ser fraccionarios significan que se deben trabajar 14 días normales laborables más 2.25 horas extras para terminar la producción en el taller 1 y 37 días con 1.14 horas en el taller 2.

Como se puede apreciar en la figura 3, los vectores se encuentran en un plano diferente al del objetivo 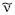; por lo que no se puede generar una solución exacta, siendo el mínimo error la proyección del objetivo sobre el plano generado por .

Aun cuando ya han sido encontrados los valores de las variables de optimización, es necesario entender qué es lo que se hizo matemáticamente, por ello, se recurre a la explicación física que va íntimamente ligada con los resultados y el procedimiento realizado. Así, al sustituir en la ecuación (8) los valores de x₁ y x₂ obtenidos con este método, se obtiene el vector aproximación

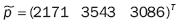
Este último vector resulta de aplicar la ley del paralelogramo de composición de fuerzas de física, también llamada Principio de Stevin, entre los vectores y que se expresa matemáticamente en las ecuaciones (15) y (16).

Al comparar la producción obtenida (16) de los contrachapados 1, 2 y 3 con la demandada por el vector objetivo 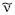= (2000 3200 3600)^T, se tiene una sobreproducción del 8.6% y 11.1% en el contrachapado 1 y 2 respectivamente, y una subproducción del 14.3% del tercer contrachapado.

Esta solución, siendo una mala aproximación, es sin embargo la mejor, pues aun sumando los porcentajes de sobreproducción y subproducción, obtenidos previamente, no superan al error del 37% de sobreproducción que representa optar por la solución calculada con el método simplex; además, nada se puede hacer bajo las actuales políticas de producción impuestas por los números en las columnas de la ecuación (2).

El vector aproximación obtenido, resulta ser la proyección del vector objetivo:

sobre el plano generado por los vectores. Se puede observar en la figura 3 que el vector error debe ser ortogonal al vector aproximación con el motivo de que el error sea mínimo y, por tanto, obtener la mejor solución al problema.

Para comprobar la ortogonalidad entre los vectores aproximación y error, y de que se obtuvo como consecuencia la mejor solución posible, se debe efectuar un producto punto entre dichos vectores, de tal modo que el resultado sea cero.

La diferencia entre los vectores objetivo y aproximación da lugar al vector error

cuya característica, como se dijo anteriormente, es que debe de ser ortogonal al plano donde se localizan , lo cual significa que se obtuvo la mejor aproximación, pues cualquier otra solución generará un vector error mayor en magnitud, que es absolutamente indeseable.

Al calcular el vector error generado con este método se obtiene lo siguiente:

y cuando se efectúa el producto punto entre y el vector aproximación se obtiene el siguiente resultado:

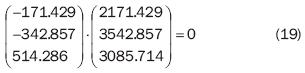
con lo que se demuestra la ortogonalidad entre la solución obtenida y el error con el método de espacios covariante y contravariante al generar el mínimo error posible.

Si se calcula el vector error que se genera al emplear la solución obtenida con el método simplex 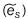, se obtendría primeramente que el vector aproximación sería

y empleando (16), se tiene

Una vez que han sido calculados los vectores error que se generan con ambos métodos, por medio del concepto de norma de un vector se pueden comparar ambos resultados de donde se tiene lo siguiente:

En la figura 4 se pueden observar las dos soluciones que se generan con ambos métodos desde el punto de vista físico, además del resultado obtenido en (23). Para no confundir entre las soluciones encontradas, los valores de las variables de optimización del método simplex se denotan con x_1S y x_2S, asimismo, para el vector aproximación se le designa con el nombre de , mientras que los encontrados por medio de los espacios covariante y contravariante son denotados por x_1C, x_2C y el vector aproximación por .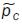

Restricciones x_i > 0

Para el último ejemplo, no se hizo uso de las restricciones x₁ > 0, x₂ > 0, debido al enfoque físico y gráfico mostrado con anterioridad; sin embargo, siendo estrictos estas dos restricciones deben de ser consideradas dentro del conjunto de restricciones del problema por lo que se tendría el siguiente planteamiento global:

minimizar C =3000 x₁ +2000x₂

sujeto a

100x₁ + 20x₂ > 2000

40x₁ + 80x₂ > 3200

60x₁ + 60x₂ > 3600              (24)

1x₁ + 0x₂ > 0

0x₁ + 1x₂ > 0

por lo que ahora se tendría, escrito a manera de combinación lineal y en la forma Ax = b:

de donde se observa que los vectores

pertenecen al espacio 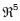, por lo que su representación gráfica resulta imposible, no así su interpretación física.

Siguiendo con la metodología de los espacios covariante y contravariante tenemos que

que al multiplicar (25) de manera similar a la mostrada en (12) y (13), se obtienen los valores de x₁= 14.287924 y x₂ = 37.137416.

Empleando estos nuevos valores y sustituyéndolos en la función costo (1) se tiene:

C= 3000(14.287924) + 2000(37.137416)
                                                                                   (27)
C= $117138.61

que resulta ser un valor más pequeño en costos respecto al valor obtenido en (14).

El vector aproximación resulta ahora de:

con lo que se puede calcular el vector error y por tanto, la norma del mismo:

La nueva solución genera un error mayor, debido a la introducción de las nuevas restricciones. Pese a lo anterior se sigue cumpliendo la ecuación mostrada en (30), así como la ortogonalidad entre los vectores aproximación y error

 

Dado que son los vectores que forman la combinación lineal en las restricciones del problema para cumplir al objetivo v, ecuaciones (8) y (25), es de esperar que si se cambian los valores que conforman los vectores antes mencionados la solución al problema también lo haga. Las restricciones del problema son las que limitan en mayor medida las posibles soluciones al mismo.

La solución del problema de optimización que se obtiene con el método de espacios covariante y contravariante, gira esencialmente en torno de la eficiencia en el cumplimiento de las restricciones y del error que se genera al verificarlas. Mientras tanto, la función objetivo funge como un resultado final cuantitativo de la calidad de las decisiones tomadas, es decir, la función objetivo engloba de manera numérica las consecuencias de tomar en cuenta los valores que pretenden satisfacer las restricciones propuestas.

La visualización y el entendimiento de los problemas de optimización, se refleja inmediatamente en las decisiones tomadas, así como en la capacidad de reacción de una empresa. El siguiente ejemplo muestra que aún cuando el objetivo no se puede alcanzar, la cuantificación del error permite tomar decisiones de qué tan eficaz es la solución presentada para su uso o, definitivamente, cancelar los planes originales de producción y efectuar cambios mínimos en los mismos que permitan alcanzar el objetivo sin error alguno, reflejándose todo ello en la función objetivo que se propone.

Ejemplo 2

Una compañía llantera tiene tres plantas en las cuales se producen llantas para autos de las siguientes medidas R15, R14, R13. Es necesario cumplir con la demanda de 1400, 1500 y 15100 unidades por semana de cada una de las medidas; sin embargo, a causa del deterioro de la maquinaria de R13 en una de las plantas (especializada en esta medida), será empleada solamente la maquinaria de las dos plantas restantes. En la planta A se producen 12, 19 y 3 llantas por hora respectivamente, y en la planta B se producen 13, 8 y 2. Debido a factores de producción, los costos varían de tal modo que el costo promedio unitario de cada llanta por hora es de $250. Con las condiciones antes señaladas se desea optimizar los costos generados tras el cierre de una de las tres plantas de dicha compañía. En la tabla 5 se concentra la información mencionada previamente.

El problema queda expresado física y matemáticamente de la siguiente manera:

Minimizar C =8500y₁ +5750y₂                            (31)

sujeto a:

Aplicando la metodología mostrada con anterioridad se tiene que:

y, con los que se obtienen los vectores del espacio contravariante:

Tomando el signo de igualdad en (32), se multiplican los vectores (33), obteniéndose los valores de y₁=108.334 y y₂=110.853, que al ser sustituidos en (32) dan por resultado el vector aproximación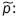

Con el vector aproximación y empleando la expresión (17) se obtiene el vector error:

Para medir qué tan grande o significativo es el error respecto de la aproximación y del objetivo

es necesario recordar que el vector aproximación y el vector error son ortogonales, por lo que se genera un triángulo rectángulo en donde cada lado tiene de magnitud la norma del vector que lo forma, es por eso que se calculan las normas de cada vector:

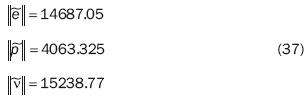
En la figura 5 se muestra el triángulo formado por las normas de los vectores (37) donde es claro que el vector error resultante es más grande que la mejor aproximación que se pueda encontrar, debido a las condiciones iniciales planteadas .

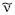El error generado es consecuencia directa del ángulo que existe entre el hiperplano formado por los vectores , y el vector objetivo , el cual se puede calcular con ayuda de la siguiente expresión:

de donde se obtiene el valor de a = 74.5353°.

Dicho ángulo, así como la magnitud del vector error, son valores que deben tenerse muy en cuenta en la toma de decisiones, pues son indicadores de la viabilidad o inviabilidad de la solución obtenida. La factibilidad de la solución es conseguida en el método simplex por medio de un análisis de sensibilidad; sin embargo, en el caso del método con espacios covariante y contravariante, el ángulo indica de manera directa dicha factibilidad puesto que el ángulo representa la relación entre el vector objetivo y la aproximación contenida en el hiperplano formado por los 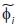. Por ejemplo, si se tuviese que el ángulo a es aproximado o tiende a 90°, se sabría que el vector aproximación tendería al vector cero , y dado que en el cálculo del vector aproximación se emplearon los escalares que proporcionan la solución al problema, se tendría una total inviabilidad de la solución, mismo resultado que arrojarían los análisis de sensibilidad del método simplex.

Regresando al problema, cuando los valores de y₁ y y₂ son sustituidos en la función costo (31) se tiene que:

C =8500(108.3)+ 5750(110.9)

C = $1558225.0                         (39)

Cuando se procede a la resolución de este problema aplicando el método simplex, se obtiene que y₁= 5033.33 y y₂ = 0.

Con las restricciones escritas de la forma mostrada en (32) se calculan los vectores aproximación y error :

de donde se tiene que 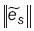= 111208.9, que al ser comparada con la norma del vector error del método con espacios covariante y contravariante (37) se observa una contrastante diferencia.

Al sustituir los valores de y₂ y y₂ obtenidos con la solución del simplex, se tiene que la función objetivo (31) asumiría el siguiente valor

C =8500(5033.33)+ 5750(0)

C=$42 783.33                         (41)

que no resulta nada agradable, sobretodo si se le compara con el resultado obtenido en (39).

Analizando las soluciones presentadas, al aplicar el método simplex, se satisfaría la demanda de llantas a un costo bastante elevado (41), además de que se tendría que cerrar la planta B de la compañía, cuestión que no sería muy aceptable debido a los costos que esto podría representar.

Al mismo tiempo, los enormes excedentes de producción de llantas R15 y R14 en la planta restante podrían desencadenar otros problemas relacionados con la maquinaria, como puede ser su deterioro inmediato (factor que propició el cierre de la planta C), o una acumulación de inventario que se ve reflejado en costos por almacenamiento.

Por otro lado, comparando los resultados obtenidos por el método de espacios covariante y contravariante se obtiene un valor muy bajo en cuanto al costo de producción de llantas (39), además de que ambas plantas A y B se mantienen operando conjuntamente sin poner en riesgo la maquinaria que en ellas se dispone. Respecto a los excesos en la producción de llantas R15 y R14 que son de 1341 y 1445 respectivamente, y que se observan en los dos primeros elementos del vector error (36), no resultan ser tan grandes como los obtenidos en el método simplex: 59000 y 94133 para las llantas R15 y R14, y que se pueden observar en los dos primeros elementos del vector en la ecuación 40.

Mientras tanto, la falta de producción de 14553 llantas R13 que se obtiene por el método con espacios covariante y contravariante, y que se muestra en el tercer elemento del vector error (36), es el reflejo del cierre de la planta C especializada en este ramo y de la incapacidad de las plantas A y B para poder suplirla.

Dado que ninguna de las dos soluciones propuestas resultan ser viables: la del método simplex por los altos costos que representa tomar dicha solución y la del método con espacios covariante y contravariante por no cumplir satisfactoriamente con la demanda; debe considerarse seriamente un cambio en los niveles de producción actuales a fin de completar la demanda propuesta inicialmente y lograr un mínimo en los costos de producción.

 

Rotación de planos (Cambios de producción)

Aunque el método con espacios covariante y contravariante no satisface la demanda, posee una ventaja amplia sobre el método simplex, pues proporciona una visualización física del problema, en la cual el resultado obtenido es la proyección del vector 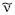sobre el hiperplano generado por los vectores. Puesto que los vectores y v no son coplanares, no se puede obtener una solución exactaal problema; sin embargo, si los vectores son proyectados sobre el hiperplano que contiene al vector 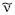, se logra que todos los vectores sean coplanares y alcanzar así una solución exacta.

La metodología presentada por Urrutia–Galicia (2003), permite realizar lo anterior con base en que el hiperplano que contiene a los vectores y será rotado un ángulo θ hasta alcanzar la posición en la que el vector 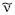se halle contenido en éste, posteriormente los vectores son proyectados en el nuevo hiperplano que contiene al vector 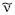, (Figura 6).

La rotación del hiperplano, así como la proyección de los vectores sobre el mismo, representan los cambios mínimos requeridos en los niveles de producción a fin de satisfacer la demanda planteada inicialmente, con lo que no se producirá error alguno después de efectuar dichos cambios.

Continuando con el ejemplo de la compañía llantera, la cual tiene serios problemas con su producción, es urgente y necesario el cambio en los niveles de producción a fin de sobrellevar su situación actual. Empleando los resultados obtenidos con el método de espacios covariante y contravariante, el primer paso es generar el hiperplano que contenga al vector objetivo 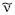de las restricciones, para lo cual se requiere de un vector normal a dicho hiperplano. Para poder calcular el vector normal, se hará uso de la matriz auxiliar de la ecuación 42.

la cual se halla integrada en la primera columna por el vector 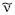normalizado y en la segunda por el vector error normalizado .

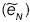Al calcular la matriz inversa de B (B^–1), se sabe que estará integrada por los vectores contravariantes

y por lo tanto, el vector

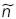es ortogonal al vector consecuentemente es el vector normal al hiperplano que contiene al vector .

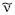Al normalizar 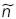se puede escribir la ecuación del hiperplano rotado como sigue:

–0.6745z₁ –0.7248z₂ +0.1345z₃ –

–0.0277z₄ –0.0283z₅ =0                         (44)

Al sustituir en (44) los valores de

Z₁ = Z₂ = Z₃ = Z₄ = 1

y despejar el valor de Z₅, se obtiene un vector arbitrario

perteneciente al hiperplano rotado que, junto con el vector

que es 100 veces más pequeño que el vector por conveniencia, será utilizado para obtener las proyecciones de los niveles de producción actuales

en el nuevo hiperplano.

Empleando una combinación lineal, cuya forma es análoga a (8) y a (32), se tiene:

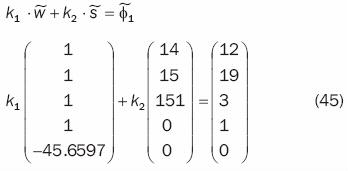
donde los valores de k₁ y k₂ se obtienen fácilmente multiplicando la matriz inversa generada con los vectores por (45), de tal modo que k₁ =0.0134 y k₂ =0.0389.

Al sustituir los valores k₁ y k₂ en (45) se obtiene la proyección de sobre el hiperplano rotado

Para obtener el valor de la proyección de sobre el hiperplano rotado, se procede de manera similar:

obteniéndose los valores de k₁ = –0.131 y k₂ – 0.0261, que al ser sustituidos proporcionan el vector proyección de :

Una vez que han sido encontrados los vectores se tiene que la situación de la compañía ha cambiado tras realizar los cambios mínimos de producción representados por los vectores anteriormente señalados.

De esta manera, el problema precisado por las restricciones queda como sigue:

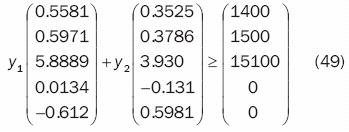
Al resolver esta situación por medio del método con espacios covariante y contravariante, se tienen los valores de y₁= 1523.7 y y₂= 1559.14, que al ser sustituidos en (49) ofrecen una solución exacta al problema con error cero:

La función de costos, después de los cambios de producción, se ve modificada por el volumen de producción de llantas por planta manteniéndose constante el costo unitario de cada llanta por hora planteado inicialmente, es decir, en promedio $250 por cada llanta fabricada en cada planta:

0=67082.71y₁ +45417.29y₂

C= 67082.71(1523.7) + 45417.29(1559.14)                   (51)

C = $173 026336.11 

Sin embargo, aun cuando el problema ha sido resuelto, es necesario manejar los números para presentarlos en la situación real propuesta por la compañía. Es por eso que al efectuar los productos señalados en (50) se tendría, en las tres primeras filas de los vectores, la producción semanal de llantas para cada una de las plantas A y B:

Considerando que en la semana se trabajan 5 días, y que cada día consta de 8 horas, se tendría que dividir la producción semanal entre 40 para obtener la producción por hora (ver tabla 7).

En resumen, para la situación que enfrenta la compañía se presentan tres opciones en donde la viabilidad de la solución propuesta depende, en gran medida, de factores inherentes a la producción que podrían ser detonantes de costos muy elevados que alterarían el resultado final; por ejemplo, los costos por almacenamiento del producto sobrante y cierre de una planta como se muestra en el método simplex, el incumplimiento de la demanda en el caso del método con espacios covariante y contravariante, o los costos que representaría un cambio de producción en la última solución propuesta, por lo que es necesario analizar profundamente cada una de las soluciones propuestas y en un caso real contemplarlo directamente en la función de costo.

Así pues, se tendrían que observar las situaciones en que podrían verse aplicadas las soluciones antes señaladas. Por ejemplo, en un caso de seguridad nacional y que en lugar de producción de llantas se produjeran distintos tipos de armas y, además se estuviese en guerra, los costos de fabricación no serían "tan" importantes (sin importar cuantos turnos diarios fueran necesarios) como la satisfacción al 100% de la demanda debido al peligro que se enfrentaría el país al no cumplirla, por lo tanto, la solución mostrada por el método simplex, y la mostrada con los cambios de producción mostrados en la tabla 7, serían las óptimas, aceptándose de entre éstas la que menor costo represente. Otro escenario, en el que la premura de cumplir la demanda no sea relativamente urgente, se podría pensar tanto en los cambios de producción como en la construcción o reparación de la fábrica C, mientras lo anterior acontece se podría producir con los niveles mostrados por la solución con los espacios covariante y contravariante (34), o con los vistos por la solución del método simplex, siendo por supuesto el óptimo, el que constituya menores pérdidas para la compañía.

 

Conclusiones

Como se vio a lo largo del artículo, existen muchas diferencias entre el método de espacios covariante y contravariante (álgebra tensorial), y el método simplex, motivo por el cual se ha hecho hincapié en los aspectos más relevantes que puedan interesar al lector, lo cual redundará en una mejor comprensión de la optimización.

Por ejemplo, en el caso del método simplex se puede hablar de la posible obtención de ceros en las variables de optimización lo que significaría el nulo funcionamiento del factor que acompaña a dichas variables, lo que representa costos o pérdidas. Otro detalle reside en la adición de más variables de optimización o en el número de restricciones, lo cual complica el tratamiento de los problemas con el método simplex, requiriendo así, paquetería de cómputo muchas veces especializada en la cual sólo se mantiene un proceso mecanizado. Por su parte, el "método tensorial" con espacios covariante y contravariante no complica su forma de operación, ya que resulta análoga a los ejemplos mostrados, aun cuando se añadan más variables de optimización o restricciones. Además, una ventaja adicional del método con espacios covariante y contravariante, se muestra en la nula participación de la función a optimizar, permitiendo reformularla y contemplar más factores que intervengan en ella, como lo fue en su momento en los cambios de producción.

Un aspecto importante que se señala es la visualización física que se puede tener para la resolución de los problemas, pues el mundo en que habitamos no es puramente matemático; es por esto que al añadir las variables de holgura, excedentes y artificiales en el método simplex, se señala que dichas variables no forman parte del problema original, por lo que el método con espacios covariante y contravariante las omite y se limita a trabajar sólo con la información proporcionada. También, dicha visualización permite la cuantificación del vector error, el cual fue calculado tanto para el método simplex como para el método con espacios covariante y contravariante, mostrándose en los ejemplos que la magnitud del vector error generado en el método simplex resulta mayor que el generado por el método de espacios covariante y contravariante, pues el primero no posee el concepto de mejor aproximación con los datos proporcionados y esto se pone de manifiesto de manera más explícita en el ejemplo de la compañía llantera; de igual forma, estos resultados se reflejan en las funciones que se deseó optimizar, siendo el método con espacios covariante y contravariante el que obtuvo las cifras económicas más ventajosas, permitiendo además realizar en cualquier caso, los cambios de producción pertinentes que, de otro modo, serían imposibles de observar con el método simplex. Cabe admitir que si bien el método simplex satisface todas las restricciones, irónicamente no arroja el resultado óptimo como se demuestra con el vector error, por lo que resulta en este sentido mucho más viable el método con espacios covariante y contravariante.

Para finalizar, existe mucha literatura acerca de optimización y programación lineal, así como de diversos métodos como el simplex que abordan estos temas (Mangasarian, 2004; Lin et al., 1998; Monteiro et al., 2004; Pan, 2005; Byrd et al, 2005). Se invita al lector a revisar dichos métodos y a compararlos con el método con espacios covariante y contravariante, notando que los primeros son abordados de manera más complicada y en su mayoría inaccesible para el entendimiento de la gran mayoría de la gente, limitándose, desgraciadamente, a ser manejados por personas especializadas en la materia.

En el caso del nuevo método presentado, todo lo que el lector necesita es la cuidadosa lectura del capítulo 1 del libro de Flügge (1972) sobre definiciones básicas de bases covariantes y contravariantes y del álgebra relacionada con ellas (Urrutia, 2003).

 

Referencias

Bhatti M.A. Practical optimization methods with mathematica® applications. NY. Springer Verlag. ISBN 0–387–98631–6. 2000.        [ Links ]

Byrd R.H., Gould N.I.M., Nocedal J. and Waltz R.A. On the conver gence of succes sive linear–quadratic programming algorithm. SIAM J. Optim., 16 (2). 2005.        [ Links ]

Cánovas M.J., López M.A., Parra J. and Toledo F.J. Distance to solvability/ unsolbavility in linear optimization. SIAM J. Optim., 16 (3). 2006.        [ Links ]

Flügge W. Tensor analysis and continuum mechanics. NY. Springer Verlag. 1972.        [ Links ]

Fraleigh J.B. and Beauregard R.A. Álgebra lineal. Addison–Wesley Iberoamericana, S.A (1989a). Chapter 9. pp. 441. Líneas 1–6 del pie de página. ISBN 0201–64420–7.        [ Links ]

Fraleigh J.B. and Beauregard R.A. Álgebra lineal. Addison–Wesley Iberoamericana, S.A. (1989b). Chapter 9. Pp. 440–443. ISBN 0201–64420–7.        [ Links ]

Fraleigh J.B. and Beauregard R.A. Álgebra lineal. Addison–Wesley Iberoamericana, S.A. (1989c). ISBN 0201–64420–7.        [ Links ]

Lin Chih–Jen, Fang Shu–Cherng and Wu Soon–Yi. An unconstrained convex programming approach to linear semi–infinite programming. SIAM J. Optim., 8 (2). 1998.        [ Links ]

Mangasarian O.L. Knowledge–based linear programming. SIAM J. Optim., 15(2). 2004.        [ Links ]

Marrero–Delgado F., Asencio–García J., Abreu–Ledón R., Orozco–Sánchez R. and Granela–Martín H.R. Herramientas para la toma de decisiones: La programación lineal (2006). (en línea). Disponible en: http//www.monografias.com/trabajos6/proli/proli.shtml        [ Links ]

Monteiro R.D. and Tsuchiya T. A new iteration–complexity bound for the MTY predictor corrector algorithm. SIAM J. Optim., 15 (2). 2004.        [ Links ]

Pan P.U. A revised dual projective pivot algorithm for linear program ming. SIAM J. Optim., Vol. 16 (1). 2005.        [ Links ]

Urrutia–Galicia J.L. La matriz inversa generalizada (el espacio contravariante) a–1 de matrices de orden mxn con m > n y la solución cerrada a este problema. Revista, Ingeniería Investigación y Tecnología, IV(1). Enero–Marzo 2003. Facultad de Ingeniería UNAM. ISSN 1405–77.        [ Links ]

 

Semblanza de los autores

José Luis Urrutia–Galicia. Obtuvo el grado de ingeniero civil en la Facultad de Ingeniería, UNAM en 1975, asimismo, los grados de maestría (1979) y doctor (1984) en la Universidad de Waterloo, en Ontario, Canadá. Es investigador del Instituto de Ingeniería, UNAM en la Coordinación de Mecánica Aplicada. Sus áreas de interés cubren: matemáticas aplicadas y mecánica teórica, análisis tensorial, estabilidad y vibraciones de sistemas discretos, vigas, placas y cascarones. Ha recibido reconocimientos como el "Premio al Mejor Artículo" de las Transacciones Canadienses de Ingeniería Mecánica (CSME) (Montreal, Canadá 1987) por el artículo "The Stability of Fluid Filled, Circular Cylindrical Pipes, Part II, Experimental", también le fue otorgada la "Medalla Duggan", que es la más alta distinción otorgada por la CSME (en la universidad de Toronto, Canadá 1990) por el artículo "On the Natural Frequencies of Thin Simple Supported Cylindrical Shells".

Juan Carlos Alcérreca–Huerta. Estudiante de la carrera de ingeniería civil en la Facultad de Ingeniería de la UNAM. Recibió la medalla Gabino Barreda por sus estudios de preparatoria en la Escuela Nacional Preparatoria "Miguel E. Schulz" de la UNAM. En 2004, obtuvo tercer lugar de informes técnicos de las estancias cortas del programa Jóvenes hacia la Investigación, en el Instituto de Ingeniería con el Dr. J.L. Urrutia Galicia, en las áreas de física, matemáticas y computación. En el mismo año ganó el segundo lugar en el concurso interpreparatoriano de Matemáticas VI área I, así como el tercer lugar de Física IV. Actualmente es discípulo del Dr. José Luis Urrutia Galicia.

Miguel Ángel Ordaz–Alcantara. Egresado de la Escuela Nacional Preparatoria No. 2 Erasmo Castellanos Quinto. Fue merecedor en 2002 de la nominación a la presea Bernardo Quintana al mérito excelencia académica. Además, durante su estancia en la preparatoria 2 perteneció al programa Jóvenes hacia la investigación realizando cuatro estancias cortas en los años de 2003 a 2006, de las cuales una fue en el Instituto de Química, otra en la FES Zaragoza y dos más en el Instituto de Ingeniería, en esta última institución actualmente es discípulo del Dr. José Luis Urrutia Galicia. En 2005, obtuvo el segundo lugar en el XIII concurso Feria de las Ciencias de la UNAM con el trabajo "Como funciona una montaña rusa". En 2006, ingresó a la carrera de física en la Facultad de Ciencias de la UNAM, en donde actualmente cursa el tercer semestre.