El modelo aditivo doble multiplicativo. Una aplicación a la mortalidad mexicana*

 

The additive double multiplicative model. An application to the mexican mortality

 

José Manuel Aburto y Víctor Manuel García-Guerrero

 

El Colegio de México, México.

 

Artículo recibido el 22 de abril de 2014.
Aprobado el 16 de febrero de 2015.

 

Resumen

El método de Lee-Carter ha sido adoptado en varios países para estimar y pronosticar las tasas de mortalidad por edad y periodo. Esta popularidad se debe a su parsimonia. Más aún, este modelo ha dado resultados satisfactorios para varios países (México, Chile, Estados Unidos, países del G7, etc.). Por otro lado, el modelo Aditivo Doble Multiplicativo propuesto por Wilmoth (1993) tiene la misma función que incorpora los efectos cohorte. En el presente trabajo ambos métodos se aplican al contexto de la mortalidad histórica mexicana y se comparan los resultados.

Palabras clave: Mortalidad mexicana, estimaciones de mortalidad, modelo aditivo doble multiplicativo, método de Lee-Carter, métodos demográficos.

 

Abstract

The Lee-Carter method has been adopted in several countries to estimate and forecast mortality rates by age and period. Such popularity is mainly due to its parsimony. Moreover, this model has been successful for several countries (Mexico, Chile, the U.S., G7 countries, etc.). Furthermore, the model proposed by Wilmoth called Additive Double Multiplicative involves the same function and incorporates the cohort effects. In this paper both methods are applied and compared to the historical Mexican mortality.

Keywords: Mexican mortality, mortality estimates, additive double multiplicative model, Lee-Carter model, demographic methods.

 

Introducción

El intento de encontrar una función para modelar la mortalidad por edades tiene una larga historia en estudios de Demografía y en las ciencias actuariales. El primer antecedente de una fórmula matemática que intentó describirlo fue realizado por De Moivre (1725), quien escribió una función de sobrevivencia de la forma S(x) = 1 - x/ω (ω es el último grupo de edades). Posteriormente, Gompertz (1825) observó que para el grupo de edades de entre 20 y 60 años, la fuerza de mortalidad se incrementaba casi exponencialmente con la edad (μ(x) = ae^bx). Desde entonces, algunos estudios han confirmado que la ley de Gompertz se cumple para varios países e inclusive para varias especies. Sin embargo, se ha encontrado que tanto para los primeros como para los últimos grupos de edades el ajuste no es tan preciso, por lo que se han propuesto diversos modelos para corregir esta falta de ajuste, particularmente en las últimas edades (Makeham, 1867; Thiele, 1872; Wittstein, 1883; Pearson, 1895; Perks, 1932; Heligman y Pollard, 1980; Hannerz, 1999; entre otros).

Existen también métodos que utilizan las funciones que establecen una relación lineal en diferentes momentos entre el logito de las funciones de supervivencia observadas y uno estándar. Cuando se tiene poca información o ésta es de mala calidad, estos métodos primero modelan la esperanza de vida al nacer mediante una función logística y luego utilizan tablas modelo de mortalidad para imputarles una estructura por edades. En casi todos esos casos, directa o indirectamente, los parámetros de los diferentes modelos son variables aleatorias (García Guerrero y Ordorica, 2012).

En los últimos 30 años se han revelado errores en las estimaciones demográficas de la mortalidad (Stoto, 1983). Keilman (1998) reportó que las primeras estimaciones no consideraban eventos importantes, como el incremento de la fecundidad después de la Segunda Guerra Mundial y el decremento en países como Grecia y España después de 1985. La reducción de la mortalidad en edades avanzadas fue subestimada y se reflejó al proyectar la esperanza de vida.

En este sentido, uno de los modelos que ha representado un hito en la modelación de la mortalidad de los últimos tiempos es el propuesto por Lee y Carter (1992). Ellos presentaron un método estocástico para estimar y proyectar la mortalidad de Estados Unidos que provee buenos resultados al ajustar la mortalidad para varios países como México (García Guerrero y Ordorica, 2012), Canadá (Lee y Nault, 1993), Chile (Lee y Rofman, 1994) y Japón (Wilmoth, 1996), entre otros. Además, por su simplicidad, este método ha sido adoptado por diversas instituciones como estándar para estimar el riesgo del envejecimiento (por ejemplo, el Fondo Monetario Internacional) (Oppers et al., 2012).

Para la estimación de los parámetros involucrados en el modelo Lee-Carter (LC) los autores proponen la Descomposición de Valores Singulares (DVS o SVD por sus siglas en inglés). Posteriormente, Wilmoth (1993) propuso utilizar Mínimos Cuadrados Ponderados (MCP) o Máxima Verosimilitud (MLE por sus siglas en inglés), aunque no fue sino nueve años después que se planteó un método para obtener la solución óptima utilizando MLE (Brouhns et al., 2002).

El modelo LC es un caso particular del propuesto por Wilmoth (1989), quien realizó un análisis de las tasas centrales de mortalidad por edad específica e incorporó las tres dimensiones demográficas básicas: edad, cohorte y periodo. De esta manera, llegó a una descripción inicial de la estructura de la matriz de datos de mortalidad con respecto a los cambios en edad y periodo. Además, complementó esta descripción con la consideración de residuales que están relacionados fuertemente con los efectos cohorte. Su investigación fue motivada por la pregunta ¿la mortalidad actual es una función de la mortalidad pasada?

Posteriormente, Wilmoth (1993) propuso el método Aditivo Doble Multiplicativo¹ (ADM) para estimar los parámetros del modelo que había propuesto. Llevó a cabo un análisis exploratorio de datos enfocado en las tres dimensiones mencionadas; el uso de un modelo que es asimétrico en edad, periodo y cohorte se justifica con una discusión de los problemas de identificación de los modelos que involucran variables perfectamente colineales.

En este artículo se modela y estima la mortalidad de México a partir de los patrones generales que muestran la información empírica disponible para el periodo 1930-2009. Para ello se utilizan el modelo ADM y el LC con el objetivo de estudiar si es posible utilizar el segundo, dada su parsimonia, en el contexto mexicano. De esta manera, en primer lugar se explica la lógica del modelo ADM y el método iterativo de estimación; después se explica el modelo LC y el LC modificado de acuerdo con la propuesta del presente trabajo, se explican tres métodos para estimar sus parámetros: Descomposición en Valores Singulares (DVS o SVD por sus siglas en inglés), Mínimos Cuadrados Ponderados (MCP) y Máxima Verosimilitud (MLE por sus siglas en inglés). Enseguida se modela y estima la información sobre la mortalidad mexicana, por sexo y edades utilizando el ADM y el LC, con cada una de sus formas de estimación; se analizan los resultados y se concluye cuál es el mejor método para la información mexicana. Estas técnicas son aplicadas a los datos "brutos", es decir, sin aplicarles a priori alguna técnica de suavizamiento. Esta decisión se tomó con el fin de no perder de vista algún efecto de edad, cohorte o periodo de los datos. Sin embargo, una vez obtenido el valor de los parámetros, estos sí fueron suavizados con el objetivo de presentar estimaciones sin errores de mala declaración de edad. Finalmente, este artículo se concluye con algunas sugerencias y reflexiones finales.

 

El modelo aditivo doble multiplicativo (ADM)

Con el propósito de demostrar que la mortalidad actual es función de la mortalidad del pasado, Wilmoth (1990) propuso modelar esta variable demográfica como una función lineal de varios parámetros: uno que determina la estructura etaria histórica de la mortalidad (α_i), donde i está en [0, ω+] se refiere a las edades que van desde los cero años hasta el último grupo abierto denotado por ω+; otro que indica la distribución promedio de las defunciones a lo largo del tiempo (β_j), donde j se refiere a los años o periodos; otro que señala el efecto cohorte sobre la mortalidad (θ_k), donde k = j - i indica el año de nacimiento de las cohortes y un conjunto de términos multiplicativos que señalan la interacción entre las dimensiones edad y periodo ϕ_m γ_im δ_jm. Matemáticamente,

Los parámetros del modelo anterior son estimados en etapas: con el fin de explorar los patrones por edad y periodo, se ajusta primero el modelo f_ij= α_i + β_j + ε_ij donde los parámetros cumplen que Σ_ij β_ij= 0, con lo que:

A esta primera fase Wilmoth la llamó fase de exploración (Wilmoth, 1990: 298).

Ahora bien, si el modelo (1) estuviese completamente especificado, los residuales deberían comportarse como ruido o como un proceso puramente aleatorio (véase Chatfield, 1995). Sin embargo, Wilmoth encontró que dichos residuales, definidos como:

siguen un patrón que podría ser modelado de la siguiente forma:

r_ij = Σ^ρ_{m = 1} ϕ_m γ_im δ_jm + ε_ij, donde los parámetros conforman un conjunto de funciones de bases ortogonales que se calculan utilizando el Método de Descomposición en Valores Singulares (DVS o SVD por sus siglas en inglés).

Así, el autor define 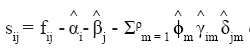de tal manera que se ajusta un modelo de la forma s_ij = θ_k + ε_ij donde k = j - i. Los parámetros θ^_k resultantes son los efectos diagonales residuales o efectos cohorte. El análisis exploratorio implica un modelo donde i, j, k, representan renglones (edades), columnas (periodos) y diagonales (cohortes), respectivamente. Las α dan la forma por debajo de la curva de mortalidad sobre el periodo entero y las β indican el nivel de la curva para el año j. La parte multiplicativa muestra una evolución lenta en la forma de la curva a través del tiempo. Finalmente, los efectos de la diagonal θ_k muestran el monto promedio de "exceso en la mortalidad" para la cohorte k sobre el periodo de estudio.

Finalmente, el modelo se ajusta de acuerdo con el siguiente procedimiento iterativo:

α_i⁽ⁿ⁾ ← 1/J ∑_j (f_ij - θ_k^{(n - 1)})

β_j⁽ⁿ⁾ ← 1/I ∑_j (f_ij - α_i⁽ⁿ⁾ - θ_k^{(n - 1)})

(ϕ_m⁽ⁿ⁾, γ_m⁽ⁿ⁾ , δ_m⁽ⁿ⁾ ) ← SVD_ρ (f_ij - α_i⁽ⁿ⁾ - β_j⁽ⁿ⁾ - θ_k^{(n - 1)})

θ_k⁽ⁿ⁾ ← 1/w_k ∑_k f_ij - α_i⁽ⁿ⁾ - β_j⁽ⁿ⁾ - ∑^ρ_{m = 1} ϕ_m⁽ⁿ⁾ γ_m⁽ⁿ⁾ δ_m⁽ⁿ⁾

donde la tercera línea indica que los términos multiplicativos son derivados de los primeros ρ términos de la DVS aplicada a la matriz (f_ij-α_i⁽ⁿ⁾-β_j⁽ⁿ⁾-θ_k^{(n - 1)}) y w_k es el número de observaciones en la k-ésima diagonal. Como datos iniciales se supone que θ_k⁽¹⁾ ≡ 0 para todo k (Wilmoth, 1995: 329-330).

 

El modelo de Lee-Carter

Para estimar y proyectar las tasas centrales de mortalidad (m_x,t), Lee y Carter (1992) propusieron un caso particular del modelo de Wilmoth indicado en la ecuación (1). Ellos definen una función de tres parámetros que captan dos dimensiones fundamentales de este fenómeno demográfico: la edad y el tiempo (Lee y Carter, 1992). El modelo de Lee-Carter (LC) se expresa matemáticamente de la siguiente manera: f_x,t = ln(m_x,t) a_x + b_xk_t + ε_x,t, donde a_x es un parámetro que indica la forma histórica promedio de la mortalidad por edades, b_x indica la intensidad de la mortalidad a cada edad, el parámetro k_t indica la tendencia temporal histórica de la mortalidad (LC lo llaman índice de mortalidad) y ε_x,t es un término de error. En este trabajo se propone una adaptación, incorporando un parámetro que describa el nivel de la curva de la mortalidad, denotado como C_t (equivalente al parámetro β_j del modelo ADM). Así, el modelo LC adaptado se expresa de la siguiente manera: f_x,t = ln(m_x,t) a_x + C_t + b_xk_t + ε_x,t (2).

Para que el modelo tenga solución única se deben cumplir las siguientes restricciones: Σ_t k_t = 0, Σ_x b_x = 1 y Σ_t C_t = 0. De esta manera, el vector a_x se calcula como el promedio sobre el tiempo y el vector C_t se calcula como el promedio sobre las edades del logaritmo de las tasas centrales de mortalidad. El resto de los parámetros son calculados con distintas técnicas estadísticas; en este trabajo se utilizan y comparan tres de ellas: Descomposición en Valores Singulares (DVS o SVD por sus siglas en inglés), Mínimos Cuadrados Ponderados (MCP) y Máxima Verosimilitud (MLE por sus siglas en inglés).

 

Estimación con Descomposición de Valores Singulares

La primera propuesta de Lee y Carter para calcular los parámetros de la ecuación r_x,t = ln(m_x,t) - â_x - Ĉ_t fue usar Descomposición de Valores Singulares (DVS). Formalmente, la DVS indica que para toda A que está en R^mxn de rango r, existen matrices ortogonales U_mxm y V_mxm, y una matriz diagonal D_rxr= diag(σ₁, σ₂,...,σ_r) tales que:

donde σ_i es el i-ésimo eigen valor de la matriz A. En la factorización anterior, a las columnas de la matriz U se le denomina eigenvectores izquierdos de la matriz A y a los renglones de V se les denomina eigenvectores derechos de la misma matriz (García Guerrero y Ordorica, 2012). En este marco:

El modelo DVS es muy popular por parsimonioso; sin embargo, Alho (2000) señala que el método no es óptimo y propone que la MLE puede producir mejores soluciones. De acuerdo con este autor, la principal razón por la cual un modelo de Poisson es óptimo para ajustar el modelo es que cuando se ajusta por medio de MCO o DVS se supone que la varianza de los residuales es constante a lo largo del tiempo y de las edades. Sin embargo, debido al bajo número de defunciones en edades avanzadas el logaritmo de la fuerza de mortalidad es mucho más volátil que en las primeras edades o en las intermedias.

 

Estimación con Mínimos Cuadrados Ponderados

Cuando el modelo (2) se ajusta por medio de Mínimos Cuadrados Ordinarios (MCO), la interpretación de los parámetros es sencilla: a_x es igual al promedio de ln(m_x,t) sobre la edad y C_t es el promedio sobre el tiempo; al igual que en la aproximación por DVS, b_x representa la intensidad de la mortalidad por edad y k_t representa la tendencia de la mortalidad en el tiempo (Wilmoth, 1993 y García Guerrero y Ordorica, 2012).

Dadas estas restricciones el modelo se ajusta minimizando la suma de cuadrados, esto es Min Σ^ω+_{x = 0} Σ^T_{t = 1}[log(m_x,t) - â_x - Ĉ_t - b_x k_t)² sujeto a que Σ^ω+_{x = 0} b_x = 1 y Σ^T_{t = 1} k_t = 0. La forma más simple de minimizar esta ecuación es, primero, calculando el vector a_x como el promedio por edad del logaritmo de las tasas centrales de mortalidad, mientras C_t representa el promedio por año del logaritmo de esas mismas tasas. Luego, se calculan b_x y k_t con DVS de la matriz log(m_x,t) - â_x - Ĉ_t. Si se define D_x,t como el número de defunciones observadas a la edad x en el año t, entonces la varianza de ln(m_x,t) es aproximadamente igual a D^-1_x,t (Wilmoth, 1989). Entonces se minimiza la ecuación Σ^ω+_{x = 0} Σ^T_{t = 1} D_x,t [log(m_x,t) - â_x - Ĉ_t - b_x k_t)². Para ello, es necesario calcular sus ecuaciones normales respecto a cada parámetro. De esta manera:

Existen soluciones simultáneas de estas ecuaciones que son más fáciles de realizar iterativamente: se seleccionan valores iniciales para los parámetros (usualmente son los ajustados por DVS) y luego, las ecuaciones anteriores se calculan de manera secuencial hasta que el cambio en el valor de los parámetros sea muy pequeño.

 

Estimación con Máxima Verosimilitud

Otra forma de ajustar el modelo LC es especificar un modelo probabilístico. Sean d_x,t una variable aleatoria que representa el número de defunciones de edad x en el año t, y D_x,t las defunciones observadas a edad x en el año t. De acuerdo con Brillinger (1986), d_x,t se aproxima a una distribución Poisson con media λ_x,t, donde λ_x,t = m_x,t E_x,t, m_x,t = exp(a_x + C_t + b_xk_t) son las tasas centrales de mortalidad y E_x,t son los expuestos al riesgo de fallecer a edad x en el tiempo t.

La función de verosimilitud de una distribución Poisson se expresa como: L(d; λ) = λ^d exp^-λ/d! De igual manera, la función de log-verosimilitud para dicha distribución se expresa como l(d; λ) = d ln(λ) - λ - ln(d!). Suponiendo que las defunciones son independientes a lo largo del tiempo y entre edades, entonces, l(d; λ) = Σ_x,t [d_x,t ln(λ_x,t) - λ_x,t]. Para maximizar la función de log-verosimilitud se pueden utilizar diversos métodos y algoritmos, como el cuasi-Newton, el simplex o el de maximización de esperanzas (EM).

Para este trabajo se utilizó el algoritmo iterativo propuesto por Brouhns et al. (2002), el cual consiste en estimar los parámetros de la forma:

En el caso del modelo LC adaptado, se tienen cuatro series de parámetros por estimar: a_x, b_x, C_t y k_t. El proceso de actualización es el siguiente: se inicia el proceso haciendo:

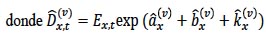es el número estimado de defunciones después de la v-ésima iteración.

Un problema operativo de este método aplicado al caso de la mortalidad es que se necesita el número de expuestos al riesgo a cada edad y en cada periodo. En el caso de los países desarrollados esto no representa problema alguno, dada la alta calidad de sus registros administrativos. Sin embargo, en países como México es necesario realizar una conciliación demográfica que proporcione coherencia entre las cifras de la población total y las de los eventos demográficos registrados. Para el caso que aquí se trata, no se dispone de esta información para los años 1930-1960, ya que la conciliación demográfica que abarca un periodo temporal más largo comienza su estimación en el año 1960 (SOMEDE, 2011). La conciliación realizada por el Consejo Nacional de Población (CONAPO, 2012) es muy corta, comienza en 1990 y existen dudas sobre su calidad (García Guerrero, 2013).

 

Aplicación a la mortalidad de México

Los datos seleccionados para ajustar el modelo son las defunciones registradas de 1930 a 2009 en México. Las cifras de mortalidad adolecen de una mala cobertura, sobre todo las más antiguas. Sin embargo, en este trabajo no se realiza ningún ajuste previo a ello considerando que las defunciones ocurridas y registradas el mismo año son una buena proxy de las dimensiones que se desean captar, aunque fue necesario omitir las edades 0, 1 y 2 debido al alto subregistro de las mismas.

 

El modelo ADM aplicado a la mortalidad mexicana

Las defunciones por edad, año y sexo son transformadas logarítmicamente; esta transformación significa que las partes de un modelo aditivo pueden ser expresadas como ajustes proporcionales a un riesgo subyacente. Como lo señalaron Emerson y Stoto (1983), una transformación seleccionada por una razón, regularmente demuestra efectos fortuitos que vienen con ella. En este caso, más allá de la ayuda de la interpretación teórica, se aprovecha la estabilización de la varianza y el incremento en la aditividad de la matriz de datos como dos argumentos a favor de la transformación mencionada (Wilmoth, 1989).

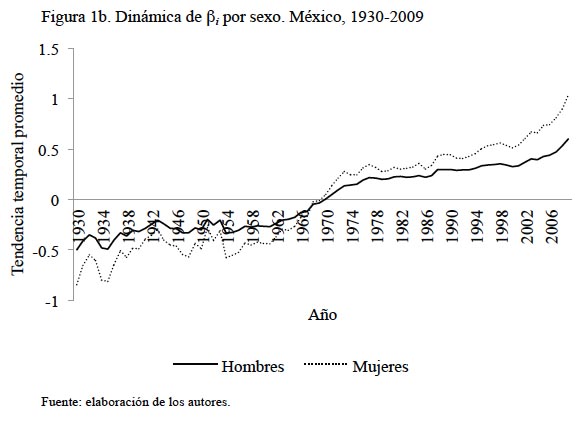
En la fase del análisis exploratorio, se ajusta una serie de modelos simples a los datos transformados. En la Figura 1a se muestra el efecto del parámetro , que representa la tendencia etaria promedio del logaritmo de las defunciones en el periodo de estudio, 1930-2009. La Figura 1b muestra el efecto del parámetro , que representa la evolución promedio de la mortalidad sobre el tiempo.

La primera de estas curvas muestra la tendencia conocida del cambio de la mortalidad sobre los rangos de edad: alta en las primeras edades, cayendo a un mínimo alrededor de los 11 años y a la baja en las edades mayores.² Se observa que entre los 17 y 85 años, el logaritmo de las defunciones oscila alrededor de siete (que serían poco más de mil defunciones en promedio anual para cada una de esas edades) para después descender. Las defunciones masculinas son ligeramente mayores hasta poco después de los 60 años y después de los 80 años se ubican por debajo de las defunciones femeninas.

Respecto a la tendencia temporal promedio, las defunciones masculinas se encontraban sobre las femeninas hasta mediados de la década de los 60, después, ese patrón se revirtió. Se observa un cambio estructural en la tendencia que predominaba hasta principios de la década de los cincuenta. Esto se debe principalmente a que fue por esos años que se consolidaron las instituciones de salud pública en México. Es importante aclarar que estos datos se refieren a los volúmenes totales de muertes por sexo a lo largo del tiempo, lo cual no indica que sea más "intensa" la mortalidad en uno u otro sexo, aquí existe un efecto del volumen total de la población expuesta al riesgo de morir que no está siendo considerado.

Por otro lado, este método le presta una atención especial a los efectos de la diagonal de los residuales que, como se mencionó, están asociados a los efectos cohorte. El primer paso del ajuste del modelo es ajustar una serie de modelos aditivos a estos efectos hasta que se estabilizan; posteriormente, se realiza el ajuste del modelo ADM utilizando el conjunto de parámetros θ_k que se muestra en la Figura 2.

En la Figura 2 se observa un patrón recurrente de observaciones atípicas cada diez años que tienden a disminuir hacia las cohortes nacidas después de 1930. Se observa también el efecto de la mortalidad en las cohortes de nacimiento de la primera década del siglo XX, aquellas que sufrieron más de cerca el movimiento armado de la Revolución Mexicana.

El modelo ADM se ajusta con la DVS utilizando las dos primeras componentes, lo que hace que el modelo explique más varianza que con sólo una; la decisión de tomar ρ = 2 se basa en la amplia diferencia en magnitud de los dos primeros valores propios respecto al resto, como se puede observar en la Tabla 1. Cabe mencionar que la incorporación de más componentes no afecta la estimación pero sí disminuye la parsimonia del modelo.

Con la DVS se calculan los demás parámetros del modelo, los cuales corresponden a los elementos de las matrices resultantes de este procedimiento. Por un lado se tienen los parámetros asociados a las edades, γ_im (Figura 3) y por otro los asociados a los periodos, δ_jm (Figura 4). Respecto a los parámetros asociados a las edades no se observan diferencias sustantivas por sexo; sin embargo, en el gráfico asociado al parámetro γ_i2, se observa que durante los primeros años de vida hay una sobremortalidad masculina.

Ahora bien, respecto a los parámetros asociados a los periodos tampoco se observan diferencias sustantivas por sexo; la gráfica asociada al parámetro δ_j1 muestra que para ambos sexos la tendencia temporal es a la baja, es decir que durante todo el periodo de análisis la mortalidad general ha disminuido continuamente. Sin embargo, la gráfica asociada al parámetro δ_j2 muestra que si bien ha habido algunas fluctuaciones en la velocidad a la que ha disminuido la mortalidad, durante la década de 1970 se observa un incremento abrupto en dicha velocidad de disminución, aunque es posible que esto refleje algún cambio estructural en la calidad de la información durante esa década.

Una vez realizada esta etapa de análisis, se confirma que la estructura de la matriz por renglones y columnas está bien representada.

 

El modelo LC aplicado a la mortalidad mexicana

En los tres procedimientos de ajuste del modelo Lee-Carter el parámetro ax es casi idéntico, con muy poca variación salvo en las últimas edades; esto se debe a que en el proceso que se realiza en los tres métodos de ajuste (SVD, MCP y MLE) se calculan siempre los términos aditivos en primer lugar. Esto se puede ver en la Figura 5a.

Además, en la Figura 5b se muestra la manera en que el parámetro multiplicativo b_x capta el comportamiento de la variación de las defunciones. Asimismo, se observa que el método MLE estima mejor la intensidad de las defunciones a las primeras edades y en las edades medias. En este sentido, el método DVS es muy similar al MCP en las edades medias, pero es posible que sobrestime la intensidad en las primeras edades y la subestime en las edades medias y envejecidas (note la similitud con el parámetro γ_i1).

En las Figuras 6a y 6b se puede notar la similitud del parámetro k_t entre los métodos de estimación con el término C_t y con el conjunto de parámetros δ_i1. En estas figuras sobresale la información que indica la estimación por MLE. Los métodos DVS y MCP señalan que ha habido un continuo e ininterrumpido proceso descendiente en la mortalidad.

En cambio con MLE se señala que durante la década de 1930 hubo un freno o estancamiento de la tendencia creciente de la mortalidad, lo cual es coherente con la primera etapa de la transición demográfica en México (García Guerrero, 2014).

Luego, la estimación señala una tendencia lineal en la disminución de la mortalidad y hacia la década de 1980, se observa una disminución en la velocidad a la que venía descendiendo. A finales de esa década y de la primera década del siglo XXI se observa un estancamiento en la disminución de la mortalidad.

El hecho de que el modelo ADM integre el efecto cohorte le proporciona una ventaja significativa en cuanto a la bondad del ajuste. Al calcular los totales estimados de las defunciones masculinas, el modelo ADM obtiene un coeficiente de determinación (R²) de 99.9 por ciento y de las femeninas de 99.8 por ciento, mientras que con MCP se obtuvo una R² = 99.8 por ciento para los hombres y 99.9 por ciento para las mujeres (se estabilizan las defunciones rápidamente y por la aproximación de los parámetros los lleva por debajo de la curva de las defunciones originales para el caso de los hombres, mientras que para las mujeres ocurre lo contrario).

Con MLE se obtuvo una R² = 99.4 por ciento para hombres y de 99.7 por ciento para las mujeres (de antemano se esperaba esto debido al supuesto de distribución Poisson utilizado) y finalmente, con DVS se obtuvo una R² = 99.1 por ciento para hombres y una R² = 99.5 por ciento para las mujeres (sobresalen algunas deficiencias ya que en los primeros años se ajusta por debajo de las defunciones originales, lo cual no es posible dado que las observaciones representan una cota mínima y en los periodos intermedios por arriba). En la Figura 7, se muestra gráficamente el ajuste de los modelos según el método que se utilice para corregir la tendencia del total de las defunciones por año. Sin embargo, las diferencias antes mencionadas son mínimas y a un nivel de significancia de uno por ciento, todas las opciones de estimación muestran un muy buen desempeño.

Con el propósito de corregir la mortalidad mexicana y brindar una tendencia demográficamente aceptable y en virtud del análisis de los resultados en los totales de las defunciones por periodo, es posible seleccionar el mejor modelo que se ajusta a los datos; de acuerdo con la Figura 7, sería razonable escoger entre el modelo ADM y el modelo LC calculado a partir de MLE; sin embargo, al interior de cada periodo, analizando los parámetros de cada modelo que dan cuenta de la distribución de las defunciones por edad (α_x para Lee-Carter y α_i para ADM).

Una vez analizadas las defunciones totales por periodo, habiendo concluido que, si bien todos los métodos de estimación proporcionan muy buenos resultados para el modelo LC, el mejor es el MLE y el mejor modelo de la mortalidad es el ADM, ya que incorpora una dimensión más en su análisis: la cohorte.

Así, el siguiente paso fue analizar la estructura por edades de las defunciones de cada periodo. Para ilustrar lo anterior, se eligieron los años 1930, 1970 y 2009 con el fin de hacer referencia a los ajustes logrados en el corto, mediano y largo plazo. Además, con ello también se analizan tres tipos de datos con diferentes calidades; se espera que los datos más difíciles de ajustar sean aquellos con mayores errores de declaración, es decir, los más antiguos.

De esta manera, como se muestra en las Figuras 8a, 8b y 8c, la mortalidad observada en las primeras edades es mayor al inicio del periodo de estudio y menor en las edades intermedias y mayores; a la mitad de cada periodo, la mortalidad infantil baja de manera considerable y comienza a verse la transición de la mortalidad en edades mayores a 50.

Por último, en el año 2009 se puede ver la estructura más reciente de la mortalidad con las defunciones registradas, la transición es evidente en la forma de la curva, donde la mortalidad en menores de cinco años disminuyó de manera sustantiva y se aprecia un máximo cerca de los 80 años de edad. El comportamiento de las edades al interior de los periodos seleccionados estimadas por el modelo LC-MLE respeta la estructura original de las defunciones; sin embargo, en las edades mayores subestima las defunciones, esto se debe a la distribución con la que se estimaron. En cambio, si bien el modelo ADM también respeta de buena manera la forma de la curva de las defunciones originales, incrementa defunciones en las últimas edades.

 

Suavizamiento de los parámetros

Usualmente, al modelar la mortalidad de un país, primero se corrige la información observada y luego se modela y se aplica algún procedimiento de estimación de parámetros (para el caso de México véase García Guerrero y Ordorica, 2012). En este trabajo se aplica una perspectiva un tanto diferente, con el fin de estudiar la información que proporcionan las observaciones empíricas históricas. Primero se modeló y se estimaron los parámetros relacionados y luego se suavizaron, con el fin de analizar la información a corto, mediano y largo plazo. Además, se suavizaron, con el objetivo de obtener una serie histórica que permita analizar de una forma más eficiente la dinámica demográfica de la mortalidad a lo largo del tiempo, eliminando los errores que subyacen.

Una de las ventajas de suavizar los parámetros es que el resultado definitivo da la estructura por edad y sexo de las defunciones para cada año es suave, lo que permite de manera más fácil observar la tendencia sin la variación que da la preferencia digital en el registro.

Sin embargo, se corre el riesgo de no identificar fenómenos de la mortalidad, tanto en la estructura como en el periodo, que afectan directamente su comportamiento o que son consecuencia de algún evento fortuito en la historia. Por lo tanto hay que poner atención especial a este procedimiento para no perder información que es importante o que puede cambiar la tendencia al realizar la combinación de los parámetros. Para garantizar un buen resultado o por el contrario desecharlo, es necesario en cada paso que se realiza detenerse para analizar cada uno de los procedimientos; en este tipo de modelos, por las complicaciones en los cálculos excesivos de parámetros, es fácil cometer errores.

Para el modelo Aditivo Doble Multiplicativo, se utilizaron distintos tipos de métodos polinomiales³ que se adecuaron a cada conjunto de parámetros: para los efectos cohorte se utilizó un suavizamiento polinomial con kernel senoidal, tratando de respetar la forma de la curva. Como resultado se obtiene un efecto similar al de medias móviles, una línea más plana, sin irregularidades de la serie original, con la cual es posible percibir mejor la tendencia de la serie. Las α_i fueron suavizados con una función polinomial con kernel Epanechnikov para respetar su comportamiento en las edades. Las β_j fueron suavizadas con una función polinomial con kernel Gaussiano para respetar la forma de la curva, aun cuando son crecientes. Por último, los términos multiplicativos fueron suavizados con un procedimiento polinomial con kernel Epanechnikov.

Al terminar este procedimiento de suavizado de los parámetros, se recalculan las defuniones corregidas y suavizadas a partir de las ecuaciones (1) y (2). Los resultados son buenos en relación a las defunciones originales. Al realizar el ajuste de este método se obtiene una descripción detallada de la estructura de una matriz de defunciones. El carácter natural de esta estructura es común en datos de mortalidad para ambos sexos y para varios países, en este caso en particular para México, las tres piezas de la descripción correspondientes a la parte aditiva, multiplicativa y diagonal del modelo han separado interpretaciones informativas que son de gran ayuda.

En la Figura 9 se muestra la estructura por edades suavizada para el modelo ADM; se observa la transición de las defunciones a través del tiempo y cómo se adaptan a las estructuras de cada año de registro. Además, la evolución de la mortalidad es evidente: por un lado, la mortalidad infantil excesiva al inicio del periodo de estudio y su reducción significativa para 2009.

Asimismo, se observa la acentuación de la misma entre los 70 y 80 años de edad para el último periodo, lo que da cuenta de lo bien que explica y corrige la mortalidad el modelo ADM.

De igual forma, el suavizamiento de los parámetros se realizó para el modelo LC-MLE. Para las defunciones totales por periodo se utilizó un suavizamiento polinomial con Kernel Epanechnikov y para los parámetros de la estructura por edad se utilizó el procedimiento propuesto por Gray (1987) con una reponderación ajustada a la curva de la estructura de las edades. En la Figura 10 se muestra la estructura por edad corregida y suavizada con los métodos antes mencionados para los años seleccionados. Resaltan ciertas diferencias en relación a los resultados del modelo ADM: el modelo LC-MLE agrupa más defunciones entre las edades 65 y 85 y en las edades mayores, cercanas a los 100, las defunciones son escasas, esto sucede debido a que se supone que las defunciones siguen una ley de Poisson, lo cual asigna una mayor probabilidad de muerte a las edades entre 65 y 85. El procedimiento de suavizamiento es más simple que el utilizado en ADM, esto se debe a que son menos los parámetros que hay que tratar.

Por último, queda la decisión de qué modelo se ajusta mejor a la mortalidad mexicana en los periodos que se estudian. Hasta el momento ambos modelos han dado resultados muy satisfactorios. Si bien hay diferencias en el proceso de estimación y ajuste de cada uno, éstas no reflejan cambios sustantivos que deban ser considerados a detalle. Esto se debe en gran medida a que la calidad de los registros administrativos sobre la mortalidad en México se ha incrementado con el tiempo.

Además, con el fin de realizar la selección del modelo, hay que tener en cuenta que el mejor será aquel que represente menor esfuerzo y tiempo y que brinde información de calidad, es decir, que sea parsimonioso. En este sentido, el modelo ADM carece de simplicidad en la estimación de parámetros, pues hay que realizar muchos cálculos para la estimación y ajuste. Se debe tener mucho cuidado a la hora del suavizamiento, ya que la interacción de todos los parámetros es la que proporciona el resultado final y, en virtud de la sensibilidad del modelo, al menor cambio de tendencia los resultados pueden variar considerablemente. Sin embargo, este modelo brinda la oportunidad de analizar los efectos cohorte sobre el tiempo.

El modelo LC-MLE proporciona resultados similares con menos parámetros, pero no es más parsimonioso, ya que el proceso de estimación de MLE es un tanto más complejo que el empleado en el ADM. Sin embargo, el suavizamiento es más simple y los parámetros que hay que suavizar resultan más homogéneos que los del ADM.

Por otro lado, existe un obstáculo importante en el modelo LC-MLE, el cual radica en que al realizar el ajuste se requiere incluir como información adicional a la población expuesta al riesgo. Este obstáculo podría ser fácilmente librado si se programase una librería ad hoc para realizar estimaciones de modelos log-bilineales para datos a nivel. Esto excede los propósitos del presente trabajo; sin embargo, se propone para futuras investigaciones.

Ahora bien, analizando la tendencia temporal del total de defunciones por año con ambos los modelos, en la Figura 11 se muestran las defunciones totales corregidas y ajustadas de cada modelo para hombres y mujeres. Es claro que el modelo LC-MLE se ajusta mejor a las defunciones originales garantizando su corrección; el modelo ADM se queda, en general, por debajo de las observadas. Esto se debe a que el suavizado de los parámetros y su interacción no es óptimo, ya que hay que considerar variables correlacionadas y tendencias que no son fáciles de observar, aun utilizando herramientas sofisticadas para el suavizamiento. En el caso de las mujeres, el modelo ADM se ajusta mejor que el de los hombres; sin embargo el modelo LC-MLE también es el que mejor se adapta a la tendencia de los datos observados.

Así, en virtud de la discusión anterior, en este caso y para la mortalidad mexicana del periodo 1930-2009, el modelo que mejor estima la mortalidad mexicana es el LC con parámetros estimados utilizando MLE, aún con la salvedad antes mencionada.

 

Conclusiones

Aplicar y comparar los métodos anteriores ofrece un panorama más amplio acerca del comportamiento de la mortalidad histórica en México. Por un lado, se presentó el modelo de Lee-Carter, el cual, por su parsimonia, ha sido ampliamente utilizado para el estudio de la mortalidad; sin embargo, esa misma parsimonia conlleva a que sólo considere las dimensiones edad-periodo de la mortalidad y elimina prácticamente la información relacionada con la dimensión cohorte. Aunque en el documento original, Lee y Carter mencionan la importancia de los efectos cohorte, terminan por no considerarlos en su ejercicio.

Por otro lado, el modelo ADM propuesto por Wilmoth da un tratamiento diferente a los residuales del modelo, de tal forma que incluye los efectos cohorte en el ajuste completo. Aunque les da prioridad a las dimensiones edad-periodo, considera de una forma particular la dimensión cohorte;⁴ además, a diferencia del modelo LC, no utiliza únicamente el primer valor singular, sino dos.

Por otra parte, se presentan diferentes métodos para ajustar el modelo LC, los cuales no son tan diferentes entre sí a pesar de las distintas maneras de calcular los parámetros; sin embargo, el método óptimo debe ser el que esté al alcance, minimice el esfuerzo y que proporcione información suficiente y de calidad para las estimaciones y proyecciones de la mortalidad.

 

Bibliografía

ALHO, Juha M., 1998, A stochastic forecast of the population of Finland, Statistics Finland, Helsinki.         [ Links ]

ALHO, Juha M., 2000, "Discussion of 'The Lee-Carter method for forecasting mortality, with various extensions and applications'", en The North American Actuarial Journal, Society of Actuaries, 4 (1).         [ Links ]

ALHO, Juha M., 2007 "Métodos empleados en la elaboración de proyecciones sobre mortalidad", en Decimoquinta Conferencia Internacional de Actuarios y Estadísticos de la Seguridad Social, Helsinki, Finlandia.         [ Links ]

BRILLINGER, David R., 1986, "The natural variability of vital rates and associated statistics", en Biometrics, (42).         [ Links ]

BROUHNS Natacha, Michel DENUIT y Jeroen K. VERMUNT, 2002, "A Poisson log-bilinear regression approach to the construction of projected lifetables", en Insurance: Mathematics and Economics (31).         [ Links ]

CONAPO, 2012, Proyecciones de la población 2010-2010, Consejo Nacional de Población, México.         [ Links ]

CHATFIELD, Chris, 1995, The Analysis of Time Series. An Introduction, Chapman and Hall, EUA.         [ Links ]

DEBÓN, Ana Aucejo, Francisco MARTÍNEZ RUIZ y Francisco MONTES SUAY, s/f, "Modelo Lee-Carter extendido", en XV Jornadas de ASEPUMA y III Encuentro Internacional, disponible en http://www.uv.es/asepuma/XV/comunica/502.pdf        [ Links ]

EMERSON, J. D. y M. A. STOTO, 1983, Transforming data. Understanding Robust and Exploratory Data Analysis.         [ Links ]

GARCÍA GUERRERO, Víctor M. y Manuel ORDORICA, 2012, "Proyección estocástica de la mortalidad mexicana por medio del método de Lee-Carter", en Estudios Demográficos y Urbanos, Centro de Estudios Demográficos, Urbanos y Ambientales, El Colegio de México, 27(80).         [ Links ]

GARCÍA GUERRERO, Víctor M., 2011, "Un análisis de las diferencias entre las proyecciones de población 2006-2050 y el censo de población 2010", en Coyuntura Demográfica. Revista sobre los procesos demográficos en México hoy, Sociedad Mexicana de Demografía, 1(1).         [ Links ]

GARCÍA GUERRERO, Víctor M., 2013, "Las nuevas proyecciones de población 2010-2050", en Boletín de la Sociedad Mexicana de Demografía, (18)        [ Links ]

GARCÍA GUERRERO, Víctor M., 2014, "Las proyecciones de la población de México", en C. RABELL (coord.) Los mexicanos. Un balance del cambio demográfico, Fondo de Cultura Económica, México.         [ Links ]

GARCÍA GUERRERO, Víctor M., 2014, Proyecciones y políticas de población en México, Centro de Estudios Demográficos, Urbanos y Ambientales, El Colegio de México, México.         [ Links ]

GIROSI Federico y Gary KING, 2007, Understanding the Lee-Carter mortality forecasting method, Working Paper, copia disponible en http://j.mp/lTXlGe        [ Links ]

GRAY, Alan, 1987, "The missing ages: adjusting for digit preference", en Asian and Pacific Population Forum, 1(2).         [ Links ]

HANNERZ, H., 1999, Methodology and applications of a new law of mortality, Department of Statistics, Lund University.         [ Links ]

HELIGMAN, L. y J. H. POLLARD, 1980, "The age pattern of mortality", en Journal of the Institute of Actuaries, 107(1), en Retrieved from http://journals.cambridge.org/abstract_S0020268100040257        [ Links ]

KEILMAN, Nico, 1998, "How accurate are the united nations world populations projections?", en Population and Development Review, 24.         [ Links ]

KOISSI, Marie-Claire y Arnold F. SHAPIRO, 2008, "The Lee-Carter model under the conditions of variables age-specific parameters", en 43rd Actuarial Research Conference.         [ Links ]

LEE, Ronald y Francois NAULT, 1993, "Modeling and forecasting provincial mortality in Canada", en World Congress of the International Union for the scientific Study of Population, Canada, Montreal.         [ Links ]

LEE, Ronald y Lawrence R. CARTER, 1992, "Modeling and forecasting U.S. mortality", en Journal of the American Statistical Association, 87 (419).         [ Links ]

LEE, Ronald y R. ROFFMAN, 1994, "Modeling and forecasting mortality in Chile", en Journal of the American Statistical Association, 22 (59).         [ Links ]

LEE, Ronald y Timothy MILLER, 2000, "Evaluating the performance of Lee-Carter Method for Forecasting Mortality forecasts", en Journal of the American Statistical Association, 38 (4).         [ Links ]

LEE, Ronald, 2000, "The Lee-Carter method for forecasting mortality, with various extensions and application", en Journal of the American Statistical Association, 4 (1).         [ Links ]

MAKEHAM, W. M., 1867, "On the law of mortality", en Journal of the Institute of Actuaries (1866), Retrieved from http://www.jstor.org/stable/41134517        [ Links ]

OEPPEN, Jim y James W. VAUPEL, 2002, "Broken limits to life expectancy", en Science 296(5570).         [ Links ]

ONU, 1958, "Multilingual demographic dictionary", en United Nations Population Studies, (29).         [ Links ]

OPPERS, Erik et al., 2012, "Chapter 4. The financial impact of longevity risk", en Global Finantial Stability Report, Fondo Monetario Internacional, EUA.         [ Links ]

PEARSON, K., 1895, Contributions to the mathematical theory of evolution. II. Skew variation in homogeneous material. Philosophical Transactions of the Royal Society of London, Retrieved from http://www.jstor.org/stable/90649        [ Links ]

PERKS, W., 1932, "On some experiments in the graduation of mortality statistics", en Journal of the Institute of Actuaries, Retrieved from http://www.jstor.org/stable/41137425        [ Links ]

R DEVELOPMENT CORE TEAM, 2011, "R: A language and environment for statistical computing", en R Foundation for Statistical Computing, Vienna, Austria, en http://www.R-project.org/        [ Links ]

SOMEDE, 2011, Conciliación demográfica de México y sus estados, Sociedad Mexicana de Demografía, México.         [ Links ]

STEENBERGEN, Marco R., 2003, Maximum likelihood programming in stata, disponible en http://monogan.myweb.uga.edu/computing/r/MLE_in_Stata.pdf        [ Links ]

STOTO, Michael A., 1983, "Accuracy of population projections", en Journal of the American Statistical Association, 78(381).         [ Links ]

THIELE, T. N. y T. B. SPRAGUE, 1871, "On a mathematical formula to express the rate of mortality throughout the whole of life, tested by a series of observations made use of by the Danish Life Insurance Company of 1871", en Journal of the Institute of Actuaries and Assurance Magazine, Retrieved from http://www.jstor.org/stable/41135308        [ Links ]

WILMOTH, John R., 1989, Fitting three-way models to two-way arrays of demographic rates, Working Paper, University of Michigan.         [ Links ]

WILMOTH, John R., 1990, "Variation in vital rates by age, period, and cohort", en Sociological Methodology, 20:295-335.         [ Links ]

WILMOTH, John R., 1993, Computational methods for fitting and extrapolating the Lee-Carter model of mortality change, Working Paper, University of California Berkeley.         [ Links ]

WILMOTH, John R., 1996, "Mortality projections for Japan: A comparison of four methods", en Health and mortality Among Elderly Populations.         [ Links ]

 

Notas

* Los autores agradecen los comentarios y sugerencias que dos árbitros anónimos hicieron a este trabajo.

¹ Una variante del modelo propuesto por Wilmoth (1990) ha sido utilizada por el Consejo Nacional de Población (CONAPO) en el pasado para la corrección de la mortalidad.

² Obviamente el comportamiento de este parámetro se debe a la transformación y a que se utiliza el conteo del evento y no tasas.

³ Este tipo de procedimientos está disponible en la mayoría de los paquetes estadísticos, los aquí utilizados fueron las funciones kdensity de STATA (Steenbergen, 2003) y density de la librería KernSmooth de R (2011).

⁴ La decisión de ponderar las dimensiones para el ajuste de un modelo, es prácticamente arbitraria, se hace por conveniencia, para el caso de México, es más fácil tener información de la mortalidad por edad y periodo que por cohorte, de hecho muy pocos países tienen sistemas de registros administrativos que provean de información de calidad por cohorte completa.

 

Información sobre los autores

José Manuel Aburto. Es egresado de la maestría en Demografía del Centro de Estudios Demográficos, Urbanos y Ambientales de El Colegio de México y Actuario por la Universidad Autónoma de Guadalajara. Durante la maestría realizó una estancia de investigación en la Universidad de Wisconsin en Madison apoyada por el Consejo Nacional de Ciencia y Tecnología. Se ha desempeñado como administrador de información cendal en el Instituto Nacional de Estadística y Geografía y analista de riesgos en AON Risk Services. Ha sido asistente de investigación del INEGI-UNICEF y asistente de materia en el curso de Análisis Matemático de la UAG. Dirección electrónica: jmaburto@colmex.mx.

Víctor Manuel García Guerrero. Es Profesor-Investigador y coordinador de la Maestría en Demografía del Centro de Estudios Demográficos, Urbanos y Ambientales de El Colegio de México (CEDUA-Colmex). Es doctor en Estudios de Población por el CEDUA-Colmex; parte de su investigación doctoral la realizó en el World Population Program del International Institute for Applied Systems Analysis en Austria y ha tomado cursos en el Max Planck Institute for Demographic Research en Alemania. Estudió actuaría, la maestría en Investigación de Operaciones y un diplomado en Econometría Avanzada en la UNAM. Fue Profesor-Investigador de la Flacso sede México y profesor de tiempo parcial en el ITAM y en la Facultad de Ciencias. Ha sido asesor y consultor en métodos demográficos para el CONAPO, distintos despachos de consultoría y bancos. Es miembro de la Somede, PAA, ALAP y IUSSP. Sus temas de investigación son: demografía formal y sus aplicaciones, estimaciones y pronósticos demográficos y sus relaciones con las políticas de población. Es candidato a investigador nacional por el Sistema Nacional de Investigadores del CONACyT. Dirección electrónica: vmgarcia@colmex.mx.