Suavizamiento controlado de tasas de mortalidad con P-splines: aplicaciones para México y el Reino Unido

 

Eliud Silva, Víctor M. Guerrero y Daniel Peña

 

Universidad Anáhuac, México, Instituto Tecnológico Autónomo de México y Universidad Carlos III de Madrid, España.

 

Artículo recibido el 30 de agosto de 2013.
Aprobado el 10 de diciembre de 2013.

 

Resumen

Se presenta un método original para controlar suavidad cuando se estiman tasas de mortalidad en un contexto bidimensional (por edades y años) con una perspectiva de P-splines. El analista puede elegir el porcentaje de suavidad deseado, ya sea en la dimensión de edad, de años o de ambas, con el objetivo de obtener tendencias suavizadas de tasas de mortalidad que sean comparables. Para ello se proponen unos índices que relacionan la suavidad deseada con los parámetros que controlan el suavizamiento. También se establecen algunos resultados teóricos que brindan soporte a los índices de suavidad y se tocan algunos aspectos de carácter numérico. Con fines ilustrativos, el método propuesto se aplica a datos de estadísticas vitales para México y a datos del Continuous Mortality Investigation Bureau del Reino Unido.

Palabras clave: Comparabilidad, índices de suavidad, mínimos cuadrados generalizados, error cuadrático medio, parámetro de suavizamiento.

 

Abstract

An original method is presented to control smoothness when estimating mortality rates in a two-dimensional context of ages and years with a P-spline perspective. The analyst can choose a desired percentage of smoothness for the dimension of age, the dimension of year or both, thus obtaining smoothed trends of mortality rates that are comparable for different datasets. To that end, some indices that relate the desired smoothness with the smoothness parameters are proposed. Some theoretical results that lend support to the indices as well as some numerical aspects are also mentioned. The proposed method is illustrated with vital statistics data from the Mexican national institute of statistics and from the UK Continuous Mortality Investigation Bureau.

Key words: Comparability, index of smoothness, generalized least squares, mean squared error, smoothness parameter.

 

Introducción

Los registros de siniestralidad en el ramo de vida o bien las estadísticas vitales de defunciones pueden tener anomalías o defectos en su registro. Su origen puede ser atribuido a la presencia de eventos extraordinarios (sismos, inundaciones, pandemias, etcétera) o a errores humanos de diversos tipos. Un registro erróneo de las muertes puede conducir a un aumento (o disminución) en la medición de la intensidad de la mortalidad en una cierta edad en detrimento de otra, lo que afecta a tener una visión clara del fenómeno y por lo tanto a la toma de decisiones. Asimismo pueden presentarse fluctuaciones de tipo irregular que tienden a oscurecer el comportamiento subyacente de los datos. El suavizamiento de datos surge como una alternativa para resolver este problema.

Como es sabido, en el sector de los seguros, en los centros de investigación demográfica y en los consejos o ministerios de población, es de suma importancia la graduación de tasas de mortalidad (que considera fidelidad a los datos y suavidad en el comportamiento de las tasas graduadas) para la planeación y toma de decisiones. Esto surge debido a la relevancia que tienen la cuantificación de riesgos y la constitución de reservas actuariales, al igual que la descripción, el análisis y el pronóstico de la mortalidad registrada. Por ello, en la literatura existen diversas propuestas metodológicas para el análisis, la estimación y la proyección de tasas de mortalidad. A continuación se mencionan algunas de éstas.

La propuesta básica para realizar graduación de carácter actuarial es la que se conoce como graduación de Whittaker y Henderson, que se describe en detalle en London (1985). Asimismo, hay modelos que abordan problemas específicos, como los establecidos en Clayton y Schifflers (1987), Brouhns et al., (2002), Wang y Lu (2005), Delwarde et al., (2007), además de aquellos expuestos en Booth y Tickle (2008) y Debón et al., (2008). En el contexto bidimensional, es decir, cuando se consideran simultáneamente la edad y los años, se ubican propuestas como la de Cleveland y Devlin (1988), Dierckx (1993), De Boor (2001), Gu y Wahba (1993) y Wood (2003). También dentro de este marco se encuentra la extensión de los llamados B-splines, que fue propuesta por Currie et al. (2004). Sin embargo, ninguna de las investigaciones anteriores brinda la posibilidad de controlar la suavidad alcanzada en las estimaciones de las tasas de mortalidad, de manera que se puedan realizar comparaciones válidas entre diferentes tendencias de mortalidad estimadas.

Con objeto de controlar la suavidad, en este trabajo se proponen varios índices relacionados con la suavidad de la tendencia, que surgen al extender un resultado establecido por Guerrero (2007) dentro de un contexto unidimensional. De hecho, al utilizar dichos índices puede medirse la precisión atribuible al elemento de suavidad de un modelo estadístico subyacente, que se supone representa la verdadera dinámica de las tasas de mortalidad. Así pues, se propone el uso de un índice de suavidad que depende sólo de dos elementos: el parámetro de suavizamiento y el número de datos disponibles. Dicho índice sirve para decidir el valor del parámetro de suavizamiento como una función del porcentaje de suavidad impuesto a priori por el analista.

En el método tradicional de suavizamiento que se encuentra implementado en diversos programas computacionales especializados se hace uso del parámetro de suavizamiento, el cual se selecciona comúnmente con base en criterios automáticos como son el AIC (Akaike Information Criterion) o el BIC (Bayesian Information Criterion) que en esencia se usan como criterios meramente numéricos (véase al respecto Hastie and Tibshirani, 1990). De hecho, al utilizar estos criterios es factible obtener datos suavizados, pero no se tiene control sobre la magnitud de la suavidad obtenida. Sin embargo, si un conjunto de datos se suaviza con un valor específico de, se debe notar que se alcanza un monto de suavidad específico. Desde un punto de vista puramente descriptivo, en este trabajo se sugiere cuantificar el monto de suavidad para poder establecer comparaciones válidas entre distintos conjuntos de datos suavizados. Además, se propone fijar a priori la misma cantidad de suavidad para todas las curvas o las tasas de mortalidad que vayan a ser suavizadas y comparadas. Esto es semejante a lo que se hace al estimar parámetros mediante intervalos de confianza, ya que en tal caso para poder realizar comparaciones se fija el mismo nivel de confianza para todos los intervalos, pues no tiene sentido comparar intervalos con distintos niveles de confianza.

En suma, la principal propuesta del trabajo consiste en fijar en primer lugar el monto de suavidad deseado para la estimación de la tendencia de la mortalidad en estudio y, a partir de ahí, determinar el valor de las constantes de suavizamiento; en segundo lugar, se trata de realizar la aplicación de los procedimientos habituales de cálculo y de análisis relacionados con la técnica de splines penalizados (conocidos como P-splines). Dentro de las principales ventajas que tiene el uso de P-splines en aplicaciones prácticas, se encuentra que no hay necesidad de postular una forma funcional específica para la curva subyacente en las tasas de mortalidad, sino simplemente utilizar un algoritmo matemático para encontrar una función suave que haga uso eficiente de los datos disponibles. Además, las ideas detrás de los P-splines se pueden extender al caso de modelos de regresión, con lo cual se genera una extensa gama de posibilidades de análisis, como lo demuestra el texto de Ruppert et al., (2003). Por otro lado, la principal desventaja del uso de P-splines radica en que se debe ser muy cuidadoso con la parte computacional y conviene estar al tanto de los avances que se realizan dentro del análisis numérico, para saber cuáles son los algoritmos más eficientes de cálculo, como señala Weinert (2007).

En la sección dos del presente artículo se presentan algunos resultados teóricos ya establecidos en la literatura sobre el tema, tanto para el caso unidimensional como para el bidimensional, que son utilizados en este trabajo. En la sección tres se realiza el estudio de un índice de suavidad bidimensional, en relación con el estimador de las tasas de mortalidad y se abordan algunos aspectos de carácter numérico para el empleo de dicho índice en la práctica. La sección cuatro ilustra la aplicación del procedimiento sugerido con datos reales de carácter demográfico para México y el Reino Unido. Por último, en la sección cinco se exponen las conclusiones finales.

 

Metodología

Suavizamiento unidimensional

El problema de suavizamiento se puede entender como la minimización de una función S, formada por dos elementos: i) la suma de diferencias al cuadrado entre datos observados y estimados, es decir la bondad del ajuste y ii) la suavidad inducida en la estimación. Estos dos elementos se minimizan en forma simultánea, pero ponderando mediante un parámetro que establece un compromiso entre bondad de ajuste y suavidad. La suavidad se induce por medio de la diferencia de segundo orden Δ² α_j = α_j -2α_j-1 + α_j-2 de manera que se obtiene

donde aparece la estimación,

que es una tendencia no observable y que en este trabajo es una combinación lineal de B-splines cúbicos. Para detalles acerca de B-splines se sugiere ver el texto de De Boor (2001). Las α_j son coeficientes constantes que deben ser estimados y p es el número de B-splines que se utilizan. De manera matricial, el problema de minimización de la función S con respecto a α, se plantea como sigue: sea B una matriz cuyas columnas son B-splines con soporte local y Ω = D₂' D₂ una matriz simétrica, donde D₂ es una matriz de tamaño (p - 2) x p que representa el operador diferencia Δ², es decir

Entonces puede escribirse S = (y - Bα)' (y - Bα) + λα' Ωα y el resultado de la minimización está dado por (véase Eilers y Marx, 1996, ecuación 13):

La solución del vector ŷ_(α)˰ puede ser escrita en términos de una base N no-singular de dimensión m x m de los denominados splines naturales, como se hace en Hastie y Tibshirani (1990: 28-29). Sea entonces β la versión de α correspondiente a este cambio de base, entonces se obtiene

donde K = D₂ N^-1.

Desde una perspectiva de modelación estadística, supóngase que los datos observados de tasas de mortalidad son la resultante de una tendencia no observable más un ruido, es decir, son una realización del siguiente modelo

con los supuestos de que E(η) = 0 y Var(η) = σ²_η I_m, donde y_α =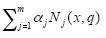

Asimismo, para inducir suavidad se considera el modelo

con E(ε) = 0 y Var(ε) = σ²_ε I_{m - 2}. Dado que E(εη') = 0, el modelo completo, formado por las dos últimas expresiones, puede escribirse como

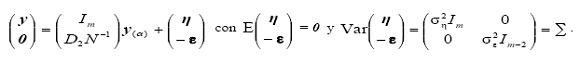
Ahora bien, si se definen

se puede escribir el modelo como Y = AX + E. De esta forma, el estimador de Mínimos Cuadrados Generalizados (MCG) que se obtiene está dado por X = (A'Σ^-1A)^-1A'Σ^-1Y, es decir,

que es el mismo resultado obtenido en (3), cuando se hace λ = σ_ε^-2/σ_η^-2. Por la teoría de MCG se puede deducir ahora que su correspondiente matriz de Error Cuadrático Medio (ECM) está dada por

Es fácil demostrar que la matriz λK'K es positiva semidefinida y, por lo tanto, I_m + λK'K es positiva definida, lo cual es un requisito necesario para la deducción de los índices de suavidad que se presentan más adelante. Adicionalmente, debe notarse que a partir de la matriz de ecm se pueden construir intervalos alrededor de la estimación puntual. Para concluir esta sección, se enfatiza que la segunda perspectiva será la que se emplee para el suavizamiento bidimensional, con la cual se llega a resultados similares a los que se obtienen con el método tradicional, pero se considera que hay una mejor interpretación estadística y se tiene la simplificación inducida por no tener que estimar el parámetro de suavizamiento.

 

Suavizamiento bidimensional

A continuación se adaptan la notación y los conceptos básicos del trabajo de Currie et al. (2004), de manera que en una tabla de mortalidad, se tiene que d = (d₁₁,..., d_m1,..., d_1n,..., d_mn)', μ = (μ₁₁,..., μ_m1,..., μ_1n,..., μ_mn)' y e = (e₁₁,..., e_m1,..., e_1n,..., e_mn)' y son los vectores que denotan las muertes ocurridas, las fuerzas de mortalidad y la exposición al riesgo de morir para las edades de 1 a m, y los años de 1 a n. Además, el vector mn apilado Y = (Y₁₁,..., Y_m1,..., Y_1n,..., Y_mn)' contiene como elementos las fuerzas crudas de mortalidad en logaritmos, es decir Y_ij = log(d_ij/e_ij) para i = 1,…, m y j = 1,…, n. Cabe notar que, en lo subsecuente, a la log (mortalidad) se le llamará simplemente mortalidad. Para extender el caso unidimensional desde la segunda perspectiva de la sección anterior, considérese el modelo

con E(Ψ) = 0 y Var(Ψ) = σ²_Ψ I_mn, donde

En este caso, para inducir suavidad en la dimensión de edad, se utiliza

Con E(Θ) = 0 y Var(Θ) = σ²_Θ I_{(m - 2)n}. Similarmente, para inducir suavidad en la dimensión de años se tiene

con E(Φ) = 0 y Var(Φ) = σ²_Φ I_{(n - 2)m}. Dado que E(ΘΨ') = 0 y E(ΦΨ') = 0, se puede escribir

Entonces, el problema de estimación por (MCG) produce la solución

con λ_a = + σ²_Ψ/σ²_Θ y λ_y = σ²_Ψ/σ²_Φ. La matriz de ecm resultante está dada por

 

Índices de Suavidad, parámetros de suavizamiento y algoritmo de estimación

La matriz inversa Γ^-1 es una matriz de precisión que se forma como suma de tres matrices de precisión: σ^-2_Ψ I_mn , σ^-2_Θ K'_aK_a , σ^-2_Φ K'_yK_y. Por ello se recurre a la idea de Guerrero (2008) de encontrar un índice que mida la proporción de P en (P + Q)^-1, donde P y Q son matrices positivas definidas de tamaño n x n. El índice apropiado está dado por

donde tr(.) denota la traza de una matriz. Cuando P y Q son matrices de precisión, este índice cuantifica la precisión relativa y tiene las siguientes propiedades: i) satisface el criterio aditivo a la unidad, es decir Λ(P; P + Q) + Λ(Q; P + Q) =1; ii) toma valores entre cero y uno; iii) es invariante bajo transformaciones lineales no-singulares de la variable involucrada y iv) se comporta de manera lineal. Las propiedades i, ii y iii son condiciones necesarias para obtener la medida y la propiedad iv asegura su unicidad, como lo demuestra Theil (1963).

Ahora se extiende (13) para producir una medida aplicable al caso de tres matrices. Esta medida permitirá definir un índice de suavidad bidimensional relacionado con edades y años. Es decir, se propone una función Λ(P; P + Q_a + Q_y) para medir la proporción de P en (P + Q_a + Q_y)^-1 y similarmente, una medida de la proporción correspondiente a Q_a o Q_y en (P + Q_a + Q_y)^-1. Con ello se establece el siguiente resultado.

Proposición 1. Sean P , Q_a y Q_y tres matrices positivas definidas o semidefinidas. Un índice escalar que mide la proporción de P en (P + Q_a + Q_y)^-1 está dado por

Esta medida satisface los cuatro criterios antes mencionados: aditividad a la unidad, ubicación entre cero y uno, invariancia bajo transformaciones no-singulares y linealidad. Se puede entonces usar (14) para cuantificar la proporción de precisión atribuible al uso de (9) y (10) en la matriz de precisión Γ^-1 = P + Q_a + Q_y con P = σ^-2_Ψ I_mn, Q_a = σ^-2_Θ K'_aK_a , Q_y = σ^-2_Φ K'_yK_y. Para ese fin, se proponen los siguientes índices de suavidad bidimensionales:

Atribuible a edades

S_a (λ_a λ_y; m, n) = Λ(Q_a; Γ^-1) = tr[λ_a K'_a K_a (I_mn + λ_a K'_a K_a + λ_y K'_y K_y)^-1]/mn

Atribuible a años

S_y (λ_a λ_y; m, n) = Λ(Q_y; Γ^-1) = tr[λ_y K'_y K_y (I_mn + λ_a K'_a K_a + λ_y K'_y K_y)^-1]/mn

En una tabla de mortalidad se considera que es conveniente suavizar conjuntamente con respecto tanto a edades como a años. Por lo tanto, se deduce también que el índice de suavidad bidimensional está dado por

Este último índice puede expresarse en términos porcentuales como S_ay%, para que se pueda interpretar como porcentaje de suavidad deseado (y alcanzado). Para apreciar el comportamiento de este índice en la Figura 1 se presenta un ejemplo del índice de suavidad conjunta para m = 30 edades y n = 30 años, conforme varían los parámetros de suavizamiento.

El índice de suavidad depende solamente de los parámetros λ_a y λ_y, así como de m y n, dado que las matrices K_a y K_y están completamente determinadas por m y n. Así pues, para alcanzar un porcentaje de suavidad conjunto para un grupo de datos dado (con m y n fijos) se necesita decidir el valor de S_ay% y resolver la igualdad que define al índice, para obtener los valores correspondientes de λ_a y λ_y. Una vez que los parámetros de suavizamiento se han encontrado se puede calcular la matriz de suavizamiento, cuya traza es conocida como la dimensión efectiva o grados de libertad (df, por su siglas en inglés) del modelo (véase al respecto Hastie y Tibshirani, 1990). Se sabe entonces que df = tr[(I_m + λK' K)^-1] en el caso unidimensional y df = tr[(I_mn + λ_a K'_a K_a + λ_y K'_y K_y)^-1] en el caso bidimensional. Dado que el índice S_ay (λ_a , λ_y; m, n) es función de la traza, se le puede considerar una reparametrización de los df del modelo. Por lo tanto, la propuesta está en línea con el argumento de Hastie y Tibshirani (1990: 52) de que “es razonable seleccionar el valor del parámetro de suavizamiento simplemente al especificar los df del suavizamiento”.

Una pregunta que le puede surgir al analista es si se puede suavizar hasta lograr 100 por ciento de suavidad. La respuesta es no. Por ejemplo, en el caso unidimensional, se sabe que tr[(I_m + λ K' K)^-1] → d cuando λ → ∞, donde d = 2 es el grado del operador diferencia (véase Eilers y Marx, 1996: 94). Asimismo, para el índice bidimensional de suavidad se deducen los límites que señala el resultado siguiente.

Proposición 2. Sea el índice bidimensional de suavidad dado por (15) y sean γ_{a , i} y γ_{y , j} los eigenvalores de K'_a K_a y K'_y K_y , respectivamente. Entonces, si se interpreta λ_a, λ_y = 0 como λ_a, λ_y → 0 y λ_a, λ_y = ∞ como λ_a, λ_y → ∞, se tiene que:

A continuación se enuncia otra proposición que complementa las propiedades que vinculan a los índices de suavidad unidimensional y bidimensional.

Proposición 3. Considérese el estimador bidimensional mn x 1 para edades, que está dado por Ŷ_(α) = (I_mn + λ_aK'_aK_a)^-1 Y. Este estimador emplea la misma matriz de suavizamiento y el mismo parámetro λ_a que usa el estimador unidimensional, dado que puede ser expresado como:

Ŷ_(α) =[I_n ⨂ (I_mλ_aK'K )^-1] Y

En cuanto a los cálculos numéricos, es bien conocido que suavizar el logaritmo de la mortalidad por Mínimos Cuadrados Penalizados (MCP) es sub-óptimo en términos de eficiencia estadística y sería preferible usar la Máxima Verosimilitud Penalizada, como lo señala Pawitan (2001). Sin embargo, para usar este último método se requiere la formulación de un modelo, cuyos supuestos deben ser verificados con los datos disponibles (en particular se debería validar el supuesto distribucional correspondiente, por ejemplo, Normalidad). En cambio, la MCP sólo requiere de la existencia de los dos primeros momentos para ser aplicable. Adicionalmente, el cálculo de splines asociado con la MCP es relativamente sencillo. En las aplicaciones que se presentan en la siguiente sección se usa el procedimiento sugerido por Currie et al., (2004) de manera que se pueden establecer comparaciones de la propuesta que aquí se presenta con la de estos autores. Ellos usan un modelo lineal generalizado (GLM) y su correspondiente función de verosimilitud penalizada, de la cual se deriva el sistema de ecuaciones B' (y - μ) = Pa. Dicho sistema se resuelve con

(B'W̃B + P)a = B'W̃B̃ã + B' (y -μ̃)

donde B es la matriz de regresión de B-splines, P = λD₂' D₂ es la matriz de penalización, ã y μ̃ son aproximaciones a la solución, W̃ es una matriz diagonal que contiene las ponderaciones w^-1_ii=(∂μ_i/∂η_i)²/ν_i, donde ν_i es la varianza de y_i dada su media μ_i, y

Estas ponderaciones surgen del supuesto de que los errores son de tipo Poisson, lo cual es común suponer con tasas de mortalidad y es lo que hacen Currie et al. (2004). De esta manera se hace uso de

W̃ = diag(μ̃)

Cuando se elige el número de nodos en los B-splines, también se elige el número de elementos para la matriz base de B-splines. Algunas propuestas para decidir el número de nodos aparecen en Eilers y Marx (1996), Currie y Durban (2002) y Ruppert (2002). Este último sugiere que para datos igualmente espaciados, se debe emplear un nodo por cada cuatro o cinco observaciones, hasta alcanzar un máximo de 40 nodos. Esta fue la regla seguida en este trabajo. Cabe citar que los cálculos se realizaron con el software Matlab (versión 7.0).

Una forma de implementar la presente propuesta de suavizamiento bidimensional es la siguiente. Considérese explícitamente el caso unidimensional por edades. Primero se debe fijar el monto de suavidad deseado S_a(λ_a; m), para lo cual debe recordarse que éste no puede ser mayor que 1-2/m. Posteriormente, dado que m y K_a son conocidos, se busca el parámetro de suavizamiento λ_a que satisfaga la relación 1 - tr[(I_m + λ_aK'_aK_a )^-1]/m = S_a(λ_a; m). La solución iterativa de esta ecuación inicia con un valor pequeño λ_a0 y se procede a incrementarlo gradualmente. El proceso se detiene cuando los lados de la ecuación previa difieren a lo más en una cantidad pequeña ε que se considera la tolerancia (en este trabajo se eligió ε = 0.001).

La idea anterior se extiende con facilidad al caso bidimensional, aunque antes debe notarse que el mismo índice de suavidad puede lograrse con diferentes combinaciones de λ_a y λ_y. Si S_ay = (λ_a , λ_y; m, n) es la suavidad bidimensional deseada, se tiene que 1 - tr[(I_mn + λ_aK'_aK_a + λ_yK'_yK_y)^-1]/ mn = S_ay = (λ_a , λ_y; m, n) donde K_a, K_y, m y n son cantidades conocidas. Se tienen las siguientes opciones: i) fijar un parámetro en la dimensión de edades, por ejemplo λ_a = λ_a0 y comenzar a buscar sobre los valores del parámetro de suavizamiento de la otra dimensión, como en el caso unidimensional; el proceso se detiene cuando se alcanza la convergencia. ii) ejecutar un proceso iterativo en el que los dos parámetros λ_a y λ_y cambien de acuerdo con incrementos definidos apropiadamente. Finalmente, se debe verificar que la diferencia entre los dos lados de la igualdad sea tan cercana como sea posible a cero (de nuevo, aquí se emplea como tolerancia ε = 0.001).

 

Acerca de los datos

En relación a los datos de los ejemplos aquí utilizados, es meritorio comentar la diferencia existente entre la añeja tradición de registros de estadísticas vitales de mortalidad entre México y el Reino Unido. Desde la perspectiva de Periodo, para el Reino Unido hay datos digitalizados desde 1922 hasta 2012 (véase www.mortality.org) en tanto que para México se cuenta con datos digitalizados en el Instituto Nacional de Estadística y Geografía (INEGI) en el Sistema Estatal y Municipal de Bases de Datos (SIMBAD) de 1990 a 2012. Es decir, hay una diferencia de experiencia demográfica de 68 años.

Por otra parte, desde el punto de vista de cohorte, en el Reino Unido se tiene información digitalizada que parte de 1842 y México no cuenta con este tipo de datos de manera oficial en la actualidad. Debe recordarse que la administración de la información de este tipo es mucho más costosa que la anterior, en distintas dimensiones. Para 1842, México tenía poco más de dos décadas de ser una nación independiente. Se debe hacer notar que aun cuando la historia demográfica digitalizada de México es relativamente reciente, es rica en cuanto a desagregación geográfica, ya que se puede obtener a nivel nacional, estatal y municipal.

El conjunto de datos de mortalidad del Reino Unido aquí empleado proviene del Continuous Mortality Investigation Bureau (CMIB) adscrito al Institute and Faculty of Actuaries (IFOA). Se trata de información de asegurados (un grupo selecto de la población) y no de la población en general. Las compañías de aquel país envían los datos de reclamaciones (defunciones) al CMBI para su recolección y análisis, cuyo principal propósito es pronosticar tablas de mortalidad por diferentes perfiles de asegurados. En la siguiente sección se consideran tanto las reclamaciones como la población de asegurados expuestos. Nótese que no necesariamente una reclamación corresponde a una defunción únicamente, ya que puede haber casos en los cuales una defunción genere varias reclamaciones porque la persona titular estaba asegurada en varias compañías.

En cuanto a la información mexicana, en el contexto de la población en general, Figueroa (2008) se nota que aun cuando es innegable el perfeccionamiento de los instrumentos tanto para recolectar, procesar y producir el dato sociodemográfico, no resultan ser así el análisis y evaluación de la calidad del mismo. Señala que muchas de las estadísticas vitales no han sido evaluadas en cuanto a su calidad y cobertura, lo cual se convierte en una tarea por realizarse para alcanzar más credibilidad y certidumbre. Asimismo, considera que la calidad de las estadísticas vitales no podrá mejorarse de manera significativa, salvo que se registren de manera oportuna y certera los eventos demográficos correspondientes.

Por otro lado, Partida (2008) hace énfasis en que tanto las estadísticas vitales como los censos (ambas fuentes necesarias para el cálculo de tasas) presentan problemas de cobertura y de declaración de edad y que, a pesar de que se hacen correcciones en los niveles de mortalidad para los primeros años vida, se ha seguido suponiendo que la calidad de ambas fuentes es la misma. Además, menciona que con base en la información disponible se está lejos de conocer con precisión los niveles y tendencias de la mortalidad en México durante el siglo XX, por lo que se hace necesario el empleo de modelos y estimaciones indirectas. El autor concluye afirmando de manera contundente que la tasa de mortalidad infantil sigue estando subestimada en el periodo de 1930 a 2000, la cobertura para mayores de tres años sobrestima los datos censales y existe una sobrestimación nacional de la esperanza de vida, que se agrava para regiones pequeñas, con lo cual se tiene un panorama distorsionado de la situación del país.

En este trabajo se utiliza la información disponible para México y el uso es exclusivamente con fines ilustrativos de la metodología aquí presentada. Si bien se ha mejorado la calidad de los datos censales y los registros de defunciones con el paso del tiempo, al hacer el supuesto de similar calidad entre fuentes de información, es decir censos y estadísticas vitales, resulta evidente el sesgo que se induce en las estimaciones de la mortalidad. En resumen, se puede afirmar que los datos del Reino Unido, al referirse a un contingente selecto donde existe un claro interés más que informativo por parte de terceras personas por declarar la defunción para tener los beneficios de seguros o pensiones, son de una calidad superior a los datos mexicanos, en los que se hace referencia a una población altamente heterogénea y desigual en cuanto a características económicas y en general sociodemográficas, aunado a los problemas ya citados (Figueroa, 2008 y Partida, 2008). Cabe decir que a pesar de que el análisis ahí expuesto no tiene un alcance hasta 2010, no resultaría desconcertante que se hayan preservado dichos problemas para años más recientes. El dimensionar las muy probables deficiencias de las fuentes mexicanas, representa un objetivo ajeno del presente trabajo.

 

Aplicaciones

En las siguientes aplicaciones se hace uso de datos de mortalidad para las edades de 11 a 100 y los años 1947-1999 del Continuous Mortality Investigation Bureau (CMBI) del Reino Unido, así como datos mexicanos provenientes de estadísticas vitales del Instituto Nacional de Estadística y Geografía (INEGI) para edades de 0 a 100 años (y más) para los años de 1990 a 2010. Para las tasas se tomaron poblaciones censales por grupo de edad y se interpolaron de manera lineal tales contingentes para los años intercensales. A fin de ilustrar el suavizamiento unidimensional se consideran dos posibilidades: i) una edad y diferentes años y ii) diferentes edades y un mismo año. En el primer caso, para los datos de Reino Unido, se usaron datos de tasas de mortalidad a edad 65 para el periodo completo. La máxima suavidad que puede ser alcanzada es 96.2 por ciento y se presentan resultados para 75 por ciento de suavidad en la Figura 2. En el segundo caso, también para Reino Unido, se eligió el año 1955 y se suavizó con respecto a las edades. La Figura 2 también presenta la estimación suavizada o tendencia a 75 por ciento (la máxima suavidad que puede ser alcanzada en este caso es 97.8 por ciento). La matriz de las estimaciones de log(d_i/e_i) está dada por Var( Ŷ_(α)) = (σ^-2_η I_m + σ^-2_ε N^-1'D'₂ D₂N^-1)^-1. Sin embargo, para tener en cuenta la base de B-splines, al igual que en Currie et al. (2004) se utiliza la aproximación Var( Ŷ_(α)) ≈ B(B'WB + λD'₂ D₂)^-1B'. Por lo tanto, un intervalo de ±3 desviaciones estándar está dado por log (d_i/e_i) ±3√Var( Ŷ_(α)), donde Var( Ŷ_(α)i) es el i-ésimo elemento en la diagonal de Var( Ŷ_(α)).

Dado que se empleó el mismo porcentaje de suavidad en ambas gráficas de la Figura 2, éstas se pueden comparar y decir entonces que hay más incertidumbre en la dimensión de años que en la de edades. Para una edad dada, el descenso de la mortalidad a través del tiempo evoluciona lentamente, mientras que para un año específico, todo el rango de variabilidad de la mortalidad (para todas las edades) está presente. Además, es claro que en el año 1955 la incertidumbre en ambos extremos de la serie es mayor que en su parte media. Esto se atribuye esencialmente al hecho de que las tasas de mortalidad en edades 10-25 y mayores a 90 tienen más alta variabilidad que en otras edades. Debe notarse que en el caso de edad 65, hay algunas observaciones que quedan excluidas de los intervalos de estimación.

Como puede apreciarse en las tasas de mortalidad mexicana de la Figura 3, existe mayor variabilidad en comparación con las de Reino Unido para la misma edad. De hecho, en el caso mexicano gran parte de los puntos observados está fuera del intervalo de estimación, situación que acontece como fue indicado sólo en unos cuantos puntos del caso del Reino Unido. Es probable que en aquel país se tenga mayor control en el registro de las defunciones de población de dicha edad, además de que se debe recordar que se trata de un grupo selecto de población que estaba asegurada. Asimismo para los años de 2000 a 2010, en el caso mexicano, para la edad de un año, casi todos los puntos pertenecen al intervalo de estimación.

A manera de contraste entre los datos mexicanos, el intervalo de la tendencia estimada para la mortalidad infantil empleada, considera ligeramente mejor a este grupo de edad que al de 65 años. Hay también menos variabilidad en estas observaciones.

Utilizando el mismo argumento expuesto anteriormente, es probable que en México se ponga un poco más de esmero en el registro de la mortalidad infantil que en la de 65 años, ya que en diversos planes nacionales de salud, recurrentemente se ponen metas en función de ella. Otra posibilidad es que en el Reino Unido haya una subestimación de la mortalidad infantil, por medio de la cual se excluyan observaciones indeseadas.

En lo tocante a superficies de mortalidad, es claro que se pueden concebir como la apreciación conjunta de experiencias anuales de mortalidad, con estructuras habituales en este tipo de fenómeno demográfico. En cada una de ellas, en escala de logaritmo natural, es posible identificar de manera exploratoria la intensidad de la mortalidad en las tres etapas de la vida humana. Puede apreciarse cómo al pasar del tiempo, en datos del Reino Unido la dispersión de los datos originales decrece en las edades más avanzadas y se observa un descenso en la mortalidad infantil.

Con lo anterior, para el caso bidimensional se encuentra lo siguiente. Para producir un grado adecuado de suavidad en ambas dimensiones se decide elegir un parámetro de suavidad mayor para la dimensión de años que para la dimensión de edades. Se tomó esta decisión porque con el suavizamiento unidimensional se mostró que λ_a = 0.1 y λ_y = 461 producen el mismo porcentaje de suavidad (véase la Figura 2) indicando que se requiere más suavidad en la dimensión de años. En la Figura 4 se aprecian algunas superficies de mortalidad suavizadas para edades 11-100, con diferentes porcentajes de suavidad. Este ejercicio replica el ejemplo de suavizamiento que aparece en Currie et al. (2004: 15 y 16) para el cual se obtienen los valores de los criterios automáticos AIC = 2306.3 y BIC = 4770, con los cuales se determinó que λ_a = 0.6, λ_y = 150 y df = 41.2 (véase la Figura 4, panel superior derecho). Ahora se puede decir también que la suavidad que se logra es de 75.6 por ciento y que el máximo porcentaje de suavidad que puede ser alcanzado con estos datos es 97.6.

También se aprecia que el conocimiento ganado del análisis unidimensional puede ser utilizado para llevar a cabo el suavizamiento bidimensional con eficacia. De hecho, puede ser empleado para: i) generar una superficie de mortalidad suavizada con un índice de suavidad fijado de antemano (por ejemplo con 75 por ciento de suavidad) y ii) sugerir el valor de λ_y (o λ_a) que mantiene la proporción unidimensional λ_y/ λ_a encontrada en el análisis unidimensional. En nuestro caso, se tiene λ_y/ λ_a = 4 610 y se puede encontrar que el valor apropiado es λ_a = 0.042, dado que λ_y= 4610 λ_a (de manera que λ_y = 193.62) para obtener una superficie de mortalidad con 75 por ciento de suavidad bidimensional (véase la Figura 4, panel inferior derecho).

Adicionalmente, la Figura 4 permite ver que la elección de los parámetros de suavizamiento conducen a 75.6 por ciento de suavidad, donde se presta más atención a suavizar en la dimensión de edades (λ_a = 0.6) y la superficie luce más suave en la dimensión de edades que en la superficie correspondiente a 78 por ciento de suavidad (con λ_a = 0.1) la cual está más balanceada en la suavidad de ambas dimensiones.

En el caso mexicano, al tener una extensión mayor de datos en relación con los de Reino Unido, se puede advertir una dinámica distinta en los extremos de las superficies. Debe recordarse que los datos para el caso extranjero son para una población selecta asegurada, de hecho se puede afirmar que en esa experiencia de mortalidad no se tiene registro de toda la mortalidad infantil y que aquellos expuestos distan mucho, en cuanto a condiciones de vida de los mexicanos, que son altamente heterogéneas según lo muestran los últimos índices de marginación publicados por el Consejo Nacional de Población (CONAPO) para el año 2010. Empleando exactamente los mismos índices que en la Figura 4, no se tienen cambios tan notables en las estructuras de las superficies mexicanas, según se aprecia en la Figura 5. Esto podría sugerir que la calidad de los datos mexicanos es relativamente homogénea de 1990 a 2010 y sistemática para todos los grupos de edad. Esto en ningún sentido supera las deficiencias de los datos mexicanos que fueron señalados anteriormente, pero sí da una idea de la estructura demográfica de la mortalidad. De hecho los datos mexicanos lucen más suaves que los correspondientes al Reino Unido.

En la Figura 6 se muestran varios ejemplos que consideran casos extremos para el suavizamiento de la mortalidad mexicana donde, con la manipulación de los parámetros de suavizamiento, se obtienen distintos índices de suavidad aproximados y se percibe el comportamiento en el límite, cuando dichos párametros tienden a infinito. Como se conoce en la literatura para el caso unidimensional, cuando el parámetro de suavizamiento crece hacia infinito se tiende a una recta, en este caso, extrapolando esa idea, se tiende a un plano. Sin embargo, el límite que tiene el índice de suavidad bidimensional está acotado, según se indica en la Proposición 2. Es decir, aun cuando se incremente indiscriminadamente uno o ambos parámetros de suavizamiento hacia infinito, se tendrá el mismo resultado en la estimación, salvo por discrepancias debidas a la precisión numérica. Cabe advertir que al utilizar los P-splines se induce a priori una cierta suavidad, la cual se pretende cuantificar en alguna investigación futura.

Para vincular el suavizamiento unidimensional con el bidimensional se sugiere lo siguiente. Primero se debe fijar un índice de suavidad en una de las dos dimensiones; luego, con base en el máximo porcentaje de suavidad que puede ser alcanzado, decidir el valor de S_ay%. Finalmente, elegir el parámetro de suavizamiento para la dimensión complementaria de tal modo que se alcance la suavidad conjunta deseada. Como ejemplo de esta sugerencia a continuación se suaviza la serie unidimensional de 30 a 70 años de edad para los años 1947-1999, con 75 por ciento de suavidad. Al establecer el índice de suavidad unidimensional se usa λ_y = 0.1 para todas las edades (la Figura 7 muestra los resultados para la edad 30). Si se busca S_ay% = 85 por ciento como suavidad conjunta, se debe encontrar el valor del parámetro λ_a que la produzca, dado que λ_y = 0.1 se ha fijado previamente. Con un proceso iterativo se elige λ_a = 2 165 000 como el valor que asegura alcanzar el porcentaje de suavidad conjunta deseado. La superficie de mortalidad en la Figura 7 muestra los mismos datos que están en la Figura 4 desde una perspectiva ligeramente distinta, la cual pretende facilitar la comparación de resultados obtenidos en dos dimensiones, con respecto a los de una dimensión. Se enfatizan los resultados para la edad 30 con los siguientes porcentajes de suavidad: 13.7 por ciento (dado que λ_a ≈ 0) 75 por ciento y 85 por ciento, respectivamente.

Las dos gráficas de la parte superior de la Figura 7 permiten comparar los resultados del suavizamiento, que puede ser considerado equivalente aunque en diferentes dimensiones. De hecho, las curvas suavizadas para la edad 30 muestran dinámicas similares. Cuando se mantiene el valor λ_y = 0.1 y se impone λ_a ≈ 0, la superficie no cambia de manera sensible. Este hecho era de esperarse, dado que no hay suavizamiento que se produzca en la dimensión de edades. Por otra parte, las dos gráficas inferiores permiten ver cómo la suavidad para la edad 30 se hace más pronunciada cuando el porcentaje de suavidad bidimensional se incrementa. Aquí también se tiene una apreciación visual de la manera en que la superficie de mortalidad se hace más plana (más suave).

 

Conclusiones

Se considera que la propuesta que aquí se presenta es útil para estimar tendencias de mortalidad con un porcentaje deseado de suavidad fijado de antemano para diversos conjuntos de datos, con la finalidad de establecer comparaciones válidas.

De esta manera, es factible comparar distintas tendencias de mortalidad seleccionando adecuadamente los parámetros de suavizamiento, con el propósito de alcanzar las suavidades que se desean, expresadas mediante los índices de suavidad, cuyas propiedades se establecen en este ensayo. Con esto, la mayor aportación de este trabajo es la propuesta de los denominados índices de suavidad en el contexto bidimensional, los cuales poseen propiedades deseables que aquí se citan.

Asimismo, se establece la relación entre los índices de suavidad unidimensional y bidimensional y se sugiere cómo puede interpretarse y utilizarse la suavidad marginal. Cabe decir que el caso bidimensional se puede entender como una generalización del caso unidimensional. Por otro lado, esta propuesta hace uso de MCG aunque se obtienen resultados idénticos a los establecidos en la literatura desde la perspectiva tradicional. De hecho, como se comentó en el documento, los índices son una reparametrización de los df. Con esta vinculación entre ambos enfoques, es factible estimar tendencias de mortalidad en dos dimensiones (edad y años) haciendo uso de métodos de suavizamiento de tipo spline, ya establecidos en la literatura sobre el tema.

Para los cálculos numéricos no se requiere usar matrices de gran tamaño, sobre todo en el uso de las bases de B-spline, sino que los resultados teóricos permiten hacer las estimaciones correspondientes. Los ejemplos buscan mostrar ilustraciones del potencial que tiene la técnica y sugieren lo que se podría hacer con datos por entidad federativa. Finalmente, debe ser claro que con las debidas adecuaciones, la metodología también se podría aplicar a otros fenómenos demográficos que se presentan en el país, como los análisis por edad, sexo y estado civil. Posteriormente se podrían efectuar comparaciones y estudiar las diferencias que se presenten entre las tendencias estimadas, desde luego, con un mismo nivel de suavidad en todas ellas.

Otro punto importante por comentar es el hecho de utilizar o no P-splines. Una ventaja es que gran cantidad de librerías en software estadístico comercial y también libre, como R, permite usar este tipo de herramientas, las cuales son relativamente sencillas de implementar para suavizar datos de distinta naturaleza, con lo cual se tiene un mecanismo altamente aceptado en la literatura especializada. Sin embargo, el analista muy probablemente conseguirá distintos niveles de suavidad para distintos conjuntos de datos, lo cual es desafortunado para efectos de comparabilidad. Como desventaja adicional, resulta que de facto se está induciendo numéricamente a un monto de suavidad que puede o no ser el deseado por el analista. Un tema futuro de investigación consiste en medir la suavidad inducida por el empleo de este tipo de herramientas numéricas, así como cuánta suavidad es debida a la inclusión o exclusión de la matriz de ponderaciones. En el caso bidimensional, se podría proponer como meta para cada una de las entidades del país la tendencia estimada de la entidad que tenga la más baja mortalidad actualmente. Con ello se podría estimar entonces una tendencia con la suavidad derivada de un criterio numérico automático e imponerla al resto de las entidades. Así sería posible analizar si se está suscitando o no una convergencia en la intensidad de la mortalidad que dé evidencia del adelgazamiento de la brecha de la desigualdad de la mortalidad al interior de los estados.

La metodología propuesta es una herramienta que aunque no corrige las deficiencias de calidad de la información puede mitigar los efectos de éstas, en cuanto a la estructura subyacente de los datos, a través de tendencias estimadas con suavidad controlada por el analista. Con esta perspectiva se podría tener una opción para el proceso de correcciones de deficiencias extremas, tanto de datos censales como de defunciones, bajo algunos supuestos por plantear. Es importante recalcar que la propuesta que aquí se presenta es una herramienta de carácter exploratorio que podría utilizarse para posteriores análisis más detallados de índole demográfico o estadístico.

 

Bibliografía

BOOTH, H. y TICKLE, L., 2008, “Mortality Modelling and Forecasting: A Review of Methods”, en Annals of Actuarial Science 3: 3–43.         [ Links ]

BROUHNS, N., DENUIT, M. y VERMUNT, J. K., 2002, “A Poisson log-bilinear regression approach to the construction of projected life tables”, Insurance: Mathematics and Economics 31: 373-93.         [ Links ]

CLAYTON, D. y SCHIFFLERS, E., 1987, “Models for temporal variation in cancer rates. II: Age-period-cohort models”, Statistics in Medicine 6: 469-81.         [ Links ]

CLEVELAND, W. y DEVLIN, S., 1988, “Locally weighted regression: an approach to regression analysis by local fitting”, Journal of the American Statistical Association 83: 597-610.         [ Links ]

CURRIE, I. y DURBAN, M., 2002, “Flexible smoothing with P-splines: a unified approach”, Statistical Modelling 2: 333-349.         [ Links ]

CURRIE, I., DURBAN, M. y EILERS, P., 2004, “Smoothing and forecasting mortality rates”, Statistical Modelling 4: 279-298.         [ Links ]

DEBÓN, A., MONTES, F. y PUIG, F., 2008, “Modelling and Forecasting Mortality in Spain”, European Journal of Operational Research 189: 624–637.         [ Links ]

DE BOOR, C. , 2001, A practical guide to splines. New York: Springer.         [ Links ]

DELWARDE, A., DENUIT, M. y EILERS, P., 2007, “Smoothing the Lee-Carter and Poisson log-bilinear models for mortality forecasting: A penalized log-likelihood approach”, Statistical Modelling 7: 29-48.         [ Links ]

DIERCKX, P., 1993, Curve and surface fitting with splines. Oxford: Clarendon Press.         [ Links ]

EILERS, P. y MARX, B., 1996, “Flexible smoothing with B-splines and penalties”, Statistical Science 11: 89-121.         [ Links ]

FIGUEROA, B. (coordinadora), 2008, El dato en cuestión. Un análisis de las cifras sociodemográficas. El Colegio de México, Centro de Estudios Demográficos, Urbanos y Ambientales, Primera edición, México.         [ Links ]

GU, C. y WAHBA, G., 1993, “Semiparametric analysis of variance with tensor product thin plate splines”, Journal of the Royal Statistical Society Series B-55: 353-368.         [ Links ]

GUERRERO, V. M., 2007, “Time series smoothing by penalized least squares”, Statistics and Probability Letters 77: 225–1234.         [ Links ]

GUERRERO, V. M., 2008, “Estimating Trends with Percentage of Smoothness Chosen by the User”, International Statistical Review 76: 187–202.         [ Links ]

HASTIE, T. y TIBSHIRANI, R., 1990, Generalized additive models. London: Chapman & Hall.         [ Links ]

LONDON, D., 1985, GRADUATION: the revision of estimates, ACTEX Publications. Connecticut: Winsted and Abington.         [ Links ]

PARTIDA, V., 2008, “Evaluación de los niveles de mortalidad en México 1930-2000” en Figueroa, B. (coordinadora) (2008) El dato en cuestión. Un análisis de las cifras sociodemográficas. El Colegio de México, Centro de Estudios Demográficos, Urbanos y Ambientales, Primera edición, México.         [ Links ]

PAWITAN, Y., 2001, In all likelihood: statistical modelling inference using likelihood. Oxford: Oxford Science Publications.         [ Links ]

RUPPERT, D., 2002, “Selecting the Number of Knots for Penalized Splines”, Journal of Computational and Graphical Statistics 11: 735-757.         [ Links ]

RUPPERT, D., WAND, M. P. y CARROLL, R. J., 2003, Semiparametric Regression. Cambridge: Cambridge University Press.         [ Links ]

THEIL, H., 1963, “On the use of incomplete prior information in regression analysis”, Journal of the American Statistical Association 58: 401-414.         [ Links ]

WANG, D. y LU, P., 2005, “Modelling and Forecasting Mortality Distributions in England and Wales using the Lee Carter Model”, Journal of Applied Statistics 32, 873-885.         [ Links ]

WEINERT, H. L., 2007, “Efficient computation for Whittaker-Henderson smoothing”, Computational Statsitics and Data Analysis 52, 959-974.         [ Links ]

WOOD, S., 2003, “Thin plate regression splines”, Journal of the Royal Statistical Society Series B-65: 95-114.         [ Links ]

 

Información sobre los autores

Eliud Silva. Actuario por la Universidad Nacional Autónoma de México (UNAM). Maestro en Demografía por El Colegio de México y Doctor en Ingeniería Matemática con especialidad en Estadística por la Universidad Carlos III de Madrid. Ha impartido cursos en la UNAM, El Colegio de México, el Instituto Tecnológico Autónomo de México (ITAM), el Instituto Tecnológico y de Estudios Superiores de Monterrey (ITESM) y en la Universidad Carlos III de Madrid. Actualmente es Profesor de tiempo completo de la Universidad Anáhuac. Es miembro del Sistema Nacional de Investigadores. Cuenta con artículos publicados en revistas nacionales y extranjeras relacionados con series de tiempo y tópicos demográficos. Entre sus publicaciones más recientes (en coautoría con Víctor M. Guerrero y Nicolás Gómez) está Building Scenarios of Multiple Time Series that Take into Account the Effects of an Expected Intervention en el Journal of Forecasting. Dirección electrónica: jsilvaurrutia@hotmail.com

Víctor M. Guerrero. Actuario por la Universidad Nacional Autónoma de México (UNAM). Maestro y Doctor en Estadística por la Universidad de Wisconsin-Madison. Desde 1990 ha sido Profesor-Investigador de Tiempo Completo en el Departamento de Estadística del ITAM, del cual fue Jefe (1997-2004). Ha sido asesor para instituciones nacionales (como el Instituto Nacional de Estadística y Geografía INEGI) e internacionales (como el Harvard Institute for International Development). Es miembro del Sistema Nacional de Investigadores y ha ganado diversos premios de investigación, como el Premio de Investigación Financiera IMEF-Ernst & Young en 2011, Premio Gustavo Cabrera 2010 de El Colegio de México, Premio de Pensiones 2007 de la Comisión Nacional del Sistema de Ahorro para el Retiro (CONSAR), Certamen Permanente de Investigación del Banco de Guatemala 1999-2000 y el Premio de Investigación en Seguros y Fianzas 1994. Entre sus publicaciones más importantes se encuentran: “Use of the Box-Cox Transformation with Binary Response Models”, en Biometrika, 1982, “Optimal Conditional ARIMA Forecasts”, en Journal of Forecasting, 1989, “Monthly Disaggregation of a Quarterly Time Series and Forecasts of its Unobservable Monthly Values”, en Journal of Official Statistics, 2003 y “Estimating Trends with Percentage of Smoothness Chosen by the User”, en International Statistical Review, 2008. Dirección electrónica: guerrero@itam.mx

Daniel Peña. Es catedrático de la Universidad Carlos III de Madrid. Doctor por la Universidad Politécnica de Madrid y cuenta con posgrados por la Universidad Complutense de Madrid y en Harvard University. Ha sido catedrático en la Universidad Politécnica de Madrid, la Universidad de Wisconsin Madison y la Universidad de Chicago. Entre diversos cargos, fue miembro del Consejo Superior de Estadística del Estado, Vicepresidente del Instituto Interamericano de Estadística y Presidente de European Courses in Advanced Statistics. Cuenta con 14 libros y más de 200 artículos de investigación publicados sobre Estadística y Econometría. Actualmente es Rector de la Universidad Carlos III de Madrid. Dirección electrónica: dpena@est-econ.uc3m.es