Ajuste matemático de la mortalidad general en México 2000, 2005 y 2010

 

Mathematical adjustment of general mortality in Mexico 2000, 2005 and 2010

 

Claudio Alberto Dávila-Cervantes

 

Facultad Latinoamericana de Ciencias Sociales México

 

Este artículo fue
recibido el 9 de agosto de 2012
aprobado el 28 de noviembre de 2012.

 

Resumen

Se presenta una propuesta del método de splines cúbicos para ajustar la curva de mortalidad general en México por sexo en todo el rango de edad para 2000, 2005 y 2010. El método consiste en ajustar un polinomio de tercer grado en las primeras cuatro edades estimándolas de manera perfecta, entre cuatro y 80 años se ajusta un spline cúbico empleando cinco nodos y se ajusta otro polinomio de tercer grado a partir de 80 años. Se emplean 24 parámetros para estimar la curva de mortalidad en todo el rango de edad. Presenta una excelente bondad de ajuste para hombres, que se incrementa con el paso de los años; para mujeres la bondad de ajuste es, en general, superior. Se destacan como ventajas del método que permite la estimación relativamente parsimoniosa de la mortalidad, respeta los cambios de concavidad de la curva de mortalidad y posibilita realizar proyecciones de la mortalidad en diferentes contextos y causas de muerte.

Palabras clave: Mortalidad, splines cúbicos, ajuste matemático, México, rango de edad.

 

Abstract

I present a methodology based on Cubic Splines to fit the general mortality curve in Mexico by sex at all ages for the years 2000, 2005 and 2010. This method consists in fitting a polynomial of third degree in the first four ages (fitting them perfectly); between ages four and 80 we fit a cubic spline using five nodes; we fit another third-degree polynomial beginning at age 80. We employ 24 parameters to estimate the mortality curve in the full age range. This model presents an excellent goodness of fit in men, which increases over the years; for women, the goodness of fit is, in general, better than that for men. It is a relatively parsimonious estimation of mortality; it maintains the mortality curve's changes in concavity and allows the realization of mortality projections in different contexts and causes of death.

Key words: Mortality, cubic splines, mathematical modeling, Mexico, full age range.

 

Introducción

Durante el siglo XX se presentaron incrementos sustanciales en la esperanza de vida de la mayoría de los países del mundo, estos fueron provocados principalmente por avances científicos, médicos y de salud pública y, en general, por una mejora en los estándares de vida. A lo largo de ese periodo la esperanza de vida se incrementó a más de 75 años en los países de altos ingresos y a más de 60 en muchos países de ingresos medios (Smith et al., 2001: 49). Estos cambios han tenido impactos dramáticos en el tamaño y composición de las poblaciones.

En México, durante ese mismo periodo, se dio también una profunda transformación de la mortalidad. Después de la Revolución Mexicana se presentó una paulatina disminución de la mortalidad gracias a muchos factores, entre los que destacan modificaciones en el nivel de vida de la población y los primeros programas de salud pública (Camposortega, 1992; 1997: 11). Esta tendencia continuó durante todo el siglo y se vio reflejada en el aumento de esperanza de vida, este indicador alcanzó un nivel alrededor de 74 años a final del siglo, cuando su nivel en 1920 era de 30 años aproximadamente. Este aumento en la esperanza de vida se presentó de forma acelerada entre 1940 y 1960, las ganancias en esperanza de vida fueron de casi 19 años en los siguientes 50 años; el ritmo de crecimiento ha sido considerablemente menor, ya que se ha incrementado en casi 18 años.

Estas trasformaciones fueron posibles gracias a que en los años cuarenta y cincuenta se contuvieron con éxito las causas de muerte más susceptibles de controlar: las enfermedades infecciosas y parasitarias. Actualmente, las enfermedades crónico-degenerativas (como enfermedades cardiovasculares, diabetes, neoplasmas, etc.), así como las muertes por causas externas (accidentes y muertes violentas), tienen cada vez mayor presencia relativa dentro del perfil epidemiológico del país (Camposortega, 1997: 11); estas causas son más difíciles de controlar, debido a que requieren de una mayor infraestructura médica y de salud pública, mayores avances técnicos, un mejor nivel de vida de la población y una cultura de prevención; esto pudiera explicar que el ritmo de aumento en la esperanza de vida se haya vuelto paulatinamente más lento. Cabe mencionar que la relación entre la estructura de causas de muerte de una población, su patrón por edad de la mortalidad y el efecto que tienen sobre la esperanza de vida de la población se formalizó en la Teoría de la Transición Epidemiológica (Omran, 1971: 509).

Entonces, la cuestión frente al menor crecimiento de la esperanza de vida es analizar cómo esta se puede continuar incrementando. Algunos investigadores creen que parte de la respuesta está en entender el comportamiento del patrón de mortalidad en una población y ajustarlo de tal forma que se pueda realizar un manejo matemático del fenómeno, lo que puede posibilitar realizar proyecciones (Halli y Rao, 1992) y desarrollar investigaciones sobre efectos, modificaciones y cambios posibles en edades específicas; se observa dentro de la comunidad científica un creciente interés en la descripción y ajuste matemático de los patrones de mortalidad. Investigaciones de este tipo que se han realizado en torno a los distintos fenómenos demográficos (en particular la mortalidad), constituyen una parte importante del desarrollo de la demografía y de la implementación de políticas públicas, programas de salud pública y planes de desarrollo (Mina, 2006). Además, con los modelos de mortalidad "se puede resumir en pocos parámetros la tabla de mortalidad, en especial la serie de sobrevivientes a edad exacta x (l_x), lo que adicionalmente permite, una vez que la tendencia histórica de dichos parámetros se tiene, proyectar el impacto de la mortalidad, obteniéndose las tablas de mortalidad a corto y largo plazo, pudiendo cuantificar las ganancias en las esperanzas de vida que en el futuro se tendrán, lo que sirve, entre otras cosas, para la legislación sobre las edades de retiro de la población económicamente activa y la legislación sobre la conveniencia de ampliarla, y hasta qué edad realmente hacerlo" (Mina, 2009: 66).

Existen varios intentos previos para modelar la curva de mortalidad en todo el rango de edad, entre ellos se destacan el modelo propuesto por Gompertz en 1825 y sus variantes Gompertz-Makeham y Lazarus (Mina, 2001; 2006); sin embargo, es conocido que la ley de Gompertz no ajusta de manera correcta la mortalidad en ciertas edades, en particular en las primeras edades de la tabla de vida y en las edades muy avanzadas, ya que las probabilidades observadas suelen ser menores que aquellas predichas por el modelo y, con ello, el número de supervivientes en edades extremas es mayor a aquel que la ley de Gompertz ajusta (Gavrilov y Gavrilova, 2002).

Asimismo, se han propuesto otras tres de esas leyes que ajustan todo el rango de edad de la mortalidad, la de Thiele en 1872, Wittstein en 1883 y la propuesta por Heligman y Pollard en 1980 (Hartmann, 1987: 19). La valía de estas leyes radica en su intento por modelar todo el rango, a diferencia de otras leyes de mortalidad que son parciales, pues ajustan bien secciones de las curvas de mortalidad, pero tienen problemas representando ciertas características de estas; sin embargo, las tres leyes referidas presentan una limitante, estiman la mortalidad por grupos de edad quinquenales, que si bien sirven para interpolar las probabilidades de muerte y obtenerlas por edad desplegada, pudieran no respetar cambios de concavidad en la curva, visibles solamente al trabajar con edades individuales (Mina, 2006).

En cuanto a la distribución por edad y sexo del total de defunciones en el país, en general, existe una sobremortalidad masculina, particularmente en las edades comprendidas entre 15 y 60 años de edad (Gráfica 1). Asimismo, las probabilidades de defunción en el país siguen el patrón regular en forma de j observado en muchas poblaciones. Este patrón está provocado por una mayor probabilidad de muerte en el primer año de vida de las personas, que disminuye hasta alcanzar su mínimo entre cinco y 10 años de edad; posteriormente se presenta un constante aumento de las probabilidades de muerte a partir de los 10 años de vida de las personas, con un incremento considerable para los hombres en la adolescencia y en edades adultas jóvenes, debido principalmente a la mayor mortalidad por accidentes y muertes violentas que se presenta en esas edades; y finalmente un crecimiento exponencial reflejado en un crecimiento casi geométrico de las probabilidades de fallecer en las edades adultas mayores (Heligman y Pollard, 1980: 73).

Bajo este marco, el objetivo de este trabajo es presentar una propuesta del método de splines cúbicos como un modelo alternativo para ajustar la curva de mortalidad general por sexo en todo el rango de edad (de cero a 100 años de edad) por edad desplegada para los años 2000, 2005 y 2010. Para ello, se calcula la bondad de ajuste entre la serie de supervivientes a edad x (l_x) observada a partir de datos de mortalidad de las estadísticas vitales y aquella estimada a partir de los splines cúbicos propuestos. Se realiza también una comparación entre la esperanza de vida observada y la estimada por medio de los splines cúbicos, con la finalidad de analizar la calidad del ajuste propuesto. Asimismo, se presentan los resultados del ajuste de las curvas de mortalidad de otros cuatro países, con la finalidad de estudiar la flexibilidad del modelo aplicándolo en otros contextos. Cabe mencionar que el ajuste se realiza por edad desplegada, ya que de esta manera se considera que se obtiene una estimación más precisa de la mortalidad, puesto que no se interpolan los valores de la curva de mortalidad en las edades no consideradas al agrupar en grupos quinquenales y con ello se respetan de mejor manera los cambios de concavidad presentados en la misma.

 

Material y métodos

Se propone una metodología que emplea un polinomio de tercer grado en las primeras cuatro edades de la serie de supervivientes a edad exacta x (l_x)¹ ajustándolas de manera perfecta, debido al cambio de concavidad en la curva provocado por la relativamente alta mortalidad infantil (en el primer año de vida) todavía existente en el país, el cual no es bien ajustado por las funciones de supervivencia como Gompertz o Gompertz-Makeham (Gavrilov y Gavrilova, 2002). Este primer polinomio presenta una unión suave con el primer polinomio del spline. Entre las edades cuatro y 80 se ajusta un spline cúbico empleando cinco nodos (o puntos de unión entre los polinomios del spline), los cuales varían en su ubicación dependiendo el año y el sexo, y se seleccionan aquellas edades en las cuales se proporciona un mejor ajuste de la mortalidad. Un polinomio de tercer grado en las últimas edades de la curva de mortalidad, a partir de los 80 años, ajusta el cambio de concavidad relacionado con la desaceleración y el nivelamiento de la mortalidad en las edades mayores de la tabla de vida (Gavrilov y Gavrilova, 2006: 23).

En los problemas de interpolación y ajuste matemático, como el que se realiza en esta investigación, se utilizan a menudo splines cúbicos debido a que emplearlos da lugar a resultados similares a los que se obtendrían con polinomios de mayor grado, pero con polinomios de bajo grado; esto conlleva una doble ventaja: se evita que aparezcan oscilaciones indeseables al ajustar la curva de mortalidad mediante polinomios de grado mayor a tres (Mina, 2011) y se calcula una menor cantidad de parámetros, logrando así una estimación más parsimoniosa² de la curva de mortalidad. Estas son algunas razones de la elección de polinomios de tercer grado para ajustar la curva de mortalidad. En cuanto a la elección de los nodos para ajustar la curva de mortalidad, esta se realiza de acuerdo a las edades que muestran diferencias en la suavización, esto es, puntos de la curva donde se presentan cambios de concavidad. El uso de cinco nodos se relaciona también con cambios en la curva mortalidad, los dos primeros nodos moldean las edades de la niñez, la adolescencia y la adultez joven en las que la mortalidad esta dominada por causas externas en hombres y por muerte materna; del segundo al cuarto nodo se modela la mortalidad adulta, la cual es todavía elevada por causas externas y enfermedades hepáticas en hombres, por cáncer de mama y cérvico-uterino en mujeres; finalmente, del cuarto al quinto se realiza el ajuste de las edades adultas y adultas mayores, donde hay un predominio de muertes por padecimientos crónico-degenerativos.

Se tomaron como puntos de corte del spline cuatro y 80 años debido, en parte, a la limitación que presentan los datos de mortalidad, puesto que es en estas edades extremas donde se presentan los mayores problemas como el subregistro de defunciones infantiles, en el caso de las personas mayores, la edad informada tiende a aumentarse a medida que avanza la edad, lo cual contribuye a subestimar la mortalidad en algunos grupos de adultos y a estimarla en exceso en grupos de personas mayores (OPS, 2003).

La bondad del ajuste de esta metodología se analiza por medio del coeficiente de determinación R² entre las series de supervivientes a edad x (l_x) observada y la estimada a partir de este método; esto también se realiza para las probabilidades de defunción a edad x (q_x) con la motivación de corroborar si el ajuste mantiene la concavidad de los datos observados a lo largo de todo el rango de edad y si ajusta de manera adecuada otra serie de la tabla de vida. Cabe recordar que entre más cercano a 1 esté el valor, el ajuste se considera mejor, por lo que la intención es obtener el máximo valor de este indicado. De la misma manera se analiza el ajuste por medio del error medio absoluto porcentual (EMAP), el cual se define como (Debon, 2003):

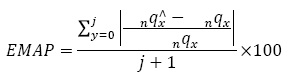
Endonde _nq_x son las probabilidades originales y _nq^∧_x las ajustadas. Es importante señalar que entre menor sea el valor de este indicador, mejor será el ajuste de la mortalidad.³

Del mismo modo, se considera importante realizar una modelación de la mortalidad en otros contextos, con la motivación de comparar los resultados de la aplicación de este método entre distintos países y de esta manera obtener una mayor validez de las estimaciones realizadas en México. Debido a ello, se llevó a cabo la estimación para los supervivientes de otros países, los cuales son: Australia, Estados Unidos, El Salvador y Brasil; los dos primeros tienen datos sobre mortalidad de muy buena calidad y los países latinoamericanos se eligieron porque su esperanza de vida es similar o menor a la mexicana. Se comparan los resultados de la R² obtenida en estos ajustes, así como de la estimación de la esperanza de vida oficial reportada en esos países.

 

Fuentes de información

La información de este estudio se obtuvo de las Estadísticas Vitales de Mortalidad del Instituto Nacional de Estadística y Geografía (INEGI) y de las proyecciones de población realizadas por el Consejo Nacional de Población de México (CONAPO). Los datos de defunciones se obtuvieron para los años 2000, 2005 y 2010, a nivel nacional, por sexo y por edad desplegada. La población a mitad de año, para calcular las tablas de mortalidad de las cuales se deriva la serie de supervivientes a edad exacta x, se obtuvo de las proyecciones 1990 a 2050 del CONAPO.

Para realizar la comparación con otros países, se obtuvieron datos provenientes de tablas de mortalidad de la Organización Mundial de la Salud (OMS) para 1990, 2000 y 2009, así como del Census Bureau en Estados Unidos para 2000 y 2005.

Para el análisis en México se tuvieron en cuenta las defunciones ocurridas al interior del país, quedando excluidos los siguientes dos casos: registros no especificados por edad y sexo y muertes ocurridas en el exterior. A partir de esto, se descartaron del total de registros 2 946 en 2000, 2 402 en 2005 y 3 006 en 2010, que corresponden a 1.21, 0.88 y 0.91 por ciento del total de las defunciones para hombres; en cambio, para mujeres no se tomaron en cuenta 1 417 registros en 2000, 950 en 2005 y 780 en 2010, que corresponden a 0.73, 0.43 y 0.30 por ciento del total. Cabe resaltar que este estudio se realiza a nivel nacional en todos los casos.

En México la información estadística proveniente del Registro Civil no es del todo confiable, esta debe evaluarse y prepararse para realizar estimaciones con un marco de certidumbre alto. Un estudio sobre de la calidad de los datos provenientes de las estadísticas de mortalidad es el de Dávila (2012), quien analiza la declaración por edad de la mortalidad en el certificado de defunción por medio del cálculo de los índices Whipple y Myers, así como un análisis de la estructura por edad y sexo de las defunciones por medio de pirámides de población, y de las principales medidas de tendencia central (media, mediana y varianza). Entre los principales resultados de ese análisis descriptivo se encuentra que los datos de mortalidad presentan una mejor calidad conforme ha avanzado el tiempo, colocándose a partir del año 2000 como información precisa y muy precisa.

 

Desarrollo de los splines

Los splines son funciones definidas por una familia de polinomios sociables, es decir, los polinomios que constituyen una función spline están estrechamente vinculados. El concepto de los splines se debe a un instrumento que utilizaban los ingenieros navales para dibujar curvas suaves, forzadas a pasar por un conjunto de puntos prefijados. La mayor dificultad radica en construir un interpolante que preserve el comportamiento de los datos, es decir, que mantenga las propiedades de monotonía y/o convexidad de los datos (Barrera et al, 1996; Mina, 2011).

Un spline es entonces una función f formada por secciones de polinomios cúbicos, por lo que tiene la forma P(x) = ax³ + bx² + cx + d, los cuales se unen con la mayor suavidad posible (sin que f sea necesariamente un polinomio único) (Barrera et al, 1996; Mina, 2011). En este caso se debe exigir que cada polinomio P_i(x) del spline cúbico satisfaga:

Donde:

g_i es el valor de la función g a ajustar.

s_i es el valor de la primera derivada de g en un conjunto de puntos {x_i} con i = l,...,n.

Si se cumple esto, no importa el valor de s_i , la función f definida por P_i(x) en cada intervalo [x_i, x_i+1;] es continuamente diferenciable. Por tanto, para que f sea un spline basta tomar los s_i de modo que la segunda derivada f '' sea continua. Como f está formada por secciones de polinomios cúbicos, los únicos puntos posibles de discontinuidad de f '' son los puntos x_i donde se empatan dos polinomios cúbicos. La continuidad de f '' es equivalente a exigir que:

f '' (x_i^-) =f '' (x_i⁺) con i = 2,...,n-1

Entonces, después del desarrollo que se presenta en Barrera et al. (2006) y en Mina (2011), las s_i deben de satisfacer las siguientes ecuaciones:

a_is_i-1+ d_is_i + (1 - a_i)s_i+1= b_ii=2,...,n-1

Donde:

Suponiendo que s₁ y s_n se eligen de alguna manera, tenemos un sistema de n-2 ecuaciones lineales para calcular las n-2 incógnitas s₂,...,s_n-1. Para obtener el valor de las incógnitas es necesario resolver el sistema de ecuaciones, el cual tiene una sola solución y puede resolverse por el método de eliminación de Gauss sin pivoteo.⁴ Los parámetros s₁ y s_n dependen de las condiciones que se impongan en la frontera. En general existen tres tipos de condiciones.

La primera condición da pie al spline cúbico completo, se deriva de conocer de antemano el valor de g' en x₁ y x_n, por lo se toma s₁= g'(x₁) y s_n= g'(x_n). En ese caso el spline no solo interpola a g en los puntos x₁,..., x_n' sino que también interpola a g' en x₁ y x_n.

La segunda condición consiste en elegir que la segunda derivada del spline en los extremos sea cero, esto es f '' (x₁) =f " (x_n) = 0. Las ecuaciones a las que da lugar esta condición se pueden ver en Barrera et al. (1996). Este tipo de spline se conoce como spline cúbico natural. Barrera et al. (1996) mencionan que, desde cierto punto de vista, éste tipo no es muy recomendable ya que la imposición arbitraria de las segundas derivadas puede provocar que cerca de los extremos x₁ y x_n el error aumente.

La tercera condición se da cuando no se tiene conocimiento sobre las derivadas de g en los extremos, entonces se eligen s₁ y s_n de tal manera que P₁ coincida idénticamente con P₂ y que P_n-1 coincida con P_n-2. En otras palabras se trata de escoger s₁ y s_n de modo que los puntos x₂ y x_n-1 no sean puntos de ruptura de la función f. Como f es un spline cúbico se sabe que:

P₁^(j)(x₂) = P₂^(j)(x₂); P_n-1^(j)(x_n-1) = P_n^(j)(x_n-1) para j = 0,1,2

Además, como P₁ y P₂ son polinomios cúbicos se pueden escribir como (Barrera et al, 2006):

P₁(x) = P₁(x₂) + P₁' (x₂)(x - x₂) + P₁ '' (x₂)(x - x₂)²/2 + P₁''' (x₂)(x - x₂)³/6

P₂(x) = P₂(x₂) + P₂' (x₂)(x - x₂) + P₂ " (x₂)(x - x₂)²/2 + P₂'''(x₂)(x - x₂)³/6

Por tanto, la condición en la frontera es equivalente a exigir que P₁'''(x₂) = P₂ '''(x₂), es decir, que f ' '' sea continua en x₂ y de manera análoga P_n-2''' (x_n-1) = P_n-1''' (x_n-1) (Barrera et al, 2006). Este estudio parte de la tercera condición para la elección de los parámetros s₁ y s_n, dado que no se tiene conocimiento sobre la función de supervivientes, debido a que los datos se han obtenido a partir de los registros administrativos, y por tanto no se dispone de información sobre la primera derivada de la función.

Para este caso se ajusta un spline cúbico con cinco nodos, que es entonces una función f formada por cuatro secciones de polinomios cúbicos, de la forma:

P(x) = ax³ + bx² + cx + d.

El spline se calcula a partir de la edad cuatro (primer nodo) hasta la edad 80 (quinto nodo) y con tres edades intermedias, las cuales indicarían el resto de los nodos (Gráfica 2). Esto implica que se van a ajustar cuatro polinomios cúbicos (números 1 a 4 en la Gráfica 2). Como se puede observar, en el punto [x₂, y₂] se intersectan los dos primeros polinomios, en el punto [x₃, y₃] se cruzan el segundo y el tercero y en [x₄, y₄] se unen el tercero y cuarto polinomios. En cambio en los puntos [x₁, y_1j] y [x₅, y₅] se tiene el inicio del primer y cuarto polinomios respectivamente. Esto se traduce en el siguiente sistema de ocho ecuaciones.

Donde los parámetros a_i , b_i , c_i y d_i , con i = 1,2,3,4 son los correspondientes a cada uno de los cuatro polinomios:

y₁ = a₁x³₁ + b₁x²₁ + c₁x₁ + d₁ ... (1)

y₂ = a₁x³₂ + b₁x²₂ + c₁x₂ + d₁ ... (2)

y₂ = a₂x³₂ + b₂x²₂ + c₂x₂ + d₂ ... (3)

y₃ = a₂x³₃ + b₂x²₃ + c₂x₃ + d₂ ... (4)

y₃ = a₃x³₃ + b₃x²₃ + c₃x₃ + d₃ ... (5)

y₄ = a₃x³₄ + b₃x²₄ + c₃x₄ + d₃ ... (6)

y₄ = a₄x³₄ + b₄x²₄ + c₄x₄ + d₄ ... (7)

y₅ = a₄x³₅ + b₄x²₅ + c₄x₅ + d₄ ... (8)

Como las discontinuidades se presentan en los puntos [x₂, y₂] , [x₃, y₃] y [x₄, y₄], se tiene que pedir la condición de que las primeras derivadas deben coincidir en estos puntos. Para tal caso se obtienen las derivadas con respecto a x de las ecuaciones (2), (3), (4), (5), (6) y (7) y se igualan las correspondientes por pares (2 y 3, 4 y 5, 6 y 7). Entonces el resultado proporciona un sistema de tres ecuaciones más, de la forma:

3a₁x²₂ + 2b₁x₂ + c₁ - 3a₂x²₂ - 2b₂x₂ - c₂ = 0 ... (9)

3a₂x²₃ + 2b₂x₃ + c₂ - 3a₃x²₃ - 2b₃x₃ - c₃ = 0 ... (10)

3a₃x²₄ + 2b₃x₄ + c₃ - 3a₄x²₄ - 2b₄x₄ - c₄ = 0 ... (11)

Estas ecuaciones resultan de igualar las derivadas y despejar los términos para igualarlas a 0. Para la siguiente condición se recuerda que, como el spline está formado por secciones de polinomios cúbicos, los únicos puntos posibles de discontinuidad de la segunda derivada son los puntos x_i donde se empatan dos polinomios cúbicos y, por tanto, se pide también que las segundas derivadas sean iguales: f " (x_i^-) = f " (x_i⁺) con i = 2,...,n. Esto se calcula a partir de las ecuaciones (9), (10) y (11), derivándolas una vez más, y de esa forma se obtiene un sistema de tres ecuaciones de la forma:

6a₁x₂ + 2b₁ - 6a₂x₂ - 2b₂ = 0 que se escribe como 3a₁x₂ + b₁ - 3a₂x₂- b₂ = 0 (12)

6a₂x₃ + 2b₂ - 6a₃x₃ - 2b₃ = 0 que se escribe como 3a₂x₃ + b₂ - 3a₃x₃- b₃ = 0 (13)

6a₃x₄ + 2b₃ - 6a₄x₄ - 2b₄ = 0 que se escribe como 3a₃x₄ + b₃ - 3a₄x₄- b₄ = 0 (14) 

Hasta el momento se tiene un sistema de 14 ecuaciones para las 16 incógnitas iniciales. Debido a que no se conoce acerca de las derivadas de la función en los puntos extremos, se utiliza la tercera condición y se igualan las terceras derivadas en los puntos [x₂, y₂] y [x₄, y₄]_,por ello es necesario calcular las terceras derivadas de (12) y (14). Entonces el cálculo de estas terceras derivadas es igual a:

3a₁ - 3a₂ = 0 (15)

3a₃ - 3a₄ = 0 (16)

Que se rescriben como:

a₁ - a₂ = 0

a₃ - a₄ = 0

Debido a esto, se cuenta ya con un sistema de 16 ecuaciones y 16 incógnitas. En términos matriciales se tiene:

AB = C

Donde A es una matriz de 16x16, B es una matriz de 16x1 que contiene los parámetros y C también es una matriz de 16x1 (la forma de las matrices se encuentra en el Anexo 1). Entonces este problema se resuelve calculando la inversa de la matriz A⁵ y por tanto:

B =A^-1 C

Una vez que se tienen los valores de los parámetros se procede a estimar los supervivientes a edad exacta x correspondientes a cada uno de los segmentos del spline por medio de las ecuaciones P_i(x) = a_ix³ + b_ix² + c_ix + d_i ., donde i =1,2,3 y 4. En estas ecuaciones cada P_i(x) equivale a la l_x y las x son las edades entre los nodos correspondientes al segmento del spline.

 

Resultados

Se ajustaron las series de supervivientes a edad x (l_x) para el total de defunciones, para hombres y mujeres en 2000, 2005 y 20j0 utilizando el método propuesto. El ajuste por medio de esta metodología es bueno para todos los años y en ambos sexos, ya que existe una alta similitud entre ambas curvas (Gráficas 3 y 4). Esto se corrobora numéricamente al analizar los valores de R² calculados entre la serie observada y la estimada, así como los resultados del EMAP (Tabla 1). Los resultados que se obtienen a partir de este método de estimación muestran una bondad de ajuste cercana a un valor máximo posible de uno en todos los casos ajustados para la R², lo que implica un ajuste satisfactorio de los datos de mortalidad en ambos sexos y para todos los años seleccionados (véase Anexo 2).

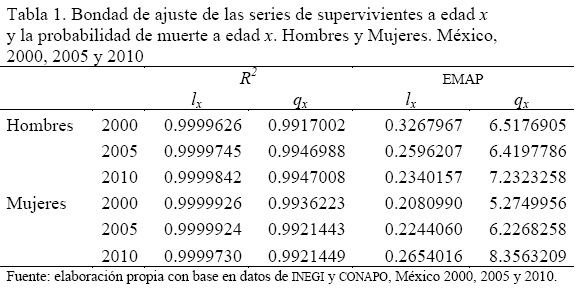
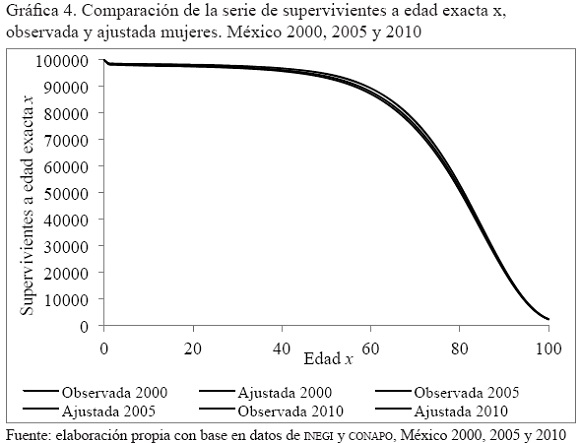
Si estos resultados se analizan con más detalle, se tiene que el valor de R² para hombres en todos los años se encuentra por encima de 0.9999 y se incrementa ligeramente de un año a otro, proporcionando un mejor ajuste en 2005 y uno todavía mejor en 2010. En cuanto al EMAP obtenido se observa que el error disminuye con el paso del tiempo, logrando el mejor ajuste en el año 2010, lo cual es consistente con el indicador anterior. En el caso de las mujeres, la bondad de ajuste es superior a la de los hombres en 2000 y 2005, no así en 2010, lo cual es descrito por ambos indicadores (R² y EMAP). Otra característica del ajuste en mujeres es que el mejor ajuste se presenta en el 2000, y su valor tiende a descender con el paso de los años (aunque continúa siendo realmente bueno).

Por otro lado, se considera indispensable estudiar la estimación del patrón de la mortalidad, tanto en su bondad de ajuste de forma numérica (con la R² o el EMAP) como de manera gráfica (Anexo 2), comparando también el ajuste por medio de otra serie de la tabla de vida (en esta investigación se utilizaron las q_x), con la finalidad de corroborar que se respeten los cambios de concavidad de la curva de mortalidad en todo el rango de edad. Por tanto, se analizó también la bondad de ajuste de la estimación propuesta utilizando la serie de probabilidades de defunción (q_x).

Las gráficas del ajuste de la serie de probabilidades de defunción,⁶ tanto para hombres como para mujeres en todos los años que abarca este estudio, se pueden observar en el Anexo 3. La estimación de las probabilidades resulta muy buena, especialmente a partir de la edad del segundo nodo del spline, para todos los casos. En las primeras edades, el cambio de concavidad que se presenta en la niñez y la adolescencia es ajustado de manera adecuada (sin dejar de ser un buen ajuste en términos generales).

Destaca una menor bondad de ajuste que con la serie l_x, pero la estimación sigue siendo buena (Tabla 1). En el caso de hombres, los valores de R² son superiores a 0.99 y consistentemente el ajuste es progresivamente mejor cada año; el ajuste mejora de 2000 a 2005, pero, a diferencia de la R², el valor del EMAP para 2010 es mayor, lo que indica que en ese año la estimación posee una menor bondad de ajuste. En el caso de mujeres se observa también una alta bondad de ajuste, siendo mejor ésta para 2000 que en los otros dos años. Lo que resulta interesante ver es que con ambos indicadores, si bien los valores para mujeres de 2000 y 2005 son superiores a los de hombres, en 2010 el ajuste de hombres resulta comparativamente mejor al de mujeres.

En cuanto a la esperanza de vida calculada por medio del ajuste por splines se obtienen valores de 71.33 y 76.48 en 2000 para hombres y mujeres respectivamente, los cuales son similares a las cifras oficiales publicadas por CONAPO (Tabla 2); para 2005 el monto es de 72.22 y 77.06 para hombres y mujeres respectivamente, valores también cercanos a los oficiales; en 2010 estos valores son 73.09 para hombres y 77.78 para mujeres. Esto indica que el método propuesto se puede utilizar de manera confiable para realizar estimaciones de este importante indicador en este y posiblemente en otros contextos o años.

Asimismo, se presentan las edades en las cuales se situaron los nodos para hombres y mujeres (Tabla 3). La ubicación de los nodos es importante en este tipo de estudios debido a que dan cuenta de los cambios que se presentan en la mortalidad, esto es, un aumento en la edad de un nodo implica una disminución de la mortalidad en el grupo de edad que ajusta. En este estudio se observa que: el segundo nodo está ubicado en edades adultas similares para hombres (33) y mujeres (37 en 2000 y 2010, y 38 años en 2005), lo que implica que el primer polinomio del spline ajusta la mortalidad en la niñez, la adolescencia y para los adultos jóvenes en ambos sexos; el tercer nodo está ubicado en la edad adulta de 37 años en hombres y 42 en 2000 para mujeres y 43 en 2005 y 2010, lo cual es indicativo de una menor mortalidad femenina en este grupo de edad y de una ligera diminución de la mortalidad en ese rango de edad; el cuarto nodo se ubica en edades distintas para ambos sexos, puesto que en hombres se localiza en la edad 49 en 2000 y se incrementa a 51 en 2005 y a 53 en 2010, mientras que para mujeres se encuentra entre los 59 y 62 años de edad significa que la mortalidad más baja de las mujeres con respecto a la de los hombres en esos rangos de edad no se presenta una caída significativa de la curva de mortalidad; por ello, para alcanzar aproximadamente el mismo nivel de supervivientes en ambos sexos la edad de los nodos es mayor para las mujeres.

Por último se realizó la estimación para los supervivientes a edad exacta x de otros países (Australia, El Salvador, Brasil y Estados Unidos), como se mencionó previamente, con el objetivo de comparar los resultados obtenidos para México mediante este ajuste con aquellos de otros contextos para tratar de obtener una mayor validez de estas estimaciones. Entre los principales resultados se observa que, en general, la estimación tiene una alta bondad de ajuste en prácticamente todos los países y años considerados (Tabla 4), lo cual se puede corroborar gráficamente (Anexo 4), hay una alta similitud entre las curvas de mortalidad estimadas y las observadas. Los países donde el ajuste en las edades de la niñez y la juventud no resulta del todo adecuado son Brasil y El Salvador, en hombres probablemente provocado por una mayor mortalidad en esas edades por causas externas, lo cual provoca un cambio de concavidad en la curva de mortalidad (claramente apreciado en El Salvador), lo que dificulta el ajuste en esas edades. En cuanto a los valores de las R² se observan valores similares a los mexicanos para la l_x , lo cual indica de que el método propuesto posee una alta flexibilidad ya que ajusta de manera correcta las curvas de mortalidad de otros países y no solamente en el contexto mexicano.

En cuanto a la estimación de la esperanza de vida se encuentra, en general, cerca del valor oficial publicado (Tabla 5). El mejor ajuste se presenta para Australia y para Estados Unidos, observándose valores estimados de este indicador muy cercanos a las cifras oficiales.

 

Discusión

La mortalidad en México ha disminuido de manera constante desde los años 1940 hasta la actualidad y la esperanza de vida ha aumentado. Esto se ha presentado a ritmos diferentes y se refleja en que a finales del siglo XX y principios del siglo XXI ha existido una disminución considerable del ritmo de ganancias en esperanza de vida de la población en general (Camposortega, 1992; 1997: 11). Esto es, si bien continúan registrándose ganancias en este indicador, el ritmo al que actualmente se presentan es considerablemente menor al de los años cincuenta y sesenta.⁷

Es por ello que el estudio de la mortalidad, específicamente de la estimación de los patrones modelo parametrizados que describan matemáticamente la estructura por edad y sexo de la mortalidad y la evolución de esta a través del tiempo, puede ayudar a profundizar en el conocimiento sobre el comportamiento de este indicador demográfico. Por tanto, este tipo de investigaciones son consideradas importantes, ya que permiten realizar un manejo matemático de los fenómenos demográficos (Halli y Rao, 1992); en otras palabras, encontrar las leyes que rigen los fenómenos demográficos para describirlos matemáticamente permite plantear de forma fundamentada escenarios futuros que sean posibles, probables o deseables si ocurriesen una serie de condiciones específicas, y a partir de ello, proponer planes de acción adecuados para intentar mitigar el impacto de la mortalidad en esas edades concretas. Los modelos, como el aquí propuesto, son útiles también para desarrollar investigaciones sobre efectos posibles en edades específicas, cambios en los determinantes demográficos y el impacto que tendrán estos sobre la tendencia de la mortalidad en la población (Halli y Rao, 1992), lo cual puede a su vez servir como insumo para el establecimiento de políticas públicas o campañas de salud pública dirigidas a mitigar o retrasar la mortalidad (Mina, 2006: 2009).

Se propuso una metodología que involucra un polinomio de tercer grado en las primeras cuatro edades y en las últimas de la serie de supervivientes, así como los cambios de concavidad observados en la curva; estos polinomios presentan una unión suave con los polinomios del spline cúbico. Entre los principales alcances del método propuesto está su buena bondad de ajuste, en consecuencia su buena descripción de la mortalidad, lo cual se ve reflejado en la estimación adecuada de la esperanza de vida al nacimiento.

El ajuste propuesto utilizando splines cúbicos se considera adecuado en tanto que estima correctamente el patrón general de la mortalidad por edad desplegada tomando en cuenta las propiedades intrínsecas de las curvas de mortalidad como el cambio de concavidad en las primeras edades de la tabla de vida provocado por una alta probabilidad de muerte en el primer año de vida, al utilizar un polinomio de tercer grado que ajuste perfectamente las primeras cuatro edades de la tabla de vida, especialmente en los países en vías de desarrollo como México, donde la mortalidad infantil y de la niñez es todavía alta, si se compara con otros países del mundo; una probabilidad descendente, a partir de esas primeras edades durante la niñez, cuando la mortalidad alcanza su mínimo valor, entre los cinco y 10 años aproximadamente; un aumento significativo en las probabilidades de fallecer a partir de los 20 años, provocado en hombres principalmente por las causas externas de mortalidad y en mujeres en los lugares donde la mortalidad materna todavía es significativa; el crecimiento exponencial de las probabilidades de muerte en edades adultas (Congdon, 1993: 242), lo cual se cumple a partir del uso del spline y la flexibilidad de estimación que conlleva esta técnica; y la desaceleración de la mortalidad que se presenta en las edades extremas de la tabla de vida (Gavrilov y Gavrilova, 2002: 10), también a través del uso de un polinomio de tercer grado para respetar este cambio de concavidad en la curva de mortalidad.

Este modelo, además de ser una estimación de la mortalidad con una alta bondad de ajuste, solamente requiere conocimientos de álgebra de matrices y el cálculo de las tablas de vida para llevarse a cabo, a diferencia de métodos para los que es necesario realizar regresiones de tipo no paramétricas o series de tiempo usando mínimos cuadrados penalizados (Guerrero, 2007); se lleva a cabo el ajuste sobre la mortalidad por edad desplegada o individual y no por grupos quinquenales, como lo realizan otras técnicas previamente presentadas, lo cual provoca que el ajuste respete la concavidad y los cambios de esta a lo largo de la curva; asimismo, la mayor ventaja del modelo, gracias a la flexibilidad que provee el uso de polinomios en la estimación matemática de la mortalidad, es la posibilidad de realizar proyecciones del fenómeno demográfico en diferentes contextos y momentos y puede ser también ocupado en el ajuste de causas de muerte (Dávila, 2012). De la misma manera, esta técnica se considera relativamente flexible, pues ajusta de manera correcta la mortalidad en otros contextos donde la curva de supervivientes a edad exacta x o las probabilidades de defunción presenten un comportamiento distinto al observado en México. Finalmente, se considera que esta técnica posibilita la realización de simulaciones, las cuales son útiles en la reproducción y análisis del fenómeno de la mortalidad de forma numérica, lo que a su vez puede permitir predecir y estudiar ciertos aspectos del comportamiento futuro del fenómeno (Mina, 2011).

 

Limitaciones

Como toda investigación, esta no se encuentra exenta de limitaciones, entre las principales destacan que en esta metodología se requiere estimar una alta cantidad de parámetros, por cada polinomio del spline hay cuatro parámetros a estimar, lo cual da un total de 24 parámetros. Esta situación provoca que este ajuste sea, hasta cierto punto, poco parsimonioso, aunque no hay que olvidar que la modelación se realizó por edad desplegada. Otra desventaja radica en la elección de los nodos, la cual se tiene que realizar de forma manual de acuerdo a los criterios mencionados de maximizar la R² entre las series estimadas y las observadas, así como minimizar el EMAP que resulta en la mejor bondad de ajuste posible del modelo y no otorga la posibilidad de generalizar por sexo, para distintas causas de muerte o para diferentes años.

Una limitación adicional se relaciona con la calidad de los datos de mortalidad provenientes de las estadísticas vitales, especialmente en las edades mayores. Estos datos tienen ciertas deficiencias, como problemas de cobertura en las zonas rurales y poco accesibles; el subregistro de defunciones, especialmente infantiles y maternas, y un largo proceso burocrático que provoca el retraso de publicación de la información (Hernández y Narro, 2010: 244). Esto puede provocar que los cálculos no se ajusten de la manera más adecuada y exista cierta incertidumbre sobre el nivel real de la mortalidad en las edades extremas especialmente.

 

Bibliografía

BARRERA SÁNCHEZ, Pablo, Claudia DURÁN SÁNCHEZ y Victoria HERNÁNDEZ MEDEROS, 1996, El ABC de los splines, Sociedad Matemática Mexicana, Serie Aportaciones Matemáticas, núm. 9, México.         [ Links ]

CAMPOSORTEGA CRUZ, Sergio, 1992, Análisis demográfico de la mortalidad en México 1940-1980, El Colegio de México, Centro de Estudios Demográficos y de Desarrollo Urbano, Distrito Federal.         [ Links ]

CAMPOSORTEGA CRUZ, Sergio, 1997, "Cambios en la mortalidad/cien años de mortalidad en México", en DemoS, Internet, recuperado de: http://www.ejournal.unam.mx/dms/no10/DMS01005.pdf        [ Links ]

CONGDON, Peter, 1993, "Statistical graduation in local demographic analysis and projection", en Journal of the Royal Statistical Society, vol. 156, núm. 2.         [ Links ]

DÁVILA, Claudio, 2012, Análisis de patrones y ajuste matemático de las principales causas de muerte en México 1979 a 2008, tesis de doctorado, El Colegio de México.         [ Links ]

DEBON, Ana 2003, Graduación de tablas de mortalidad. Aplicaciones actuariales, tesis de doctorado, Universitat de Valencia, España.         [ Links ]

GAVRILOV, Leonid A. y Natalia S. GAVRILOVA, 2002, "The quest for the theory of human longevity", en The actuary.         [ Links ]

GAVRILOV, Leonid A. y Natalia S. GAVRILOVA, 2006, Reliability theory of aging and longevity, en Edward J. MASORO y Steven N. AUSTAD (eds.), Handbook of the biology of aging, Elsevier Academic Press, San Diego.         [ Links ]

GUERRERO, Victor M., 2007, "Time series smoothing by penalized least squares", en Statistics and Probability Letters, vol. 77, núm. 12.         [ Links ]

HARTMANN, Michael, 1987, "Past and recent attempts to model mortality at all ages", en Journal of Official Statistics, vol. 3, núm. 1.         [ Links ]

HALLI, Shiva y K. Vaninahha RAO, 1992, Advanced techniques of population analysis, Plenum Press, The plenum series on demographic methods and population analysis. Nueva York.         [ Links ]

HELIGMAN, Larry y John H. POLLARD, 1980, The age pattern of mortality, en Journal of the Institute of Actuaries, núm. 107.         [ Links ]

HERNÁNDEZ-BRINGAS, Héctor y José NARRO-ROBLES, 2010, "El homicidio en México", 2000-2008, en Papeles de Población, vol. 16, núm. 63, Toluca.         [ Links ]

MINA, Alejandro, 2001, "Funciones de sobrevivencia empleadas en el análisis demográfico", en Papeles de Población, abril-junio, núm. 28.         [ Links ]

MINA, Alejandro, 2006, "Ley de mortalidad mexicana. Funciones de supervivencia", en Estudios Demográficos y Urbanos, mayo-agosto, vol. 21, núm. 2, Toluca.         [ Links ]

MINA, Alejandro, 2009, "Uso de las funciones de supervivencia en las ciencias sociales y en los estudios de población. Aplicación al caso de México", en Papeles de Población, vol. 15, núm. 61, Toluca.         [ Links ]

MINA, Alejandro, 2011, "La obtención y proyección de tablas de mortalidad empleando curvas spline", en Papeles de Población, vol. 17, núm. 69, Toluca.         [ Links ]

OMRAN, Abdel R., 2005, "The epidemiologic transition: a theory of the epidemiology of population", en The Milbank Quartely, vol. 83, núm 4.         [ Links ]

OPS, 2003, "Sobre la estimación de tasas de mortalidad para países de la Región de las Américas", en Boletín Epidemiológico, vol. 24, núm. 4, Organización Panamericana de la Salud.         [ Links ]

SIEGEL Jacob S. y Henry S. SHYOCK y David SWANSON, 2004, The methods and materials of demography, Elsevier Academic Press, California.         [ Links ]

SMITH, Stanley K. Jeff, TAYMAN, y David A. SWANSON, 2001, State and local population projections: methodology and analysis, Kluwer Academic, Durham.         [ Links ]

 

Notas

¹ Las series de supervivientes a edad exacta x se obtuvieron por medio de la relación entre las tasas de mortalidad y las probabilidades de defunción sin realizar corrección o modelaje alguno para no modificar el nivel de la mortalidad (Siegel y Swanson, 2004).

² El concepto estadístico "parsimonia" se refiere a la obtención del mejor modelo (aquel que presenta la mayor bondad de ajuste) utilizando la menor cantidad posible de parámetros. Normalmente hay un intercambio entre estos dos criterios, debido a que si el número de parámetros utilizado para ajustar los datos se incrementa, entonces el ajuste de los datos mejora también, pero, a medida que se incrementa el número de parámetros, la estabilidad estadística se va perdiendo (Congdon, 1993).

³ Al emplear estos indicadores de R² y EMAP lo que se realiza es la minimización de los errores producidos en la estimación matemática de la curva de mortalidad.

⁴ La explicación y solución de este tipo de sistemas se puede ver en Barrera et al. (1996).

⁵ La matriz A es no singular, excepto cuando x₁, x₂, x₃, x₄ y x₅ fueran iguales, por lo tanto, los sistemas de ecuaciones tienen solución única.

⁶ Las probabilidades de defunción se presentan en escala logarítmica.

⁷ Las cifras sobre el incremento de la esperanza de vida a lo largo del siglo XX y principios del XXI se presentaron previamente.

 

Información sobre el autor:

Claudio Alberto Dávila Cervantes. Doctor en Estudios de Población (con especialización en mortalidad, temas de salud, mortalidad por causas y ajuste matemático de los fenómenos demográficos) por parte de El Colegio de México; Maestro en Demografía (con especialización en mortalidad y mortalidad por causas) por parte de El Colegio de México; Licenciado en Actuaría, por parte del Instituto Tecnológico Autónomo de México. Actualmente es profesor investigador dentro del programa de Maestría en Población y Desarrollo de la Facultad Latinoamericana de Ciencias Sociales (FLACSO sede México). Entre sus publicaciones recientes se encuentran: "Análisis de la mortalidad por causas en México: Ganancias en esperanza de vida 2000 y 2005 y proyecciones al 2015" publicado en la Editorial Académica Española en 2011. Los artículos "Diabetes en México y Colombia: Análisis de la tendencia de años de vida perdidos, 1998-2007" en la Revista de Salud Pública de la Universidad Nacional de Colombia en 2011; "Diferencias socioeconómicas en los años de vida perdidos por cáncer de mama y cérvico-uterino en Colombia, 1997 y 2007" en la Revista en Gerencia y Políticas en Salud de la Universidad Javeriana en Colombia en 2010; y "Cambios en los años de vida perdidos por cáncer de mama y cérvico-uterino en México según grado de marginación estatal, 1997 y 2007" en la Revista de Salud Pública de Chile en 2010. Dirección electrónica: claudio.davila@flacso.edu.mx