Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Papeles de población
versão On-line ISSN 2448-7147versão impressa ISSN 1405-7425
Pap. poblac vol.16 no.66 Toluca Out./Dez. 2010
Limitantes de los índices de marginación de Conapo y propuesta para evaluar la marginación municipal en México
Limits of the marginalization indexes by Conapo and a proposal to assess municipal marginalization in México
Humberto Gutiérrez–Pulido* y Viviana Gama–Hernández**
* Universidad de Guadalajara. Correo electrónico: humpulido@yahoo.com
** Consejo Estatal de Población Jalisco. Correo electrónico: lilvampi7@yahoo.com.mx
Este artículo fue
recibido el 20 de abril de 2010
aprobado el 6 de octubre de 2010.
Resumen
El índice de marginación desarrollado por el Consejo Nacional de Población en la década de 1990 tiene algunas limitantes, entre las que destacan el que la influencia de los indicadores de marginación sobre el IM es muy variable y que los valores del IM no son comparables sobre el tiempo. Esto hace que el IM sea de poca utilidad para evaluar los cambios en la marginación. Para atender esto, Conapo desarrolló el índice absoluto de marginación. Sin embargo, el IAM da igual ponderación a indicadores que de sí son diferentes; esto causa que los indicadores tengan una influencia muy diferente sobre el valor del IAM. En este artículo se analiza la problemática de estos índices a nivel municipal, y propone como alternativa el denominado índice de marginación para evaluación (IME). Con el índice propuesto se evalúa la evolución de la marginación municipal en México entre 1990 y 2005.
Palabras clave: índice absoluto de marginación, medición de la pobreza, análisis de componentes principales, marginación municipal, México.
Abstract
The marginalization index (IM) developed by the National Population Council (Conapo) in the 1990's has the problems that the influence of marginalization indicators on the IM greatly varies and that the IM values are not comparable over time. These problems cause that the IM is not useful to evaluate changes in marginalization. As an alternative, Conapo developed the absolute index of marginalization (IAM). However, the IAM gives equal weight to indicators which are different on their own; and then the indicators have a very different effect on IAM values. The objective of this paper is to analyze the problems of these indexes at the municipal level; and it proposes an alternative index called marginalization index for evaluation (IME). With the proposed index it is evaluated the evolution of municipal marginalization in México between 1990 and 2005.
Key words: absolute marginalization index, poverty measurement, principal components analysis, municipal marginalization, Mexico.
Antecedentes de la medición de la marginación
El indicador más comúnmente utilizado para medir el desarrollo de un Estado o una nación fue durante mucho tiempo el producto interno bruto (PIB), el cual cuantifica la capacidad de una economía para generar satisfactores a su población. Sin embargo, durante la segunda mitad del siglo XX se fue afianzando la idea de que el PIB tenía limitaciones para reflejar el desarrollo en un sentido más amplio, debido a que fue ganando terreno dentro de los enfoques del desarrollo la idea de que el sistema de mercado crea desigualdades y situaciones de exclusión social que no son temporales ni corregidas por el propio crecimiento del PIB, y tampoco constituyen un acicate competitivo individual que desemboque en un progreso social (Conapo, 1993). De esta manera fue ganando aceptación la propuesta de medir el desarrollo con una visión más amplia, considerando la calidad y las condiciones de vida, además de las necesidades satisfechas.
En años recientes se ha demostrado que el crecimiento económico es necesario para mejorar las condiciones de una comunidad, pero insuficiente, es decir, para elevar su desarrollo (Martínez Pellégrini et al., 2008), lo cual ha consolidado la necesidad de medir éste con una visión más amplia. Sobre el particular, un parteaguas a nivel internacional fue el trabajo desarrollado por el Programa de las Naciones Unidades para el Desarrollo (PNUD), al proponer en 1990 el primer informe sobre el desarrollo humano (PNUD, 1990), en donde se establece por primera vez el cada vez más utilizado índice de desarrollo humano (IDH), que incluye en su medición los componentes de salud, educación e ingresos.
Durante la segunda mitad del siglo XX, particularmente en la primera mitad de la década de 1980, ocurre la crisis de la deuda externa de los países subdesarrollados, fenómeno que terminó en forma abrupta con tres décadas de relativos progresos socioeconómicos y dio paso a una profunda recesión que en México duró buena parte del decenio de 1980. Esto provocó un sensible empeoramiento de las condiciones de vida e importantes retrocesos sociales (Conapo, 1993; Márquez, 2006) y llevó a ajustar las políticas de desarrollo. A partir de esto y dado el cambio de paradigma de ver el desarrollo en forma más integral, se introdujeron en las políticas gubernamentales el componente de alivio de la pobreza y la atención a las necesidades básicas de la población. Esto incrementó la necesidad de medir la pobreza y la marginación social. Sobre el particular, en México la principal medición ha sido el índice de marginación (IM), que toma en cuenta nueve indicadores socioeconómicos de carencias (cuadro 1) y que fue desarrollado en 1993 por el Consejo Nacional de Población (Conapo, 1993) y tuvo como antecedentes directos una propuesta de Coplamar (1982) y otra del Conapo (1990).
Sobre el tema de medición de la pobreza en México es importante recordar la creación en 2004 del Consejo Nacional de Evaluación de la Política de Desarrollo Social (Coneval), junto con sus antecedentes directos que se remontan al año 2001 (Coepo, 2010). El Coneval se ha encargado de medir la pobreza por ingresos y el índice de rezago social (Coneval, 2006; Coepo, 2010) y ha reconocido que la pobreza es multidimensional, por ello desarrolló una metodología para la medición multidimensional de la pobreza (Coneval, 2009).
Adicionalmente se han generado otros índices, como el de 'bienestar', propuesto por el INEGI, y el de 'masas carenciales', plasmado en la Ley de Coordinación Fiscal. Algunos detalles de estos dos índices se pueden consultar en López–Calva et al. (2006).
El índice de marginación de Conapo y sus limitantes
El IM se estableció en México con la finalidad de apoyar las tareas de la planeación del desarrollo y de la política de población a nivel regional y local (Conapo, 1993). Partiendo de que los procesos que modelan la marginación conforman una precaria estructura de oportunidades sociales para los ciudadanos, sus familias y comunidades, y los exponen a privaciones, riesgos y vulnerabilidades sociales que a menudo escapan al control personal, familiar y comunitario y cuya reversión requiere el concurso activo de los agentes públicos, privados y sociales. El IM es una medida–resumen que permite diferenciar entidades federativas, municipios y localidades según el impacto global de las carencias que padece la población. Este índice se calcula a partir de información de los censos de población y vivienda desde 1990, y tiene cuatro versiones o niveles de desagregación: para entidades federativas, municipios, localidades y áreas geoestadísticas básicas urbanas (Gutiérrez et al., 2008). El IM estatal o municipal considera cuatro dimensiones estructurales: 'falta de acceso a la educación', 'residencia en viviendas inadecuadas', 'percepción de ingresos monetarios insuficientes' y 'vivir en localidades con menos de cinco mil habitantes'. A partir de estas dimensiones se generan los nueve indicadores socioeconómicos de marginación que se muestran en el cuadro 1. Para sintetizar la información de estos indicadores y generar con ellos una medida–resumen, se ha aplicado en todas las ocasiones el análisis de componentes principales (ACP), que expresa la información de los nueve indicadores en un menor número de nuevas variables que son independientes entre sí, y que tienen otras propiedades deseables (Peña, 2002). Estas nuevas variables reciben el nombre de componentes principales. Este mismo procedimiento se siguió en 1990, 1995, 2000 y 2005 (Conapo, 1993; Conapo, 1995; Conapo, 2001, y Conapo, 2005).
El análisis de componentes principales
En forma breve, la idea del ACP es la siguiente, en cada ocasión que se ha calculado el IM, lo primero que se requiere es el valor (en porcentaje) de cada uno de los indicadores del cuadro 1, para los diferentes municipios. Enseguida, para eliminar el efecto de la diferente magnitud de los indicadores, se estandarizan las variables originales de la siguiente manera:
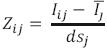
donde:
Zij es el indicador estandarizado j (j = 1,... ,9) de la unidad de observación i, que en este caso son los municipios del país, que en 1990 eran 2403, por lo que i = 1,...,2403.
Iij es el indicador socioeconómico j del municipio i, en porcentaje.
 y dsj son la media y desviación estándar, respectivamente, de los valores del indicador j considerando todos los municipios.
y dsj son la media y desviación estándar, respectivamente, de los valores del indicador j considerando todos los municipios.
Denotando las nuevas variables estandarizadas como vectores de n = 2403 entradas, el ACP consiste en transformar el espacio de los vectores Z en uno nuevo Yk, es decir, encontrar (k= 1,...,m; con m ≤ 9) tales que sean combinaciones lineales de las variables estandarizadas.

Las nuevas variables Yk, llamadas componentes principales, deben cumplir algunos requisitos, tal como no estar correlacionadas (Peña, 2002).
Limitantes del IM
Una primera tarea del ACP es elegir el número de componentes principales que serán utilizados para explicar el fenómeno analizado. Sin embargo, en el caso del IM sólo se ha seleccionado el primer componente, lo cual es una primera limitante, porque la valoración del nivel de carencias que diferencia a los municipios se ha hecho sólo con parte de la información disponible. En efecto, en el cuadro 1 se muestra que el porcentaje de la variación que explicaba el primer componente de la marginación municipal para los años 1990, 2000 y 2005 ha sido de 62.4, 58 y 54 por ciento, respectivamente. Por lo que, dado que los municipios se han agrupado en cinco categorías de grado de marginación (baja, muy baja, media, alta y muy alta), en el establecimiento de estas categorías sólo se ha usado un poco más de la mitad de la información de los indicadores de marginación. Obviamente, para clasificar en cinco grupos los municipios del país en función de los nueve indicadores de marginación hay alternativas multivariadas más eficientes desde el punto de vista matemático; por ejemplo, el análisis de conglomerados (Peña, 2002).
Por otro lado, el IM está dado por el primer componente de la siguiente manera:

donde los coeficientes cj son los pesos o importancia que se le da a cada indicador para cuantificar la marginación de un municipio. En el cuadro 1 se muestran estos pesos para los años 1990, 2000 y 2005. De donde queda claro que el primer componente y con ello el IM le ha dado un mayor peso a los indicadores de educación, seguido por porcentaje de viviendas con piso de tierra y la variable de ingresos. En cambio, a las que se les asigna menor importancia para definir la magnitud de la marginación son sin drenaje ni servicio sanitario, población en localidades con menos de cinco mil habitantes y sin agua entubada. La diferencia en el peso de los coeficientes se ha incrementado con el paso del tiempo, hasta llegar a que la población con primaria completa tiene más del doble de importancia que el de servicio sanitario. Se puede demostrar que la determinación de las ponderaciones depende tanto de los valores de las variables como de su estructura de correlación (Peña, 2002; Aparicio, 2004).
Así, los pesos del cuadro 1 han determinado cuáles son los factores que definen el nivel de marginación de un municipio, pero se ha hecho recurriendo sólo a consideraciones estadísticas y además utilizando sólo parte de la información disponible, ya que, por ejemplo, en el año 2005 sólo se explica 53.95 por ciento de la variación de los datos.
Es importante señalar que el hecho de que a ciertos indicadores de marginación se les dé menor importancia en el primer componente no quiere decir que sea una carencia con niveles bajos, sino que más bien tiene que ver con otra forma en la que se aprehende la marginación. Ya que los indicadores con menor peso en el primer componente tienen un mayor peso en los siguientes (véase Conapo, 2005; 332). Esto se debe a que la correlación entre los diferentes indicadores de marginación municipal es distinta, como se muestra en la matriz de correlación del cuadro 2. Es notable que, para 1990, el indicador I2 (sin primaria completa) sea el que tiene más altas correlaciones con el resto, le sigue I7 (piso de tierra) e I1 (analfabetismo), que son justamente los tres indicadores con mayor peso en el índice de marginación de ese año. En contraste, los que tienen menores correlaciones con el resto son I8 (porcentaje de población en localidades con menos de cinco mil habitantes) y el I4 (sin energía eléctrica), que están entre los que tienen menor peso en el IM del mismo año.

El impacto que ha tenido la definición del índice de marginación sólo con el primer componente principal para la orientación de políticas públicas ha sido fuerte, toda vez que con el paso del tiempo varios programas públicos se han orientado exclusivamente a municipios o localidades con alta o muy alta marginación.
Finalmente, la otra limitante del IM es que no permite evaluar los cambios en la marginación a lo largo del tiempo, en virtud de que está medido en una escala de intervalo, por lo que las comparaciones que se presentan con base en esta metodología solamente son válidas en términos relativos, pero no absolutos. La implicación práctica de esta cuestión metodológica es que no pueden ser comparados de manera directa los cambios observados en el valor de los índices de marginación de una unidad geográfica particular en dos momentos en el tiempo. Es decir, los valores del IM correspondientes a 1990, 2000 y 2005 para algún municipio no son comparables entre sí. Sólo tienen sentido al compararlos con los de otros municipios dentro del mismo año. Por ejemplo, para el municipio de Guadalajara, los valores del IM son –2.1446, –2.0295 y –1.9766, respectivamente, para los años referidos. Lo que muestra que el IM para Guadalajara tuvo cambios marginales, pero esto no quiere decir que la marginación no haya disminuido.
En efecto, en el cuadro 3 se muestran los valores de las nueve variables que dan origen al IM para Guadalajara en el periodo 1990–2005, y es claro que todas las variables disminuyeron en forma importante, y con ello el nivel de carencias y marginación.
El uso del primer componente principal para definir índices es frecuente, véase, por ejemplo, el índice de rezago social del Coneval (Coneval, 2006), el índice de marginación urbana de Conapo (Conapo, 2009) y el propuesto por Álvarez Ayuso y Cadena Vargas (2006). La ventaja de esto es que facilita la construcción de los índices al ser un procedimiento matemático directo, pero lleva a las desventajas que ya se describieron para el IM. Lo anterior contrasta con otras formas de definir índices, que van desde propuestas académicas como la de Morales y Morales (2008), o propuestas instrumentadas por instituciones, como son el caso del IDH (véase PNUD, 2005), el índice de desarrollo municipal del Instituto del Federalismo en México (Martínez Pellégrini et al., 2008) y el índice de vulnerabilidad social (IVS) definido por el DIF Nacional (México). En estos tres casos, de acuerdo con consideraciones socioeconómicas, se define la ponderación o importancia que tendrán los diferentes indicadores de desarrollo o carencias. Por ejemplo, el IVS involucra un total de trece variables o indicadores agrupadas en cinco subcategorías de vulnerabilidad: 'familiar', 'de género', 'por discapacidad y tercera edad', 'educativa infantil' y 'por salud infantil'. El peso o ponderación porcentual de cada una de estas subcategorías en el IVS son: 20, 13, 7, 30 y 30 por ciento, respectivamente. Estas ponderaciones se decidieron con criterios sociológicos.
En Cárdenas (2010) también se analiza la limitante del IM, en el sentido de que no es posible emplearlo para medir la efectividad de programas gubernamentales orientados a disminuir el rezago social. Como alternativa, a partir del IM genera un índice reparametrizado, que este autor llama 'cardenalización', el cual supera la limitante referida. Un poco en la misma dirección, Camberos y Bracamontes (2007) utilizan métodos de regresión para relacionar el IM de año base con los indicadores de otras fechas con objeto de superar la limitación del IM para evaluar la evolución de la marginación. Los dos trabajos anteriores muestran que el peso o ponderación que toman los indicadores de marginación puede variar en forma importante. Además, estos trabajos no sólo muestran las limitaciones del IM, sino también el poco conocimiento del IAM.
Otra crítica al IM es la que hace Bistrain (2010), quien cuestiona la precisión de los criterios de estratificación de los municipios en función del valor del IM en 2005, al aplicar la técnica de Dalenius y Hodges (1959). Esta estratificación es un aspecto central de los objetivos del IM, ya que existen múltiples programas gubernamentales dirigidos a municipios con alta o muy alta marginación. El autor señala que existen múltiples herramientas que permiten delimitar los estratos con mayor precisión para garantizar el cumplimiento de los objetivos metodológicos y de planeación estipulados en los índices de marginación, y propone una alternativa basada en la interpolación por diferencias divididas de Newton.
En un sentido similar, Bustos (2009) cuestiona el resultado de la estratificación y jerarquización de las entidades geográficas que se logra con el IM, sobre todo al dej ar patente que e sto se hace con la información parcial que representa el primer componente principal, como ya se comentó antes. Este autor propone un indicador compuesto, basado en la determinación de ponderaciones óptimas, que permite realizar comparaciones de una misma realidad en distintos momentos.
Además, Bistrain (2008) cuestiona los indicadores del IM para medir la marginación en el medio rural, y como alternativa propone usar siete indicadores que tienen ciertas diferencias respecto a las usadas en el IM.
Índice absoluto de marginación (IAM)
Como vimos antes, el IM no es útil para valorar los avances en la disminución de la marginación de una entidad geográfica. Por lo que, si se quiere evaluar estos avances, es necesario analizar en su conjunto los nueve indicadores, y ver cuáles avanzaron y cuáles siguen manteniendo niveles altos. Pero es deseable contar con una medida sintética, construida a partir de los indicadores de marginación, que resuma los avances en la reducción de la marginación y que sea comparable a lo largo del tiempo. Es con ese propósito que en el Conapo se propuso el índice absoluto de marginación, IAM, véase Aparicio (2004). Este índice se obtiene directamente de los porcentajes de carencias de cada entidad geográfica, ponderando con la misma importancia los nueve indicadores, es decir, cj = 1/9, por lo que el IAM está dado por

Por ejemplo, a partir del cuadro 3 se obtiene que el IAM para el municipio de San Miguel Coatlán, Oaxaca, correspondiente a los años 1990, 2000 y 2005 es de 80.9, 65.8 y 60.5, respectivamente. Lo anterior implica que este municipio redujo su marginación 25 por ciento, según el IAM. En 1990, San Miguel Coatlán estaba entre los cincuenta municipios del país más marginados. En contraste, el municipio de Guadalajara tenía valores del IAM de 13.9, 9.3 y 7.6, respectivamente, para los años indicados antes. Lo que implica que este municipio redujo su marginación 45 por ciento en forma relativa.
El autor de la propuesta del IAM señala:
...la decisión de utilizar la misma ponderación para cada uno de los indicadores obedece al reconocimiento de que las dimensiones que se incorporan al cálculo de los índices de marginación constituyen todas ellas garantías constitucionales que deben ser atendidas por el Estado, por lo que se considera apropiado otorgarles una misma ponderación... El IAM tiene una interpretación absoluta y no solamente relativa, ya que si todos los indicadores de marginación mostraran una carencia absoluta el valor del índice sería de 100, mientras que, en el extremo opuesto, si todos los indicadores mostraran un valor óptimo, el valor del índice sería cero. De esta manera, el valor del índice absoluto de marginación es una medida directa de qué tan alejada se encuentra una unidad geográfica de la situación óptima (Aparicio, 2004: 20).
Sin embargo, el IAM tiene una falla estructural muy importante que lo convierte en un mal instrumento para medir los avances en la reducción de la marginación, ya que otorga ponderación (1/9) a indicadores que de por sí son diferentes. En efecto, del cuadro 3 se ve que, considerando los 2403 municipios del país, en 1990 el valor promedio del primer indicador (porcentaje de población analfabeta) era de 23, mientras que en el promedio del último indicador (porcentaje de población con ingreso menor a dos salarios mínimos) tenía un valor de 77.2. Por lo tanto, al dividir estos valores entre nueve se ve que el impacto promedio que estos dos indicadores tienen en el valor del IAM es totalmente diferente, ya que el primero es de apenas 2.6 y el último de 8.6, lo que implica que el noveno indicador tiene 3.4 veces más impacto en el IAM que el primero. Además de los ingresos, otros indicadores muy dominantes en el IAM son 'localidades de menos de cinco mil habitantes', 'hacinamiento' y 'sin primaria completa'. Estos cuatro indicadores determinan en promedio 63, 72 y 75 por ciento del valor del IAM para los años 1990, 2000 y 2005, respectivamente. Pero el impacto de estos cuatro indicadores en el IAM para un municipio en particular puede ser todavía más alto, por ejemplo, para el municipio de Guadalajara es del 92, 94 y 94 por ciento para 1990, 2000 y 2005, respectivamente; mientras que para el municipio de Valladolid, Yucatán, estas influencias son de 61 (1990), 76 (2000) y 75 por ciento (2005). Por lo tanto, al evaluar los esfuerzos en la reducción de la marginación se estará evaluando en gran medida los logros en estos cuatro indicadores, dejando un tanto de lado a los otros cinco. Incluso puede darse el caso de que en un municipio pequeño, donde todas las localidades tengan menos de cinco mil habitantes, ese solo indicador decida en gran medida el valor del IAM. Por lo anterior, el IAM queda lejos de ser un buen indicador para evaluar los avances en la reducción de la marginación.
Esta problemática del IAM no es identificada por otras propuestas que buscan corregir problemáticas del IM. Por ejemplo, Bistrain (2008) aplica diferentes métodos multivariados para obtener el índice de marginación, pero al final prefiere usar uno muy similar al IAM. Además, el IAM hereda algunos de los problemas que se han reportado en la literatura para el IM, tales como los indicadores utilizados (Bistrain, 2008) y el método de estratificación que se aplica (Bustos, 2009; Bistrain, 2010).
Índice de Marginación para Evaluación (IME)
Con las fallas estructurales del IM y el IAM se justifica la necesidad de contar con un mejor índice que esté en una escala de razón que refleje el nivel de logro y así poder medir los avances en la reducción de la marginación en cualquier tiempo. Además, dado que la falla del IAM es tratar como iguales a indicadores que de por sí son diferentes, se pensó en una alternativa que lograra que los nueve indicadores tuvieran una importancia similar. Esto por lo menos para una fecha considerada, que para el caso de la marginación en México puede ser 1990 o el año 2000.
Propuesta 0
Una forma típica de transformar variables para normalizarlas y lograr magnitudes similares entre las mismas es mediante la siguiente fórmula, aplicada en este caso a cada indicador de marginación Ij,

Donde minj y maxj son valores mínimo y máximo que se pueden establecer en función de los valores de Ij o incluso recurriendo a consideraciones socioeconómicas, como se ha hecho para establecer el IDH (véase PNUD, 2005); y cj es un coeficiente de ponderación, que pudiera ser diferente de uno para algunos de los indicadores. Lo importante en la elección de minj, maxj y cj es construir una escala normalizada para todos los indicadores, de tal forma que en promedio todos los Wj tiendan a tener el mismo valor. Así, valores grandes de Wj indicarán mucha marginación, y valores pequeños, poca. Esta forma de normalizar indicadores es la utilizada para definir el IDH (PNUD, 2005) y el índice de desarrollo municipal del Instituto Nacional del Federalismo en México (Martínez Pellégrini et al., 2008).
De acuerdo con lo anterior, la primera propuesta para el índice de marginación para evaluación (IME0) es que esté dado por

Es decir, IME0 es igual al promedio de los Wj. Además, es importante que en la transformación para obtener cada Wj se busque que el valor del IME0 sea similar al IAM, para que el primero tenga una interpretación directa e intuitiva, y se pueda leer como el promedio o nivel de marginación de ese municipio. Con todo esto, si se logra definir adecuadamente cada Wj, cada indicador de marginación tendrá un impacto similar en los cambios del IME0.
A partir de las anteriores consideraciones y observando los mínimos, máximos, así como percentiles altos de los valores de los indicadores de marginación para los 2403 municipios del país en 1990; se proponen los valores minj maxj y cj para definir los nuevos indicadores normalizados Wj que se muestran en la parte inferior del cuadro 3. Nótese que minj es cero para casi todos los indicadores, excepto para aquéllos que por la realidad de la carencia que representan mantienen valores muy grandes, como es el caso de ingreso y hacinamiento, donde, para ambos, el mínimo propuesto es de 10. En cuanto a maxj es igual a 50 para 'analfabetismo'; 60 para 'sin energía eléctrica'; 80 para 'sin primaria completa', 'sin drenaje ni servicio sanitario' y 'sin agua entubada', y 100 para los restantes cuatro indicadores. Además, en cuanto al coeficiente de ponderación, es igual a uno para los indicadores de carencias que tienen niveles promedio bajos, y menor que uno para los que tienen valores altos, que, como ya se ha dicho, son 'ingreso', 'hacinamiento', 'sin primaria completa', 'localidades con menos de cinco mil habitantes' y 'sin drenaje ni servicio sanitario dentro de la vivienda'.
En el cuadro 3 se ilustra el cálculo del IME0 para tres municipios seleccionados y con los promedios municipales del país.
Propuesta IME
Otra forma típica de normalizar las variables para lograr magnitudes similares entre las mismas es ponderándolas por el inverso de su promedio. Para los indicadores de marginación Ij habría que decidir tomar el promedio municipal de qué año: 1990, 2000 o 2005. Aquí, con la idea de hacer más estable la transformación, se propone que tal promedio se tome igual a 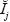 que es igual al valor medio de las medias de cada indicador para los años 1990 y 2005, de esta forma la normalización estaría dada por
que es igual al valor medio de las medias de cada indicador para los años 1990 y 2005, de esta forma la normalización estaría dada por

Por ejemplo, en el caso de analfabetismo, de acuerdo con el cuadro 3, el promedio municipal para los años 1990 y 2005 era de 23.03 y 16.71, respectivamente; por lo que 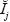 = 19.87. De forma similar, del cuadro 3 se obtiene que
= 19.87. De forma similar, del cuadro 3 se obtiene que 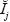 para los restantes indicadores de marginación, del dos al nueve, están dados, respectivamente, por: 48.33, 26.35, 14.65, 26.05, 58.77, 33.14, 75.08 y 71.96. La propuesta es que estas ponderaciones se dejen establecidas, de tal forma que no cambien en cada evento censal y se pueda medir el cambio futuro respecto a este valor base.
para los restantes indicadores de marginación, del dos al nueve, están dados, respectivamente, por: 48.33, 26.35, 14.65, 26.05, 58.77, 33.14, 75.08 y 71.96. La propuesta es que estas ponderaciones se dejen establecidas, de tal forma que no cambien en cada evento censal y se pueda medir el cambio futuro respecto a este valor base.
Con esta transformación, la segunda alternativa para el índice de marginación para evaluación (IME) viene dado por

donde k = 0.40. Este valor de k se requiere para que el valor promedio inicial del IME sea muy similar al valor promedio del IAM (véase cuadro 3), y con esto se facilite la interpretación del IME, que estaría dado por una escala de razón, donde su valor mínimo sería cero, en cuyo caso indicaría cero carencias respecto a los nueve indicadores de marginación.
En el cuadro 3 se ilustra el cálculo del IME para tres municipios seleccionados y con los promedios municipales del país.
Comparación de los índices
Una de las críticas que se le hizo al IAM fue la gran influencia que sobre el mismo tienen los indicadores que por su naturaleza tienen valores altos, como son los de 'ingresos', 'localidades de menos de cinco mil habitantes', 'hacinamiento' y' sin primaria completa'. Además, es importante considerar que la influencia de un indicador de marginación sobre un índice cambia con el tiempo, debido a que la forma en la que evolucionan los indicadores de marginación es diferente. Enseguida se analiza esto con mayor detalle, y se contrasta con lo que ocurre para los dos índices propuestos arriba.
Para comparar los índices (IAM, IME0 e IME), se calcula el impacto promedio relativo que tiene cada indicador de marginación, transformado o no, sobre el correspondiente índice en cada año. Para ello primero se calcula el promedio municipal del índice para un año dado, y a partir de la fórmula general del índice se deduce con cuánto contribuye cada indicador en términos relativos. Por ejemplo, de el cuadro 3 se ve que el promedio municipal del IAM en 1990 era de 49.2, por lo que a este valor el primer indicador, analfabetismo, contribuye con 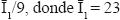 es el promedio del porcentaje de analfabetismo en los municipios del país para ese año. Por lo tanto, el primer indicador contribuye en promedio al IAM con
es el promedio del porcentaje de analfabetismo en los municipios del país para ese año. Por lo tanto, el primer indicador contribuye en promedio al IAM con

En el cuadro 4 se puede notar la contribución de los otros indicadores al IAM en 1990, donde resalta que precisamente es 'analfabetismo' el indicador que contribuye en promedio menos al IAM; en contraste, los indicadores ocho y nueve ('localidades con menos de cinco mil habitantes' e 'ingreso'), son los que, en promedio, contribuyen más, con un porcentaje de 17.4 cada uno. Por lo tanto, estos últimos indicadores contribuyen un 335 por ciento más que 'analfabetismo'. En el mismo cuadro 4 se observa que, para 2005, el indicador 4 ('sin energía eléctrica') contribuye en promedio al IAM apenas un 1.8 por ciento, mientras que el indicador ocho ('localidades con menos de cinco mil habitantes') contribuye en promedio con 24.0 por ciento, lo que implica que éste último indicador contribuye 1334 por ciento más que 'sin energía eléctrica', lo cual ratifica la gran diferencia que ante el IAM tienen las variables de marginación.
De manera similar se calcula la contribución de los indicadores sobre los índices propuestos. Por ejemplo, para calcular la contribución de analfabetismo al IME0 en 1990, se toman los datos apropiados del cuadro 3 y se aplica la siguiente fórmula
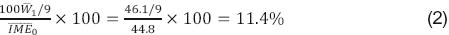
En el cuadro 4 se ve que en 1990 todos los indicadores tienen una contribución muy similar al IME0, yaque fue uno de los objetivos propuestos. Aunque para el año 2005 esta paridad se pierde un tanto para algunos indicadores, toda vez que mientras los indicadores tres y cuatro contribuyen en promedio con 4.7 y 3.7 por ciento, respectivamente; el indicador ocho aporta 17.6 por ciento, lo que genera una discrepancia máxima de 480 por ciento en la aportación promedio al IME0. Si se consideran las discrepancias en el IAM y que la mayoría de los indicadores tienen una contribución similar sobre el IME0, entonces este índice propuesto sigue siendo una alternativa mejor que el IAM. Además, se podrían buscar valores del min y max para el cálculo del IMEQ, que atenuaran su sensibilidad para los diferentes años.
Por otro lado, para calcular la aportación promedio de los indicadores al IME se aplica la siguiente fórmula, que se ejemplifica para analfabetismo en el año 1990,

El cuadro 4 muestra una mayor similitud en la contribución de los diferentes indicadores de marginación al IME, registrándose la mayor discrepancia en el 2005 entre la aportación de los indicadores tres y cuatro contra la del indicador ocho. Pero esta discrepancia máxima, de 260 por ciento, contrasta con la que se da para el IAM, que es de 1 334 por ciento, y la del IME0, que es de 480 por ciento.
Considerando lo anterior, así como los resultados del cuadro 4, y dada la mayor sencillez del IME, aquí optamos por este índice para analizar la evolución de la marginación municipal en México a partir de 1990.
Para comprender el funcionamiento del IME y sus ventajas respecto al IAM, se analizan los casos de tres municipios del país que tienen un nivel de marginación muy diferente entre sí: San Miguel Coatlán (Oaxaca), Valladolid (Yucatán) y Guadalajara (Jalisco). En el cuadro 3 se muestran los valores de los indicadores de marginación de 1990 a 2005 para estos municipios, junto con el valor del IAM e IME.
Si se recuerda que una de las críticas enderezadas contra el IAM fue la gran influencia de los indicadores de 'ingresos', 'localidades de menos de cinco mil habitantes', 'hacinamiento' y 'sin primaria completa'. Al aplicar la fórmula (1) para los cuatro indicadores en el municipio de Valladolid en 1990, se tiene que

De ahí que, en 1990, los cuatro indicadores de referencia determinen 61 por ciento del valor del IAM para Valladolid; mientras que para 2005 es de 75 por ciento. Lo que implica que en este caso la evolución de la marginación entre 1990 y 2005 la terminan decidiendo en buena medida tales indicadores. Esto queda más claro con el cálculo del siguiente recuadro obtenido a partir del cuadro 3 para el municipio de Valladolid.

En este recuadro se muestra que el promedio de los cuatro indicadores de mayor impacto (I2, I6, I8, I9) tenían un valor en 1990 de 56.0; mientras que en 2005 fue de 48.6, lo que significa que la marginación medida por estos cuatro indicadores sólo tuvo una reducción de 13 por ciento en quince años. En contraste, si la evaluación de la evolución de la marginación se hace con base en los restantes cinco indicadores, se alcanza una reducción de 56 por ciento. Pero esta reducción queda subvalorada debido a la gran influencia de los otros indicadores, toda vez que el IAM completo sólo logra una reducción de 30 por ciento.
En cambio, si se utiliza el IME, los indicadores 'sin primaria completa', 'hacinamiento', 'localidades de menos de cinco mil habitantes' e 'ingresos' sólo tienen un impacto del 38 por ciento sobre el valor del IME, y como en 1990 el valor del mismo para Valladolid era de 43.2, y para 2005, 26.1 (véase cuadro 3), entonces la reducción de la marginación en términos del IME fue de 39.5 por ciento, que es una evaluación más prudente respecto a lo que le pasó a la mayoría de los indicadores de marginación en el periodo señalado.
San Miguel Coatlán, Oaxaca, es un municipio con alto nivel de marginación en 1990, los valores del IAM e IME fueron ahí de 80.9 y 97.3, respectivamente. Ambas mediciones indican un elevado nivel de marginación, donde la medición del IME supera a la del IAM, con 16.4 puntos. Parael año 2005, los valores de los índices para este mismo municipio son 60.5 y 64.8; por lo que las reducciones relativas de la marginación de San Miguel Coatlán, en términos de IAM e IME, para el periodo 1990–2005 fueron de 25.0 y 33.4 por ciento, de manera respectiva. Esto muestra que, por las desventajas que tiene el IAM de Conapo, la reducción de la marginación en 25 por ciento está subestimada, y si se da una importancia menos dispar a los indicadores de marginación, en realidad la disminución de la marginación es mayor, como lo reporta el IME, con una reducción de 33.4 por ciento, lo que es una mejor medición de lo que realmente ha pasado en este municipio.
Esta tendencia de subvaloración que hace el IAM en la reducción de la marginación en Valladolid y San Miguel Coatlán se mantiene en los valores promedios de los municipios del país, ya que con el IAM el descenso en el periodo de referencia fue de 31 por ciento, mientras que con el IME fue de 41.8. En efecto, si se calcula el promedio de los indicadores I2, I6, I8 y I9 en 1990 se obtiene un valor de 69.5; mientras que en 2005 fue de 57.5, lo que implica que en estos indicadores sólo se da una disminución de 17 por ciento. En contraste, en los restantes cinco indicadores, la reducción relativa promedio fue de 54.5 por ciento. Esta subvaloración de la reducción de la marginación que hace el IAM se centra más en los municipios altamente marginados o pequeños.
En el municipio de Guadalajara, los valores del IAM en 1990 y 2005 son 13.9 y 7.6, respectivamente; mientras que para el IME son 10.3 y 5.5, correspondientemente; con lo que las reducciones relativas en la marginación, en términos de estos dos respectivos índices, son muy similares: 45.8 y 46.6 por ciento.
Por otro lado, uno de los hechos relevantes del IM es que ha logrado influir en la focalización de programas públicos, ya que existen diversos programas gubernamentales que entre sus criterios de aplicación incluyen el grado de marginación del municipio o la localidad. En Conapo, para establecer en qué grado de marginación cae cada municipio, se aplica al conjunto de valores del índice de marginación la técnica de estratificación óptima de Dalenius y Hodges (1959) —véase, por ejemplo: Conapo, 2000—, y de esta manera los municipios son agrupados en las cinco categorías o grados de marginación. Sin entrar a cuestionar esta técnica, como sí se hace en otros estudios (Bustos, 2009; Bistrain, 2010), en el cuadro 5 se muestran los resultados de aplicar la metodología de Dalenius y Hodges (1959) a los valores del IME, IAM e IM.

En el cuadro 5 se ve que la medición del IM para 2005 determinó la existencia de 1 251 municipios con alta o muy alta marginación, mientras que 702 estaban en baja o muy baja (Conapo, 2005).
En cambio, para el IME e IAM hay 743 y 992 municipios, respectivamente, con alto o muy alto grado de marginación. Por lo que hay diferencias notorias en cuanto a la cantidad de municipios que caen en cada categoría para cada índice. Estas diferencias son el resultado de la distribución de cada índice y de la forma en que los indicadores de marginación los influyen, como ya se dijo. En general, entre mayor sea la discrepancia con la que los indicadores de marginación influyen sobre cada índice, mayores serán las diferencias de clasificación del grado de marginación de un municipio. Sobre el particular, ya se ha argumentado que, en promedio, en el conjunto de municipios del país el índice que aquí se propone, el IME, es en el que los diferentes indicadores de marginación tienen un impacto menos dispar, y que por lo tanto sería el índice que estaría haciendo una categorización más prudente.
Para profundizar en la información que se muestra en el cuadro 5 se obtuvo el cuadro 6. En éste se muestran las coincidencias y discrepancias en el grado de marginación que se le asigna a 2 454 municipios del país en 2005, a partir de los índices de marginación. Así, los municipios que están en las diagonales (sombreadas) son a los que se les determina el mismo grado. Por ejemplo, en el caso del IM e IME, hay 321 municipios que con ambos índices se les asigna muy alto grado de marginación, y hay 332 clasificados de igual manera en el grado alto. En general, un total de 1 591 municipios (65 por ciento del total) se clasifican de la misma manera con IM e IME. Al contrastar IAM e IME, se encuentran 1 786 municipios (73 por ciento del total) que se clasifican de la misma manera con ambos índices.
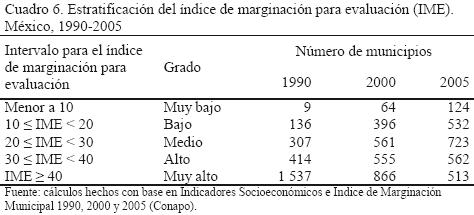
Las cantidades que están por arriba de las diagonales del cuadro 6 representan a aquellos municipios a los que el IME les asigna mayor grado de marginación que los dos índices de Conapo. Y los que están por debajo de las diagonales muestran lo contrario: el IME les asigna un menor grado de marginación que la decidida con los índices de Conapo. Así, por ejemplo, en el caso del IM, hay 44 municipios que con el IM son catalogados como de muy alta marginación, pero con el IME se clasifican sólo en el grado alto. Algo similar le ocurre a 169 municipios que con el IAM se les clasifica en grado muy alto, y con el IME sólo alto.
Así, el hecho de que el IAM esté fuertemente influido por pocos indicadores afecta tanto el nivel reportado de la marginación para un municipio (cuadros 5 y 6), como la valoración que se le da a la evolución de la marginación a través del tiempo, como se ejemplificó para los tres municipios del cuadro 3.
Análisis de la evolución de la marginación con el IME
La evolución de la marginación municipal entre 1990 y 2005, de acuerdo con el IME, se resume en el cuadro 7. Por ejemplo, en 1990, el IME varió entre 5.4 y 118.3, con una media de 50.6; para 2005, este rango de variación se reduce al ir de 2.5 a 99.4, con un promedio de 29.4. Esto implica que el promedio del IME se redujo en forma relativa 41.8 por ciento, que corresponde a una reducción de 21.2 puntos en el valor del IME. En el cuadro 7 también se da cuenta de la evolución de diferentes estadísticos del IME, como el mínimo, el percentil 10, la mediana, el percentil 90, el máximo y la desviación estándar, con la idea de mostrar la evolución de los diferentes niveles de marginación. Es claro que todos los estadísticos muestran una disminución de la marginación, por ejemplo, el valor del percentil 90 para 1990 era igual a 81.9, esto indica que, en ese año, noventa por ciento de los municipios tenía un IME menor de 81.9; para el año 2005, 90 por ciento de los valores del IME fueron menores a 47.5, lo cual implica una compactación de 41.9 por ciento del grueso (90 por ciento) de los valores del IME. Lo anterior, junto con la reducción en la variabilidad (desviación estándar), muestra una disminución en las brechas de desigualdad entre los municipios en términos del IME.

Estratificación
Algo que ha caracterizado al IM es que cada vez que se calcula se clasifican los municipios de acuerdo con su grado de marginación en cinco niveles, siendo muy bajo, bajo, medio, alto y muy alto. Pero este grado de marginación es relativo al mismo año, por lo que independientemente del nivel real de marginación en el país, habrá municipios catalogados en cada una de las cinco categorías. Por esto, para propósitos de evaluación de los resultados de las políticas públicas es mejor catalogar los municipios de acuerdo con la intensidad con la que se manifiesta la marginación. En particular, para el IME se plantean las cinco categorías dadas por los intervalos que se muestran en el cuadro 8. Donde un municipio es catalogado con un grado muy bajo de marginación si el IME es menor a 10, en nivel bajo si su IME está entre 10 y menos de 20, en grado medio si 20 ≤ IME < 30, en el grado alto si 30 ≤ IME < 40; y por último, si el IME indica que el municipio tiene una marginación mayor o igual a 40 entonces será catalogado con muy alta marginación.

De acuerdo con esta categorización, en 1990 había 1 951 municipios en las categorías de alta o muy alta marginación, mientras que sólo 145 tenían baja o muy baja marginación. Para 2005 todavía había 1 075 municipios en las categorías alta y muy alta; y 656 alcanzaron las categorías de baja o muy baja marginación.
Las cuadros 7 y 8 muestran claramente que, en términos generales, hubo una reducción importante de la marginación en los municipios del país. Con una reducción promedio de 41.8 por ciento. Sin embargo, al hacer un análisis de los logros individuales de cada municipio por medio del IME destacan notorios contrastes. En el cuadro 9 se muestran los diez municipios con mayores y menores reducciones en el valor del IME. Siendo cuatro municipios de Puebla (Camocuautla, Coatepec, Atlequizayan y Tlapacoya) los que tuvieron mayores reducciones en el valor de su IME, con disminuciones de 68.6, 66.7, 60.4 y 60.1 puntos. En contraste, son tres municipios de Oaxaca los que tienen menores avances: San Blas Atempa, San Antonino Castillo Velasco y Villa de Zaachila. En este último municipio incluso se dio un empeoramiento del valor de su IME, al pasar de 30.55 a 33.14 puntos. Resulta lógico que, en general, los municipios que tienen mayores reducciones en el valor del IME presentan la particularidad de que en 1990 tenían valores grandes del IME. Sin embargo, lograr estas reducciones tiene un gran mérito, ya que hay muchos otros municipios que a pesar de su valor alto en el IME no lograron tales avances.

La perspectiva de la evolución cambia si se calcula la reducción relativa en el IME, como se muestra en el cuadro 10. En esta perspectiva, las tres mayores reducciones fueron de 74.5, 71.2 y 68.1 por ciento para los municipios de San lacinto Amilpas, Oaxaca; Altamira, Tamaulipas, y Ramos Arizpe, Coahuila, respectivamente. En contraste, los menores avances relativos se presentan en los mismos municipios de Oaxaca del cuadro 9.

Con los datos contenidos en los cuadros 8, 9, 10 puede concluirse que el IME es capaz de evaluar los cambios en la marginación tanto en forma relativa como en el valor absoluto del mismo.
Conclusiones
El índice de marginación (IM) desarrollado por Conapo en la década de 1990 se ha usado como una medida–resumen para diferenciar entidades geográficas según el impacto global de las carencias que padecen sus pobladores. Para los municipios, el IM se forma con una suma ponderada de nueve indicadores de carencias, la ponderación se ha hecho aplicando el análisis multivariado de componentes principales, considerando únicamente el primer componente. Esto genera dos problemas, el primero es que para definir el IM sólo se utiliza parte de la información, por ejemplo, en 2005, sólo 54 por ciento de la variación de los nueve indicadores es explicada por el primer componente principal, y segundo, el peso o contribución de estos indicadores al IM es diferente en cada evento censal; por ejemplo, los indicadores de educación pesan el doble que la carencias de drenaje y servicio sanitario en 2005. Otro problema del IM es que sus valores no son comparables a través del tiempo, lo que dificulta su uso para evaluar los avances en la reducción de la marginación.
Para atender esta problemática, en el propio Conapo se propuso el índice absoluto de marginación (IAM), que resulta de una suma sin ponderación de los nueve indicadores de carencias. Sin embargo, el IAM tiene una falla estructural muy importante, ya que se le da igual ponderación a indicadores que de sí son diferentes. Esto causa que el valor del IAM para un municipio esté fuertemente influido por el valor de los indicadores que por su naturaleza presentan niveles altos de carencias, como ingresos, localidades de menos de cinco mil habitantes y hacinamiento; dejando en un segundo o un tercer planos al resto de las carencias. Por ejemplo, en este trabajo se ha demostrado que los indicadores de marginación sin energía eléctrica y localidades con menos de cinco mil habitantes tienen una discrepancia del 1 334 por ciento en cuanto a su influencia promedio sobre el valor del IAM en 2005 (cuadro 4).
Por lo anterior, como alternativa a los índices de Conapo, se ha propuesto el índice de marginación para evaluación (IME), construido a partir de normalizar los indicadores de marginación municipal, de manera que tengan un impacto promedio similar en el IME. Se han hecho dos propuestas. Una de ellas, las más sencilla y fácil de aplicar, consiste en transformar cada indicador de un municipio dividiéndolo por el valor medio correspondiente y considerando todos los municipios del país.
Con base en el IME, se ha visto que la marginación en los municipios del país se redujo en forma relativa 41.8 por ciento entre 1990 y 2005, al pasar de un valor promedio de 50.6 a uno de 29.4. Sin embargo, al hacer un análisis de los logros individuales de cada municipio, destacan notorios contrastes. Ya que las reducciones relativas van desde 74.5 por ciento hasta un aumento de 8.5 por ciento.
Finalmente, se han propuesto intervalos para que se clasifique el grado de marginación de un municipio en función del valor del IME. Esto contrasta con el enfoque seguido por Conapo, donde cada periodo censal se vuelve a agrupar a los municipios en función del valor del IM, lo que hace que siempre se tengan municipios en muy alta y muy baja marginación.
Bibliografía
ÁLVAREZ AYUSO, Inmaculada y Edel CADENA VARGAS, 2006, "Índice de vulnerabilidad social en los países de la OCDE", en Economic Analysis Working Papers 01/2006 Series. Departamento de Análisis Económico, Teoría Económica e Historia Económica. Universidad Autónoma de Madrid. [ Links ]
APARICIO, Ricardo, 2004, Índice absoluto de marginación, 1990–2000. Consejo Nacional de Población, México. [ Links ]
BISTRAIN CORONADO, César, 2008, Análisis de la marginación en la población rural de México, 1990–2000. Tesis de Maestría en Población y Desarrollo, Flacso. México. [ Links ]
BISTRAIN CORONADO, César, 2010, "Revisión de los índices de marginación elaborados por el Conapo", en Estudios Demográficos y Urbanos, vol. 25, núm. 1 (73). [ Links ]
BUSTOS Y DE LA TIJERA, Víctor Alfredo, 2009, "Indicadores sintéticos para seguir la evolución en el tiempo de fenómenos multidimensionales: una propuesta metodológica", en Boletín del Sistema Nacional de Información Estadística y Goegráfica, vol. 2, núm. 3. [ Links ]
CAMBEROS, Mario y Joaquín BRACAMONTES, 2007, "Marginación y políticas de desarrollo social: un análisis regional para sonora", en Problemas del Desarrollo, vol. 38, núm. 149. [ Links ]
CÁRDENAS RODRÍGUEZ, Oscar Javier, 2010, "Cardenalización del índice de marginación: una metodología para evaluar la eficiencia del gasto ejercido en el Ramo 33", en EconoQuantum, vol. 7, núm. 1. [ Links ]
COEPO, 2010, Desarrollo humano y demografía de grupos vulnerables de Jalisco, Dirección de Publicaciones del Gobierno de Jalisco, Guadalajara. [ Links ]
CONAPO, 1990, Comportamiento reproductivo y marginación en áreas rurales y urbanas de México, Consejo Nacional de Población, México. [ Links ]
CONAPO, 1993, Indicadores sociodemográficos e índice de marginación municipal, 1990, Consejo Nacional de Población y Comisión Nacional del Agua. México. [ Links ]
CONAPO, 1995, Indices de marginación 1995, Consejo Nacional de Población y Programa de Educación, Salud y Alimentación, México. [ Links ]
CONAPO, 2001, Indices de marginación, Colección índices Sociodemográficos. Consejo Nacional de Población, México. [ Links ]
CONAPO, 2005, Indices de marginación 2005, Colección índices Sociodemográficos, Consejo Nacional de Población, México. [ Links ]
CONEVAL, 2006, Mapas de pobreza por ingresos y rezago social 2005. Consejo Nacional de Evaluación de la Política de Desarrollo Social, México. [ Links ]
CONEVAL, 2009, Metodología para la medición multidimensional de la pobreza en México, Consejo Nacional de Evaluación de la Política de Desarrollo Social. México. [ Links ]
COPLAMAR, 1982, Geografía de la marginación, Siglo XXI Editores, México. [ Links ]
DALENIUS, Tore y Joseph L. HODGES, 1959, "Minimumvariance stratification", en Journal of the American Statistical Association, vol. 54. [ Links ]
GUTIÉRREZ PULIDO, Humberto, Mónica MARISCAL, Marcela AYALA, Pedro ALMANZOR y César COSSIO, 2008, Panorama demográfico de Jalisco. Gobierno de Jalisco, Guadalajara. [ Links ]
LÓPEZ–CALVA, Luis Felipe, Lourdes RODRÍGUEZ–CHAMUSSY y Miguel SZÉKELY, 2006, "Introducción", en Luis Felipe LÓPEZ–CALVA y Miguel SZEKELY (comps.), Medición del desarrollo humano en México. FCE, México. [ Links ]
MÁRQUEZ, Miguel 2006, "El desarrollo humano desde la perspectiva integral y su proyección mundial", en Desarrollo Humano Local, York University, Toronto. [ Links ]
MARTÍNEZ PELLÉGRINI, Sárah, Laura FLAMAND, y Alberto HERNÁNDEZ, 2008, "Panorama del desarrollo municipal en México. Antecedentes, diseño y hallazgos del Índice de Desarrollo Municipal Básico", en Gestión y Política Pública, vol. XVII, núm. 1, México. [ Links ]
MORALES–RAMOS, Marco Antonio y Eduardo MORALES–RAMOS, 2008, "La teoría de conjuntos difusos como una opción para medir la pobreza, el caso de México", en El Trimestre Económico, vol. LXXV (3), núm. 299. [ Links ]
PEÑA, Daniel 2002, Análisis de datos multivariantes, Mc Graw Hill, Madrid. [ Links ]
PNUD 1990, Desarrollo Humano, Informe 1990, Tercer Mundo Editores, Bogotá [ Links ].
PNUD 2005, Informe sobre Desarrollo Humano México 2004, Programa de las Naciones Unidas para el Desarrollo, México. [ Links ]
Información sobre los autores:
Humberto GUTIÉRREZ PULIDO. Doctor en probabilidad y estadística. Profesor en la Universidad de Guadalajara y secretario técnico del Consejo Estatal de Población Jalisco. Miembro del Sistema Nacional de Investigadores. Áreas de interés: mejora de procesos, aplicaciones de la Estadística y Demografía. Algunas publicaciones recientes: Gutiérrez et al. (2010), Desarrollo humano y demografía de grupos vulnerables en Jalisco, Dirección de Publicaciones del Gobierno del Estado de Jalisco; H. Gutiérrez Pulido y M. Mariscal González, (2010), "Evolución de la marginación y la pobreza", en Dos décadas de desarrollo en Jalisco 1990–2010; Cecilia Garibay, Humberto Gutierrez y Arturo Figueroa (2010), Evaluation of a digital library by means of quality function deployment (QFD) and the kano model, The Journal of Academic Librarianship, vol. 36, núm. 2.
Viviana GAMA HERNÁNDEZ. Licenciada en Matemáticas. Analista en el Consejo Estatal de Población, Jalisco.














