Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Papeles de población
versión On-line ISSN 2448-7147versión impresa ISSN 1405-7425
Pap. poblac vol.15 no.61 Toluca jul./sep. 2009
En la búsqueda del estado estacionario de la población del planeta
In the search for the steady state of the planet population
Manuel Ordorica–Mellado
El Colegio de México. Correo electrónico: mordori@colmex.mx
Resumen
El objetivo del presente trabajo es construir una función matemática que describa la evolución de la población mundial hasta el año 2050, a fin de establecer escenarios de lo que pudiera ocurrir en el corto, mediano y largo plazo, en el caso de llegar al estado estacionario. Se utiliza la función logística para describir la dinámica de la tasa de crecimiento demográfico. Se establecerá una hipótesis de crecimiento demográfico cero, con tres alternativas en los valores de la asíntota superior. Los escenarios en términos del número de habitantes en las tres hipótesis de la cota superior no son muy diferentes. El mundo llegaría a nueve mil millones en los tres supuestos. Además, en este artículo se analiza desde el punto de vista teórico, la incorporación de la edad en el modelo logístico.
Palabras clave: crecimiento demográfico, esperanza de vida, población mundial, población estacionaria.
Abstract
The objective of the present work is to build a mathematical function that describes the evolution of the world's population up to the year 2050, so as to establish scenarios of what might occur in the short, mid and long terms, in the case of reaching the steady state. A logistic function is utilized to describe the dynamics of the demographic growth rate. The hypothesis of a zero demographic growth is established with three alternatives in the values of the superior asymptote. The scenarios in terms of the number of inhabitants in the three hypotheses of the superior limit are not so different. The world will reach nine million in the three suppositions. What is more, in this article the incorporation of age into the logistic model is analyzed from the theoretical viewpoint.
Key words: demographic growth, life expectancy, world population, steady population.
Introducción
... 4 Generación va, y generación viene: mas la Tierra siempre permanece.
5 Y sale el sol, y pónese el sol, y con deseo vuelve a su lugar donde torna a nacer..
7 Los ríos todos van a la mar, y la mar no se hinche; al lugar de donde los ríos vinieron, allí tornan
para correr de nuevo... 9 ¿Qué es lo que fue? Lo mismo que será; ¿Qué es lo que ha sido hecho? Lo
mismo que se hará: yjiada hay nuevo debajo del sol..
La Santa Biblia. Eclesiastés I: 4, 5, 7 y 9
El deseo de predecir y explorar el futuro constituye una parte central de lo que nos hace seres humanos. Somos la única especie en el planeta Tierra que demuestra un vivo interés por el tiempo por venir. Conocer el futuro nos ayuda a tomar decisiones respecto al presente. Sabemos que dentro de 7 600 millones de años, la Tierra será engullida por el Sol. Para ese entonces no habrá vida sobre el planeta. Los astrofísicos pueden hacer proyecciones a periodos muy largos, mientras que los demógrafos sólo podemos aproximarnos al futuro unas cuantas décadas.
Durante miles de siglos el crecimiento demográfico se mantuvo lento. La preocupación se centraba en la escasez de personas. El crecimiento de la población estaba vinculado a un gran imperio. Fue hace aproximadamente un siglo y medio cuando el estudio de los aspectos demográficos pasó a ser un tema de gran importancia y adquirió rango científico al alcanzarse, a mitad del siglo XIX, los primeros mil millones de habitantes. En la tercera década del siglo XX la población mundial ascendió a dos mil millones de personas. El 12 de octubre de 1999, el planeta llegó a seis mil millones de individuos; poco más de cinco siglos después de que Cristobal Colón descubriera el Nuevo Mundo. En este periodo de doce años, entre 1987 y 1999, la población de la Tierra aumentó en 1000 millones de personas. Según estimaciones de Naciones Unidas, en el 2012 habría 7000 millones de individuos. Hoy, la esperanza de vida en el mundo es de 67 años, cuando hace medio siglo era 20 años menor. El número medio de hijos por mujer es de 2.5 y hace dos decenios era del doble. El crecimiento demográfico actual del planeta es de 1.1 por ciento anual, lo cual significa que la población se duplicaría en ciclos de un poco más de 60 años, si continúa ese ritmo de incremento anual.
Una ventaja que tenemos quienes realizamos proyecciones de población es que éstas tienen una inercia notable, por lo que las previsiones a varios lustros de distancia son altamente posibles. Por ejemplo, las personas que demandarán el pago de sus pensiones en 2050, en el caso de que tengan esa prestación, nacieron en 1985.
A fin de descubrir el futuro demográfico se ha construido un elevado número de modelos matemáticos que intentan replicar el pasado y el presente para determinar escenarios posibles sobre el futuro. Existen diversos métodos para hacer prospectiva demográfica, entre los que destacan los de tipo matemático, los económicos y las proyecciones a través del método de los componentes. Este último es el que se utiliza con mayor frecuencia porque permite incorporar la estructura por edad de la población, planteando hipótesis de cada uno de los componentes que intervienen en el cambio demográfico. En el presente trabajo se desarrollará un modelo de tipo matemático en el que se construirá una función con el fin de analizar la dinámica poblacional e intentar construir relaciones entre las variables demográficas y, en consecuencia, avanzar en la teoría de las poblaciones no estables. Además, intentaremos responder a la pregunta: ¿hacia qué población se dirige el mundo cuando llegue al crecimiento estacionario?
Parecería que las personas siempre estamos en busca de los equilibrios, de la armonía, como ocurre en las ciencias físicas. Cuando encendemos una vela, la llama crece y luego decrece. Pronto se instala en un estado estacionario, siempre y cuando haya suficiente oxígeno. La balanza comercial de un país está en equilibrio si las importaciones son iguales a las exportaciones. La población ha crecido aceleradamente en algunas partes del planeta y luego en esos lugares han buscado tender hacia el equilibrio. En otras partes se han presentado niveles de crecimiento demográfico por debajo del reemplazo y han planteado acciones para crecer. Los seres humanos vamos buscando siempre el estado estacionario.
En 1977, en nuestro país, por ejemplo, en el marco de la política migratoria, se planteó la necesidad de impulsar el crecimiento demográfico de las zonas costeras que se encontraban en equilibrio, y que tenían recursos naturales y productivos, a fin de establecer una política de reordenamiento del territorio. Este es un ejemplo de rompimiento del equilibrio con el fin de buscar la estabilidad en la distribución de la población.
Un buen ejemplo de que ciertas cuestiones de los seres humanos están vinculadas al equilibrio es la distribución normal. Muchas características siguen un comportamiento parecido a la distribución gaussiana, es decir, gran parte de los datos están alrededor de una media y con menor probabilidad se encuentra información en las colas de la distribución. Este también es un ejemplo de que el equilibrio se ubica en muchas de nuestras actividades.
En Física, el equilibrio es el estado de un sistema sometido a fuerzas contrarias que se contraponen, de tal suerte que las variables que describen el sistema no evolucionan más y luego éste cesa todo movimiento. En Geografía, se observan más bien estados estacionarios, cuando la igualdad de los flujos que entran y salen de un sistema abierto implica que no hay variación del mismo. Otro ejemplo de estado estacionario se presenta en el análisis de series de tiempo. Para poder utilizar el instrumental de los procesos estocásticos se transforman las series para llevarlas al estado estacionario y poder utilizar la teoría que subyace a estos modelos. En teoría de colas también se intenta tener el mismo número de llegadas que de salidas para que las personas en la cola puedan ser atendidas. Una región que recibe tantos inmigrantes de otras regiones como de emigrantes se calificará como en equilibrio, y en Demografía, una población es estacionaria si los nacimientos en el transcurso de un periodo dado son iguales a las muertes. El proceso estacionario se encuentra en muchas de las decisiones que tomamos en la vida.
Otra característica de los seres humanos es que siempre han estado interesados en los números de las poblaciones. Por ejemplo, los números dan su nombre a una parte de la Biblia en la cual la estadística ocupa un lugar importante y aparecen repetidos conteos de población. Yavé dijo a Moisés y a Eleazar: "... Registra a toda la comunidad de los hijos de Israel por casas paternas y hagan el recuento de todos los de más de veinte años, útiles para la guerra..." Esto muestra el interés por la población para fines militares.
Otro rasgo de los individuos es la búsqueda de leyes en la naturaleza que nos permitan anticiparnos al porvenir. A lo largo de la historia de la Demografía se han desarrollado diversas funciones matemáticas con el fin de describir dos posiciones extremas entorno a la evolución de la población, entre las cuales sobresalen como las más conocidas la exponencial y la logística, aplicadas a la descripción de la población total. La primera crece indefinidamente, mientras que la otra tiene un límite. Los esfuerzos por establecer leyes matemáticas que representaran el crecimiento demográfico se promovieron debido a la creciente disponibilidad de información y al desarrollo de modelos matemáticos para la descripción de datos. Ninguna de las representaciones matemáticas mencionadas se ajusta fielmente a la realidad, debido a que las hipótesis no reproducen la dinámica de los componentes del crecimiento de la población. Sin embargo, han posibilitado avanzar en la teoría matemática de la demografía, como es el caso de las poblaciones estables desarrollada por Lotka (1969), que es una de las teorías más sólidas en esta disciplina.
La construcción de modelos matemáticos agregados que describen la dinámica demográfica permiten analizar las posibles trayectorias de la población total y seleccionar la deseada, de acuerdo con las condiciones socioeconómicas. Lo ideal es disponer de la población y sus componentes por sexo y edad, lo que permite conocer las causas de la evolución poblacional. Es importante señalar que la representación matemática de la evolución de la población es un primer acercamiento analítico antes de llegar a la modelación con información más específica.
La ecuación diferencial más sencilla es la siguiente:

En donde r0 es una constante. Alfred Lotka analizó con profundidad esta función, con sus implicaciones en la composición por edad de la población.
Cuando se supone que la tasa de crecimiento demográfico es función lineal de la población, se desprende la ecuación logística:

Es importante destacar que es más fácil hacer supuestos sobre la evolución de la tasa de crecimiento de la población que sobre la población misma o sobre la tasa de mortalidad. Es aceptable la hipótesis de que la dinámica en el ritmo de crecimiento demográfico total se comportará como la función logística. Podemos plantear que el crecimiento demográfico cero podría ser la asíntota inferior, mientras que es casi imposible decir cuál es el límite de la población.
¿Es posible usar la logística para representar la dinámica de la tasa de crecimiento demográfico en el caso de la población del planeta? Este es el propósito de este trabajo. Sabemos que desde finales de la década de 1960 empezó a descender la tasa de crecimiento demográfico. Debido a su forma gráfica, esta función permite describir la trayectoria de la intensidad del crecimiento poblacional después de mediados de la década de 1960, puesto que dicha tasa se incrementó hasta el segundo quinquenio de los años sesenta, cuando se observó el máximo y luego inició su declinación. Sólo es posible utilizarla cuando se encuentra en su fase descendente en la intensidad del crecimiento poblacional, porque es poco probable que en el corto y mediano plazos revierta su tendencia y empiece a crecer nuevamente. Es difícil pensar que la tasa de crecimiento de la población podría en el corto y mediano plazos cambiar su tendencia decreciente, debido a la inercia demográfica.
Objetivo
El objetivo del presente trabajo es desarrollar una función matemática que describa la dinámica de la tasa de crecimiento demográfico y, en consecuencia, la evolución de la población entre 1980 y el año 2005, y sus perspectivas, a fin de establecer escenarios de lo que pudiera ocurrir en el corto, mediano y largo plazos, bajo el supuesto de que se alcance la población estacionaria en el planeta. Además, se incorporará la edad al modelo.
Metodología
Sea

Donde r(t) es la tasa instantánea de crecimiento de la población y es función del tiempo. Supongamos que se puede representar una declinación mediante la logística, bajo la hipótesis de que la dinámica de este componente es lineal en el tiempo, de la siguiente forma:

Resolviendo la ecuación diferencial tenemos:

En la función de r(t) se observa que cuando t tiende a infinito, r(t) tiende a k1 Esto significa que k1 es la tasa de crecimiento demográfico a la que tiende la población cuando t tiende a infinito. Los dos primeros factores de la función Ρ(t) son constantes y quedan definidos cuando se realiza el cálculo de la función para t = 0, es decir, cuando se establecen las condiciones iniciales. Es importante aclarar que el momento t = 0 representa el año de 1980, que es el punto de arranque.
La función P(t) está compuesta de dos constantes y dos funciones en t.
La función

es creciente, puesto que es una función exponencial, mientras que la función

es decreciente, por lo que amortigua o frena el aumento de la población.
Resultados y su análisis
Para estimar a y b se parte de la ecuación:

Despejando a + b t se tiene

La transformación de la ecuación a una forma lineal permite la aplicación del modelo de regresión, el cual posibilita la estimación de a y b mediante el método de regresión lineal simple. Los datos utilizados son las tasas de crecimiento demográfico del mundo calculadas a partir de la publicación de Naciones Unidas en 2005.1
La población estimada por Naciones Unidas (Naciones Unidas, 2005) para 1980 fue de 4 442 millones, de 4 844 millones en 1985, de 5 279 millones en 1990, de 5 692 millones en 1995, de 6 086 millones en 2000 y de 6 465 millones de personas en 2005.

Se elaboraron escenarios para diversos valores de la asíntota superior. El valor de k1 es igual a cero y los de k2 son: 2.5 por ciento, tres por ciento y 3.5 por ciento. Esto nos da un total de tres escenarios posibles de proyecciones de población.
Los valores de los parámetros son:

En todos los casos el coeficiente de determinación es de 0.96, lo que muestra un excelente ajuste. Esto significa que 96 por ciento se explica por la regresión, y sólo cuatro por ciento por los errores.
Es posible señalar que los resultados estimados de las poblaciones, derivados de la función matemática, son semejantes a los observados, lo que significa que el modelo reproduce de manera adecuada la dinámica demográfica mundial del periodo 1980–2005. En el cuadro 1 se presentan los resultados de los tres escenarios.

Incorporando la edad en el modelo
Sea c(x, t) la estructura de la población a la edad x; B(t – x), el número de nacimientos en el momento t – x, y p(x, t), la probabilidad de que una persona sobreviva desde el nacimiento hasta la edad x, en el momento t.
La población de edad x en el momento t se puede expresar mediante la siguiente igualdad: p(t) c(x, t) = B(t – x) p(x, t).
Del lado izquierdo de la igualdad se tiene el producto de la población total por el porcentaje de población de edad x. El resultado es la población de edad x en el momento t. Del lado derecho se tiene la multiplicación de los nacimientos en el momento t – x, por la probabilidad de que esos nacimientos lleguen con vida a la edad x. El resultado es también la población a la edad x. Son dos caminos alternos que llegan al mismo resultado, uno es de momento y el otro generacional.
Bajo el supuesto de que la tasa de crecimiento demográfico siga una logística, tenemos que:

Despejando c(x,t) y sustituyendo el valor de P(t), tenemos:
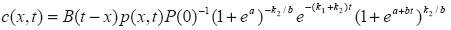
Por tanto, es posible calcular la estructura por edad a partir de los nacimientos, de una tabla de vida y de una constante. A continuación se presenta un ejemplo del cálculo de la estructura por edad para una edad dada.
Consideremos el año de 1980, es decir, el valor de t es igual a 0, para una edad cumplida de 0 años. Portanto, se desea calcular c(0,0) en el caso discreto.

Se simplifica y queda lo siguiente:
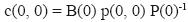
La estructura por edad a la edad 0 es igual a:
123916000 (0.94961) (4442000000)-1 = 0.026
¿Qué más podemos encontrar? Si integramos entre o y w, tenemos que:
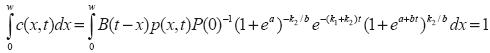
Sacando fuera de la integral los valores que no dependen de x se tiene que:

El límite superior de la integral, definido por w, es la edad máxima de la vida a la que se supone puede llegar un individuo.
Pasando para el otro lado de la ecuación el valor de la constante, tenemos:

Cálculo de la esperanza de vida al nacer
Aplicando el teorema del valor medio, es posible sacar B(t – ξ) fuera de la integral, donde ξ es un punto en el intervalo de 0 a w. Por tanto, tenemos que:

Sabemos que: 
Por tanto

Esto significa que la esperanza de vida al nacer se puede expresar en función de los nacimientos y una constante que depende de los parámetros. La dificultad en el cálculo de la esperanza de vida al nacer, en este caso, es encontrar el valor de ξ .
A manera de reflexión
Es posible señalar que la función logística muestra adecuadamente la dinámica de las tasas de crecimiento de la población mundial, lo cual se puede constatar con los elevados coeficientes de correlación. La población proyectada para el año 2050, según Naciones Unidas (2005) es de nueve mil millones de personas, cifra que concuerda aproximadamente con las proyecciones obtenidas con el modelo presentado en este documento (véanse gráfica 1 y cuadro 1). Esta será el doble de la población mundial de principios de la década de 1980. Cuando nazca el habitante nueve mil millones, Gaspar Matej —el habitante cinco mil millones, nacido en 1987— se encontrará ya en la etapa de su jubilación a mediados del siglo XXI. En 2050, en muchas partes del mundo, no se escucharán los llantos de los bebés. Los temas de conversación que se discutirán son: ¿vale la pena casarse o unirse?, ¿cuándo es el mejor momento para tener un hijo? y ¿es buena idea tenerlo? Las mujeres podrían estar pensando en tener un hijo al final de su vida fértil, pero solas. Habrá muchos geriatras, prácticamente no habrá ginecólogos. Aumentará de forma legal la emigración laboral hacia los países con estructura por edad envejecida. Se sancionará económicamente a parejas que no tengan hijos. ¿Cuál es el mundo demográfico que queremos tener?

Bibliografía
COONTZ, Sidney H., 1960, Teorías de la población y su interpretación económica, FCE, México. [ Links ]
KEYFITZ, Nathan, 1979, Introducción a las matemáticas de la población, Centro Latinoamericano de Demografía, Santiago de Chile. [ Links ]
LOTKA, Alfred, 1969, Teoria analítica de las asociaciones biológicas, Centro Latinoamericano de Demografía, Santiago de Chile. [ Links ]
ORDORICA, Manuel, 1990, "Ajuste de una función expologística a la evolución de la población total de México, 1930–1985", en Estudios Demográficosy Urbanos, vol. 5, núm. 3, El Colegio de México. [ Links ]
ORDORICA, Manuel, 2006, "Cuatro escenarios de la población de México para fines del siglo XXI construidos a través de una función exponencial", en José Luis LEZAMA y José B. MORELOS (coords.), Población, ciudad y medio ambiente en el México Contemporáneo, CEDUA, El Colegio de México. [ Links ]
ORDORICA, Manuel, 2008, "Evolución de la población de México, 1980–2005, conforme a la hipótesis de una tasa de crecimiento demográfico logística", en Estudios Demográficos y Urbanos, vol. 23, núm. 3, El Colegio de México. [ Links ]
ORDORICA, Manuel, 2009, "¿Qué escenario demográfico se quiere para el mundo: crecimiento lento, población estacionaria o la extinción?", en Ciencia Ergo Sum, vol. 15, núm. 3, Universidad Autónoma del Estado de México. [ Links ]
PEARL y REED, 1920, On the rate of growth of the population of the United States since 1790 and its mathematical representation, FUENTE INCOMPLETA. [ Links ]
NACIONES UNIDAS, 1953, "Factores determinantes y consecuencias de las tendencias demográficas", en Estudios sobre población, número 17, FUENTE INCOMPLETA. [ Links ]
NACIONES UNIDAS, 2005, World Population Prospects, The 2004 Revision, vol. I, Comprehensive Tables, FUENTE INCOMPLETA. [ Links ]
SÜSSMILCH, Johann Peter, 1761, An illustration of population growth. Die gottliche Ordnung, vol. 1, Berlin. [ Links ]
VERHULST, 1838, Notice sur la loi que la population suit dans son accroissement, FUENTE INCOMPLETA. [ Links ]
VERHULST, 1845, Recherches mathématiques sur la loi d'accroissement de la population, FUENTE INCOMPLETA. [ Links ]
1 Las tasas de crecimiento demográfico para los años exactos, se estimaron tomando un promedio aritmético entre las tasas quinquenales de incremento poblacional de dos periodos consecutivos del libro (Naciones Unidas, 2005).
Información sobre el autor
Manuel Ordorica Mellado. Maestro en Demografía por El Colegio de México y doctor en Ingeniería por la Universidad Nacional Autónoma de México. Ha sido director del Área de Estudios de Población en el Consejo Nacional de Población, 1977 a 1987; consultor en educación en la Unesco, 1987 a 1988; coordinador de la Maestría en Demografía y del Doctorado en Estudios de Población del Centro de Estudios Demográficos, Urbanos y Ambientales de El Colegio de México. Es miembro del Sistema Nacional de Investigadores y Premio Nacional de Demografía. Entre sus publicaciones más importantes destacan Evaluation of the mexican fertility survey, 1976–1977 (en coautoría con Joseph E. Potter); The impact of rapidfertility decline on the geographical redistribution of the population in developing countries, y Ajuste de una función expologística a la evolución de la población total de México, 1930–1985.














