Funciones de sobrevivencia empleadas en el análisis demográfico

 

Alejandro Mina Valdés

 

El Colegio de México.

 

Resumen

El manejo de las funciones de sobrevivencia tipo Gompertz y tipo Makeham son presentadas a partir de su origen, considerando sus antecedentes, así como la determinación de los parámetros de cada una de éstas, empleando para ello el método de los grupos no superpuestos, comunmente utilizado en ciencias actuariales.

También se presenta el método iterativo que permite depurar, logrando un mejor ajuste, los resultados obtenidos, lo que permite proyectar los parámetros de las funciones de sobrevivencia, obteniendo tablas abreviadas de mortalidad por grupos quinquenales de edad tanto para los hombres como para las mujeres en México, a nivel nacional, para los años 1995, 2000, 2005 y 2010. Finalmente, se presentan las ganancias en las esperanzas por edad entre los años 1995 y 2010.

 

Abstract

The handling of survival functions as Gompertz and Makeham type are presented since its origin, considering its antecedents, as well as the determination of the parameters of each one of this functions, using the method of not superimposed groups, commonly employee in actuarial sciences.

The iterativo method is also presented that allows to purify, obtaining a better adjustment of the obtained results, what allows to project the parameters of the survival functions, obtaining abbreviated charts of mortality for five-year groups of age as much for the men as for the women in Mexico, at national level, for the years 1995, 2000, 2005 and 2010. Finally are presented the increases in prospects age life between 1995 and 2010.

 

Introducción

Algunas de las leyes más conocidas en el ámbito actuarial son, sin duda, las asociadas a la mortalidad y, particularmente, aquellas que describen la información resumida en una tabla de mortalidad.

En 1724 Moivre presentó su hipótesis conocida como "hipótesis de decremento uniforme", la que se resume en la expresión: L(x) = K(w-x), donde: l(x) representa la serie de las personas sobrevivientes a edad z; k la pendiente o velocidad con que decrece la población resumida en la tabla de mortalidad, y w la edad límite de sobrevivencia de dicha población.

La recta de Moivre fue recomendada para un rango de edades de 12 a 86 años, en el cual se ajustaba de mejor manera.

Supóngase que k = 800 y w = 90, entonces, bajo la hipótesis de Moivre, L(x) = 800(90 - x) (gráfica 1):

La hipótesis lineal de Moivre fue superada por Benjamín Gompertz en 1825, quien se apoyó en las dos causas generales de muerte: la casualidad y la creciente incapacidad del hombre para resistir la muerte.

Las causas biológicas fueron consideradas por Gompertz, dejando de considerar las causas fortuitas. Así, la hipótesis de Gompertz quedó planteada de la siguiente manera: "La resistencia que tiene el hombre para evitar la muerte disminuye a una tasa proporcional a ella misma, en el tiempo".

Denotando por Mx la tasa instantánea de mortalidad, donde:

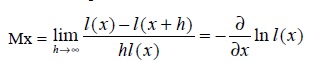
Gompertz toma su recíproco (1/Mx) como la medida que cuantifica la resistencia del hombre a la muerte. El planteamiento matemático de su hipótesis es:

Donde h es la tasa a la que disminuye la resistencia del hombre a la muerte. Resolviendo (1) para Mx, Gompertz obtiene:

y resolviendo (2) para l(x), obtiene:

la que comúnmente es llamada ley de Gompertz.

William M. Makeham incorporó en 1860 las causas de muerte no consideradas por Gompertz, modificando (2) al incrementar su valor con la suma de la constante A, la que hipotéticamente involucra dichas causas fortuitas.

Así, para Makeham:

Y resolviendo (4) (Mina, 1982: 191) para l(x), obtiene:

La que comúnmente es llamada ley de Makeham.

La utilidad que tienen las leyes de Gompertz y Makeham van más alla de la descripción de la serie de los sobrevivientes de una tabla de vida l(x). En el presente trabajo se muestra alguna de las aplicaciones de trabajos hechos o dirigidos por el autor, que los actuarios y demógrafos han hecho de las leyes de Gompertz y Makeham tanto para el fenómeno demográfico mortalidad como para otros fenómenos.

Para desarrollar la ecuación (1) se considera lo siguiente:

a) Se dividen ambos miembros de la igualdad entre el recíproco de la Tasa Instantánea de Mortalidad, es decir, entre 1/Mx y se integra respecto a x para obtener el siguiente resultado:

b) Con las leyes de los logaritmos se obtiene:

c) Aplicando antilogaritmo en ambos lados de la igualdad:

d) Se multiplica por los inversos de e-hx y 1/Mx, es decir, por ehx y Mx para obtener la siguiente expresión para Mx:

e) Si denotamos a eh como C, la expresión para Mx es la siguiente:

Hasta aquí se ha encontrado una expresión para la Tasa Instantánea de Mortalidad a partir del supuesto de Gompertz. Si ahora se parte de la definición de Tasa Instantánea de Mortalidad, considerando el cambio que se observa en los sobrevivientes de una población (lx), se tiene el siguiente límite donde h tiende a cero:

Por la definición de derivada se tiene:

Se ha logrado expresar la Tasa Instantánea de Mortalidad (Mx) como la derivada respecto a x del logaritmo de la función l(x); ahora se buscará encontrar una expresión para l(x). Si se integra y evalúa la expresión (11) respecto a y en el intervalo (0, x) se obtiene:

Por las leyes de los logaritmos tenemos que:

Multiplicando por -1 la expresión (15):

Para eliminar el logaritmo del primer miembro de nuestra igualdad se aplica el antilogaritmo:

Finalmente, se despeja l(x) obteniendo el siguiente resultado:

Hasta este momento se conoce la expresión que define la Ley de Gompertz; sin embargo, es necesario considerar los supuestos que Makeham estableció en su ley.

Makeham propone integrar, en el modelo que define la ley de Gompertz, la primera de las dos causas de muerte supuestas por Gompertz, la cual no fue considerada en el modelo. Es decir, propone considerar dentro de un modelo matemático, tanto las causas independientes de la edad como las independientes.

Makeham establece la siguiente ley:

Donde:

Mx = Tasa Instantánea de Mortalidad bajo los supuestos de Makeham.

A = Parámetro asociado al efecto de las causas de muerte independientes de la edad, las cuales no fueron consideradas en la determinación de la ley de Gompertz.

BC^x = Expresión que define la ley de Gompertz.

Desarrollando la expresión (19), se integran ambos miembros de la igualdad en el intervalo (0, x), es decir:

Se resuelven las integrales y se evalúan:

Simplificando la expresión (23) y multiplicándola por -1 se obtiene:

Se renombran los siguientes términos para expresar la igualdad (24) en términos de logaritmos; para ello, realizamos lo siguiente: -A denotará como ln S y -B/ln C como ln g, por lo que la expresión (24) queda:

La cual se puede simplificar utilizando las leyes de los logaritmos para obtener:

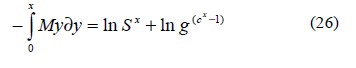
Este resultado permite encontrar una nueva definición para la expresión (18):

Así, sustituyendo la expresión (27) en la expresión (18) tenemos:

Si denotamos l(0)/g como K, tenemos la siguiente expresión:

Esta expresión (32) es la Ley de Makeham, siendo entonces la función de Makeham la siguiente:

La ley de Makeham fue utilizada en un principio para describir el cambio relativo de la línea (lx) de supervivientes de una tabla de mortalidad, la cual supone que podría ser descrita por una función de la forma Mx = A + BC^x.

 

Presentación de la metodología

Combinación de los parámetros k, a, b y d de la función Makeham

Para determinar los parámetros k, a, b y d de la función Makeham, se utilizará el método de los grupos no superpuestos, para el cual es necesario determinar las siguientes condiciones:

a) Los datos se dividirán en cuatro grupos de observaciones sucesivas (yx).

b) Cada grupo deberá contar con el mismo número de valores observados (m). Por lo que, para aplicar este método, se necesita conformar los siguientes grupos:

Primer grupo:

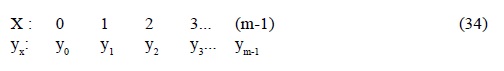
Segundo grupo:

Tercer grupo:

Cuarto grupo:

c) Para linealizar la expresión (33) del apartado anterior, se calculan los logaritmos decimales de las y_x en cada uno de los grupos definidos en el inciso anterior, es decir:

d) A continuación se calculan las sumas de los logaritmos de cada uno de estos grupos y se denotan sumas como S₀ , S₁ , S₂ y S₃ , respectivamente.

e) Para el primer grupo, tenemos: Si se desarrolla cada término del miembro derecho:

para toda i, donde es una progresión aritmética con el primer término de la sucesión igual a cero, la diferencia común es 1 y el número de observaciones es m. La suma de esta sucesión es m(m-1)/2; por tanto:

donde es una progresión geométrica con el primer término de la sucesión igual a d⁰, la razón común es d y el número de observaciones es m. La suma de esta sucesión es d⁰(d^m-1)/(d-1) y, por tanto:

Así, la suma para el primer grupo de observaciones es:

Siguiendo el procedimiento anterior, se obtienen las sumas para el resto de los grupos:

4. Ahora se calculan las primeras diferencias de la suma S₀, S₁, S₂ y S₃ y denotándose estas diferencias con DS₀, DS₁ y DS₂:

La expresión anterior se puede reducir para obtener:

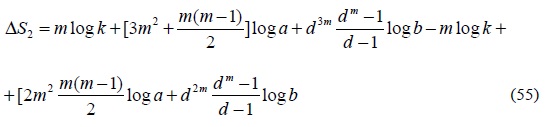
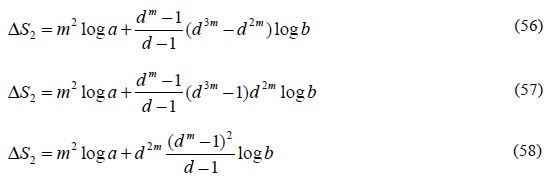
5. Se continúa el proceso calculando las segundas diferencias, las cuales se denotarán como D²S₀ y D²S₁

6. Con los resultados anteriores se encontrarán las expresiones para los parámetros a, b y d. Para encontrar el parámetro d se utiliza la expresión (66) y el resultado encontrado en (62), de la siguiente manera:

Despejando d^m y calculando la raíz m-ésima, se tiene que d puede expresarse como:

Para encontrar el parámetro b se retoma el resultado obtenido en (62). Primero se despeja el logaritmo de b y después se aplica el antilogaritmo y se obtiene b:

El parámetro a se calculará a partir de las expresiones (48) y (62):

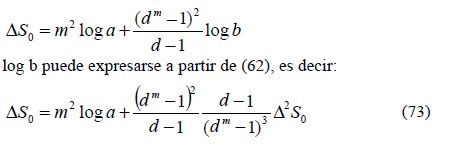
Se despeja el log a y se aplica antilogaritmo:

Por último, el parámetro k se obtendrá a partir de la condición de mínimos cuadrados, es decir:

Para simplificar la expresión, se denota como Vxa a^xb^dx , por tanto, (77) se expresa como:

Desarrollando (y_x - kVx)² se obtiene:

Este resultado permite expresar (78) como:

Para eliminar el cuadrado de k, se sabe que y_x = kVx según la expresión (78), por lo tanto, es posible expresar (84) como:

Dada la expresión (85) es posible estimar K de la siguiente manera:

 

Método de corrección de los valores estimados para los parámetros k, a, b y d

Una vez obtenidos los valores de los parámetros k, a, b y d de la función Makeham, es posible realizar variaciones en ellos con el objetivo de calcular una mejor aproximación de los valores observados.

La función Makeham presentará, con estas variaciones, cambios significativos que se denotarán con dy. Dichos cambios se podrán obtener a través del proceso que a continuación se describe:

Sea

Se obtiene el logaritmo natural de la función (1):

Hay que calcular la derivada de la expresión (2):

Al calcular la derivada se puede considerar que:

Mientras que la derivada del miembro derecho se puede expresar como:

El último término de la expresión (5) se puede presentar según el siguiente razonamiento: de acuerdo con las propiedades de los logaritmos se expresa:

Ln d^x = Ln xLnd

Al obtener la derivada de la expresión anterior se observa que:

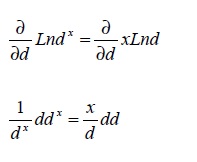
Por lo tanto, la derivada de dx con respecto a d es:

Dado lo anterior, la expresión (5) se puede escribir como:

En consecuencia, la derivada de dy_x es:

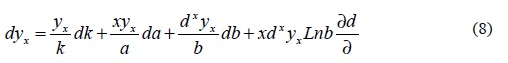
Para calcular los valores de los parámetros a partir de la expresión (8), se procede a linealizar dicha expresión; para ello se denota como:

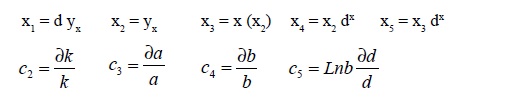
Una vez hecho lo anterior, se sustituye en (8) estas variables, por lo que puede expresarse en forma de regresión múltiple lineal, como se presenta a continuación:

x₁ = c₂ x₂ + c₃ x₃ + c₄ x₄ + c₅ x₅

Se denotan las diferencias entre los valores observados y los valores teóricos como dyx, de tal forma que sea posible calcular los coeficientes de la regresión, c₂ , c₃ , c₄ y c₅ , a través de las siguientes ecuaciones normales:

Para resolver este sistema de ecuaciones lineales simultáneas de cuatro incógnitas puede emplearse el método de matrices, donde para encontrar la solución al sistema es necesario conocer la matriz integrada por los coeficientes de la regresión.

Las ecuaciones normales antes presentadas pueden expresarse en forma matricial de la siguiente manera:

Para encontrar los coeficientes de la matriz V, se realiza la siguiente operación:

V = A^-1 G

De esta manera se calculan los valores de las c_j y, por consiguiente, las primeras correcciones a los parámetros k, a, b y d de la función Makeham. Estas correcciones permiten obtener nuevas aproximaciones para los parámetros. Por tanto, los nuevos valores para éstos son:

k₁ = k(1+c₁) a₁= a(1+c₃) b₁ = b(1+c₄) d₁ = d(1+c₅ / Lnb)

A partir de estos valores se obtienen nuevos valores teóricos y, por lo tanto, nuevas diferencias dyx. Lo anterior implica el empleo de un proceso iterativo que permitirá ir obteniendo aproximaciones cada vez más satisfactorias. Es decir, el proceso deberá repetirse hasta que la magnitud de las correcciones alcancen un valor reducido tal que no logren cambiar sensiblemente los valores teóricos obtenidos usando los valores de los parámetros hasta esa iteración.

En general, se observa que si ki, ai, bi y di son valores de la iteración (i), los valores de esos parámetros a la iteración (i+1) serán:

La aplicación que aquí se presenta de la función de Gompertz-Makeham es sobre la tendencia histórica de la esperanza de vida al nacimiento para hombres y mujeres México de 1995 al año 2010. Con dichas esperanzas se obtuvieron las tablas abreviadas de mortalidad por sexo para cada uno de los años de referencia.

Los valores de los parámetros de las funciones de ajuste Gompertz-Makeham obtenidas son los siguientes:

Con las funciones Gompertz-Makeham se obtuvieron los márgenes de la esperanza de vida para los hombres y para las mujeres, los que sirvieron para obtener las tablas abreviadas de mortalidad que se presentan en el anexo.

 

Bibliografía

APOSTOL, Tom, 1987, Calculus, Cálculo en varias variables con aplicaciones a las probabilidades y al análisis vectorial, vol. 2, Reverté, México.         [ Links ]

CORONA, V. Rodolfo, y Alberto Minunjin Z., 1982, Técnicas de evaluación y ajuste de información estadística, FCE, México.         [ Links ]

INSTITUTO NACIONAL de ESTADÍSTICA, GEOGRAFÍA e INFORMÁTICA, 1992, XI Censo Nacional de Población y Vivienda, México.         [ Links ]

INSTITUTO NACIONAL de ESTADÍSTICA, GEOGRAFÍA e INFORMÁTICA, 1996, Conteo 95, Resultados, México.         [ Links ]

CURTIS, F. Gerard, 1997, Análisis numérico, Alfa Omega, México.         [ Links ]

MINA Valdés, Alejandro, 1982, Uso y abuso de los modelos de ajuste en la demografía, El Colegio de México, México.         [ Links ]

MINA Valdés, Alejandro, 1982, "Consideraciones sobre modelos de ajuste empleados en la demografía matemática", en Demografía y Economía, El Colegio de México, vol. XVI, núm. 2(50).         [ Links ]

MINA Valdés, Alejandro, 1990, "Las funciones de Gompertz y Makeham en el análisis actuarial y demográfico en México", en La Actuaría en México. Antología de algunos trabajos relevantes, Colegio Nacional de Actuarios, México.         [ Links ]

MINA Valdés, Alejandro, 1996, Dinámica de la población mexicana del 12 de marzo de 1990 al 5 de noviembre de 1995, El Colegio de México, Centro de Estudios Demográficos y de Desarrollo Urbano.         [ Links ]

MINA Valdés, Alejandro, s/f, "Simulación de los cambios demográficos de una población entre dos fechas", en Estudios Demográficos y Urbanos, núm. 42, El Colegio de México, México.         [ Links ]

 

Información sobre el autor

Alejandro Mina Valdés. Actuario y Matemático por la Universidad Nacional Autónoma de México, y Maestro en Demografía por El Colegio de México. Actualmente es profesor-investigador de tiempo completo del Centro de Estudios Demográficos y de Desarrollo Urbano de El Colegio de México; pertenece al Sistema Nacional de Investigadores desde 1986; ha sido director de 115 tesis de licenciatura y 14 de maestría, y es autor de 63 artículos y tres libros sobre temas de análisis demográfico. Correo electrónico: amina@colmex.mx.