Introducción
Una de las funciones principales de la escuela es proporcionar contextos significativos de resolución de problemas, en los que las y los estudiantes1 empleen estrategias matemáticas, que los preparen para afrontar situaciones problemáticas de la vida diaria. No obstante, como se detalla en informes estandarizados internacionales, como el reciente estudio PISA (OECD, 2019), los estudiantes poseen dificultades para resolver problemas cuyas situaciones planteadas hacen referencia al mundo que les rodea (Vicente, Van Dooren y Verschaffel, 2008).
El aprendizaje de las matemáticas es necesario para dotar de sentido a las situaciones que nos rodean, por lo que debe conectarse la verosimilitud de los problemas presentados con las experiencias vividas por el estudiante (Greer, Verschaffel, Van Dooren y Mukhopadhyay, 2009). Consecuentemente, los problemas de la escuela deben caracterizarse por tratarse de situaciones auténticas, no aquellas que reproduzcan un procedimiento algorítmico, así como describir situaciones con sentido para el alumnado, es decir, próximas a su vida cotidiana (Jiménez y Ramos, 2011).
Los problemas en los que el conocimiento sobre el mundo que nos rodea desempeña un papel relevante se denominan realistas (Verschaffel, Van Dooren, Chen y Stessens, 2009). En esta tipología, para obtener una solución matemática correcta, el individuo debe considerar las características reales del contexto descrito en el enunciado del problema (Verschaffel et al., 2009). Un ejemplo de problema realista es el siguiente: “El mejor tiempo de John al correr 100 m es 17 segundos. ¿Cuánto tiempo tardará en recorrer 1 km?” (Verschaffel, De Corte y Lasure, 1994:276). Para darle solución se debe considerar que, en la vida real, una persona no puede mantener la velocidad mencionada en el enunciado a lo largo de un recorrido de 1 km. Así, cualquier individuo que use el sentido común de la realidad, no daría como respuesta “170 segundos”. Sin embargo, esta respuesta es la que se obtuvo en el 90% de los estudiantes de la investigación realizada por Verschaffel, De Corte y Lasure (1994). Este elevado porcentaje de respuestas no realistas muestra las dificultades del alumnado cuando debe resolver estos problemas.
Entre los primeros estudios en esta línea de investigación cabe destacar el de Greer (1993) y el de Verschaffel, De Corte y Lasure (1994), ambos con una metodología similar. En el estudio de Greer participaron 100 estudiantes de 13 a 14 años de edad y, en el de Verschaffel, De Corte y Lasure, 75 alumnos, de 10 a 11 años. En ambos trabajos los participantes respondieron una prueba escrita con pares de ítems. En cada par, el primer ítem presentaba una situación estándar, que podía resolverse mediante operaciones aritméticas, y el segundo era un problema realista que debía ser interpretado por el resolutor para obtener la solución correcta. Sin embargo, mientras que en el estudio de Greer todos los problemas eran de tipo multiplicativo, en el de Verschaffel, De Corte y Lasure se incluyeron también problemas de tipo aditivo. A pesar de estas diferencias, los resultados obtenidos fueron similares, pues los estudiantes resolvieron los ítems sin tener en cuenta las características del contexto de la situación.
Tras el estudio de Verschaffel, De Corte y Lasure (1994) se originó una línea de investigación internacional centrada en analizar el éxito que presentan los estudiantes en la resolución de problemas realistas (Reusser y Stebler, 1997; Xin, Lin, Zhang y Yan, 2007), y en cómo incrementar el número de respuestas que tuvieran en cuenta el contexto de la situación (respuesta realista): modificando parte de la metodología usada originalmente (Dewolf, Van Dooren, Ev Cimen y Verschaffel, 2014; Xin et al., 2007; Yoshida, Verschaffel y De Corte, 1997), modificando la presentación de los problemas o el proceso de resolución (Fitzpatrick, Hallett, Morrissey, Yıldız et al., 2019; Van Dooren, Lem, De Wortelaer y Verschaffel, 2019) o aumentando la autenticidad de las condiciones experimentales (DeFranco y Curcio, 1997; Mellone, Verschaffel y Van Dooren, 2017).
El principal foco de los estudios previos ha sido examinar el éxito de los estudiantes en problemas realistas de tipo aditivo y multiplicativo. En este estudio, nos centraremos en problemas de estructura multiplicativa y, en particular, en los de división-medida y de división-partitiva con resto. Además, no solo se analizará el éxito de los estudiantes, sino las estrategias que emplearon y su evolución desde tercero a sexto grado de educación primaria.
Marco teórico
El marco teórico se organiza en tres apartados. En primer lugar, se presenta una categorización de los problemas de estructura multiplicativa. En segundo lugar, se expone una revisión de resultados de investigaciones previas sobre el uso de estrategias en la resolución de problemas de división-medida y división-partitiva. Por último, se presentan investigaciones en las que se ha estudiado el nivel de éxito de estudiantes en problemas de división con resto.
Tipos de problemas de estructura multiplicativa
El campo de las estructuras multiplicativas y la investigación implementada sobre la adquisición de conceptos y relaciones de tipo multiplicativo se ha realizado desde diversos enfoques (Greer, 1992). En nuestro estudio nos centraremos en el aportado por Vergnaud (1983). Vergnaud clasifica la adquisición del conocimiento en campos conceptuales, los cuales concibe como el conjunto de problemas, situaciones, conceptos, relaciones, estructuras, contenidos y operaciones del pensamiento que están interconectados a lo largo del proceso de adquisición. Uno de los campos conceptuales de su interés fue el de las estructuras multiplicativas, entendido como el conjunto de situaciones que pueden analizarse como problemas de proporcionalidad simple y múltiple que comportan como operaciones aritméticas una multiplicación, una división o la combinación de ambas. En dicho campo conceptual, Vergnaud distingue tres tipos de problemas: isomorfismo de medidas, un solo espacio de medidas y producto de medidas.
Este estudio lo focalizaremos en los problemas de isomorfismo de medidas, que son aquellos que describen situaciones de proporción directa entre dos espacios de medida (M1 y M2), cada uno con dos cantidades. Esta relación entre espacios de medida puede observarse en la Figura 1.

Fuente: elaboración propia basada en información de Vergnaud (1983).
Figura 1 Tabla de correspondencia entre espacios de medida en problemas de isomorfismo de medidas
Una de las cuatro cantidades (x en la Figura 1) suele reducirse a una unidad. Consecuentemente, en función de cuál de las otras cantidades sea la incógnita, se obtienen tres clases de problemas (Vergnaud, 1983): multiplicación, división (búsqueda de la cantidad de unidades) y división (búsqueda del valor unitario). En el presente estudio se analizarán los dos últimos subtipos, a los que Greer (1992) denominó como división-medida y división-partitiva, respectivamente.
En primer lugar, los problemas de división-medida se caracterizan por conocer, de la Figura 1, f (x) y f (x’) y ser x’ la incógnita del problema. Por ejemplo, Tengo 24 yogures. Hay 6 yogures en cada paquete. ¿Cuántos paquetes de yogures tengo? (Figura 2).
Los problemas de división-partitiva responden al esquema de la Figura 1, dándose el caso concreto en que x’ y f (x’) son datos conocidos y f (x) es la incógnita del problema. Un ejemplo sería: Tengo 24 yogures en 4 paquetes, con el mismo número de yogures en cada paquete. ¿Cuántos yogures hay en cada paquete? (Figura 3).
Estrategias utilizadas por los estudiantes en la resolución de problemas de división-medida y división-partitiva
En las últimas décadas se han realizado investigaciones centradas en estudiar las estrategias empleadas por estudiantes de educación primaria al resolver problemas de estructura multiplicativa (Ivars y Fernández, 2016; Kouba, 1989; Mulligan, 1992) y, en particular, en problemas de división-medida o división-partitiva (Downton, 2009; Hulbert, Petit, Ebby, Cunningham et al., 2017).
En la resolución de problemas de estructura multiplicativa, Mulligan (1992) analizó la evolución de las estrategias utilizadas por estudiantes de 7 a 8 años mediante cuatro entrevistas realizadas en un periodo de dos años. En este estudio longitudinal, las estrategias obtenidas se clasificaron en tres grupos: modelización con conteo; estrategias de conteo, aditivas y sustractivas; y aplicación de hechos numéricos conocidos y derivados de la adición y multiplicación. Estrategias similares fueron obtenidas por Ivars y Fernández (2016) con alumnos de primero a sexto grado (6-12 años). Mulligan (1992) observó, en las entrevistas iniciales, una tendencia a modelizar con conteo en los problemas de división-medida y división-partitiva, además de emplear estrategias de conteo y aditivas en los de división-partitiva. Sin embargo, en la cuarta entrevista se observó una fuerte manifestación de los hechos numéricos, tanto derivados de la adición como de la multiplicación. En Ivars y Fernández (2016) se observó que en los primeros grados prevalecía el uso de estrategias de modelización y de conteo. Sin embargo, a medida que los grados avanzaban, el empleo de estas estrategias fue remplazado mayoritariamente por el uso de un algoritmo. De hecho, Kouba (1989) ya mostró, con estudiantes de 6 a 9 años, que la estrategia de modelización decrece mientras que estrategias de adición/sustracción repetida y de hechos numéricos aumentan a partir de los 7 a 8 años.
Centrándonos únicamente en los problemas de división-medida y división-partitiva, Downton (2009) mostró que el alumnado de 8 a 9 años empleó, como estrategia más frecuente para resolver estos problemas, hechos numéricos conocidos y derivados. No obstante, un número similar de estudiantes utilizó la modelización en ambos tipos de problemas y también se usaron estrategias de conteo, aunque su empleo fue mayor en los de división-medida. La adición/sustracción repetida solo se usó en problemas de división-partitiva. Carretero (1989) también observó con estudiantes de 8-11 años un uso amplio de los hechos numéricos. No obstante, fue el uso del algoritmo de la división el procedimiento de resolución que destacó sobre el resto.
Los resultados de estas investigaciones muestran que, al inicio de la etapa de educación primaria (6-8 años), los estudiantes son capaces de utilizar una gran variedad de estrategias para resolver los problemas de isomorfismo de medidas, principalmente, estrategias de modelización y conteo. Sin embargo, conforme avanzan los grados predomina el uso de hechos numéricos o algoritmo. Estos estudios únicamente han considerado situaciones en las que las divisiones, bien con el significado de partición o de medida, eran exactas, lo que conlleva la no necesidad de interpretar la solución en el contexto del problema.
Problemas de división con resto
En los problemas de división con un resto diferente a cero la solución no requiere tan solo una ejecución correcta de la división, sino que esta debe interpretarse y evaluarse de acuerdo con la situación problemática presentada en el enunciado del problema (Chen, Van Dooren, Chen y Verschaffel, 2011; Yoshida, Verschaffel y De Corte, 1997). Podemos encontrar tres tipos de situaciones diferentes en las que la consideración del resto desempeña un papel importante (Verschaffel et al., 2009):
Situaciones en las que la presencia del resto obliga a reconocer como solución el valor del cociente más una unidad más (tipo 1): 100 niños son transportados en minibuses a un campamento de verano en la playa. Cada minibús puede transportar un máximo de 8 niños. ¿Cuántos minibuses se necesitan?
Situaciones en las que el resto no es considerado, siendo la solución el cociente no decimal (tipo 2): Un abuelo regala a sus 6 nietos una caja con 80 globos. Si los comparten por igual, ¿cuántos globos obtiene cada nieto?
Situaciones en las que el resultado es el cociente más la parte fraccionaria del resto (tipo 3): Un sastre vendió una gran pieza de tela con una longitud de 50 metros. Quiere cortarla en 4 piezas de la misma longitud. ¿Cuánto medirá cada pieza?
En la tercera Evaluación Nacional del Progreso Educativo de los Estados Unidos (NAEP, por sus siglas en inglés; Carpenter, Lindquist, Matthews y Silver, 1983) se presentó por primera vez un problema realista de división con resto de tipo 1. Los participantes, estudiantes de 13 años, debían averiguar cuántos autobuses de 36 plazas se necesitaban para transportar a un total de 1 128 soldados. Aunque aproximadamente el 70% de los participantes realizó correctamente la división 1 128: 36 = 31.
Verschaffel, De Corte y Lasure (1994) presentaron dos problemas de división con resto a estudiantes de 10-11 años: uno de reparto de personas en autobuses (tipo 1), que obtuvo 49.3% de respuestas realistas, y otro de reparto de globos entre personas (tipo 2), con 58.7% de respuestas realistas. Reusser y Stebler (1997), usando los mismos problemas que Verschaffel, De Corte y Lasure (1994), pero con estudiantes de 10 a 12 años obtuvieron, en el problema de tipo 1, 49.3% de respuestas realistas y, en el de tipo 2, 74.6% y; con estudiantes de 13 años, en el de tipo 1, 77.6% y en el de tipo 2, 74.4%. Con estos mismos problemas, pero con estudiantes de 9 a 13 años, Xin et al. (2007) obtuvieron 67.7% de respuestas realistas en el problema de los autobuses y 68% en el de los globos.
Verschaffel et al. (2009) analizaron las respuestas de estudiantes de 9 a 12 años en la resolución de tres problemas, cada uno perteneciente a uno de los tipos mencionados previamente. El porcentaje medio de respuestas realistas obtenidas fue de 57%: 29% en estudiantes de 9 a 10 años, 62%, en los de 10 a 11, y 83% en los de 11 a 12. Asimismo, considerando el porcentaje medio de respuestas realistas en cada tipo de problema, en este estudio los participantes resolvieron más exitosamente el de tipo 2 (cociente no decimal); después el de tipo 3 (cociente más parte fraccionaria) y, por último, el de tipo 1 (cociente más uno).
Lago, Rodríguez, Enesco, Jiménez et al. (2008), aunque con estudiantes de 12 a 13 años, también analizaron el orden de dificultad de los diferentes tipos de problemas de división con resto. Los estudiantes resolvieron más exitosamente aquellos que requerían como solución el cociente no decimal o el cociente más la parte fraccionaria (tipos 2 y 3, respectivamente) que los problemas que requerían como solución el cociente más una unidad (tipo 1). Los autores atribuyeron estos resultados a que los estudiantes identificaban los de tipo 2 y 3 como problemas estándar de división en los que la respuesta numérica correcta era el cociente.
Además, Lago et al. (2008) también analizaron si el modelo de división subyacente en los distintos problemas de división con resto influía en el nivel de éxito alcanzado en estos. Para su análisis, la mitad de los participantes resolvieron problemas de división-partitiva con resto (uno de cada tipo) y la otra mitad, de división-medida con resto (uno de cada tipo). Aunque generalmente los participantes no mostraron dificultades para identificar el algoritmo de la división como procedimiento de resolución, el rendimiento en los problemas de división-medida descendió debido a un análisis superficial del enunciado que los habría llevado a buscar semejanzas con el modelo de división adquirido, que parecía ser el partitivo. De esta forma, obviaron información esencial del enunciado en los problemas de división-medida, por lo que se incrementaron las respuestas numéricas incorrectas al no utilizar los decimales en los problemas de tipo 3 y sí indebidamente en los problemas de tipo 1 y 2.
Aunque investigaciones previas han mostrado el nivel de éxito para algunas tipologías de problemas realistas, son menos los estudios centrados en analizar las estrategias usadas. Li y Silver (2000) mostraron que estudiantes de 8 a 9 años, para resolver un problema de división con resto del tipo 1 (cociente más una unidad), empleaban correctamente la adición/sustracción repetida y era menos frecuente el uso de hechos numéricos conocidos.
El objetivo de esta investigación es analizar el nivel de éxito y las estrategias usadas en la resolución de problemas realistas de división-medida y división-partitiva con resto, por alumnado de educación primaria de 8 a 12 años. El objetivo general mencionado lo concretamos en las siguientes preguntas de investigación:
¿Cómo evoluciona el nivel de éxito en la resolución de problemas realistas de división con resto a lo largo de la etapa de educación primaria?
¿Qué estrategias usan los estudiantes de educación primaria al resolver problemas realistas de división con resto?
¿Cómo evoluciona el uso de estrategias al resolver problemas realistas de división con resto a lo largo de educación primaria?
Método
Participantes y contexto
En este estudio participaron 177 estudiantes españoles de educación primaria, con una edad comprendida entre los 8 y 12 años. La elección de participantes con este perfil de edad está determinada por ser el periodo en que se introduce y trabaja la división en el sistema educativo en España. La Tabla 1 muestra la distribución de los participantes por grado.
Instrumento
Los participantes respondieron a un cuestionario con seis problemas de estructura multiplicativa adaptados de Verschaffel et al. (2009); dos de ellos de división-medida y cuatro de división-partitiva en los que el resto es diferente a cero. El cuestionario contenía dos problemas para cada tipo de situación que puede generarse al considerar el resto de los problemas (Tabla 2).
Tabla 2 Problemas del cuestionario y características
| Problemas | Características |
|---|---|
| Problema 1 (P1). 9 aficionados quieren desplazarse al estadio de otra ciudad. Cada taxi puede llevar a 4 aficionados. ¿Cuántos taxis necesitan? | División-medida. El resto obliga a reconocer como resultado el valor del cociente más una unidad más (tipo 1) |
| Problema 2 (P2). En una feria artesanal se han sorteado 7 kilos de turrón. El sorteo lo han ganado 3 amigos y han decidido repartir el premio por igual. ¿Cuántos kilos de turrón ha ganado cada amigo? | División-partitiva. La solución es el resultado del cociente y la parte fraccionaria del resto (tipo 3) |
| Problema 3 (P3). Una academia de baile ha repartido en una clase 8 entradas para un musical. Los bailarines de la clase eran 3 y todos han recibido el mismo número de entradas. ¿Cuántas entradas ha recibido cada bailarín? | División-partitiva. El resto no se considera. La solución es el cociente no decimal (tipo 2) |
| Problema 4 (P4). Una diseñadora ha comprado 35 metros de tela. Quiere cortarla en 6 piezas de la misma longitud. ¿Cuánto medirá cada pieza? | División-partitiva. La solución es el resultado del cociente y la parte fraccionaria del resto (tipo 3) |
| Problema 5 (P5). Una librería ha donado 95 libros a 4 colegios. Los colegios han recibido el mismo número de libros. ¿Cuántos libros ha recibido cada colegio? | División-partitiva. El resto no se considera. La solución es el cociente no decimal (tipo 2) |
| Problema 6 (P6). 80 alumnos se alojarán en un albergue durante el viaje de fin de curso. En cada habitación se pueden alojar un máximo de 6 alumnos. ¿Cuántas habitaciones necesitan? | División-medida. El resto obliga a reconocer como resultado el valor del cociente más una unidad más (tipo 1) |
Fuente: elaboración propia adaptada de Verschaffel et al. (2009).
Los participantes dispusieron de 50 minutos para resolver el cuestionario individualmente. La única indicación que se les ofreció es que debían justificar sus respuestas y que no podían utilizar calculadora ni dispositivos electrónicos.
Análisis
El análisis se llevó a cabo en dos fases. En la primera, se analizó si la respuesta dada por los estudiantes era realista o no realista, por problema y grado. De esta manera, las respuestas fueron clasificadas en: reacción realista, reacción no realista y otras reacciones.
La reacción realista (RR) son respuestas en las que el resolutor, además de emplear un procedimiento de cálculo correcto, aporta una respuesta realista al atender a la situación descrita en el enunciado del problema para interpretar el resto. En particular, en los problemas de tipo 1, el resolutor interpreta el resto añadiendo una unidad al cociente. En los de tipo 2, identifica como respuesta el cociente no decimal y en los problemas de tipo 3, añade al cociente la parte fraccionaria. Por ejemplo, el estudiante de la Figura 4 ofrece una respuesta realista atendiendo a la situación del problema 6; él se da cuenta de que no pueden quedar 2 alumnos “sin habitación”, añadiendo una unidad al cociente. Se incluyen más ejemplos de este tipo de respuesta en la sección de resultados.

Fuente: respuesta de estudiante (6º grado).
Figura 4 Ejemplo de reacción realista en el P6 (6º grado)
La reacción no realista (RNR) involucra aquellas respuestas en las que, a pesar de haber empleado un procedimiento de cálculo correcto, el alumno no realiza una interpretación realista del resto acorde con la situación descrita en el enunciado. Por ejemplo, en la Figura 5 se observa que el estudiante ofrece como respuesta el cociente en un contexto de reparto de personas en el que la existencia del resto obliga a reconocer como resultado el cociente más una unidad más (problema 6).

Fuente: respuesta de estudiante (5º grado).
Figura 5 Ejemplo de reacción no realista en el P6 (5º grado)
Otras reacciones (OR) son las respuestas en blanco y aquellas en las que el estudiante hacía uso de procedimientos incorrectos. Por ejemplo, en la Figura 6, el alumno usa el algoritmo de la multiplicación en un contexto de reparto de libros (problema 5).
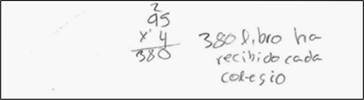
Fuente: respuesta de estudiante (5º grado).
Figura 6 Ejemplo de otras reacciones en el P5 (5º grado)
En la segunda fase el análisis se centró en las estrategias usadas por los estudiantes. Inicialmente, tres investigadores analizaron individualmente una muestra de los diferentes problemas para generar descriptores de las estrategias utilizadas en cada tipo de problema. Posteriormente, y de forma conjunta, se discutieron las similitudes y diferencias de los descriptores identificados por cada uno de los investigadores en cada problema, y se fueron refinando según se iban analizando nuevas respuestas (triangulación). Este proceso se repitió para cada uno de los problemas hasta llegar a un consenso y considerar las estrategias de todos los problemas en conjunto para identificar evidencias de solapamiento entre ellas. De este proceso de triangulación, emergieron seis categorías, que son presentadas en la sección de resultados.
Resultados
Los resultados obtenidos, que serán discutidos posteriormente en la sección final, se presentan en tres apartados. En el primero mostraremos el porcentaje de cada tipo de reacción por tipo de problema y grado; en el segundo, las estrategias empleadas por el alumnado en las RR y en las RNR y, por último, la evolución de dichas estrategias a lo largo de la educación primaria (3º a 6º grado).
Tipo de reacción por tipo de problema y grado
Los resultados obtenidos globalmente (Tabla 3) muestran que el porcentaje medio de reacciones realistas fue de 46.2%. Asimismo, los participantes resolvieron más exitosamente los problemas cuyo resultado es el cociente no decimal (68.8%); después aquellos en los que había que añadir una unidad al cociente (42.3%) y, por último, los problemas cuyo resultado es el cociente más una parte fraccionaria (27.5%).
Tabla 3 Porcentajes de RR por grado y tipo de problema
| Cociente más 1 (Tipo 1) |
Cociente no decimal (Tipo 2) |
Cociente más parte fraccionaria (Tipo 3) |
Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RR | RNR | OR | RR | RNR | OR | RR | RNR | OR | RR | RNR | OR | |
| 3º | 37.5 | 43.7 | 18.8 | 64.6 | 10.4 | 25.0 | 0.0 | 77.1 | 22.9 | 34.0 | 43.7 | 22.3 |
| 4º | 22.1 | 53.5 | 24.4 | 81.4 | 1.1 | 17.5 | 1.2 | 77.9 | 20.9 | 34.9 | 44.2 | 20.9 |
| 5º | 53.4 | 35.3 | 11.3 | 62.5 | 20.5 | 17.0 | 37.5 | 50.0 | 12.5 | 51.1 | 35.3 | 13.6 |
| 6º | 56.0 | 36.9 | 7.1 | 66.7 | 22.6 | 10.7 | 71.4 | 23.8 | 4.8 | 64.7 | 27.8 | 7.5 |
| Total | 42.3 | 42.3 | 15.4 | 68.8 | 13.6 | 17.6 | 27.5 | 57.2 | 15.3 | 46.2 | 37.7 | 16.1 |
Fuente: elaboración propia.
En cuanto a la evolución, se observa en global, un incremento de las reacciones realistas desde 34.0% en el tercer grado a 64.7% en el sexto. Esta tendencia se repite en cada uno de los tres tipos de problema por separado. Sin embargo, esta progresión se ve limitada en dos momentos. Por un lado, se observa un descenso de 37.5 a 22.1% de las RR de tercero a cuarto grado en los problemas de tipo 1 (cociente más 1). Este descenso coincide con el aumento de OR, generado por el uso erróneo de estrategias por parte del alumnado, y de RNR en las que el uso del procedimiento correcto no se acompaña de una interpretación realista de la situación. Por otro lado, en los problemas de tipo 2 (cociente no decimal), entre cuarto y quinto grado, las RR disminuyen de 81.4 a 62.5%. Esta disminución coincide con el aumento de RNR en quinto grado en las que el alumnado resuelve los problemas dando como solución el cociente decimal sin considerar el contexto de reparto.
Tipos de estrategias utilizadas
Se obtuvieron seis categorías de estrategias. Estas estrategias o procedimientos de cálculo fueron utilizados tanto en las reacciones realistas como en las no realistas. A continuación, se muestran ejemplos de estas estrategias en reacciones realistas.
Uso de algoritmo. Respuestas en las que se resuelve el problema mediante el algoritmo de la división. Por ejemplo, la respuesta de la Figura 7 muestra cómo el estudiante utiliza el algoritmo de la división hasta las centésimas para repartir las ocho entradas entre los tres bailarines. Además, considera el contexto del problema (repartir entradas), ofreciendo como respuesta la parte entera (dos entradas a cada uno).

Fuente: respuesta de estudiante (6º grado).
Figura 7 Reacción realista. Uso de algoritmo en el P3 (6º grado)
Estrategia gráfica. Respuestas que ofrecen una solución gráfica. Por ejemplo, el estudiante de la Figura 8, dibuja las ocho entradas y las va repartiendo entre los tres bailarines. Da como resultado (gráficamente) dos entradas para cada bailarín y como resto, las dos que sobran, considerando de este modo el contexto de la situación.

Fuente: respuesta de estudiante (3er grado).
Figura 8 Reacción realista. Estrategia gráfica en el P3 (3er grado)
Uso de algoritmo y estrategia gráfica. Combinación de las dos estrategias anteriores, es decir, respuestas que incluyen el algoritmo de la división y una solución gráfica (Figura 9).

Fuente: respuesta de estudiante (4º grado).
Figura 9 Reacción realista. Uso de algoritmo y estrategia gráfica en el P1 (4º grado)
Uso de sumas-restas sucesivas. Uso iterativo de sumas o restas. En la Figura 10, el estudiante usa sumas sucesivas (sumando grupos de 4) para identificar que con dos taxis pueden viajar ocho personas (4 + 4 = 8, 2 taxis). Después añade 1 taxi más al considerar el contexto del problema en el que tienen que viajar las 9 personas. El estudiante de la Figura 11 usa restas sucesivas (restando grupos de 4) para identificar el número de taxis necesarios (9 - 4 = 5, 1 taxi y 5 - 4 =1, 1 taxi). Además, considera el contexto del problema añadiendo un taxi más para la persona que queda sin formar un grupo de 4.

Fuente: respuesta de estudiante (5º grado).
Figura 10 Reacción realista. Uso de sumas sucesivas en el P1 (5º grado)

Fuente: respuesta de estudiante (3er grado).
Figura 11 Reacción realista. Uso de restas sucesivas en el P1 (3er grado)
Regla de tres. Respuestas que relacionan los datos de forma multiplicativa igualando los productos cruzados. La Figura 12 muestra cómo el estudiante usa una regla de tres (multiplicando en cruz) para calcular el resultado (2.25). Además, tiene en cuenta el contexto de la situación y da como resultado una unidad más de la parte entera obtenida.

Fuente: respuesta de estudiante (6º grado).
Figura 12 Reacción realista. Utilización de la regla de tres en el P1 (6º grado)
Hechos numéricos. Uso del conocimiento de las tablas de multiplicar. La Figura 13 muestra que el estudiante usa los hechos numéricos conocidos (tablas de multiplicar) para identificar que en 3 taxis pueden viajar 12 personas, por lo tanto, al ser 9 los pasajeros, concluye que pueden viajar en tres taxis.
Evolución de las estrategias empleadas a lo largo de educación primaria
La Figura 14 muestra el porcentaje de uso de las estrategias en las reacciones realistas en cada tipo de problema por grado y la Figura 15, el porcentaje de uso de las estrategias en las reacciones no realistas. El alumnado usó más variedad de estrategias en los problemas de tipo 1 (cociente más uno), que en los de tipo 2 (cociente no decimal) y 3 (cociente más parte fraccionaria). En estos dos últimos, el algoritmo fue casi la única estrategia empleada por el alumnado. No obstante, el uso de algoritmo fue la más utilizada en todos los tipos de problemas y en todos los grados.
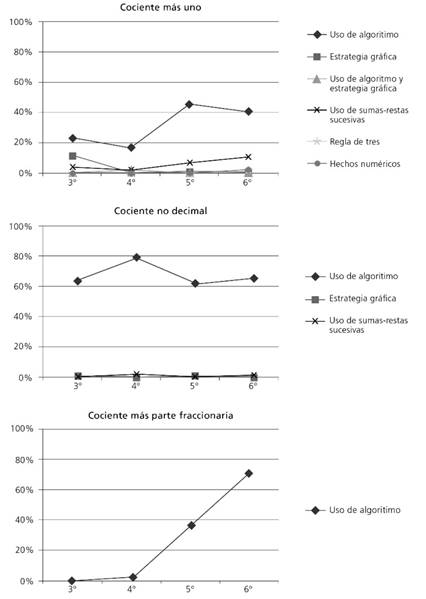
Fuente: elaboración propia.
Figura 14 Porcentajes de uso de las estrategias en las RR en cada tipo de problema por grado
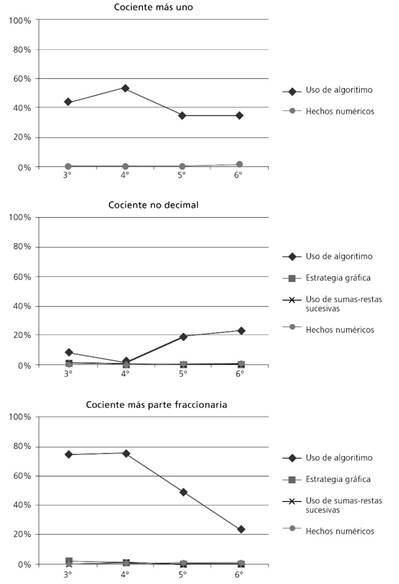
Fuente: elaboración propia.
Figura 15 Porcentajes de uso de las estrategias en las RNR en cada tipo de problema por grado
Con respecto a la evolución del uso de las estrategias en los problemas de tipo 1, se observa que en tercer grado los estudiantes usaron otros procedimientos como estrategia gráfica en las reacciones realistas (Figura 14). A medida que se avanza en la etapa de educación primaria, desaparece esta estrategia y se observa un uso prácticamente único del algoritmo. Además, el descenso en el uso de la estrategia gráfica entre tercero y cuarto grado en las reacciones realistas coincide con un aumento del algoritmo en las reacciones no realistas entre estos grados (Figura 15). Este hecho podría explicar el descenso de las reacciones realistas entre tercer y cuarto grado.
En los problemas de tipo 2, la mayoría de los estudiantes utilizaron el uso de algoritmo en las reacciones tanto realistas como no realistas. Por tanto, el descenso en las RR de cuarto a quinto grado se explica porque un número de estudiantes de quinto, aunque aplicaron el algoritmo (procedimiento correcto), no proporcionaron una respuesta realista, en este caso, el cociente no decimal.
El uso de algoritmo en los problemas de tipo 3 es muy bajo en los primeros grados viéndose incrementado en quinto, cuando se introduce el algoritmo de la división con decimales.
Discusión y conclusiones
Para dar respuesta a las preguntas de investigación, discutiremos dos aspectos. Por un lado, el nivel de éxito en los diferentes tipos de problemas de división con resto y su evolución a lo largo de la etapa de educación primaria. Por otro, las estrategias surgidas en los distintos tipos de problemas y su evolución a lo largo de los grados.
Reacciones realistas a lo largo de la educación primaria (3º a 6º grado)
Los resultados obtenidos muestran un bajo porcentaje de reacciones realistas en problemas de división con resto, obteniendo una media de 64.7% de reacciones realistas en sexto grado. Estos resultados apoyan investigaciones previas que muestran las dificultades de los estudiantes al afrontar la resolución de problemas realistas (e.g. Carpenter et al., 1983; Reusser y Stebler, 1997; Verschaffel, De Corte y Lasure, 1994; Xin et al., 2007). Nuestro análisis muestra que los estudiantes siguen teniendo dificultades al resolver problemas de división-medida y división-partitiva en los que es necesario tener en cuenta el contexto de la situación. Por tanto, estos resultados revelan la necesidad de iniciar una formación específica en la educación primaria en la resolución de problemas realistas. Aunque la resolución de problemas es un contenido incluido en el currículo, no se potencia la resolución de problemas realistas, aun siendo uno de los contenidos importantes y evaluados, por ejemplo, en los estudios PISA (OECD, 2019).
Además, los resultados muestran que los estudiantes no poseen las mismas dificultades según el tipo de problema de división con resto. Resolvieron más fácilmente los problemas de tipo 2 (cociente no decimal), después los de tipo 1 (cociente más uno) y, por último, los de tipo 3 (cociente más parte fraccionaria). Estos hallazgos apoyan los obtenidos por Lago et al. (2008), Verschaffel, De Corte y Lasure (1994), Verschaffel et al. (2009) y Xin et al. (2007), quienes afirmaron que los problemas de tipo 1 presentaron una mayor dificultad que los de tipo 2. Sin embargo, nuestros resultados parecen discrepar de los obtenidos por Lago et al. (2008) y Verschaffel et al. (2009) con relación a que los problemas de tipo 3 se resuelven con mayor facilidad que los de tipo 1. Únicamente, los estudiantes de sexto grado (11-12 años) de nuestro estudio resolvieron con más éxito los problemas de tipo 3. Esta discrepancia en los resultados podríamos interpretarla desde dos puntos de vista. Por un lado, mientras que los problemas de tipo 1 requieren de una interpretación del resultado obtenido según el contexto de la situación para ofrecer una respuesta correcta, los de tipo 3 podrían afrontarse como problemas estándar en los que la respuesta es el cociente obtenido en la división (Lago et al., 2008). Por otro lado, los problemas de tipo 1 de este estudio son los únicos de división-medida. De acuerdo con Lago et al. (2008), el modelo de división subyacente podría suponer mayor dificultad en los problemas de división-medida (tipo 1) que en los de división-partitiva (tipo 3).
De los resultados se percibe un incremento global de las reacciones realistas, desde 34.0% en tercer grado (8-9 años) hasta 64.7% en sexto (11-12 años). Asimismo, esta disposición también se observa si se atiende a cada tipología de problema. Por tanto, de estos resultados podría extraerse que las RR tienden a aumentar progresivamente conforme se avanza en la etapa de educación primaria, de acuerdo con Verschaffel et al. (2009), quienes afirman que el nivel de éxito aumenta con la edad.
Estrategias y evolución a lo largo de la educación primaria (3º a 6º grado)
Los resultados han mostrado las estrategias utilizadas por el alumnado al resolver problemas de división con resto. Esto nos ha permitido identificar, coincidiendo con Mulligan (1992) y Ivars y Fernández, el uso de estrategias de modelización con conteo (estrategia gráfica), en las que el participante se apoya en una representación gráfica de la situación/acción para dar con la respuesta correcta; estrategias aditivas y sustractivas (uso de sumas-restas sucesivas); y hechos numéricos conocidos y derivados de la adición y multiplicación (hechos numéricos), donde los participantes emplean su conocimiento sobre las tablas de multiplicar. Además, en nuestro estudio se ha identificado el uso de otras estrategias: regla de tres y uso de algoritmo.
La estrategia más frecuente desde tercero a sexto grado de educación primaria en todos los tipos de problemas fue uso de algoritmo, siendo la única utilizada en los problemas de cociente más parte fraccionaria. Este uso limitado de estrategias podría explicar por qué los estudiantes tuvieron tan poco nivel de éxito en los problemas de cociente más parte fraccionaria en tercero y cuarto grado, ya que el algoritmo de la división con decimales no se introduce hasta quinto grado (10-11 años) en España. Estos resultados parecen sugerir que, si los estudiantes hubieran tenido un repertorio más amplio de estrategias a su disposición, diferentes al uso de un algoritmo, quizás el nivel de éxito en este problema hubiera sido mayor. Por ejemplo, el uso de estrategias gráficas para la representación del problema facilita a los estudiantes la identificación de la estructura que subyace al problema planteado (Santos, 1997).
En los problemas de tipo 1 (cociente más uno) y 2 (cociente no decimal) también se observa el uso de otras estrategias como estrategia gráfica y uso de sumas-restas sucesivas. Estudios previos indicaban un empleo similar de estrategias de modelización (en nuestro estudio estrategia gráfica) tanto en problemas de división-medida como de división-partitiva (Downton, 2009). Sin embargo, nuestros resultados muestran que las estrategias de modelización tuvieron una mayor presencia en los problemas de división-medida (de tipo 1), mientras que en los de división-partitiva (en este caso, los de tipo 2 y 3) su uso fue residual. Otra diferencia respecto del estudio de Downton, es que la estrategia uso de sumas-restas sucesivas también se utilizó en los problemas de división-medida (tipo 1) y no solo en los de división-partitiva. Sin embargo, este resultado concuerda con el obtenido por Carretero (1989).
La evolución en el uso de las distintas estrategias reflejadas en este estudio coincide y extiende los resultados obtenidos por Ivars y Fernández (2016) con problemas de división-medida y división-partitiva con resto, ya que en los primeros grados (8-9 años) prevalece el uso de estrategias de modelización (estrategia gráfica) que se va reemplazando por estrategias más eficientes como las sumas-restas sucesivas (uso de sumas-restas sucesivas) y, finalmente, por el del algoritmo de la división (uso de algoritmo).
Finalmente, cabe destacar dos aspectos importantes de nuestro estudio. En primer lugar, el descenso en las reacciones realistas de tercer a cuarto grado en los problemas de tipo 1 se explica por el descenso del uso de estrategia gráfica y un aumento del uso del algoritmo de la división sin interpretación del resto (uso de algoritmo en RNR) en cuarto grado. Luego, parece que cuando los estudiantes comienzan a usar el algoritmo en cuarto no interpretan la respuesta en el contexto real del problema. En cambio, usar estrategias de modelización como estrategia gráfica en tercero, parece que les lleva a considerar el contexto real (y por tanto a un mayor nivel de éxito). Los estudiantes de cuarto grado comienzan a sustituir el uso de la estrategia gráfica por estrategias, en principio, más eficientes como el uso de algoritmo. Sin embargo, la aplicación del algoritmo no deriva en una RR. Estos resultados podrían estar vinculados a la falta de comprensión conceptual producida por la aplicación sistemática de procedimientos de cálculo (Erlwanger, 2004), como en este caso la división.
En segundo lugar, hay una disminución del número de reacciones realistas en los problemas de tipo 2 de cuarto a quinto grado. En quinto se observa un índice mayor de RNR debido a que el alumnado, aunque usa un procedimiento correcto como es el algoritmo, no tiene en cuenta consideraciones realistas. Una posible causa es que al introducirse en quinto grado el algoritmo de la división con decimales, los estudiantes resuelven los problemas dando como solución el cociente decimal, anteponiendo la aplicación del algoritmo de la división con decimales a una RR al enunciado del problema. Es decir, el alumnado prioriza el cálculo frente al razonamiento en la resolución de problemas (Cerda, Pérez, Aguilar y Aragón, 2018). Esta causa podría ser consecuencia directa de una perspectiva escolar reduccionista, centrada en la resolución de problemas estándar, y del enfoque computacional dado a la resolución de problemas (Cooper y Harries, 2005), o bien, vincularse a las dificultades del alumnado a lo largo de la educación formal para resolver tareas que conllevan el aprendizaje mediante textos (Vega, Bañales y Reyna, 2013).
Implicaciones para la enseñanza y propuestas de futuro
Nuestros resultados tienen implicaciones para la enseñanza de la resolución de problemas en las aulas de educación primaria. Más allá de la ejecución mecánica de un algoritmo de cálculo, método generalizado en la enseñanza tradicional, la resolución de problemas en las aulas debería incluir una serie de procesos necesarios como son la representación para comprender el enunciado del problema, la planificación de la estrategia, la ejecución de la estrategia o la evaluación de la respuesta (Lago et al., 2008). Particularmente, en la resolución de problemas realistas sería conveniente establecer dinámicas de trabajo colaborativo (Mellone, Verschaffel y Van Dooren, 2017), así como la simulación de situaciones de la vida cotidiana (DeFranco y Curcio, 1997) por su capacidad para facilitar un entorno óptimo de aprendizaje significativo.
Para finalizar, somos conscientes de algunas limitaciones de nuestro estudio. En primer lugar, no se ha hecho un estudio longitudinal. La realización de este tipo de estudio nos puede ofrecer información más detallada y posibles causas sobre cambios en el uso de estrategias a lo largo de los grados. Por otro lado, entrevistar a los participantes nos permitiría indagar sobre los motivos que conducen al alumnado a usar un tipo de estrategia u otra en cada tipo de problema. Además, sería conveniente profundizar en las diferencias observadas con respecto a investigaciones previas en cuanto a las dificultades que presentan los estudiantes en los diferentes problemas (Lago et al., 2008; Verschaffel et al., 2009).











 nueva página del texto (beta)
nueva página del texto (beta)






