Investigación

 

El aula de matemáticas: un rico ámbito de estudio para el desarrollo profesional de los profesores en servicio

 

Tenoch Esaú Cedillo Ávalos*

 

* Profesor-investigador del área académica Aprendizaje y enseñanza en matemáticas, ciencias y artes. Universidad Pedagógica Nacional, Carretera al Ajusco núm. 24, col. Héroes de Padierna, Tlalpan, México DF, CP 14200. CE: tcedillo@upn.mx.

 

Artículo recibido: 14 de marzo de 2007
Dictamen: 13 de julio de 2007
Segunda versión: 31 de julio de 2007
Aceptado: 16 de agosto de 2007

 

Resumen

Este artículo reporta una investigación realizada para evaluar los resultados de un programa de desarrollo profesional dirigido a profesores de matemáticas de secundaria en servicio. Para ello se prepararon y videograbaron 20 sesiones de trabajo en el aula con alumnos de segundo grado de secundaria, donde se abordaron temas cruciales del currículo y se les confrontó con una serie articulada de situaciones problemáticas no rutinarias, cuya solución no requería un nivel avanzado de conocimientos, sino matemáticas elementales y creatividad. Después se organizaron 10 sesiones con maestros, también filmadas, y se les pidió resolver los mismos problemas; en la parte final observaron los videos de los alumnos y se discutieron preguntas preparadas para guiar una reflexión sobre su práctica partiendo del trabajo realizado por ellos y los alumnos. El análisis sugiere que hubo cambios relevantes en sus concepciones sobre la enseñanza-aprendizaje de las matemáticas y fortalecieron su conocimiento matemático.

Palabras clave: matemáticas, estrategias de enseñanza-aprendizaje, educación media, México.

 

Abstract

This article reports on an evaluation of the results of a development program for secondary school mathematics teachers. Twenty classroom sessions with students in the second year of secondary school were prepared and videotaped. During the sessions, crucial topics on the curriculum were addressed and the students were given a series of non-routine problem situations to solve. Their solutions required elementary mathematics and creativity, rather than advanced knowledge. Subsequently, ten sessions with teachers were organized and filmed. After solving the same problems as the students, the teachers watched the videos of the student sessions. The teachers then discussed prepared questions to guide their reflections on their practice, based on the problem-solving they and the students had done. The analysis suggests that relevant changes occurred in the teachers' conceptions of teaching and learning mathematics, along with improvement in their knowledge of mathematics.

Key words: mathematics, teaching and learning strategies, secondary education, Mexico.

 

Introducción

Uno de los propósitos centrales de este estudio fue obtener evidencias que muestren en qué medida es posible poner en práctica los preceptos de las teorías actuales sobre la enseñanza y aprendizaje de las matemáticas. El cumplimiento de tal propósito requiere ir más allá de elaborar novedosos materiales y proponer sensatas recomendaciones para la enseñanza y el aprendizaje de las matemáticas escolares; además, consideramos que un factor esencial es poder mostrar, mediante datos obtenidos en situaciones reales del salón de clases, el papel que requiere desempeñar el profesor para que los estudiantes adquieran aprendizajes que les permitan construir redes conceptuales basadas en sólidos conocimientos matemáticos. Mucho se ha dicho acerca de que los alumnos deben construir su propio conocimiento, que no deben recibir conocimientos previamente "digeridos" por los profesores y que éstos deben modificar el papel que desempeñan en el aula.

El problema que nos propusimos enfrentar requiere crear un ambiente de aprendizaje donde se pongan en práctica estrategias didácticas que muestren cómo pueden lograrse esos ambiciosos objetivos. La estrategia que decidimos adoptar fue propiciar que los estudiantes generaran conocimientos de manera similar a como lo hace un matemático para producir un conocimiento nuevo. Brevemente expuesto, asumimos que en el proceso de construcción de un nuevo resultado, un matemático empieza por enfrentar un problema que aún no tiene resuelto, explora las relaciones que se dan en ese problema, analiza casos particulares, formula conjeturas para intentar generalizar lo que observó y, finalmente, se ocupa de la búsqueda de argumentos irrefutables que den sustento a sus conjeturas.

Teniendo como marco de referencia esa estrategia, diseñamos una serie de actividades de aprendizaje basadas en la resolución de problemas no triviales que representaran un fuerte reto para los estudiantes pero que, a la vez, motivara su curiosidad intelectual para hacerlos "sentir" que son capaces de superar las dificultades si ponen en juego todo su empeño apoyados por una adecuada conducción del profesor.

La investigación realizada durante los últimos treinta años sobre el aprendizaje de las matemáticas destaca la necesidad de generar formas de enseñanza, paradigmas para la educación de los profesores, planes de estudio para la educación básica y procedimientos de evaluación nuevos (Kilpatrick, 1992). Los resultados de esas investigaciones han influido en reformulaciones del currículo de las matemáticas escolares que presentan nuevas exigencias para el trabajo docente. Las posturas teóricas basadas en el constructivismo social también han tenido un impacto en los programas educativos. Estas teorías conciben que el conocimiento es un producto del trabajo intelectual de comunidades formadas por individuos creativos; estas ideas se reflejan en cursos y materiales que se proponen hacer que los profesores abandonen su rol como transmisores de conceptos, hechos básicos y habilidades, para convertirse en tutores en el desarrollo del pensamiento matemático de sus estudiantes (Cobb, Word y Yackel, 1990). Los nuevos paradigmas en educación demandan que los profesores cambien significativamente su conocimiento matemático y sus concepciones sobre cómo enseñar y aprender matemáticas. Esas posturas teóricas se sustentan en la premisa de que cada estudiante llega al salón con sus propias ideas y esto exige que el maestro esté preparado para proporcionar nuevas experiencias que induzcan a sus alumnos a recopilar y analizar información que les ayude a confirmar o refutar las conjeturas que generan, con base en sus acercamientos intuitivos al conocimiento formal de las matemáticas.

Lo anterior requiere que los profesores demuestren en su práctica diaria que están convencidos de que sus alumnos no son "recipientes que esperan ser llenados" y que los consideren sujetos intelectualmente creativos, capaces de hacer preguntas no triviales, de resolver problemas y de construir teorías y conocimiento razonable. Satisfacer esos requerimientos demanda que los docentes remuevan, tanto del libro de texto como de ellos mismos, sus roles como autoridades intelectuales en la clase y que depositen esa autoridad en argumentos rigurosos que ellos produzcan con sus alumnos (Thompson, 1992). Hay estudios que se han enfocado en el rol que desempeñan los maestros en el mejoramiento educativo (Linares y Krainer, 2006). En particular, durante los últimos 15 años el currículo de matemáticas para la enseñanza secundaria en México ha introducido reformas que requieren que los profesores desarrollen enfoques didácticos basados en métodos de enseñanza que se centran en el aprendizaje de los estudiantes.

Este artículo reporta un trabajo que realizamos en México con profesores de secundaria en servicio en los últimos cuatro años. Empezaremos con una discusión de nuestra experiencia previa con docentes, ya que esto influyó de manera importante en la elección del método y el diseño de los instrumentos que usamos. En la segunda sección describimos y discutimos los elementos principales del programa de desarrollo profesional en cuyo contexto se llevó a cabo la investigación que aquí se reporta: las preguntas que guían este trabajo, los perfiles de los sujetos que participaron en el proyecto y las actividades de enseñanza-aprendizaje que usamos. La tercera sección aborda los hallazgos que hemos obtenido hasta ahora. Finalmente, presentamos una serie de señalamientos considerando el trabajo que hemos llevado a cabo y los estudios futuros que consideramos necesario realizar.

 

Antecedentes

Nuestro trabajo inicial con profesores fue a través de un programa de desarrollo profesional que se llevó a cabo durante cuatro años en 100 escuelas secundarias mexicanas (Cedillo, 2003). Desde el principio del proyecto nuestros datos confirmaron que uno de los mayores retos que habría que afrontar era lograr que los docentes genuinamente sintieran que había razones importantes para cambiar (Cobb y Mc Clain, 2001; Cedillo y Kieran, 2003). La información recopilada durante las sesiones de capacitación mostró que el factor de más impacto en convencer a los maestros para que participaran activamente en el proyecto fue la oportunidad que tuvieron de observar lo que llamaron "logros matemáticos no esperados de los estudiantes", estos eventos ocurrieron durante las clases conducidas por los instructores del proyecto (Cedillo, 2003).

El estilo de enseñanza adoptado por los instructores consistió en orientar los eventos en el salón de clases siguiendo la forma de razonamiento de los estudiantes. Al adoptar ese principio asumimos que el aprendizaje es un proceso de construcción socialmente compartido por los alumnos y el maestro. Esto requiere que el profesor adopte un rol que describimos mediante ver la actividad en el salón como una partida múltiple de ajedrez, donde él es el jugador experto que enfrenta de manera simultánea a 30 jugadores que pueden comunicarse y discutir entre ellos antes de hacer un movimiento. El experto hace la primera jugada (propone la actividad) y debe estar preparado para recibir hasta 30 diferentes respuestas; en la segunda jugada el experto (maestro) tiene que dar respuestas específicas que impliquen un reto para cada uno de los jugadores, y así sucesivamente. Una diferencia importante entre el juego convencional de ajedrez y la versión que nosotros usamos como metáfora es que, en el nuestro, el profesor debe manejar las cosas de forma que, con el tiempo, los estudiantes legalmente ganen.

Esta metáfora implica ver la enseñanza de las matemáticas como una confrontación activa de los estudiantes con retos matemáticos que los desafían. Para adoptar esa postura es necesario considerar el conocimiento previo de los alumnos y del maestro:

[...] es improductivo ignorar el conocimiento reciente y las ideas frescas de los estudiantes; asimismo, es improductivo ignorar el conocimiento producido por generaciones de matemáticos. Por lo tanto, enseñar matemáticas es una situación que presenta un continuo dilema para los profesores: por un lado, ellos necesitan empezar donde están los alumnos y por el otro, ellos tratan de ayudar a los alumnos a desarrollar una comprensión de conceptos que son parte de un cuerpo de conocimiento matemático construido socio históricamente (Krainer, 2004:87).

La evidencia empírica que recopilamos en estudios previos indica que los profesores casi no le dan valor a los experimentos exitosos de enseñanza que se han realizado en otras partes, en contextos escolares distintos a los que ellos tienen en su trabajo cotidiano. Esto concuerda con lo reportado por Cobb y Mc Clain (2001). Sin embargo, nuestros datos muestran que los docentes confieren un valor importante a la experiencia de tener reuniones con sus pares de otras escuelas. Encontramos que si atestiguan que otro maestro puede lograr que sus alumnos aprendan, entonces es más probable que modifiquen sus prácticas y fortalezcan su conocimiento matemático. Los datos que recabamos indican que el proceso de hacer que los docentes cambien toma bastante tiempo. Las primeras evidencias del cambio fueron observadas después de un año de trabajo continuo y las transformaciones más significativas se presentaron después de tres años (Cedillo, 2003).

 

El estudio actual

La investigación que presentamos se realizó durante la instrumentación del programa Enseñanza de las Matemáticas. La hipótesis en que éste se basó es que un incremento en la calidad de la enseñanza puede tener efectos positivos en el aprendizaje de los estudiantes. También se asumió como premisa que conocer las formas de razonamiento matemático de los alumnos proporcionaría a los profesores bases más sólidas para su instrucción y para su desarrollo profesional (Carpenter y Fennema, 1989). Este programa fue financiado por el Banco Interamericano de Desarrollo y apoyado por la Secretaría de Educación Pública, el Instituto Latino Americano de la Comunicación Educativa y la Universidad Pedagógica Nacional.

Los resultados que aquí reportamos se refieren a los efectos de la estrategia metodológica empleada en el programa de desarrollo profesional; el método para recolección de datos que usamos se basó en observar críticamente las sesiones en que se proporcionaron oportunidades a los profesores para contrastar sus formas de razonamiento con las de los estudiantes. Para esto se pidió a docentes y alumnos que resolvieran por separado los mismos problemas matemáticos. Estos aspectos del estudio se presentan con mayor detalle más adelante.

Preguntas de investigación

Las siguientes preguntas guiaron el estudio que aquí se reporta:

• ¿Qué efectos produce en las concepciones sobre el aprendizaje y la enseñanza de las matemáticas de los profesores contrastar sus formas de razonamiento con las de los alumnos?

• ¿Qué efectos produce en el conocimiento matemático de los profesores observar las clases donde los alumnos resolvieron los mismos problemas matemáticos que ellos previamente abordaron?

 

Método

Para las sesiones de trabajo con los alumnos se usó una estrategia didáctica basada en conducir las actividades de la clase haciendo ajustes sobre la marcha, siguiendo sus formas de razonamiento. En las realizadas con los profesores se propició que concentraran su atención en los avances de los estudiantes para orientar la reflexión sobre su práctica. Nuestra expectativa fue que esto, eventualmente, daría lugar a cambios favorables en el conocimiento matemático y pedagógico de los docentes.

Ese modelo didáctico se empleó para conducir 20 sesiones de clase con estudiantes de secundaria que cursan segundo grado en escuelas oficiales; todas las sesiones fueron videograbadas para posteriormente hacer posible su uso en tantas locaciones como fuera necesario durante las siguientes fases del programa de desarrollo profesional. Los talleres con los profesores también fueron filmados; los videos fueron la principal fuente de datos para el proyecto de investigación. Consideramos que estos materiales serán un valioso recurso en estudios posteriores donde participen maestros en servicio y como material didáctico para los formadores de futuros docentes.

Sesiones en el salón de clases

Para decidir el contenido matemático de las sesiones en el salón de clases fue necesario revisar la literatura en investigación y el currículo oficial de matemáticas en América Latina. La información obtenida de este análisis nos condujo a seleccionar los temas comunes en el currículo de matemáticas que han sido objeto de estudio, ya sea porque son temas difíciles para su aprendizaje o su enseñanza o debido a su rol como antecedentes relevantes en niveles de educación subsecuentes.

También fue necesario considerar las restricciones financieras y el tiempo asignado para el proyecto. Esto nos condujo a seleccionar las áreas curriculares y los temas que se describen a continuación:

 

Se dedicaron dos sesiones de 50 minutos para tratar cada tema. Las sesiones en el salón de clases se realizaron en dos escuelas secundarias públicas de la Ciudad de México que voluntariamente participaron en el proyecto. Los directivos de cada plantel nos permitieron intervenir en la escuela siempre y cuando el proyecto no perturbara sus actividades cotidianas, lo que hizo necesario que trabajáramos con grupos escolares dentro de su horario normal de clases; esto fue una situación no esperada que resultó muy valiosa para el proyecto, porque propició de manera natural que hubiera frescura y espontaneidad en el trabajo de los estudiantes. Otra ventaja que se derivó de esa situación es que los alumnos que tomaron parte en las clases no fueron seleccionados en forma alguna por el director de la escuela, los profesores, o por el equipo responsable del proyecto.

La población se formó por los grupos escolares que estaban disponibles en el horario en el que fueron programadas las sesiones de trabajo, y estos horarios se determinaron por el tiempo que tenía disponible el equipo técnico que grababa con calidad profesional las sesiones. Los profesores que condujeron las sesiones en el aula no son parte del personal de la escuela. Deliberadamente desempeñaron el papel del maestro tres investigadores del equipo académico responsable del proyecto. Esto fue un requerimiento para llevar a cabo una fase piloto en la que se realizaron intensivas reuniones de trabajo con los responsables del proyecto para someter los métodos que usamos a un proceso de refinamiento. La etapa piloto se realizó en escuelas que no participaron en el estudio principal.

Las sesiones en el salón de clases fueron conducidas siguiendo las respuestas que dieran los alumnos al enfrentar una serie de problemas articulados; las acciones del maestro fueron guiadas por la metáfora de la partida múltiple de ajedrez que se describió anteriormente. Esta metáfora implica un método similar al ciclo de enseñanza propuesto por Simon (1995) y al concepto de secuencias instruccionales desarrollado por Cobb y Mc Clain (2001). Simon describe el ciclo de enseñanza como un proceso en el que: "[...] en todo momento el maestro tiene una agenda pedagógica y por lo tanto un sentimiento de dirección. Sin embargo, esta agenda está sujeta a una continua modificación en el acto de enseñar [...]". Cobb y Mc Clain (2001:215) también hacer referencia a este aspecto, en particular enfatizan que: "Esta manera de actuar en el aula incluye un propósito y una actitud permanente de apertura ante las posibilidades ofrecidas por las reacciones de los alumnos a las actividades que se les proponen" .

Consideramos importante señalar que esta postura didáctica no sugiere de ninguna manera que las actividades deben ser llevadas a cabo sin objetivos claros; en todo momento de la clase el maestro debe tener en mente una meta principal y los medios para alcanzarla.

Otro aspecto metodológico que se tomó en cuenta fue la selección de los problemas matemáticos; éstos debían ser suficientemente complicados tanto para los profesores como para los estudiantes. El criterio que utilizamos para seleccionarlos fue tomar los que nos permitieran abordar los temas del currículo en formas no convencionales.

Por ejemplo, en el caso de la aritmética se eligió el tema de divisibilidad. De acuerdo con la revisión documental que realizamos, en los países de América Latina este tema es abordado tomando como punto de partida las definiciones formales de divisor, múltiplo y número primo. Esto es seguido por una serie de ejercicios para reforzar la comprensión de estas definiciones. Para presentar un tratamiento alternativo, decidimos abordar el tema de múltiplos y divisores usando un conjunto de preguntas dirigidas a propiciar que los estudiantes enfrentaran situaciones que retaran su curiosidad matemática y capacidad intelectual y les condujeran a "descubrir" las relaciones entre los conceptos involucrados, a proponer generalizaciones con base en la observación de regularidades numéricas y, finalmente, a expresar y justificar esas generalizaciones por medio del uso del código algebraico. Es importante mencionar que se permitió a los estudiantes trabajar cooperativamente en pequeños grupos si ellos así lo querían.

 

Problemas matemáticos propuestos

A continuación se describen los problemas que usamos para cada tema, abordaremos algunos más detalladamente con la finalidad de exponer con mayor precisión el tratamiento didáctico empleado, el resto de los problemas se presentan de manera más general.

Múltiplos y divisores

Estos temas se abordaron con base en las respuestas que dieron los alumnos a las siguientes preguntas y actividades:

• ¿Puedes encontrar números que tengan exactamente dos divisores? En los próximos cuatro minutos haz una lista de esos números tan extensa como te sea posible. El reto es que tu lista sólo incluya números que cumplan esa condición.

• ¿Puedes encontrar números que tengan exactamente tres divisores? ¿Puedes proponer una regla que nos permita construir muchos números que tengan exactamente tres divisores? ¿Hay más de una regla que nos permita hacer eso?

• ¿Puedes encontrar números que tengan exactamente cuatro divisores? ¿Puedes proponer una regla que nos permita construir muchos números que tengan exactamente cuatro divisores? ¿Hay más de una regla que nos permita hacer eso?

• ¿Puedes encontrar números que tengan exactamente n divisores? ¿Puedes mostrarnos una regla que nos permita construir muchos números que tengan exactamente n divisores? ¿Hay más de una regla que nos permita hacer eso?

• ¿Puedes encontrar un número natural diferente de 1 que no puedas factorizar usando exclusivamente números primos como factores?

Máximo común divisor

Este concepto se abordó por medio de un conocido problema que consiste en tener tres recipientes (A, B y C), ninguno está graduado, lo único que se conoce es la capacidad de cada uno de los recipientes A y B. La capacidad del C es mayor que la de los otros dos juntos. El problema consiste en encontrar una regla general que nos permita saber qué cantidades enteras de litros pueden obtenerse pasando líquido del recipiente A al B a partir de que conoces la capacidad de cada uno de ellos. Usamos este problema para que los estudiantes recrearan la noción del concepto de máximo común divisor y los alentamos a encontrar regularidades numéricas que eventualmente les permitieran proponer soluciones generales. Cada equipo de estudiantes fue provisto con jarras y agua que podrían usar si lo consideraban necesario. El problema se extendió hasta abordar intuitivamente la solución de ecuaciones diofantinas. Las preguntas y la secuencia en la que fueron planteadas a los estudiantes se describen a continuación.

• Tienes tres jarras, A, B y C. La jarra A tiene una capacidad de tres litros, la jarra B tiene una capacidad de 5 litros. La jarra C puede usarse para guardar la cantidad de líquido que quieras o para pasar líquido a ella de alguna de las jarras A o B. ¿Puedes obtener 4 litros pasando líquido de la jarra A a la B? ¿Puedes encontrar una manera para registrar la secuencia de los movimientos que hiciste de una jarra a otra para convencernos de que tu respuesta es correcta?

• Considera que tienes las mismas condiciones que en el problema anterior, pero ahora la jarra A es de 2 litros y la jarra B es de 4 litros. ¿Puedes obtener 1 litro pasando líquido de la jarra A a la B? ¿Puedes encontrar una forma para registrar la secuencia de los movimientos que hiciste de una jarra a otra para convencernos de que tu respuesta es correcta?

• Ahora la jarra A es de 6 litros y la B de 9 litros. ¿Puedes obtener 1 litro pasando líquido de una jarra a la otra? ¿Puedes encontrar una manera de registrar la secuencia de los movimientos que hiciste de una jarra a la otra para convencernos de que tu respuesta es correcta? ¿Puedes hacer una lista con las diferentes cantidades de litros que pueden obtenerse al pasar líquido de la jarra de 6 litros a la de 9 litros? ¿Puedes proponer un método para saber qué cantidades enteras de litros puedes obtener pasando líquido de la jarra de 6 litros a la de 9 litros?

• Ahora la jarra A es de 7 litros y la B es de 10 litros. ¿Puedes obtener 1 litro pasando líquido de una jarra a la otra? ¿Puedes encontrar una manera de registrar la secuencia de los movimientos que hiciste de una jarra a la otra para convencernos de que tu respuesta es correcta? ¿Puedes hacer una lista con las diferentes cantidades de litros que pueden obtenerse al pasar líquido de la jarra de 7 litros a la de 10 litros? ¿Puedes proponer un método para saber qué cantidades enteras de litros puedes obtener pasando líquido de la jarra de 7 litros a la de 10 litros?

• Observa cuidadosamente las listas que hiciste para mostrar las diferentes cantidades de litros que puedes obtener al pasar líquido de una jarra a la otra. ¿Notas alguna regularidad en estos números? ¿Podrías encontrar una estrategia general que te permita saber si puedes o no obtener una cantidad dada de líquido sólo con saber la capacidad de cada jarra?

Mínimo común múltiplo

Este tema se abordó usando el conocido problema de los engranes. La versión que propusimos fue considerar dos engranes como los que se muestran en la figura 1, el número de dientes en cada engrane puede ser diferente. La pregunta que se hizo a los estudiantes fue que encontraran el menor número de vueltas que deben dar cada uno de los engranes para coincidir otra vez en el punto donde empezaron a girar. Este problema se extendió al caso de más de dos engranes y a problemas del tipo "un amigo mío compró manzanas y naranjas. Por cada manzana pagó 5 pesos y por cada naranja 3 pesos. Pagó lo mismo por las manzanas que por las naranjas. ¿Cuál es la menor cantidad de cada fruta que compró?"

 

Preálgebra y álgebra

Incluimos cuatro temas, dos de ellos inducen la necesidad de emplear el código algebraico para expresar y justificar generalizaciones (patrones numéricos, juegos y regularidades algebraicas). Las sesiones sobre patrones numéricos y generalización consistieron en que los alumnos encontraran una función que cumpliera con la secuencia numérica sugerida por un diagrama como el que se muestra en la figura 2.

 

Para introducir la actividad se les planteó a los estudiantes preguntas como las siguientes: ¿Cuántos cuadrados tendrá la cuarta figura? ¿Cuántos cuadrados tendrá la décima figura? Una figura en esta secuencia tiene 225 cuadrados, ¿cuál es el lugar de esta figura en la secuencia? ¿Puedes expresar la regla que usaste para contestar las preguntas anteriores usando el lenguaje algebraico?

Otros problemas que se usaron en esta sección fueron del tipo "piensa en un número". Por ejemplo: piensa en un número entero que esté entre 0 y 10. Suma 10 al número que pensaste y guarda el resultado. Ahora resta a 10 el número que pensaste y guarda el resultado. Suma los dos resultados que obtuviste. ¿Puedo adivinar el resultado final que obtuviste? ¡Es 20! ¿Estoy en lo correcto?, ¿por qué pude hacer esto? ¿Podría adivinar el número que pensaste si éste fuera mayor que 10? ¿Podría adivinar el número que pensaste si fuera menor que 0? ¿Podría adivinarlo si éste no fuera un número entero?, ¿por qué?

Las sesiones sobre juegos y regularidades algebraicas fueron abordadas por medio del problema de las torres Hanoi (figura 3). La meta fue que los estudiantes encontraran la regla que gobierna este juego: la función f(n) = 2ⁿ-1. Para realizarlo se les proporcionó material manipulable y una pieza de software que simula los movimientos de los discos de una torre a la otra. Podrían usar alguno o ambos de estos recursos según ellos eligieran.

 

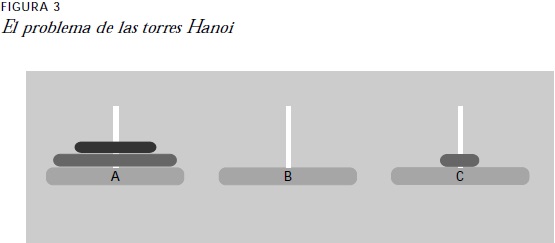
El juego se inició pidiendo a los alumnos que pasaran tres discos de una torre, las reglas del juego son que en ningún momento puede estar un disco sobre otro de menor tamaño y que la mejor estrategia es la que emplea el menor número de movimientos. Las preguntas que se les hicieron fueron como las siguientes: ¿Cuál es el número mínimo de movimientos que se necesitan para pasar los tres discos de una torre a la otra? Si los discos estuvieran en la torre A, ¿hacia qué torre harías el primer movimiento? Se incrementó la dificultad del juego al aumentar el número de discos.

El tema de las ecuaciones de primer grado se abordó pidiendo a los estudiantes que encontraran "el número perdido" en una ecuación dada. Consideramos importante señalar que ellos no habían tenido ninguna instrucción sobre los métodos convencionales para resolver ecuaciones al momento de la sesión. Se incrementó la dificultad de la actividad gradualmente hasta abordar casos en los que las ecuaciones contenían paréntesis y barras de división como signos de agrupación. Otro tipo de actividad que se usó en esta sesión fue pedir a los alumnos que redactaran un problema que pudiera ser resuelto mediante una ecuación dada y viceversa.

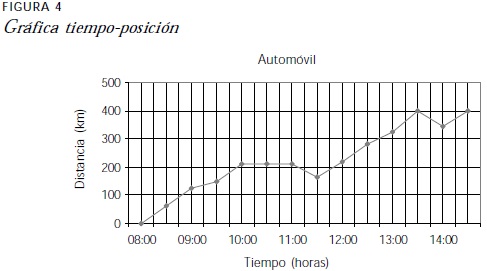
El tema lectura y construcción de gráficas cartesianas se abordó pidiendo a los estudiantes que crearan historias que correspondieran a la información que se presentaba en gráficas de tiempo-posición y viceversa (como la de la figura 4). Otro tipo de actividad que se usó en estas sesiones fue encontrar la regla de correspondencia de una función a partir de la información que se daba en una gráfica lineal.

 

Geometría

Las sesiones de geometría se desarrollaron en torno al concepto de medición. Se abordaron las nociones centrales de semejanza de triángulos, el teorema de Pitágoras y razones trigonométricas en triángulos rectángulos como herramientas de medición. Estos temas no están incluidos en el plan de estudios de segundo grado, por lo que estábamos seguros de que los alumnos tendrían su primer acercamiento a ellos en las sesiones del proyecto.

Se les introdujo a esos temas por medio de una estrategia de indagación tratando de que descubrieran por sí mismos las nociones centrales involucradas, en una forma similar a la que se emplea en un laboratorio de ciencias naturales. Para apoyar este tipo de actividad el salón fue equipado con geoplanos manipulables, un software que simula un geoplano y otro de geometría dinámica y calculadoras científicas. Por ejemplo, para abordar el tema de razones trigonométricas, se les pidió dibujar un triángulo rectángulo dadas las medidas de sus ángulos internos; después calcularon los cocientes tomando por pares las longitudes de los lados del triángulo y comparando sus resultados con los de sus compañeros. El software de geometría dinámica les permitió hacer esto ágilmente y explorar sus conjeturas usando tantos casos particulares como creyeran necesario antes de formular sus conclusiones.

El uso de calculadoras científicas les permitió confirmar los resultados que habían obtenido y saber los nombres técnicos de las razones trigonométricas que estaban usando. Una vez hecho esto, se les pidió que dieran argumentos matemáticos que pudieran explicar las regularidades numéricas que habían observado. Para cerrar la sesión, los alumnos se enfrentaron a problemas cuya solución requería encontrar algunas longitudes o medidas de ángulos en un triángulo rectángulo. Un método similar se usó para tratar los temas de semejanza de triángulos y el teorema de Pitágoras.

Talleres con los profesores

Se realizaron diez talleres mensuales de cinco horas cada uno en el periodo febrero-noviembre de 2005. Los profesores de matemáticas en servicio participaron de manera voluntaria y aceptaron que las sesiones se videograbaran. Como apuntamos antes, las mismas actividades y problemas que se usaron con los estudiantes fueron incluidas con los maestros. En los talleres, los docentes hicieron exploraciones matemáticas trabajando a partir de las indicaciones que se dieron en hojas de trabajo; decidieron trabajar en equipos pequeños.

Los talleres se estructuraron de la siguiente manera: los profesores tuvieron una hora para abordar los problemas propuestos para esa sesión. Las siguientes dos horas fueron asignadas para ver los videos de las dos sesiones con los estudiantes; antes de verlos, se les preguntó si creían que los alumnos de segundo grado serían capaces de resolver los problemas que ellos acababan de trabajar. Si la respuesta es sí, ¿en qué medida?, ¿cómo?, ¿por qué? Las dos últimas horas fueron asignadas para que los profesores discutieran lo que ellos hicieron en el contexto de lo que observaron en los videos. Para guiar su atención mientras observaban los videos se les pidió tomar notas sobre los siguientes puntos:

• las estrategias no esperadas que usaron los alumnos;

• los factores que más influyeron en el éxito de los estudiantes al resolver los problemas;

• los factores que provocaron confusión en los estudiantes o la producción de respuestas incorrectas;

• las formas de razonar de los estudiantes que diferían de las que él o ella, como profesor, hubiera utilizado para enfrentar el mismo problema; y

• otros eventos en el salón de clases que consideraran importantes.

Los docentes que participaron en los talleres trabajan en escuelas secundarias públicas en la Ciudad de México. El profesor con mayor experiencia en este grupo había enseñado matemáticas durante 20 años, y el de menor, llevaba dos años dando clases. Dos de estos maestros trabajaban en las escuelas en las que se llevaron a cabo las sesiones con estudiantes. Este hecho agregó un factor de credibilidad a los eventos en el salón de clases que observaron en los videos.

 

Resultados

Una vez que analizamos los datos de los videos y las hojas de actividades que completaron los profesores encontramos que, en general, sus intervenciones interrelacionaban reflexiones sobre el contenido matemático, el pedagógico y las habilidades de los estudiantes. Tomando en consideración estas restricciones, tratamos de organizar la presentación de los resultados dentro de las siguientes secciones: a) las expectativas de los profesores sobre las capacidades sus alumnos y b) sus reflexiones sobre su conocimiento matemático y su práctica docente.

Expectativas de los profesores

El hecho de que tanto profesores como estudiantes enfrentaran los mismos problemas nos dio información importante acerca de las expectativas de los docentes en cuanto a las habilidades de sus alumnos. Los datos recabados indican que centran la valoración de las capacidades de aprendizaje de los estudiantes en sus propias habilidades para enseñar. Como se apuntó previamente, antes de ver el video de las sesiones con alumnos se les preguntó a los maestros si pensaban que los jóvenes serían capaces de resolver los problemas. La primera vez que contestaron esta pregunta hicieron énfasis en que no creían que los resolverían, especialmente aquellos que requerían formular alguna generalización y generar argumentos sólidos para aceptarla o rechazarla. Por ejemplo, en el caso del tema de divisibilidad, sostuvieron que para que los estudiantes pudieran alcanzar una meta tan ambiciosa era necesario enseñarles previamente las reglas de divisibilidad, un método para obtener números primos y mostrarles cómo usar el álgebra para trabajar con números generalizados. Pensaron que no era factible que contestaran preguntas que requerían álgebra porque sus conocimientos a este respecto eran aún incipientes. Dijeron estar suficientemente seguros de que eso era lo que mostrarían los videos y que solamente era importante observar hasta qué punto confirmarían su hipótesis.

Una vez que los profesores vieron hasta qué punto los estudiantes fueron capaces de trabajar con los problemas usando las rudimentarias herramientas matemáticas que tenían, empezaron a discutir buscando encontrar por qué su percepción inicial de las capacidades de los alumnos estaba tan alejada de lo que ellos pudieron hacer. Por ejemplo, les sorprendió que pudieran analizar los factores de un número dado usando el código algebraico. Al discutir esto hacían referencia a casos como el de un estudiante que pasó al pizarrón para explicar su descubrimiento: "si decimos que p es un número primo... p⁴ tiene exactamente cinco divisores, porque p⁴÷1=p⁴; p⁴÷p=p³; p⁴÷p²=p²; p⁴÷p³=p y p⁴÷p⁴=1..." Este estudiante abundó en su explicación: "Primero exploramos con muchos números como ése y funcionó, después alguien del equipo lo hizo con letras y nos dimos cuenta que es más fácil con las letras que con números".

Esta clase de evidencia condujo a los profesores a buscar explicaciones plausibles para estos hechos; llegaron a la conclusión de que había sido la manera en la que el instructor guió su razonamiento aritmético lo que les permitió ganar confianza en sí mismos, "esto hizo que los estudiantes empezaran a producir ideas, como analizar casos particulares que finalmente les dejaron ver posibles generalizaciones". Por ejemplo, uno de los profesores destacó lo siguiente:

[...] vean, el maestro [el instructor del proyecto] nunca dijo no a ninguno de los estudiantes, siempre fue paciente [...] Si un estudiante decía algo incorrecto el maestro preguntaba al grupo si estaba de acuerdo con la respuesta que ese alumno estaba dando [...] Actuó de la misma manera aun cuando un alumno estaba dando una idea brillante. De esta forma el maestro les iba dando muchas oportunidades para corregir o confirmar sus respuestas por ellos mismos [...] Esta actitud del maestro les da a los alumnos una oportunidad para aprender más [...] De esta manera los estudiantes se aventuran a dar argumentos para rechazar o aceptar sus soluciones.

El grupo de profesores concluyó que pensaban que los alumnos no serían capaces de enfrentar estos problemas porque ellos tomaban como referencia su propia experiencia y recursos que empleaban cuando enseñaban esos temas. Dijeron que: "estaban seguros de que las secuencias didácticas que ellos usaban eran buenas, y que consideraban que si los estudiantes enfrentarían los problemas de la manera en que nosotros se los propusimos a ellos, les parecía casi imposible que los estudiantes pudieran resolverlos con éxito". El siguiente extracto de la intervención de un maestro ilustra lo anterior:

Es la manera en la que enseñamos la que nos hizo pensar que los alumnos no serían capaces de dar respuestas correctas a preguntas tan complejas [...] Cuando enseño estos temas empiezo por darles a los estudiantes los procedimientos necesarios y las definiciones y conceptos acerca del contenido de lo que quiero que ellos trabajen [...] Después les doy un buen número de ejemplos tratando de reafirmar su entendimiento. Las reglas de divisibilidad se necesitan para hacer que ellos sean buenos para encontrar factores, así que les enseño estas reglas [...] Cuando ustedes dijeron que se les darían estos ejercicios a los alumnos de la manera en que lo hicieron con nosotros, nos fue muy difícil pensar que los estudiantes lo pudieran hacer bien.

Esperábamos que la opinión de los profesores acerca de las capacidades de los estudiantes cambiara después de la primera sesión de los talleres, pero no fue así. El cambio que observamos fue que se tomaban más tiempo para responder acerca de lo que pensaban que ocurriría en la clase con los alumnos. Por ejemplo, en la clase del "problema de las jarras" dudaban que pudieran enfrentarlo con éxito. Los presionamos para que dieran una respuesta más precisa y finalmente acordaron que:

[...] no creían que los estudiantes fueran capaces de resolver el problema debido a que sabían muy poco acerca del máximo común divisor, y la actividad requería no sólo el manejo de la definición de este concepto, sino hacer un registro claro de los cambios de líquido de una jarra a otra y encontrar relaciones entre los números que se involucraran en el problema.

Una vez más, los logros de los estudiantes contradijeron fuertemente su pronóstico.

Hacia el final del estudio, 9 de los 25 profesores que participaron en los talleres informaron que habían tratado de utilizar un método distinto de enseñanza intentando emular lo que aprendieron en los talleres. Entre los principales obstáculos que mencionaron se puede destacar que "preparar y presentar una clase como la que condujo el instructor del proyecto les tomaba demasiado tiempo"; otra dificultad que mencionaron fue "el dominio que se requiere tener sobre el contenido matemático del tema para poder atender las preguntas y respuestas de los alumnos de manera que sus intervenciones les ayudaran a los estudiantes a fortalecer su pensamiento matemático [...] Con tiempo, cuando hayamos dado varias veces la misma clase podremos hacerlo".

Los profesores que no trataron de poner en marcha un nuevo método de enseñanza argumentaron que la manera de enseñar del instructor del proyecto así como los avances de los alumnos mostraban ser positivos, pero que un enfoque como el que propusimos no era viable para ellos debido a que la organización en sus escuelas no estaba preparada todavía para llevar a cabo un programa de esta clase. El argumento de los docentes en este sentido fue que ellos no se sentían con la confianza suficiente en sus propios conocimientos como para hablar con el director de la escuela, o explicarle al supervisor cómo podrían cubrir mediante este enfoque los temas del programa y alcanzar las metas del currículo oficial. Nuestros datos sugieren que esta falta de confianza tiene que ver con debilidades en su conocimiento pedagógico y matemático. El siguiente extracto lo ilustra:

Estoy impresionado con los logros de los estudiantes; encuentro muchos puntos favorables en la manera en que los instructores condujeron la clase, cómo manejaron el contenido y ajustaron sobre la marcha sus intervenciones de acuerdo con las respuestas de los alumnos. No creo que yo pueda hacer esto, la escuela en la que trabajo no está tan bien organizada como las escuelas en las que se tomaron los videos, conozco bien esas escuelas. Mis alumnos no se comportan como los alumnos que vimos en los videos, es muy difícil para mí mantenerlos concentrados. He dicho antes que me gustaron mucho las clases que vimos en los videos, particularmente me gustó la clase de las torres Hanoi y traté de trabajar esto con mis estudiantes. Ese día la directora de la escuela entró inesperadamente a mi salón y se quedó a observar la clase. Comentó mi trabajo con el inspector y me ordenaron que no volviera a hacer esto. Se me dijo que limitara mi trabajo a los temas que se incluyen en el currículo. Estoy seguro de que intentaré de nuevo más adelante, ahora necesito tiempo para superarme y aprender más sobre las matemáticas y su enseñanza [...] Una cosa es jugar el juego de las torres Hanoi y otra completamente diferente es desentrañar los conceptos matemáticos que éste involucra, esto es necesario para preparar la clase de manera que los alumnos puedan jugar el juego matemáticamente. Esto requiere que el maestro tenga, además de un buen conocimiento de las matemáticas, una notable habilidad para enseñar. El problema que yo veo es que mi carga de trabajo es muy pesada, como lo es para muchos de mis compañeros, de cualquier forma, trataré de organizarme para hacer esto y seré voluntario nuevamente para participar en esta clase de programas siempre que me den la oportunidad.

Reflexiones de los profesores sobre su práctica

Las intervenciones de los profesores durante los talleres sugieren que los logros de los estudiantes fueron un factor importante para motivarlos a reflexionar críticamente sobre su práctica y su conocimiento matemático y pedagógico. Este hallazgo confirma lo que nos propusimos al diseñar el presente estudio. Como mencionamos antes, al concluir las sesiones de los talleres (un año de trabajo), algunos de los docentes se involucraron en intentar métodos de enseñanza diferentes al que habían estado utilizando; esto fue uno de los resultados de las discusiones y el análisis del enfoque de enseñanza que se presentó en este estudio. Incluso los que manifestaron no tener intención de cambiar hicieron referencia en sus intervenciones a la manera en la que el hecho de observar los logros de los estudiantes les motivó a revisar sus formas de enseñar.

Los datos recabados sugieren que el principal factor que los motivó a que probaran un método de enseñanza distinto fue observar cómo cambian las actitudes de los alumnos en la medida en que se les daban oportunidades para explorar, cometer errores, ir hacia delante y hacia atrás, siempre sintiéndose seguros porque había un maestro que estaba con ellos para ayudarlos. Uno de los profesores se refirió las actitudes de los alumnos de la siguiente manera:

Creo que las actitudes favorables de los alumnos están estrechamente relacionadas con su desempeño matemático [...] Vimos cómo los alumnos iban ganando confianza en ellos mismos en la medida en que el grupo aceptaba sus ideas [...] Fue notable la manera en que participaban entusiastamente proponiendo ideas y discutían acaloradamente con sus compañeros y el maestro. Los alumnos que observamos en los videos parecían felices en la clase de matemáticas [...] Me pregunto por qué mis alumnos casi nunca se ven así. Estoy impresionado de lo lejos que puede ir el aprendizaje de los alumnos cuando el maestro los guía como vimos en los videos [...] Me gustaría que mis alumnos se comportaran de esa manera y estoy convencido de que eso depende mucho de mí.

Las reacciones de los profesores indican que al principio su atención se centró de manera importante en las respuestas de los estudiantes, pero pronto dejaron de enfocarse exclusivamente en las respuestas y empezaron a analizar cómo razonaban los alumnos para dar esas respuestas; esto los condujo a concluir que era importante discutir la manera en la que los instructores condujeron las clases. En muchas de las sesiones los profesores trataron de encontrar razones plausibles que explicaran por qué los jóvenes podían generar soluciones matemáticas a los problemas que se les plantearon. Los maestros destacaron en sus debates que el instructor procuraba no dar respuestas a los estudiantes; en cambio, les respondía con una nueva pregunta "tratando de hacer que los alumnos vieran por sí mismos cuál era el error". Nuestro análisis sugiere que los profesores se dieron cuenta de estos eventos porque ellos no actúan de la misma manera que el instructor en los videos.

El punto que más discutieron los profesores fue la posibilidad que ellos tienen de poner en práctica el enfoque de enseñanza que observaron en los videos. Llegaron a la conclusión de que los estudiantes que tomaron parte en los videos no son diferentes a los suyos. Este tipo de discusiones les permitió concluir que no son sólo las habilidades pedagógicas del maestro lo que permite que las actividades en el aula sean fructíferas; notaron que esas habilidades se manifiestan en otros factores importantes, como los materiales que usa el profesor para la actividad, el criterio para seleccionar o diseñar los problemas, la forma en la que la clase fue planeada, y cómo esta manera de estructurar la clase puede ayudar al maestro a anticipar las respuestas que pueden producir los alumnos. La siguiente intervención de un maestro ilustra lo anterior:

Después de haber discutido estos temas me di cuenta de la importancia de preparar cuidadosamente la clase. Me di cuenta de que planear una clase consiste en poner juntos mis conocimientos pedagógicos y matemáticos para ayudar a los estudiantes a aprender más significativamente [...] Lo que quiero decir es que planear una clase requiere que el maestro traduzca su conocimiento matemático de manera que lo pueda llevar a un contexto de enseñanza-aprendizaje.

 

Consideraciones finales

Nuestro estudio estuvo influido por otros trabajos realizados en programas de desarrollo profesional para docentes donde se asume que la resolución de problemas matemáticos suficientemente difíciles puede tener efectos positivos en el conocimiento pedagógico y matemático de los profesores (Zaslavsky, Chapman y Leikin, 2003; Murray, Olivier y Human, 1995; Schifter, 1993). Los resultados arrojados por este estudio resaltan la importancia de este tipo de problemas matemáticos como un instrumento para que los maestros mejoren sus prácticas de enseñanza. Nuestros datos confirman también algunos hallazgos previos sobre el rol que juega la resolución de problemas matemáticos no rutinarios como un medio para hacer que los profesores reflexionen sobre sus prácticas y, eventualmente, las mejoren. Una fuente importante para nuestro estudio fue la investigación realizada por Carpenter y Fennema (1989), su trabajo asume que el conocimiento del pensamiento matemático de los estudiantes proporcionará a los docentes una base más sólida para su tarea docente y para su desarrollo profesional.

Una suposición en el presente estudio es que estamos convencidos de que los profesores deben aprender matemáticas de la misma manera en la que se espera que las enseñen. Dado que nuestro estudio estuvo dirigido a maestros en servicio, debíamos utilizar un método que nos permitiera proveerles una oportunidad de aprender matemáticas de la misma manera en la que esperamos que las enseñen. Para nosotros fue un reto que los sujetos con los que trabajamos estaban dando clases. El hecho de ponerlos en la posición de confrontar su conocimiento con el de sus estudiantes les permitió analizar críticamente su práctica en el marco de cómo están enseñando. Los resultados del presente estudio confirman lo reportado en otras investigaciones acerca de que una componente relevante en el desarrollo profesional de los profesores es su conocimiento matemático. El matiz que nuestros datos sugieren a este respecto es que es más probable que participen activamente en el proceso de fortalecimiento de su conocimiento matemático si éste se aborda situándolo adecuadamente en su práctica de enseñanza. Nuestros datos ratifican la necesidad de un sólido conocimiento matemático para que los maestros sean capaces de diseñar, o retomar, actividades que propicien oportunidades para que sus alumnos aprendan matemáticas de una manera más significativa. Consideramos necesario enfatizar en que este estudio indica que si queremos fortalecer el conocimiento matemático y pedagógico de los profesores en servicio, es importante que los motivemos involucrándolos en propuestas didácticas que produzcan resultados que se reflejen en la calidad de los aprendizajes de los estudiantes.

Los resultados del presente estudio confirman que el cambio en las concepciones, prácticas y conocimientos de los profesores no es un evento, sino el resultado de un largo proceso. Después de un año de trabajo con maestros en servicio sólo tenemos evidencia de cambios incipientes en sus prácticas y concepciones. Esta experiencia indica claramente que las reuniones de trabajo mensuales proporcionaron un ambiente favorable para aprender unos de otros y resalta la pertinencia de seguir promoviendo la creación de comunidades profesionales de enseñanza. En México esto es un enorme reto porque nuestros profesores usualmente trabajan aislados unos de otros.

 

Referencias

Carpenter, T. P. y Fennema, E. (1989). "Building on the knowledge of students and teachers", en G. Vergnaud, J. Rogalski y M. Artigue (eds.), Proceedings of the 13th PME International Conference, 1, 34-45.         [ Links ]

Cedillo, T. y Kieran, C. (2003). "Initiating students into algebra with symbol-manipulating calculators", en J. T. Fey (ed.), Computer algebra systems in secondary school mathematics education, Reston, VA: National Council of Teachers of Mathematics, pp. 219-239.         [ Links ]

Cedillo, T. (2003). "El álgebra como lenguaje alternativo y de cambio en las concepciones y prácticas de los profesores de matemáticas", Perfiles Educativos (México: IIESU-UNAM), núm. 101, pp. 50-65.         [ Links ]

Cedillo, T. (2006). "La enseñanza de las matemáticas en la escuela secundaria: Los sistemas algebraicos computarizados", Revista Mexicana de Investigación Educativa (México: COMIE), 11 (28), pp. 129-154.         [ Links ]

Cobb, P. y McClain, K. (2001). "An approach for supporting teachers' learning in social context", en F. L. Lin y T. J. Cooney (eds.) Making Sense of Mathematics Teacher Education, 207-231, Países Bajos: Kluwer Academic Publishers.         [ Links ]

Cobb, P.; Wood, T. y Yackel, E. (1990). "Classroom as learning environments for teachers and researchers", en R. Davis, C. Maher y N. Noddings (eds.), Constructivist views on the teaching and learning of mathematics. Journal for Research in Mathematics Education Monograph, 4, 125-146.         [ Links ]

Kilpatrick, J. (1992). "A history of research in mathematics education", en Grouws, D. A. (ed.), Handbook of Research on Mathematics Teaching and Learning, parte I, Nueva York: National Council of Teachers of Mathematics/Macmillan Library Reference, Simon & Schuster Macmillan, pp. 3-38.         [ Links ]

Krainer, K. (2004). "On giving priority to learners' prior knowledge and our need to understand their thinking", Journal of Mathematics Teacher Education (Países Bajos: Kluwer Academic Publishers), 7:87-90.         [ Links ]

Llinares, S. y Krainer, K. (2006). "Mathematics (student) teachers and teacher educators as learners", en A. Gutiérrez y P. Boero (eds.), Handbook of Research on the Psychology of Mathematics Education. Past, Present and Future, Rotterdam/Taipei: Sense Publishers,pp. 429-460.         [ Links ]

Murray, H.; Olivier, A., y Human, P. (1995). "Teachers' mathematical experiences as links to children's needs", en L. Meira y D. Carraher (eds.), Proceedings of the 19th PME International Conference, 3, 312-319.         [ Links ]

Schifter, D. (1993). "Mathematics process as mathematic content. A course for teachers", Journal of Mathematical Behavior, 12(3), 271-283.         [ Links ]

Simon, M.A. (1995). "Reconstructing mathematics pedagogy from a constructivist perspective", Journal for Research in Mathematics Education, 26, 114-145.         [ Links ]

Thompson, A. (1992). "Teacher's believes and conceptions: A synthesis of the research", en D. A. Grows (ed.) Handbook of Research on Mathematics Teaching and Learning,Reston, VA: National Council of Teachers of Mathematics.         [ Links ]

Zaslavsky, O.; Chapman, O. y Leikin, R. (2003). "Professional development in mathematics education: Trends and tasks", en A. J. Bishop, et al. (eds.), Second international handbook of mathematics education (2). Dordrecht: Kluwer, pp. 877-915.         [ Links ]