1 Introduction
Bio-inspired algorithms are computational techniques inspired by nature, primarily the simulation or emulation of simple and intelligent processes of certain animals, insects, or bacteria in search of food or shelter.
These algorithms arise to improving search algorithms to solve numerical and combinatorial optimization problems [9]. These algorithms are classified as metaheuristics and incorporate techniques and strategies to design or improve mathematical procedures aimed at obtaining high performance. [18].
Metaheuristics generate a set of results for a particular problem that is totally or approximately global optimum.
These algorithms are classified into two groups based on different natural phenomena: Evolutionary Algorithms (EAs) emulate the evolutionary process of the species [2] and Swarm Intelligence Algorithms (SIAs) emulate the collaborative behaviour of certain simple and intelligent species such as bacteria [14], bees [8], ants [1], among others [3]. Metaheuristics were created to solve unconstrained optimization problems.
However, to handle this problems, mechanisms such as feasibility rules, special operators, decoders, among others are implemented. The use of metaheuristics is an effective alternative for solving Constraint Numerical optimization Problems (CNOPs) [12].
Generally, a CNOP is known as a general nonlinear programming problem and can be defined as:
subject to:
where
If we denote by
There are different EAs techniques used to solve CNOP, highlighting: Genetic Programming (GP), Genetic Algorithms (GA), Evolutionary Programming (EP) and Differential Evolution Algorithm (DEA).
DEA is a simple and easy to implement technique using the basic operators of genetic algorithms: mutation, crossover and selection. Despite its simplicity and smallthe number of parameters, it generates good results in CNOPs.
Since then, DEA has been proven in competitions such as the International Contest on Evolutionary optimization (ICEO) of the IEEE [15, 16] and in a wide variety of real-world applications, such as the optimization of the four-bar mechanism [19] or for global optimization of engineering and chemical processes [10].
The Bacterial Foraging Optimization Algorithm (BFOA) is a SIA based on foraging of Escherichia Coli bacteria [14], which simulates the process of chemotaxis (swim and tumble), swarming, reproduction, and elimination-dispersal.
These bacteria in the process face several problems in their search for food [11]. From this algorithm, significant modifications were made: the number of parameters was reduced, an operator for handling constraints was incorporated [13] and a mutation operator similar to an EAs [6]; this is called Two-Swim Modified-BFOA (TS-MBFOA).
This metaheuristic allows competitive and favourable results when solving CNOPs, with a good configuration of its parameters. This approach has been successfully used to solve engineering design problems, such as the well-known Tension Compression Spring [7], the generation of healthy menus [4] and optimization of a Smart-Grid [5].
In the real world, TS-MBFOA and DEA have implementations for solving optimization problems, however, these algorithms are not fully exploited in different áreas where researchers are not aware of their adaptation and implementation.
Therefore, this research is motivated to explore the capabilities of both algorithms in the solution of particular CNOPs known as: Pressure Vessel, Process Synthesis MINLP, Tension Compression Spring and Quadratically constrained quadratic program. These algorithms are implemented in a free and cross-platform programming language.
Results obtained were validated using basic statistics such as best value, mean, median, standard deviation and worst value.
Also, the nonparametric Wilcoxon Signed Rank Test (WSRT) was applied to measure the consistency of the results.
Finally, convergence graphs of the median number of executions for each algorithm in each problem are presented to notice the performance of the algorithms.
2 Two-Swim Modified Bacterial Foraging Optimization Algorithm (TS-MBFOA)
The TS-MBFOA is a proposed algorithm for solving CNOPs [7], where bacteria
The chemotaxis process is interleaved with exploitation or exploration swim in each cycle.
The process begins with the classic swim (exploration and mutation between bacteria) and is calculated with Eq. 3, where a bacterium will not necessarily interleave exploration and exploitation swims, because if the new position of a given swim
Otherwise, a new tumble will be calculated. The process stops after
The swim operator is calculated with Eq. 4:
where
where
where
In the middle cycle of the chemotaxic process, the swarming operator is applied with Eq. 7:
Bacteria are ordered in the reproduction process, eliminating the worst bacteria
In elimination-dispersión, the worst bacteria are eliminated from the population
3 Differential Evolution Algorithm (DEA)
DEA, developed by Storn and Price in 1995, was proposed to solve numerical optimization problems [17].
This algorithm is competitive in global optimization problems, its strategy is based on population search. The algorithm starts from a population of
An individual of the
where
Initialization process: individuals are randomly generated within the search space limited by the upper and lower limit of each problem variable, i.e.:
Mutation process: the search direction controls the magnitude of displacement in the search space and the speed of convergence to the optimal solution. The mutated vector is constructed from two vectors weighted by a scaling factor, as shown in Eq. 9:
where
Crossover process: controls the recombination of the mutation of individuals to generate a new descendant, where the CR operator is an end-user-defined parameter, which can be randomly or statically defined.
In the selection process: the descendant is evaluated in the problem function. If the descendant obtains a better result than the parent, then it replaces the parent in the next generation of the algorithm, otherwise the parent is kept (Eq. 10):
where
4 Experimentation and Results
TS-MBFOA and DEA were implemented in the Java programming language, a free and cross-platform language.
The CNOPs to solve by both algorithms have their own characteristics, such as: different numbers of variables, number and types of constraints, ranges of variables, among others; as presented below in its mathematical model.
Problem 1: Pressure Vessel.
Minimize:
subject to:
where: 1 ≤
Problem 2: Process Synthesis MINLP.
Minimize:
subject to:
where:
Problem 3: Tension Compression Spring. Minimize:
where: 0.05 ≤ d ≤ 2, 0.25 ≤ D 1.3 and 2 ≤ N ≤ 15:
Problem 4: Quadratically constrained quadratic program.
Minimize:
subject to:
where:
Each algorithm has parameters that must be calibrated to generate competitive results.
Previously, we performed tests in search of a good calibration, to run each algorithm on the test problems.
Tab. 1 presents the parameter settings of the TS-MBFOA and DEA. TS-MBFOA and DEA, where a number of 500 fixed generations were established for each algorithm.
Table 1 TS-MBFOA and DEA Parameters
| TS-MBFOA | DEA | ||
| Parameter | Value | Parameter | Value |
| 15 | Population | 50 | |
| 0.0005 | 0.7 | ||
| 8 | 0.8 | ||
| 1.95 | 500 | ||
| 1 | |||
| 100 | |||
| 500 | |||
This yields to around 60,500 evaluations for each algorithm, which allows a fair comparison between the results and to plot the convergence of the algorithms.
In the tests conducted with each algorithm, 30 independent iterations were adjusted to measure the consistency of the results.
The results of the independent runs of each algorithm with the four CNOPs are presented in Tab. 2, where CNOP is the problem to solve,
Table 2 Best result found by the TS-MBFOA and DEA in 30 independent executions to each CNOPs
| CNOP | Nv | Alg | Bv | T |
| 44 | ||||
| Problem 1 | 4 | TS-MBFOA | 8796.84951 | 20 |
|
|
DEA | 9375.75820 | ||
| 55 | ||||
| Problem 2 | 7 | TS-MBFOA | 4.26075 | 31 |
|
|
DEA | 3.73269 | ||
| 96 | ||||
| Problem 3 | 3 | TS-MBFOA | 0.012665 | 21 |
|
|
DEA | 0.012665 | ||
| 22 | ||||
| Problem 4 | 2 | TS-MBFOA | -118.70485 | 27 |
|
|
DEA | -118.70485 | ||
TS-MBFOA obtained better results than DEA in most of the runs. However, the runtime of DEA was smaller in many cases.
In problem 1, the TS-MBFOA obtained a result of
For problem 2, DEA finds the best optimal solution of 3.73269. With TS-MBFOA, the best value found is 4.26075, a non-competitive solution. For problems 3 and 4, both algorithms find the global optimum of the problem similar to the optimal solution known in the state-of-the-art.
Generally speaking, both algorithms generate results in less than 60 seconds, except for problem 3. With TS-MBFOA this experiment tooked 96 seconds, but it is a reasonable time with a competitive result.
For each experiment performed with both metaheuristics, basic statistics were applied to check the consistency of the results obtained.
Tab. 3 shows the basic statistics of the 30 iterations performed for each CNOPs with both algorithms. The TS-MBFOA obtains better results in problem 1. In problems 3 and 4, both algorithms obtain equal results.
Table 3 Basic statistics of the best results of the 30 iterations of the TS-MBFOA and DEA. The best values are highlighted in bold
| CNOP | Measure | TS-MBFOA | DEA |
|
Problem 1 |
Media | 8796.84982 | 9375.75820 |
| Median | 8796.84951 | 9375.75820 | |
| Std. dev. | 0.00166 | 5.45696E-12 | |
| Worst | 8796.85879 | 9375.75820 | |
|
Problem 2 |
Media | 4.27758 | 3.73305 |
| Median | 4.27485 | 3.73305 | |
| Std. dev. | 0.01223 | 2.01891E-4 | |
| Worst | 4.32189 | 3.73348 | |
|
Problem 3 |
Media | 0.012665 | 0.012665 |
| Median | 0.012665 | 0.012665 | |
| Std. dev. | 0.0000013 | 7.110684E-12 | |
| Worst | 0.012672 | 0.012665 | |
|
Problem 4 |
Media | -118.7048 | -118.70485 |
| Median | -118.7048 | -118.70485 | |
| Std. dev. | 7.21821E14 | 4.26325E-14 | |
| Worst | -118.7048 | -118.7048 | |
In problem 2, DEA obtains a better result. According to the standard deviation, the consistency of the solutions found by DEA is better than TS-MBFOA.
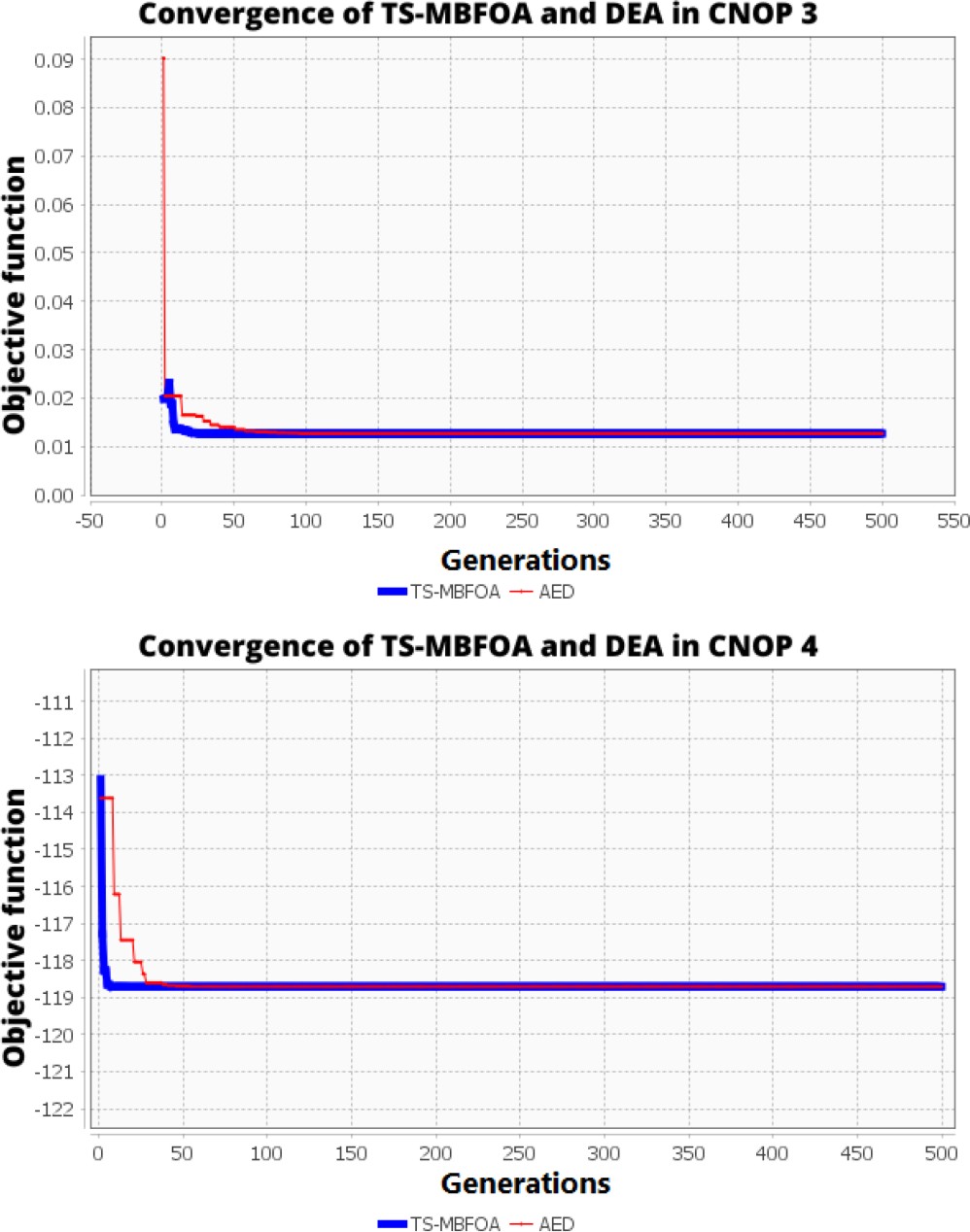
Figs. 1 and 2 present the behavior of both algorithms at each CNOP of iteration number 15 of the 30 runs performed independently (median).
The convergence of both algorithms is similar in 3 of the 4 CNOPs, both algorithms from the first 50 generations already reach optimal solutions.
Only in problem 2 both algorithms require more than 200 generations to converge to an optimal solution. It is worth mentioning that CNOP 2 is a highly constrained problem. The WSRT non-parametric test was applied with a 95% confidence level, being 5% the significant level.
The result obtained in CNOP 1, 2, and 3 is p-value = 0.00001, a value lower than the significant level.
This indicates a significant difference between the results of both algorithms. Therefore, the lower the p-value, the more significant the result. For CNOP 4 the p-value = 0, this indicates that there is no significant difference.
5 Conclusion and Future Work
In this work, two metaheuristics were implemented to solve a set of numerical optimization problems with constraints: TS-MBFOA, a swarm intelligence algorithm, and DEA, an evolutionary algorithm. Four benchmark problems were tested on both algorithms, programmed in Java Language.
30 independent runs were performed by each algorithm on each test problem with a number of 500 generations and approximately 60,500 evaluations.
The parameters of each algorithm were adjusted to the number of evaluations allowed in this work. Basic statistics and a non-parametric test called Wilcoxon Signed Rank Test was applied to know the quality and consistency of the results, where both algorithms obtained similar results.
DEA has better consistency of results according to the standard deviation obtained in each problem. TS-MBFOA and DEA obtained better quality results in 1 of the 4 problems. The non-parametric test indicates that there is no significant difference between the results of both algorithms in problem 4.
In the remaining three problems, there is a significant difference (problem 1, 2 and 3). With respect to execution times, both algorithms generate solutions in seconds, however, DEA is the one that generates results in less time with respect to TS-MBFOA and this is due to the simplicity of the processes and the small number of parameters of the evolutionary algorithm.
The convergence graph of each algorithm shows that the TS-MBFOA and DEA after 50 generations begin to converge, but in problem 2, both algorithms converge after 200 generations.
It is necessary to perform a finer adjustment of the parameters of each algorithm and to test both algorithms in more benchmark problems.











 nova página do texto(beta)
nova página do texto(beta)