1 Introduction
The off-line one-dimensional Bin Packing Problem (1D-BPP) is a well-known grouping optimization problem with many applications in logistics, industry, telecommunications, transports, among several others. Given an unlimited number of bins with a fixed capacity
It implies that there is no efficient algorithm to find an optimal solution for every instance of 1D-BPP. Searching for the best possible solutions to 1D-BPP, a wide variety of algorithms have been designed. The proposals range from simple heuristics to hybrid strategies, including branch and bound techniques [7], metaheuristics [20] and special neighbourhood searches [4].
However, despite the efforts of the scientific community to develop new strategies, there is not yet an efficient algorithm capable of finding the best solution for all possible 1D-BPP instances, so it is then important to try to identify the characteristics that define the behavior of the algorithms to understand and improve their performance.
One of the suggested methods to solve BBP is the Grouping Genetic Algorithm (GGA) proposed by Falkenauer in 1996 [10], who presented a design of three new components: (1) a representation scheme for solutions in which groups are seen as genes; (2) a fitness function that evaluates the exploitation of bins’ capacity; and, (3) grouping variation operators to modify and re-combine the group-based solutions, including a Segment-level crossover. Later, in 2015, Quiroz-Castellanos et al. [20] proposed the algorithm known as Grouping Genetic Algorithm with Controlled Gene Transmission (GGA-CGT).
Unlike Falkenauer, Quiroz-Castellanos et al. proposed the application of the variation operators in a controlled way, inducting the fullest-bin pattern. GGA-CGT is one of the best algorithms found in the state-of-the-art to solve 1D-BPP; it focuses on the transmission of the best genes on the chromosomes (the fullest-bin pattern), keeping a balance between selective pressure and diversity in the population, in order to favor the generation and evolution of high-quality solutions. GGA-CGT includes an intelligent grouping crossover operator, called Gene-level crossover, which gives the best genes (the fullest bins) a higher probability of being preserved.
The experimental results presented by Quiroz-Castellanos et al. [20] exposed that the Gene-level crossover showed an effectiveness improvement of 30% when compared with the Segment-level crossover proposed by Falkenauer [10]. Despite the success of the Gene-level crossover, the performance of the GGA-CGT is related mainly to the mutation operator, which alone is capable of finding quality solutions.
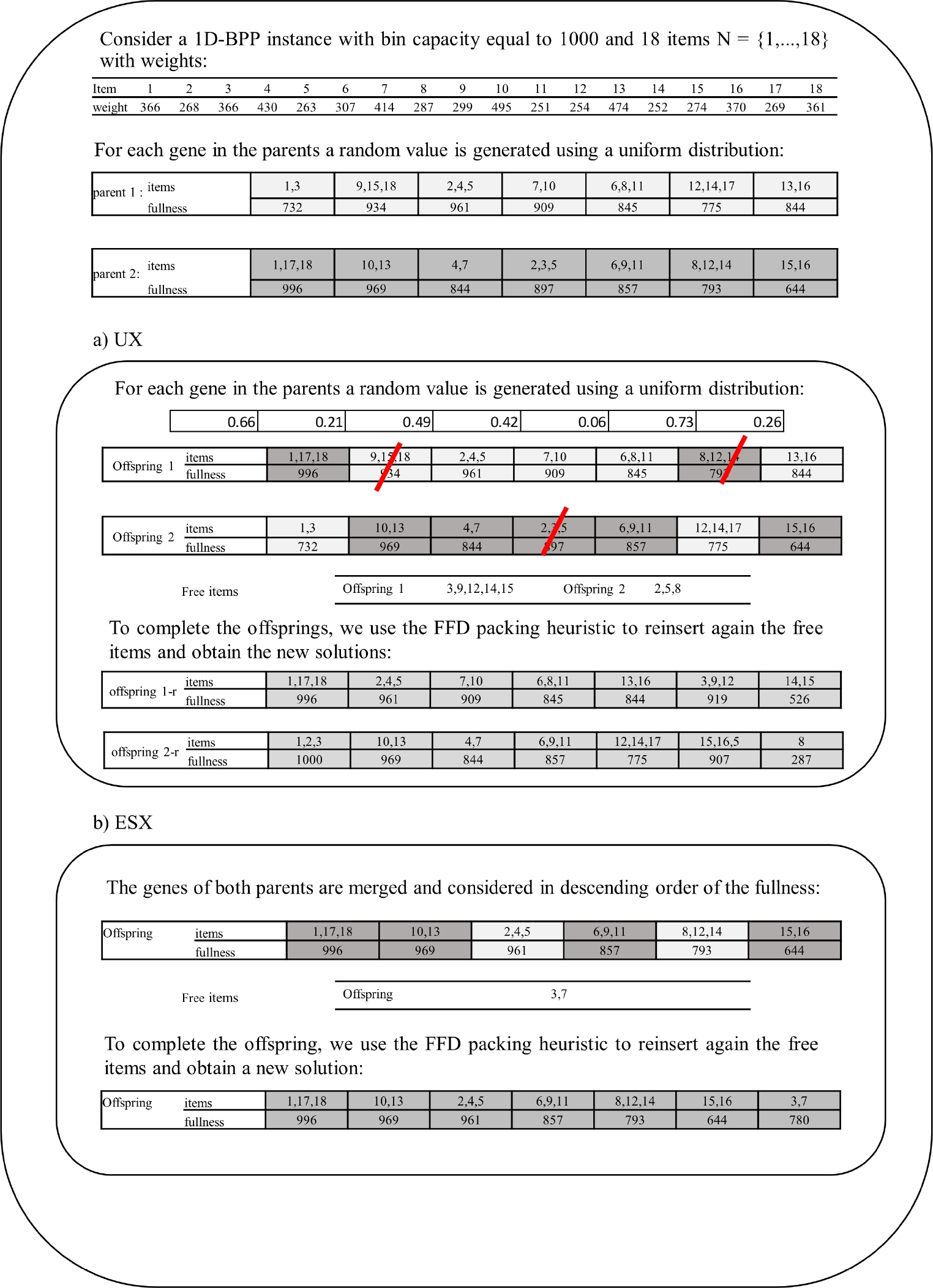
In the present work, three well-known grouping crossover operators are implemented to solve 1D-BPP: Uniform crossover, Exon Shuffling crossover and Greedy Partition crossover. These operators have never been implemented within the GGA-CGT algorithm before. Furthermore, the Uniform crossover has not been used to solve the 1D-BPP. The goal of the implementation is to measure the performance of these crossover operators whit respect to the predefined Gene-level crossover operator. The performance of the GGA-CGT is studied by replacing the original Gene-level crossover operator with each of these state-of-the-art crossovers as well as new versions of the Gene-level and the Uniform crossover operators.
The paper structure is as follows. Section 2 presents the most relevant state-of-the-art algorithms for 1D-BPP; Section 3 comprises a brief definition of the components of the GGA-CGT; Section 4 includes an explanation for the state-of-the-art grouping crossover operators that will be implemented afterwards; Section 5 contains the experimental proposal to analyze the performance of the mentioned grouping crossover operators; finally, Section 6 summarizes the conclusions and future research paths.
2 Releated Work
In the last three decades, different techniques have been implemented in order to find the best solution for the BPP, as it is one of the most interesting problems of the optimization field. Among the techniques that stand out the most are hybrid algorithms and heuristics. For the 1D-BPP study, most algorithms proposed in the literature have been evaluated using a well-studied trial benchmark [8]; it includes 1615 instances in which the number of items
The specialized literature includes approximation algorithms, which had their performances math-ematically analyzed, being the most successful ones: (1) First-Fit Decreasing (FFD), (2) Best-Fit Decreasing (BFD) and (3) Minimum Bin Slack (MBS) [13]. The proposals also include many exact algorithms using dynamic programming, LP relaxation, branch-and-bound, branch-and-price and constraint programming methods [7, 17]. The most relevant results have been obtained by means of metaheuristic and hybrid algorithms covering proposals based on local search [2, 4], evolutionary algorithms [3, 10, 20, 15, 5] and swarm intelligence algorithms [1, 16, 18, 11]. The most exploited approaches, which have allowed obtaining the best results, consist mainly of: (1) the use of simple 1D-BPP heuristics; (2) the application of search space reduction methods; (3) the inclusion of local search techniques based on the dominance criterion; (4) the use of lower bounding strategies; and (5) the induction of the fullest-bin pattern.
The review of the results obtained by the best 1D-BPP solution algorithms revealed that there are still instances of the literature that present a high degree of difficulty and the strategies included in the procedures do not seem to lead to better solutions. After the literature analysis, it was observed that none of the state-of-the-art strategies had been analyzed to explain the reason for its high-grade or poor performance. Few studies have centered on the analysis of the relationships between the effectiveness of the algorithms and the structure and complexity of the 1D-BPP instances [6]. It is important to understand the algorithms’ behavior and evaluate the strategies that allow them to achieve their performance. This work aims at studying the performance of different grouping crossover operators trying to identify the strategies that they use and that positively impact their performance.
3 Grouping Genetic Algorithm with Controlled Gene Transmission (GGA-CGT)
The GGA-CGT proposed in 2015 by Quiroz-Castellanos et al. [20] uses a group-based representation in which each gene represents a group of items or bin. The GGA-CGT is aimed at maximizing the fitness of the individuals in the population. The fitness function is described as follows:
where
GGA-CGT uses a controlled selection regarding the choice of individuals to cross and mutate. The strategy consist of an elitist approach together with two inverted rankings to give all the solutions a chance to contribute to the next generation but forcing the survival of the best solutions. For the crossover,
GGA-CGT includes a new crossover operator that is referred to as Gene-level crossover, which generates two children
Regarding the mutation, it consists of an Elimination operator which works at the gene level, promoting the transmission of the best genes on the chromosome. The Adaptive mutation operator, which considers the bins in descending order of their filling, eliminating the
where
The replacement strategy preserves the population diversity and the best solutions by replacing duplicated fitness individuals and the worst fitness solutions with new offspring. The controlled replacement method for the crossover consists of introducing the
When the mutation operator is applied, some of the elite solutions whose age is less than a predefined
The details of the heuristics used to generate the population, the rearrangement heuristics to repair solutions, as well as the remaining mechanisms and the parameter settings can be consulted in the work of Quiroz-Castellanos et al. [20].
In order to identify the impact of the Gene-level crossover operator (GLX) on the GGA-CGT per-formance, an experimental study was performed by using nine different values for the crossover rate, to vary the number of individuals selected for the crossover process
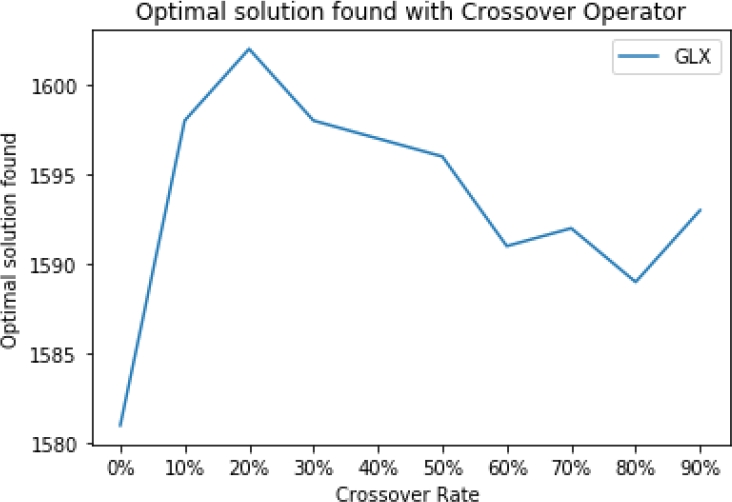
Fig. 1 Number of optimal solutions obtained by the GGA-CGT with the original Gene-level crossover (GLX) for different crossover rates
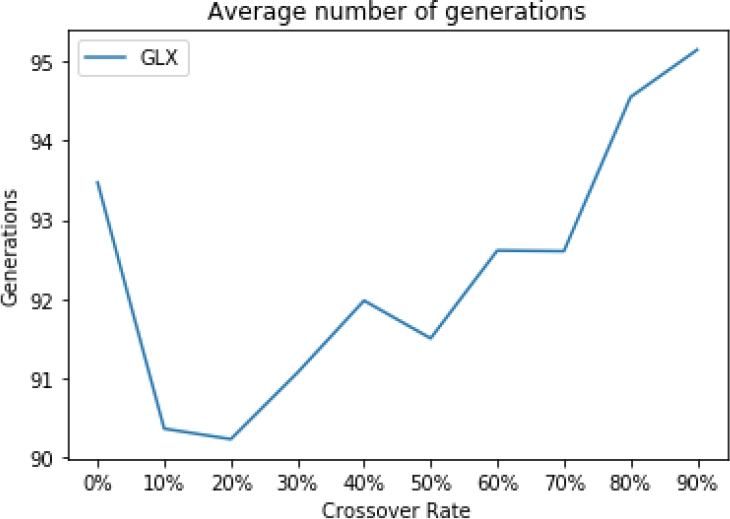
Fig. 2 Average number of generations executed by the GGA-CGT with the original Gene-level crossover (GLX) for different crossover rates
The following sections will present a series of studies consisting of: (1) implementing the state-of-the-art crossover operators in the GGA-CGT algorithm; (2) performing experimentation with different crossover percentages within the algorithm; and (3) analyzing the results of the GGA-CGT algorithm with each operator.
4 Grouping Crossover Operators
The crossover is one the most frequently used genetic operators. This operator combines the information of two or more solutions (called parents) to produce descendants (called children or offspring). The state-of-the-art algorithms includes different grouping crossover operators (see Ramos-Figueroa et al. [21] for a survey of grouping genetic operators). Grouping crossover operators perform the transmission of the genetic material considering the characteristics of every gene, performing a more controlled combination process, by giving the best genes a higher probability of being preserved.
The state-of-the-art algorithms present four grouping crossover operators that work with the group-based encoding: Gene-level crossover (GLX), Uniform crossover (UX), Exon Shuffling crossover (ESX), and Greedy Partition crossover (GPX). GLX was described in Section 3. The following sections describe the general procedure of the other three operators.
4.1 Uniform Crossover
The Uniform crossover (UX) variation operator generates two children
4.2 Exon Shuffling Crossover
The Exon Shuffling crossover (ESX), was proposed by Kolkman and Stemmer (2001) [14]. It has been often used to tackle 1D-BPP [9, 25, 19]. This is an operator that generates a single child
4.3 Greedy Partition Crossover
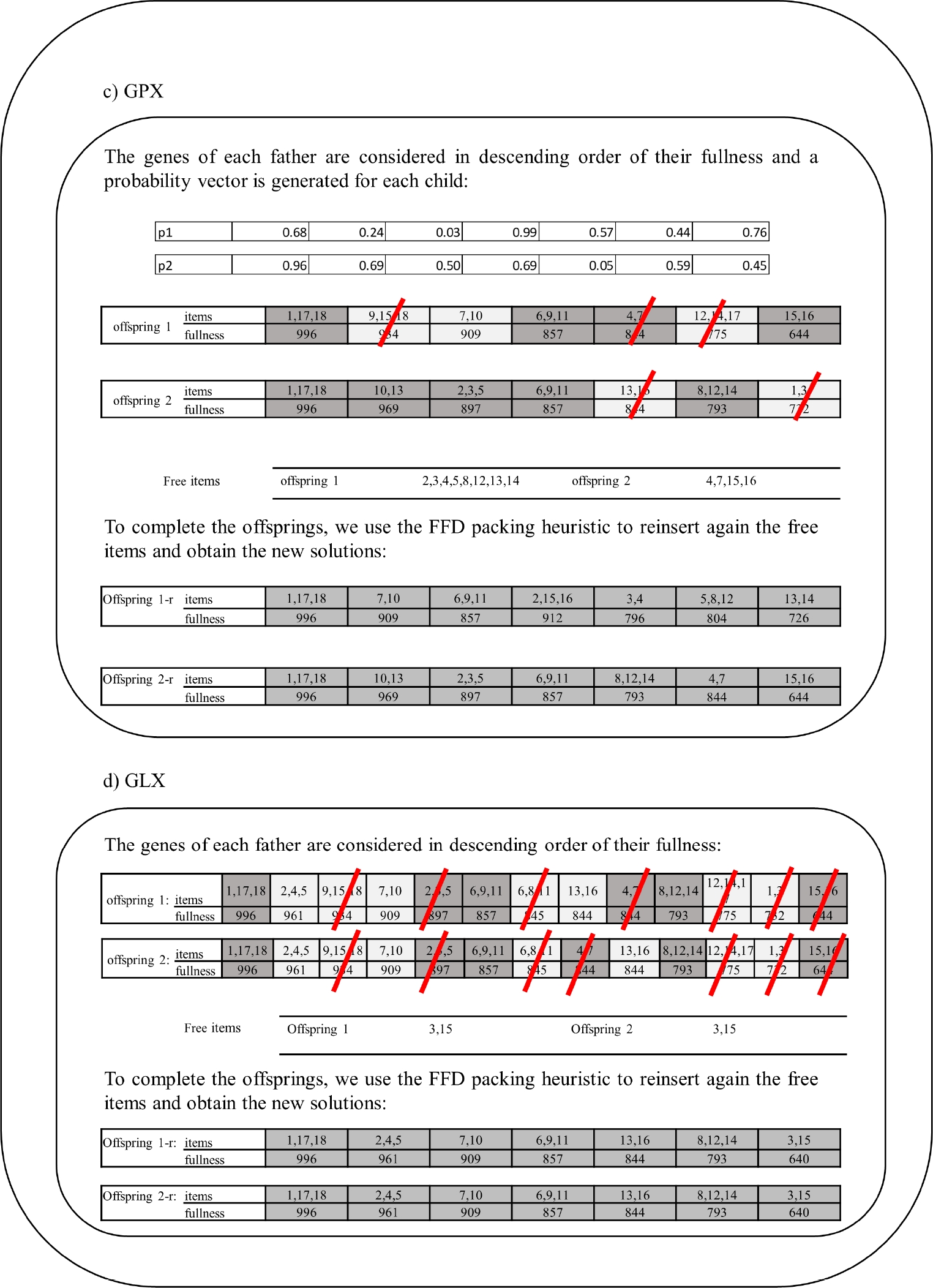
The Greedy Partition crossover (GPX), is also among the state-of-the-art grouping oriented crossover operators that have been used to tackle 1D-BPP in other Grouping Genetic Algorithm [23]. This particular operator has two versions and this paper focuses on the group oriented one. Given two parent solutions
4.4 Gene-Level Crossover
The operator is described in Section 3. This operator was proposed by Quiroz-Castellanos et al. [20] for the GGA-CGT algorithm and has been used several times to solve the 1D-BPP due to its performance [15, 22, 24]. Figure 4d depicts an example of the crossover process followed by GLX.
Since the above operators, are considered the best grouping crossover operators amongst the state-of-the-art, the next section comprises an analysis of these operators to determine which one enables the GGA-CGT to reach the best performance for 1D-BPP. The experiments cover: (1) the integration of the operators in the GGA-CGT algorithm; (2) the study of different crossover percentages; and, (3) the robustness analysis of the results of the best crossover operators inside the GGA-CGT algorithm.
5 Experimentation and Results
This section presents the experiments to analyze the way the different crossover operators can impact on the performance of GGA-CGT. The experimental design consists of three phases. The first one covers the analysis of the state-of-the-art grouping crossover operators (UX, ESX, GPX and GLX) to determine which ones have the best impact on the effectiveness of GGA-CGT. The second one comprises an analysis of the best operators to observe the influence of the number of children generated and their reinsertion to the population. Finally, the third one studies the robustness of the GGA-CGT with the best crossovers, comparing with the original GLX operator.
The performance assessment of each operator involves solving the 1615 standard instances [8], which are distributed among nine sets: data set 1 (720 instances), data set 2 (480 instances), data set 3 (10 instances), triplets (80 instances), uniform (80 instances), hard28 (28 instances), was 1 (100 instances), was 2 (100 instances), and gau 1 (17 instances). Sets data set 1, data set 3, gau 1 and hard28, have shown to have test cases with a high degree of difficulty. Standing out hard28, where there is a higher number of instances that the algorithms cannot solve optimally.
To analyze the performance of each operator on the GGA-CGT, for each instance, a single execution of the algorithm GGA-CGT was run, with the initial seed for the random number generation set to 1. For each operator ten different crossover rates were explored, from 0% to 90% of the population. For all the parameters, different from the crossover rate, we used the configuration proposed by Quiroz-Castellanos et al. [20].
5.1 State-of-the-Art Grouping Crossover Operators
The GGA-CGT employs the controlled reproduction technique proposed by Quiroz-Castellanos et al. [20], for the state-of-the-art crossover operators we used the same strategy. Both, the UX operator and the GPX operator, generate a set
Table 1, Table 2, Table 3, and Table 4 show the results obtained by the GGA-CGT with each of the state-of-the-art crossover operator (UX, ESX, GPX and GLX, respectively). For every class of instances, each table first shows the number of test cases (Inst.), followed by the number of optimal solutions found by the GGA-CGT with each crossover rate. The last row of each table shows the total number of optimal solutions obtained by each configuration. Moreover, Fig. 5 and Fig. 6 show the number of optimal solutions that are found and the average number of generations executed, when we explore ten different crossover rates (from 0% to 90%) over the four different crossover operators.
Table 1 Results obtained by the GGA-CGT with the Uniform crossover (UX) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 718 | 719 | 719 | 718 | 718 | 718 | 718 | 719 | 718 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 479 | 480 | 479 |
| data set 3 | 10 | 9 | 9 | 10 | 10 | 10 | 10 | 10 | 9 | 10 | 10 |
| triplets | 80 | 80 | 80 | 80 | 80 | 79 | 80 | 78 | 78 | 78 | 69 |
| uniform | 80 | 80 | 80 | 80 | 80 | 79 | 80 | 80 | 80 | 79 | 80 |
| hard28 | 28 | 9 | 11 | 9 | 10 | 8 | 8 | 7 | 6 | 7 | 5 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| Total | 1615 | 1581 | 1591 | 1591 | 1592 | 1587 | 1589 | 1586 | 1583 | 1586 | 1574 |
Table 2 Results obtained by the GGA-CGT with the Exon Shuffling crossover (ESX) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 719 | 719 | 719 | 718 | 718 | 719 | 719 | 718 | 720 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 |
| data set 3 | 10 | 9 | 9 | 10 | 9 | 9 | 10 | 9 | 10 | 9 | 9 |
| triplets | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 |
| uniform | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 |
| hard28 | 28 | 9 | 9 | 10 | 10 | 10 | 12 | 9 | 10 | 9 | 8 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 15 | 16 | 16 | 16 | 16 | 15 | 15 | 15 | 15 |
| Total | 1615 | 1581 | 1592 | 1595 | 1594 | 1593 | 1596 | 1592 | 1594 | 1591 | 1592 |
Table 3 Results obtained by the GGA-CGT with the Greedy Partition crossover (GPX) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 720 | 719 | 718 | 719 | 718 | 719 | 719 | 718 | 718 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 478 |
| data set 3 | 10 | 9 | 9 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 9 |
| triplets | 80 | 80 | 80 | 79 | 80 | 79 | 80 | 79 | 80 | 75 | 73 |
| uniform | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 79 | 80 | 80 | 79 |
| hard28 | 28 | 9 | 11 | 12 | 8 | 9 | 6 | 8 | 6 | 6 | 6 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 15 | 14 | 14 | 13 | 13 | 14 | 14 | 13 | 13 |
| Total | 1615 | 1581 | 1595 | 1594 | 1590 | 1590 | 1587 | 1589 | 1589 | 1582 | 1576 |
Table 4 Results obtained by the GGA-CGT with the Gene-level crossover (GLX) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 719 | 720 | 719 | 718 | 718 | 718 | 718 | 718 | 719 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 |
| data set 3 | 10 | 9 | 9 | 10 | 9 | 9 | 9 | 9 | 9 | 8 | 9 |
| triplets | 80 | 80 | 80 | 80 | 79 | 79 | 78 | 76 | 77 | 74 | 78 |
| uniform | 80 | 80 | 80 | 80 | 80 | 79 | 80 | 79 | 79 | 79 | 80 |
| hard28 | 28 | 9 | 14 | 16 | 15 | 16 | 15 | 13 | 14 | 14 | 12 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 16 | 16 | 16 | 16 | 16 | 16 | 15 | 16 | 15 |
| Total | 1615 | 1581 | 1598 | 1602 | 1598 | 1597 | 1596 | 1591 | 1592 | 1589 | 1593 |

Fig. 5 Number of optimal solutions obtained by the GGA-CGT with each state-of-the-art crossover for different crossover rates
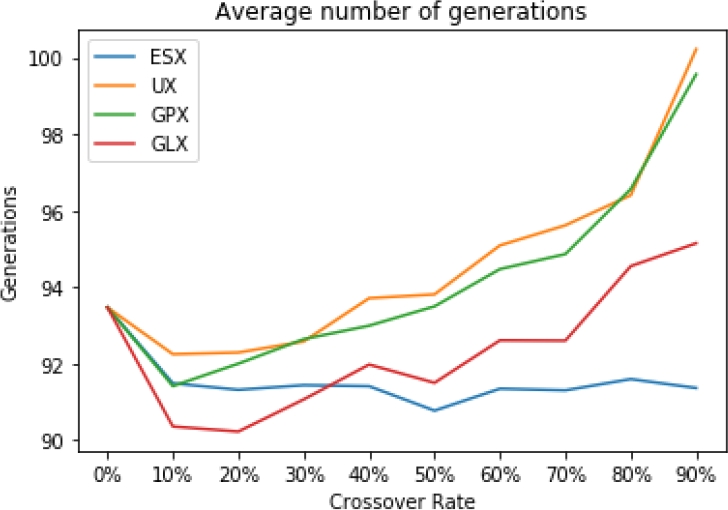
Fig. 6 Average number of generations executed by the GGA-CGT with each state-of-the-art crossover for different crossover rates
The results obtained from implementing the UX variation operator in the GGA-CGT algorithm, are shown in Table 1. As can be seen, the highest number of instances solved is 1592, with a crossover rate of 30%, however, with 90% of crossover rate, the performance of the GGA-CGT is affected since it only solves 1574 of the 1615 instances less than those solved with 0% crossover rate. In terms of the average number of generations, with a 90% of crossover rate, the algorithm iterates 100.22 generations per instance, as it is shown in Fig. 6.
The results obtained from implementing the ESX variation operator in the GGA-CGT algorithm are shown in Table 2. As can be seen, the highest number of the optimally solved instances is 1596, with a 50% crossover rate. Something interesting in this operator is that the optimally solved instances are between 1592 and 1596, and it is not affected with any crossover rate. Concerning to the average number of generations, the algorithm performs a maximum of 91.6 generations, corresponding to a crossover rate of 80%, as it is shown in Fig. 6.
The results obtained from implementing the GPX operator in the GGA-CGT algorithm, are shown in Table 3. The operator solves optimally at most 1595 instances with a 10% crossover rate. As the UX operator, the performance of the GGA-CGT is affected with a 90% crossover rate, since it only finds the optimal solution of 1576 instances less than those solved with 0% crossover rate. It is important to mention that it performs 99.56 generations on average with a 90% crossover rate, as it is shown in Fig. 6.
The same experiment was performed for the crossover operator of the GGA-CGT algorithm, GLX [20]. The results are presented in the Table 4, which with a 20% crossover rate solves optimally 1602 instances out of 1615. The minimum number of optimal solutions is found with a crossover rate of 80%, being 1589, and it indeed benefits the algorithm, since without crossover, it finds only 1581 optimal solutions.
From Fig. 5 and Fig. 6 it can be observed that ESX and GLX outperformed the performance of the other two crossover operators, presenting a more stable behavior with different crossover rates.
After the execution of the GGA-CGT with the four crossover operators it was concluded that the ESX operator with a configuration of a 50% of crossover rate and the GLX operator with a 20% crossover rate, found a higher number of optimal solutions, which is why a series of experiments were performed, based on these results and they are described below.
5.2 Reinsertion of Children to the Population
Considering that the GLX algorithm generates two offspring for each pair of crossed parents, for the following experiments, the replacement criteria within the GGA-CGT algorithm were considered. Two versions of the GGA-CGT algorithm were implemented, where the GLX crossover operator generates only one child for each pair of parents.
For the implementation of the following experimentation, the following three cases were addressed: (1) when the ESX algorithm reinserts offspring into the population by replacing individuals with repeated fitness and, if there are still offspring without reinsertion, by replacing the worst solutions; (2) when the GLX algorithm reintegrates the created offspring into the population by replacing individuals within the set of random parents
The case where ESX reinserts the children into the population by replacing individuals within the set of random parents

Fig. 7 Number of optimal solutions with different replacements. ESX-1 GLX-1: children replace the individuals in the set of the random parents. ESX-2, GLX-2: children replace the individuals with duplicated fitness and also the worst solutions

Fig. 8 Average number of generations with different replacements. ESX-1 GLX-1: children replace the individuals in the set of the random parents. ESX-2, GLX-2: children replace the individuals with duplicated fitness and also the worst solutions
The results obtained by the ESX variation operator, corresponding to the case when using reinsertion into the population by replacing the solutions within the repeated fitness group and worst solutions (ESX-2), are shown in Table 5. The GGA-CGT algorithm manages to solve optimally a maximum of 1593 instances with crossover rates of 30% and 40%. The lowest number of instances that it solves optimally is 1589 with a 10% crossover rate.
Table 5 Results obtained by the GGA-CGT with the Exon Shuffling crossover with replacement to individuals with duplicated fitness and the worst solutions (ESX-2) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 718 | 719 | 719 | 718 | 718 | 718 | 718 | 718 | 718 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 |
| data set 3 | 10 | 9 | 9 | 9 | 10 | 10 | 9 | 10 | 9 | 9 | 10 |
| triplets | 80 | 80 | 80 | 80 | 80 | 80 | 79 | 79 | 79 | 80 | 79 |
| uniform | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 |
| hard28 | 28 | 9 | 8 | 9 | 9 | 10 | 9 | 10 | 10 | 10 | 9 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 14 | 15 | 15 | 15 | 16 | 15 | 15 | 15 | 15 |
| Total | 1615 | 1581 | 1589 | 1592 | 1593 | 1593 | 1591 | 1592 | 1591 | 1592 | 1591 |
On the other hand, the results of the imple-mentation of the GLX operator with the reinsertion into the population by replacing the parents of the random group (GLX-1) are presented in Table 7. As it can be seen, the operator implemented within the algorithm finds a maximum number of 1599 optimal solutions with a 20% crossover rate, while the lowest number of optimal solutions is 1591 with a 80% crossover rate.
Table 6 Results obtained by the GGA-CGT with the Gene-level crossover with replacement to individuals with duplicated fitness and the worst solutions (GLX-2) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 719 | 719 | 719 | 718 | 719 | 719 | 719 | 720 | 719 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 |
| data set 3 | 10 | 9 | 10 | 9 | 9 | 10 | 10 | 10 | 9 | 10 | 9 |
| triplets | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 79 |
| uniform | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 |
| hard28 | 28 | 9 | 12 | 13 | 13 | 14 | 12 | 13 | 11 | 12 | 13 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 15 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 15 |
| Total | 1615 | 1581 | 1596 | 1597 | 1597 | 1598 | 1597 | 1598 | 1595 | 1598 | 1595 |
Table 7 Results obtained by the GGA-CGT with the Gene-level crossover with replacement to individuals in the set of the random parents R(GLX-1) for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 719 | 720 | 719 | 720 | 719 | 718 | 718 | 718 | 719 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 480 |
| data set 3 | 10 | 9 | 10 | 10 | 9 | 9 | 9 | 10 | 9 | 9 | 9 |
| triplets | 80 | 80 | 79 | 79 | 79 | 78 | 79 | 76 | 78 | 75 | 79 |
| uniform | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 79 | 79 | 79 |
| hard28 | 28 | 9 | 13 | 14 | 14 | 15 | 13 | 14 | 15 | 15 | 11 |
| was1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 16 | 16 | 16 | 16 | 16 | 15 | 16 | 15 | 16 |
| Total | 1615 | 1581 | 1597 | 1599 | 1597 | 1598 | 1596 | 1593 | 1595 | 1591 | 1593 |
The last experiments, corresponding to the GLX with the reinsertion of the offspring in the population replacing the solutions with repeated fitness and worst fitness (GLX-2), are shown in Table 6. This operator allows the GGA-CGT to find a maximum of 1598 optimal solutions with crossover rates of 40%, 60% and 80%, while the minimum number of instances optimally solved is 1595 for 70% and 90% crossover rates, without taking into account the results when there is no crossover.
Based on the results discussed earlier in this section, with respect to the implementation of the two versions of the ESX operator, it is concluded that the ESX operator using a reinsertion of the children in the group of random parents (ESX-1), has a better performance, since it solves on average 1593.22 instances in an optimal way out of 1615. Moreover, the highest number of optimal solutions found by the ESX operator are solved with this reinsertion (1596). On the other hand, the other reinsertion, replacing parents with repeated and worst fitness solves an average of 1591.55 instances in an optimal way.
Regarding the results of the implementation of the GLX operator in the version that only creates one child for every two parents, when the reinsertion into the population is performed by replacing the solutions with repeated and worst fitness (GLX-2), it has better results, finding on average 1596.77 optimal solutions. In the case of the GLX operator with reinsertion to the population by replacing the set of random parents (GLX-1), an average of 1595.44 optimal solutions are found. Moreover, by means of this replacement the highest number of optimal solutions are found by the GLX operator (1599).
5.3 Uniform Crossover with Ordered Genes
After analyzing the different features involved in the crossover operators, we observe that the UX operator was the only one that did not sort the parent solutions in descending order before performing the crossover process. A final implementation of the UX operator was done, where the genes of the parents were first sorted in descending order of their filling, and then the usual crossover process of the operator was performed (UX-sorted). The results are shown in the Table 8. As we can see, the algorithm with a 10% crossover rate solves a total of 1596 instances in an optimal way, while with a 90% crossover rate it affects the performance of the algorithm as it only solves 1574 instances. In addition to the above, a comparison was made between the UX operator and UX-sorted. The results are shown in two tables, one presenting the maximum number of instances solved per class in the (Table 9) and the other with respect to the minimum number of instances solved per class in the (Table 10).
Table 8 Results obtained by the GGA-CGT with the UX-sorted crossover for different crossover rates
| Class | Inst. | Crossover rate | |||||||||
| 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| data set 1 | 720 | 708 | 719 | 720 | 719 | 719 | 719 | 719 | 718 | 718 | 718 |
| data set 2 | 480 | 480 | 480 | 480 | 480 | 480 | 480 | 479 | 480 | 480 | 478 |
| dataset 3 | 10 | 9 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 9 |
| triplets | 80 | 80 | 80 | 80 | 80 | 78 | 79 | 77 | 77 | 76 | 71 |
| uniform | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 79 | 79 | 79 | 79 |
| hard28 | 28 | 9 | 13 | 10 | 8 | 9 | 7 | 7 | 7 | 7 | 6 |
| was 1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| gau 1 | 17 | 15 | 14 | 13 | 13 | 13 | 13 | 13 | 14 | 14 | 14 |
| Total | 1615 | 1581 | 1596 | 1593 | 1590 | 1589 | 1588 | 1584 | 1585 | 1584 | 1575 |
Table 9 Results of the highest number of optimally solved instances by the GGA-CGT with the UX and UX-sorted crossover operators
| Class | Inst. | UX | UX-sorted |
| Crossover rate | |||
| 30% | 10% | ||
| data set 1 | 720 | 719 | 719 |
| data set 2 | 480 | 480 | 480 |
| dataset 3 | 10 | 10 | 10 |
| triplets | 80 | 80 | 80 |
| uniform | 80 | 80 | 80 |
| hard28 | 28 | 10 | 13 |
| was 1 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 |
| gau 1 | 17 | 13 | 14 |
| Total | 1615 | 1592 | 1596 |
Table 10 Results of the lowest number of optimally solved instances by the GGA-CGT with the UX and UX-sorted crossover operators
| Class | Inst. | UX | UX-sorted |
| Crossover rate | |||
| 90% | 90% | ||
| data set 1 | 720 | 718 | 718 |
| data set 2 | 480 | 479 | 478 |
| dataset 3 | 10 | 10 | 9 |
| triplets | 80 | 69 | 71 |
| uniform | 80 | 80 | 79 |
| hard28 | 28 | 5 | 6 |
| was 1 | 100 | 100 | 100 |
| was 2 | 100 | 100 | 100 |
| gau 1 | 17 | 13 | 14 |
| Total | 1615 | 1574 | 1575 |
5.4 Robustness of Crossover Operators
To evaluate all of the potential of the best crossover operators, we performed a robustness test by executing three versions of the GGA-CGT thirty times with different seeds of random numbers. These last experiments arose from the comparison of the ESX and GLX operators.
For the GLX operator we used the version in which the children are reinserted in the population by replacing the random parents (GLX-1) with a 50% crossover rate, as well as the original version of the GLX included in the the GGA-CGT algorithm by Quiroz-Castellanos et al. [20], that generates two children with a 20% crossover rate. On the other hand, for the ESX operator we also used the version in which the children are reinserted in the population by replacing the random parents (ESX-1) with a crossover rate of 50%. These operators were selected as they are within the group of operators that showed the higher effectiveness. The experiment consists of 30 executions of the GGA-CGT algorithm (48,450 runs) with each crossover operator.
The results of the experiments are shown in Table 11, Table 12 and Table 13. The second column (Inst.), corresponds to the total number of instances belonging to the class in the first column. The column “Optimal solutions in the 30 executions” includes the total number of optimal solutions found in the 30 executions.
Table 11 Results for the 30 executions of the GGA-CGT with the ESX when it generates only one child
| Class | Inst. | Optimal solutions in the 30 executions | Average number of optimal | % |
| data set 1 | 720 | 21562 | 718.73 | 99.82% |
| data set 2 | 480 | 14400 | 480.00 | 100.00% |
| data set 3 | 10 | 282 | 9.40 | 94.00% |
| triplets | 80 | 2396 | 79.87 | 99.83% |
| uniform | 80 | 2400 | 80.00 | 100.00% |
| hard28 | 28 | 299 | 9.97 | 35.60% |
| was 1 | 100 | 3000 | 100.00 | 100.00% |
| was 2 | 100 | 3000 | 100.00 | 100.00% |
| gau 1 | 17 | 467 | 15.57 | 91.57% |
| 1615 | 47806 | 1593.53 | 98.67% |
Table 12 Results for the 30 executions of the GGA-CGT with the GLX when it generates only one child
| Class | Inst. | Optimal solutions in the 30 executions | Average number of optimal | % |
| data set 1 | 720 | 21562 | 718.73 | 99.82% |
| data set 2 | 480 | 14400 | 480.00 | 100.00% |
| data set 3 | 10 | 281 | 9.37 | 93.67% |
| triplets | 80 | 2370 | 79.00 | 98.75% |
| uniform | 80 | 2393 | 79.77 | 99.71% |
| hard28 | 28 | 394 | 13.13 | 46.90% |
| was 1 | 100 | 3000 | 100.00 | 100.00% |
| was 2 | 100 | 3000 | 100.00 | 100.00% |
| gau 1 | 17 | 476 | 15.87 | 93.33% |
| 1615 | 47876 | 1595.87 | 98.82% |
Table 13 Results for the 30 executions of the original GGA-CGT with the GLX that generates two children
| Class | Inst. | Optimal solutions in the 30 executions | Average number of optimal | % |
| data set 1 | 720 | 21571 | 719.03 | 99.87% |
| data set 2 | 480 | 14400 | 480.00 | 100.00% |
| data set 3 | 10 | 291 | 9.70 | 97.00% |
| triplets | 80 | 2391 | 79.70 | 99.63% |
| uniform | 80 | 2400 | 80.00 | 100.00% |
| hard28 | 28 | 430 | 14.33 | 51.19% |
| was 1 | 100 | 3000 | 100.00 | 100.00% |
| was 2 | 100 | 3000 | 100.00 | 100.00% |
| gau 1 | 17 | 477 | 15.90 | 93.53% |
| 1615 | 47960 | 1598.67 | 98.99% |
The column “Average number of optimal” corresponds to the average number of instances optimally solved in each set. Finally, the column “%” corresponds to the percentage of optimal solutions found.
It is observed that the GGA-CGT algorithm with the GLX operator, which generates two children, found on average a higher number of optimal solutions, with a 98.99% percentage.
While the GLX and the ESX that generate one child found 98.8% and 98.67% of the optimal solutions, respectively. Furthermore, on average, the original GGA-CGT with the GLX operator that generates two children resolves in an optimal way an average of 1598.67 instances out of 1615. Regarding to the GLX and the ESX that generate one child, they found on average 1595.87 and 1593.53 optimal solutions, respectively.
5.5 Statistical Analysis of the Effectiveness of GGA-CGT with the Best Crossover Operators
A series of statistical tests were applied to the results of the 30 executions of the GGA-CGT algorithm with the ESX, GLX and GLX-V1 operators. The statistical test applied was the Wilcoxon Rank-sum test with a 95% confidence. These tests were performed on two result sets. First, the error of the results was calculated for each instance in each execution, which was determined as the relative difference defined as:
For the first set of experiments, the average error of the 30 executions was obtained for each instance.
Next, the Wilcoxon test was applied to the average errors of the algorithm per class of instances with the three operators: ESX vs GLX-V1, ESX vs GLX and GLX-V1 vs GLX, obtaining 9
Table 14 Instances for which the GGA-CGT does not find the optimal solution with each operator for any of the crossover rates
| Class | Inst. | UX | ESX | GPX | GLX | Class | Inst. | UX | ESX | GPX | GLX |
| data set 1 | N3c1w2_r | X | triplets | t501_17 | X | ||||||
| N3c3w4_c | X | X | X | X | t501_18 | X | X | ||||
| N4c3w4_s | X | X | X | X | t501_19 | X | |||||
| data set 2 | N2w1b2r5 | X | X | Uniform | u250_12 | X | X | X | |||
| N2w1b2r8 | X | hard28 | h1D-BPP832 | X | X | X | |||||
| data set 3 | Hard2 | X | h1D-BPP40 | X | X | X | X | ||||
| triplets | t60_00 | X | h1D-BPP360 | X | X | X | |||||
| t60_01 | X | X | h1D-BPP645 | X | X | X | X | ||||
| t60_05 | X | h1D-BPP742 | X | X | X | ||||||
| t60_06 | X | X | h1D-BPP766 | X | X | X | X | ||||
| t60_07 | X | h1D-BPP60 | X | X | X | X | |||||
| t60_08 | X | h1D-BPP13 | X | X | X | X | |||||
| t60_10 | X | h1D-BPP195 | X | X | X | X | |||||
| t60_11 | X | h1D-BPP709 | X | X | X | X | |||||
| t60_12 | X | h1D-BPP785 | X | X | X | X | |||||
| t60_13 | X | h1D-BPP47 | X | X | X | X | |||||
| t60_14 | X | h1D-BPP181 | X | X | X | X | |||||
| t60_15 | X | h1D-BPP485 | X | X | X | X | |||||
| t60_17 | X | h1D-BPP640 | X | X | X | X | |||||
| t60_18 | X | h1D-BPP144 | X | X | X | X | |||||
| t60_19 | h1D-BPP561 | X | X | X | |||||||
| t120_03 | X | h1D-BPP781 | X | X | X | X | |||||
| t120_14 | X | h1D-BPP900 | X | X | X | X | |||||
| t249_04 | X | h1D-BPP178 | X | X | X | X | |||||
| t501_00 | X | h1D-BPP419 | X | X | X | X | |||||
| t501_04 | X | h1D-BPP531 | X | X | X | ||||||
| t501_05 | X | X | X | h1D-BPP814 | X | X | X | ||||
| t501_08 | X | gau1 | TEST0058 | X | X | ||||||
| t501_09 | X | TEST0014 | X | X | X | X | |||||
| t501_14 | X | X | TEST0030 | X | X | X | X | ||||
| t501_16 | X | TEST0005 | X | X | X | ||||||
| Total | 46 | 25 | 39 | 36 | |||||||
Table 15 p-value of the Wilcoxon test for the error of the GGA-CGT with the ESX, GLX-V1 and GLX crossovers in the different classes of instances
| Class | p-value for the average error | ||
| ESX vs GLX-V1 | ESX vs GLX | GLX-VI vs GLX | |
| data set 1 | 0.9637 | 0.9636 | 1 |
| data set 2 | 1 | 1 | 1 |
| data set 3 | 0.9698 | 0.9698 | 0.9698 |
| triplets | 0.2459 | 0.1557 | 0.8618 |
| uniform | 0.8914 | 0.8914 | 0.9986 |
| hard 28 | 0.5552 | 0.5121 | 0.9151 |
| was 1 | 1 | 1 | 1 |
| was 2 | 1 | 1 | 1 |
| gau 1 | 0.7828 | 0.7828 | 0.9862 |
For the second set of tests, all instances were considered separately. A Wilcoxon test was performed for each instance with the results obtained from the algorithm with the different operators, i.e.: ESX vs GLX-V1, ESX vs GLX and GLX-V1 vs GLX. The Table 16 shows the results of the instances where a significant difference was observed in the results obtained with the different operators.
Table 16 p-value of the Wilcoxon test for the error of the GGA-CGT with the ESX, GLX-V1 and GLX crossovers in the most difficult instances
| Class | Instance | p-value of the error of the 30 executions | ||
| ESX vs GLX-V1 | ESX vs GLX | GLX-V1 vs GLX | ||
| hard 28 | h1D-BPP360.txt | 0.0147 | 0.147 | 1 |
| h1D-BPP742.txt | 0.0039 | 0.0009 | 0.6574 | |
| h1D-BPP47.txt | 3.3853x10-7 | 2.9537x10-8 | 0.6574 | |
| h1D-BPP640.txt | 0.01471 | 0.01471 | 1 | |
| h1D-BPP531.txt | 2.9537x10-8 | 2.9537x10-8 | 1 | |
| h1D-BPP814.txt | 0.0039 | 0.0039 | 1 | |
| gau 1 | TEST0030.txt | 0.0358 | 0.069 | 0.6574 |
The Wilcoxon test, at the class level, shows no significant difference between the operators, which would indicate that the performance is the same among the three. However, the test at the instance level does show a difference, in some instances of the Hard28 and Gau 1 classes, between the ESX operator and the GLX-V1 and GLX operators, indicating that for these instances the ESX operator is the worst operator.
5.6 Difficult 1D-BPP Instances
Finally, with the objective to identify the features of the 1D-BPP instances that present the highest degree of difficulty for the four state-of-the-art grouping crossovers, Table 16 shows the set of instances for which the optimum was not found. These results were obtained from the set of experiments performed with the different crossover rates, selecting those instances that were not solved optimally in at least one of the configurations.
The first column includes the name of the sets of instances that include cases for which the optimal solutions could not been found for some of the configurations of the four crossover operators. The second column contains the name of the difficult instances, and the following columns include an X for each operator that fails to find the optimal solutions for each instance in one of its configurations. The instances belong to the classes: data set 1, data set 2, data set 3, triplets, uniform, hard28 and gau 1. The highest number of instances where the optimum is not found belong to the triplets class. With respect to the class data set 3 and uniform, only one instance is not optimally solved.
As it can be seen, the instances belonging to the hard28 class are the most complicated for the 4 operators. The operator with the lowest number of optimally solved instances is the ESX operator. Although the GLX operator optimally solves the highest number of instances, these instances tend to be more variable with different crossover percentages.
The UX operator, on the other hand, is the one that has the greatest diversity with respect to the number of instances not optimally resolved, being a total of 46. With respect to the instances belonging to the triplets class, the ESX operator is the only operator that has no problem in finding the optimum, besides being the only one to solve optimally all the instances of the Uniform class.
Although the GGA-CGT algorithm finds the optimal solution of most of the well-known benchmark instances within the state-of-the-art, it has been shown that it does not perform well with the 2800 new difficult instances, referred to as
6 Conclusion and Future Work
In this research we propose an experimental study about the GGA-CGT for the 1D-BPP, in which different grouping crossover operators were used to compare and mesure the performance. The conclusions of this research are presented as follows.
From the experiments carried out in Section 5, it is concluded that the original Gene-level crossover operator (GLX), when generating two children, outperforms the other state-of-the-art grouping crossovers, achieving a better performance with respect to the number of optimal solutions found, being 1602 out of 1615. The second experiment, also explained in Section 5, on the implementation of the ESX and GLX operators in their two versions (generating only one child, with replacement to random parents, and, with replacement to solutions with repeated fitness and worst solutions), shows that the best operator is the GLX operator with the reinsertion to the population through the replacement to random parents, since it solves optimally a total of 1599 instances out of 1615.
The last experiment allow us to validate that the original GLX operator, that generates two children, is the one that achieves the best performance, showing a robust behavior in different runs of the GGA-CGT. Finally, it can be concluded that the GLX operator performs better within the GGA-CGT algorithm.
Although the GLX operator solves a larger number of instances, per class there is no significant difference between the operators. But there is a difference for some instances of the Hard 28 class, where it has been shown that the GLX operator has the best performance of the operators.
For future work, a detailed review of the operators is planned to identify the strategies that allow for them to improve their performance in the different classes instances, with the objective of using this knowledge to design a new crossover operator with a better performance in terms of time, number of generations and number of optimal solutions found for instances of different classes. It is also intended that the GGA-CGT algorithm with the operator to be designed will improve the performance of the algorithm for the











 nova página do texto(beta)
nova página do texto(beta)