SciELO - Scientific Electronic Library Online
 
vol.26 número2Analysis of CNN Architectures for Human Action Recognition in VideoAn Experimental Study of Grouping Crossover Operators for the Bin Packing Problem índice de autoresíndice de assuntospesquisa de artigos 		Home Pagelista alfabética de periódicos  

Serviços Personalizados

Journal

Artigo

Indicadores

Links relacionados

  • Não possue artigos similaresSimilares em SciELO

Compartilhar

Computación y Sistemas

versão On-line ISSN 2007-9737versão impressa ISSN 1405-5546

Comp. y Sist. vol.26 no.2 Ciudad de México Abr./Jun. 2022  Epub 10-Mar-2023

https://doi.org/10.13053/cys-26-2-4247 

Articles of the thematic issue

Fuzzy Flower Pollination Algorithm: Comparative Study of Type-1 and Interval Type-2 Fuzzy Logic System in Parameter Adaptation Optimization

Héctor Carreón-Ortiz1 

Fevrier Valdez1 

Óscar Castillo1 

11 Tijuana Institute of Technology, Mexico. fevrier@tectijuana.mx.

Abstract:

State-of-the-art algorithms are competitive, because they get the most out of available resources. Metaheuristic algorithms solve optimization problems from a search space. The proposal in this research work is to use the algorithm bio-inspired by nature Flower Pollination Algorithm (FPA) for the optimization of the membership functions of an Interval Type-2 Fuzzy Logic system, which we will call IT2FLS-FPA (Interval Type-2 Fuzzy Logic System-Flower Pollination Algorithm). This work is presented to continue with one that we developed before [6], in this investigation we made a comparison between a non-optimized IT2FLS-FPA and an optimized IT2FLS-FPA where we demonstrate that the latter is better by means of statistical hypothesis tests.

Keywords: Bioinspired algorithm; flower pollination algorithm; optimization; interval type-2 fuzzy logic

1 Introduction

Optimization minimizes or maximizes a function by randomly choosing the values of the variables within an admissible range [94, 96]. Research continues to develop algorithms that achieve the above purpose. The development of algorithms for real problems is of interest to many research studies. In the beginning optimization techniques used gradient based algorithms, where the main idea was to find a range of solutions near the origin [2, 55], these methods provide accurate solutions and fast convergence, better than stochastic approaches. The problem is that this type of algorithms will only tend to local minima and not to the global minimum.

The resource constraint is faced in daily competition to all types of systems, in this struggle different strategies have been employed to change the established order. Optimization is used to handle the problem of limited resources (producing more with less). In the search for optimization, goals must be achieved with few resources [3, 4]. The objective function is the set goal that varies depending on the problem [5, 6]. The goal of optimization is to find the parameter values that minimize or maximize a specific objective, for example, in an engineering design is to find the parameter values that satisfy the needs of the design with minimum cost, optimization solves this type of requirement.

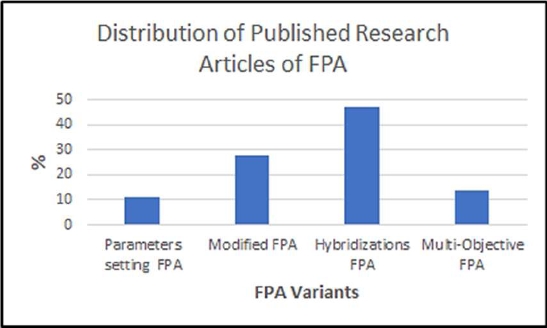
FPA is a very popular optimization method among researchers because of its characteristics as it has few parameters and has demonstrated a robust performance when applied to various optimization problems, that is why we decided to use this metaheuristic inspired by nature, besides that we have worked previously with this algorithm [7] and has proven to be very good and we can see it in the work done by [8, 17, 36, 37, 41, 42, 50, 51, 52, 64, 87, 88, 89, 90], there are variants of FPA developed by [59, 60, 61, 62, 63], in Figure 1 we can see a graphical summary of the variants [86], also hybrid algorithms have been developed with the FPA as [64, 65, 66, 67, 68], the applications of the FPA in the areas Chemical Engineering, for thermodynamic systems [69], in petroleum industry [70] where FPA is one of the effective algorithms in this area, in the preparation of triaxial porcelain from Palm Oil Fuel Ash (POFA) [71] and POFA was used as the cement filler for enhancing the EMI absorption of cement-based composites [72].

Fig. 1 Distribution of published research articles of FPA 

In civil engineering it is one of the most important areas of applied optimization, because nonlinear design problems with complex constraints, costs, architectural design constraints, physical requirements often generate a complex engineering problem [73, 74, 75]. In mechanical engineering FPA has contributed in solving speed reducer, gear train, tension-compression spring design problems using hybrid algorithms with FPA with local search [66, 74, 76, 77, 78].

In Electronical and Communication Engineering, metaheuristic methods have also been employed in wireless communication systems such as [79, 80], using global pollination, enhanced local pollination and dynamic shift probability FPA was improved by [81], also FPA was used to solve radio spectrum optimization problems. In Energy and Power Systems, Dubey et al [59] modified FPA to solve practical power system test cases, Prathiba et al [82] employed FPA to minimize fuel cost in a bus system.

Lenin et al [67] hybridized FPA with harmony search algorithm to optimize reactive power dispatch. In Computer Science, FPA was employed in image compression Kaur et al [83], for multilevel image FPA was used for Ouadfel and Taleb-Ahmed [84].

A binary FPA was employed for Rodrigues et al [85] for solutions across the corner in electro encephalogram, Jensi and Jiji [68] proposed a hybrid approach combining K-Means algorithm and FPA that finds the center of the optimal cluster.

The main contribution of this work is to use the metaheuristic Flower Pollination Algorithm (FPA) and the Type 2 Fuzzy Logic System (IT2FLS) to dynamically adjust the parameters of the FPA in order to obtain better results than in the previous work [6], where experiments with FPA and Fuzzy Logic were performed.

In other published works [30, 31, 32, 33, 34] and in the most recent ones [35, 36] it has been shown that the use of Fuzzy Logic can be better because good results are obtained than not using it but using (IT2FLS) in the dynamic adaptation of the parameters in the FPA metaheuristic is much better by the results obtained in this research.

The remainder of this article is organized as follows. Section 2 describes works that other authors have done on the FPA algorithm and the IT2FLS method, Section 3 gives a very general review of the bio-inspired algorithms, Section 4 is basic information on the FPA algorithm, Section 5 describes the origin and development of the type-1 and interval type-2 fuzzy systems, Sections 6 and 7 present the model and the proposed parameters, in Section 8 we show the results of this research and finally in Section 9 we present the conclusions of this paper.

2 Related Works

Several researches on the Flower Pollination Algorithm (FPA) and a Fuzzy System (FS) have been developed in the 8 years, one of them is where the optimization of the parameters of the membership functions is performed using the FPA algorithm to simulate the motion of a robot [8], according to [7] in the simulation the FPA algorithm calls the model and, in the process, updates the variables. In another paper [9] where a hybrid approach for fire outbreak detection based on FPA algorithm and IT2FLS using meteorological parameters is proposed.

According to fire information, numerous grammatical uncertainties can be assumed in type-2 membership functions, so that the accuracy of fuzzy systems can be increased [50]. In a work we conducted in 2020 [6] where we used the FPA Algorithm and a FS to solve a water tank control problem, by means of the FPA algorithm, the parameters of the membership functions of the fuzzy system simulating the water tank were optimized.

3 Bioinspired Optimizations

Bio-inspired optimization is based on biological systems, which have been the inspiration for solving optimization problems. The subsets of natural computation according to [10, 53] are biological computation and optimization. Metaheuristic optimization simulates the biological behaviors of animals or plants and has been used to find the optimal solution to a problem. A metaheuristic is a heuristic strategy to solve complex optimization problems.

Optimization methods according to Fevrier Valdez, et al. 2020 [11, 58] in 1960 Holland at the University of Michigan started working with Genetic Algorithms (GAs) [12, 93, 95], in 1995 Eberhart and Kennedy, inspired by the social behavior of bird flocking or fish schooling, developed Particle Swarm Optimization (PSO) [13], in 1983 Kirkpatrick et al. And in 1985 Cerny proposed the simulated annealed probabilistic (SA) method [14] and the Pattern Search developed by Robert Hooke and T. A. Jeeves [15] is a family of numerical optimization methods that does not require the gradient of the problem to be optimized, so it can be used on functions that are not continuous or differentiable.

4 Flower Pollination Algorithm (FPA)

FPA was developed by Xin-She Yang in 2012, inspired by the pollination process of flowering plants [16, 17, 36, 37], let us analyze the general pollination behavior of plants, there are two forms of pollination: biotic and abiotic.

Biotic pollination: pollen is transported to the stigma by insects and animals. Abiotic pollination: wind and water are the means of pollination. Research says that 10% of pollination has an abiotic pollination process and, therefore, does not require any pollinator.

There are two ways of pollination: self-pollination and cross-pollination. Self-pollination occurs from the pollen of the same flower or from different flowers of the same plant, in this process local pollination occurs and cross-pollination occurs through a flower of a different plant and can occur over long distances by means of bees, bats, birds, flies, etc., which fly long distances, these pollinators make global pollination possible [17, 38, 39, 40]. The author of the algorithm describes the flower constancy and the behavior of pollinators in the pollination process with the following four rules [17, 41, 42, 43, 44, 45]:

  1. Global pollination process takes place by biotic and cross-pollination and pollinators perform Lévy flights [17, 46, 47].

  2. Local pollination process is considered abiotic and self-pollinating.

  3. Flower constancy, pollinators visit plants with specific flowers to increase reproductive success.

  4. A probability of change p ∈ [0, 1] that controls global and local pollination.

The basic idea is the fact that each plant has a flower and each flower originates a gamete, so it is established is that it is not necessary to distinguish between a plant, a flower or a gamete [51]. Birds, insects, etc. (pollinators) can fly enormous distances for biotic and cross-pollination to occur. Lévy's flight perfectly describes the flight of pollinators, rules 1 and 3 using Levy's distribution [52] describe global pollination to plot random step sizes (L) as Eq. (1).

The mathematical modeling of the 4 rules is as follows; the processes of global pollination (Rule 1) and flower constancy (Rule 3) are represented by the following equation:

xit+1=xit+γL(λ)(g*−xit), (1)

where:

xit+1 is the generated solution vector at iteration t+1, xit is the pollen i or the solution vector xi at iteration t, g* is the current best solution, γ is a scaling factor used to control the step size, L(λ) is the Lévy flights-based step size, it corresponds to the strength of the pollination. In reality, pollinators can fly long distances with different lengths (step size), this can be modeled using a Lévy distribution according to the following equation:

L~λΓ(λ)sin(πλ2)π1s1+λ(s≫s0>0), (2)

where:

Γ(λ) is the standard gamma function, and this distribution is valid for large steps s>0.

Local pollination (Rule 2), and flower constancy (Rule 3) can be represented as follows:

xit+1=xit+ε(xjt−xkt), (3)

where:

xjt and xkt are pollen gametes obtained from different flowers of the same plant species, randomized between 0 and 1 to approximate this selection to a local random walk. (xjt−xkt) is used to imitate the flower constancy in a limited neighborhood.

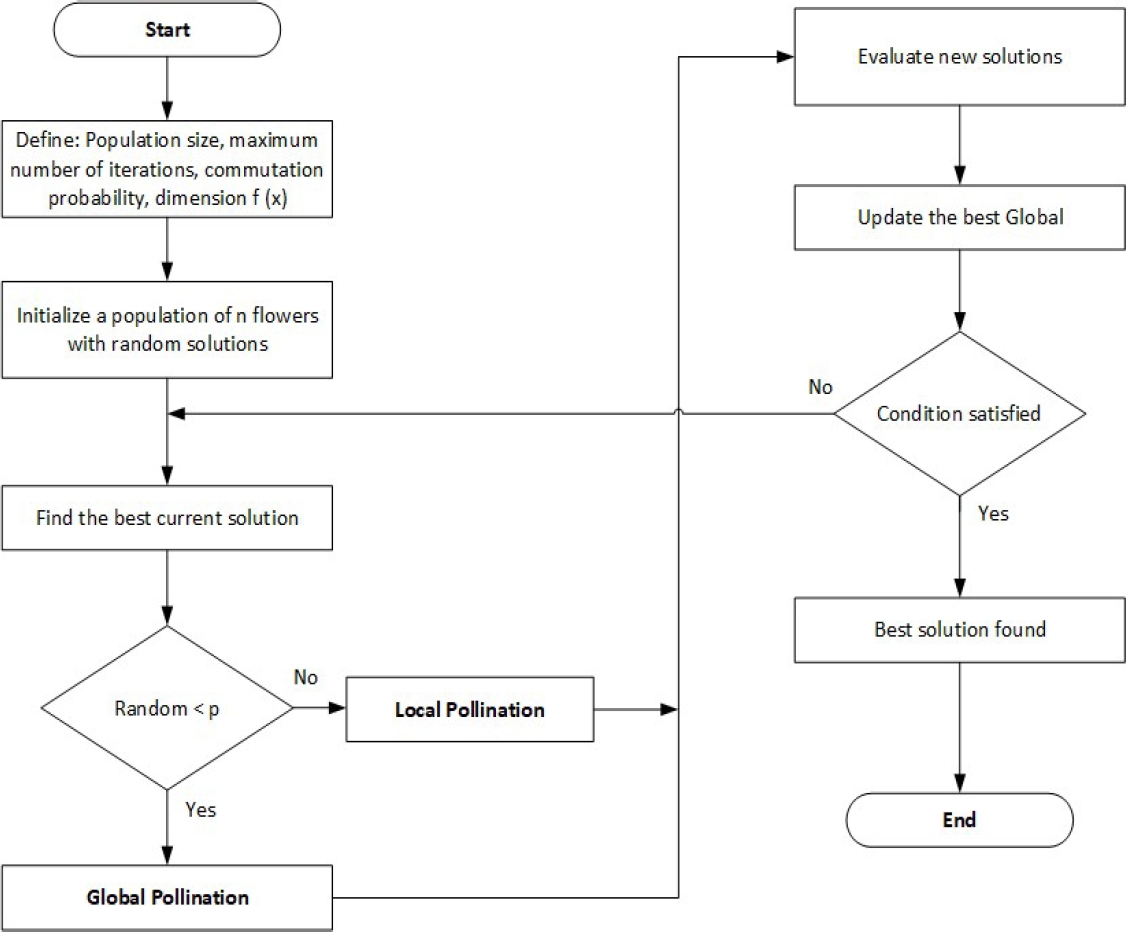
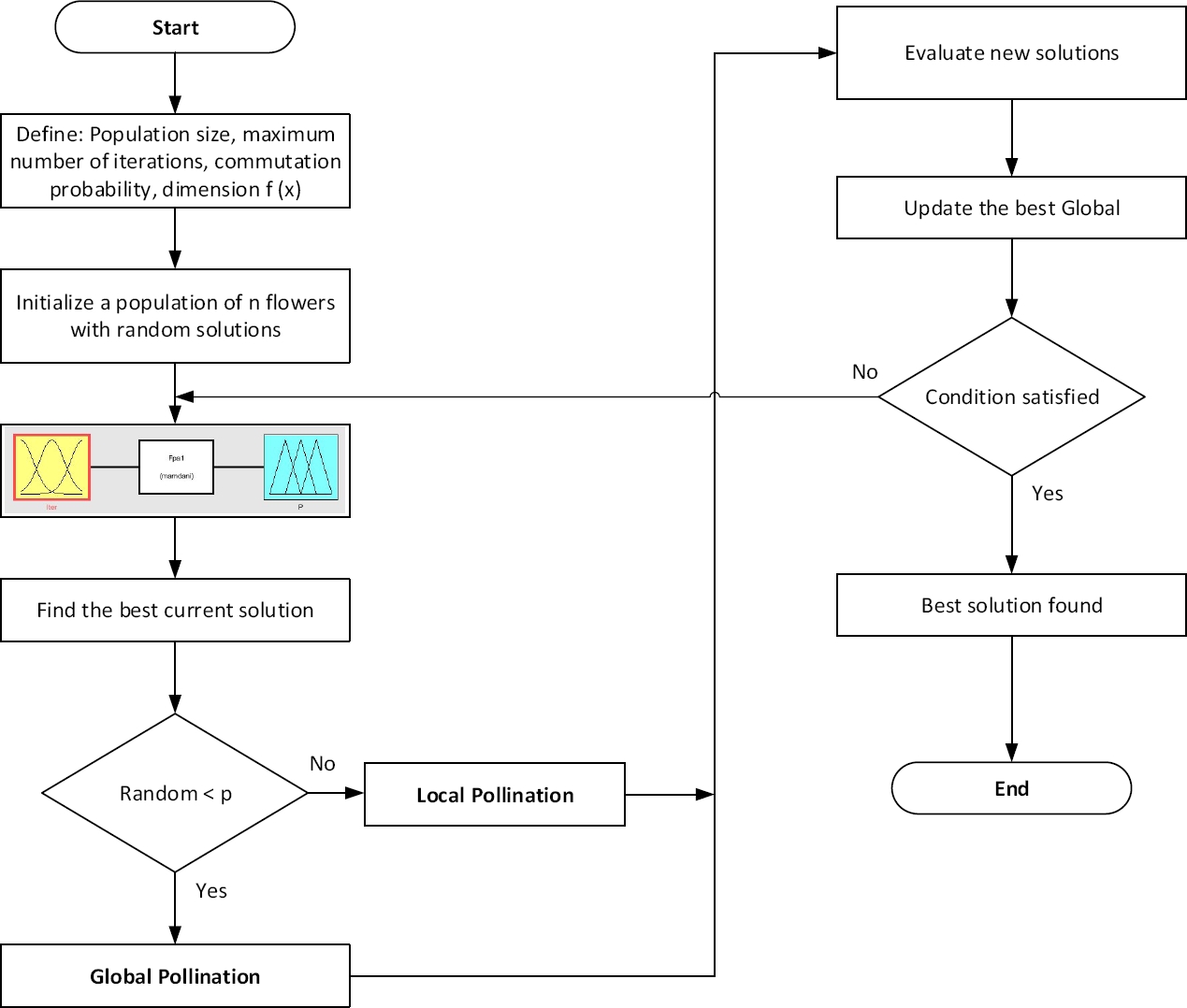
Fourth rule, flower pollination processes can occur randomly at all scales, both in the local and global case. Therefore, to emulate this biorientation, a switching parameter p chosen randomly from [0,1] can be effectively used.

In the following, the flowchart and pseudocode of the flower pollination algorithm are shown in Figures 2 and 3.

Fig. 2 Flower Pollination Algorithm Flowchart 

Fig. 3 Pseudo code of the proposed Flower Pollination Algorithm (FPA) 

5 Fuzzy Logic

Uncertainty, doubt, skepticism, suspicion, imprecision, approximation and distrust mean lack of certainty about someone or something. Uncertainty can range from lack of certainty to almost total lack of conviction or knowledge, especially about an outcome. Uncertainty has always been present in human life, one of the main advances on uncertainty in recent years is the introduction of fuzzy logic, which means a deep understanding of approximate reasoning [18], the origin of fuzzy logic comes from fuzzy set theory, its principles come from two sources of the last century [19]:

  • – First: Charles S. Peirce, who applied the term "Logic of vagueness" and was unable to develop and complete his theory before his death [19]. The mathematician and philosopher Max Black (1937) took up the concept of "Logic of vagueness" [20]. In 1923, the philosopher Bertrand Russell proposed that "vagueness" is a matter of value [21]. Therefore, the "Logic of vagueness" turned out to be the subject of interest of other researchers such as Brock [22], Nadin [23, 24], Engel-Tiercelin [25] and Merrell [26, 27] [19]

  • – Second source: the mathematician Lofti A. Zadeh used in 1960 for the first time the term "Fuzzy Sets" and continued to develop this idea for the next 40 years, in his first paper published in 1965 on Fuzzy Sets [28], it was the beginning of a new stage of his scientific career, in the publication of this first article, the answer generated in the scientific community a lot of controversy.

From 1965 onwards, all published articles focused on the process and use of the fuzzy set thesis [19]. Professor Richard Bellman, renowned mathematician, was its main advocate and one of its most important contributors to the analysis and control of systems, in general this theory "Fuzzy Sets" was received with hostility and skepticism.

5.1 Basic Theory

The idea of Fuzzy Logic is not to determine whether the variable X is true or false, but to determine to what degree ∈ [0,1] it is true. We call this degree of certainty the degree of membership, although in some texts it is called possibility and, in this case, special emphasis is usually made on the difference between probability (empirical measure of the frequency with which an observation is repeated in a set of measurements) and possibility (degree of membership of an observation to a fuzzy set), we also speak of confidence level since it is the degree to which we are sure that the observation belongs to the defined set. The degree of membership is assigned by the membership function (f: X → R).

Fuzzy set theory allows us to gradually evaluate the membership of elements relative to a set. The fuzzy set 'A' in a nonempty space X(A⊆X) can be defined as [19]:

A={(x,uA(x))|X∈U}, (4)

where uA:X→[0,1] is a function of each element of X that establishes the extent to which it belongs to the set A. This function is called the membership function of the fuzzy set A.

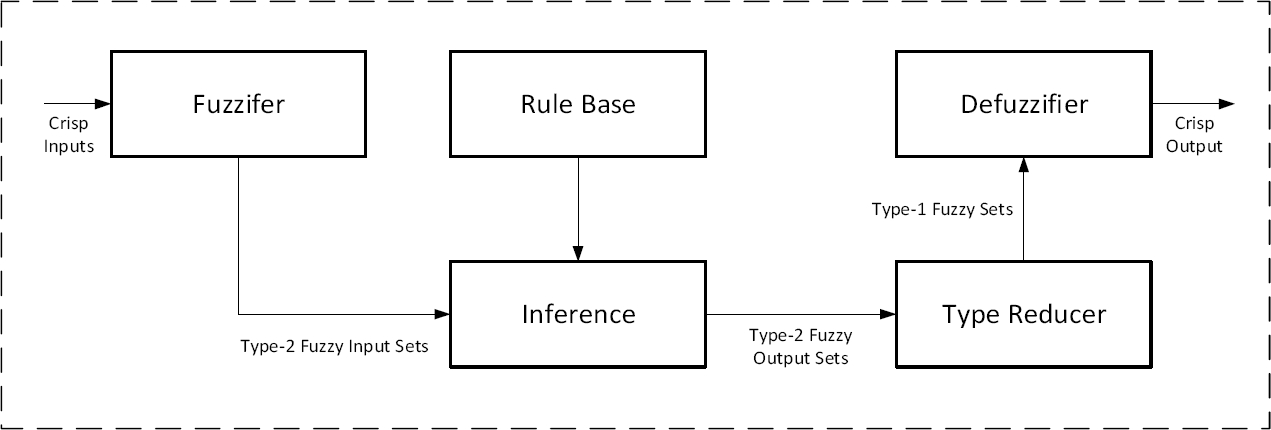
Figure 4 shows us the basic structure of a fuzzy control system [96, 97, 98], which are detailed below:

  • – Fuzzification: Fuzzifies the system inputs.

  • – Rule base: Contains the selection of fuzzy rules.

  • – Mechanism of inference (Rule Inference Module): It contains a database that defines the membership functions used in the rules and a reasoning mechanism that performs the inference procedure (fuzzy reasoning).

  • – Defuzzification: Converts the (fuzzy) result of the inference process to a real value (crisp) within the domain of the output variable [31].

Fig. 4 General sketch for a fuzzy controller 

5.2 Interval Type-2 Fuzzy Logic System

It is known that Type-2 fuzzy systems (T2FLS) allow us to model and minimize the effects of uncertainty in Type-1 Fuzzy Systems (T1FLS) [32, 49]. We also understand that Type-2 fuzzy systems are more difficult to use and understand, so their use is still not very common [48, 54, 56, 98].

Figure 6 shows structure of Type-2 Fuzzy Control System T2FLS [1, 33, 34, 35, 57, 92]:

A˜={(x,uA˜(x))|∀x∈X}, (5)

Fig. 5 Membership Function for IT2 

Fig. 6 Scheme of a Type-2 FLC 

The interval type 2 fuzzy sets proposed by Zadeh [91] and continued by Liang and Mendel [35], provide the mathematical approach to handle uncertainty by means of a secondary domain describing the uncertainty of the data. Mathematical equation of IT2FLS (6):

A˜={((x,u),1)|∀x∈X,∀u∈Jx⊆[0,1]}, (6)

X is the primary domain representing the degree of membership of the fuzzy set and Jx is the secondary domain related to the uncertainty and is always equal to 1. An IT2 MF can be defined from two limiting T1 MFs, and they are known as the upper MF and the lower MF and the Footprint of Uncertainty (FOU) (Mendel and John, 2002), which is the area between the two, and Figure 5 illustrates these concepts. In an IT2 FIS, the inference is very similar to that of a T1 FIS.

6 Mathematical Modeling of Fuzzy Flower Pollination Algorithm (FFPA)

Figure 7 shows the FPA flow diagram where the type-2 fuzzy system is included in the algorithm process by intervals.

Fig. 7 Fuzzy Flower Pollination Algorithm Flowchart 

7 Parameter Adaptation

This research uses the optimization algorithm inspired by the nature FPA, the method to optimize the parameters applies small adjustments in the optimization process, for the adjustment of the parameters, it uses Interval Type-2 Fuzzy Logic System (IT2FLS) to verify the value of one or more parameters in each iteration of the algorithm.

The fuzzy system uses as input the percentage of iterations in which p is evaluated, to know the new values of the parameters and thus to know if it is a global or local pollination.

To evaluate the error of these metrics, the parameter E (epsilon) is used, which represents the flower constancy, all these parameters are used as input for the fuzzy system defined by equations (7) and (8):

Iteration=Current iterationMaximum of iteration, (7)

Mean Square Error (MSE):

MSE=1n∑i=1n(Yi−Y^i)2, (8)

where:

Yi = Current result at time i.

Y^i = Forecast of the value at instant i.

n = Total number of samples considered.

8 Simulation Results

All the experiments carried out in this investigation were done with 8 mathematical functions, Figure 8, shows the 8 Benchmark functions: Sphere, Ackley, Rastrigin, Zakharov, Griewank, Sum of Different Powers, Michalewickz and Rosenbrock, FPA-T1FLS and FPA-IT2FLS as indicated in the table.

Fig. 8 Benchmark functions that were used for the experiments 

Tables 1 and 2 show the results: Best, Worse, Mean, and Standard Deviation for 30 and 100 dimensions of the FPA-T1FLS.

Table 1 Experiments with FPA and T1FLS 

30 – Dimensions – FPA-T1FLS
Function Best Worse Mean Std
1-Sphere 1.650E-04 2.080E-02 4.350E-03 5.000E-03
2-Ackley 1.690E-02 2.210E+00 7.620E-01 9.830E-01
3-Rastrigin 2.630E-02 1.070E+02 9.800E+00 2.530E+01
4-Zakharov 2.790E-03 1.380E-01 3.890E-02 3.670E-02
5-Griewank 2.530E-06 6.310E-04 1.410E-04 1.320E-04
6-Sum of Dif Powers 5.010E-17 2.510E-11 1.120E-12 4.550E-12
7-Michalewicz -9.520E+00 -1.310E+01 -1.180E+01 8.360E-01
8-Rosenbrock 2.370E+01 4.690E+01 3.230E+01 4.370E+00

Table 2 Experiments with FPA and T1FLS 

100 – Dimensions – FPA-T1FLS
Function Best Worse Mean Std
1 Sphere 3.570E-01 1.490E+00 7.520E-01 2.830E-01
2 Ackley 3.960E-01 7.430E-01 5.890E-01 7.740E-02
3 Rastrigin 5.890E-01 1.030E+00 7.910E-01 1.060E-01
4 Zakharov 1.110E+00 4.100E+00 2.080E+00 6.090E-01
5 Griewank 2.660E-03 6.530E-03 4.020E-03 8.870E-04
6 Sum of Dif Powers 6.630E-14 1.090E-08 7.840E-10 2.170E-09
7 Michalewicz -1.400E+01 -2.350E+01 -1.910E+01 2.050E+00
8 Rosenbrock 1.270E+02 2.170E+02 1.680E+02 2.090E+01

Tables 3 and 4 show the results: Best, Worse, Mean, and Standard Deviation for 30 and 100 dimensions of the non-optimized FPA-IT2FLS.

Table 3 Experiments with FPA and non-optimized IT2FLS 

30 – Dimensions – FPA-IT2FLS
Function Best Worse Mean Std
1-Sphere 3.910E-04 2.150E-02 5.100E-03 5.150E-03
2-Ackley 9.390E-02 1.220E-01 7.270E-02 3.390E-02
3-Rastrigin 3.170E+01 3.840E+01 3.500E+01 1.880E+00
4-Zakharov 1.010E-02 1.240E-01 5.230E-02 3.010E-02
5-Griewank 2.880E-05 6.800E-04 1.820E-04 1.520E-04
6-Sum of Dif Powers 1.210E-17 3.570E-11 1.650E-12 6.450E-12
7-Michalewicz -8.510E+00 -1.170E+01 -9.760E+00 7.620E-01
8-Rosenbrock 7.470E+01 1.110E+02 8.920E+01 9.260E+00

Table 4 Experiments with FPA and non-optimized IT2FLS 

100 – Dimensions – FPA-IT2FLS
Function Best Worse Mean Std
1-Sphere 5.710E-01 1.640E+00 1.010E+00 2.900E-01
2-Ackley 5.950E-01 4.950E-01 5.700E-01 1.090E-01
3-Rastrigin 2.260E+02 2.540E+02 2.360E+02 6.470E+00
4-Zakharov 1.300E+00 3.450E+00 2.190E+00 4.740E-01
5-Griewank 5.760E-03 1.440E-02 9.690E-03 2.270E-03
6-Sum of Dif Powers 6.690E-15 4.510E-08 3.010E-09 8.940E-09
7-Michalewicz -1.260E+01 -1.640E+01 -1.460E+01 9.380E-01
8-Rosenbrock 1.080E+03 1.320E+03 1.210E+03 5.390E+01

Tables 5 and 6 show the results: Best, Worse, Mean, and Standard Deviation for 30 and 100 dimensions of the FPA-IT2FLS optimized for the FPA13T2330 architecture.

Table 5 Experiments with FPA and optimized IT2FLS 

30 – Dimensions – FPA-IT2FLS – FPA13T2330
Function Best Worse Mean Std
1.Sphere 1.410E-03 5.229E-02 7.968E-03 9.250E-03
2.Ackley 4.223E-02 1.671E-01 8.219E-02 3.312E-02
3.Rastrigin 2.900E+01 3.840E+01 3.434E+01 2.194E+00
4.Zakharov 6.703E-03 1.502E-01 5.799E-02 3.535E-02
5.Griewank 4.354E-05 1.100E-03 3.038E-04 2.270E-04
6.Sum of Dif Powers 2.488E-19 8.314E-09 3.116E-10 1.491E-09
7.Michalewicz -1.129E+01 -8.452E+00 -9.932E+00 7.098E-01
8.Rosenbrock 9.051E+01 1.379E+02 1.077E+02 1.099E+01

Table 6 Experiments with FPA and optimized IT2FLS 

100 – Dimensions – FPA-IT2FLS – FPA13T2330
Function Best Worse Mean Std
1 Sphere 4.395E-01 1.486E+00 9.833E-01 2.426E-01
2 Ackley 4.748E-01 1.030E+00 7.034E-01 1.275E-01
3 Rastrigin 2.273E+02 2.624E+02 2.476E+02 8.315E+00
4 Zakharov 1.210E+00 3.469E+00 2.106E+00 5.325E-01
5 Griewank 6.794E-03 2.323E-02 1.362E-02 3.384E-03
6 Sum of Dif Powers 3.800E-14 3.892E-07 2.653E-08 8.098E-08
7 Michalewicz -1.686E+01 -1.313E+01 -1.474E+01 1.008E+00
8 Rosenbrock 1.412E+03 1.714E+03 1.549E+03 6.847E+01

Tables 7 and 8 show the results: Best, Worse, Mean, and Standard Deviation for 30 and 100 dimensions of the FPA-IT2FLS optimized for the FPA13T2B130 architecture.

Table 7 Experiments with FPA and optimized IT2FLS 

30 – Dimensions – FPA-IT2FLS – FPA13T2B130
Function Best Worse Mean Std
1.Sphere 5.676E-04 2.330E-02 6.731E-03 5.871E-03
2.Ackley 2.583E-02 1.895E-01 8.226E-02 3.306E-02
3.Rastrigin 2.839E+01 3.940E+01 3.478E+01 2.408E+00
4.Zakharov 1.476E-02 1.722E-01 5.126E-02 3.528E-02
5.Griewank 2.525E-05 9.736E-04 2.843E-04 2.096E-04
6.Sum of Dif Powers 1.491E-17 4.638E-10 1.915E-11 8.446E-11
7.Michalewicz -1.075E+01 -8.854E+00 -9.916E+00 4.734E-01
8.Rosenbrock 9.574E+01 1.376E+02 1.132E+02 1.028E+01

Table 8 Experiments with FPA and optimized IT2FLS 

100 – Dimensions – FPA-IT2FLS – (FPA13T2B130)
Function Best Worse Mean Std
1-Sphere 5.798E-01 1.327E+01 9.797E+00 4.478E+00
2-Ackley 4.947E-01 8.192E-01 6.573E-01 9.349E-02
3-Rastrigin 2.315E+02 2.643E+02 2.521E+02 7.748E+00
4-Zakharov 8.883E+01 1.077E+02 9.939E+01 4.088E+00
5-Griewank 7.521E-03 2.346E-02 1.283E-02 3.657E-03
6-Sum of Dif Powers 5.444E-15 3.533E-08 1.470E-09 6.361E-09
7-Michalewicz -1.828E+01 -1.275E+01 -1.489E+01 1.142E+00
8-Rosenbrock 1.474E+03 1.802E+03 1.638E+03 8.748E+01

Table 9 shows the results: Best, Worse, Mean, Standard Deviation and Z-Test, for 30 dimensions, hypothesis tests were performed with non-optimized FPA-T1FLS and FPA-IT2FLS, it can be observed that only in 4 mathematical functions there were significant evidence that FPA-IT2FLS is better than FPA-T1FLS.

Table 9 Comparison FPA-T1FLS with non-optimized FPA-IT2FLS 

COMPARATIVE 30 Dim FPA-T1FLS FPA-IT2FLS Z-Test
Function Mean Std Mean Std
1.Sphere 4.350E-03 5.000E-03 5.100E-03 5.150E-03 N
2.Ackley 7.620E-01 9.830E-01 7.270E-02 3.390E-02 Y
3.Rastrigin 9.800E+00 2.530E+01 3.500E+01 1.880E+00 Y
4.Zakharov 3.890E-02 3.670E-02 5.230E-02 3.010E-02 N
5.Griewank 1.410E-04 1.320E-04 1.820E-04 1.520E-04 N
6.Sum of Dif Powers 1.120E-12 4.550E-12 1.650E-12 6.450E-12 N
7.Michalewicz -1.180E+01 8.360E-01 -9.760E+00 7.620E-01 Y
8.Rosenbrock 3.230E+01 4.370E+00 8.920E+01 9.260E+00 Y

Table 10 shows the results: Best, Worse, Mean, Standard Deviation and Z-Test, for 100 dimensions, hypothesis tests were performed with non-optimized FPA-T1FLS and FPA-IT2FLS, it can be observed that only in 5 mathematical functions there were significant evidence that FPA-IT2FLS is better than FPA-T1FLS.

Table 10 Comparison FPA-T1FLS with non-optimized FPA-IT2FLS 

COMPARATIVE 100 Dim FPA-T1FLS FPA-IT2FLS Z-Test
Function Mean Std Mean Std
1 Sphere 7.520E-01 2.830E-01 1.010E+00 2.900E-01 Y
2 Ackley 5.890E-01 7.740E-02 5.700E-01 1.090E-01 N
3 Rastrigin 7.910E-01 1.060E-01 2.360E+02 6.470E+00 Y
4 Zakharov 2.080E+00 6.090E-01 2.190E+00 4.740E-01 N
5 Griewank 4.020E-03 8.870E-04 9.690E-03 2.270E-03 Y
6 Sum of Dif Powers 7.840E-10 2.170E-09 3.010E-09 8.940E-09 N
7 Michalewicz -1.910E+01 2.050E+00 -1.460E+01 9.380E-01 Y
8 Rosenbrock 1.680E+02 2.090E+01 1.210E+03 5.390E+01 Y

Table 11 shows the results: Best, Worse, Mean, Standard Deviation and Z-Test, for 30 dimensions, hypothesis tests were performed with FPA-T1FLS and optimized FPA-IT2FLS (FPA13T2330), it can be observed the following.

Table 11 Comparison FPA-T1FLS with optimized FPA-IT2FLS 

COMPARATIVE 30 Dim FPA-T1FLS FPA-IT2330 Z-Test
Function Mean Std Mean Std
1 Sphere 4.350E-03 5.000E-03 7.968E-03 9.250E-03 Y
2 Ackley 7.620E-01 9.830E-01 8.219E-02 3.312E-02 Y
3 Rastrigin 9.800E+00 2.530E+01 3.434E+01 2.194E+00 Y
4 Zakharov 3.890E-02 3.670E-02 5.799E-02 3.535E-02 Y
5 Griewank 1.410E-04 1.320E-04 3.038E-04 2.270E-04 Y
6 Sum of Dif Powers 1.120E-12 4.550E-12 3.116E-10 1.491E-09 N
7 Michalewicz -1.180E+01 8.360E-01 -9.932E+00 7.098E-01 Y
8 Rosenbrock 3.230E+01 4.370E+00 1.077E+02 1.099E+01 Y

Only in 7 mathematic functions there was significant evidence that the FPA-IT2FLS (FPA13T2330) is better than the FPA-T1FLS. Table 12 shows the results: Best, Worse, Mean, Standard Deviation and Z-Test, for 100 dimensions, hypothesis tests were performed with FPA-T1FLS and optimized FPA-IT2FLS (FPA-IT2330), it can be observed that only in For 7 mathematical functions, there was significant evidence that the FPA-IT2FLS (FPA-IT2330) is better than the FPA-T1FLS.

Table 12 Comparison FPA-T1FLS with optimized FPA-IT2FLS 

COMPARATIVE 100 Dim FPA-T1FLS FPA-IT2330 Z-Test
Function Mean Std Mean Std
1.Sphere 7.520E-01 2.830E-01 9.833E-01 2.426E-01 Y
2.Ackley 5.890E-01 7.740E-02 7.034E-01 1.275E-01 Y
3.Rastrigin 7.910E-01 1.060E-01 2.476E+02 8.315E+00 Y
4.Zakharov 2.080E+00 6.090E-01 2.106E+00 5.325E-01 N
5.Griewank 4.020E-03 8.870E-04 1.362E-02 3.384E-03 Y
6.Sum of Dif Powers 7.840E-10 2.170E-09 2.653E-08 8.098E-08 Y
7.Michalewicz -1.910E+01 2.050E+00 -1.474E+01 1.008E+00 Y
8.Rosenbrock 1.680E+02 2.090E+01 1.549E+03 6.847E+01 Y

Table 13 shows the results: Best, Worse, Mean, Standard Deviation and Z-Test, for 30 dimensions, hypothesis tests were performed with FPA-T1FLS and optimized FPA-IT2FLS (FPA-IT2B130), it can be observed that only in For 6 math functions, there was significant evidence that the FPA-IT2FLS (FPA-IT2B130) is better than the FPA-T1FLS. Table 14 shows the results: Best, Worse, Mean, Standard Deviation and Z-Test, for 100 dimensions, hypothesis tests were performed with FPA-T1FLS and optimized FPA-IT2FLS (FPA-IT2B130), it can be observed that only in 7 mathematical functions there was significant evidence that the FPA-IT2FLS (FPA-IT2B130) is better than the FPA-T1FLS.

Table 13 Comparison FPA-T1FLS with optimized FPA-IT2FLS 

COMPARATIVE 30 Dim FPA-T1FLS FPA-IT2B130 Z-Test
Function Mean Std Mean Std
1 Sphere 4.350E-03 5.000E-03 6.731E-03 5.871E-03 Y
2 Ackley 7.620E-01 9.830E-01 8.226E-02 3.306E-02 Y
3 Rastrigin 9.800E+00 2.530E+01 3.478E+01 2.408E+00 Y
4 Zakharov 3.890E-02 3.670E-02 5.126E-02 3.528E-02 N
5 Griewank 1.410E-04 1.320E-04 2.843E-04 2.096E-04 Y
6 Sum of Dif Powers 1.120E-12 4.550E-12 1.915E-11 8.446E-11 N
7 Michalewicz -1.180E+01 8.360E-01 -9.916E+00 4.734E-01 Y
8 Rosenbrock 3.230E+01 4.370E+00 1.132E+02 1.028E+01 Y

Table 14 Comparison FPA-T1FLS with optimized FPA-IT2FLS 

COMPARATIVE 100 Dim FPA-T1FLS FPA-IT2B130 Z-Test
Function Mean Std Mean Std
1.Sphere 7.520E-01 2.830E-01 9.797E+00 4.478E+00 Y
2.Ackley 5.890E-01 7.740E-02 6.573E-01 9.349E-02 Y
3.Rastrigin 7.910E-01 1.060E-01 2.521E+02 7.748E+00 Y
4.Zakharov 2.080E+00 6.090E-01 9.939E+01 4.088E+00 Y
5.Griewank 4.020E-03 8.870E-04 1.283E-02 3.657E-03 Y
6.Sum of Dif Powers 7.840E-10 2.170E-09 1.470E-09 6.361E-09 N
7.Michalewicz -1.910E+01 2.050E+00 -1.489E+01 1.142E+00 Y
8.Rosenbrock 1.680E+02 2.090E+01 1.638E+03 8.748E+01 Y

9 Conclusions and Further Research

We have seen in other research that when we use a Type-1 Fuzzy Logic System (T1FLS) in parameter optimization of a bio-inspired algorithm, good results are obtained, but when we use a Type-2 Fuzzy Logic System (T2FLS) for parameter optimization, better results are obtained.

In this research, we used the bio-inspired algorithm FPA and an Interval Type-2 Fuzzy Logic System (IT2FLS). The experiments were performed with 8 benchmark functions: Sphere, Ackley, Rastrigin, Zakharov, Griewank, Sum of different powers, Michalewicz and Rosenbrock for 30 and 100 dimensions.

Once the hypothesis tests are done, we can observe that the methods that use interval type-2 fuzzy systems are better than type-1 fuzzy systems and even better results are obtained when interval type-2 fuzzy systems are optimized, in this research the FPA-IT2330 architecture was the best architecture obtained for an interval type-2 fuzzy system, of the 8 membership functions in 7 the IT2FLS was better for 30 and 100 dimensions (Tables 11 and 12).

As future work, we can perform experiments with more mathematical functions CEC2013 and CEC2017, we can also perform experiments with other dimensions: 5, 10, 50, 50, 200 and 500 with these last two surely the computational cost will be high, we can also perform experiments with other architectures of interval type-2 fuzzy systems and finally we can perform experiments with generalized type-2 fuzzy systems.

References

1. Castillo, O., Melin, P., Ontiveros, E., Peraza, C., Ochoa, P., Valdez, F., Soria, J. (2019). A high-speed interval type 2 fuzzy system approach for dynamic parameter adaptation in metaheuristics. Engineering Applications of Artificial Intelligence, Vol. 85, pp. 666–680. DOI: 10.1016/j.engappai.2019.07.020. [ Links ]

2. Kirsch, U. (1993). Structural optimization: fundamentals and applications. Springer-Verlag, pp. 57–124. [ Links ]

3. Faturechi, R., Miller-Hooks, E. (2014). A mathematical framework for quantifying and optimizing protective actions for civil infrastructure systems. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, No. 8, pp. 572–589. DOI: 10.1111/mice.12027. [ Links ]

4. Aldwaik, M., Adeli, H. (2014). Advances in optimization of highrise building structures. Structural and Multidisciplinary Optimization, Vol. 50, No. 6, pp. 899–919. DOI: 10.1007/s00158-014-1148-1. [ Links ]

5. Gao, H., Zhang, X. (2013). A Markov-based road maintenance optimization model considering user costs. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, No. 6, pp. 451–464. DOI: 10.1111/mice.12009. [ Links ]

6. Zhang, G., Wang, Y. (2013). Optimizing coordinated ramp metering—A preemptive hierarchical control approach. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, No. 1, pp. 22–37. DOI: 10.1111/j.1467-8667.2012.00764.x. [ Links ]

7. Carreon, H., Valdez, F., Castillo, O. (2020). Fuzzy Flower Pollination Algorithm to Solve Control Problems. Hybrid Intelligent Systems in Control, Pattern Recognition and Medicine, Studies in Computational Intelligence, Vol. 827, pp. 119–154. DOI: 10.1007/978-3-030-34135-0_10. [ Links ]

8. Carvajal, O., Castillo, O., Soria, J. (2018). Optimization of Membership Function Parameters for Fuzzy Controllers of an Autonomous Mobile Robot Using the Flower Pollination Algorithm. Journal of Automation, Mobile Robotics and Intelligent Systems, Vol. 12, No. 1, pp. 44–49. DOI: 10.14313/JAMRIS_1-2018/6. [ Links ]

9. Sharma, K.R., Honc, D., Dušek, F. (2015). Predictive control of differential drive mobile robot considering dynamics and kinematics. 30th European Conference on Modelling and Simulation, pp. 354–360. DOI: 10.7148/2016-0354. [ Links ]

10. Umoh, U.A., Inyang, U.G., Nyoho, E.E. (2019). Interval Type-2 Fuzzy Logic for Fire Outbreak Detection. International Journal on Soft Computing, Artificial Intelligence and Applications, Vol. 8, No. 3, pp. 27–46. DOI: 10.5121/ijscai.2019.8303. [ Links ]

11. Rai, D., Tyagi, K. (2013). Bio-inspired optimization techniques: a critical comparative study. ACM SIGSOFT Software Engineering Notes, Vol. 38, No. 4, pp. 1–7. DOI: 10.1145/2492248.2492271. [ Links ]

12. Valdez, F. (2015). Bio-Inspired Optimization Methods. Springer Handbook of Computational Intelligence, pp. 1533–1538. DOI: 10.1007/978-3-662-43505-2_81. [ Links ]

13. Holland, J.H. (1992). Adaptation in Natural and Artificial Systems: an introductory analysis with applications to biology, control, and artificial intelligence. MIT Press. [ Links ]

14. Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. International Conference on Neural Networks (ICNN), Vol. 4, pp. 1942-1948. DOI: 10.1109/ICNN.1995.488968. [ Links ]

15. Kirkpatrick, S., Gelatt, C.D., Vecchi, M.P. (1983). Optimization by Simulated Annealing. Science, Vol. 220, No. 4598, pp. 671–680. DOI: 10.1126/science.220.4598.671. [ Links ]

16. Hooke, R., Jeeves, T.A. (1961). Direct search solution of numerical and statistical problems. Journal of the ACM (JACM), Vol. 8, No. 2, pp. 212–229. DOI: 10.1145/321062.321069. [ Links ]

17. Yang, X.S. (2012). Flower pollination algorithm for global optimization. 11th International Conference on Unconventional Computation and Natural Computation, Lecture Notes in Computer Science, Vol. 7445, pp. 240–249. DOI: 10.1007/978-3-642-32894-7_27. [ Links ]

18. Sabahi, F., Akbarzadeh-T, M.R. (2013). A qualified description of extended fuzzy logic. Information Sciences, Vol. 244, pp. 60–74. DOI: 10.1016/j.ins.2013.03.020. [ Links ]

19. Zadeh, L.A. (1965). Fuzzy sets. Information and Control, Vol. 8, pp. 338–353. [ Links ]

20. Nikravesh, M. (2007). Evolution of fuzzy logic: From intelligent systems and computation to human mind. Studies in Fuzziness and Soft Computing, Vol. 217, pp. 37–54. [ Links ]

21. Black, M. (1937). Vagueness, an exercise in logical analysis. Philosophy of Science, Vol 4, No. 4, pp. 427–455. [ Links ]

22. Russell, B. (1923). Vagueness. The Australian Journal of Psychology and Philosophy, Vol. 1, No. 2, pp. 84–92. DOI: 10.1080/00048402308540623. [ Links ]

23. Brock, J. (1979). Principle themes in Peirce’s logic of vagueness. Peirce Studies, Vol. 1, No. 1, pp. 41–50. [ Links ]

24. Nadin, M. (1982). Consistency, completeness and the meaning of sign theories: The Semiotic Field. The American Journal of Semiotics, Vol. l, No. 3, pp. 79–98. DOI: 10.5840/ajs1982135. [ Links ]

25. Nadin, M. (1980). The logic of vagueness and the category of synechism. The Monist, Library of Philosophy, Vol. 63, No. 3, pp. 351–366. [ Links ]

26. Engel-Tiercelin, C. (1992). Vagueness and the unity of C.S. Peirce’s Realism. Transactions of the Charles S. Peirce Society, Vol. 28, No. 1, pp. 51–82. [ Links ]

27. Merrell, F. (1995). Semiosis in the Postmodern Age. Purdue University Press. [ Links ]

28. Merrell, F. (1996). Signs Grow: Semiosis and Life Processes. University of Toronto Press. [ Links ]

29. Kaveh, A. (2017). Applications of Metaheuristic Optimization Algorithms in Civil Engineering. Springer, Cham. [ Links ]

30. Surjanovic, S., Bingham, D. (2013). Virtual Library of Simulation Experiments: Test Functions and Datasets. Simon Fraser University. [ Links ]

31. Reznik, L. (1997). Fuzzy Controllers. Victoria University of Technology. [ Links ]

32. Mendel, J.M., John, R.I. (2002). Type-2 fuzzy sets made simple. IEEE Transactions on Fuzzy Systems, Vol. 10, No. 2, pp. 117–127. DOI: 10.1109/91.995115. [ Links ]

33. Mendel, J.M., Hagras, H., John, R.I. (2006). Standard background material about interval type-2 fuzzy logic systems that can be used by all authors. IEEE Computational Intelligence Society. [ Links ]

34. Hagras, H.A. (2004). A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots. IEEE Transactions on Fuzzy Systems, Vol. 12, No. 4, pp. 524-539. DOI: 10.1109/TFUZZ.2004.832538. [ Links ]

35. Liang, Q., Mendel, J.M. (2000). Interval type-2 fuzzy logic systems: theory and design. IEEE Transactions on Fuzzy Systems, Vol. 8, No. 5, pp. 535-550. DOI: 10.1109/91.873577. [ Links ]

36. Khursheed, M., Nadeem, M.F., Khalil, A., Sajjad, I.A., Raza, A., Iqbal, M.Q., Bo, R., Rehman, W.U. (2020). Review of Flower Pollination Algorithm: Applications and Variants. International Conference on Engineering and Emerging Technologies (ICEET), pp. 1–6. DOI: 10.1109/ICEET48479.2020.9048215. [ Links ]

37. Madasu, S.D., Kumar, M.L.S.S., Singh, A.K. (2018). A flower pollination algorithm based automatic generation control of interconnected power system. Ain Shams Engineering Journal, Vol. 9, No. 4, pp. 1215–1224. DOI: 10.1016/j.asej.2016.06.003. [ Links ]

38. Kaur, G., Singh, D. (2012). Pollination Based Optimization or Color Image Segmentation. International Journal of Computer Engineering and Technology (IJCET), Vol. 3, No. 2, pp. 407–414. [ Links ]

39. Kumar, S., Singh, A. (2012). Pollination based optimization. 6th International Multi Conference on Intelligent Systems, Sustainable, New and Renewable Energy Technology and Nanotechnology (IISN), pp. 269–273. [ Links ]

40. Waser, N.M. (1986). Flower constancy: definition, cause and measurement. The American Naturalist, Vol. 127, No. 5, pp. 593–603. DOI: 10.1086/284507. [ Links ]

41. Abdel-Raouf, O., Abdel-Baset, Mohamed, El-Henawy, I. (2014). A Novel Hybrid Flower Pollination Algorithm with Chaotic Harmony Search for Solving Sudoku Puzzles. International Journal of Engineering Trends and Technology (IJETT), Vol. 7, No. 3, pp. 126–132. DOI: 10.14445/22315381/IJETT-V7P225. [ Links ]

42. Kalra, S., Arora, S. (2016). Firefly algorithm hybridized with flower pollination algorithm for multimodal functions. Proceedings of the International Congress on Information and Communication Technology, Advances in Intelligent Systems and Computing (AISC), Vol. 438, pp. 207–219. DOI: 10.1007/978-981-10-0767-5_23. [ Links ]

43. Pavlyukevich, I. (2007). Lévy flights, non-local search and simulated annealing. Journal of Computational Physics. Vol. 226, No. 2, pp. 1830-1844. DOI: 10.1016/j.jcp.2007.06.008. [ Links ]

44. Bell, A.D., Bryan, A. (2008). Plant form: an illustrated guide to flowering plant morphology. Timber Press. [ Links ]

45. Glover, B. (2007). Understanding flowers and flowering: An integrated approach. Oxford University Press. [ Links ]

46. Pavlyukevich. (2007). Lévy flights, non-local search and simulated annealing. Journal of Computational Physics, Vol. 226, No. 2, pp. 1830–1844. DOI: 10.1016/j.jcp.2007.06.008. [ Links ]

47. Dinkar, S.K., Deep, K. (2018). An efficient opposition based Lévy Flight Antlion optimizer for optimization problems. Journal of Computational Science, Vol. 29, pp. 119–141. No. 10.1016/j.jocs.2018.10.002. [ Links ]

48. Castillo, O., Aguilar, L.T. (2019). Fuzzy Lyapunov Synthesis for Nonsmooth Mechanical Systems. Type-2 Fuzzy Logic in Control of Nonsmooth Systems, Studies in Fuzziness and Soft Computing, Vol. 373, pp. 43-54. DOI: 10.1007/978-3-030-03134-3_3. [ Links ]

49. Sadat Asl, A.A., Zarandi, M.H.F. (2018). A Type-2 Fuzzy Expert System for Diagnosis of Leukemia. Fuzzy Logic in Intelligent System Design, NAFIPS, Advances in Intelligent Systems and Computing, Vol. 648, pp. 52–60. DOI: 10.1007/978-3-319-67137-6_6. [ Links ]

50. Umoh, U.A., Inyang, U.G., Nyoho, E.E. (2020). A Hybrid Framework for Fire Outbreak Detection Based on Interval Type-2 Fuzzy Logic and Flower Pollination Algorithm. Soft Computing for Problem Solving 2019, Advances in Intelligent Systems and Computing, Vol. 1139, pp. 27–145. DOI: 10.1007/978-981-15-3287-0_3. [ Links ]

51. Fouad, A., Gao, X.Z. (2019). A novel modified flower pollination algorithm for global optimization. Neural Computing & Applications, Vol. 31, No. 8, pp. 3875–3908. DOI: 10.1007/s00521-017-3313-0. [ Links ]

52. Kayabekir, A.E., Bekdaş, G., Nigdeli, S.M., Yang, X.S. (2018). A Comprehensive Review of the Flower Pollination Algorithm for Solving Engineering Problems. Nature-Inspired Algorithms and Applied Optimization, Studies in Computational Intelligence, Vol. 744, pp. 171–188. DOI: 10.1007/978-3-319-67669-2_8. [ Links ]

53. Okwu, M.O., Tartibu, L.K. (2021). Metaheuristic Optimization. Nature-Inspired Algorithms Swarm and Computational Intelligence, Theory and Applications, Studies in Computational Intelligent, Vol. 927, pp. 1–4. [ Links ]

54. Ontiveros-Robles, E., Melin, P., Castillo, O. (2021). An Efficient High-Order α-Plane Aggregation in General Type-2 Fuzzy Systems Using Newton–Cotes Rules. International Journal of Fuzzy Systems, Vol. 23, No. 4, pp. 1102–1121. DOI: 10.1007/s40815-020-01031-4. [ Links ]

55. Olivas, F., Valdez, F., Melin, P., Sombra, A., Castillo, O. (2019). Interval type-2 fuzzy logic for dynamic parameter adaptation in a modified gravitational search algorithm. Information Sciences, Vol. 476, pp. 159–175. DOI: 10.1016/j.ins.2018.10.025. [ Links ]

56. Ontiveros, E., Melin, P., Castillo, O. (2018). High order α-planes integration: A new approach to computational cost reduction of General Type-2 Fuzzy Systems. Engineering Applications of Artificial Intelligence, Vol. 74, pp. 186–197. DOI: 10.1016/j.engappai.2018.06.013. [ Links ]

57. Liang, Q., Mendel, J.M. (2000). Interval type-2 fuzzy logic systems: theory and design. IEEE Transactions on Fuzzy Systems, Vol. 8, No. 5, pp. 535-550. DOI: 10.1109/91.873577. [ Links ]

58. Valdez, F., Castillo, O., Melin, P. (2021). Bio-Inspired Algorithms and Its Applications for Optimization in Fuzzy Clustering. Algorithms, Vol. 14, No. 4, pp. 1–21. DOI: 10.3390/a14040122. [ Links ]

59. Dubey, H.M., Pandit, M., Panigrahi, B.K. (2015). A biologically inspired modified flower pollination algorithm for solving economic dispatch problems in modern power systems. Cognitive Computation, Vol. 7, No. 5, pp. 594–608. DOI: 10.1007/s12559-015-9324-1. [ Links ]

60. Yamany, W., Zawbaa, H.M., Emary, E., Hassanien, A.E. (2015). Attribute reduction approach based on modified flower pollination algorithm. IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), pp. 1–7. DOI: 10.1109/FUZZ-IEEE.2015.7338111. [ Links ]

61. Zhou, Y., Wang, R., Luo, Q. (2016). Elite opposition-based flower pollination algorithm. Neurocomputing, Vol. 188, pp. 294–310. DOI: 10.1016/j.neucom.2015.01.110. [ Links ]

62. Sarjiya, Putra, P.H., Saputra, T.A. (2015). Modified flower pollination algorithm for nonsmooth and multiple fuel options economic dispatch. 8th International Conference on Information Technology and Electrical Engineering (ICITEE), pp. 1–5. DOI: 10.1109/ICITEED.2016.7863285. [ Links ]

63. Regalado, J.A., Emilio, B.E., Cuevas, E. (2015). Optimal power flow solution using modified flower pollination algorithm. IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), pp. 1–6. DOI: 10.1109/ROPEC.2015.7395073. [ Links ]

64. Dubey, H.M., Pandit, M., Panigrahi, B.K. (2015). Hybrid flower pollination algorithm with time-varying fuzzy selection mechanism for wind integrated multi-objective dynamic economic dispatch. Renewable Energy, Vol. 83, pp. 188–202. DOI: 10.1016/j.renene.2015.04.034. [ Links ]

65. Zainudin, A., Sia, C.K., Ong, P., Narong, O.L.C., Nor, N.H.M. (2017). Taguchi design and flower pollination algorithm application to optimize the shrinkage of triaxial porcelain containing palm oil fuel ash. IOP Conference Series: Materials Science and Engineering, Vol. 165. DOI: 10.1088/1757-899X/165/1/012036. [ Links ]

66. Abdel-Baset, M., Hezam, I. (2016). A hybrid flower pollination algorithm for engineering optimization problems. International Journal of Computer Applications, Vol. 140, No. 12, pp. 10–23. DOI: 10.5120/ijca2016909119. [ Links ]

67. Lenin, K., Ravindhranath, R.B., Surya, K.M. (2014). Shrinkage of active power loss by hybridization of flower pollination algorithm with chaotic harmony search algorithm. Control Theory and Informatics, Vol. 4, No. 8, pp. 31–38. [ Links ]

68. Jensi, R., Jiji, G.W. (2015). Hybrid data clustering approach using K-means and flower pollination algorithm. Advanced Computational Intelligence: An International Journal (ACII), Vol. 2, No. 2, pp. 15–25. DOI: 10.48550/arXiv.1505.03236. [ Links ]

69. Merzougui, A., Labed, N., Hasseine, A., Bonilla-Petriciolet, A., Laiadi, D., Bacha, O. (2016). Parameter identification in liquid-liquid equilibrium modeling of food-related thermodynamic systems using flower pollination algorithms. The Open Chemical Engineering Journal Vol. 10, No. 1, pp. 59–73. DOI: 10.2174/1874123101610010059. [ Links ]

70. Shehata, M.N., Fateen, S.E.K., Bonilla-Petriciolet, A. (2016). Critical point calculations of multi-component reservoir fluids using nature-inspired metaheuristic algorithms. Fluid Phase Equilibria, Vol. 409, pp. 280–290. DOI: 10.1016/j.fluid.2015.10.002. [ Links ]

71. Zainudin, A., Sia, C.K., Ong, P., Narong, O.L.C., Nor, N.H.M. (2017). Taguchi design and flower pollination algorithm application to optimize the shrinkage of triaxial porcelain containing palm oil fuel ash. International Conference on Applied Science (ICAS), IOP Conference Series: Materials Science and Engineering, Vol. 165. DOI: 10.1088/1757-899X/165/1/012036. [ Links ]

72. Narong, L.C., Sia, C.K., Yee, S.K., Ong, P., Zainudin, A., Nor, N.H.M., Kasim, N.A. (2017). Optimization of the EMI shielding effectiveness of fine and ultrafine POFA powder mix with OPC powder using flower pollination algorithm. International Conference on Applied Science (ICAS), IOP Conference Series: Materials Science and Engineering, Vol. 165. DOI: DOI: 10.1088/1757-899X/165/1/012035. [ Links ]

73. Nigdeli, S.M., Bekdaş, G., Yang, X.S. (2016). Application of the flower pollination algorithm in structural engineering. Yang, X.S., Bekdaş, G., Nigdeli, S.M. (eds.), Metaheuristics and Optimization in Civil Engineering, Modeling and Optimization in Science and Technologies, Vol. 7, pp. 25–42. DOI: 10.1007/978-3-319-26245-1_2. [ Links ]

74. Meng, O.K., Pauline, O., Kiong, S.C., Wahab, H.A., Jafferi, N. (2017). Application of modified flower pollination algorithm on mechanical engineering design problem. International Conference on Applied Science (ICAS), IOP Conference Series: Materials Science and Engineering, Vol. 165. DOI: 10.1088/1757-899X/165/1/012032. [ Links ]

75. Bekdaş, G., Nigdeli, S.M., Yang, X.S. (2015). Sizing optimization of truss structures using flower pollination algorithm. Applied Soft Computing, Vol. 37, pp. 322–331. DOI: 10.1016/j.asoc.2015.08.037. [ Links ]

76. Kavirayani, S., Kumar, G.V. (2017). Flower pollination for rotary inverted pendulum stabilization with delay. Telecommunication Computing Electronics and Control (TELKOMNIKA), Vol. 15, No. 1, pp. 245–253. DOI: 10.12928/TELKOMNIKA.v15i1.3403. [ Links ]

77. Xu, S., Wang, Y., Huang, F. (2017). Optimization of multi-pass turning parameters through an improved flower pollination algorithm. International Journal of Advanced Manufacturing Technology, Vol. 89, No. 1, pp. 503–514. DOI: 10.1007/s00170-016-9112-4. [ Links ]

78. Acherjee, B., Maity, D., Kuar, A.S. (2017). Parameters optimisation of transmission laser welding of dissimilar plastics using RSM and flower pollination algorithm integrated approach. International Journal of Mathematical Modelling and Numerical Optimisation, Vol. 8, No. 1, pp. 1–22. DOI: 10.1504/IJMMNO.2017.083656. [ Links ]

79. Chakravarthy, V., Rao, P.M. (2015). On the convergence characteristics of flower pollination algorithm for circular array synthesis. 2nd International Conference on Electronics and Communication Systems (ICECS), pp. 485–489. DOI: 10.1109/ECS.2015.7124953. [ Links ]

80. Chakravarthy, V., Paladuga, S.R., Prithvi, M.R. (2015). Synthesis of Circular Array Antenna for Sidelobe Level and Aperture Size Control Using Flower Pollination Algorithm. International Journal of Antennas and Propagation, Vol. 2015, pp. 1–9. DOI: 10.1155/2015/819712. [ Links ]

81. Singh, U., Salgotra, R. (2017). Pattern Synthesis of Linear Antenna Arrays Using Enhanced Flower Pollination Algorithm. International Journal of Antennas and Propagation, Vol. 2017, pp. 1–11. DOI: 10.1155/2017/7158752. [ Links ]

82. Prathiba, R., Moses, M.B., Sakthivel, S. (2014). Flower pollination algorithm applied for different economic load dispatch problems. International Journal of Engineering and Technology (IJET), Vol. 6, No. 2, pp. 1009–1016. [ Links ]

83. Kaur, G., Singh, D., Kaur, M. (2013). Robust and efficient ‘RGB’ based fractal image compression: flower pollination-based optimization. International Journal of Computer Applications, Vol. 78, No. 10, pp. 11–15. DOI: 10.5120/13524-1215. [ Links ]

84. Ouadfel, S., Taleb-Ahmed, A. (2016). Social spiders optimization and flower pollination algorithm for multilevel image thresholding: a performance study. Expert Systems with Applications, Vol. 55, pp. 566–584. DOI: 10.1016/j.eswa.2016.02.024. [ Links ]

85. Rodrigues, D., Silva, G.F.A., Papa, J.P., Marana, A.N., Yang, X.S. (2016). EEG-based person identification through binary flower pollination algorithm. Expert Systems with Applications, Vol. 62, pp. 81–90. DOI: 10.1016/j.eswa.2016.06.006. [ Links ]

86. Alyasseri, Z.A.A., Khader, A.T., Al-Betar, M.A., Awadallah, M.A., Yang, X.S. (2018). Variants of the Flower Pollination Algorithm: A Review. Yang, X.S., eds., Nature-Inspired Algorithms and Applied Optimization, Studies in Computational Intelligence, Vol. 744, pp. 91–118. DOI: 10.1007/978-3-319-67669-2_5. [ Links ]

87. Balasubramani, K., Marcus, K. (2014). A Study on Flower Pollination Algorithm and Its Applications. International Journal of Application or Innovation in Engineering & Management, Vol. 3, No. 11, pp 230–235. DOI: 10.2648/IJAIEM.303.609. [ Links ]

88. Chiroma, H., Shuib, N.L.M., Muaz, S.A., Abubakar, A.I., Ila, L.B., Maitama, J.Z. (2015). A Review of the Applications of Bio-Inspired Flower Pollination Algorithm. Procedia Computer Science, Vol. 62, pp. 435–441. DOI: 10.1016/j.procs.2015.08.438. [ Links ]

89. Himanshukumar, R.P., Vipul, A.S. (2020). Comparative Study of Interval Type-2 and Type-1 Fuzzy Genetic and Flower Pollination Algorithms in Optimization of Fuzzy Fractional Order PIλD μ Controllers. Yang, Yi, editor, Intelligent System and Computing, IntechOpen. DOI: 10.5772/intechopen.90359. [ Links ]

90. Umoh, U., Abayomi, A., Udoh, S., Abdulazeez, A. (2021). Flower Pollination Algorithm in Optimization of Interval Type-2 Fuzzy for Telemedical Problem. Abraham, A., Sasaki, H., Rios, R., Gandhi, N., Singh, U., Ma, K. (eds.), Innovations in Bio-Inspired Computing and Applications (IBICA), Advances in Intelligent Systems and Computing, Vol. 1372, pp. 43–54. DOI: 10.1007/978-3-030-73603-3_4. [ Links ]

91. Zadeh, L.A. (1975). The concept of a linguistic variable and its application to approximate reasoning—I. Information Sciences, Vol. 8, No. 3, pp. 199–249. DOI: 10.1016/0020-0255(75)90036-5. [ Links ]

92. Olivas, F., Valdez, F., Castillo, O., Melin, P. (2016). Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic. Soft Computing, Vol. 20, No. 3, pp. 1057–1070. DOI: 10.1007/s00500-014-1567-3. [ Links ]

93. Roeva, O., Zoteva, D., Castillo, O. (2021). Joint set-up of parameters in genetic algorithms and the artificial bee colony algorithm: an approach for cultivation process modelling. Soft Computing, Vol. 25, pp. 2015–2038. DOI: 10.1007/s00500-020-05272-1. [ Links ]

94. Lagunes, M. L., Castillo, O., Soria, J., Valdez, F. (2021). Optimization of a fuzzy controller for autonomous robot navigation using a new competitive multi-metaheuristic model. Soft Computing, Vol. 25, pp. 11653–11672. DOI: 10.1007/s00500-021-06036-1. [ Links ]

95. Hidalgo, D., Cervantes, L., Castillo, O., Melin, P., Martínez-Soto, R. (2020). Fuzzy Parameter Adaptation in Genetic Algorithms for the Optimization of Fuzzy Integrators in Modular Neural Networks for Multimodal Biometry. Computación y Sistemas, Vol. 24, No. 3, pp. 1093–1105. DOI: 10.13053/CyS-24-3-3329. [ Links ]

96. Valdez, F., Castillo, O., Peraza, C. (2020). Fuzzy Logic in Dynamic Parameter Adaptation of Harmony Search Optimization for Benchmark Functions and Fuzzy Controllers. International Journal of Fuzzy Systems, Vol. 22, pp. 1198–1211. DOI: 10.1007/s40815-020-00860-7. [ Links ]

97. Castillo, O., Amador-Angulo, L.A. (2018). A generalized type-2 fuzzy logic approach for dynamic parameter adaptation in bee colony optimization applied to fuzzy controller design. Information Sciences, Vol. 460–461, pp. 476-496. DOI: 10.1016/j.ins.2017.10.032. [ Links ]

98. Ontiveros, E., Melin, P., Castillo, O. (2018). High order 𝜶-planes integration: A new approach to computational cost reduction of General Type-2 Fuzzy Systems. Engineering Applications of Artificial Intelligence, Vol, 74, pp. 186–197. DOI: 10.1016/j.engappai.2018.06.013. [ Links ]

Received: June 08, 2021; Accepted: November 17, 2021

Creative Commons License This is an open-access article distributed under the terms of the Creative Commons Attribution License

 
Av. Juan de Dios Bátiz s/n esq. M. Othón de Mendizábal, U.P. "Adolfo López Mateos" Zacatenco, Ciudad de México, Ciudad de México, MX, 07738, (52-55) 5729-6000 ext. 56571