1 Introduction
Clustering methods are defined as unsupervised learning processes used to divide a set of observations into clusters [36, 38, 31, 28]. Clusters are groups of similar observations which are sufficiently far from each other. Several clustering methods are defined in the literature and all share a common nature - the difficulty in their analytical evaluation [39, 3, 9, 23, 14].
The discrete frequencies of observations and the measures of similarities between entities and clusters produce many local minima which disturb the process of clustering to converge to the correct results. Therefore, one avenue is to evaluate clustering algorithms using artificially constructed data. Many authors have categorized unsupervised classification based on criteria such as similarity or dissimilarity measures, the nature of data, and the function to be optimized [18]. Based on evaluation, the two principal categories are hierarchical methods and mobile centers methods.
The ultra-metric inequality is one of the most often used methods to generate artificial data to evaluate hierarchical algorithms [10, 22]. A large number of popular methods are based on employing the mixture model and particularly the Gaussian mixtures [15, 2, 25, 26]. The mixture models must satisfy some properties that conform with the clustering methods [24]. These patterns are summarized in two criteria: the internal cohesion and the external isolation.
Internal cohesion ensures observations within the same cluster have similar properties. External isolation ensures observation from different clusters are very dissimilar. Several works in the literature considered the Gaussian distribution as design block for clustering algorithms due its well-known properties [15, 2]. On the other hand, several approaches have been proposed to generate artificial data. Salem and Nandy [30] proposed different structures for producing artificial observations in 2D spaces. The main rule to preserve the internal cohesion of the components mixture is to introduce empty space between the clusters despite the fact that empty space is not a sufficient condition to guarantee external isolation. In the case where the mixture components have close enough centers, no clustering method has the ability to identify the components [30]. In [34, 35], well separated data is generated for 2D and 3D cases.
The two criteria characterizing the cluster structure are strongly respected. Milligan [23] developed an algorithm for generating artificial data but was only able to avoid the total overlap for the first dimension. The claim is that avoiding overlap for the first dimension allows by transitivity to avoid total overlap for the rest of the dimensions [8, 29]. Milligan’s algorithm is verified by visual inspection. Kuiper and Fisher [20] and Bayne et al. [5] directly manipulated a variable which measured certain parameters as separability for a simple covariance matrix of normal clusters. Blashfield [6] and Edelbrock [13] used unconstrained multivariate Gaussian mixture with fairly complex covariance structures.
This allows to obtain cluster structure and the clusters are well separated [14]. Other authors have inserted noise in well separated data to add some complexity to the obtained simulated data [30, 34, 35]. Baudry et al. [4] proposed a verification method to estimate the Gaussian mixture model. This work clearly distinguishes cluster structures of the mixture where the components are well separated from the Gaussian mixtures in case of total overlap. In [17, 37], the authors proposed a new artificial data generator that embeds the notion of the rate of overlap for uncorrelated 2D artificial Gaussian data.
In this paper, we propose a new automatic method for generating artificial data by controlling mixture components overlap. This work tackles two main problems: the design of an artificial data generator for correlated 2D data, and the study of the behavior of clustering algorithms and their respective validity indices by varying the rate of overlap between the mixture components. We are interested in correlated data because of the growing number of applications in computer vision and image processing, as clustering is used as the core solution to solve problems such as segmentation and image matching. In these applications, correlated data that revealed useful when combined and could be used in the clustering process are pixel gray-level, local window gray-level, and local variance.
In this paper, we will show how the overlap rate is quantified and its use as the basis block in the artificial data generator. The rest of this paper is organized as follows: section 2 briefly presents the Gaussian mixture; section 3 deals with components separation; section 4 presents the quantification of component overlap; in section 5, the control of overlap is developed; the generation algorithm and the experimental results are shown in sections 6 and 7 respectively. Finally, the conclusion is drawn with some perspectives.
2 Bivariate Correlated Gaussian Mixture Model
Mixture models are widely used in many applications because many real and natural phenomena as well as sets of data in many disciplines are based on such distributions [14, 1, 3, 25, 30]. A mixture of M Gaussian 2D components is given by:
where
where
3 Well Separated Components
Initially, the clustering methods and the validity indices were evaluated by using well separated data before using any other simulated data. Most works are not based on a formal way to generate artificial data and the main technique to construct isolated mixture components is visual inspection [35, 34, 11, 4].
The objective is to propose a definition that helps qualify and quantify well separated components by involving all the mixture parameters. Mixture components are considered well separated if they exhibit a minimum overlap between clusters [25, 26]; we define:
where
In [17], we presented in 2D the
minimum overlap between two components
As in the 1D case, more than 99.7% of the observations are located inside the ellipse
defined by the intersection of the plane defined by
The probability density function of the generated data (pdf ) is constrained to have the same configuration for the well separated components so that:
Definition 1: Two adjacent Gaussian components
Formally,
where
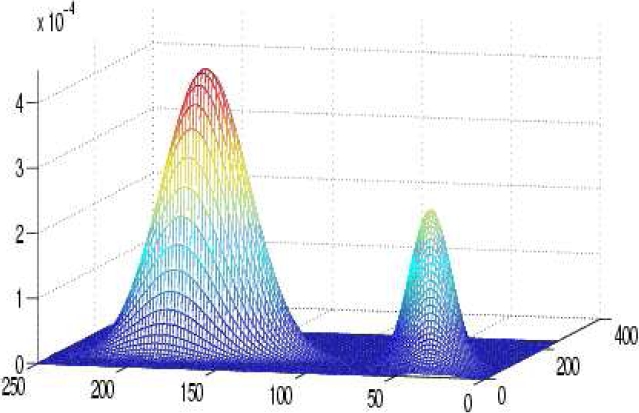
Fig. 1 An example illustrates the minimal overlap between two components of
a mixture.
3.1 Components Overlap
During the generation of a large set of data, it is important to ensure that the generated mixture components are not in a case of total overlap. Components in a case of total overlap violate the two criteria of internal cohesion and external isolation.
To better explain the meaning of total overlap, let us examine the example of figure 2. In figure 2 (a), the mixture is composed of three components; however, only two are visible; the total overlap can only be detected by visual inspection. A case of maximum overlap is shown in figure 2 (b). We can still distinguish that there are three components. In figure 2 (c), there is a partial overlap between the three components of the mixture. It is clear that the mixture is composed of three components:
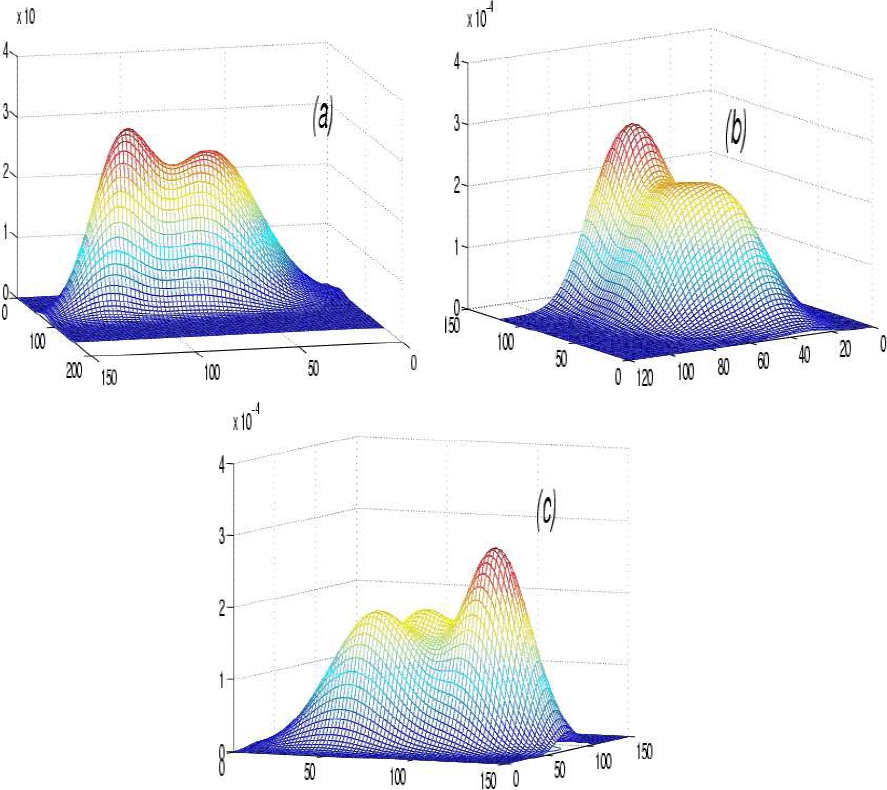
Fig. 2 Overlap Between Three Components of the Mixture in the Three
Cases. (a): Total overlap between
It is meaningless to evaluate clustering algorithms on total overlapped structures.
Two components in a case of total overlap indicate that these two components form a unique component having different distribution parameters, hence it important to avoid this case.
3.2 Overlap Between Two Equivalent Bivariate Gaussian Components
In order to control components overlap, a formal quantification is needed.
In a bivariate space, let us consider two components
For two equivalent components, we propose the following condition for the maximum overlap:
where
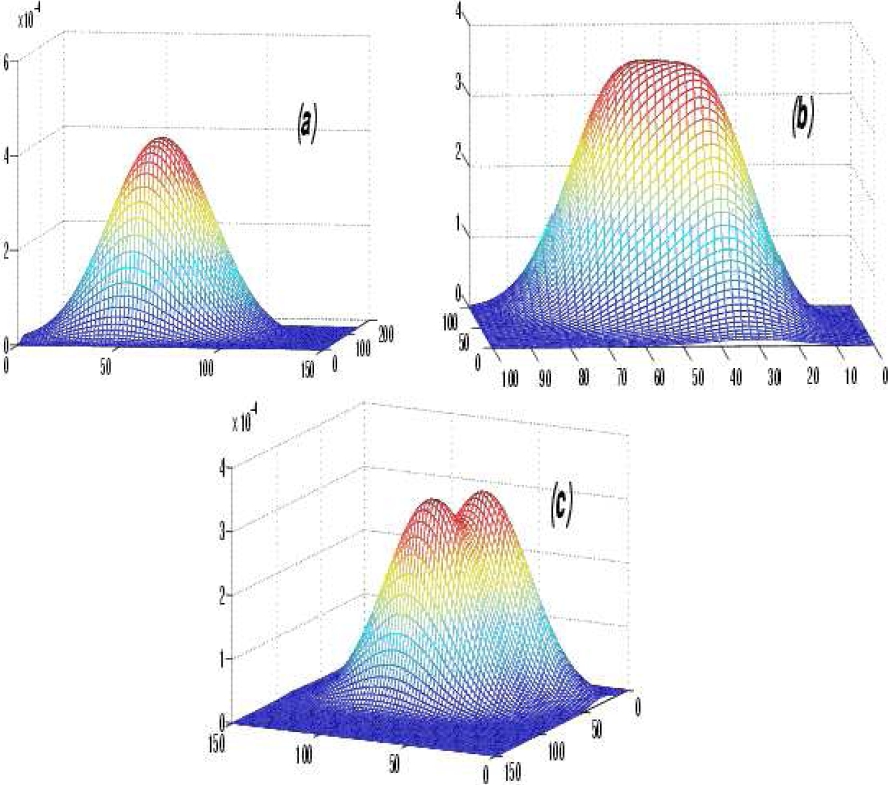
Fig. 3 Generalization and illustration of the condition (3) for two
mixture equivalent components. (a) Total overlap:
The value at the intersection point is lower than the value given in condition
(4). This results form a relationship between the visual inspection and the
formal quantification. We will propose in the next section a definition
characterizing the overlap cases. In the rest of this paper, we will use the
notation
4 Formal Quantification of the Overlap
We propose the definition of the maximum overlap. Later we formalize the degree of overlap by the notion of rate. This definition is similar to that proposed in [17] except that in our case, the definitions are more general in order to support correlated and uncorrelated data. The overlap between components must be controlled to avoid the case of total overlap. We consider the overlap only between the two adjacent components. We will exploit the results of the previous section to propose the definitions.
4.1 Maximum Overlap
The maximum overlap is considered as a limit between the undesirable case of total overlap and the case of partial overlap. The condition of equation (4) is extended to support non-equivalent components and we set the following definition.
Definition 2: Two adjacent Gaussian bivariate components
4.2 Rate of Overlap
In the literature, the notion of overlap is not quantified in a way that an
artificial data can be constructed. On the other hand, there are many indices
proposed to measure the shared observations or resemblance between clusters. For
the most popular model, the Gaussian model, an interesting description of the
fretquently used indices for computing the overlap rate between clusters is
presented in [12, 32]. The Mahalanobis distance,
We propose the definition of overlap rate
— The rate of overlap takes values between 0 and 1, so that the value of 1 implies the presence of maximum overlap and the value of 0 implies that the two components are ”well separated”.
— The overlap rate must include all the parameters of the two components: the mixture coefficients, the centers, the standard deviations and the coefficients of correlation.
Definition 3: The rate of overlap between two adjacent bivariate Gaussian components is defined as the ratio of the value at the highest intersection point to the value at the highest intersection point in the case of maximum overlap. Formally, the rate of overlap can be written as:
These three definitions are very interesting because they employ visual
inspection as a basis for the generation and verification of artificial data.
Additionally, the rate of overlap definition involves symmetrically all the
parameters of the two adjacent Gaussian components. We propose an algorithm for
generating artificial data in order to avoid the case of total overlap and
control the overlap rate
5 Controlling Mixture Overlap
As mentioned above, we randomly generate the parameters of the first component - the
mixture coefficients, the standard deviations and the coefficients of correlation
with the other components. We also introduce the angles of intersection between the
components randomly. The angles of intersection are used to measure the deviation of
the intersection points from the
5.1 Fixing Partial Overlap Rate
For two components
Case 1: For
which means that:
where:
We have:
where:
From the inequality
For the second component, by applying the same reasoning, we find:
where:
Case 2: In this case, we find the same equations (5,7), but with these parameters for the first component:
and these parameters for the second component:
In this case,
In the plane defined by the equation
We proceed to translate the referential
We obtain an ellipse which center is the center of referential. After translating
the referential, we proceed to the rotation in which the major axis of the
ellipse will be parallel to the
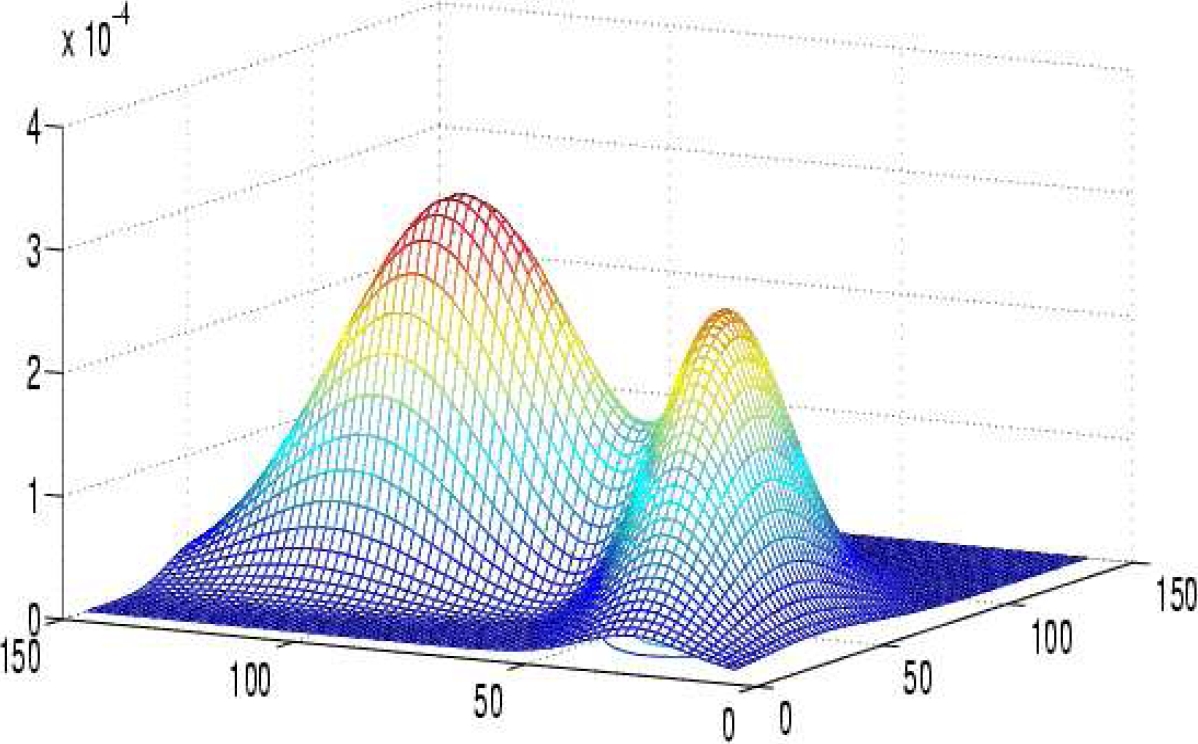
Fig. 5 Partial overlap between two bivariate Gaussian components
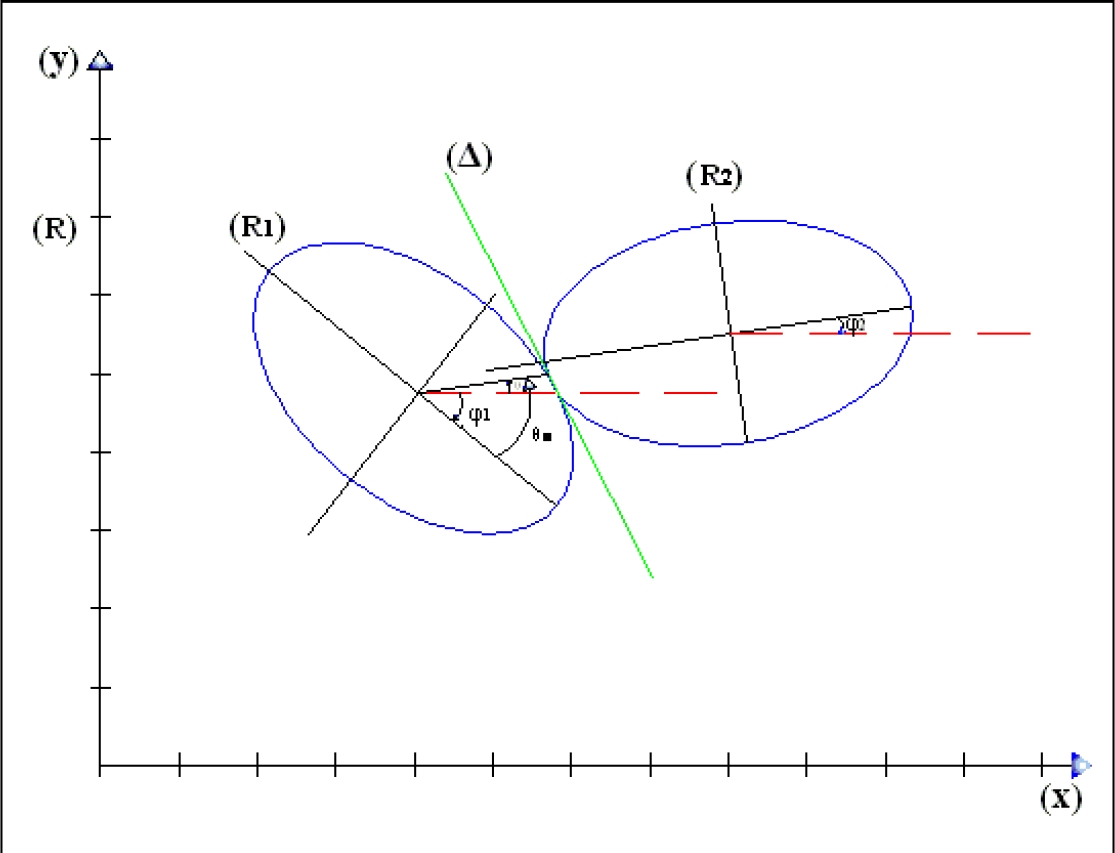
Fig. 6 Illustration of the ellipses’ intersection, the different references and the angles used for the rotation
where
where
From equations 11, 12, and 13 and after some transformations, we have:
where the angle
To avoid the ternary overlap,
In order to compute the second component’s center, we need the value of the
obliqueness at the intersection point. The obliqueness tangent is the tangent of
the angle between the line tangent at the intersection point and the
The value of the tangent obliqueness
For the second case, we find that the function presenting this part of ellipse is:
and the obliqueness of the line tangent on
For the third case, where
In
where
We proceed to compute the intersection point
The treatment of the second ellipse is identical to that of the first ellipse
(result of the projection of the component onto the
We compute the angle
where the strictly positive real numbers
The value of the line obliqueness
For the special case where
We compute the coordinates
It is possible to substitute
By applying the definition of well separated components to the two components
where:
For the second component, we find that:
where:
The two equations 24 and 26 are characteristic equations of
two ellipses in the plane
6 Generation Algorithm for Gaussian Bivariate Artificial Correlated Data
In this section, the algorithm of generation of the artificial data is summarized. The general algorithm starts by introducing random values to the parameters of the first component.
We also introduce the mixture coefficients, the standard deviations of the components, the coefficient of correlation and the deviation angles of the other components. The components’ centers are derived afterwards.
In order to avoid the overlap between three components, we suggest to introduce the
deviation angles
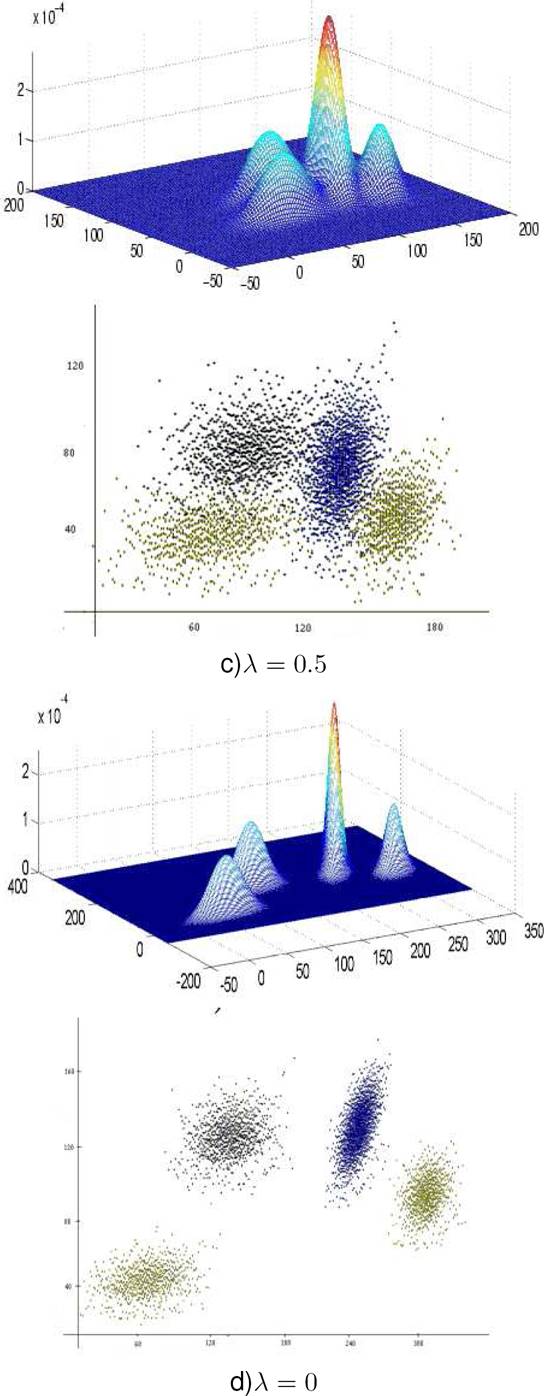
Figures 8 and 9 show a mixture of four components for each rate of overlap. If we
exclude the centers of the components, the mixture components have the same
parameters. Table 1 shows the generator
initializations. The columns represent the mixture coefficients
Table 1 Generator initialization to obtain mixture of four components according to the variation of the overlap rate
| mixt coef | angle | ||||
| comp 1 | 0.25 | 23 | 12 | 0.3 | 1.016 |
| comp 2 | 0.25 | 25 | 20 | 0.2 | 0 |
| comp 3 | 0.35 | 15 | 15 | 0.4 | -1.016 |
| comp 4 | 0.15 | 15 | 20 | -0.2 | — |
We choose to give the same first component center
Table 2 illustrates the centers computed by
the generator according to the different overlap rate values. Figures 8 and 9 show both
the probability density function pdf and the density scatter plots.
We can clearly observe that the scatter approaches each other as
Table 2 The centers obtained after the generation of bivariate artificial data
| 0 | 0.5 | 075 | 1 | ||
| comp. 1 | 60 | 60 | 60 | 60 | |
| 40 | 40 | 40 | 40 | ||
| comp. 2 | 111.34 | 82.50 | 79.25 | 76.53 | |
| 167.97 | 93.74 | 85.23 | 77.95 | ||
| comp. 3 | 241.93 | 143.40 | 133.05 | 125.63 | |
| 159.82 | 87.97 | 79.47 | 71.80 | ||
| comp. 4 | 327.64 | 186.94 | 172.74 | 163.47 | |
| 129.27 | 73.46 | 66.5 | 59.89 |
7 Experimental Results
In this section, we present the experimental protocol and results. We propose to use k-Means, Fuzzy C-Means (FCM) and FCM-based splitting Algorithm (FBSA) [27, 19]. For validity indices, we propose to use R-Square (RS), Partition Coefficient (PC), Davies-Bouldin (DB), Xie-Benie (XB), WSJ and Classification Entropy (CE) [40].
7.1 Determination of the Number of Components
As mentioned previously, the influence of the overlap rate on clustering results is discussed. The ability of the clustering methods and the validity indices to determine the number of components is also examined.
In order to give equal opportunity to all the clustering methods to reach the
correct cluster structure, we use a unique configuration for choosing the
initial centers. We arrange the set of observations according to the first
dimension. The
Tables 3 and 4 illustrate the results obtained by the proposed algorithm.
The first column represents the clustering methods used in this study: FCM, FBSA
and K-Means. The second column contains the value of validity indices RS, PC,
DB, XB, WSJ and CE. For each components’ number, we compute the result in group
according to the rate of overlap
In previous contributions [26, 17], we obtained the same result for
the uni-variate and uncorrelated data. In [33], a study concerning the WSJ is presented. It is based on
Bersdak suggestion, where the number of observations
We also show that by increasing the number of components or the overlap rate, the quality of the results decrease. If we look at the experimental results in Table 3, we observe that the validity indices DB, XB, PC determine the component number to be 3, but with the same overlap rate in Table 4 the above validity indices do not have the ability to identify the true number of components.
Table 3 Results for three components
| 3 components | ||||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 3 | 3 | 10 | 3 |
| fcm | 2 | 10 | 3 | 3 | 10 | 3 |
| db | rs | |||||
| k-means | 3 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| FBSA | 2 | 10 | 3 | 3 | 8 | 3 |
| FCM | 2 | 10 | 3 | 3 | 8 | 3 |
| db | rs | |||||
| k-means | 3 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| FBSA | 2 | 10 | 4 | 10 | 10 | 2 |
| FCM | 2 | 10 | 4 | 9 | 10 | 2 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| FBSA | 2 | 10 | 2 | 2 | 10 | 2 |
| FCM | 2 | 10 | 2 | 2 | 10 | 2 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 2 | 2 | 8 | 2 |
| fcm | 2 | 10 | 2 | 2 | 10 | 2 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
Table 4 Results for 5 components
| 5 components | ||||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 5 | 2 | 10 | 3 |
| fcm | 2 | 10 | 5 | 2 | 10 | 2 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 3 | 3 | 8 | 3 |
| fcm | 2 | 10 | 3 | 3 | 8 | 3 |
| db | rs | |||||
| k-means | 3 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 3 | 3 | 10 | 3 |
| fcm | 2 | 10 | 3 | 3 | 10 | 3 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 2 | 2 | 10 | 2 |
| fcm | 2 | 10 | 7 | 8 | 10 | 2 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
| rs | pc | db | xb | wsj | ce | |
| fbsa | 2 | 10 | 2 | 2 | 10 | 2 |
| fcm | 2 | 10 | 2 | 2 | 10 | 2 |
| db | rs | |||||
| k-means | 2 | 2 | ||||
A large number of components means that there are relatively a large number of global minima to locate, so that between these global minima a large set of local minima exist where the clustering methods could wrongly converge.
From Table 3, we can easily observe that the determination of the component number becomes less and less accurate as the overlap rate increases.
From the results illustrated in Table 3,
we find that all the non-monotonous validity indices are able to find the number
of components when the overlap rate
Contrary to the 1D experiences presented in [26], the process of clustering, in this case, cannot converge towards the true models. The curse of dimensionality affects the process for two main reasons. The first one concerns the frequency of dispersion of the data.
For the same number of observations, in 1D space, the data is distributed only on
one dimension which causes the data to be more compact and the
In [26], in 1D, it is confirmed that the worst situation in which clustering methods encounter difficulty in determining the exact components number is the one where there is a component with a small deviation between two components with large standard deviations. In these circumstances, the first component overlaps beyond the second adjacent component and reaches the third component.
In 2D, there are more chances of such ternary overlap. Suppose we have three 2D
components such that the intersection angle between the first and the second
components is
In this situation, the first component is so close to the third component that
they are in case of total overlap. For this reason, we limited the intersection
angles to be within
7.2 Determination of the Clusters’ Centers
In this section, we study the ability of clustering methods to determine the model parameters by knowing the number of components. The model parameters includes the mixture coefficients, the centers, the standard deviations and the correlation coefficients. The most important parameter is the centers because a small deviation from its real value has a significant influence on the other parameters.
Another point to take into consideration is that a given deviation of the components centers in the case of minimal overlap does not have the same influence in the case of maximum overlap. Because the data in maximum overlap is more compact, an error which appears negligible in minimal overlap case results in significant divergence in the mixture parameters in the maximum overlap case.
For these reasons, we have introduced a new measure
where
Before computing
The second is to minimize the function defined as
Table 5 Results
| 2 clusters | |||||
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| k-means | 0.03 | 0.15 | 0.18 | 0.13 | 0.24 |
| fcm | 0.0205 | 0.024 | 0.0678 | 0.11 | 0.16 |
| 3 clusters | |||||
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| k-means | 0.007 | 0.006 | 0.015 | 0.0178 | 0.0185 |
| fcm | 0.0025 | 0.0040 | 0.0055 | 0.007 | 0.0762 |
| 4 clusters | |||||
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| k-means | 0.12 | 0.11 | 0.0723 | 0.0705 | 0.053 |
| fcm | 0.0812 | 0.00421 | 0.0051 | 0.00822 | 0.00842 |
| 5 clusters | |||||
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| k-means | 0.00052 | 0.00481 | 0.0052 | 0.041 | 0.0026 |
| fcm | 0.0012 | 0.00551 | 0.015 | 0.0017 | 0.0183 |
| 6 clusters | |||||
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| k-means | 0.054 | 0.0077 | 0.0033 | 0.049 | 0.018 |
| fcm | 0.044 | 0.0018 | 0.0241 | 0.035 | 0.032 |
| 7 clusters | |||||
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| k-means | 0.004 | 0.0087 | 0.01 | 0.013 | 0.0048 |
| fcm | 0.004 | 0.00465 | 0.00612 | 0.0086 | 0.012 |
The results are proportional to the overlap rate. As the overlap rate increases,
the
A large value of
8 Conclusion and Future Work
We have proposed an artificial data generator for evaluating the performance of clustering methods. The generator is used to produce artificial data for the mobile centers methods. It also benefits the hierarchical methods where the number of observations is relatively important.
Our approach is based on a formal definition and quantification of mixture components overlap. These definitions are extracted by a formal method in order to have a relationship between visual inspection of the overlap and its formal representation. We have selected three clustering algorithms to be benchmarked (FCM, FBSA and K-Means) and the validity indices RS, PC, DB, XB, WSJ and CE are used in this study.
The experiments are conducted under the same conditions including the initialization parameters and the artificial mixtures. The experimental results have shown the effectiveness and the accuracy of the produced observations especially when the overlap rate increases between components: some algorithms and validity indices outperform others and the monotonic nature of the validity indices is confirmed.











 nueva página del texto (beta)
nueva página del texto (beta)