1 Introduction
The MTSP is an extension of classical traveling salesmen problem (TSP) [1]. In classical TSP, a salesman visits every city exactly only once in fully connected networks of city and return back to start city such that tour cast is minimum. In MTSP, m (>1), salesman travels the fully connected network of cities such that at a time a group of city is visited exactly once by only one salesman out of m salesman and salesman return to start city i.e. tours of each salesman have distinct city. Each salesman must have starting and ending position is same. Given a collection of n cities and the distance (cost), of travel between every pair of city must be partitioned into m tours for m>1 salesmen to serve a set of n>m cities. The objectives of MTSP are:
Sum of the cost of m tours of the m salesman is minimum.
Maximum tour cost travel by any one salesman is minimized.
We have also considered two additional constraints on the solution, similar to Crater et al. [6]: start and end city is the same for all salesmen and this city is called as home city, every salesmen visit at least one city other than home city. The second objective is related to the balancing of workload among the salesman. Clearly, MTSP is NP-Hard as classical TSP (m = 1), which is well known NP-Hard.
A number of real life problem are modeled using MTSP, which is useful for many applications business, industry and engineering. The most common application of MTSP are in the area of scheduling and routing e.g. print press scheduling [14], interview scheduling [12], crew scheduling[2], hot rolling scheduling[34], workload balancing [25], design of global navigation satellite system surveying networks [30], school bus routing [2], and vehicle scheduling problem [23, 27].
In recent years, many heuristic or meta-heuristic algorithms have been developed for solving the NP-hard optimization problems, such as Simulated Annealing [7, 18], Genetic Algorithms [1, 22], Ant Colony Optimization [36] and Particle Swarm Optimization [24]. These methods are also exploited to solve MTSP [4, 5, 6, 21, 32, 33, 35, 36].
Finding global solution for NP-Hard problems within affordable time and computing resources is intractable. Instead of global optimal solution, a suboptimal solution with reasonable computational load is obtained and it will further pruned for better solution using some heuristic about the solution. During recent years, researcher has shown great interest in finding effective algorithms in heuristic framework to solve MTSP and TSP. A comprehensive survey on heuristic methods is available in [19], and references there in. In this paper we focused on the development of algorithm for MTSP in Genetic Algorithm (GA), framework. GA is an iterative, population based, heuristic search technique. Several GA based methods are proposed depending on the different way of representing chromosome and genetic operations.
Tang et al. [34] proposed a GA with one chromosome representation for MTSP to solve the hot rolling production scheduling problem. Malmborg et al. [23] and Park et al [27] used a two chromosome representation in their genetic algorithm based approaches for MTSP and applied it for vehicle scheduling. Carter et al. [6] developed a genetic algorithm for MTSP with his proposed two-part chromosome representation and corresponding genetic operators. Brown et al. [5] proposed a grouping GA that uses a chromosome presentation. Singh et al. [31] proposed a grouping GA, in this they represented chromosome as set of m tours and their proposed crossover and mutation operator. Chromosome representation of Singh et al. [31] is similar to multi chromosome representation, except that tours are not assigned to specific salesmen. Yuan et al. [37] proposed genetic algorithm for MTSP with two-part chromosome and a new crossover, he named it as two-part crossover (TCX).
Novelty of all the aforementioned method is use of new chromosome representation and modified form of genetic operator (crossover, mutation), which was used in classical TSP [37]. But, these chromosome representations have many redundant solutions, i.e., many chromosome seems to be different but they represent the same MTSP solution. The set of all possible chromosomes (representation space / search space), is much larger than the set of all possible solution to the problem (problem space). However, GA is searching based method and it works on representation space, therefore it has to explore the larger space, and hence, the performance of the GA degraded severely. The detail pros and cons of chromosome representations used in these methods are discussed in Section 2.
In this paper, we proposed the genetic algorithm for the MTSP. Our proposed genetic algorithm uses group theory to generate initial population and a proposed new crossover operator. We use muti-chromosome representation scheme for encoding the representation space [1]. In multi-chromosome representation, the size of the search space is same as the size of two-part chromosome representation. However, multi-chromosome encoding is much similar to the characteristics of MTSP, salesmen are separated from each other “physically”, i.e., each salesman visit different city except start and end city. This representation more easily interpretable to the MTSP solution space. Upon use of group theory method for chromosome initialization, the multi chromosomes representation has no redundancy (duplicate solutions) in search space.
We have compared the results our proposed method with the result reported in Yuan et al. [38] using two part chromosome crossover (TCX), ordered crossover operator with an asexual crossover (ORX +A), cycle crossover operator with an asexual crossover (CYX +A), and the partially-matched crossover operator with an asexual crossover (PMX +A).
The rest of the paper is organized as follows: Section 2 presents the mathematical formulation of the MTSP. Section 3 reviews the different chromosome representations techniques reported so far the MTSP problem along with their pros and cons. Section 4 presents the framework of genetic algorithm with proposed group theory for population initialization and crossover. Section 5 presents the experimental results. Finally, Section 6 provides concluding remark of the study.
2 Formulations of Multiple Traveling Salesman Problem (MTSP)
In the MTSP, given a set of n nodes (cities) and m salesmen located at a single start (source), node. In this process the MTSP consists of finding tours for all m salesmen, who all start and end at the same source node, such that each city must be visited exactly once by only one salesman and the objective is to minimize the total cost of visiting all the nodes. This type of problem is modeled in graph theory as a weighted graph G = (V, E, w), where V is the set of vertices representing cities, E is the set of edges representing roads and w is weight (cost), between each pair of vertices.
A closed tour in which all the vertices are distinct which is known as Hamiltonian cycle. Finding set of m Hamiltonian cycles with minimum travel cost in the weighted graph gives the desired solution. i. e. total cost of visiting all nodes is minimized. The cost between cities is represented by matrix, known as cost matrix C = (cij), i, j = 1, 2, · · ·, n.
In cost matrix C the (i, j)th entry c ij, represents the cost of travel from i th to j th city. The matrix C is said to be symmetric when c ij=c ji, ∀ (i, j) ∈ E and asymmetric otherwise. In Integer Linear Programming framework the MTSP is formulated as follows [1]:
Let us define following decision variable
Consider
The MTSP problem can be mathematically formulated as constraint optimization problem as follows:
subject to
Equation (3, 4) corresponds to the objective criterion i, ii of MTSP, as discussed in Section 1. The constraint given by Equation (7, 8) are usual city assignment constraint: at a time, a group of cities is assigned to exactly one salesman out of m salesmen. The constraint (5, 6), ensure that exactly m salesmen depart from and return back to home city (here it is represented by index 1). Constraint represented by Equation (9), is used to prevent sub-tours, which are degenerate tours that are formed between intermediate nodes and not connected to the home.
3 Chromosome Representations for the MTSP
The convergence and quality of solution obtained from GA is depends on the diversity in the search space. Thus, using an efficient encoding scheme for search space is necessary for success of GA. In general, in search space the solution / chromosomes are represented such that there is least chance to have multiple copy of the same solution i.e., search space have less redundancy and high diversity in the population. Here we present a brief review of different techniques for chromosome representation, which are commonly employed for solving MTSP, with their advantages and disadvantages. In proposed method, we used multi-chromosome representation technique, which is similar to the characteristic of the problem.
3.1 One Chromosome Technique
This method represents a solution for the MTSP using a single chromosome of length n + m − 1, where n represents a permutation (tour) of n cities with integer value ranging from 1 to n and m represents number of salesman. The solution chromosome is divided into m sub-tours by inserting m−1 dummy negative integers that represents the change from one salesman to another.
For example, in Fig.1 (where n = 10 and m = 3), the first salesman will visit cities 1, 3, and 6, the second salesman will visit cities 10, 5 and 9, and third salesman will visit 7, 4, 8 and 2. All visit in the order that the city appears. The number of possible solutions is (n + m - 1)!. However, many of the possible chromosomes are redundant. The detail of this technique is available in [5, 10, 31].
3.2 Two Chromosome Technique
This method represents a solution for the MTSP using a two chromosome of length n. one-chromosome represents a permutation (tour) of n cities with integer value ranging from integer 1 to n and the other chromosome represents city assigned to a salesman, and value ranging from integer 1 to m. For example, in Fig. 2, for n = 10 and m =3, the first salesman will visit cities 3, 10 and 2, the second salesman will visit cities 6, 5, 7 and 8, and third salesman will visit 1, 9 and 4. The visit is taken place in the same order as the cities appear in the permutation.
In this method, there are
3.3 Two-Part Chromosome Technique
In this method, MTSP solution represented by two part of a chromosome of length n+m, where n is the number of city and m is the number of salesman used in MTSP. The first part of the chromosome of length n represents a permutation (tour), of n cities, in which each gene takes integer value ranging from 1 to n. Second part of chromosome of length m gives the number of cities assigned to each salesman.
The values assigned to the genes of the second part of the chromosome are constrained to be m positive integers, such that their sum is equal to the total number of cities to be visited. For example in Fig.3, the first salesman will visit cities 1, 5, 9 and 7, second salesman will visit cities 4, 8 and 6, and third salesman will visit 10, 3 and 2.
In the two-part chromosome technique for the MTSP, there are n! possible permutations for the first part of the chromosome. The second part of the chromosome represents a positive vector of integers
There are
3.4 Multi-Chromosome Technique
This method uses as many chromosomes as number of salesman [1]. The length of chromosome is variable and depends on the number of cities assigned to the particular salesman. Let the length of first chromosome is k
1
, the length of second chromosome is k
2
, and so on. Therefore, total number of cities in multi-chromosome representation equals to
Determining number ways the cities assigned to the first chromosome is equal to the problem of obtaining an ordered subset of k
1
elements from a set of n elements. There are
The length of the each chromosome represents a positive vector of integers
There are
Thus, size of the solution space for the multi-chromosome representation is
Here we use multi chromosome representation [38] for encoding the solution / search space for the MTSP. The multi chromosomes representation has lesser number of duplicate solutions in search space, i.e., less redundancy, in comparison to other three chromosomes representation discussed so far [1, 5, 6, 10, 31].
4 The Genetic Algorithm for MTSP
We have developed a Genetic Algorithm for MTSP using a proposed group theory based method for tour construction and a new crossover operator. The proposed new crossover operator is inspired by the distance preserving crossover [11].
4.1 Group Theory for Tour Construction
There are various possible methods for generating the initial population [6, 23, 31, 34, 39, 40]. One of them is random generation of the initial population [6, 23, 31, 34], while another approach is to apply greedy constructive heuristic [39, 40] with Karp’s patching [20] to construct a feasible tour. Simplest and most straight forward method for generating the initial population is nearest neighbor tour construction heuristic [28].
But all aforesaid initialization methods suffer from inherent redundancy due to random initialization of the population. Singh et al. [31] try to overcome problem of redundancy, but it requires additional checking for uniqueness of newly generated chromosome against population members generated so far.
In this study, we generate the initial population using following iterative procedure. We assign label to the vertices of the weighted graph using the element of group of integers, Z n , with integer modulo n.
where the addition on the right-hand side of equation is the ordinary addition of integers, the operation “+ n " is called addition modulo n. By using this function, we generate group table. In group table no two rows or columns are identical, it follows that every row of the composition table is obtained by a permutation of Z n and that each row / columns is a distinct permutation of n symbols [29]. The function P, which generates initial population, is defined as follows:
where i=1 to population size, and j=1 to n. In the group tour construction method, each individual in the initial population are unique that gives a wide diversity of genetic materials by exploring the whole search space. This due to initial heterogeneous population created using group theory that control diversity in generations and promote the exploration. Moreover, this method does not require any additional checking procedure for uniqueness of the population member.
4.2 Fitness
Our fitness function is same as the objective function. There are mainly two different objectives for the MTSP as discussed in introduction section and mathematically given by Equation (3) and (4), therefore, we have two different fitness functions. The objectives of MTSP are:
(i) Sum of the cost of m tours of the m salesman is minimum.
(ii) Maximum tour cost travel by any one salesman is minimized.
In both cases, we have to minimize the value of the fitness function.
4.3 Proposed Crossover Operator
The crossover operator is a method for sharing information between chromosomes. It combines the features of two parent chromosomes to form two offspring with the possibility that good chromosomes may generate better ones. Goldberg [13], described several order-based operators, such as the Partially Matched Crossover (PMX). The order crossover (OX) was suggested by Davis [9]. The position-based crossover (PBX) was introduced by Syswerda [33]. The cycle crossover (CX) was suggested by Oliver et al. [26]. Freisleben et al. [11] introduced a distance preserving crossover (DPX).Yuan et al. proposed a two-part chromosome crossover (TCX) [37].
In this paper, we propose a new crossover inspired by DPX crossover. In proposed crossover, the first city of chromosome s1 is copied to the last position on child c2 and last city of chromosome s1 is copied to the first position on child c2. Similarly, the first city of chromosome s2 is copied to the last position on child c1 and last city of chromosome s2 is copied to the first position on child c1.
The remaining cities changed as given algorithm in Fig. 6. For example, in Fig. 5, the first position of parents s1, s2 are copied to the last position in child c2 and c1 respectively and the last position of parent s1, s2 are copied to the first position in child c2 and c1 respectively, remaining positions 2, 3, 4, 5, 6, 7, and 8 cities are swapped as procedure given in Fig. 6.
The rationale behind this crossover is based on the intuitive idea that the city in sub optimal / optimal tours occurs at same position. In this crossover the Hamming distance is preserved. Upon use of this crossover there is very less chance to have duplicate members in the population.
4.4 2-Opt Optimal Mutation
Croes, G. A. [8] proposed 2-opt optimal mutation, and in literature it mostly named as 2-opt mutation. The 2-opt mutation replaces two edge from a tour by two new edges that are not in tour such that the cost of new tour is less than the original tour. This replacement process is continued till no further improvement in the cost of the new tour is possible, this is often referred to as 2-opt optimal. Here important to note that 2-opt mutation keeps the feasible tour corresponding to a reversal of a subsequence of the cities.
The method proceeds by replacing two non-adjacent edges
For example, inverting the sub tour
The change in cost,
The 2-opt optimal mutation, which is sequential move and have chance of producing less diversify population for next generation i.e. increase in redundant solution in search space. The group theory tour construction algorithm for initial population generation has inherent capability of eliminating the redundant solutions.
Combination of 2-opt optimal mutation and Group theory tour construction algorithm, the exploration space for optimal tour gets reduced and hence the search time as well. Therefore, the combination of Group theory tour construction algorithm and 2-opt optimal mutation refines the tour for global optimality and decreases the time to get the optimal solution. We found that the proposed method gives better result in comparison to other heuristic methods reported in [37].
4.5 Proposed Algorithm
The first step of algorithm is population generation i.e. set of tour initialized using tour construction method described in Section 4.1. For multi-chromosome representation we randomly generate population of break-points of the tours for assigning the number of cities to each salesman for each tour. In the second step of algorithm, the fitness value is obtained for each tour in the population.
In the third step, randomly select ten tours and its corresponding break-points from the population. After then replace first tour and its corresponding break-points with minimum cost among selected ten tours and its break- points for crossover.
In the fourth step, apply proposed crossover operator on the first two tours from the ten tours obtained in step 4, with crossover probability rate (pc). After the crossover, the break points for both children are generated randomly.
In the last step, apply 2-opt optimal mutation operator on the tour having minimum cost among selected first two parents used for crossover in step four or new individuals that generated after crossover. After then update the population and its corresponding break-points. These processes repeated until specified generation is reached.
5 Experimental Results
5.1 Experimental Setup
For evaluating the performance of experimental results, Intel (R) Core (i5) 3.20 GHz processor, 2GB RAM on MATLAB is used. In this experiment, test problems are selected benchmark instances taken from the TSPLIB and reported in [6, 31, 37]. These test problems are Euclidean two-dimensional symmetric problem with 51, 100, and 150 cities. Here these problems are denoted as MTSP-51, MTSP-100, and MTSP-150. Number followed by MTSP indicates the number of city in the instance.
In Table 1, the experimental conditions of 12 different problem of sizes (n) and salesmen (m) combinations along with the number of generation used for each type of problem. The termination criterion is the number of generations. The value of parameters used in experiment are: population size (P) =100, tournament selection (k) =10, and crossover probability rate =0.85. The performance of methods compared based on best tour cost (Best), average tour cost (Mean), and standard-deviation (SD). Total 30 trails are made in order to collect the statistics of the result. A better method is considered to be those having lower value of Mean and Best than the other method.
5.2 Experimental Results and Analysis
To evaluate the benefits of the proposed crossover operator and initial population generation technique, computational experiments were conducted and results are compared with the four crossover namely TCX, ORX +A, CYX +A and PMX +A reported in [35] on a set of MTSP problems. We conducted experiments considering both objective functions of MTSP.
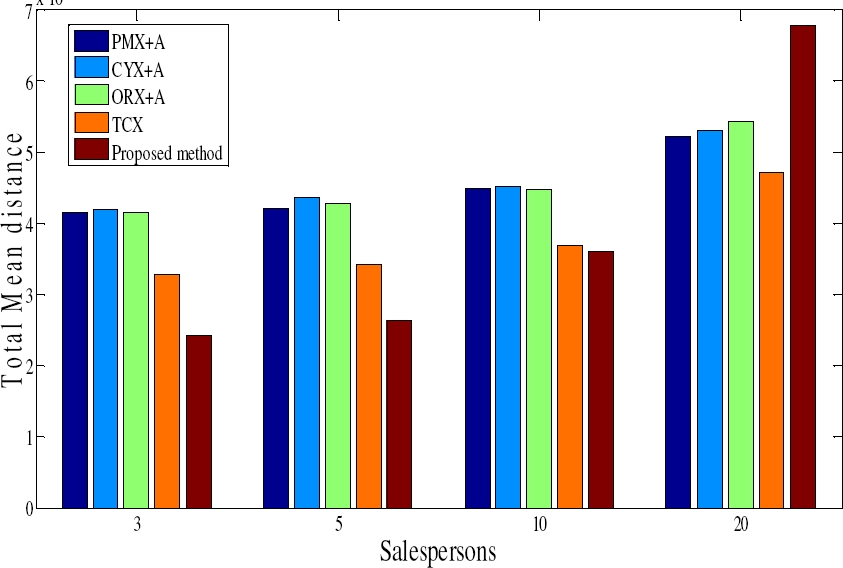
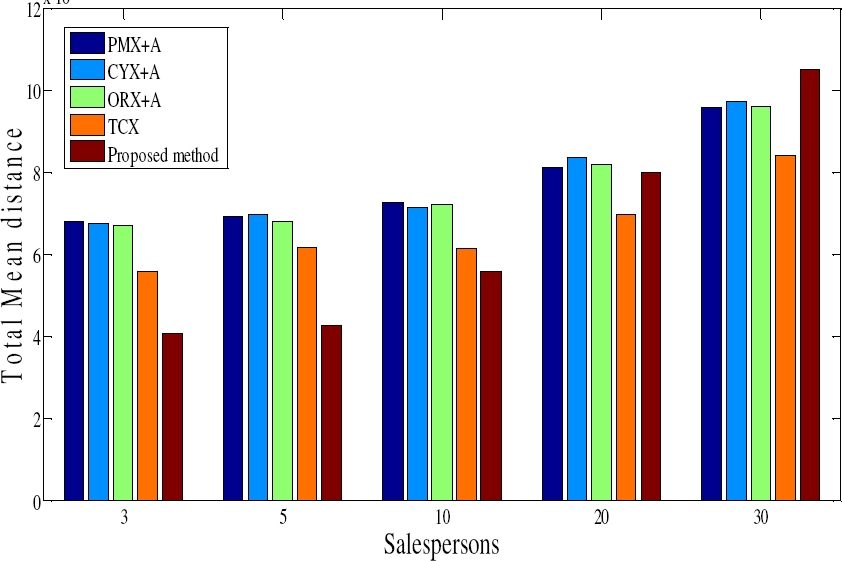
The experimental result for first objective criterion - minimize the total travel distance of all the salesmen given by Equation (3) - is presented in Table 2 and graphically in Figure 7, Figure 8, and Figure 9. The cases where our proposed method obtains better result i.e. lower value of Mean and Best, than the all other method is shown in bold, while dash (-) values are not reported.
Table 2 Experimental Results for Minimisation of Total Travel Distance
| Instance | Crossover | m=3 | m=5 | m=10 | m=20 | m=30 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Best | Mean | SD | Best | Mean | SD | Best | Mean | SD | Best | Mean | SD | Best | ||
| MTSP-51 | Proposed | 466 | 6 | 460 | 515 | 10 | 499 | 693 | 20 | 669 | ||||||
| TCX | 510 | 24 | 466 | 536 | 26 | 499 | 636 | 17 | 602 | - | - | - | - | - | - | |
| ORX+A | 584 | 29 | 517 | 621 | 39 | 551 | 709 | 33 | 648 | - | - | - | - | - | - | |
| CYX+A | 591 | 43 | 511 | 622 | 44 | 530 | 710 | 42 | 633 | - | - | - | - | - | - | |
| PMX+A | 601 | 38 | 513 | 606 | 40 | 537 | 705 | 34 | 625 | - | - | - | - | - | - | |
| MTSP-100 | Proposed | 24071 | 690 | 22959 | 26220 | 755 | 24559 | 35943 | 1221 | 33136 | 67623 | 2038 | 62963 | - | - | - |
| TCX | 32708 | 2267 | 28943 | 34179 | 2006 | 30941 | 36921 | 1964 | 32802 | 46976 | 1773 | 44112 | - | - | - | |
| ORX+A | 41516 | 3356 | 36713 | 42716 | 2806 | 36196 | 44631 | 2997 | 38717 | 54265 | 3059 | 47971 | - | - | - | |
| CYX+A | 41911 | 3195 | 35791 | 43634 | 2804 | 35421 | 45150 | 3241 | 40894 | 52916 | 2884 | 46466 | - | - | - | |
| PMX+A | 41441 | 3423 | 33802 | 42063 | 3931 | 33908 | 44786 | 3467 | 39785 | 52142 | 2588 | 46212 | - | - | - | |
| MTSP-150 | Proposed | 40697 | 826 | 39504 | 42639 | 1825 | 39862 | 55895 | 1765 | 50892 | 79734 | 1138 | 77668 | 105072 | 922 | 102880 |
| TCX | 55851 | 2588 | 51126 | 61596 | 4759 | 51627 | 61360 | 3888 | 54473 | 69701 | 4340 | 62456 | 84008 | 5285 | 76481 | |
| ORX+A | 67037 | 3745 | 60090 | 68018 | 3377 | 62539 | 72113 | 3637 | 63899 | 81696 | 5372 | 71933 | 96122 | 4562 | 88515 | |
| CYX+A | 67463 | 4454 | 55335 | 69860 | 4342 | 61521 | 71584 | 4845 | 63126 | 83471 | 4197 | 75146 | 97106 | 3911 | 89008 | |
| PMX+A | 68152 | 5140 | 58303 | 69112 | 4011 | 60761 | 72620 | 4334 | 64975 | 81178 | 4920 | 73281 | 95752 | 4923 | 87402 | |
For all instance our proposed method gives better performance, with respect to all performance parameter for cases m = 3, 5. For m =10 our method gives slightly inferior solution in terms of Best for instance MTSP-51 and MTSP -100 of TCX, but it gives better average solution almost in all cases except TCX of MTSP -51. For m = 20, performance of proposed method degraded in terms of Best, but gives better Mean for instance MTSP-150 except the case TCX. For m = 30, the performance degraded with respect to all parameter.
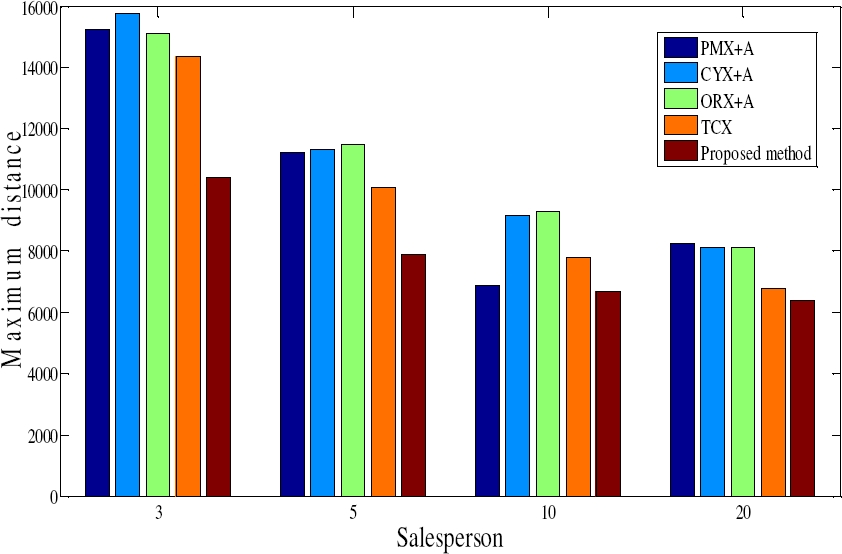
The results for second objective criterion - minimizing the longest individual tour, which is also called make-span [37], given by Equation (4) - is presented in Table 3, and graphically in Figure 10-Figure 12. Clearly, proposed method outperforms all others method with respect to all parameters for all cases except TCX of MTSP- 100 for Best parameter.
Table 3 Experimental Results for Minimizing the Longest Tour
| Instance | Crossover | m=3 | m=5 | m=10 | m=20 | m=30 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Best | Mean | SD | Best | Mean | SD | Best | Mean | SD | Best | Mean | SD | Best | ||
| MTSP-51 | Propose | 188 | 4 | 184 | 139 | 3 | 129 | 112 | 0 | 112 | - | - | - | - | - | - |
| TCX | 207 | 13 | 182 | 153 | 10 | 135 | 113 | 2 | 112 | - | - | - | - | - | - | |
| ORX+A | 216 | 12 | 191 | 165 | 11 | 139 | 128 | 13 | 112 | - | - | - | - | - | - | |
| CYX+A | 222 | 16 | 188 | 161 | 12 | 138 | 131 | 16 | 112 | - | - | - | - | - | - | |
| PMX+A | 218 | 11 | 191 | 161 | 10 | 141 | 130 | 12 | 112 | - | - | - | - | - | - | |
| MTSP-100 | Propose | 10384 | 194 | 10031 | 7907 | 137 | 7728 | 6688 | 65 | 6581 | 6404 | 43 | 6363 | - | - | - |
| TCX | 14365 | 1013 | 12645 | 10086 | 674 | 8730 | 7768 | 492 | 6796 | 6768 | 433 | 6358 | - | - | - | |
| ORX+A | 15137 | 1462 | 12997 | 11459 | 1053 | 9415 | 9286 | 1385 | 7373 | 8123 | 881 | 6666 | - | - | - | |
| CYX+A | 15759 | 1242 | 13467 | 11333 | 1278 | 9507 | 9151 | 1364 | 7111 | 8109 | 936 | 6516 | - | - | - | |
| PMX+A | 15238 | 1371 | 12249 | 11233 | 1177 | 9267 | 6890 | 1482 | 7187 | 8265 | 8608 | 6570 | - | - | - | |
| MTSP-150 | Propose | 15389 | 334 | 14804 | 13077 | 2539 | 10106 | 6884 | 99 | 6684 | 5546 | 36 | 5483 | 5251 | 5 | 5248 |
| TCX | 22523 | 1226 | 20556 | 16054 | 1227 | 14096 | 10722 | 927 | 8475 | 9640 | 789 | 8423 | 8759 | 806 | 7169 | |
| ORX+A | 24766 | 1689 | 22015 | 17646 | 1519 | 15266 | 15150 | 2006 | 11788 | 13669 | 1816 | 10274 | 12204 | 1376 | 9182 | |
| CYX+A | 23906 | 1941 | 20915 | 17608 | 1563 | 14029 | 14738 | 1750 | 10779 | 14111 | 1872 | 8365 | 13091 | 1295 | 10694 | |
| PMX+A | 24216 | 1802 | 20347 | 17741 | 1235 | 15418 | 14489 | 2139 | 10738 | 13810 | 1315 | 11722 | 12608 | 1667 | 10080 | |
We observe that, as number of salesman (m) increases the performance of the proposed method with respect to first objective degraded. This is due to minimizing the longest tour balances the cities (or workload), among the salesmen and also minimizes the distance travelled by the salesmen. Minimization of the longest tour affects the fitness value as it gets decreased with the increasing number of salesmen.
6 Conclusion
In this paper, we developed a new crossover and initial population generation using group theoretic concept for solving multiple traveling salesperson problem (MTSP), using genetic algorithm (GA). Proposed method of initial population generation, gives the wide diversity in the population by ensuring uniqueness of the members in the population and thus redundancy due to random initialization is removed. Moreover, use of proposed crossover over this population has very less chance of producing redundant member in search space. We have compared the performance of the GA using proposed crossover and population initialization with the method using crossover TCX, ORX +A, CYX +A and PMX + A. Computational results reveals that the proposed technique outperform over all other method for second objective criterion, however, slightly inferior result for first objective in few cases (m =30 and m=20).











 nueva página del texto (beta)
nueva página del texto (beta)