1 Introduction
In real situations, it is necessary to place elements, always looking for an optimal way to do it. For this, some storage medium is used, such as bags, boxes, containers, among others. These elements, commonly called objects, are of different size or type. This feature allows storage to be a complex problem, since it is always necessary to place them in the best way to save space. For example: storage problems, loading problems and containers, the problem of change, assembly lines, business problems, cutting patterns, among others. In general, these types of problems are known as cutting and packing problems. These problems, are included in a family of combinatorial problems, which can be applied to different areas such as: Health, Financial, Technological Development, Textile, Metal, among others, and this has given rise to disciplines such as: Computer science, Engineering, Operations Research, among others, propose or develop new algorithms that allow to obtain good solutions.
1.1 The One-Dimensional Bin Packing Problem (1DBPP)
The pioneers in working on this cutting problem were Gilmore and Gomory, in 1961 formulated this family of problems, known as cutting stock or trim loss problems. Subsequently, Garey and Johnson in [1], defined the one-dimensional Bin Packing problem (1DBPP).
The Bin Packing problem can be conceptually defined as follows:
Given a set of objects O (of different sizes), two constants B (container size) and N (number of containers), it is possible to place all the objects inside the N containers, such that the sum of the objects does not exceed the Capacity of each of the containers.
The problem of 1DBPP is classified as NP-hard, see [1]. Given this complexity, it is difficult to develop algorithms that obtain optimal results, such as those reported by the specialized literature [2, 3, 4, 5, 6], or close to the optimum, and even better, in a polynomial time. Proof of this are the different approaches that have been used to solve the 1DBPP, some of them are: Heuristic algorithms, Metaheuristics and Exact methods. Next, the works that have reported the best results to solve the 1DBPP are presented.
The section 2, describes the relevant works that solve some instances of the Hard28 set of 1DBPP and test sets that are difficult to solve. For its part, section 3, explains the characteristics of the analysis tool, through which the storage patterns of the objects are discovered. In section 4, the proposed algorithm that solves some instances of Hard28 of 1DBPP is detailed. The section 5, on the other hand, shows the experimental results and finally the conclusions and the work to be done are discussed in section 6.
2 State of the Art
To date, different algorithms have been proposed that solve the problem of 1DBPP, in this section, it evaluates those that have solved the largest number of instances of the Hard28 dataset, comparing the behavior of the algorithms and the quality of the solution.
2.1 Algorithms that Solve the Problem of 1DBPP
According to the specialized literature, the work developed in [12, 13], has reported a set of algorithms that have proven to be the best to obtain optimal solutions from some of the most referenced instances in the state of the art. Particularly, the instances of the Hard28 set have been reported as those that have been the most difficult to solve by metaheuristic algorithms.
The algorithm Hybrid Grouping Genetic Algorithm Bin Packing (HGGA-BP), discussed in [8], is a hybrid-genetic clustering algorithm. Which is inspired by the algorithm of Falkenauer, reported in [14]. The HGGA-BP uses heuristics (FFD, WFD, BFD, among others), to generate the initial population. Subsequently, it uses intensification and diversification to find the best individuals in the population, applying crosses and mutations to improve the quality of the solution. The HI-BP algorithm, reported in [7], is a hybrid metaheuristic algorithm, which has two stages: construction and improvement. In the first stage, it uses a hybrid heuristic and in the stage of improvement uses the tabu search algorithm reported in [11].
Weigth Anneling [9], is a metaheuristic algorithm that uses five steps to solve the 1DBPP problem. The first step generates an initial solution using the FFD heuristic. The second step distorts the sizes of objects; the third step performs local searches and exchanging objects between pairs of containers, in the fourth step reassigns weights and finally checks whether the stoppage criterion has been reached.
On the other hand, Pert-SAWMBS developed in [10], proposes a method of solution oriented to the container, this is done by controlling the average weight of the objects that are inside each container. As well as using reduction methods for each of the solutions generated.
The research work developed in [12], proposes a method based on patterns, data mining and iterative, to find the optimal values of the set of instances Hard28.
It is important to highlight the method of solution that is posed by in [13], in it a new strategy is proposed that allows finding optimal values reported in the literature [12]. This work proposes an exploration strategy that uses different approaches to solve the instances of the Bin Packing problem. To do this, it uses a hybrid algorithm that takes as its main elements: a mathematical model, a heuristic, reduction criteria and finally a metaheuristic algorithm, the latter calculates the lower limit of an instance. One of the limitations of this work is the computation time that it uses to obtain the optimal values.
2.2 1DBPP Instances
To date, there is no consensus to determine which sets of instances are difficult to resolve. In the work developed in [12], several investigations have been reported in which sets of instances considered by the authors as difficult to solve are proposed.
For example, the datasets proposed in [14]: Uniform [OR Library] and Triplets [OR Library]. In the first, the files binpack1 to binpack4 consist of objects whose size are uniformly distributed in (20,100), to be packed in containers of Size 150. And in the second, the files binpack5 to binpack8 consists of 'triplets' of objects distributed in (25, 50), to be packaged in 100 size containers.
The work reported in [15], proposes three sets of instances Data_Set_1, Data_Set_2 and Data_Set_3, each of these sets presents characteristics that make them difficult to solve.
The first set consists of 720 instances, each one of which is constructed similarly to those used in [19]. The objective of set number two is to obtain an average of 3, 5, 7 and 9 objects per container and the last set has instances considered as hard, since the weights of the objects are widely dispersed and the values are obtained in the interval from 20,000 to 35,000.
It is important to note that in [17], the data set Wae_Gau1 is proposed for the first time, which consists of 17, instances with different characteristics in each of them and which are considered as difficult to resolve by the authors.
In the work developed in [16], the data sets Was_1 and Was_2 are proposed, which are considered difficult to solve.
Finally, the research discussed in [18], proposes to the data set 53NIRUP and the data set Hard28. The set Hard28 consists of 28 instances, which have been considered as the most difficult to solve by the current metaheuristic algorithms.
The following explains the elements that are used to detect the different storage patterns of objects in containers.
3 Storage Patterns
The next section presents the visualization tool that was used to discover the storage patterns developed.
3.1 Visualization Tool
Given the large amount of information generated by the metaheuristic algorithms applied to the 1DBPP problem, the tool called MEVIZ was developed, which performs analysis and monitoring of the results generated by an algorithm. MEVIZ receives as input a set of instances and a metaheuristic algorithm.
The metaheuristic algorithm that to date has solved more instances of the Hard28 dataset is the HGGA-BP, proposed in [8]. These two elements are the input data to the visualization tool. To perform the monitoring, a listening agent is embedded in the metaheuristic algorithm.
Figure 1, shows an example of how objects are distributed within the containers by the HGGA-BP algorithm. And in Table 1, the total number of solutions generated by the same algorithm is shown.
Table 1 Number of solutions generated by the HGGA-BP algorithm
| Instance name | Number of solutions generated |
|---|---|
| hBPP14 | 537455 |
| hBPP832 | 533409 |
| hBPP40 | 842109 |
| hBPP360 | 545123 |
| hBPP645 | 831429 |
| hBPP742 | 548413 |
| hBPP766 | 538262 |
| hBPP60 | 544368 |
| hBPP13 | 536140 |
| hBPP195 | 531753 |
| hBPP709 | 534363 |
| hBPP785 | 541316 |
| hBPP47 | 539677 |
| hBPP181 | 546009 |
| hBPP359 | 546560 |
| hBPP485 | 541622 |
| hBPP640 | 543313 |
| hBPP716 | 551829 |
| hBPP119 | 532743 |
| hBPP144 | 528376 |
| hBPP561 | 528306 |
| hBPP781 | 530417 |
| hBPP900 | 531077 |
| hBPP175 | 544497 |
| hBPP178 | 539753 |
| hBPP419 | 567358 |
| hBPP531 | 553283 |
| hBPP814 | 541937 |
As this algorithm is genetic, it considers many solutions, since it depends on the size of the initial population. With the tool developed in the present investigation, it is possible to visualize the whole set of solutions generated by the metaheuristic algorithm.
In Table 2, the segment of a solution generated by the HGGA-BP algorithm of the hBPP13 instance of the Hard28 set is shown and based on these results storage patterns can be obtained.
Table 2 Extract of a solution generated by the HGGA-BP algorithm applied to the HBPP13 instance
| Number of solution |
Container | Objects | Total Sum |
|---|---|---|---|
| 15513 | 0 | -596-332-72 | 1000 |
| 1 | -85-444-471 | 1000 | |
| 2 | -194-555-251 | 1000 | |
| 3 | -649-36-315 | 1000 | |
| 4 | -652-51-297 | 1000 | |
| 5 | -385-426-189 | 1000 | |
| 6 | -128-572-300 | 1000 | |
| 7 | -499-341-160 | 1000 | |
| 8 | -662-122-216 | 1000 | |
| 9 | -674-28-298 | 1000 | |
| 10 | -641-169-190 | 1000 | |
| 11 | -690-281-29 | 1000 | |
| 12 | -378-126-496 | 1000 | |
| 13 | -635-62-303 | 1000 | |
| 14 | -660-167-173 | 1000 | |
| 15 | -316-628-56 | 1000 | |
| 16 | -651-181-168 | 1000 | |
| 17 | -691-95-214 | 1000 | |
| 18 | -458-541-1 | 1000 | |
| 19 | -626-144-230 | 1000 | |
| 20 | -634-84-282 | 1000 |
3.2 Pattern Discovery
Next, the results generated by the metaheuristic algorithm through the MEVIZ tool are analyzed and it is possible to discover storage patterns of objects in containers and that are the basis of the algorithm proposed in this research work.
Analyzing the solutions generated and taking as reference Table 2, container number
11 is filled with 3 objects, two of which have a weight whose value are prime numbers (281 and 29) and the other object has a weight whose value is an even number (690).
This is also true for container number 14, at its maximum capacity. In container number zero, the weight of the three objects are even numbers (596, 332 and 72), as well as container number six.
Another common pattern that has been discovered is that of 2 objects with weight whose value is an odd number and an object with a weight whose value is an even number.
It is important to mention that these patterns are meet whenever a container is full to its maximum capacity.
From the results obtained by the tool, it has been found that these patterns are presented in the different solutions that are obtained for an instance of Hard28, as well as for all instances of the same dataset. All this allows to generalize the storage patterns of the objects in the containers for the data set Hard28.
In the next section, we propose an algorithm that uses the properties of the natural numbers, this proposal reduces the dimensionality of the instances of the data set Hard28. Subsequently the FFD heuristic algorithm is applied and in this way the optimal is obtained for some of the instances of the Hard28, in practically negligible times.
4 Proposed Algorithm
After analyzing the results generated by the HGGA-BP algorithm and visualized with the MEVIZ tool, an algorithm is developed that reduces the dimensionality of the instances and, together with the FFD heuristic, allows to obtain the optimal value of some of the data set instances Hard28.
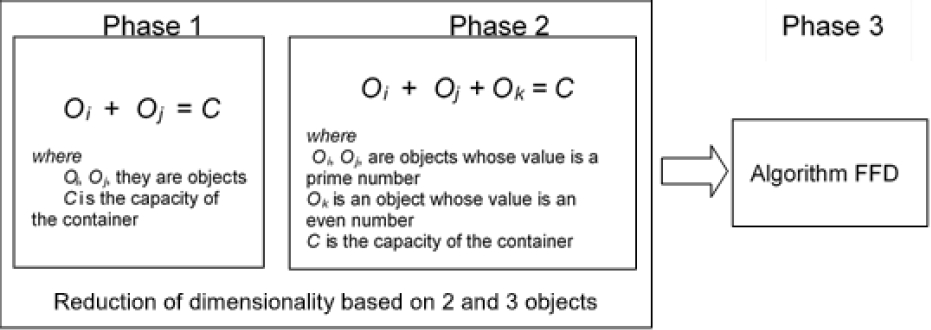
A general scheme of the proposed algorithm is shown in Figure 2, it uses the storage pattern (2 objects whose weight is a prime number and an object whose weight is an even number), to fill containers at their maximum capacity using only 3 objects.
One of the basic elements of the proposed algorithm is to divide the list of objects into sublists, this allows grouping objects that have common characteristics, without the need to perform excess combinations, as in the case of using a single list of objects. In addition, this reduces the dimensionality of instances. The general elements of the proposed algorithm are described below.
Phase 1. Fill a container with 2 objects. One of the characteristics of the set of instances of the Hard28 is that the values of some objects are greater than half the capacity of the container, this allows to traverse the list of objects and fix them in containers.
Subsequently, to be able to fill them to their maximum capacity the problem is reduced to using a search algorithm, i.e., takes the residual capacity of the container and searches that value in the list of free objects. This phase reduces the dimensionality of the instance.
Phase 2. Fill a container with 3 objects. Based on the detected pattern, containers are filled with 3 objects, of which the weight of 2 objects are prime numbers and the other object is an even number; this is valid because the capacity of the container, for the case of the set of instances Hard28, is an even number. Subsequently, the strategy of divide and conquer is used, this strategy is applied to the list of free objects of Phase 1.
For this, the reduced list is divided into 3 sublists; objects whose weight value is an even number and objects whose weight value are prime numbers. From this a combinatorial algorithm is developed, using the list of prime objects with the list of even objects. This fills some other containers and further reduces the dimensionality of the instance.
Phase 3. Heuristic algorithm. The three lists of objects left over from phase 2: primes, pairs and odd are concatenated, and the FFD heuristic algorithm is applied.
Next, the proposed algorithm is shown, which allows to obtain the optimum value of some instances of the dataset HARD28.
Step 1. The instance is reduced by filling the containers with 2 objects
For all objects in the instance:
Let O i and O j be the weights associated with the i-th and the j-th object of the instance and let C be the capacity of the container
If O i + O j = C then place them in a container and remove the O i and O j objects from the instance.
Step 2. The instance is reduced by filling the containers with 3 objects
Split the list into 3 sublists:
List of even objects,
List of prime objects,
List of odd objects.
For all objects in the list of primes and list of pairs.
Let O k , be an object that belongs to the list of even objects.
Let O i and O j , be two objects belonging to the list of prime objects and C the capacity of the containe.
If O i + O j + O k = C then place them in a container and delete the objects O i , O j and O k , from the instance.
Step 3. Join the lists of even, odd and prime objects.
Step 4. Apply to the First Fit Decreasing (FFD) algorithm.
In the next section, the experimental results are discussed.
5 Experimental Results
The tests were performed using the C# programming language and the VS.NET 2010 IDE on an Intel Core i7 2.80 GHz computer with 4GB of RAM, using the Windows 7 operating system.
Each of the instances of the Hard28 set contains different numbers of objects, 160, 180 or 200. The range of weights is from 1 to 800, with a container capacity equal to 1000.
Table 3 shows the percentage of objects that have a prime, even or odd value, as well as the percentage of objects that are above half the container capacity of the instances of the Hard28 dataset. This percentage corresponds to the objects that were left, after filling the containers with 2 objects.
Table 3 Percentage of objects with even values, odd, primes and total number of objects
| Name of instance |
Percentage of prime objects |
Percentage of odd objects |
Percentage of even objects |
Percentage of objects greater than half of the container |
Objects |
|---|---|---|---|---|---|
| hbpp13 | 0.17 | 0.53 | 0.46 | 0.33 | 180 |
| hbpp14 | 0.20 | 0.48 | 0.51 | 0.31 | 160 |
| hbpp40 | 0.22 | 0.48 | 0.51 | 0.28 | 160 |
| hbpp47 | 0.22 | 0.51 | 0.48 | 0.35 | 180 |
| hbpp60 | 0.12 | 0.51 | 0.48 | 0.32 | 160 |
| hbpp119 | 0.19 | 0.44 | 0.54 | 0.30 | 200 |
| hbpp144 | 0.17 | 0.48 | 0.51 | 0.27 | 200 |
| hbpp175 | 0.15 | 0.43 | 0.56 | 0.36 | 200 |
| hbpp178 | 0.19 | 0.52 | 0.47 | 0.35 | 200 |
| hbpp181 | 0.17 | 0.47 | 0.52 | 0.34 | 180 |
| hbpp195 | 0.18 | 0.51 | 0.48 | 0.26 | 180 |
| hbpp359 | 0.17 | 0.50 | 0.49 | 0.34 | 180 |
| hbpp360 | 0.13 | 0.54 | 0.45 | 0.36 | 160 |
| hbpp419 | 0.14 | 0.54 | 0.45 | 0.34 | 200 |
| hbpp485 | 0.16 | 0.51 | 0.48 | 0.34 | 180 |
| hbpp531 | 0.16 | 0.48 | 0.51 | 0.38 | 200 |
| hbpp561 | 0.20 | 0.53 | 0.46 | 0.26 | 200 |
| hbpp640 | 0.14 | 0.60 | 0.39 | 0.37 | 180 |
| hbpp645 | 0.14 | 0.50 | 0.49 | 0.29 | 160 |
| hbpp709 | 0.09 | 0.61 | 0.38 | 0.28 | 180 |
| hbpp716 | 0.18 | 0.48 | 0.51 | 0.39 | 180 |
| hbpp742 | 0.17 | 0.5 | 0.5 | 0.35 | 160 |
| hbpp766 | 0.12 | 0.54 | 0.45 | 0.28 | 160 |
| hbpp781 | 0.18 | 0.47 | 0.52 | 0.31 | 200 |
| hbpp785 | 0.19 | 0.43 | 0.56 | 0.33 | 180 |
| hbpp814 | 0.17 | 0.52 | 0.47 | 0.38 | 200 |
| hbpp832 | 0.11 | 0.5 | 0.5 | 0.27 | 160 |
| hbpp900 | 0.19 | 0.47 | 0.52 | 0.32 | 200 |
Of the 28 instances of the Hard28 data set the optimum was found in 5 of them: hBPP14, hBPP359, hBPP716, hBPP119, hBPP175, as shown in Table 4. These same instances were solved with the algorithms: HI-BP [7], WA [9] and Pert-SAWMBS [10], but the time it took the algorithm proposed in this paper is less than the algorithms mentioned above. In the case of the HGGA-BP algorithm [8], it solves 6 more, but in a much longer time, as shown in Table 5, it shows the total time consumed by the HGGA-BP algorithms [8], HI- BP [7], WA [9] and Pert-SAWMBS [10] in solving all set of instances Hard28.
Table 4 Results generated by the proposed strategy, compared with other algorithms
| Instance | Optimal | HI_BP | WABP | Pert-SAWMBS | HGGA-BP | Proposed Algorithm |
|---|---|---|---|---|---|---|
| hBPP14.txt | 62 | 62 | 62 | 62 | 62 | 62 |
| hBPP832.txt | 60 | 61 | 61 | 61 | 61 | 61 |
| hBPP40.txt | 59 | 60 | 60 | 60 | 60 | 60 |
| hBPP360.txt | 62 | 63 | 63 | 63 | 62 | 63 |
| hBPP645.txt | 58 | 59 | 59 | 59 | 59 | 59 |
| hBPP742.txt | 64 | 65 | 65 | 65 | 64 | 65 |
| hBPP766.txt | 62 | 63 | 63 | 63 | 63 | 63 |
| hBPP60.txt | 63 | 64 | 64 | 64 | 64 | 64 |
| hBPP13.txt | 67 | 68 | 68 | 68 | 68 | 68 |
| hBPP195.txt | 64 | 65 | 65 | 65 | 65 | 65 |
| hBPP709.txt | 67 | 68 | 68 | 68 | 68 | 68 |
| hBPP785.txt | 68 | 69 | 69 | 69 | 69 | 69 |
| hBPP47.txt | 71 | 72 | 72 | 72 | 71 | 72 |
| hBPP181.txt | 72 | 73 | 73 | 73 | 73 | 73 |
| hBPP359.txt | 76 | 76 | 76 | 76 | 76 | 76 |
| hBPP485.txt | 71 | 72 | 72 | 72 | 72 | 72 |
| hBPP640.txt | 74 | 75 | 75 | 75 | 74 | 77 |
| hBPP716.txt | 76 | 76 | 76 | 76 | 76 | 76 |
| hBPP119.txt | 77 | 77 | 77 | 77 | 77 | 77 |
| hBPP144.txt | 73 | 74 | 74 | 74 | 74 | 74 |
| hBPP561.txt | 72 | 73 | 73 | 73 | 73 | 73 |
| hBPP781.txt | 71 | 72 | 72 | 72 | 72 | 73 |
| hBPP900.txt | 75 | 76 | 76 | 76 | 76 | 76 |
| hBPP175.txt | 84 | 84 | 84 | 84 | 84 | 84 |
| hBPP178.txt | 80 | 81 | 81 | 81 | 81 | 81 |
| hBPP419.txt | 80 | 81 | 81 | 81 | 81 | 81 |
| hBPP531.txt | 83 | 84 | 84 | 84 | 83 | 85 |
| hBPP814.txt | 81 | 82 | 82 | 82 | 81 | 83 |
| Total | 5 | 5 | 5 | 5 | 11 | 5 |
Table 5 Comparative table of the solution times
| Proposed Algorithm | HGGA-BP | HI_BP | WA | Pert-Saw MBS |
|---|---|---|---|---|
| 10 ms. | 4.31 seg | 0.48 seg. | 0.59 seg. | 0.24 seg. |
Although the optimal was not obtained for the remaining instances, the solution is close to the optimum (a container), except for instances hBPP814, hBPP531, hBPP640, hBPP781 whose difference is larger than a container. Particularly the instance hBPP640 is to 3 containers of the optimal value.
6 Conclusions
Many of the works that try to solve the problem 1DBPP have focused on giving solution to the set of instances Hard28, which have been reported in the specialized literature as the most difficult.
The algorithm proposed in this research is novel and promising. Unlike the ones reported in the literature, the algorithm uses the characteristics of each of the weights of the objects to be located, that is, the weight of the objects can be: a prime number, an even number or an odd number. Also used is the fact that the weights of some of the objects have a value higher than half the capacity of the container. This type of patterns allows to reduce the dimensionality of instances.
The first reduction of dimensionality is achieved by filling a container with two objects, depending on the size of the instance, but in general this allows to reduce the size of instances between 5% and 10%.
One of the results that is important to highlight is the discovery of storage patterns of objects in containers. A container is filled with 3 objects: 2 objects whose weight are prime numbers and an object whose weight is an even number, this is due to the implemented tool, MEVIZ, and that allowed to analyze the whole set of solutions generated by the algorithm HGGA-BP.
The algorithm proposed in this paper finds the optimal value for 5 instances, reported in the specialized literature [6, 7, 8, 9], and the computation time was in milliseconds, which is practically negligible, see Table 5.
The measured times for each of the instances are less than one millisecond, except for the instance hBPP14. But in instances hBPP716, hBPP119, hBPP175 and hBPP359 the computation time is one millisecond. For other instances, it is almost insignificant. In other related works, the reported times are in seconds and greater.
The results generated, see Table 4, allow to continue in this line, that is, to work with the characteristics of the objects. Find patterns of combinations for three objects and make it unique; two odd and one pair, or three objects whose weight is an even value.
As well as working with number theory and characterizing objects to determine three objects that must necessarily go together inside a container; two objects whose weight is a prime number and an object whose weight is an even number or three objects whose weight is an even number.











 nueva página del texto (beta)
nueva página del texto (beta)