1 Introduction
The use of optimization problems arise in different fields such as manufacturing, engineering design, control, optimization, economics etc., provide practical use in real life therefore there is a real need for efficient and robust computational algorithms which help to solve that kind of problems. Several NP-hard combinatorial optimization problems, such as assignment problem, the traveling sales problem, minimum spanning tree, vehicle routing problem, can be modeled as the Quadratic Assignment Problem (QAP) (Said, Mahmoud, El-Horbaty, 2014).
Optimization is a process that finds a best or optimal solution for a problem. An combinatorial optimization is a topic that consist of finding an optimal object from a finite set of objects (Schrijver, 2006) find values of variables that minimize or maximize the objective function while satisfying the constrains. The principal factors of optimization problems are: an objective function which is to be minimized or maximized, a set of unknown or variables that affect the objective function and a set of constrains that allow the unknowns to certain values but exclude others.
There is more than one local solution in most optimization problems, in order to choose a good optimization method that look only in the neighborhood of the best solution rather than be a greedy one that mislead the search process and leave it stuck at a local solution. Nowadays there are multiple methods to solve optimization problems of both mathematical and combinatorial types, but if the optimization problem is difficult or the search space is large, it will become difficult to solve using conventional mathematics.
As a result of these problems many meta-heuristic optimization methods have been developed to solve such difficult problems (Alazzam and Lewis, 2013).
To understand combinatorial optimization is necessary define Combinatorial that in general means that the state space is discrete, now combinatorial optimization problems (COP), are those problems that have a finite set of possible solutions, experts in combinatorial optimization tend to search for particular poly nominal solvable version of NP- hard problems and research mechanisms to measure the difficulty of problem instances (Loila et. Al 2007). To solve combinatorial optimization problems, it´s necessary to check all feasible solutions in the search space. However, is not always possible to check all feasible solution especially when the search space is large, therefore many meta-heuristics algorithms haven been devised and modified to solve these problems. Due to the Meta heuristics does not provide a guarantee to find an optimal solution, but they try to explore different areas in the search space in a smart way to get a near optimal solution in less cost and time (Baghel, Agrawa, Silakari, 2012).
Many real world applications require the solution of optimization problems which belong to a special class NP- complete problems as the quadratic assignment problem (QAP), which is one of the most difficult problems in the NP-hard class, (Shani and Gonzalez, 1978), models real life problems in several areas such facilities location, combinatorial data analysis and parallel and distributed computing. Combinatorial optimization problems such as maximal clique and graph partitioning can be formulated as a QAP.
The main contribution of this paper is centered on the search for solutions to a complex problem belonging to the NP-hard class (QAP), through the Greedy Randomized Adaptive Search Procedure metaheuristic (GRASP).
This paper is organized as follows. In section 2 the related work is presented with the methodology, solution, applications and in general some advances in the QAP. Section 3 the mathematical model for QAP is presented. In section 4 the development of the GRASP meta-heuristic, section 5 the design of GRASP for QAP, section 6 describes the experimental results obtained by the application of the presented model and finally in section 7 some conclusions and future work are presented.
2. Related Work
Koopmans and Beckmann(1957), first proposed the QAP as a mathematical model related with economic activities, since then, it has appeared in several applications: Steinberg (1961), used the QAP to minimize the number of connections between components in a backboard wiring; Heffley (1972,1980), applied as a Koopmans and Beckmann in economic problems; Francis and White (1974) developed a decision framework for assigning a new facilities here some of the applications: police pots, supermarkets, schools, hospitals in order to serve a given set of clients; Geofrrion and Graves (1987), focused on scheduling problems; Pollatschek et al.(1976), used the QAP to define the best design for typewriter keyboard and control panels; Krarup and Pruzan(1978), applied it to archeology; Hubert (1987), in a statistical analysis; Forsberg et al. (1994), used it in the analysis of reaction chemistry; Brusco and Stahl (2000), in numerical analysis. However, the most popular application for the QAP is the facilities layout problem, Dickey and Hopkins (1972), applied the QAP to the assignment of buildings in a university campus, Elshafei (1977), in a hospital planning and Bos (1993), in a related problem to forest park. Benjaafar (2002), introduced a formulation of the facility layout design problem in order to minimize work in process (WIP), in that work it shows that layouts obtained using a WIP- based formulation can be very different in comparison of the conventional QAP formulation because the QAP- optimal layout can be WIP Infeasible.
During the decade of the 90´s there was new application related with the QAP, Bland and Dawson (1991,1994), Taboo search and design optimization, Layout of facilities using a heuristic hybrid algorithm, Balakrishnan et al. (1992), applied to solutions for the constrained dynamic facility layout problem; Lacksonen and Enscore (1993), used the quadratic assignment algorithm for the dynamic layout; Philips and Rosen (1994), invoked the quadratic assignment formulation of the molecular conformation problema;Bozer and Suk- Chul (1996), applied to branch and bound method for solving the bidirectional circular layout problem; Talbot and Cawley (1996), used a quadratic index assignment algorithm for vector quantization over noisy transmission channels; White(1996), in a lagrangean relaxation approach for a turbine design quadratic assignment problem; Ball et al. (1998), in Network -based formulation of quadratic assignment problems; Haghani and Chen (1998), used to optimize the gates assignment at airport terminal; Kochhar et al. (1998), applied to a genetic algorithm for the unequal area facility layout problem; Sarker et al. (1998), applied to one dimensional machine location problems in a multi-product flowline with equidistant location; Tansel and Bilen (1998), in move based heuristic for the unidirectional loop network layout problem; Tavakkoli - Moghaddain and Shayan (1998), in Facilities layout design by genetic algorithm; Urban (1998), use to solve procedures for the dynamic facility layout problem; Gong et al. (1999), in a genetic algorithm method for one- dimensional machine location problems; Rossin and Klein (1999), applied in a complexity measure for the facility layout problem.
The applications of the QAP are extensive and have been of great interest for the researchers in real scenarios for that reason they are still looking for new alternatives that allow to have new inventions on this subject, for the decade of the 2000 researchers continue with this hard work implementing new methods: Bartolomei and Egbelu (2000), used quadratic assignment problem QAP with adaptable material handling devices; Ho and Moddie (2000), applied a hybrid approach for concurrent layout design of cells and their flow paths in a tree configuration; Urban et al. (2000), used to integrated machine allocation and layout problem; Hahn and Krarup (2001), used in a hospital facility layout problem; Ji and MacGregor (2001), applied to observe the customers traffic inside a mall; Siu and Chang (2002). In an optimal assignment in wavelength division multiplexing network with fixed regular virtual topologies; Wang and Sarker (2002), used to locating cells with bottleneck machines in cellular manufacturing systems; Ciriani et al. (2004), in Room allocation polynomial subcase of the quadratic assignment problem; Solimanpur et al. (2004), applied to an Ant colony optimization algorithm to the inter-cell layout problem in cellular manufacturing.Recent work shows the new trends and applications for these optimization problems that are modeled with the QAP: Nickel and Puerto (2005), did an extended and comprehensive study in the continuous area of networks based on location and distribution models mainly on medium problems of location and distribution; Another interesting application in logistics concerns the assignment of doors to minimize the cost of loading materials in a rectangular cross dock (Bozer y Carlo 2008).
In the design of logistics networks, there is a special problem of location and design problems, which consists of finding the optimal location of the facilities and assigning customers to the facilities in such a way as to minimize the costs of satisfying customer demand (Bozer y Carlo 2008); hospital design (Murat et al. 2010). Bathi and Rasool (2014), applied to the airport design, container location in shipping yards, interior customs. In recent years’ metaheuristics have proven to be robust tools for solving difficult optimization problems as is shown in this section.
3. Mathematical Model QAP
Next we present the mathematical model of combinatorial optimization.
Given a set ℵ= {1, 2, n} and n × n matrices F= (f ij ) and D= (d kl ) the QAP can be stated as follows:
The objective is to find and optimal assignment of n facilities to n locations.
Here Πℵ is the set of all permutations of
In this article, we will implement the GRASP metaheuristics to find solutions to the QAP by means of a random combining approach of neighborhood structures, which will be tested for the instances taken from QAPlib.
4. GRASP Meta-Heuristic
GRASP is a metaheuristic that emerged during the 1980´s in order to solve difficult problems in the field of combinatorial optimization.
It was originally developed by Feo and Resende in 1989, with the article a probabilistic heuristic for a computationally difficult set covering problem.
GRASP is an iterative process. Each GRASP iteration consists of two steps: the construction phase and the post-processing phase. Once the two phases have been executed, the obtained solution is stored and iteration is carried out, saving each time the best solution that has been found so far.
The objective of the construction phase is to generate a feasible solution of good quality and it is expected that the work of the post-processing phase will be less, so each GRASP iteration would occur faster in the construction phase, GRASP generates a list of candidates formed by elements of high quality, this list is called candidate restriction list (CRL). The initial solution is constructed iteratively.
In each iteration of the constructive procedure, an element is randomly chosen from the list of candidates to be added to the substructure as part of the solution being constructed, better say the method is greedy, random and adaptive.
In the post-processing phase, local search algorithms are used to improve the solution produced in the first phase to obtain local optimization.
5. GRASP for QAP
According with Li et al. The first phase of GRASP has components that are linked together into an iterative method that constructs a feasible solution. This solution will be improved in a second phase through a local search strategy.
The first phase consists of two stages, in the first one generates a restricted list of candidates that needs two parameters alpha and beta, from this process the first two assignments are given in the permutation of the solution being constructed, in step 2 The remaining n-2 are added, the process ends when the whole permutation is complete, then we have an initial solution ready to improve it.
Construction phase for the QAP:
The elements of the flow matrix are arranged in a list in ascending order and the elements of the distance matrix are arranged in a list in decreasing order, the two lists are constrained by an alpha (α), parameter and both lists are multiplied from component to component.
To generate a new list with the elements
The second phase of the construction consists in including one by one the new assignments by calculating the cost of each of the possible assignments and selecting from a list the ones of lesser value, thus being continued until the permutation is complete. See procedure 2 modified from figure 2 of Li, Pardalos and Resendes (1994).
The input parameters for this algorithm are two assignments obtained from the restricted list of candidates, as can be seen the cardinality of the gamma set in line 1 is 2, while the permutation is not complete, a procedure is followed to calculate the costs of possible assignments of the following components of the permutation in this way is selected the lowest cost.
The second phase of GRASP called post-processing consists of improving the solution produced in the first phase by means of a local search algorithm that depends on the designed neighborhood structure. In Procedure 3, the solutions P, s and the neighborhood structure N (s).
This paper implements the random combination of neighborhood structures
Table 1 Neighborhood from initial solution s
| N(s)= 2-Exchange | Cost | |||||
|---|---|---|---|---|---|---|
| s | 2 | 3 | 5 | 1 | 4 | 74 |
| s1 | 3 | 2 | 5 | 1 | 4 | 74 |
| s2 | 5 | 3 | 2 | 1 | 4 | 90 |
| s3 | 1 | 3 | 5 | 2 | 4 | 60 |
| s4 | 4 | 3 | 5 | 1 | 2 | 62 |
| s5 | 2 | 5 | 3 | 1 | 4 | 74 |
| s6 | 2 | 1 | 5 | 3 | 4 | 72 |
| s7 | 2 | 4 | 5 | 1 | 3 | 50* |
| s8 | 2 | 3 | 1 | 5 | 4 | 61 |
| s9 | 2 | 3 | 4 | 1 | 5 | 80 |
| s10 | 2 | 3 | 5 | 4 | 1 | 74 |
6. Experimental Results
In this section, we report experimental results describing the testing of a Java implementation of the GRASP described in this paper on a wide range of tested problems, including most instances from the suite of QAP tested problems QAPLIB (Li, Pardalos, Resendes, 1994)).
The experiment was conducted on Intel (R) Core (TM) i7-7500 CPU 2, 7 GHz, 2.90 GHz with RAM of 16 GB.
Throughout the experiment we used the following parameters:
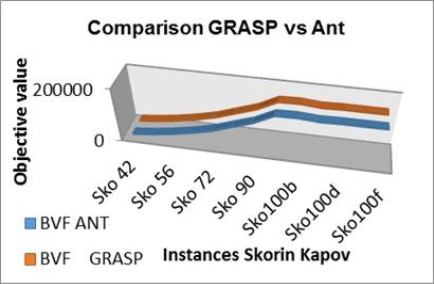
The Figure 1, shows the comparison of the algorithms, the instance and the target value obtained by GRASP and Ant, as it is observed the difference that is recorded is not great.
Table 2, shows the results obtained of the execution of the sequential program in Java code to solve the QAP by means of GRASP and combination of neighborhoods, in the first column the large scale instances proposed by Skorin Kapov from n=42 to N=100 and its different variants, it is worth mentioning that these instances are the most complex to obtain robust results. The second column shows the combination of the neighborhood represented by N applied in the local search in the second phase of GRASP where C.R. means Combination Random, λ-E: Lambda Exchange, 2-E: 2 exchange, SW: swap, In the third column the best known objective values with the acronyms BKV are shown and in the fourth column the results are shown with the abbreviations GRF, the fifth column shows the gap less than 1% in all cases, Finally the CPU time in seconds.
Table 2 GRASP results
| Instance | N | BKV | BVF GRASP | GAP | CPUT |
|---|---|---|---|---|---|
| Sko 42 | C. R. | 15812 | 15862 | 0.32 | 319 |
| Sko 49 | C. R. | 23386 | 23552 | 0.71 | 64 |
| Sko 56 | λ- E. | 34458 | 34694 | 0.68 | 121 |
| Sko 64 | λ- E. | 48498 | 48686 | 0.39 | 207 |
| Sko 72 | λ- E. | 66256 | 66686 | 0.65 | 283 |
| Sko 81 | 2- E. | 90998 | 91640 | 0.71 | 538 |
| Sko 90 | C. R. | 115534 | 116176 | 0.56 | 860 |
| Sko 100a | Sw. | 152002 | 152830 | 0.54 | 1718 |
| Sko 100b | 2- E. | 153890 | 154916 | 0.67 | 1263 |
| Sko 100b | C.R. | 153890 | 154928 | 0.67 | 1060 |
| Sko 100c | 2- E. | 147862 | 148736 | 0.59 | 1290 |
| Sko 100d | C. R. | 149576 | 150772 | 0.80 | 1197 |
| Sko 100e | λ- E. | 149150 | 150454 | 0.87 | 1141 |
| Sko 100f | λ- E. | 149036 | 150320 | 0.86 | 470 |
In Table 3, the GRASP results are shown with the combination of neighborhood structures for n=64 to n=250 instances and their variants proposed in QAPLIB for which the optimum values were obtained in a minimum time of computation.
Table 3 Other GRASP´s results
| Instance | N | BKV | BVF GRASP | GAP | CPUT |
|---|---|---|---|---|---|
| Sko 42 | C. R. | 15812 | 15862 | 0.32 | 319 |
| Sko 49 | C. R. | 23386 | 23552 | 0.71 | 64 |
| Sko 56 | λ- E. | 34458 | 34694 | 0.68 | 121 |
| Sko 64 | λ- E. | 48498 | 48686 | 0.39 | 207 |
| Sko 72 | λ- E. | 66256 | 66686 | 0.65 | 283 |
| Sko 81 | 2- E. | 90998 | 91640 | 0.71 | 538 |
| Sko 90 | C. R. | 115534 | 116176 | 0.56 | 860 |
| Sko 100a | Sw. | 152002 | 152830 | 0.54 | 1718 |
| Sko 100b | 2- E. | 153890 | 154916 | 0.67 | 1263 |
| Sko 100b | C.R. | 153890 | 154928 | 0.67 | 1060 |
| Sko 100c | 2- E. | 147862 | 148736 | 0.59 | 1290 |
| Sko 100d | C. R. | 149576 | 150772 | 0.80 | 1197 |
| Sko 100e | λ- E. | 149150 | 150454 | 0.87 | 1141 |
| Sko 100f | λ- E. | 149036 | 150320 | 0.86 | 470 |
Finally, Table 4 shows the same results as in Table 2, but now for the ant algorithm implemented by Tillard and adapted to compare it.
Table 4 Ant results
| Instance | BKV | BVF ANT | GAP ANT | CPUT ANT |
|---|---|---|---|---|
| Sko 42 | 15812 | 15812 | 0 | 19,573 |
| Sko 49 | 23386 | 23386 | 0 | 53,185 |
| Sko 56 | 34458 | 34520 | 0,18 | 38,993 |
| Sko 64 | 48498 | 48498 | 0 | 16,05 |
| Sko 72 | 66256 | 66356 | 0,15 | 50,932 |
| Sko 81 | 90998 | 91118 | 0,13 | 72,304 |
| Sko 90 | 115534 | 116010 | 0,41 | 103,26 |
| Sko100a | 152002 | 152396 | 0,26 | 58,856 |
| Sko100b | 153890 | 153914 | 0,02 | 79,32 |
| Sko100c | 147862 | 148454 | 0,4 | 37,51 |
| Sko100d | 149576 | 150106 | 0,35 | 180,12 |
| Sko100e | 149150 | 150106 | 0,64 | 180,12 |
| Sko100f | 149036 | 150106 | 0,71 | 180,12 |
7. Conclusions
In this paper we describe the important aspects of a GRASP implementation to find solutions to the QAP, adapting the improvement phase through the combination of the 2-exchange, λ-exchange, exchange, combinatorial random neighborhood structures, the implemented algorithm In java was tested for a set and instances obtained from sko42, sko49, sko 56, sko 64, sko72, sko81, sko 90, sko 100 a, sko100b, sko 100c, sko 100d, sko100e, sko100f and esc 64a, esc 128Tai, 250.
The contribution of this paper is the execution of a basic GRASP methodology with the variants in their post-processing phase through the combination of different neighborhood structures which led us to obtain approximate solutions with an error of no more than 1% In 90% of the cases and was executed for all type of arrays considered of great scale.
The main difficulties faced were the CPU time for the Sko100a arrays up to Sko100f, as its execution time varied between 1060 and 1717 seconds, however the error taken as a reference of the best known value is less than 1%.
As future work, it is proposed to modify the improvement phase with the same neighborhood structures by formulating a union of local structures and on the other hand to apply variable speed search with the four neighborhood structures and to generate instances for the case of the stochastic QAP problem to model the traffic in a shopping center.
Also the execution of the algorithm is presented in (Tillard, 1998).
The GRASP results shows that with neighborhood combination has a robust consistency because it was implemented in large scale arrays with a gap of less than 1% in most cases in relation with the best known values and in comparison with the fant algorithms. It is shown that the simplicity of GRASP is competitive with bioinspired algorithms.











 nueva página del texto (beta)
nueva página del texto (beta)