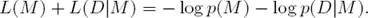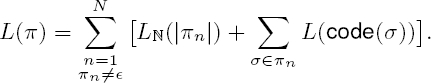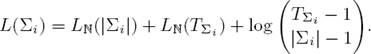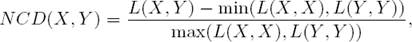1 Introduction
Systematic correspondences between related languages form the basis for much linguistic work. Researchers employ them to e.g. improve teaching, analyze the similarity or relatedness of languages qualitatively, or to formulate hypotheses about their mutual intelligibility. Beyond that, they are relevant to tasks such as machine translation.
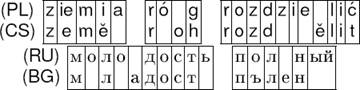
Correspondence rules could be established on the basis of various linguistic features, such as the languages’ alphabets, their orthographies, their phonologies, or their inflectional and derivational morphologies. As an example, the Polish, Czech, Russian, and Bulgarian forms of the pan-Slavic word for happiness could be analyzed with the following correspondences, reflecting orthographic and (slight) phonetic differences:
In our project, we focus on modeling the mutual intelligibility of related Slavic languages. In the current stage of the project, we focus on the reading intercomprehension setting, i.e. a scenario where a native speaker of one Slavic language, such as Polish, is reading e.g. a newspaper written in a related language he or she has never learned or otherwise been exposed to, such as Czech or Croatian. It it clear that in such a scenario, successful intercomprehension requires a high degree of cognacy between the involved languages. However, different cognates may have gone through various changes throughout the languages’ evolutions, e.g. due to spelling reforms, or they may have been adapted by the languages differently in the first place, e.g. loanwords being adapted according to the orthographic versus phonetic principle depending on the time of borrowing. Thus, a reader will be faced with having to decipher many different correspondences to his or her native language(s). We hypothesize that native readers will encounter more difficulties with some of these correspondences than with others, and we want to find information-theoretic baselines for predicting the correspondences’ degrees of difficulty and thus the languages’ expected mutual intelligibility.
For this endeavour, we first require the lists of correspondences between the languages. While much linguistic work has been done on the Slavic family, we have shown in previous work that the existing collections of correspondence rules from historical linguistics are highly incomplete in terms of coverage of modern cognate words [7]. Since the sheer amount of correspondences is staggering, we require to automatically identify the correspondence rules present in available data. Regular correspondences have often been addressed in previous work and the proposal to learn them automatically from data goes back as far as the 1960s ([10]). Newly-available computational power has faciliated much progress over the past two decades, and topics as diverse as cognate identification/reconstruction or transliteration generation (cf., e.g. [2, 18, 13]), discovery or quantification of etymological relationships ([23, 14, 3]), lost languages decipherment ([21]) or discovery of pseudo-morphological sub-word alignments ([20]) have been addressed. However, the existing approaches do not fulfill our requirements – for our purposes, correspondences cannot be limited to a maximum number of characters or to a maximum number of languages, and fully disjoint character sets must be possible.
Since existing systems overwhelmingly focus on the phonetic modality, they typically impose a maximum length on correspondences of at most two by two characters and assume that all data uses the same alphabet. However, the orthographic modality is different from the phonetic. Firstly, since languages may employ digraphs or trigraphs for representing single phone(me)s, orthographic correspondences clearly cannot be limited in this way. Secondly, used scripts may be completely disjoint. For example, some Slavic languages employ the Cyrillic alphabet and some employ the Latin alphabet, and many even modify either script with various diacritics. Furthermore, in intercomprehension, we cannot assume that only correspondences to one single language are relevant. Native readers may be multilingual and we can reasonably assume that many also possess some knowledge of other languages, such as Russian or – nowadays – English, which may influence their intercomprehension process both positively or negatively. One way to quantify the influence of multiple languages on intercomprehension would be to consider the entropies of the adaptation process between cognates in each known language and the target language, which would posit that readers use their knowledge of each language separately. However, it may be that individually, two languages, call them A and B, have a high entropy when transforming words into a third language, call it C, whereas taking the knowledge from A and B together, i.e. transforming words from A and B jointly into C, has much lower or even zero entropy. In order to capture this fully, we require three-way correspondences between all the languages, and more generally N-way correspondences between any N languages, which is a feat we have not found in any of the systems we reviewed. While marginalization can and has been used to construct N-way correspondence rules (e.g. in [14]), we found that this approach can quickly magnify small errors and we thus want to handle N-way rules natively.
We want to use these correspondences to compute meaningful, objective baseline expectations regarding the mutual intelligibility of languages and language groups, taking into account a reader’s knowledge of any number of other languages. In other words, we aim to define similarity measures not only for pairs, but groups of languages.
This leaves us with the following questions: How can we find correspondences of arbitrary sizes between an arbitrary number of languages which employ arbitrarily different alphabets? And how can we use these correspondences to objectively quantify linguistic similarity between not only pairs, but groups and even families of languages? These are the questions we answer in this paper. For this, we employ the Minimum Description Length (MDL) principle [9]. MDL is a statistically well-founded approach to identifying the best model for given data, and has e.g. been used to model changes in etymologically related words [23].
Using MDL, we deem the set correspondences that describes the data most succinctly to be the best. We propose an efficient, deterministic algorithm to infer good sets of correspondence rules directly from data. We then show how their coding-theoretic complexity and regularity can be used to quantify similarity in a fine-grained fashion. We present two experiments: In a pairwise analysis of 13 Slavic languages, we confirm that the notion of linguistic similarity captured by our algorithm is a strong reflection of linguistic classification. In a four-language experiment between Czech, Polish, Russian, and Bulgarian, we find that our algorithm efficiently and intuitively quantifies linguistic similarity between subsets of all analyzed languages. The four-language experiment shows us that our approach is well suited to assessing the orthographic regularity of closely-related languages, and we discuss in detail how this works.
The rest of the paper follows the usual structure: we give an overview of our key ideas and some terminology in Section 2. Then, we present our model and describe our learning algorithm in Section 3. We report learned correspondences and provide an information-theoretic analysis of language similarities in Section 4, and set our model in relation to previous work in Section 5 before concluding in Section 6.
2 Key Ideas and Terminology
Our central idea is that if two languages L1 and L2 are highly related, then they will share a great deal of their sequential structures. Here, we focus on the sequential similarity between cognate words. That is, we assume that for every cognate realized in different languages there is some underlying sequence of latent variables that governs its exact surface realization. These underlying sequences will manifest as correlating sequences of the symbols of the languages, and we want to learn them automatically from data.
To this end, we employ the Minimum Description Length (MDL) formalism, which posits that the optimal model is the one resulting in the most concise description of the modeled data, i.e. induction is performed by compressing the data. Importantly, in MDL-based modeling, we use only the data as evidence for our models and forego making assumptions about the nature of models in the form of prior probabilities.
For our model, we employ a two-part code [15], posing the optimization problem
Here, D is the data at hand, M the explaining model, and M the model class we draw our models from. L(M) is the length, in bits1, of the description of model M.
Similarly, L(D|M) is the length, in bits, of the data given model M. Description lengths are simply code lengths: Shannon’s source coding theorem [19] tells us that the best prefix-free code for some data is derived from the probabilities of the data, i.e.
From this, we see that two-part MDL can be considered to be a regularized maximum likelihood approach very similar to Bayesian inference.
We aim to find correspondence rules exploratively, i.e. without imposing a generative model that governs their shape or distribution. Concretely, we treat correspondences simply as associated strings of characters with no assumed underlying distribution at all. Doing this allows to observe the actual distributions of correspondence rules in data and to compute objective, unbiased string-level measures of linguistic similarity via the joint compressibility of cognates in various languages.
2.1 Evaluating and Inferring Rules
In order to evaluate how good a given set of correspondence rules is, we should evaluate how well these rules describe the data. However, this is not entirely unproblematic. For example, if we are given the Polish-Czech correspondences (s,š), (sz, š), (c,t), (cz,t), and (szcz,št), then we can segment the sub-strings szcz and št e.g. as shown below.
We call any such segmentation an alignment. Lacking an evaluation function, we cannot tell which of the three example alignments above is the best. However, if we are given the best alignment of our data, then we can straightforwardly compute probabilities for each of the correspondence rules, from which we can then compute the optimal rule costs. Similarly, knowing the costs of the rules allows to compute the optimal alignment.
Thus, our problem lends itself well to an Expectation-Maximization (EM) [5] approach. The expectation step is straightforward; we simply align the data with the current model. The maximization step can be explained intuitively as follows: If the optimal alignment is c), using rule (szcz, št), then any of the rules in alignments a) and b) could be used at least as often in the data as (szcz,št). Thus, if the rules in alignment c) are the optimal ones, i.e. better than those in b), the rules in b) will also be better than the ones in a). Assuming that the complexity of larger rules is higher than that of any of the smaller rules they contain, we can combine smaller rules into larger ones to see if merged rules’ utility in describing the data outweighs their increased complexity. Using this approach, we will deterministically obtain good results as long as the best alignments with the current rule set do not exclude too much evidence needed to discover competing rules.
With this in mind, initialization of this model is straightforward: if we start by assuming no structure at all, then we will find the dominant structures in the data. Thus, we start training from an alignment in which every symbol in the data is placed solely in one correspondence rule. We call such an alignment a null alignment and call rules which contain exactly one symbol from exactly one language singleton rules.
3 MDL Code for Regular Correspondences
Mathematically, our model class is the set of sets of tuples associating strings from the individual languages’ alphabets. We use a two-part code and must define both L(M) and L(D|M). Our code must ensure that a) shorter rules are rated less complex than longer ones, b) rules using very common letters are rated less complex than those using rare letters, and c) there is no bias against sparsely-populated rules.
In the following, we use count(x) to indicate the number of occurrences of x, and use code(x) to indicate the shortest possible code word for x. We are interested only in measuring complexity, so we ignore the exact code words for any element and instead focus only on their optimal lengths. We begin by discussing our model code L(M).
3.1 Model Code
Let N be the number of languages. Our models consist of N alphabets Σi and a correspondence rule table, which we call Π. Our total model description length is
In order to describe the rules from Π, we require the code lengths for all letters σ from all alphabets Σi. However, for ease of exposition, we first discuss L(Π). In essence, our Π is a list of independent correspondence rules. We group rules by which languages they are defined on in order to identify many rules even when N is large. To explain why we do this, let us first explain in detail how we encode rules.
Encoding a Correspondence Rule Rules π ∈ Π are of the form π = (π1,
..., πN) with πi ∈ 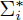 . To encode one such rule, we
must include the information a) how long the string from each of the languages
is and b) which letters it contains.
. To encode one such rule, we
must include the information a) how long the string from each of the languages
is and b) which letters it contains.
It is important to note that rules can be partially empty, i.e. undefined on some languages. If we were to specify explicitly that a rule has a length of 0 on some channel, we would impose a bias particularly against very sparsely-populated rules – specifying a rule containing one symbol on two languages each would incur N − 2 times the overhead of specifying a length of 0 for all the empty languages. However, if for every rule we already know which language sub-group it is defined on, then we can avoid this bias by only sending lengths where they are non-zero. This helps to find rules with few carrier languages – a fact that is especially important since our rules grow from small (and having few carrier languages) to large (and having many carrier languages).
Let π ∈ Π, π = (π1, ..., πN) with
πi ∈ 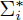 be a rule. To transmit π, we
send all N entries independently of each other, specifying lengths and character
sequences only where they are non-empty:
be a rule. To transmit π, we
send all N entries independently of each other, specifying lengths and character
sequences only where they are non-empty:
We encode each element’s length with LN, the universal code for the integers [16], which is the MDL-optimal code for natural numbers of unknown size. For transmitting the strings themselves, we use code(σ), i.e. the Shannon code for symbol usages in all rules.
Encoding the Rule Table As mentioned above, we specify for every rule which subset of languages it is defined on in order to avoid bias against sparse rules. We can straightforwardly classify each rule according to which subset it is defined on. Then, we must encode how many rules defined on each of the different subsets there are.
There are 2N − 1 different language subsets on which a rule may be defined. We encode the number of rules of each kind via LN. These numbers must be offset since LN(n) is defined for n ≥ 1 and there may be zero rules of a certain kind.
Additionally, to describe our data items using rules, we must include the counts for the Shannon code for using each of these rules in our description. We specify these counts by a data-to-model code [22]. Data-to-model codes are used to code uniformly from an enumeration of models, i.e. without preference towards any particular model. Since we know that none of the rules described in the model will have a count of zero, the appropriate data-to-model code is given by the number composition of the distribution’s total counts over the number of rules. Thus:
where 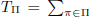 count(π) and where
ΠCi is the set of rules
defined on the i-th subset of languages as enumerated in some
canonical way.
count(π) and where
ΠCi is the set of rules
defined on the i-th subset of languages as enumerated in some
canonical way.
Encoding the Alphabets For describing the strings of each rule, we again use the Shannon-optimal code for the individual alphabets’ symbols. Thus, we must first transmit the unigram code(σ)∀σ ∈ Σi for every alphabet Σi. We again do this by a data-to-model code, i.e. by coding uniformly from all possible distributions.
Setting  , the total
transmission cost relating to some Σi becomes
, the total
transmission cost relating to some Σi becomes
The alphabet sizes are constant for any given data set and do not have to be included in the code to be able to do meaningful inference, but nonetheless quantify the complexity of the individual languages and should thus be included.
3.2 Data Code L(D|M)
To encode data with our model, we simply transmit the correspondences the current model uses to describe each data entry. We model our data as a list of independent sequences correspondence rules, i.e.
For individual data entries, we transmit their lengths via LN and specify the used correspondence rules via the best usage code for the rules, code(π). We next discuss how to find the best such segmentations for data entries, and how to infer rules.
3.3 Alignment Procedure
Computationally, finding the best description for a data item d requires finding the best alignment for it. We here formulate this as a shortest-path problem in a weighted, directed graph and used Dijkstra’s algorithm [6] to find optimal alignments. Nodes in the graph represent index tuples, while edges describe the applicable rules. By partial order reduction, we make these graphs as small as possible. Nonetheless, due to the combinatorial nature of the problem, bottlenecks exist in memory consumption and runtime. With the current implementation, we can obtain exact results for up to five languages within a few hours on a 4GB RAM, 2.5GHz single core desktop machine.
3.4 Training Procedure
Inferring correspondences of arbitrary length is a combinatorial, non-convex optimization problem defined over a large, unstructured search space. However, as we argued in Section 2, we can compute optimal alignments for all data if we are given a rule table with costs, Likewise, if we are given an alignment of all data, we can improve our model from it. Therefore, we can find good solutions by Expectation-Maximization [5].
At the beginning of training, we initialize our model with a null alignment. A null alignment is one in which only singleton rules are used, i.e. only rules which consist of exactly one character from exactly one language.
3.4.1 Expectation Step
In the Expectation step, we align all data items with the rules from the current rule table Π and the current usage costs for the rules. This results in new counts for all rules from which we compute costs in the next step. We employ Laplace correction in order to ensure that the algorithm is always able to explain all data and may choose to not use locally suboptimal patterns.
The time complexity of our E step is O(|D| · |R|2), where R is the maximum number of rules simultaneously applicable in a single data entry.
3.4.2 Maximization Step
In the Maximization step, we optimize our code table. We do this by merging together the two patterns with the highest decrease in overall description length. The intuition behind this is the observation that if a longer pattern is useful, then any sub-pattern of it will be at least as or more useful. It is important to note that in this way, the learned correspondences grow according to their statistical significance. Thus, in this fashion, we deterministically learn the most important structures in the data.
The time complexity of our M step is O(|D| · A2/2), where A is the maximum number of rules used to align a single data entry.
4 Experiments & Results
Firstly, we present a standard pairwise analysis for a group of languages for which we have collected data we deem representative. We compute pairwise distances, construct a phylogenetic tree, and compare it to linguistic classifications, which we find the algorithm fully reproduces. Secondly, we present a detailed analysis of four languages simultaneously, showing how we can quantify and characterize linguistic similarity in much more detail than previously possible. For both cases, we also report some of the learned correspondences.
We considered comparing to phylogenetic trees computed by other models. However, our approach is completely novel in that it allows to assess language sub-set similarity, which is the aspect we wish to focus on. Therefore, we opted to only compare the phylogenetic tree to the linguistic classification as a sanity check.
4.1 Data Sets
We compiled two data sets for our experiments. Firstly, we use Swadesh lists for 13 modern Slavic languages taken from the wiktionary.2 The languages are Czech, Polish, Slovak, Lower Sorbian, Upper Sorbian (west Slavic), Russian, Belarussian, Ukrainian, Rusyn (east Slavic), Bulgarian, Macedonian, Slovenian, and Serbo-Croatian (south Slavic). For Serbo-Croatian, we have both a version in Latin script and one in Cyrillic script.
Secondly, we add a set of Slavic cognates containing internationalisms and pan-Slavic words for Czech, Polish, Russian, and Bulgarian.3
All our data is in raw orthographic form without transcriptions of any kind. It consists mostly of verbs, adjectives, and nouns. For all of our experiments, we use only those entries that contain words for all languages in question. While our algorithm is agnostic to gaps in data, this makes for easier comparison.
4.2 Experiment 1: Classic Pairwise Analysis
For a pairwise analysis, we require some measure of distance between pairs of languages. In MDL-based modeling, it is common to use Normalized Compression Distance (NCD) [4] for this. Intuitively, NCD measures how hard it is to describe X and Y together compared to how hard it is to describe them separately. It is defined as
where L(X, Y) is the description length when encoding languages X and Y jointly. NCD is a mathematical distance; lower values mean that two data sets are more similar.
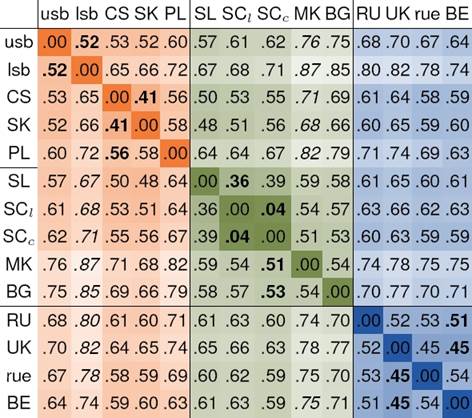
We show the NCD values for all pairwise comparisons for the 13 languages in Table 2. We use ISO 639-1 and ISO 639-3 codes to identify the languages, except for Serbo-Croatian, which we denote by SCl in its Latin version and and SCc in its Cyrillic version. We indicate lowest and highest NCDs per row in bold and italic text, respectively.
Our table reveals that languages from the same linguistic group tend to have lower NCD than languages from differing groups. The south Slavic group is linguistically further divided into a southwestern group (Slovene and Serbo-Croatian) and a southeastern sub-group (Macedonian and Bulgarian). Indeed Slovenian and Serbo-Croatian are more similar to languages from the west Slavic group than to the east Slavic group. Serbo-Croatian in Latin script was assessed to be slightly closer to the other languages that use Latin script, while the Cyrillic version is more similar to other Cyrillic languages.
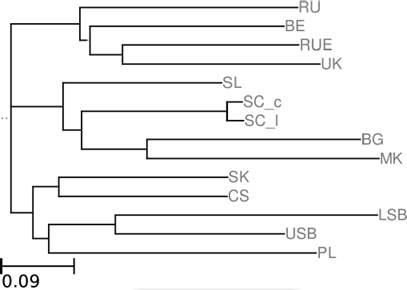
For easier viewing, we construct a phylogenetic tree from the NCDs by the neighbor joining method [17] and place the root manually. It is shown in Figure 1.4 The greater the horizontal distance between languages, the less similar they are.
The algorithm groups the languages according to their linguistic classification [11]. It identifies Bulgarian and Macedonian as slight outliers in the south Slavic group, and Polish, Upper and Lower Sorbian as such in the west Slavic group. This is an expected result. Bulgarian and Macedonian are outliers in that they have largely lost case. Words from these languages oftentimes employ zero endings or comparatively shorter endings than the other languages. This leads to overall very low BG-BG and MK-MK description lengths, but still high NCDs to the other languages. Polish is more complex than Slovak and Czech are, which is likely due to its frequent use of digraphs. This leads to an increased complexity of Polish patterns. Finally, Lower Sorbian in particular uses a number of etymologically different words in the Swadesh list, which seems to be the cause for its outlier status. Its word forms nonetheless share enough structure with Upper Sorbian, Polish, and the other West Slavic languages to be grouped accordingly.
In Figure 2, we present example alignments from the models for the CS-PL and RU-BG language pairs. The discovered correspondences are of slightly different granularities. More complex rules are learned only if the data warrants their use for compression.5 We next show how this can be exploited for fine-grained analysis of similarity.
4.3 Experiment 2: Quantifying Similarities of Subsets of Four Languages
Restricting ourselves to pairwise analyses and grouping the most similar languages together in a phylogeny may cause us to miss many subtle similarities. Our algorithm is agnostic to the number of input languages and can be used to efficiently analyze more than two languages at a time. This allows for highly detailed information-theoretic quantification of the similarities among groups of languages. To illustrate how this works, we first present some four-way CS-PL-RU-BG alignments in Figure 3.
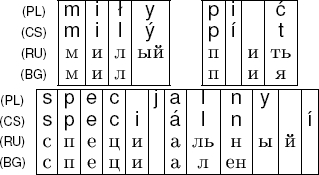
Some of the discovered rules link only two or three languages, leaving the other language(s) to be described by separate rules. We have selected some examples to highlight the differences in i vowels. In our Polish-Czech-Russian-Bulgarian data, there is enough evidence to discover various rules, such as (,,и, и) or (,i, и,и), but not enough evidence to include a four-way rule (j,i, и, и). In consequence, the internationalism specjalny (special) is analyzed with the three-way i correspondence plus a Polish singleton rule (j,,,) – despite the individual phonetic realizations of the internationalism being nearly identical.6 In other cases, using two rules – such as (i,í,,) plus (,,и,и) in pić (to drink) – is a good choice, showing that both of these rules are regular enough to be discovered. A four-way rule combining them is not selected as its complexity surpasses its utility.
This reflects the fact that while there is an underlying latent variable, namely the i vowel, the realizations employed by each of the languages differ in entropy. In some cases, the joint entropy, relative to the amount of available data, between all four languages is low enough for a four-way rule to be discovered. In other cases, the joint entropy between some groups of the languages, e.g. the two groups Polish and Czech as well as Russian and Bulgarian, is low enough to warrant a rule linking these language groups, but the overall four-way joint entropy prevents a larger rule from being learned. Thus, the information-theoretic complexity and regularity of the discovered rules directly reflect the degree of statistical regularity in the parallel realizations. At the same time, the discovered rules themselves provide an elegant and intuitive avenue for human interpretation.
To quantify the amount of structure that individual languages share, we define the shared Description Length (sDL) of languages Li1, ..., LiK as
where Q(Li1, ..., LiK) contains all rules which are non-empty (i.e. contain symbol sequences) exactly for languages Li1, ..., LiK. sDL values quantify the relative complexity and importance of the rules for a specific sub-group of languages.
Figure 4 shows sDLs for the CS-PL and RU-BG models. It reveals that RU diverges more than BG does from the RU-BG joint description, and that CS does so for CS-PL. Because we chose only cognate tuples defined for all four languages for this experiment, we can also compare the two language pairs meaningfully. There, we see that CS-PL requires a larger description, and that Czech alone takes up a somewhat larger fraction of total description length.
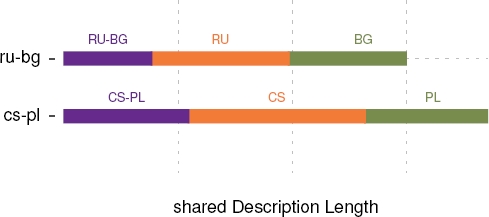
Fig. 4 sDLs for Czech-Polish and Russian-Bulgarian. Total sDLs: CS-PL 1852.43 bits vs. RU-BG 1496.62 bits
The four-way Shared Description Lengths shown in Figure 5 are a quantification of the similarities between all language sub-sets from our Czech-Polish-Russian-Bulgarian set. Four-way sDL is the biggest contributor overall. It quantifies the prevalence and complexity of the structure shared by all four languages. Each of the individual languages have significant overheads to the four-way shared description length.
Czech is the language with the highest individual description length. This appears to be caused in part by the larger alphabet of Czech, stemming from the large number of diacritically-modified symbols. For example, every Czech vowel can be marked as long with the čárka, giving us e.g. é as long version of e. Investigating the alignments, we also see that there are a few words where the Czech cognate has an additional morpheme over the Polish one, causing series of Czech singletons.
The algorithm furthermore identifies a significant proportion of correspondences between Czech and Polish and between Russian and Bulgarian. The sDLs of these two language pairs are almost equal, with Russian-Bulgarian slightly outweighting Czech-Polish at 623.43 bits for CS-PL, 638.87 bits for RU-BG. If we interpret this as evidence for a significant (disjoint) grouping between the two languages, there is as much evidence for grouping Czech and Polish as there is for grouping Russian and Bulgarian.7 Beyond this, we identify further, more subtle similarities, many of them between Russian and other, not-yet-covered language subsets. This indicates that Russian very often shares a regular structure with some of the other languages, possible evidence of either Russian being a dominant language exerting heavy influence on the others, or of Russian having diverged the least from a common ancestor.
Causes of Sub-Group sDLs: If we go back to our example correspondences in Figure 3, we can see two different effects that lead to three-way correspondences: Firstly we see the already-discussed fragmentation of larger rules due to differences in entropies of orthographic realizations8 (as in specjalny (special)), and secondly we can observe the influence of morphological differences. Bulgarian regularly employs zero endings where the other languages use non-zero endings, as is the case in miły (nice, smooth). In the example, this leads to a three-way correspondence rule (y,ý, ЫЙ, ) between Polish, Czech, and Russian, which is empty for Bulgarian.
It is easy to see that divergences in phonology, orthography, morphology, and lexis may all influence the results of our analyses. If we were to compare languages with highly similar derivational morphologies but completely different lexicons, we would be able to identify only the corresponding affixes or endings and be left with single-language rules for the stems. Likewise, if we were to compare languages that share their stem lexicon but employ radically different derivational morphologies, we would be able to identify correspondences only within the stems. This indicates that our algorithm in its current form is perfectly suited for capturing and assessing the orthographic regularity of closely-related languages: If we exclude, to the extent possible, the other factors that may cause rule fragmentation and use our algorithm to analyze only words that are morphologically and phonetically highly regular, then we will be able to quantify the regularity of the parallel orthographic realizations of the words.
5 Relation to Previous Work
The previous work most related to ours is the correspondence-based models presented by Wettig et al. ([23]) and by Nouri and Yangarber ([14]). Similar to them, we leverage the statistical regularity present in cognate data to assess linguistic similarity. Similar to theirs, our algorithm discovers statistically meaningful correspondence rules directly from data. Unlike theirs, our model does not limit the size of correspondences and allows for direct discovery of correspondences between any number of languages.
Many of the existing approaches that discover correspondences make strong generative assumptions in modeling, e.g. via use of Poisson distributions or Dirichlet processes ([21, 20, 3]). This imposes unwarranted biases on the distribution and shape of discovered correspondences and thus precludes objective quantification of shared structures. In contrast, we forego imposing assumptions, which allows for objective quantification of linguistic similarity.
In this work, we focus on correspondences as a means to the end of quantifying cross-linguistic similarity. Nonetheless, the algorithm may produce useful correspondences: a similar model was recently shown ([8]) to allow for efficient discovery of linguistically meaningful correspondences between pairs of languages, even allowing for selection of rules at different levels of linguistic granularity. We have not found this feature in any of the algorithms we reviewed, which focus on fixed linguistic granularities motivated either morphologically ([20]) or phonologically ([21, 3]).
6 Conclusion
We studied the problem of automatically quantifying the amount of structure shared by sets of languages. We started from the assumption that if languages are highly related, then they will share a great deal of their sequential structure. To capture these sequential structures, we inferred objective string-level correspondences of arbitrary size from cognate tuples for arbitrarily many languages and leveraged their information-theoretic complexity and regularity for highly detailed analysis of linguistic similarity. We introduced an MDL-based approach and an efficient inference algorithm.
Our experiments show that the approach works well in practice. In our pairwise experiment, we constructed a sensible phylogeny for the analyzed Slavic languages. In our four-way experiment, we showed that our algorithm quantifies similarity between groups of languages in a highly detailed fashion and argued that it is ideally suited to capture the information-theoretic regularity of parallel orthographic realizations of cognate words.
We are currently undertaking a large-scale analysis of the orthographic regularity of the Slavic languages using our approach. In future work, we will extend our model to account for morphological differences information-theoretically and to accomodate phenomena such as metatheses, in which sequences of elements may change order.











 text new page (beta)
text new page (beta)