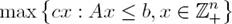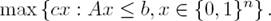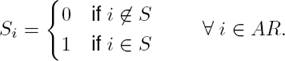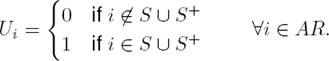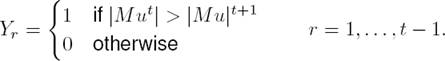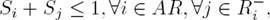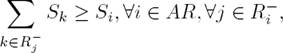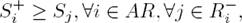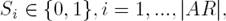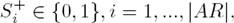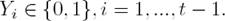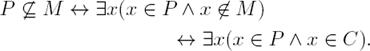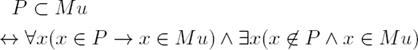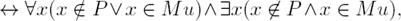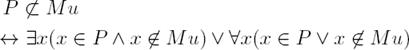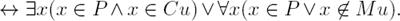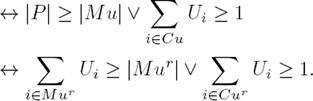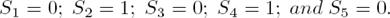Corresponding author is Alejandro Santoyo.
1 Introduction
Argumentation theory has become an increasingly important and exciting research topic in Artificial Intelligence (AI), with research activities ranging from developing theoretical models, prototype implementations, and application studies [3], [28]. The main purpose of argumentation theory is to study the fundamental mechanism humans use in argumentation and to explore ways to implement this mechanism on computers.
Argumentation theory is related to debate, dialogue, negotiation, conversation, and persuasion; it searches conclusions through logical reasoning [25]. In fact, argumentation theory has been successfully used in a variety of applications such as organ transplantation [24], democratic decision support [1], multi-agent systems [21], legal reasoning [22] [29], machine learning [23], as well as debate and argument mining [19].
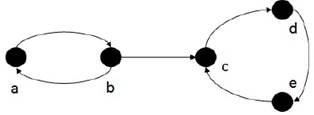
Currently, formal argumentation research has been strongly influenced by abstract argumen-tation theory of Dung [15]. This approach is mainly orientated to manage the interaction of arguments by introducing a single structure called Argumentation Framework (AF). An AF basically is a pair of sets: a set of arguments and a set of disagreements between arguments called attacks. Indeed, an AF can be regarded as a digraph in which the arguments are represented by nodes and the attack relations are represented by arcs. In Figure 1, one can see an example of an AF and its graph representation.
In [15], four argumentation semantics were intro-duced: grounded, preferred, stable, and complete semantics. The central notion of Dung’s semantics is the acceptability of the arguments. Even though each of these argumentation semantics represents different patterns of selection of arguments, all of them are based on the basic concept of admissible set. Informally speaking, an admissible set presents a coherent and defendable point of view in a conflict between arguments. For instance, by considering the AF of Figure 1, one can find the following admissible sets: ∅, {a}, {b}, {b, d}.
One research branch in abstract argumentation has been to find new methods for computing its different semantics, i.e. the search for acceptable (w.r.t. certain criteria) sets of arguments. Charwat et al. [12] survey the approaches that have been used so far for computing AF semantics, and divide them into reduction and direct approaches. The direct approach consists in developing new algorithms for computing AF semantics, and the reduction approach consists in using the software that was originally developed for other formalisms [12].
Our interest is in the reduction approach. Thus, a given AF has to be formalized in the targeted formalism such as constraint-satisfaction [13], constraint-programming [6], propositional logic [4], and answer-set programming [7, 30]. But, our interest is particularly in the answer-set-programming and binary integer programming approaches.
To the best of our knowledge, there is only one previous work [27] where authors indirectly used 0-1 integer programming for computing preferred semantics. Their approach was based on a mapping from an argumentation framework AF into a logic program with negation as failure Π AF . After that, authors computed the Clark’s completion Comp(Π AF ) [26], and finally they created the 0-1 integer program lc(Π AF ) [2] which then was solved by a mathematical programming solver.
In this work, we present a novel method, to the best of our knowledge, for directly computing semi-stable (SS) semantics using 0-1 integer programming with no mapping. Our approach is based on 0-1 integer programming i.e. a mathematical programming formulation which models the semi-stable semantics. This work presents the mathematical model and explains it in terms of Dung’s abstract argumentation notions [15], i.e. the mathematical constraints model conflict-freeness, acceptability, and the semi-stable extension definition itself [10]. This work explains the objective function and each constraints’ role.
It is worth mentioning that semi-stable semantics has been regarded as an alternative for stable semantics by Caminada et al. [10] [9] because of the following:
- Every stable extension is also a semi-stable extension.
- There exists at least one semi-stable extension, while it is possible to have no stable extensions.
- Preferred semantics has also been proposed as an alternative [15], but additional non-stable extensions can be introduced, even in situations where stable extensions already exist.
- Additionally, Caminada and Gabbay [11] also state that every semi-stable extension is also a preferred extension.
Therefore the semi-stable semantics is closer and more adequate for being an alternative for stable semantics.
In this work, we also experimentally compare our approach against an answer set programming (ASP) approach: the ASPARTIX approach [17] using its general encoding for SS semantics1. The results we obtained indicate that our new method performed well.
However, we must say that ASPARTIX has been proved against tools from other approaches [5] such as Dung-O-Matic2 which is based on well-known algorithms (direct approach), and ConArgs23 which is based on constraint-programming (reduction approach). The results showed that ASPARTIX outperformed Dung-O-Matic, but ConArg2 outperformed ASPARTIX.
The selection of Clingo in our research is due to the following reasons. Clingo is an answer set solver for (extended) normal and disjunctive logic programs. It combines the high-level modeling capacities of ASP with state-of-the-art techniques from the area of Boolean constraint solving. The group that developed Clasp won the 2014 Artificial Intelligence Dissertation Award4. Furthermore, the software has several trophies5.
The paper is organized as follows. Section 2 gives some background on argumentation. Section 3 presents a procedure based on solving a series of 0-1 integer programming problems for computing SS semantics. Section 4 presents the preliminary results as well as the used methodology. Section 5 presents our approach for addressing different decision problems. Finally, Section 6 presents some conclusions and future work.
2 Background
We assume that readers are familiar with the basic notions of answer set programming, otherwise readers can find good introductions in [7], and additionally in [30] one can find a survey of ASP approaches for computing argumentation semantics.
2.1 0-1 Integer Programming [31]
A linear programming problem (LP) is a class of mathematical programming problem, a constrained optimization problem, in which we seek to find a set of values for continuous variables (x 1, x 2, ..., x n ) that maximizes or minimizes a linear objective function z, while satisfying a set of linear constraints (a system of simultaneous linear equations and/or inequalities) [14]. Mathematically, an LP is expressed as follows:
where A is an m by n matrix, c an n-dimensional row vector, b an m-dimensional column vector, and x an n-dimensional column vector of variables or unknowns.
If all variables are integer, we have an Integer Program (IP) written as
and If all variables are restricted to 0-1 values, we have a 0-1 or Binary Integer Program (BIP):
2.2 Formulation of a 0-1 Integer Program
Translating a problem description into a formulation should be done systematically, and a clear distinction should be made between the data of the problem instance, and the variables (or unknowns) used in the model: (1) Define what appear to be the decision variables, (2) Define a set of constraints which will define the feasible solutions space, (3) Using the decision variables, define the objective function.
If something goes wrong, define an alternative set of decision variables and iterate. Once the formulation is ready, it can be coded in any mathematical programming modeling language such as AMPL.
2.3 Abstract Argumentation
Readers with no background on argumentation semantics can find a gentle introduction in [25]. We will use some concepts of Dung’s argumentation approach, the main of them is an Argumentation Framework (AF), which captures the relationships between arguments.
Definition 1. [15] An AF is a pair AF: = ⟨AR, attacks⟩, where AR is a finite set of arguments, and attacks is a binary relation on AR, i.e. attacks ⊆ AR × AR.
Any AF can be regarded as a digraph. For instance, if AF: = ⟨{a, b, c, d, e}, {(a, b), (b, a), (b, c), (c, d), (d, e), (e, c)}⟩, then AF is represented as it is shown in Figure 1. We say that a attacks b (or b is attacked by a) if attacks(a, b) holds. Similarly, we say that a set S of arguments attacks b (or b is attacked by S) if b is attacked by an argument in S.
Dung defined his argumentation semantics based on the basic concept of admissible set, which can be understood in terms of defense of arguments and in terms of conflict-free sets, as follows:
Definition 2. [10] Let AF: = ⟨AR, attacks⟩ be an argumentation framework, A ∈ AR and S ⊆ AR, then:
A + as {b ∈ AR: a attacks b} and
S + as {b ∈ AR: a attacks b for some a ∈ S}.
A − as {b ∈ AR: b attacks a} and
S − as {b ∈ AR: b attacks a for some a ∈ S}.
S is conflict-free iff S ∩ S + = ∅.
S defends an argument a iff A − ⊆ S + .
F: 2 AR → 2 AR as F (S) = {a ∈ AR: a is defended by S}.
It is possible to define the semantics in terms of admissible sets as follows:
Definition 3. [10] Let AF: = ⟨AR, attacks⟩ be an argumentation framework and S ⊆ AR be a conflict-free set of arguments, then:
S is admissible iff S ⊆ F (S).
S is a complete extension iff S = F (S).
S is a preferred extension iff S is a maximal (w.r.t. set inclusion) complete extension.
The SS semantics is similar to the preferred semantics [10], but instead of maximizing S it is required to maximize S ∪ S +, as the following definition states:
Definition 4. [10] Let AF: = ⟨AR, attacks⟩ be an argumentation framework and S ⊆ AR be a conflict-free set of arguments, then: S is called a SS extension iff S is a complete extension where S ∪ S + is maximal.
The semi-stable semantics accepts an equiva-lent statement, as follows:
Definition 1. [10] Let AF: = ⟨AR, attacks⟩ be an argumentation framework and let S ⊆ AR. The following statements are equivalent:
3 Computing Semi-Stable Semantics by 0-1 Integer Programming
In this section we show the 0-1 integer program-ming formulation for the SS semantics problem and its encoding in Mosel6, which is the modeling language of the mathematical solver Xpress7 that we used for this work. This section also explains the objective function and constraints, as well as the iterative process for computing all the extensions of the SS semantics.
3.1 Semi-Stable Semantics Problem Formulation
A mathematical programming solver works with mathematical formulations which in turn work with decision variables. These formulations are coded using the solver’s modeling language. In our case, the values that decision variables can take on are restricted to {0, 1} since we use 0-1 integer programming.
The task of the solver is to determine the values that the decision variables should take on in order to optimize (maximize or minimize) the objective function of its underlying mathematical model. It is possible to have several feasible solutions, but the solver has to find the optimal one, if it exists. Therefore, the first step is to define the required binary decision variables.
Considering that Definition 4 and Proposition 1 state an SS extension in terms of an admissible set S such that S ∪ S + is maximal, then it is required a decision variable for S and another for S + as follows:
When the solver executes the mathematical model’s program and finds an optimal solution, we should interpret the values of the decision variables in terms of a solution of the modeled problem. Thus, in our case, if the variable S i = 1, the associated argument i is in the set S, otherwise it is not. Once we have this solution we define
Definition 5. The set M = {i ∈ AR: S i = 1 in the optimal solution}, and C = {i ∈ AR: S i = 0 in the optimal solution} is M’s complement.
Accordingly, we define the decision variable for S + as follows:
Definition 6. The set M + = {i ∈ AR: S + i = 1 in the optimal solution}, and C + = {i ∈ AR: S + i = 0 in the optimal solution} is M + ’ complement.
In this way, the optimal solution of the 0-1 integer problem formulation for the SS semantics can be stated in terms of maximizing S∪S +. Additionally, it is required to have a decision variable for the union of these sets as follows:
Definition 7. The set Mu = {i ∈ AR: U i = 1 in the optimal solution}, and Cu = {i ∈ AR: U i = 0 in the optimal solution} is Mu’s complement.
Now, in order to have a mechanism to work with attacks more suitable than working with the adjacency matrix of a given AF, we define the following:
Definition 8. Let AF: = ⟨AR, attacks⟩ be an argumentation framework, then R −i = {j ∈ AR: (j, i) ∈ attacks} ∀i ∈ AR, is the set of nodes attacking node i, and the set of sets R − = {R − i: i ∈ AR}.
Considering Definitions 2 and 3, we restate the admissible set definition in terms of Definition 8 in order to be able to derive the linear constraint that assures admissibility, thus we have the following Lemma:
Lemma 1. Let AF: = ⟨AR, attacks⟩ be an argumentation framework, and set S ⊆ AR, then S is admissible iff ∀i ∈ S, ∀j ∈ R − i, ∃k ∈ S, ((k, j) ∈ attacks)).
It is important to take into account that a mathematical solver searches in the solution space for just one optimal solution for a given problem formulation, i.e. just one extension. Therefore, if we want all the extensions of a given AF, it is required to solve a series of binary programming models, one for each extension. Therefore, we can think of the SS semantics problem formulation in terms of a series of solutions that the solver finds in a series of iteration.
Since SS semantics is made up of several sets, we use M t to denote the solution of the binary subproblem in iteration t and q to denote the amount of SS extensions that a given argumentation framework has such that q ≥ 1, thus:
This expression states that the Mu 1 has the largest possible cardinality, and that Mu q has the smallest possible cardinality. Therefore, it is clear that in order to get all SS extensions it is required to iterate q times, and the problem formulation will use t to denote a given iteration.
Additionally, it is also required to have a decision variable for a couple of either/or constraints [20] which will be added per each iteration (see Section 3.3) in order to assure S ∪ S + maximality w.r.t. set inclusion, i.e. they help us just to avoid that solution Mu t+1 be the same than the solutions found in iterations t, t − 1, . . . , 1 or any subset of them as follows:
This way, the following 0-1 integer problem for-mulation to compute the t th semi-stable extension of a given AF is the following (including (1), (2), (3), (5)):
subject to:
Note that (1), (2), (3) and (5) are the decision variables definition, and constraints (15), (16), (17), (18) define the problem’s domain.
Note also that constraints (12), (13), and (14) are going to be added in iteration t, once the model was solved, in order to be active in iteration t + 1, while the remaining constraints are always active. The following paragraph explains the objective of these constraints, but they are explained with more detail in Section 3.3.
Now, let us explain each constraint within the context of Dung’s abstract argumentation notions and the semi-stable definition:
Maximality with regard to set inclusion. The model’s objective function (OF)(6) guar-antees us that we will find a maximum cardinality set, which will be the solution Mu t . This set is made up of S ∪ S +. Constraints (12), (13), and (14) along with the objective function will avoid that M t+1 and Mu t+1 be any subset of M t and Mu t respectively, thus they guarantee us maximality with regard to set inclusion. Subsection 3.3 explains how constraints (13) and (14) were defined and why they are added after the computation of each additional extension in order to compute the whole semantics.
Conflict-Freeness. Note that the definition of a conflict-free set in Definition 2 item 5 is not stated in terms of attacks’s directions but just in terms of attacks between arguments, without considering the directions of them. In this way, such a definition considers an arc just as an edge, and therefore the whole AF can be regarded as an undirected graph, at least with regard to the conflict-free set problem. Note that the expression S i + S j ≤ 1 in constraint (7) will be fulfilled only when S i = 1 or S j = 1 but not both and when S i = 0 and S j = 0, therefore at most one argument will be selected. Thus, this constraint guarantees us that solution will be a conflict-free set.
Admissibility. The intuition of Definitions 1, 2, and 3 is that an admissible set S should defend each of its arguments, and Lemma 1 only restates it in terms of Definition 8. Note that in Lemma 1 the existential quantifier suggests that constraint (8) should be
 , but we used
, but we used  since the constraint must be fulfilled ∀i ∈ AR8. This way, the translation from this definition to constraint (8) is a straightforward task, this constraint guarantees us that the set M
t
is admissible.
since the constraint must be fulfilled ∀i ∈ AR8. This way, the translation from this definition to constraint (8) is a straightforward task, this constraint guarantees us that the set M
t
is admissible.Creation of S + . So far, we have a conflict-free and admissible set, and it is still required to build S +i as in Definition 2 item 2 ∀i ∈ M +. It should be done by decision variables (2) such that the objective function can be executed. This way, S +i should take on value 1 if argument i is attacked by some argument j ∈ R − i such that S j = 1. This is the same that d = d i ∨ d 2 . . . ∨ d n as a logical expression which can be linearized as follows [20]:
Note that (19) and (20) become (9) and (10) respectively. Additionally to (19) and (20) we should have d ≤ 1, but it is redundant due to (16). Thus, constraints (9), (10), and (16) will determine the values of decision variables (2) from values on decision variables (1).
Thus, M 1 is a conflict-free and admissible set, considering that (6) guarantees a maximum cardinality set, and according to Definition 4 and Preposition 1, M 1 is an SS extension.
Construction of U = S ∪S + . In order to avoid that Mu t+1 be a subset of Mu t , it is required to have as decision variables the union of (1) and (2), as defined in (3). To this end, and in order to ease this process, consider that it is not possible that S i = 1 and S +i = 1 at the same time, since it would mean that M is not a conflict-free set. Thus, the value that U i will take on should be S i + S +i . Considering Definition 7, constraint (11) guarantees that Mu will have the whole solution.
3.2 Semi-Stable Extensions Program
Notice that the problem formulation was made up of (1)-(11), and (15)-(18) already can be used for computing the first SS extension of a given AF. To this end, this program should be coded using a mathematical programming language like Mosel9, this is a straightforward task, since the mathematical language was developed for expressing mathematical formulas. The following code stands for the whole mathematical model:
We will denote this program as BIP in order to make reference to it.
3.3 Semi-Stable Semantics
As it was stated, once the model is implemented in a mathematical programming language, the program computes only one SS extension. In order to compute an additional extension it is required to iterate, but adding additional constraints to avoid getting previous solutions, these constraints will force to get another different extension. In this setting, it is required to iterate to find all the extensions of a given AF until no feasible solution exists. Thus, we have to take care of getting no subsets of M t (Case No. 1), and no proper subsets of Mu t (Case No. 2).
Case No. 1. Then, in order to find the constraint that we have to add to avoid that M t+1 ⊆ M t , consider Definitions 5, and let P be the solution in iteration t + 1, and M the solution in iteration t, thus:
The intuition of this result is that it is required that the solution in iteration t + 1 has at least one element from solution’s complement in iteration t. Constraint (12) is defined from this intuition. Note that the Mosel code must take care of the special case where |M| = |AR|.
Case No. 2. Additionally, we have to add another constraint to avoid that Mu t+1 ⊂ Mu t . In order to find such a constraint(s), consider Definition 7 and let P be the solution in iteration t + 1 and Mu the solution in iteration t, thus:
Note that the intuition of the expression in (22) should be the same as that of the first part of the disjunction in (26). Consider also that we wanted to find an expression that led us to a linearized constraint to avoid getting proper subsets of previous solutions. Thus, we can have a proper subset when |P | < |Mu| holds, and therefore we must apply the expression ∃x(x ∈ P ∧ x ∈ Cu), otherwise apply the expression ∀x(x ∈ P ∨ x ∉ Mu), whose intuition is that the new solution P can have any element, this means that it requires no constraint. Thus, we have just to work with the first part of the disjunction. Therefore, we have to linearize the expression
as follows [14]:
that in turn can be transformed as follows:
This means that only either 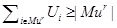 or
or  will be active, but to satisfy the simultaneousness assumption of binary integer programming, they must be transformed considering the following general format [20]:
will be active, but to satisfy the simultaneousness assumption of binary integer programming, they must be transformed considering the following general format [20]:
where B is a big number, in our case B = |AR|, and y is the binary variables defined in (18). This transformation becomes constraints (13) and (14).
Now, let SSE be a set of all the SS extensions of a given AF, and MC a set of additional (12), (13), and (14) constraints, then the algorithm for computing the q extensions of a given AF is Algorithm 1:
Now it is possible to state the following theorem:
Theorem 1. Let AF be an argumentation framework, R − as in Definition 8, M, M +, and Mu is a solution of BIP , and SSE is computed as described in Algorithm 1, then SSE is the set of all SS extensions of AF .
Proof. Sketch: From the above discussion consider the following items:
By constraints (7), (8) we know that M is a conflict-free and admissible set. See Section 3.1 item 2 and 3.
By constraints (9) and (10) we know that M + is made up from M. See Section 3.1 item 4.
By constraint (11) we know that Mu = M ∪ M+. See Section 3.1 item 5.
By the Objective Function (6) we know that M ∪ M + is a maximum cardinality set. See Section 3.1 item 1.
By Definition 4 and Proposition 1 we know that if a set M is a conflict-free and admissible set and M ∪ M + is maximal, then M is an SS extension.
Now, notice that in each iteration, due to the constraints added to MC in steps 6, 7, and 8 in iteration t, the solution Mu (if exists) obtained in step 4 must not be a superset or subset of any previous solutions already in SSE, and Mu must be of maximum cardinality among the solutions that satisfy BIP ∪ MC, therefore Mu is maximal w.r.t. set inclusion.
By previous items and according with (4), there is no any possible solution between solutions found in iteration t and t+1, therefore SSE is the set of all SS extensions of AF.
4 Preliminary Results
In order to measure the performance of the 0-1 integer programming approach, it was compared with an ASP approach: the ASPARTIX [18] which we will refer to as ASP1. Additionally, the approach based on 0-1 integer programming will be called BIP (Binary Integer Programming).
4.1 Experiment Description
For the readers interested in the code used to compute the SS extensions, it is available at ASPARTIX’s web page10. It is worth mentioning that ASPARTIX is the de facto benchmark for argumentation systems.
The solver used by the ASP approach was Clingo11 due to its great performance in several ASP competitions [8], while the 0-1 integer programming approach used the ad-hoc Xpress12 solver. Both solvers were used without any special configuration parameter. The computers used in the experiment had the following configuration: An AMD Phenom II X3 2.80 Ghz processor, 4GB of RAM, and 32-bit Windows 7 professional operating system.
The given time for solving each instance was 1000 seconds. In order to compute the global time when a solver fails solving a given instances, the time assigned is 1000 seconds.
The instances that were used during all the experiments were taken from the ASPARTIX web page13. The name of each instance gives us some information about its inherent difficulty to be solved and it has the form inst_G_n_p1_p2_i, that should be interpreted as follows [16]:
- G: Generator used: 2: arbitrary AFs (does not use p2); 4: 4-grid AFs; 8: 8-grid AFs.
- n: Number of arguments
- p1: Probability for each pair of arguments (a,b) that the attack (a,b) is present for the arbitrary graphs. For the grid graphs this parameter indicates one dimension of the grid. The other is calculated with n.
- p2: Present only for grid AFs. It indicates the probability that a given attack is a mutual attack.
- i: Index for AFs with the same parameters, i.e. AFs generated with the same parameters are distinguished with this index.
ASPARTIX project’s goal was to find ”new methods for analyzing, comparing, and solving argumentation problems”14, and with this goal in mind the project’s team created the instances that we used.
4.2 Performance Results
A total of 1,118 instances were used, the instances ranged from 20 arguments to 100 arguments with increments of 10 arguments. There were 132 instances of 20 arguments, 44 of each kind of instances, and so on for the rest of the instances.
In Figure 2 we present average computation times for each approach and for each kind of instances (arbitrary, 4-grid, and 8-grid). Figure 2 shows also that ASP1 had the best performance (near zero) for arbitrary instances, while the Binary Integer Program (BIP) was very close to it for the same kind of instances.
The performance of both solvers solving 4-grid and 8-grid instances were close to zero until 60-arguments instances, where the BIP approach started to have difficulties to solve them. The ASP1 approach started to have problems until the 70-arguments instances for 4-grid instances, and 80-arguments instances for 8-grid instances. Both solvers had no problem solving arbitrary instances, even with the 100-argument ones.
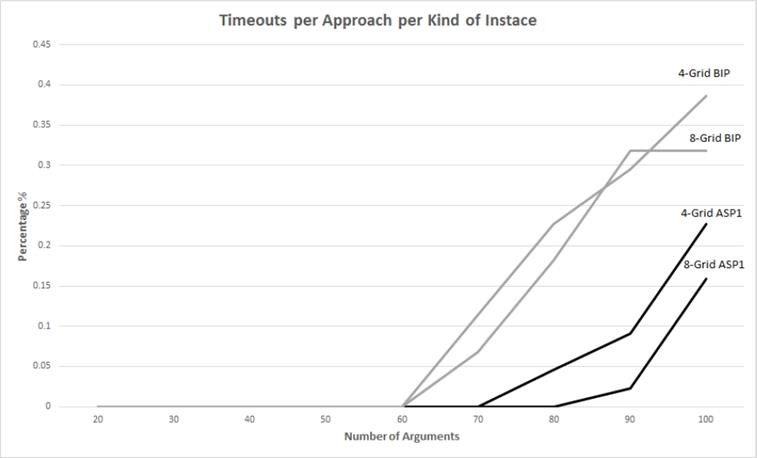
Figure 3 shows timeouts per approach and per kind of instance. Note that there are no timeouts for arbitrary instances and that the behavior is similar to that of average execution times. Note also that though BIP’s timeouts started at 60 arguments instances and ASP’s at 70 arguments, the rate of growth is almost parallel from 90 arguments instances.
Figures 2 and 3 seem to show that the rate of growth of both solvers is similar with a constant difference between the performance of them, and though we have observed that the execution time for BIP approach for arbitrary instances at n arguments t(n) BIP ,2 is never larger than 2.691 times the time of the ASP approach t(n) ASP ,2 (i.e. t(n) BIP ,2 ≤ 2.691 * t(n) ASP ,2), Figure 4 suggests that at some point both lines are going to cross. With regard to the other instances, it is difficult to say if there is also a constant difference since timeout actually indicate a lack of reliable times to determine if this constant exists or not.
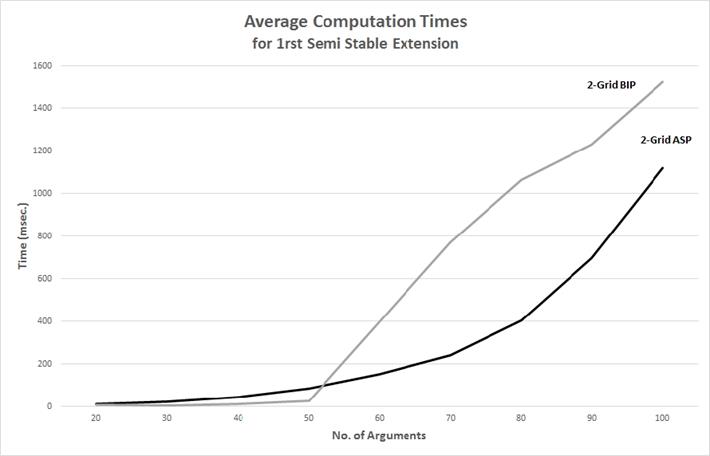
On the other hand, Figure 5 shows average execute times for finding just the first extension for arbitrary instances, note that the ASP solver was faster than the BIP solver, while Figure 6 shows that for 4-Grid and 8-Grid instances it was the other way around, i.e. the BIP solver had a better performance.
It is important to say that the average amount of extensions corresponding to arbitrary instances (2-Grid) is very small, while the average amount of extensions for 4-Grid and 8-Grid instances is larger. Note the great similarity of Figures 4 and 5 which also suggest that the BIP performance is as good as the ASP’ performance, but there is a difference in how solvers compute the remaining extensions: the ASP solver keeps enough information to ease the search of the remaining extensions, while the BIP solver starts with no information from previous searches.
At this moment, we can say that this problem could be addressed either by programming the whole solution using ad-hoc libraries or by configuring the solver for keeping information of previous searches and adding additional Mosel code.
5 Addressing Decision Problems
In order to have a more complete view of our approach to calculate the semi-stable semantics, we decided to analyze its behavior with the decision problems that Caminada et al. [10] described in his paper. Such a description is as follows.
Given an argumentation framework 𝓗 = (AR, attacks), let 𝓔 be its SS semantics. Table 1 describes a number of general decision problems relative to 𝓔.
Let 𝓗 be the argumentation framework shown in Figure 1, which has {b, d} as the only SS extension. Let S 1, ...S 5 be the set of decision variables as in Definition 1, such that the set {b, d} corresponds to the set S = {0, 1, 0, 1, 0}.
1. Verification. In order to decide if {b, d} ∈ 𝓔(𝓗) just add the following constrains:
In this case, if the solver finds an optimal solution, then {b, d} is an SS extension, otherwise it is not. Algorithm 1 is not required since we are asking for the first extension, i.e. the one the solver finds with no iteration.
2. Credulus Acceptance. Let x = b. In order to decide if there is any S ∈ 𝓔(𝓗) for which x ∈ S, add the following constraint:
In this case, if the solver finds an optimal solution, then the condition we are asking for holds, otherwise it is not. Again, Algorithm 1 is not required.
3. Sceptical Acceptance. In this case it is not required to add more constraints, but it is required to use Algorithm 1.
Additionally, it is required to add code to the algorithm in order to test if x ∈ S. On the other hand, it is not required to compute all SS extensions of 𝓗, since it is enough to find the first extension where x ∉ S holds in order to stop.
4. Non-emptyness. It is not required to add more constraints neither Algorithm 1 is required. It is enough to attempt to compute the first extension and test if the solver found an optimal solution.
6 Conclusions
We have presented a novel method for computing SS semantics using binary integer programming. The performance of the new method was good although the ASP approach outperformed it at finding all the SS extensions of a given argumentation framework.
However, the BIP approach had a performance that was as good as that of the ASP approach at finding just the first extension. It means that our approach is good for solving decision problems, at least in those cases where it is enough to compute the first extension.
The reason for the difference between both approaches for computing all extensions of the SS semantics lies in their designs. The mathematical solver was designed to efficiently compute only the first optimal solution, while the ASP solver was designed to compute all models of a logic program. Despite this difference, it is possible that a mathematical solver can take advantage of the information used for computing the first optimal solution in order to compute the remaining ones more efficiently.
It is well known that binary integer programs can be improved in order to compute more efficiently its objective function by using mathematical programming techniques such as relaxation or adding strong valid inequalities. Therefore, there is a great opportunity space for improving this approach for computing the semi-stable semantics.
This new approach constitutes an alternative for computing AF semantics using mathematical programming, and even though we used a state of the art mathematical programming solver, there exist several libraries for Java, C++, and other general purpose languages.











 nova página do texto(beta)
nova página do texto(beta)