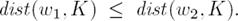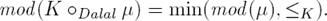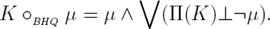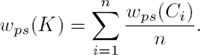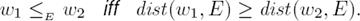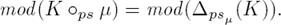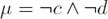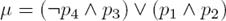Corresponding author is Oscar Chávez-Bosque.
1 Introduction
Belief change can be characterized in two ways: in terms of postulates, which are the properties that a changing process must follow in order to produce rational results, and in terms of processes, which consists of a set of predefined steps in order to generate the results. The latter process indeed defines an operator that is also expected to satisfy a set of postulates previously defined in the literature [15].
Belief revision is a framework that characterizes the process of belief change in which an agent revises its beliefs when new evidence is received. Revision always considers new evidence as a better belief [11]. Such new evidence is usually represented in the form of a propositional formula which must be preserved after the revision.
Logic-based belief revision has been extensively studied [1, 3, 10, 11, 19, 28]. An agent’s beliefs are usually represented as a belief base and with the help of some order-based strategy the new piece of information is integrated to the belief base to reach a new coherent revised belief base.
Classical belief revision always prefers the new information and thus revises the current beliefs to accommodate new evidence. Most studies of belief revision are based on the AGM (Alchourron, Gardenfors & Makinson) postulates [1] which capture this notion of priority and describe the minimal properties a revision process should have. The AGM postulates formulated in the propositional setting in [19], denoted as R1-R6 (see section 3.1), characterize the behavior that a revision operator should comply with. For example, R1, called the success postulate, captures the priority of new evidence over the belief base, which requires that the revision result of a belief base K by a proposition µ (new information) should always maintain µ being believed.
Another belief change approach, belief merging, studies strategies for combining information contained in a set of, possibly inconsistent, belief bases (profile) obtained from different sources in order to produce a single consistent belief base.
In this case, the better belief is taken as the collective one, i.e. the result of merging the bases, which according with the approach can be a set of formulae or a single formula.
Several merging operators have been defined and characterized in a logical way. Among them, model-based merging operators [22, 25, 26, 27, 36] obtain a belief base from a set of worlds with the help of a distance measure on worlds and an aggregation function over distances. The closest worlds to the input belief profile are the result of the operator. This framework has a good level of generality, due to the variety of distance functions that may be chosen, however, in the literature almost every proposed operator uses the classical Dalal distance [10]. Implementation of Dalal based frameworks faces a big issue: the computation of the models of every base in the profile, which could be very expensive. Interested readers can refer to [16] for approaches to deal with the implementation of such operators.
An alternative distance between possible worlds has been defined in [5]. This distance is based on the notion of Partial Satisfiability (PS). A merging operator based on PS-distance is also proposed in [5]. The PS-operator has been implemented avoiding the computation of the models of the belief profile. Moreover, this operator can deal with inconsistent bases which have no models, which is an advantage over Dalal based operators that operate only over the profile’s models and hence cannot handle inconsistent bases.
In the literature, we found that belief merging can be extended to support integrity constraints, which are typically represented as a set of formulae or a single formula that must be respected by the merging result1. In [5], however, the support of integrity constraints is not considered by the proposed operator. Note that as showed in [22], a model-based merging operator can be naturally extended to support integrity constraints. That is, to make the result of the merging fulfil a formula representing the integrity constraints2 µ, we only need to restrain the search of worlds to the ones that satisfy µ and choose the closest to the input belief profile.
In a previous work [34], we proposed an extension of the ∆ps (PS-Merge) belief merging operator and provided a preliminary analysis of its properties. In this paper we (i) further elaborate its characterization, (ii) discuss the properties of our extension, called 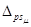 (∆ps under constraints), (iii) describe corresponding test examples in practical scenarios, and (iv) develop a software prototype, called Belief Reviser, to implementing our proposed operators.
(∆ps under constraints), (iii) describe corresponding test examples in practical scenarios, and (iv) develop a software prototype, called Belief Reviser, to implementing our proposed operators.
We made a comparison of
This paper is organized as follows. In section 2 we give some definitions and notations on logic and knowledge bases. In section 3 we introduce belief revision and we define BHQ and Dalal operators. In section 4 we introduce belief merging. We describe partial satisfiability and define 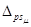 . In section 5 we propose revision through merging via concrete test scenarios which are also described in colloquial language; we compare
. In section 5 we propose revision through merging via concrete test scenarios which are also described in colloquial language; we compare 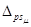 against the other two operators and discuss the results. In section 6 we describe the software prototype developed. Finally in section 7 we give some conclusions and discuss future work.
against the other two operators and discuss the results. In section 6 we describe the software prototype developed. Finally in section 7 we give some conclusions and discuss future work.
2 Preliminaries
We consider a language 𝓛 of propositional logic using a finite set of atoms or variables P := {p1, p2, . . . , pn}. The logic connectives ρ = {¬, ∧, ∨} are defined as usual.
A Well Formed Formula (WFF), also called formula or sentence, is a propositional formula ψ containing a subset of variables from P and a subset of operators from ρ. Parentheses are used in the traditional way [13]. We can define a formula as follows:
— Each propositional variable is a formula.
— If ψ is a formula, then ¬ψ is a formula.
— If ψ and φ are formulae, then ψ ∧ φ and ψ ∨ φ are formulae.
Unnecessary parentheses may be eliminated in the traditional way.
A belief base or belief theory K is a finite set of formulae of 𝓛 representing the beliefs from a source. In this paper we sometimes identify K with the conjunction of its elements, for example if K = {ψ1, ψ2, . . . , ψn} then K = ψ1 ∧ ψ2 ∧ · · · ∧ ψn
A literal l is an atom or the negation of an atom. A term D is a conjunction of literals such that D = l1 ∧ · · · ∧ lk, with li = pj or li = ¬pj. Every formula ψ ∈ L(P ) can be transformed into a Disjunctive Normal Form (DNFψ), such that ψ ≡ DNFψ, where DNFψ is a disjunction of terms such that DNFψ =D1 ∨ · · · ∨ Dm.
A term D is an implicant of a formula ψ iff D ⊨ ψ, and it is a prime implicant iff for all implicants D′ of ψ, we have D′ ⊨ D. The set of all the prime implicants of a formula ψ is denoted by Ξ(ψ).
Similarly, a clause C is a disjunction of literals C = l1 ∨ · · · ∨ lk, with li = pj or li = ¬pj. Every formula ψ ∈ L(P ) can be transformed into a Conjunctive Normal Form (CNFψ), such that ψ ≡ CNFψ, where CNFψ is a conjunction of clauses such that CNFψ =C1 ∧ · · · ∧ Cm.
A clause C is an implicate of a formula ψ iff ψ ⊨ C, and it is a prime implicate iff for all implicates C′ of ψ, we have C ⊨ C′. The set of all the prime implicates of a formula ψ is denoted by Π(ψ).
The set of worlds or models of the language is denoted by W, its elements will be denoted by vectors of the form (w(p1), . . . , w(pn)), where w(pi) = 1 or w(pi) = 0 for i = 1, . . . , n and the set of models of a formula ψ is denoted by mod(ψ). K is satisfiable (consistent) iff there is a model of K. If ψ is a propositional formula or a set of propositional formulae then P(ψ) denotes the set of atoms appearing in ψ. |P| denotes the cardinality of set 𝓟.
A belief profile E = {K1, . . . , Km} is a multiset (bag) of m belief bases.
Let ≤ψ a pre-order relation over worlds; x =ψ y is a notation for x ≤ψ y and y ≤ψ x, and x <ψ y is a notation for x ≤ψ y and y ≰ψ x.
3 Belief Revision
Belief revision is a central topic in knowledge representation and reasoning. Belief revision consists in incorporating a new belief, changing as few as possible the original beliefs while preserving consistency [9].
3.1 Belief Revision Characterization
In [1] eight postulates have been proposed to characterize the process of belief revision, which are known as the AGM postulates. Assuming a propositional setting, in [19] this characterization is rephrased yielding the following R1-R6 postulates, where K, K1 and K2 are belief theories to be revised and µ, µ1 and µ2 are pieces of new evidence and o is a belief revision operator:
R1. K o µ implies µ.
R2. If K ∧ µ is satisfiable, then K o µ ≡ K ∧ µ.
R3. If µ is satisfiable, then K o µ is also satisfiable.
R4. If K1 ≡ K2 and µ1 ≡ µ2, then K1oµ1 ≡ K2oµ2.
R5. (K o µ1) ∧ µ2 implies K o (µ1 ∧ µ2).
R6. If (K o µ1) ∧ µ2 is satisfiable, then K o (µ1 ∧ µ2) implies (K o µ1) ∧ µ2.
[33] introduced the notion of faithful assignment and provided a representation theorem which shows an equivalence between the six postulates and a revision strategy based on total pre-orders, the formal definitions are as follows [18]:
Definition 1 Let 𝓦 be the set of all worlds (interpretations) of a propositional language 𝓛. A function that maps each sentence ψ in 𝓛 to a total pre-order ≤ψ on worlds 𝓦 is called a faithful assignment if and only if:
Theorem 1 (Representation Theorem)
A revision operator o satisfies postulates R1-R6, iff there exists a faithful assignment that maps each sentence ψ into a total pre-order ≤ψ such that:
A belief revision operator can be seen as a function where inputs are a set of beliefs K and a formula µ, and outputs a new set of revised beliefs K o µ. In the literature, a number of concrete belief revision operators have been proposed, deploying either semantic or syntactic approaches.
3.2 Dalal Operator
The most prominent belief revision operator, Dalal operator [10] performs a model-based revision measuring minimal change by the cardinality of model change, i.e. it uses a “distance” metric which operates over two worlds w1, w2 by counting the number of atoms whose values differ from each other, known as the Hamming distance dist(w1, w2). Then this distance helps to define a distance between a belief base K and any possible world w as follows:
Then a total pre-order ≤K over possible worlds can be defined as: w1 ≤K w2 iff
Definition 2 The revision operator oDalal is defined as:
3.3 BHQ Operator
BHQ operator is a prime implicate-based belief revision operator, formula-based yet syntax-insensitive, and do not rely on background information [3]. The operator is defined by first compiling the belief base in its set of prime implicates and then applying the revision operator.
Definition 3 Let K be a belief base and µ be a formula, Π(K) the set of prime implicates of K and K⊥µ the set of maximal subsets of K consistent with ¬µ. Then the prime implicate-based revision operator, written oBHQ , is defined as follows:
The operator conjoins the input µ and the disjunction of the maximal subsets of Π(K) consistent with µ. Instead of dealing directly with the formulae in the belief base, it deals with the prime implicates of the belief base.
4 Belief Merging
Belief merging aims at combining several pieces of (possibly inconsistent) information coming from different sources [24]. The goal is to produce a single consistent set of information, trying to keep the most of the information.
Belief merging addresses important issues in artificial intelligence and databases, as its applications are many and diverse [4]. For example, a belief merging operator in a multiagent system may reach an agreement on the inputs of a group of agents based on the contradictory beliefs of each member in the group. When agents have conflicting beliefs about the “true” state of the world, belief merging can be used to determine the “true” state of the world for the group [33].
Several merging operators have been defined and characterized in a logical way. Among them, ∆ps (PS-Merge) is a versatile operator which can be used to solve real-world problems, with the ad-vantage of having an efficient implementation [31].
4.1 Partial Satisfiability Merging
Without loss of generality the operator considers only normalized languages so that each belief base is taken as the disjunctive normal form (DNF) of the conjunction of its elements or the conjunctive normal form (CNF) of the disjunction of its elements.
In [5] the notion of Partial Satisfiability (PS) is introduced which is a generalization of satisfiability, in which the valuation function w : 𝓛 → {0, 1} is extended to wps : 𝓛 → [0, 1], i.e. the range in a PS-valuation could be any number between 0 and 1. Instead of indicating satisfaction with a Boolean value, partial satisfaction yields a number representing the degree of satisfaction of a formula. If a formula is unsatisfied, its partial satisfiability is 0. If a formula is satisfiable completely (Boolean satisfiable), its partial satisfiability is 1. The partial satisfiability of any other case is between these two values. The authors have proposed two definitions of partial satisfiability: one considers only formulae in DNF and the other, called normal partial satisfiability, considers both forms DNF and CNF. Even when there is a small difference in the valuation of conjunctions, in this paper we consider only normal partial satisfiability, so when we refer partial satisfiability we refer the case of normal partial satisfiability. The difference in the valuation of conjunctions considers a degree of satisfiability when the formula K is unsatisfied and does not contain all the atoms of the language (|𝓟(K)| < |𝓟|), i.e. when the agent is not satisfied at all in its own beliefs, the partial satisfiability considers a small degree of satisfaction for the atoms not appearing in the formula representing its beliefs [31].
Definition 4 (Normal Partial Satisfiability) Let K ∈ 𝓛(P ) in DNF or CNF, w ∈ 𝓦, the Normal Partial Satisfiability of K for w, denoted as wps(K), is defined as follows:
— If K is a literal
— If K := D1 ∨ · · · ∨ Dn
— If K := C1 ∧ · · · ∧ Cn
Example 1 The Partial Satisfiability of the belief base K = (¬a ∧ ¬c) ∨ (b ∧ ¬c) given P = {a, b, c} and w = (1, 1, 1) is
Example 2 Notice that we can find the Partial Satisfiability of inconsistent belief bases such as K = a ∧ (¬a ∨ b) ∧ ¬b, given P = {a, b} and w = (1, 0), it is
This intuitively means that two out of three conjuncts are satisfied.
4.2 ∆ps Operator
In classical model-based belief merging, the process of merging a profile ∆(E) defines three distances: a distance from a world to another one dist(w1, w2), a distance from a world to a belief base dist(w, K) based on dist(w1, w2) and a distance from a world to a profile dist(w, E) based on dist(w, K). The latter distance allows us to define a pre-order between possible worlds with regards to the profile (≤E). The closest worlds to the profile are the models of the merging result. Partial satisfiability merging is quite similar. The only difference is that we define a distance from a world w to a base K directly without the help of distances between worlds. More precisely, we first define:
then a distance from a world w to a profile E is defined as follows:
i.e. the distance from a world to a profile is the sum over all the partial satisfiability of every belief base. Finally, a pre-order between possible worlds w.r.t. a profile E is defined as follows:
The models of the merging result are the worlds that are closest to the profile.
4.3 ∆ps under Constraints
The merging process can be extended straightfor-wardly when an integrity constraint µ is imposed. To assure that the result of the merging will satisfy the integrity constraints, we can restrict the search to the constraint’s models mod(µ) as follows:
We suppose that the integrity constraint is self-consistent. Moreover, without loss of generality we only consider constraints represented by a single formula µ. If there are n constraints µ1, µ2, . . . , µn we will represent them by the conjunction of the constraints, i.e. we shall consider only the belief merging case under one constraint µ = µ1 ∧ µ2 ∧ · · · ∧ µn.
Example 3 (Konieczny & Pino-Pérez, 2002 [23]) At a meeting of co-owners of a block of flats, the chairman proposes for the coming year the construction of a swimming-pool, a tennis-court and a private-car-park. But if two of these three items are built, the rent will increase significantly. We will denote by s, t and p the construction of the swimming-pool, the tennis-court and the private car-park respectively and i will denote the increase of the rent. Two co-owners want to build the three items, and they do not care about the rent increase, K1 = K2 = s ∧ t ∧ p, the third thinks that building any item will cause at some time an increase of the rent and wants to pay the lowest rent so he is opposed to any construction, so K3 = ¬s ∧ ¬t ∧ ¬p ∧ ¬i and finally the last one thinks that the flat really needs a tennis-court and a private car-park but does not want a rent increase i.e. K4 = t ∧ p ∧ ¬i.
The chairman outlines that building two or more items will increase the rent significantly, this fact can not be ignored and worlds in which this fact is falsified must be ignored. These kind of facts are known as integrity constraints.
Let µ be the set of the integrity constraints of the example, it is represented by the single formula ((s ∧ t) ∨ (s ∧ p) ∨ (t ∧ p)) → i. If we consider P the ordered set {s, t, p, i} then the worlds (1, 1, 1, 0), (1, 1, 0, 0), (1, 0, 1, 0) and (0, 1, 1, 0) can not be considered as a possible ∆ps(E) model since these worlds falsify the integrity constraint. It is enough to calculate the Partial-Satisfiability of the bases for worlds in mod(µ).
The answer given by ∆ps of Example 3 (see table 1) is the world (1, 1, 1, 1), i.e. the decision that satisfies the majority of the group is to build the three items no matter if the rent increases. This decision is also the one obtained using the integrity constraint majority merging operator based on the Σ aggregation function in [23].
5 Revision through Merging
Now, for adapting PS-based framework to a belief revision context it is enough to consider revision as a particular case of merging under constraints, where the profile E is a singleton3 E = K and constraints µ represents the new information. Thus, revising a belief base K by the new information µ can be defined through merging as follows:
Definition 5 Let K be a knowledge base and µ be a formula, then the PS-Merge revision of K by µ is defined as:
Given the profile is a singleton, the sum of partial satisfiability of the belief base is not necessary, i.e. 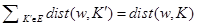 , so we can redefine the pre-order in terms of distance from a world to a base as follows:
, so we can redefine the pre-order in terms of distance from a world to a base as follows:
which in terms of implementation will reduce the complexity.
5.1 Satisfaction of Postulates
We show now that the operator satisfies, under certain restrictions, postulates R1-R6. To prove that we use the representation theorem showed in Theorem 1.
Note that in the settings in Definition 1 and Theorem 1, we only need to consider ≤ψ instead of considering ≤K for a general belief base K. Clearly the ≤ψ is a total pre-order on the possible worlds given that Equation (6) is defined based on a relation over real numbers.
To show that the mapping from ψ to ≤ψ is faithful, we need to prove the three conditions required in Definition 1. For the first condition, i.e. w1, w2 ⊨ ψ only if w1 =ψ w2, suppose that w1, w2 ⊨ ψ holds, then the partial satisfiability values of ψ for both w1 and w2 are 1, i.e. dist(w1, ψ) = 1 and dist(w2, ψ) = 1 which means w1 =ψ w2.
For the second condition suppose that w1 ⊨ ψ and w2 ⊭ ψ hold, then the partial satisfiability of ψ for w1 is 1 and the partial satisfiability of ψ for w2 is less that 1 by the definition of partial satisfiability, i.e. dist(w1, ψ) > dist(w2, ψ), which means that w1 <ψ w2.
However, we must note that the third condition does not hold in general because partial satisfia-bility is syntax sensitive while condition 3 imposes syntax independence. Nevertheless, for ease of computation, formulae are usually compiled into the disjunction of all its prime implicants (a particular case of DNF) or the conjunction of all its prime implicates (a particular case of CNF) for practical implementation. In this setting we can prove the third condition.
Indeed, in the literature prime implicants decomposition is often used to decide whether two formulae are equivalent or not. The main property satisfied by prime implicants of ψ (denoted by Ξ(ψ)) and prime implicates of ψ (denoted by Π(ψ)) is shown as follows [30]:
Proposition 1 φ ≡ ψ iff Ξ(φ) = Ξ(ψ) iff Π(φ) = Π(ψ).
The representation in prime implicants is unique in the sense that, given a set P of propositional symbols, every proposition built up with symbols of P has exactly one representation in prime implicants that represents a whole family of congruent propositions [30], a similar result can be found using conjunctions of prime implicates.
Therefore, if φ ≡ ψ, let φ′ and ψ′ be the the disjunction of prime implicants of ψ and ψ, respectively, then due to the uniqueness of the prime forms (up to the order of the terms and of the literals that occur within them), we should have φ′ and ψ′ are essentially the same, hence we have ≤φ′ =≤ψ′ because by definition the order of the terms and literals does not affect the partial satisfiability values. Similar results hold for prime implicates.
Given the above analysis, we have the following theorem:
Theorem 2 If every formula considered have been compiled into the disjunction of all its prime implicants or the conjunction of all its prime implicates, then ops satisfies R1-R6.
While the approach requires compilation to CNF or DNF, it can deal with inconsistent belief bases, which is a significant issue rarely addressed in the literature [21]. Moreover, compilation to DNF or CNF is a problem widely studied and well implemented, so compilation is not a bottleneck in the whole problem. Interested readers can refer to [17, 20] for the compilation problem from a formula to its prime implicants.
5.2 Test Scenarios Adapted to Revision
In order to validate the ops operator and demon-strate some advantages over other operators, we use the following four examples shown in the frames below. The first two examples were borrowed from [3]. The third example shows how our operator can deal with contradictory bases that rarely can any belief merging operator deal with them [21]. The fourth example is taken from [30].
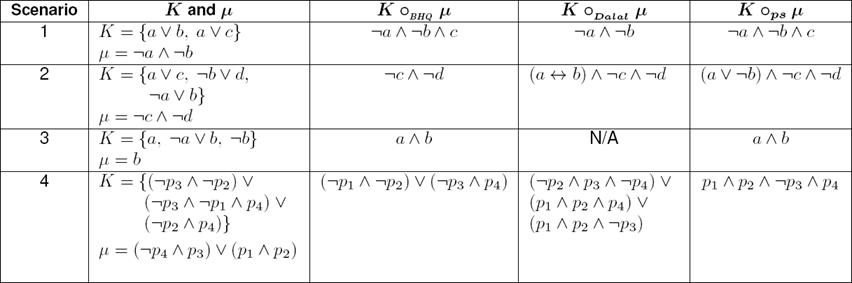
Scenario 1 (Bienvenu, Herzig & Qi, 2008) [3]. A person is dead. An initial review indicates the death is caused by asphyxiation or by suffocation. A latest review indicates the death is caused by asphyxiation or by cardiopulmonary arrest.
a = death by asphyxiation.
b = death by suffocation.
c = death by cardiopulmonary arrest.
Then, a forensic analysis excludes the possibilities of death by asphyxiation and death by suffocation.
Scenario 2 (Bienvenu, Herzig & Qi, 2008) [3]. A family wants to go on vacation and they are planning their journey. The child wants to swim in a beach or taking a flight during the journey. The mother will not go to a colonial city unless she goes shopping in the journey. The father will not go to a beach unless he goes to a colonial city.
a = Beach.
b = Colonial city.
c = Flight.
d = Shopping.
After checking the listed preferences and revising the budget, the family finds that neither taking a flight nor shopping is affordable.
We have taken examples from the literature to make a fair comparison and not to bias the results, also, given the interesting results of BHQ operator which differ from results of the classical Dalal operator.
For ease of understanding, we translate these examples, originally in propositional notations, to real-life situations/scenarios expressed in natural language.
Scenario 3 In an accident, a witness claims that the car starts normally. But the owner argues that the car cannot start or the car has been turned off. Later, the owner’s partner remembers that the car is not turned off.
a = Car starts.
b = Car turned off.
A technical revision by a mechanic indicates that the car has been turned off.
Scenario 4 (Marchi, Bittencourt & Perrussel, 2010) [30]. A patient visits a nutritionist for diet advice, and exposes his tastes/dietary habits in the breakfast for a typical day: no watermelon and citrics at all, or no watermelon and no plain water and milk, or no citrics and milk.
K = {(¬p3∧¬p2)∨(¬p3∧¬p1∧p4)∨(¬p2∧p4)}
p1 = Plain water.
p2 = Citrics.
p3 = Watermelon.
p4 = Milk.
The nutritionist then issues his recommendation: no milk and watermelon, or plain water and citrics.
Results of ops are compared with existing techniques such as oBHQ [3] and the well known Dalal [10] approach.
Table 2 shows the results of each operator. We will expose the use of the three belief revision operators in scenario 1. They apply similarly in the other three scenarios.
Example 4 The BHQ operator applied to scenario 1 involves the computation of prime implicantes of K, say Π(K). In this case Π(K) = K. Then, the maximal subsets of Π(K) consistent with µ are {{a ∨ c}}. Finally, K oBHQ µ is ¬a ∧ ¬b ∧ (a ∨ c) ≡ ¬a ∧ ¬b ∧ c.
Example 5 The Dalal’s operator returns the set of worlds with minimum distance of the models of µ with respect to K. So K oDalal µ from scenario 1 is {(¬a, ¬b, c), (¬a, ¬b, ¬c)} despite the models of K, So K oDalal µ is ¬a ∧ ¬b ≡ µ.
Example 6 ops over scenario 1 considers computing the models of µ: (0, 0, 1) and (0, 0, 0), on the assumption that atoms are ordered alphabetically. We can easily verify that the model of K ops µ is (0, 0, 1), as shown in Table 3. Then, K ops µ is ¬a ∧ ¬b ∧ c.
In scenario 1, Dalal’s revision result ¬a∧¬b loses information concerning c. Instead, results of BHQ and PS operators ¬a ∧ ¬b ∧ c preserve information on c. This result means that K oBHQ µ and K ops µ conclude no death by asphyxiation nor death by suffocation but death by cardiopulmonary arrest.
In scenario 2, BHQ revision result is the same as the constraint µ, instead the result of the Dalal operator is (a ↔ b) ∧ ¬c ∧ ¬d, which considers an equivalence between a and b. Result of PS-operator (a ∨ ¬b) ∧ ¬c ∧ ¬d considers a disjunction between a and ¬b which assures satisfaction of two conjunctions of input K = (a ∨ c) ∧ (¬b ∨ d) ∧ (¬a ∨ b), i.e. we assure that two members of the family are satisfy on their holidays. The advice of K opsµ is that the family should travel to a beach or not to a colonial city, and avoid taking a flight and shopping. Dalal results also assure the satisfaction of two members but give priority to the father.
Scenario 3 considers the revision of an inconsistent belief base, so Dalal’s revision does not apply in this case. Results of BHQ and PS operators retract ¬b in order to produce the consistent belief base a ∧ (¬a ∨ b) ∧ b ≡ a ∧ b. In this case both operators result in both the car starts normally and the car has been turned off.
Scenario 4 is an interesting case since it is a more complex example in terms of number of atoms and formulae. Dalal’s approach yields a complex recommendation intake for the patient (p1∧¬p2∧p3∧¬p4)∨(¬p1∧¬p2∧p3∧¬p4)∨(p1∧p2∧ p3 ∧p4)∨(p1 ∧p2 ∧¬p3 ∧p4)∨(p1 ∧p2 ∧¬p3 ∧¬p4) ≡
(¬p2 ∧ p3 ∧ ¬p4) ∨ (p1 ∧ p2 ∧ p4) ∨ (p1 ∧ p2 ∧ ¬p3) Although simplied, it is still a complex formula. oBHQ results in (¬p1∧¬p2)∨(¬p3∧p4), a simpler breakfast menu, but PS approach results in the most elegant solution: p1 ∧ p2 ∧ ¬p3 ∧ p4: plain water and citrics and no watermelon and milk.
6
6.1 Algorithm
We modified the algorithms proposed in [6, 32] to consider constraints and then formalized the Algorithm 1 mentioned in [34]. The inputs of the algorithm are shown below:
— V : Number of variables of profile E,
— B : Number of bases of E,
— C : Vector of number of conjuncts of each base in E,
— L : Matrix of occurrences of literals by each conjunct of each base in E,
— M : Number of conjuncts of constraints µ,
— LM : Matrix of occurrences of literals by each conjunct of constraints µ.
Example 7 Consider the base of scenario 1, with E = {K} = {(a ∨ b) ∧ (a ∨ c)}, and µ = ¬a ∧ ¬b then the input data accepted by Algorithm 1 are as follows:
Complexity of Algorithm 1 is polynomial in V, B and M inputs.
6.2 Software Prototype
For users’ convenience, we have also developed a software prototype implementing 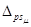 . We call it Belief Reviser prototype. The prototype considers the operators in ρ and considers the two missing classical operators → and ↔, i.e ρ = ρ ∪ {→, ↔}.
. We call it Belief Reviser prototype. The prototype considers the operators in ρ and considers the two missing classical operators → and ↔, i.e ρ = ρ ∪ {→, ↔}.
Algorithm 1 is implemented in language M using GNU Octave 3.6.2, as it is an open alternative to Matlab® with similar characteristics and performance [14]. We based on existing source code4, and we design a User Interface (UI) based on the Belief Merger prototype5 described in [7].
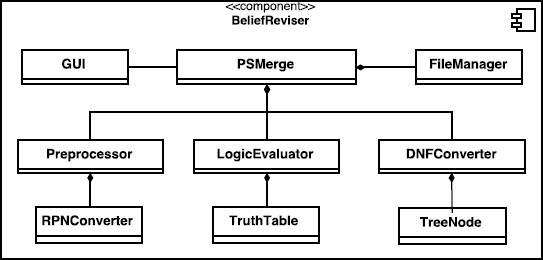
Figure 1 outlines the UML diagram of the Belief Reviser where main classes and its relations are depicted. The prototype was developed under the Open Java Development Kit (OpenJDK) 7 since it is a relatively easy to learn development platform and its object-oriented design. It has multithreaded and platform-independent capabilities, and it is active and robust. Moreover, the platform is free [37].
PSMerge class handles all the revision process, instantiating all classes involved while verifying the correct configuration of the running environment. The classes shown in Figure 1 perform different functionalities of the prototype.
6.2.1 Data Preprocessing
Preprocessor class parses the belief base and the constraints to build a pair of lists with formulae in Reverse Polish Notation (RPN) notation (postfix notation). Postfix notation, while less common than infix notation in written mathematics, is more explicit in the sense that the operands belonging to a particular operation can be expressed without the need for brackets or operator precedence
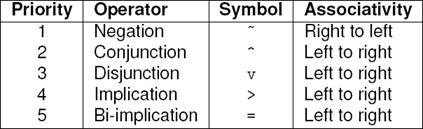
[12]. Class RPNConverter implements Algorithm 2 which shows the implementation of the Dijkstra’s Shunting-yard algorithm [41] applied to logical operators in ρ. Operator precedence is shown in Table 4.
6.2.2 Logic Formulae Evaluation
LogicEvaluator class performs the evaluation of logic formulae in RPN notation with the help of
TruthTable class, which contains the matrix of size n × m where n = |𝓟(K)| and m = 2n. Algorithm 3 sets up the truth table as follows: column under the first variable should alternate 2n−1 true’s with with 2n−1 false’s; column under the second variable should alternate 2n−2 true’s with with 2n−2 false’s; continuing until we reach the last column variable.
The explicitness of the RPN formulae obtained by Algorithm 4 allows us to implement the algorithm for evaluating postfix notation in a straightforward manner. Algorithm 4 shows the RPN evaluator developed using a stack as a helper data structure.
6.2.3 DNF Conversion
DNFConverter class performs the process of conversion in two steps. In the first step, an algorithm parses the formula and creates a binary tree according to the operator’s precedence (Table 4). In the second step, another algorithm converts the formula to DNF by building the DNF binary tree while walking through the formula binary tree built in the first step. Each node of the tree is an instance of TreeNode class. The conversion of a formula to its DNF is based on the JavaScript code from the Theorem Proving in Propositional Logic (WFFs) web site [2].
6.2.4 PS-Merge Interface
FileManager class is the interface between the Java code and the language M implementation of 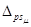 . We use JavaOctave 0.6.4 bridging from Java to Octave to run
. We use JavaOctave 0.6.4 bridging from Java to Octave to run 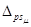 in PSMerge.m file. As
in PSMerge.m file. As 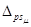 implementation requires an input file with the precise structure (see subsection 6.1), this class builds the input file (problem.txt) and runs
implementation requires an input file with the precise structure (see subsection 6.1), this class builds the input file (problem.txt) and runs 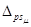 and the solution is obtained via an output file (solution.txt). Figure 2 illustrates this process.
and the solution is obtained via an output file (solution.txt). Figure 2 illustrates this process.
6.2.5 User Interface (UI)
Figure 3 shows the main elements of the prototype UI. A belief base K is introduced into the top left input box. Constraint µ is introduced into the bottom left input box. Variables are represented by the alphabetical letters (except the ‘v’ letter), with uppercase and lowercase letters being treated differently. Logical operators are represented by the symbols shown in Table 4. Each belief is separated by commas. An output panel is presented on the right side of the UI where results and debug information are displayed. When needed, formulae is converted to DNF as required by ∆ps.
All the scenarios presented in this paper were solved in this prototype, loaded via text files for each scenario. For example, file format of scenario 1 shown in Figure 3 consists of a first line representing K and a second line representing µ:
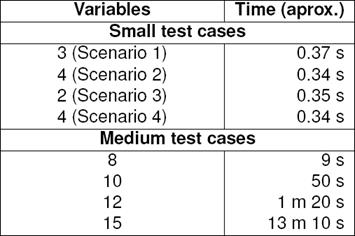
Average case performance running the four scenarios is 0.3 seconds. Table 5 shows the test cases executed in the Belief Reviser running on an Alienware M17x laptop with Intel Core i7@2GHz processor, 8 GB RAM, Ubuntu Linux 14.10 OS.
First four test cases correspond to the scenarios, respectively, considering a minimum number of variables. The following four test cases are generated within the prototype and consider a larger number of variables which are unlikely to be solved manually. The performance results of these tests indicate that they can be handled in a reasonable computational time with common hardware.
Time employed by the prototype is much lower than the time (in minutes) that a human being would spend in solving these scenarios, assuming that the user is familiarized with belief revision concepts. Moreover, examples with greater number of variables and size of K may be unmanageable and error-prone for human beings.
7 Conclusion
Classical belief revision always results in trusting the new evidence. Some approaches need extra information, such as priorities between formulae, in order to process the revision. However, in many cases this extra information is not available. We propose a new revision method considering “flat” belief bases without extra information.
We adapt belief merging in order to carry out belief revision by using belief merging under constraints, which always results in holding the constraints. Instead of creating a new belief revision operator, we consider revision as a particular case of belief merging under constraints where only one a priori base is to be merged.
We have taken into account of the revision postulates that must be satisfied and proved that under certain syntactical restriction our approach satisfies the AGM postulates. Also, the PS approach is elegant and simple in computation.
We present a comparison of our proposal, ∆ps under constraints, 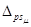 , against the well-known Dalal operator, which is a model-based operator, and the BHQ operator, which is formula-based and considers inconsistent formulae; describing in natural language a set of examples with different characteristics. Results are explained and interpreted demonstrating the potential of the PS approach. The three operators shown present dissimilar features, and ops was proved to be easier to implement and more appropriate to some scenarios. For example, ops in scenario 1 retains properly the information of c, in scenario 2 shows to be fair given no preference to the father desires, for scenario 3 handles an inconsistent K and for scenario 4 provides a clear and unambiguous nutritional advice.
, against the well-known Dalal operator, which is a model-based operator, and the BHQ operator, which is formula-based and considers inconsistent formulae; describing in natural language a set of examples with different characteristics. Results are explained and interpreted demonstrating the potential of the PS approach. The three operators shown present dissimilar features, and ops was proved to be easier to implement and more appropriate to some scenarios. For example, ops in scenario 1 retains properly the information of c, in scenario 2 shows to be fair given no preference to the father desires, for scenario 3 handles an inconsistent K and for scenario 4 provides a clear and unambiguous nutritional advice.
It is worth noticing that many revision ap-proaches in the literature use models of operations and hence cannot apply to situations involving an inconsistent belief base. However, PS-based revision can deal with the inconsistency (see scenario 3).
A Belief Reviser software prototype was developed. It automates the process of belief revision given that it is a user-friendly interface implementing 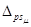 . We tested the prototype with a set of test cases in different sizes, namely small and medium test cases. Results indicate that problems of medium sizes can be handled by the prototype. The Belief Reviser is free software available online at http://www.sourceforge.net/ p/beliefreviser.
. We tested the prototype with a set of test cases in different sizes, namely small and medium test cases. Results indicate that problems of medium sizes can be handled by the prototype. The Belief Reviser is free software available online at http://www.sourceforge.net/ p/beliefreviser.
Future work considers a deep analysis of PS definition in order to propose a new definition that avoids the restriction concerning prime implicant forms, since formulae expressed in prime implicant form satisfy the principle of independence of the syntax. Also, we plan to compare the PS operator against classical operators [38, 40] as well as against more recent proposals [30, 29].
problems, from frameworks for identifying quality knowledge in the Web [39] to model multi-agent systems [35]. Belief revision is one of the most important concepts in studying human reasoning. mathematics are the basis that hold for many other sciences, we believe that many problems could be solved using logic, and belief revision is a promissory technique with a number of applications to real life scenarios.
Finally, we propose to model real-life scenarios, taking examples from different areas such as decision-making from strategic planning [7], or menu planning from nutrition sciences [8]. By this, real scenarios will be validated by experts of each field and comparison of operators will be more interesting and valuable.











 nova página do texto(beta)
nova página do texto(beta)