1. Introducción
Los problemas de clasificación están cobrando particular importancia en la actualidad puesto que en muchos casos se requiere agrupar elementos que presenten un conjunto de características específicas. Existen varios modelos de clasificación reportados en la literatura, por ejemplo: los basados en redes neuronales, en redes bayesianas, los árboles de clasificación, la regresión logística y el análisis discriminante, por solo mencionar algunos.
En la actualidad existen campos multidisciplinarios como la Bioinformática, con problemas grandes y muy complejos, que no se logran solucionar de forma satisfactoria con el uso de un solo clasificador. Con frecuencia ocurre que la precisión, exactitud o la característica que se desee medir, de un único clasificador no satisface los requerimientos del problema. Esa es la razón principal que ha conllevado al auge en el uso conjunto de sistemas compuestos por varios clasificadores para tratar de alcanzar resultados superiores a los de un único clasificador.
En investigaciones recientes muchos autores introducen el término multi-clasificador como un "clasificador" que combina las salidas de un conjunto de clasificadores individuales, utilizando algún criterio (ej.; promedio, voto mayoritario, mínimo, etc.). Los sistemas multi-clasificadores logran satisfacer muchas veces la necesidad de desarrollar clasificadores exactos, precisos y confiables para muchas aplicaciones prácticas.
Se han reportado numerosos artículos que los han utilizado con éxito en la solución de problemas reales 1.
La idea inicial para mezclar conjuntos de clasificadores es muy sencilla. Ella parte del hecho de combinar respuestas que se complementen unas con otras. Los clasificadores que deben combinarse no son los más precisos o los más exactos, sino los más diversos. Una muestra mal clasificada por uno o varios clasificadores puede estar correctamente clasificada por otro u otros 2. Mezclar un grupo de clasificadores idénticos no producirá mejores resultados que uno solo de ellos. La idea es entonces combinar un grupo de clasificadores diversos entre sí, para garantizar que al menos uno de ellos brinde la respuesta correcta cuando el resto esté equivocado. Por tal razón resulta sumamente importante estudiar la diversidad entre los clasificadores bases a combinar. Existen numerosas fórmulas estadísticas reportadas en la literatura, conocidas como "medidas de diversidad". Comprenderlas para cuantificar la diversidad existente en un conjunto de clasificadores es un aspecto imprescindible en la combinación de clasificadores.
Por otro lado, la cantidad de clasificadores existentes en la actualidad hacen muy difícil escoger cuáles combinar pues la cantidad de combinaciones posibles es un número muy alto por tanto surge la idea de usar una meta heurística que nos ayude a resolver el problema combinatorio. Algunas de las metas heurísticas existentes son: Optimización basada en Colonias de Hormigas (ACO por las siglas en inglés Ant Colony Optimization), Optimización basada en Colonias de Abejas (ABC por Artificial Bee Colony) y Algoritmos Genéticos (GA por Genetic Algorithms) 3, 4, 5, 6.
Estos últimos se destacan por ser ampliamente usados en una gran variedad de aplicaciones y técnicas de modelación u optimización, pues ellos son una de las meta heurísticas más sencillas 7. Están inspirados en la evolución biológica y su base genético-molecular. Este tipo de algoritmo hace evolucionar una población de individuos sometiéndola a acciones aleatorias semejantes a las que actúan en la evolución biológica (mutaciones y cruzamientos), así como también a una selección de acuerdo a algún criterio, en función del cual se decide cuáles son los individuos más adaptados y cuáles no 8. Las soluciones que se encuentran en cada generación se evalúan según su calidad y las mejores de ellas se almacenan para la próxima generación. Esta forma de guardar estas soluciones puede ser determinista, eligiendo siempre las mejores k soluciones, o aleatoria eligiendo las soluciones según un valor probabilístico asociado 9.
La meta heurística ofrece la posibilidad de no tener que explorar todo el espacio de búsqueda de las "posible soluciones". Los algoritmos genéticos, como una meta heurística de mejora, permiten partir de un conjunto de soluciones iniciales; sobre las cuales se aplican iterativamente determinados operadores con el objetivo de modificarlas y obtener como resultado final un óptimo, que si bien puede no ser el global, que sea lo suficientemente cercano a él.
A continuación se detallan las medidas de diversidad existentes para cuantificar la diversidad en un conjunto de clasificadores, aspecto que se incluye más adelante en la modelación de la meta heurística mencionada anteriormente.
2. Medidas de diversidad
Resulta intuitivo pensar que el resultado de combinar un grupo de clasificadores idénticos no va a ser mejor que el resultado de uno solo de sus miembros. Al contrario, resultaría más conveniente si combináramos un grupo de clasificadores diferentes entre sí, dado que al menos uno de ellos debe dar la respuesta correcta cuando el resto falle. Dicha diferencia, conocida principalmente como diversidad, también se le conoce como ortogonalidad, independencia, dependencia negativa o complementariedad. A pesar de que no existe una definición formal de lo que es intuitivamente percibido como diversidad, no al menos en el vocabulario de la Ciencia de la Computación, es ampliamente aceptado por la comunidad científica el hecho de que la existencia de diversidad en un grupo de clasificadores base es una condición necesaria para la mejora del desempeño de un ensamblado de clasificadores. Un ensamblado de clasificadores diversificados conduce a errores no correlacionados, que a su vez mejoran la precisión de la clasificación. Comprender y cuantificar la diversidad que existe en un ensamblado de clasificadores es un aspecto importante en la combinación de clasificadores. En la literatura existen diferentes medidas usadas para tal propósito, cuyo objetivo es cuantificar la dependencia existente entre clasificadores 10.
En 10 se plantea que no hay una medida de diversidad involucrada en forma explícita en los métodos de generación de clasificadores, aunque asumen que la diversidad es el punto clave en cualquiera de los métodos.
Estas medidas para cuantificar la diversidad, pueden ser categorizadas en dos tipos: medidas en forma de pares (pairwise) y medidas para todo el conjunto (non pairwise) 10. A continuación se explica en qué se basan las medidas en forma de pares.
2.1. Medidas de diversidad en forma de pares
Las medidas en forma de pares se calculan por pares de clasificadores usando sus salidas, las cuales son binarias (1,0) que indican si la instancia fue correctamente clasificada o no por el clasificador. A continuación se indica el resultado de dos clasificadores (Ci, Cj) en una instancia para conocer si la clasificaron correctamente o no, ver Tabla 1.
Tabla 1 Matriz binaria para una instancia
| Cj correcto (1) | Cj incorrecto (0) | |
| Ci correcto (1) | a | B |
| Ci incorrecto (0) | c | D |
| a + b + c + d = 1 | ||
Si se suman para todas las instancias los valores de a, b, c, d, entre el par de clasificadores (Ci, Cj), se obtendrá el siguiente resultado, a partir del cual se calculan las medidas en forma de pares, ver Tabla 2.
Tabla 2 Matriz binaria para N instancias
| Cj correct (1) | Cj incorrecto (0) | |
| Ci correcto (1) | A | B |
| Ci incorrecto (0) | C | D |
| A +B + C + D = N | ||
Donde A sería igual a la suma total de los valores de a para todas las instancias y así respectivamente con los valores de B, C y D. N es el número total de instancias. Un conjunto de L clasificadores produce L(L-1)/2 pares de valores. Para obtener un único resultado habría que promediar estos valores.
A continuación se muestra la Tabla 3 donde se destacan algunas características generales de estas medidas. Luego se detallan cada una de ellas.
En la primera columna se muestra el símbolo usado en la literatura para representar a la medida correspondiente.
Luego la siguiente columna representa el crecimiento (↑) o decrecimiento (↓) del valor de la medida para obtener la mayor diversidad, a continuación se detalla aún más este criterio.
- ↑: el conjunto de clasificadores es más diversos mientras mayor sea el valor de la medida.
- ↓: el conjunto de clasificadores es más diversos mientras menor sea el valor de la medida.
La última columna de la tabla muestra los intervalos de valores que pueden tomar cada una de estas medidas, como se puede apreciar no todas tienen el mismo intervalo.
2.1.1. Coeficiente de correlación (ρ)
El coeficiente de correlación entre dos clasificadores Ci y Cj se calcula como:
La medida final para un conjunto de clasificadores sería el promedio de los valores asociados a cada combinación de dos clasificadores que se extraigan del conjunto. Mientras menor sea el valor de p, mayor será la diversidad 11.
2.1.2. El estadístico Q
El estadístico Q (Q Statistics) es otra de las medidas en forma de pares. Se calcula de la siguiente forma:
En general, el valor de Q va a oscilar entre -1 y 1. Aquellos clasificadores que tienden a reconocer los mismos objetos correctamente tendrán un valor positivo de Q, y aquellos que comentan errores en diferentes objetos poseerán un valor negativo de Q. La mayor diversidad de esta medida se alcanza mientras menor sea su valor 11. Para cualquier par de clasificadores, los valores de ρ y Q tendrán el mismo signo y se puede probar que |ρ| < |Q|. 10.
2.1.3. Medida de desacuerdo
La medida de desacuerdo (The Disagreement Measure) introducida por Skalak 12, es la más intuitiva de las medidas entre un par de clasificadores, y es igual a la probabilidad de que los dos clasificadores discrepen en sus predicciones. Mientras mayor sea su valor mayor será la diversidad:
2.1.4. Medida de doble fallo
La medida de doble fallo (The Double-Fault Measure), introducida por Giacinto y Roli 13, considera el fallo de los dos clasificadores al mismo tiempo. En 14 definen a esta medida como una medida no-simétrica. Esto quiere decir que si se intercambian los unos con los ceros en los resultados de los clasificadores, el valor de la medida no va a ser el mismo. Esta medida está basada en el concepto de que es más importante conocer cuando errores simultáneos son cometidos que cuando ambos tienen clasificación correcta. Mientras menor sea el valor, mayor será la diversidad:
2.2. Medidas de diversidad para todo el conjunto (non-pairwise)
Estas medidas consideran a todos los clasificadores a la vez y calculan un único valor de diversidad para todo el conjunto, ellas se conocen también como medidas de grupo o grupales.
A continuación se muestra la Tabla 4 donde se destacan algunas características generales de ellas. Luego se detallan cada una de ellas.
Tabla 4 Características generales de las medidas para todo el conjunto
| Medidas | Nomenclatura | (↑/↓) | Intervalos |
|---|---|---|---|
| Entropía | E | ↑ | 0 ≤ E ≤ 1 |
| Varianza de Kohavi-Wolpert | KW | ↑ | 0≤ KW< +∞ |
| Desacuerdo entre expertos | K | ↓ | -1 ≤ K ≤ 1 |
| Medida de dificultad | Ө (DIF) | ↓ | 0 ≤ Dif ≤ 1 |
| Diversidad generalizada | GD | ↑ | 0 ≤ GD ≤ 1 |
| Diversidad de Coincidencia de fallos | CFD | ↑ | 0 ≤ CFD ≤ 1 |
| Diversidad de distintos fallos | DFD | ↑ | 0 ≤ DFD ≤ 1 |
| Diversidad Global | OD | ↑ | 0 ≤ OD ≤ 1 |
| Medida de Variabilidad | VAR | ↑ | 0 ≤ Var ≤ 1 |
2.2.1. Entropía
La medida de Entropía (The Entropy Measure), explicada en 10, se basa en la idea intuitiva de que en un conjunto de N instancias y L clasificadores la mayor diversidad se obtendrá si L/2 de los clasificadores clasifican una instancia correctamente y los otros L- L/2 la clasifican incorrectamente. Fue introducida por Cunningham y Carney en 15:
donde Yi,j tendrá valor 1 si el clasificador i clasificó correctamente el caso j y 0 en caso contrario. Si E tiene valor 0 esto indica que no hay diversidad entre los clasificadores y un valor 1 indica la mayor diversidad posible.
2.2.2. Varianza de Kohavi-Wolpert
La varianza de Kohavi-Wolpert (Kohavi-Wolpert Variance), fue inicialmente propuesta por Kohavi y Wolpert 16. Esta medida es originada de la descomposición de la varianza del sesgo del error de un clasificador.
Kuncheva y Whitaker presentaron en 10 una modificación para medir la diversidad de un ensamblado compuesto por clasificadores binarios, quedando la medida de diversidad como:
con esta medida, la diversidad disminuye a medida que el valor de KW aumenta.
2.2.3. Medida de desacuerdo entre expertos
La medida de desacuerdo entre expertos (Measurement interrateragreement) 17, es otra de las medidas de diversidad que se basan en todo el conjunto. Se desarrolla como una medida de fiabilidad entre clasificadores. Puede usarse para medir el nivel de acuerdo dentro de un conjunto de clasificadores, por consiguiente está también basada en el supuesto de que un conjunto de clasificadores debe discrepar entre sí para ser diverso. La diversidad disminuye cuando el valor de k aumenta. El k se calcula por:
donde el término de la derecha es la medida de concordancia de Kendall y p es la media de la exactitud de la clasificación individual, y se calcula como:
2.2.4. Medida de dificultad
La medida de dificultad (The Measure of "difficulty" e) viene del estudio realizado por Hansen y Salmon 18. Se calcula a través de la varianza de una variable aleatoria discreta que toma valores en el conjunto (0/L, 1/L, 2/L,..., 1) y denota la probabilidad de que exactamente i clasificadores hayan clasificado bien todas las instancias.
Para conveniencia, θ suele ser escalada linealmente en el intervalo [0,1] tomando p (1-p) como el mayor valor posible, donde p es la precisión individual de cada clasificador. La diversidad del ensamblado aumenta con el decremento del valor de la medida de dificultad.
La intuición de esta medida puede ser explicada de la siguiente manera: un ensamblado de clasificadores diverso tiene un valor pequeño de medida de dificultad, dado que cada muestra de entrenamiento puede al menos ser clasificada correctamente por una proporción de todos los clasificadores base, lo cual es más probable con una baja varianza de X:
2.2.5. Medida de diversidad generalizada
La medida de diversidad generalizada (Generalized Diversity) se enunció por Partridge y Krzanowski 19.
Sea Y una variable aleatoria que representa la proporción de clasificadores que clasificaron incorrectamente una muestra x ∈ Rn extraída aleatoriamente del conjunto de datos. Denotemos por pi la probabilidad de que Y=i/L y p(i) la probabilidad de que i clasificadores extraídos de manera aleatoria fallen en clasificar correctamente un objeto X extraído aleatoriamente. Supongamos que dos clasificadores son tomados de forma aleatoria del ensamblado, los autores exponen en su trabajo que la máxima diversidad es lograda cuando uno de los dos clasificadores se equivoca en clasificar un objeto y el otro lo clasifica correctamente. En este caso la probabilidad de equivocarse los dos clasificadores es p(2)=0. Por otra parte argumentan que la mínima diversidad se lograría cuando el fallo de un clasificador es siempre acompañado con el fallo del otro, entonces la probabilidad de que los dos clasificadores fallen es la misma que la probabilidad de que un clasificador escogido de forma aleatoria falle, esto es p(1):
donde
el valor de GD varía entre 0 y 1, siendo 0 la menor diversidad cuando p(2)=p(1) y 1 la mayor diversidad cuando p(2)=0 y L la cantidad de clasificadores.
2.2.6. Medida de diversidad de coincidencia de fallos
Esta medida (Coincident Failure Diversity) se enuncia por Partridge y Krzanowski 20, como una mejora a la medida anterior.
Esta medida está diseñada de tal forma que tenga un valor mínimo 0 cuando todos los clasificadores siempre clasifiquen correctamente, o cuando todos los clasificadores, lo mismo clasifiquen correcta o incorrectamente al mismo tiempo. Su máximo valor 1 es alcanzado cuando todos los errores de clasificación son únicos, es decir cuando al menos un clasificador va a clasificar incorrectamente cualquier objeto aleatorio:
aquí po = 1 cuando todos los clasificadores siempre son simultáneamente correctos o incorrectos, p[i] es el mismo término de la medida anterior y L es la cantidad de clasificadores. El valor de CFD está entre 0 y 1 y mientras mayor sea, mayor será la diversidad.
2.2.7. Medida de diversidad de distintos fallos
Esta medida (Distintic Failure Diversity) fue igualmente enunciada por Partridge y Krzanowski 20, como una mejora a la medida anterior, pues ahora se tiene en cuenta a todas las instancias donde los clasificadores no coinciden en las clases asignadas, es decir, se consideran las distintas posibilidades de fallo teniendo en cuenta las clases:
aquí t es un vector de probabilidades en el que cada posición se calcula determinando la cantidad de i clasificadores que hayan fallado en asignar la clase correcta, dividido por el total de fallos ocurridos y L es la cantidad de clasificadores. El valor de DFD está entre 0 y 1 y mientras mayor sea, mayor será la diversidad.
2.2.8. Medida de la diversidad global
La medida de la diversidad global (Overall Diversity) fue enunciada en 20, como una versión "pesada" de la medida de diversidad de distintos fallos. Dicha medida se calcula como:
Cada posición de w representa el promedio de valores d para cada fila donde i clasificadores fallaron. Los valores d se calculan para cada instancia como:
donde K es la cantidad de clases o categorías que se asignan a los casos, Ck indica la cantidad de clasificadores que asignaron la clase k a la instancia i, siendo k una clase incorrecta y ni es el total de fallos ocurridos en la instancia i. El valor de OD está entre 0 y 1 y mientras mayor sea, mayor será la diversidad.
2.2.9. Medida de variabilidad
Esta medida (The Measure of Variability) tiene en cuenta si las clases asignadas por los clasificadores en cada instancia son distintas o no. Mientras mayor sea su valor, mayor será la diversidad:
donde N es el total de instancias y EL(i) es la etiqueta (clase) asignada a la instancia i, por el clasificador i-ésimo 11.
3. Combinación de varias medidas de diversidad
Para hacer posible el trabajo con más de una medida de diversidad, es necesario garantizar primero su estandarización, de forma tal que todas se ubiquen en un mismo intervalo y alcancen la mayor diversidad hacia un mismo extremo de dicho intervalo; y segundo utilizar alguna función que agrupe cada uno de estos valores en uno solo.
3.1. Estandarización de las medidas de diversidad
Para llevar cada una de las medidas anteriores a un mismo intervalo, se puede emplear la siguiente transformación lineal. Sea el intervalo (a; b) y x un real cualquiera. La representación de x en el intervalo (a; b) está dada por la fórmula:
Luego, la transformación del extremo del intervalo en el que alcanzan la diversidad a otro puede hacerse restando la medida estandarizada al extremo más a la derecha. O sea, si fuese en el intervalo (0; 1) sería 1- x'.
3.2. Agrupamiento de las medidas en un solo valor
Para combinar varias medidas de diversidad y obtener un solo valor pudieran utilizarse los operadores que se muestran en la Tabla 5.
Tabla 5 Operadores para combinar medidas de diversidad
| Operador | Descripción |
|---|---|
| Promedio | Calcula el promedio de un conjunto de medidas |
| Máximo | Determina el máximo de un conjunto de medidas |
| Producto | Calcula el producto de un conjunto de medidas |
| Operador borroso (Fuzzy operator) | Utiliza los conceptos de Inteligencia Artificial referentes a los conjuntos borrosos 21,9. |
Combinar varias medidas de diversidad puede ser un método interesante de aplicar porque puede dar una idea de cómo se comporta la diversidad teniendo en cuenta varios criterios que reflejen cuán diversos son los clasificadores individuales. La primera forma de lograr lo anterior pudiese ser calculando el promedio de las medidas de diversidad, resumiéndose en un valor que indique de forma general la diversidad contenida entre los clasificadores. Otro pudiese ser determinar el producto y el máximo de las medidas usadas. Como tal este último no es una forma de combinación pero resulta útil ya que no se sabe de antemano cuál medida es la más adecuada en términos de diversidad para el multi-clasificador y no necesariamente la misma medida tiene que ser la más diversa en todas las combinaciones de clasificadores que se formen.
El operador Fuzzy trabaja con los conceptos de conjuntos borrosos y funciones de membrecía de la teoría de la lógica difusa. En la combinación de varias medidas de diversidad, se propone la utilización de dos conjuntos borrosos definidos por los términos lingüísticos "baja diversidad" y "alta diversidad". Las funciones de pertenencia usadas fueron las triangulares 21.
A continuación se detalla la modelación de la meta heurística Algoritmo Genéticos para la construcción de un multi-clasificador que garantice la diversidad en el conjunto de clasificadores combinados y una mayor exactitud en la solución.
4. Modelación del problema
En muchas aplicaciones reales de la actualidad, sobre todo en el campo de la bioinformática y quimio-informática, se cuenta con grandes grupos de clasificadores individuales y es muy difícil seleccionar la mejor combinación de ellos pues mientras mayor sea la cantidad de clasificadores individuales, mayor cantidad de combinaciones se hacen posibles y por tanto se hace más difícil explorar todo el espacio de búsqueda, lo que nos conlleva a un problema combinatorio, los cuales son comúnmente resueltos mediante el uso de alguna meta heurística.
Nuestro problema consiste en lograr combinar un conjunto de clasificadores que supere la mejor exactitud individual en la clasificación y a la vez sean lo más diverso posible entre ellos.
Por tanto, lo que se quiere optimizar es la exactitud en la clasificación del conjunto de clasificadores y a la vez la diversidad existente entre dichos clasificadores, dicha diversidad puede ser cuantificada mediante las medidas de diversidad descritas en las secciones anteriores.
A continuación se muestra la función a optimizar:
donde x representa el conjunto de clasificadores y se pretende maximizar el valor de f(x) , es decir, obtener la combinación de clasificadores donde la exactitud y la diversidad sean la mayor posible.
En nuestro problema tenemos las siguientes restricciones:
Ex > Ei , es decir, la exactitud del conjunto de clasificadores Ex debe ser superior a la mejor exactitud individual Ei .
║x║ ≥ 2, es decir, la cardinalidad del conjunto de clasificadores debe ser mayor o igual a 2, pues no tendría sentido un conjunto de un solo clasificador.
4.1. Configuración con algoritmos genéticos
Luego de realizado un estudio de los métodos heurísticos más comunes la razón de la selección de esta meta heurística se basa en la facilidad de la modelación del problema con la misma respecto a las demás.
La configuración del algoritmo genético depende mucho del tipo de problema al que se le va a dar solución.
Una vez definida la configuración y la representación de cada uno de los elementos necesarios, se procede a establecer los operadores genéticos que serán los encargados de que cada población evolucione, y en cuyo proceso debe encontrase la solución esperada.
Estos operadores deben responder a las restricciones del problema y, por tanto, deben ser en ocasiones adaptados.
El cromosoma será el encargado de representar las posibles soluciones del problema que se quiere resolver. En este caso, se trata de decidir qué clasificadores usar en el multi-clasificador de forma que se alcance una exactitud mayor que la ofrecida por los clasificadores individuales.
Además, se debe garantizar que esta combinación posea la mayor diversidad posible entre las predicciones de los clasificadores individuales. Por ello, se decide utilizar la representación basada en cadenas de bit donde un cromosoma Cx es configurado de la siguiente forma:
4.2. Descripción de la función objetivo
Esta función responde a la función de optimización definida anteriormente, donde ahora el conjunto de clasificadores está representado como un cromosoma (Cx). Por ello, la función que determina la calidad de un cromosoma x se define como:
donde el primero de los sumandos indica la exactitud del multi-clasificador al combinar los clasificadores que están contenidos en el cromosoma Cx y el segundo parámetro es el valor resultante de aplicar una medida de diversidad (o un conjunto de ellas) a los mismos clasificadores de Cx. Por tanto la función objetivo a través del proceso evolutivo será:
donde P es el tamaño de la población. Supuestamente, al finalizar el proceso evolutivo de la población, el individuo (o cromosoma) de mayor valor en la función objetivo deberá ser portador en sus genes de la mejor combinación que se está buscando. No obstante, en estudios previos a esta investigación se ha determinado que no necesariamente el incremento de la diversidad está acompañado de un aumento en la exactitud del multi-clasificador. De ahí que, en muchos casos se van a obtener valores en esta función que dicen que la combinación que ofrece ese cromosoma es la mejor; sin embargo, cuando se analiza solamente la exactitud se puede apreciar que no supera la mejor exactitud de los clasificadores individuales.
Esto se debe a que pueden darse casos en que el primer parámetro de la ecuación 19 sea pequeño y el valor de f(Cx) sea muy alto porque existe una gran diversidad entre los clasificadores.
Por la problemática anterior, se agregó la restricción número 1 donde se obliga a que la exactitud del conjunto de clasificadores de la solución supere la mejor clasificación individual.
4.3. La población como objeto evolutivo: elementos principales
El análisis de la población incluye varios elementos. Goldberg obtuvo en su investigación que el tamaño óptimo de una población de cadenas binarias, crece exponencialmente con la longitud de la cadena 22. Sin embargo, en diferentes resultados empíricos muchos autores sugieren tamaños de poblaciones tan pequeños como 30 individuos. La modelación que se propone utiliza el tamaño de la población igual a 2L/2 donde L es la cantidad de clasificadores; o sea, el tamaño del cromosoma.
La población inicial se genera usando un híbrido entre la generación aleatoria y el sembrado de individuos. Cada cromosoma se genera aleatoriamente, tomando cada gen valor 0 ó 1 en dependencia de un número r generado aleatoriamente; si r es mayor que 0.5 se incluye el clasificador representado por el i-ésimo gen; en caso contrario, no se incluye.
En experimentos realizados en 23 se evidencia que el clasificador de mayor exactitud, era incluido en el conjunto de clasificadores usado por el multi-clasificador. Es por eso que una vez generado el cromosoma de la forma anterior, se debe obligar además a que los mejores clasificadores se incluyan en la combinación, poniendo el gen correspondiente con valor 1.
En caso de que más de la mitad de los clasificadores tengan la misma exactitud y a la vez sea la mayor solo se incluirán en la combinación la mitad del total de clasificadores que estén en esas condiciones.
Cada iteración simple del AG se inicia con una población con la cantidad especificada anteriormente. Los nuevos cromosomas generados a partir de los operadores genéticos de recombinación serán agregados a la población.
Finalmente la población será "limpiada" de aquellos cromosomas que probabilísticamente son los de menor valor en la función objetivo, hasta quedarse con el tamaño establecido. Dado que la modelación fue pensada para aplicar con cualquier cantidad de clasificadores, se restringió la posibilidad de que en la población existiesen cromosomas repetidos. Esto se debe a que en una primera versión, cuando se ejecutaba el algoritmo con pocos clasificadores y muchas iteraciones, el algoritmo tendía a estancarse a partir de determinada generación con todos los cromosomas iguales, perdiéndose la posibilidad de explorar soluciones no vistas hasta el momento.
Una vez generada la población inicial se forma una población intermedia mediante el operador de selección, y sobre esta población se aplican determinados operadores para obtener nuevos individuos y con mejor adaptabilidad expresada en términos de la función objetivo. Cada individuo es seleccionado, en dependencia de su calidad, para competir en el proceso evolutivo. A partir de estos cromosomas seleccionados, son creados nuevos cromosomas por medio del cruzamiento y la mutación, pudiéndose incluir o no en la nueva población. A continuación se explican brevemente los operadores utilizados para simular la recombinación genética y el mecanismo de selección natural.
4.4. Operador de cruzamiento
En el caso del cruzamiento, se permite seleccionar fragmentos del genotipo de cromosomas que independientes no son muy buenos pero que al mezclarlos pueden resultar en una solución mejor que la que se tenía. Según la bibliografía consultada, existen varias formas de definir este operador. En la modelación se tuvo en cuenta el operador clásico de cruzamiento en un punto y el cruzamiento uniforme 24.
Si cuando concluya el proceso de recombinación genética por medio del cruzamiento, los nuevos cromosomas ya existían en la población, se fuerza a que ocurra una mutación para obtener cromosomas nuevos y diferentes.
4.5. Operador de mutación
La implementación de este operador es muy sencilla dado que solamente se tiene que intercambiar el alelo del gen que se va a mutar. Así, si en un cromosoma el quinto gen indica que ese clasificador estaba incluido en la combinación, luego de aplicar una mutación en ese locus resultaría que ese clasificador ya no se incluye en la combinación.
4.6. Operador de selección natural
En este proceso se forma una población intermedia de cromosomas sobre los cuales se aplicarán los operadores anteriores para obtener una nueva población, con cromosomas de más calidad que los existentes. Para la selección de los cromosomas que formarán parte de esta población intermedia se usa la función objetivo, la que evaluada en cada uno de los individuos determinará su selección para participar en la recombinación genética.
Una vez formada la población intermedia, se aplican los operadores de mutación y cruzamiento atendiendo a la probabilidad de que puedan ocurrir o no, y los cromosomas resultantes se agregan a la población original. Teniendo en cuenta las características del problema que se quiere solucionar el proceso de selección se divide o ejecuta en dos momentos; antes de efectuar la recombinación y después de haberla aplicado. La primera se hace con el objetivo de que solo los mejores individuos sean los que se reproduzcan y la segunda es debida a que los individuos nuevos, dentro de la población original, pueden o no tener las capacidades adaptativas para sobrevivir a la próxima generación y por tanto, algunos de ellos son desechados.
En la primera selección se toman los cromosomas de mayor valor en la función objetivo de la población inicial y en la segunda selección se aplica el método de la ruleta sobre la población aumentada con los cromosomas resultantes de aplicar la recombinación genética; de forma que se reduzca su tamaño al tamaño especificado en el sub-epígrafe 4.3, no permitiéndose en este caso la selección de un mismo cromosoma más de una vez. Más información sobre el método de la ruleta puede encontrarse en 25.
5. Experimentos y resultados
A continuación se muestra cómo, utilizando la modelación de AG propuesta para construir un multi-clasificador, se hace un estudio del resultado de las medidas de diversidad, de los operadores que se proponen para combinarlas y de su valor predictivo en la construcción de un sistema multi-clasificador.
Los resultados principales, con respecto a los operadores que se proponen para combinar las medidas se resumen en la Tabla 9, mientras que analizando el comportamiento individual de las medidas se destacaron las medidas DF y DIF por encima de las demás.
Para evaluar el comportamiento de las combinaciones de medidas de diversidad que se proponen se decide aplicar un experimento en el que se estudia la correlación existente entre todas las combinaciones posibles de un conjunto de medidas y las combinaciones posibles de un conjunto de clasificadores, definido en la Tabla 6.
Tabla 6 Conjunto de clasificadores del experimento
| Nombre de clasificadores |
|---|
| weka.classifiers.bayes.NaiveBayes |
| weka.classifiers.functions.Logistic |
| weka.classifiers.lazy.IBk |
| weka.classifiers.trees.J48 |
| weka.classifiers.functions.MultilayerPerceptron |
| weka.classifiers.trees.ADTree |
Dichos modelos de clasificación fueron tomados todos del WEKA1, al igual que el multi-clasificador usado fue el "Vote" también tomado desde esta plataforma.
Además se seleccionaron todas las medidas de diversidad implementadas y enunciadas anteriormente, las reglas de combinaciones utilizadas fueron: promedio, máximo y producto de los valores de diversidad y el operador Fuzzy.
Se utilizaron nueve bases de datos del Repositorio de Aprendizaje Automático de la Universidad de California, Irvine-UCIML2, ver Tabla 7.
Tabla 7 Bases de datos usadas en los experimentos
Como puede apreciarse las bases son diferentes entre sí: dos tienen rasgos numéricos, otras tres tienen rasgos nominales y cuatro presentan combinación de ellos. Todas tienen dos clases. La cantidad de casos varía también en las bases de datos, desde bases con 132 casos hasta bases con 1000 casos. Todas son bases binarias.
En total se calcularon 16369 combinaciones de medidas en 57 combinaciones de clasificadores por cada una de las 10 bases. Una vez obtenido todos los datos necesarios, se determinó el máximo y el mínimo de las correlaciones en cada base utilizada y en cada combinación de medida.
Luego de haber determinado el coeficiente de correlación de Pearson para cada una de las combinaciones de medidas de diversidad y con cada combinación de clasificadores del conjunto definido en la Tabla 6, se determinó el máximo y el mínimo de estos en cada base por cada regla de combinación.
La Tabla 8 muestra un análisis descriptivo aplicado a estos resultados. Según los valores de la desviación estándar, las combinaciones Promedio, Producto y Máximo de los valores de diversidad, estuvieron más dispersos en su intervalo; mientras que el operador Fuzzy mostró pequeños valores en ese sentido, significando que las correlaciones determinadas en este operador estuvieron muy cercanas a la media aritmética. Si tenemos en cuenta que en este operador el valor de la media fue de 0.717 y -0.752 en las correlaciones positivas y negativas respectivamente, entonces se puede decir que con el operador Fuzzy se obtienen valores de diversidad que demuestran una buena correlación tanto positiva como negativa con respecto a la exactitud del multi- clasificador.
Tabla 8 Estadísticos descriptivos de los valores máximos y mínimos de la correlación de Pearson obtenidos en cada una de las reglas de combinación
| ρ | Regla de combinación | Estadísticos | |||
| Mínimo | Media | Máximo | Desv. Estándar | ||
| + | AVG | 0.170 | 0.550 | 0.854 | 0.261 |
| PROD | 0.162 | 0.548 | 0.857 | 0.266 | |
| MAX | 0.253 | 0.618 | 0.926 | 0.228 | |
| Fuzzy | 0.717 | 0.900 | 0.110 | 0.110 | |
| - | AVG | -0.609 | -0.256 | 0.149 | 0.149 |
| PROD | -0.650 | -0.273 | 0.159 | 0.159 | |
| MAX | -0.648 | -0.280 | 0.149 | ||
| Fuzzy | -0.752 | -0.538 | 0.113 | ||
Sin embargo, sería bueno determinar cuáles de las medidas de diversidad son las más factibles de usar para obtener los resultados anteriores. Utilizando el Promedio como la regla de combinación de los valores de diversidad se determinó que en seis, de las 9 bases de casos, la máxima correlación positiva se obtenía combinando las medidas DF (doble fallo) y DIF (medida de dificultad) obteniéndose una media 0.672 en los valores resultantes de aplicar este operador y con una desviación estándar de 0.255.
Algo parecido sucedía en la combinación de las medidas DIF y VAR (medida de variabilidad). Se determinó además, que en cuatro de las bases si DF se combinaba con E (Entropía) se obtenía que mientras aumentaba la diversidad disminuía la exactitud del multi-clasificador (correlación negativa). En menor medida sucedía lo mismo combinando E y KW (Kohavi-Wolpert).
Utilizando el Producto de los valores de diversidad se encontró que en siete de las bases mientras aumentaba la diversidad aumentaba la exactitud del sistema multi-clasificador usando las medidas DIF y DF, obteniéndose valores con una media de 0.629 en los valores resultantes de aplicar este operador y una desviación estándar de 0.265. Además, se obtuvo en algunos casos que al igual que la regla de combinación anterior la utilización de DIF y VAR tienen una correlación positiva con la exactitud. En cuanto a la correlación negativa, en tres de las bases la utilización de las medidas E y DF producen valores bajos en la correlación, al igual que la utilización de DIF y E.
Calculando el Máximo de los valores de diversidad, se obtuvo que en ocho de las bases la medida DIF fue la que aportó más diversidad al multi-clasificador en cualquier combinación que se probara, siempre que DF no estuviera presente, no sucediendo lo contrario cuando DF se incluía. La dispersión de los valores de correlación fue de 0.243 con respecto a una media aritmética de 0.588. A pesar de ello la máxima correlación (0.848) fue obtenida en la base Echocard usando DF en cualquier combinación de GD (diversidad generalizada), CFD (diversidad de coincidencia de fallos), DFD (diversidad de distintos fallos), VAR y OD (diversidad global) o en cualquier combinación de k (desacuerdo entre expertos), KW, D (medida de diferencias), Q (estadístico q) y E. En relación a la correlación negativa no hubo una combinación de medidas que destacara por encima de otras. Solo decir que las medidas que más se incluían en las combinaciones de mayor correlación negativa con la exactitud fueron KW (aparecía en todas las bases), Q y D.
Por último, con el operador Fuzzy no se obtuvo ninguna combinación común en las bases que indicara una correlación positiva. No obstante, teniendo en cuenta las características vistas con los estadísticos descriptivos, las combinaciones de medidas que fueron aplicadas con este operador, por lo general, establecen una buena correlación positiva.
Además, en dichas combinaciones había una fuerte presencia de las medidas en forma de pares.
Igual situación ocurre en la correlación negativa, ya que no fue precisa la existencia de una combinación de medidas que determinara una correlación negativa.
No obstante, en tres de las bases se obtuvo una correlación media de -0.76 usando las medidas DIF y DF. Al contrario de la correlación positiva, en este caso muchas de las medidas que se encontraban en las combinaciones eran medidas grupales y si había alguna pareada era DIF o Q.
Se muestra la Tabla 9 con los principales resultados vistos anteriormente, donde Sol representa el conjunto de medidas combinadas.
Tabla 9 Análisis de correlación entre la exactitud del multi-clasificador y la combinación de medidas de diversidad con cada operador
| Operador | Correlación positiva | Correlación negativa |
|---|---|---|
| Promedio | DF y DIF | DF y E |
| DIF y VAR | E y KW | |
| Producto | DF y DIF | DF y E |
| DIF y VAR | E y DIF | |
| Máximo | (DIFe Sol ) | KW ∈ Sol |
| && DF ∉ Sol | ||
| Operador Fuzzy | Mayor presencia de medidas pareadas | Mayor presencia de medidas grupales |
5.1. Comportamiento individual de las medidas de diversidad
En el mismo se observó la prevalencia de algunas medidas como DIF, KW y DF.
Es por eso que se decide diseñar un experimento en el que se calculan todas las medidas de diversidad para todas las combinaciones de clasificadores de los conjuntos definidos en la Tabla 10 y la Tabla 11, donde los mejores resultados se encontraron con la medida pareada DF y la medida no pareada DIF, lo cual se corrobora con las figuras mostradas más adelante en este epígrafe.
Tabla 10 Conjunto de 12 clasificadores usados
| Nombre de clasificadores |
|---|
| weka.classifiers.bayes.NaiveBayes |
| weka.classifiers.functions.Logistic |
| weka.classifiers.lazy.IBk |
| weka.classifiers.trees.J48 |
| weka.classifiers.functions.MultilayerPerceptron |
| weka.classifiers.trees.ADTree |
| weka.classifiers.functions.SGD |
| weka.classifiers.trees.RandomTree |
| weka.classifiers.functions.SMO |
| weka.classifiers.lazy.KStar |
| weka.classifiers.functions.VotedPerceptron |
| weka.classifiers.bayes.BayesNet |
Tabla 11 Conjunto de 18 clasificadores usados
| Nombre de clasificadores |
|---|
| weka.classifiers.trees.FT |
| weka.classifiers.lazy.LWL |
| weka.classifiers.bayes.BayesNet |
| weka.classifiers.trees.RandomForest |
| weka.classifiers.lazy.IBk |
| weka.classifiers.functions.SPegasos |
| weka.classifiers.trees.REPTree |
| weka.classifiers.bayes.NaiveBayes |
| weka.classifiers.functions.Logistic |
| weka.classifiers.lazy.IBk |
| weka.classifiers.trees.J48 |
| weka.classifiers.functions.MultilayerPerceptron |
| weka.classifiers.trees.ADTree |
| weka.classifiers.functions.SGD |
| weka.classifiers.trees.RandomTree |
| weka.classifiers.functions.SMO |
| weka.classifiers.lazy.KStar |
| weka.classifiers.functions.VotedPerceptron |
Dichas medidas fueron calculadas a partir de los resultados de la clasificación hecha en las bases Breast-C Wisconsin, Echocard y German Credit, por ser estas bases ejemplos extremos de los resultados obtenidos; es decir, en Breast-C Wisconsin nunca se obtuvo un multi-clasificador cuya exactitud superase la exactitud individual, en Echocard no se obtienen mejoras en el conjunto de seis clasificadores (ver Tabla 6) pero al aumentar a 12 y 18 clasificadores sí se encuentran mejoras y en German Credit se encuentran buenas soluciones en cualquiera de estos conjuntos sin coincidir entre sí.
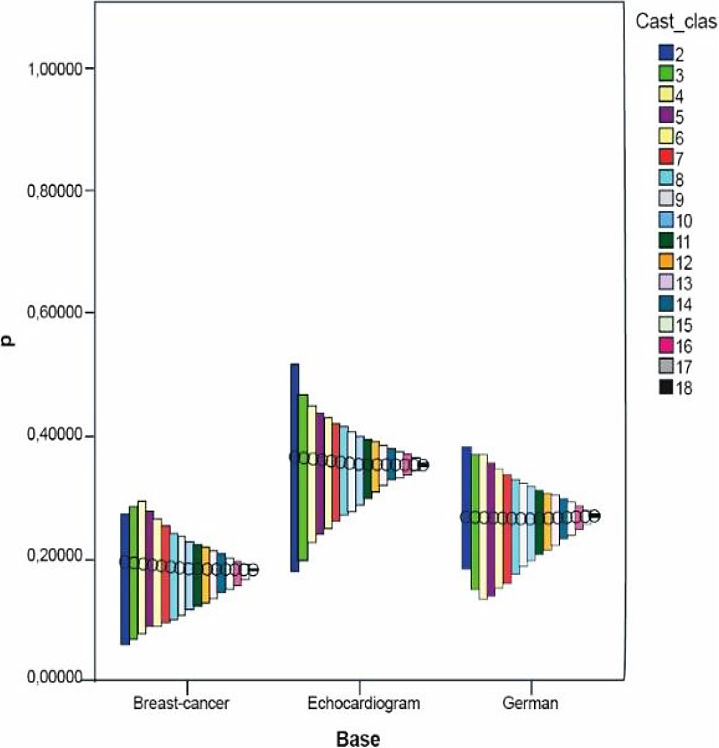
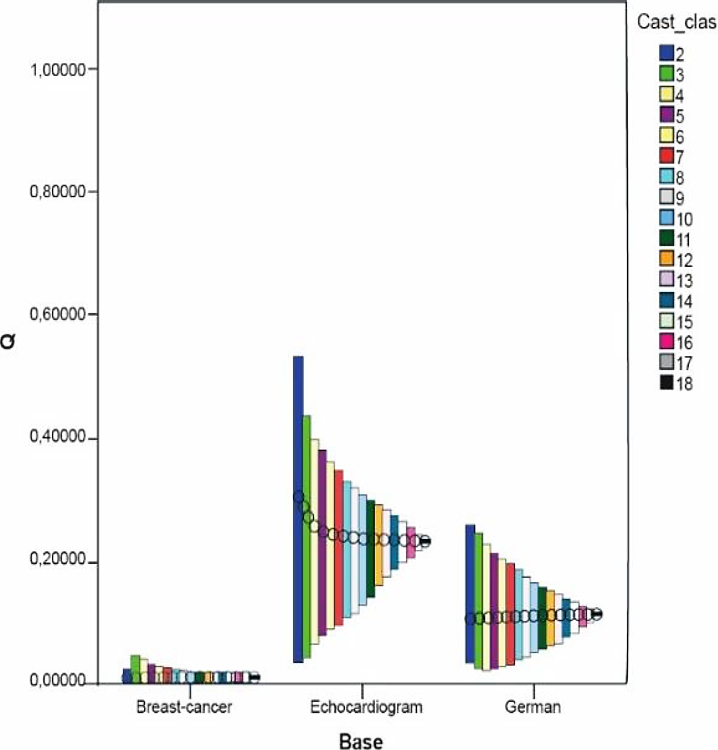
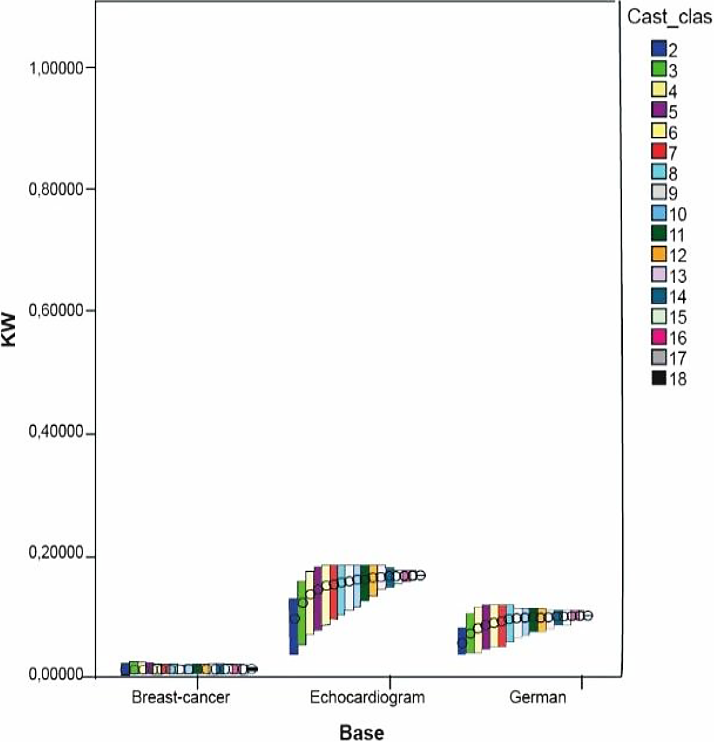
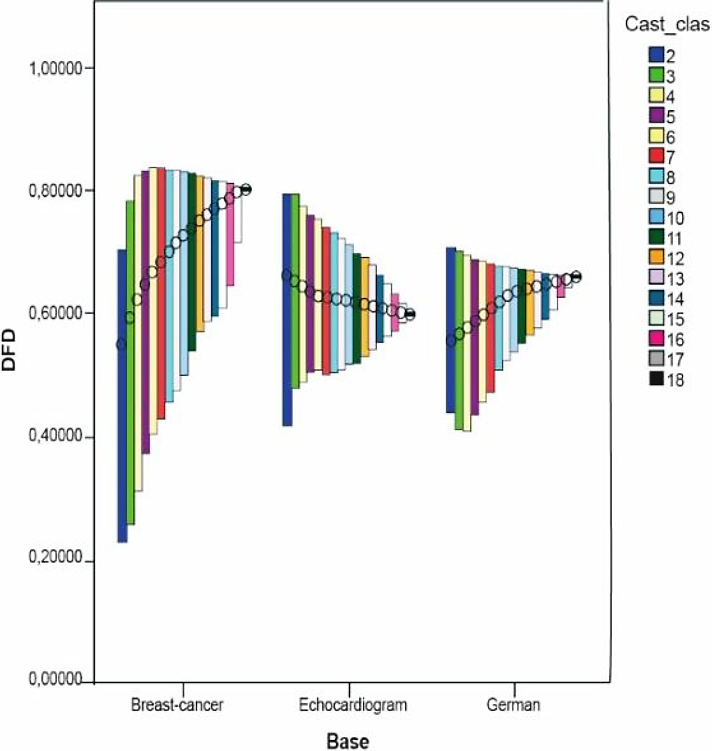
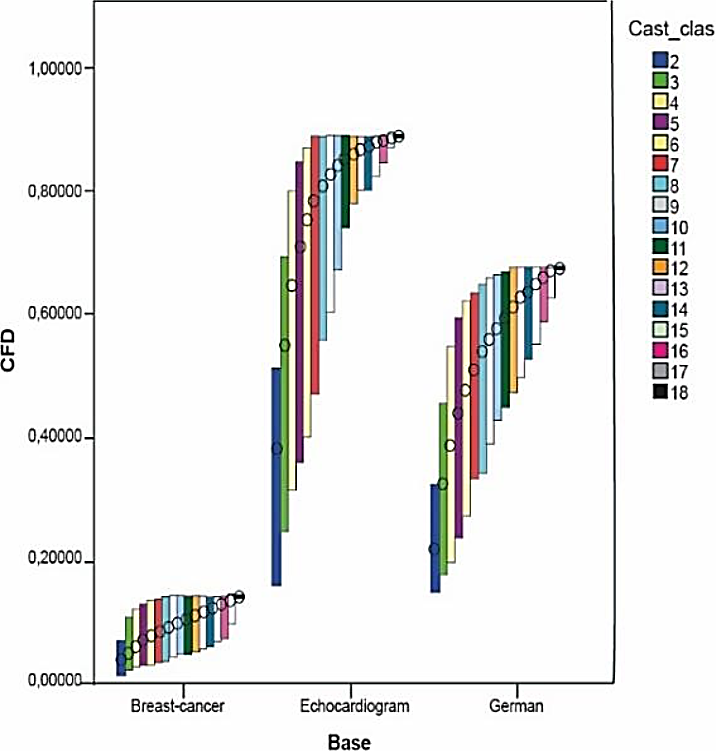
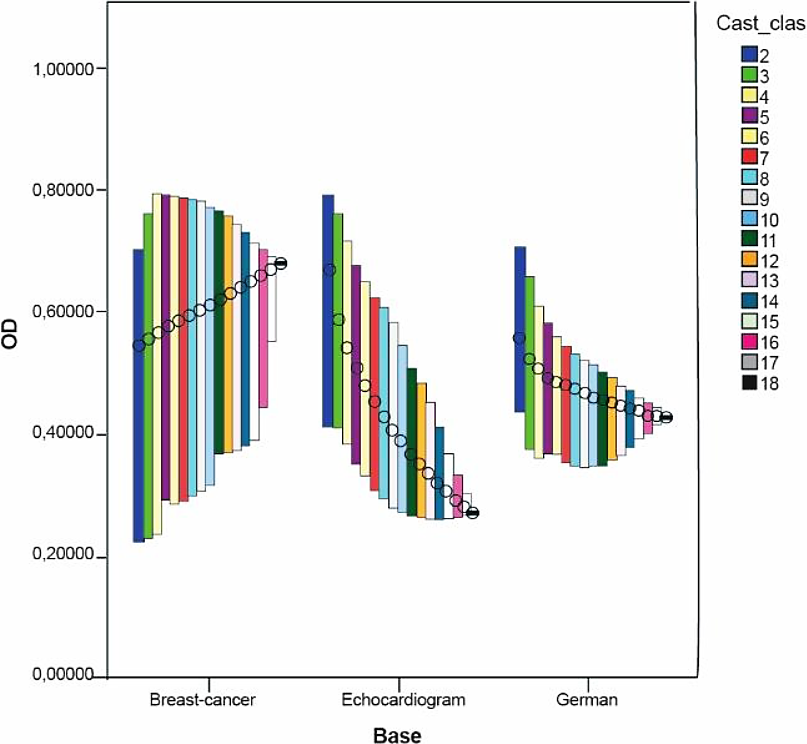
El análisis fue establecido utilizando los gráficos de Máximos-Mínimos-Cierre el cual resulta útil para mostrar el intervalo de una variable comprendido entre dos valores. En este tipo de gráficos se usa una barra de rangos que es dibujada entre los valores máximos y mínimos de una variable. Adicionalmente, se puede especificar dibujar el cierre que normalmente es determinado con una medida de tendencia central. En nuestro caso se usó la media de los valores de la variable.
Se estudió el comportamiento de las medidas de diversidad en cada una de las bases según la cantidad de clasificadores. Los resultados de todas las medidas se muestran en las siguientes figuras mostradas.
Se puede observar en las figuras como tendencia que en las tres bases mencionadas anteriormente no se obtienen muy buenos valores de diversidad excepto en las medidas DF y DIF.
En las tres bases, mientras aumenta el número de clasificadores el rango en el que se mueven los valores de diversidad se reduce y en la mayoría de las medidas disminuye su media. Excepto en las medidas DF, DIF y VAR, se observó lo anterior. Esto puede deberse a que según aumenta el número de clasificadores, la formulación matemática de cada medida conduce a valores más pequeños, lo cual requiere de un estudio más preciso de las particularidades matemáticas de dichas medidas.
En el caso de las dos últimas bases la diversidad mantuvo el mismo comportamiento; es decir, en todas era menor o viceversa.
En el caso de la base Breast-C Wisconsin los resultados fueron heterogéneos pues en la mayoría de las medidas se obtienen valores muy pequeños de diversidad en intervalos donde el valor de la media desciende mientras que se obtiene en medidas como DF y DIF que la diversidad sobrepasaba a 0.9 y los valores presentan una desviación estándar cerca de 0.0017; sin embargo en otras medidas como CFD, DFD y OD la media de los valores de diversidad ascendió y el rango en el que se movieron dichos valores fue un poco mayor. No obstante, a pesar de esto no fue posible encontrar una combinación de clasificadores que mejorara la mejor exactitud individual utilizando esta base, donde también influye que la mejor exactitud individual obtenida en ella por un solo clasificador fue del 98 %, lo cual constituye un valor suficientemente bueno y alto para ser mejorado.
6. Conclusiones
Se presentan en este trabajo las medidas de diversidad existentes para conocer la diversidad en un conjunto de clasificadores, además se muestra la modelación de la meta heurística Algoritmos Genéticos para construir sistemas multi-clasificadores que garanticen diversidad en el conjunto de clasificadores y una mayor exactitud en la solución. También se exponen dos experimentos en los que se analiza el comportamiento individual de las medidas de diversidad y su combinación con alguna regla de las que se proponen.
En esto último, el operador Fuzzy resultó ser el que aporta valores de diversidad altamente correlacionados con la exactitud del multi-clasificador.
Se destacan además, algunas medidas que reinciden en algunas combinaciones cuando se utilizó el promedio o el producto de los valores de diversidad. De igual forma dichas medidas presentaron altos valores de diversidad cuando se analizaron individualmente.
Sin embargo, en algunas bases de casos el comportamiento de las medidas de diversidad no es el mismo.











 text new page (beta)
text new page (beta)