1 Introduction
Millions of people in North America live with varying degrees of irreversible vision loss because they have an untreatable, degenerative eye disorder, which affects the retina. In these conditions, the delicate layer of tissue that lines the inside back of the eye is damaged affecting its ability to send light signals to the brain. When the blood vessels are damaged by high blood sugar levels and initially become defective, later they may become blocked off. The defective vessels can lead to hemorrhages (spots of bleeding), fluid and exudates (fats) to escape from the blood vessels over the retina. The blocked vessels can starve the retina from oxygen (ischaemia), leading to the growth of new abnormal vessels in the retina 1.
Actually, there are several screening eye exams that help to find any illness, among the exams are amsler grid, autofluorescence, dilated eye exam, fundoscopy or ophthalmoscopy, eye fundus photography, fluorescence angiography, optical coherence tomography (OCT), and tonometry 2, 3. In recent researches diverse techniques like the Hough transform, mathematical morphology techniques, illumination correction and histogram equalization 4, 5, 6, 7, 8, 9, 10 have worked in eye fundus photography to find blood vessels, exudates, and hemorrhages. Other works enhance the image and detect edges using Gaussian filters, the watershed transform, and the Canny edge finder 11, 12, 13, 14. More recently, the use of spatial frequency filters as edge detector has been reported in 15, 16.
In this paper, we use the databases DIARETDB0 and DIARETDB1 (Standard Diabetic Retinopathy Database Calibration Level {0,1}) from Lappeenranta University (Finland). We remark that the image data contained in these databases were clinically validated by several experts. Each image in these databases has a size of 1152 x 1500 pixels. Knowing that the area of the optic disk is 2.47 mm2 (radius = 0.88 mm), the corresponding approximate spatial resolution is of 4.746μm per pixel 17.
The purpose of this work is to extract exudates and blood vessels in eye fundus color images. Basically, our proposal consists of the following steps. First, a binary image mask is created to obtain the boundary of the eye fundus in the acquired color image by clipping the effective area taken by the camera. Second, an homomorphic filter in the Fourier domain and in the discrete cosine transform (DCT) 18 domain are applied to homogenize the image illumination, after which a super-Gaussian bandpass filter in the frequency DCT domain is proposed and applied to distinguish between foreground objects and the corresponding eye fundus image background. Third, two procedures are proposed for the different types of pathologies mentioned earlier.
The first procedure that determines exudates employs a gamma correction to enhance contrast, the Otsu's global threshold method is applied to binarize the image, and a logical operation between the binary mask and the thresholded image is realized to get the segmented image. The second procedure is for blood vessels, in which we first use the negative of the filtered image, then a median filter to reduce noise and artifacts is applied, also a gamma correction is applied to enhance contrast, and image thresholding (Otsu's method) is performed using global statistics to obtain the desired object regions including their edges. Segmentation of the blood vessels is obtained applying a morphological closing and a logical operation between the binary mask and the thresholded image.
The paper is organized as follows: Section 2 explains in detail the different image processing steps involved in the proposed frequency filtering based method for the segmentation of the aforementioned pathologies and several representative examples are provided. In Section 3 we present the segmentation results obtained including our segmentation algorithm in pseudocode format. We close the paper with Section 4 of conclusions and some pertinent comments.
2 Segmentation of Exudates and Blood Vessels
2.1 Theoretical Background
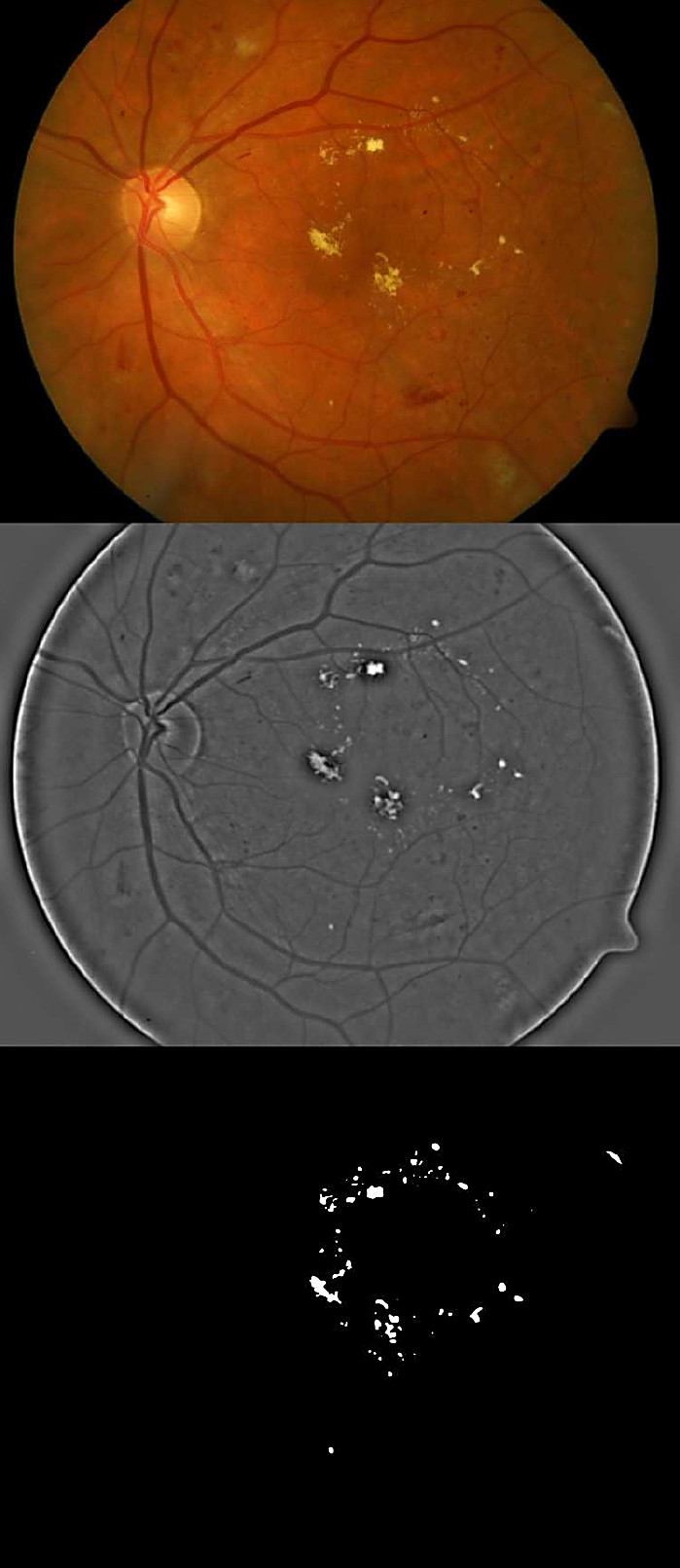
A binary mask is build to delete the effective area taken by the eye fundus camera. The corresponding Algorithm 1 is given next and an example of a mask is shown in Fig. 1.
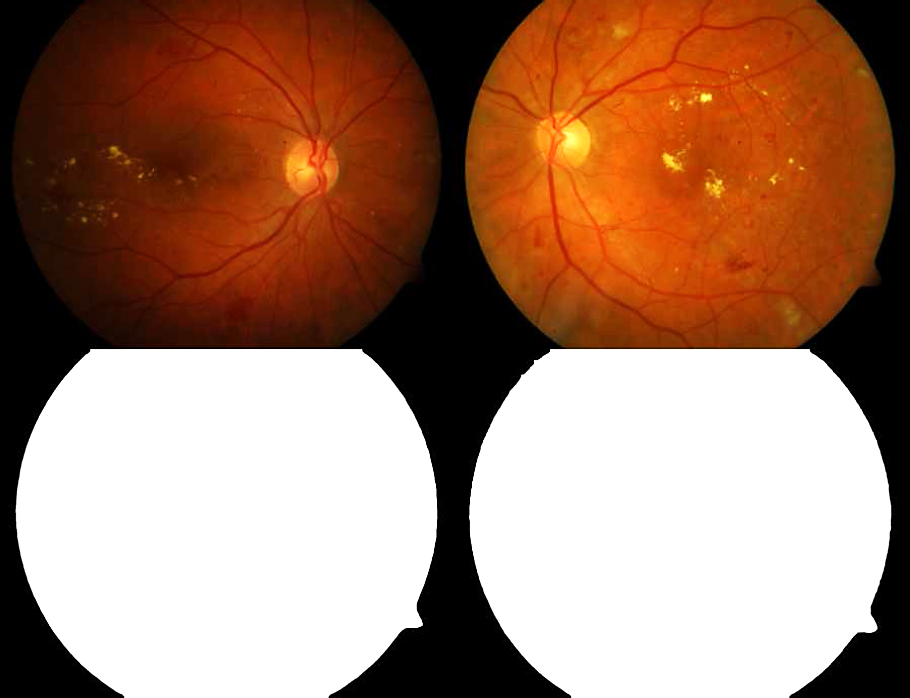
Fig. 1 Top: original eye fundus color images (right eye and left eye). Bottom: eye fundus binary masks
In a segmentation process it is possible to discriminate objects of interest from the background by dividing the image in regions that satisfy certain conditions 19. In general, due to the presence of non-uniform illumination in eye fundus images, we propose the use of a Fourier or DCT homomorphic filter to homogenize illumination.
The discrete cosine transform (DCT) is a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies and amplitudes. DCTs are important to numerous applications in science and engineering. Formally, the DCT is a linear, invertible function in the real domain ℝ2 to the real domain ℝ2, which is also equivalent to an array of M x N elements. The two dimensional DCT is given by:
where,
Recall that the two dimensional discrete Fourier transform (DFT) is given by
where, f(x, y) is an image of size M x N, u = 0, 1, .., M - 1, and υ = 0, 1, .., N - 1 for both transforms. Also, f(x, y) is multiplied by (-1)(x+y) to center the transform that is computed with a Fast Fourier Transform (FFT) algorithm.
In each case the filtered image, denoted by g(x, y), is computed as follows:
where, IDFT is the inverse discrete Fourier transform, F(u, υ) is the DFT of the input image f(x, y), and C(u, υ) is the inverse discrete cosine transform IDCT of the input image f(x, y), using Eq. 1, with u, v changed by x, y, respectively, and H(u, υ) is a specific homomorphic filter in the Fourier or DCT domain. For numerical computation, the functions C, F, H, and g are matrices of the same size as the given image. A high pass Butterworth homomorphic filter (HF) is defined as
where, γL < 1, γH > 1, and n (filter order) is the slope of the function between the given gamma bounds. The particular values we use for filtering with Fourier the eye fundus color images are γL = 0.75, γH = 1.75, n = 2, and D0 = 10 for the cutoff spatial frequency. The values used for filtering the eye fundus color images with DCT are γL = 0.75, γH = 1.75, n = 2, and D0 = 20 for the cutoff spatial frequency. An example of illumination correction for an RGB color image is shown in Fig. 2.
Fig. 2 Top: example color image. Middle: illumination corrected color image with DFT. Bottom: illumination corrected color image with DCT
We introduce a super-Gaussian function 20 as a novel filter for processing images in the frequency domain. The advantages of the use of this filter is explained next in comparison with a Butterworth filter.
In Fig. 3, we show several Butterworth bandpass and super-Gaussian bandpass filter profiles of different orders in the DCT domain, the specific parameters values are D0 = 200 (cutoff frequency), and W = 150 (bandwidth) for both filters. As we can see on the given graphs, the bandwidth value is better delimited with the super-Gaussian filter (i.e., a better selective bandwidth), hence, its curve is more sharpened than the Butterworth filter profile. We remark, that the values of D, D0, W are in pixels.
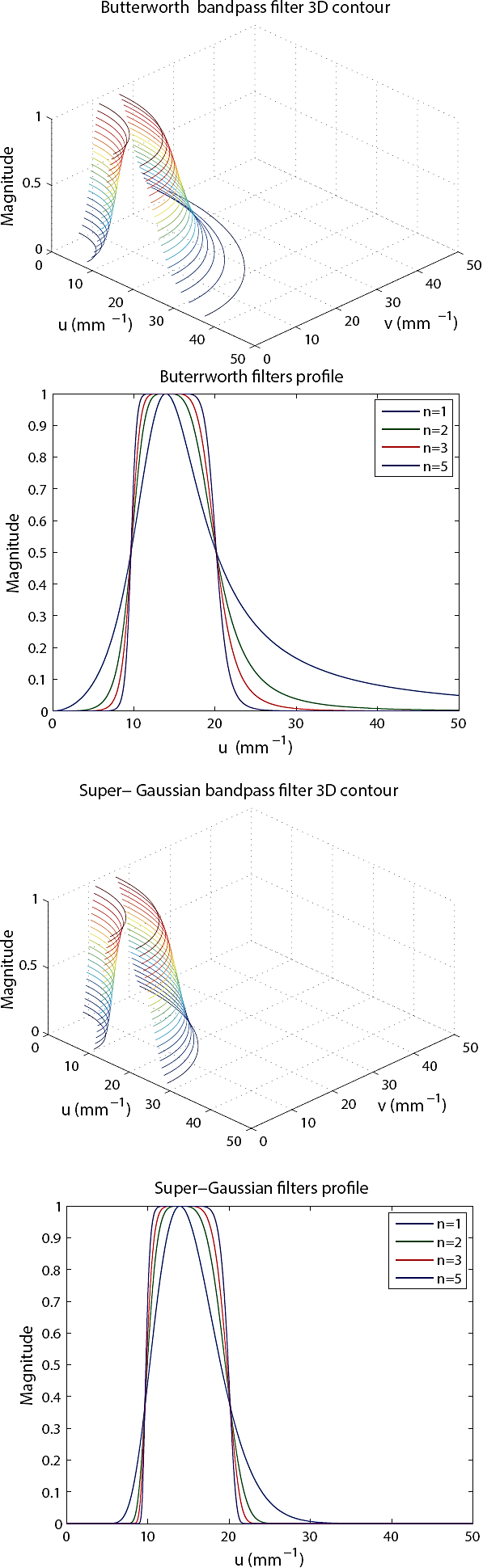
Fig. 3 From top to bottom: Butterworth bandpass filter 3D contour (n = 2), Butterworth filter profiles, super-Gaussian bandpass filter 3D contour (n = 2), and super-Gaussian filter profiles
We can observe in Fig. 2 that the homomorphic filtered image using the DCT is better, because its illumination is more uniform than the DFT filtered image. For that reason we will work with the DCT instead of the DFT filtered image.
Once the illumination is corrected, the segmentation process is facilitated by filtering with the discrete cosine transform to intensify the foreground objects against the surrounding background of the corresponding green channel in a given eye fundus color image. The proposed super-Gaussian bandpass (SGBP) filter is given by:
where, n is the order of the filter, W is the bandpass width,
The filtering stage based on the DCT is the same for segmenting exudates as well as blood vessels. The specific steps to segment each type of pathology is described in the following subsections.
2.2 Segmentation of Exudates
For this type of pathology, we apply on image gscBP a 3 x 3 median filter with the purpose to emphasize exudates contrast. Then, a gamma correction is applied to med(gSGBP(x, y)) with value 2 and Otsu's method 19, based on global and local statistics, is used to calculate a global threshold value for the computed image.
In particular, the binary output image is determined as:
where, the subindex label E refers to exudates.
The segmented exudates image is found by masking the previous image with the initially binary mask M. That is to say, SE = BE ∧ M, where A is the logical AND operation. An illustrative example of exudates is displayed in Fig. 4.
2.3 Segmentation of Blood Vessels
In order to remark blood vessels, we take the negative of the previous filtered image computing. That is, gNSGBP(x, y) = (L - 1) - gSGBP(x, y), where L is the maximum value of the corresponding grayscale dynamic range. Then, as in exudates, we apply again on image gNSGBP a 3 x 3 median filter, with the purpose to emphasize contrast of blood vessels present in the image. Then a gamma correction is applied med(gNSGBP(x, y)) with value 2. In the next step, an image thresholding is performed using Otsu's method to obtain a binary image using the global threshold value provided by this method. Specifically, the binary output image is computed as:
where, the subindex label V refers to blood vessels.
A binary closing morphological operation 21 is used to connect object edges in the corresponding regions of BV(x, y), i. e., BV • S = (BV ⊕ S) ⊖ S, where the structuring element S is an isotropic square of size 3 x 3 pixels. Finally, the segmented image SV containing the blood vessels is obtained by masking the previous image. Hence, SV = BV ∧ M. An example is shown in Fig. 5. We remark that with this same technique, it is possible to segment simultaneously aneurysms which are localized blood filled balls of variable size in the wall of a blood vessel 22.
3 Image Segmentation Results
To test our proposed segmentation technique, we use six eyes fundus color images taken from the free domain databases DIARETDB0 and DIARETDB1. The first database consists of 130 eye fundus color images, of which 20 are normal and 110 contain signs of diabetic retinopathy (hard exudates, soft exudates, microaneuyrysms, hemorrhages and neovascularization). The database DIARETDB1 consists of 89 eye fundus color images, from which 84 images contain at least mild non-proliferate signs of diabetic retinopathy. The other 5 images are considered normal since these do not contain any signs of diabetic retinopathy, according to all experts who participated in the evaluation.
The eye fundus color images were captured using the same 50 degree field-of-view digital fundus camera with varying imaging settings 23. As mentioned earlier, each image has a size of 1152 x 1500 pixels, with an approximately spatial resolution of 4.756 micrometers per pixel. We remark that the global threshold value obtained by applying Otsu's method value is different for each image. Figures 6 to 11 show illustrative examples of exudates and blood vessels segmentations.
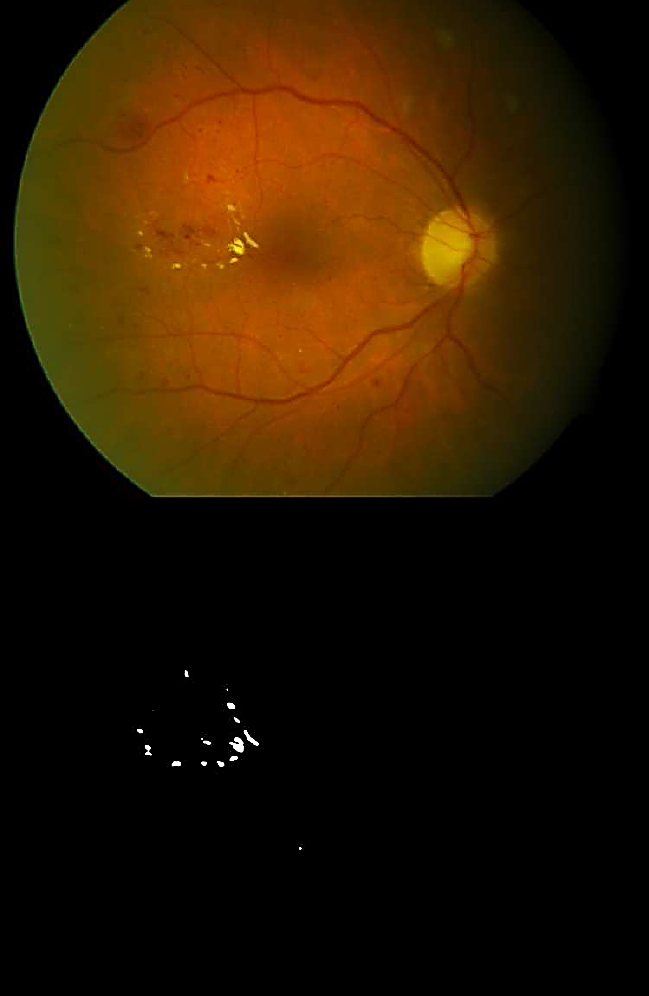
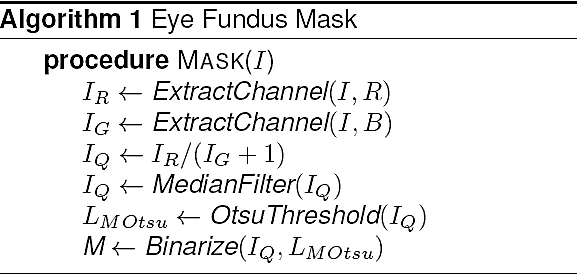
Fig. 6 Top: Eye fundus color image with hard exudates (database: diaretdb0_v1_1/image003). Bottom: Binary image with segmented hard exudates
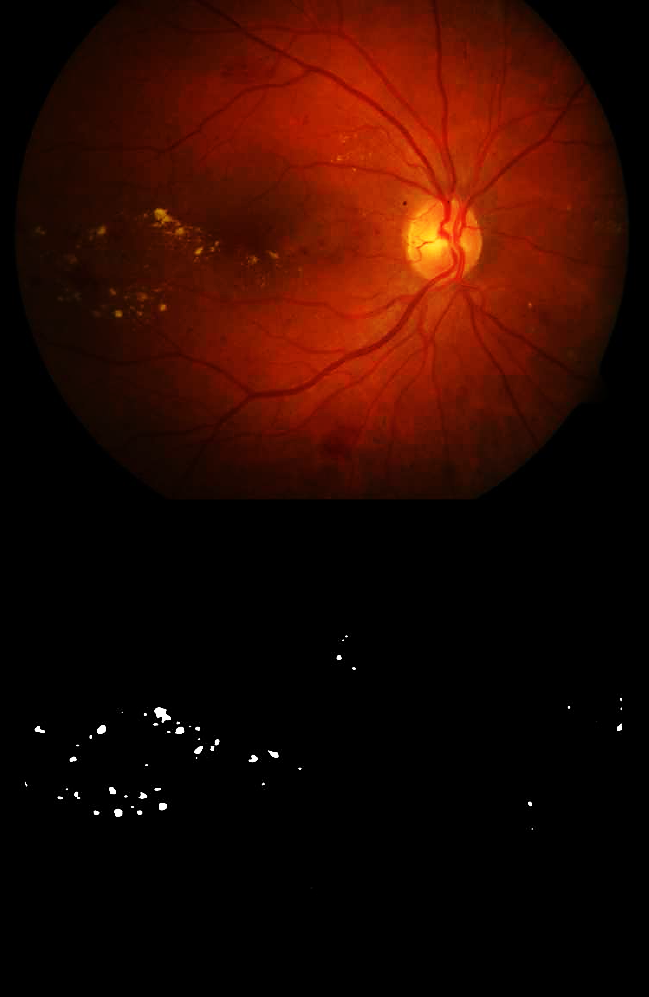
Fig. 7 Top: Eye fundus color image with hard exudates (database: ddb1_v02_01/image064). Bottom: Binary image with segmented hard exudates
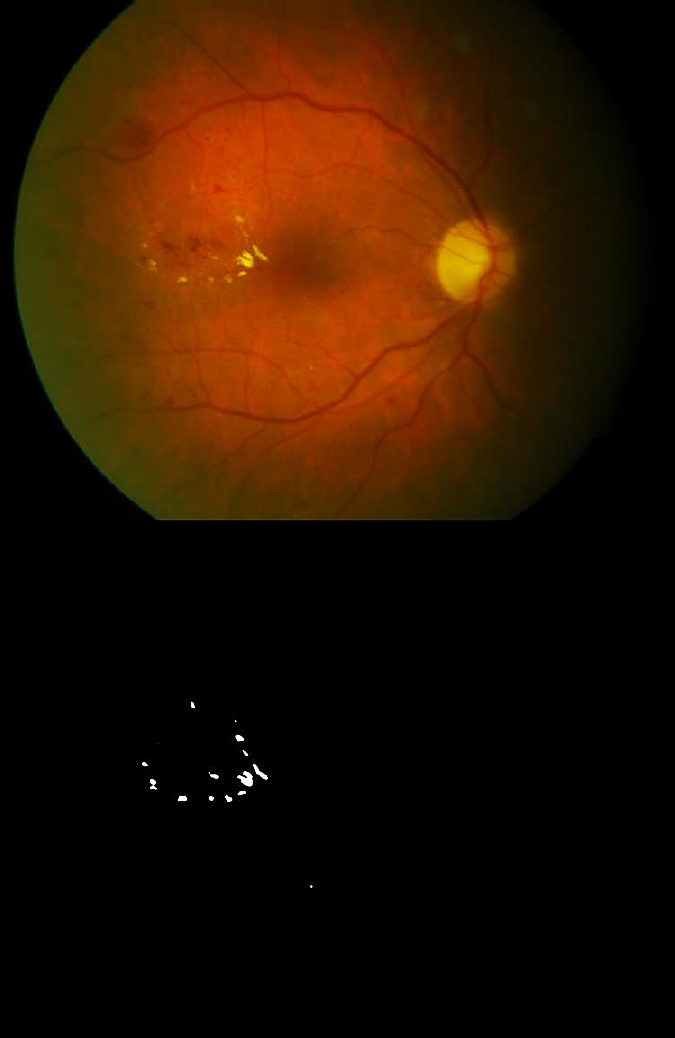
Fig. 8 Top: Eye fundus color image with blood vessels and aneurysms (database: diaretdb0_v1 _1/image005). Bottom: Binary image with segmented blood vessels and aneurysms
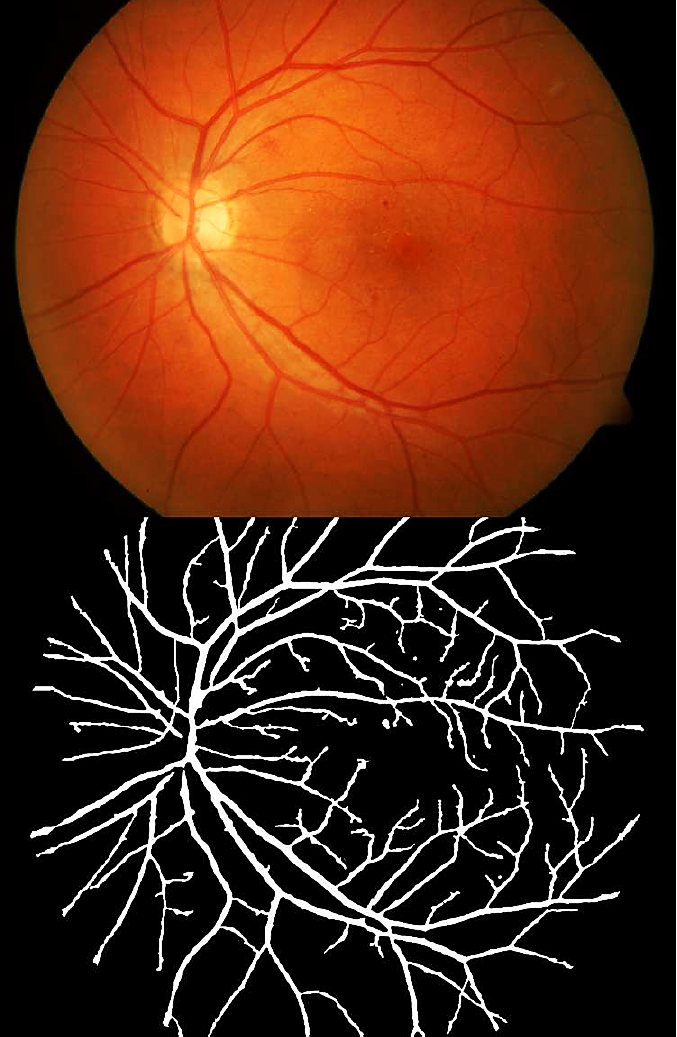
Fig. 9 Top: Eye fundus color image with blood vessels and aneurysms (database: diaretdb0_v1_1/image006). Bottom: Binary image with segmented blood vessels and aneurysms
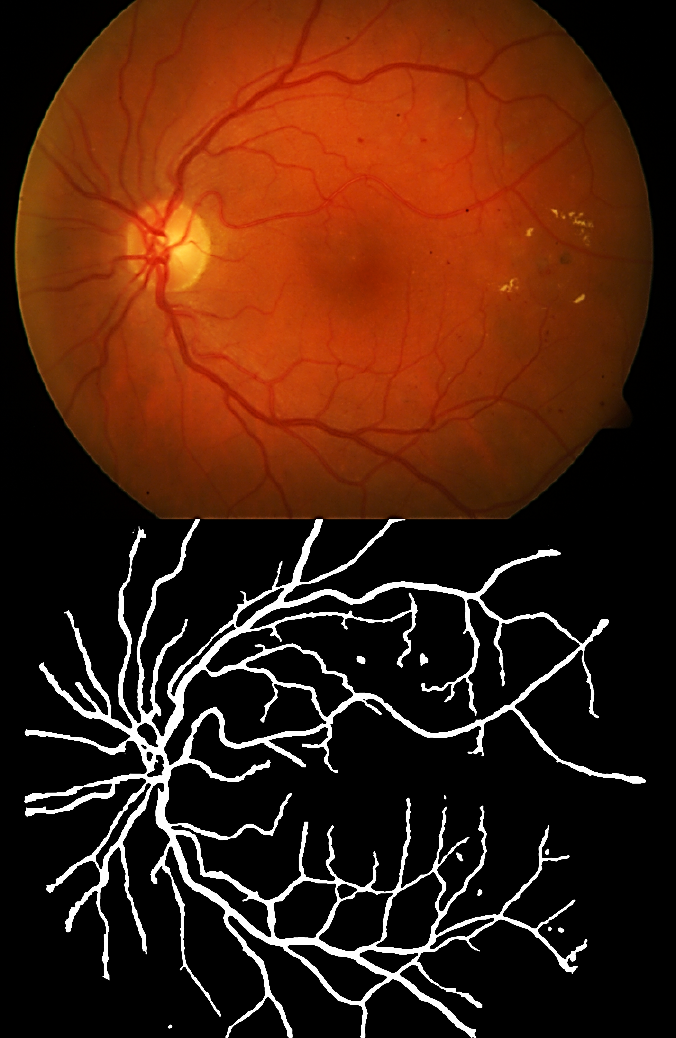
Fig. 10 Top: Eye fundus color image with blood vessels and aneurysms (database: diaretdb1 _v1 _1/image006). Bottom: Binary image with segmented blood vessels and aneurysms
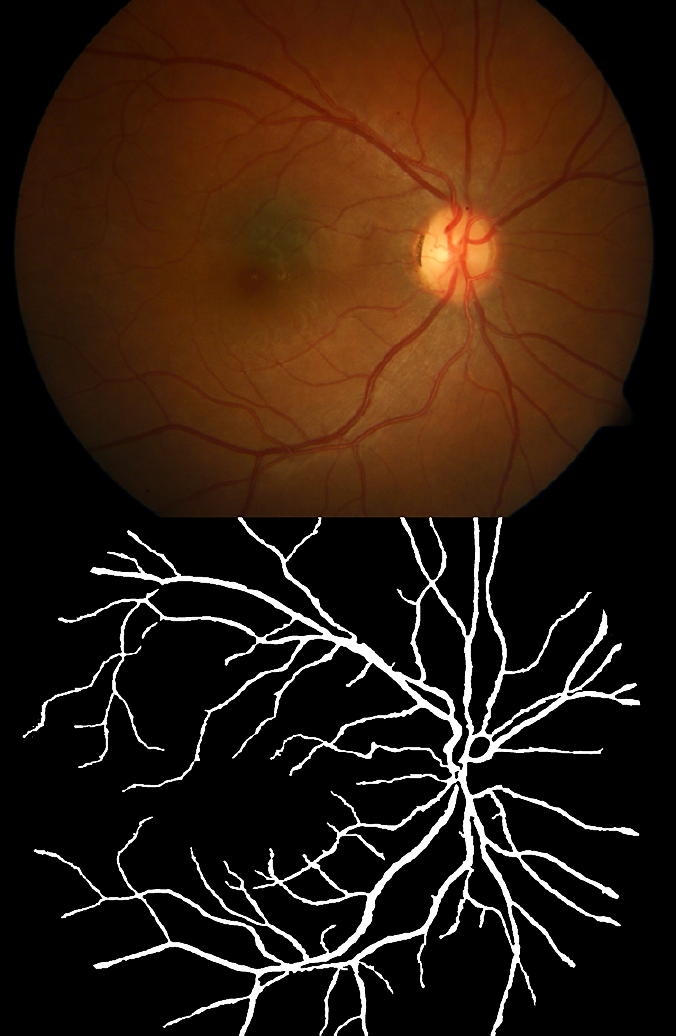
Fig. 11 Top: Eye fundus color image with blood vessels (database: diaretdb1 _v1 _/image093). Bottom: Binary image with segmented blood vessels
Table 1 shows the segmentation parameters and numerical values used for exudates and blood vessels.
Table 1 Gamma correction and threshold values for segmenting exudates and blood vessels
| Exudates (γ = 2) | |
| Figure Number & Pathology | LEOtsu |
| 4 : Hard & Soft Exudates | 0.19 |
| 6 : Hard Exudates | 0.20 |
| 7 : Hard Exudates | 0.17 |
| Blood Vessels (γ = 3) | |
| Figure Number & Pathology | LVOtsu |
| 5 : Blood Vessels | 0.29 |
| 8 : Blood Vessels & Aneurysms | 0.32 |
| 9 : Blood Vessels & Aneurysms | 0.31 |
| 10 : Blood Vessels & Aneurysms | 0.36 |
| 11 : Blood Vessels | 0.32 |
In the exudates segmentation images obtained, we can observe that the optic disk has a similar color as exudates, however our technique does not segment the optic disk. In Figs. 8 to 10 (9) besides blood vessels segmentation, aneurysms are also observed in the segmentation and correspond to small amorphous regions not connected to the blood vessels. Algorithm 2 provides the sequence of steps of our technique.
Soft exudates (Fig. 4) are nerve fiber layer infarcts or pre-capillary arterial occlusions. On the other hand, hard exudates (Figs. 4, 6, and 7) represent the accumulation of lipid in or under the retina secondary to vascular leakage, this is due to the aqueous portion of the fluid that is absorbed more quickly than the lipid component. Thus, the lipid that builds up in or under the retina becomes visible as yellowish deposits. In Figs. 5 to 11, we can observe the segmentation of the blood vessels (temporal arcades), and aneurysms are shown in Figs. 8 to 10, they look like islands and are easily seen where the macula is located.
The confusion matrix contains information about actual and predicted classifications realized by a pattern recognition system 24. Performance of such systems is commonly evaluated using the data in the matrix shown below.
The entries in the confusion matrix are: the number TP of correct objects (exudates or blood vessels) that a tested group sample gives positive, the number TN of incorrect objects that a tested group sample is negative, the number FP of correct objects that classification is negative, and the number FN of incorrect objects that objects are positively classified.
The confusion matrix allows us to find the sensitivity or true positive rate (TPR), i.e., the "positive cases" which refers to the proportion of objects that give positive test results, and the specificity or true negative rate (TNR) meaning that, the "negative cases" which refers to the proportion of objects that give negative test results (see Eqs. 10 and 11):
To obtain the sensitivity and specificity rates of our test examples, 20 eye fundus color images hand marked of exudates and blood vessels were used as ground-truth. In Table 2 the values of sensitivity and specificity of the method proposed (DTBS) are compared with other methods taken from the technical literature, both for the segmentation of exudates and blood vessels.
Table 2 Sensitivity (TPR) and specificity (TNR) rates for the segmentation of exudates and blood vessels in eye fundus images vs. other segmentation techniques.
| Exudates sensitivity & specificity | ||
| TPR | TNR | |
| Garaibeh (6) | 0.9210 | 0.9901 |
| Jaafar (4) | 0.8930 | 0.9930 |
| Kande (25) | 0.8600 | 0.9800 |
| Welfer (7) | 0.7048 | 0.9884 |
| Youssef (10) | 0.8000* | 1.0000* |
| Kumar (14) | 0.9710 | 0.9830 |
| Nugroho (15) | 0.9015 | 0.9999 |
| DTBS | 0.9412 | 0.9910 |
| Blood vessels sensitivity & specificity | ||
| TPR | TNR | |
| Niemeijer (26) | 0.6898 | 0.9696 |
| Rangayyan (27) | 0.8579 | 0.9000 |
| Saleh (9) | 0.8423 | 0.9658 |
| Staal (28) | 0.7194 | 0.7793 |
| Youssef (10) | 0.8000* | 1.0000* |
| DTBS | 0.8517 | 0.9832 |
In Table 2, the entries marked with an asterisk (*) means that the sensitivity and specificity given by Youssef were calculated taking into account both exudates and blood vessels. Also, TNR= 1.000 results from considering finite number of regions of interest (ROI's) versus a complete image as in the rest of table entries.
4 Conclusion
In this work, we have introduced a discrete cosine transform based filtering approach to the problem of extracting exudates and blood vessels in eye fundus color images. A Fourier transform or CDT homomorphic filter is proposed for illumination correction of the input images and a binary mask of the effective area of the retinography is constructed as a quotient between the red and green channels. An important step in the proposed method is the (DCT) spatial frequency domain processing using a super-Gaussian bandpass filter with carefully selected parameters. This novel type of filtering achieves an adequate contrast of the foreground objects against the background. We choose the DCT over the Fourier transform since its computation deals only with real values instead of complex numbers; in addition, the result obtained with the corresponding homomorphic DCT based filter is visually better. For blood vessels a negative of the filtered image is preliminary obtained, then a median filter is applied for both pathologies to reduce background noise and artifacts. There after a gamma correction is applied to enhance the resulting image contrast.
A binary image is determined using Otsu's simple statistics method for both cases and, before the final masking operation is realized, an intermediate operation is used only for blood vessels. In this case, a closing morphological operation is required. Several illustrative examples are given that demonstrate the results obtained with the proposed method. Notice that high sensitivity and specificity rate values have been obtained in our segmentation examples. Future work contemplates extending the number of tests on other clinical databases available such as DRIVE 29 and STARE [30] as well as pathology recognition (e.g., diabetic retinopathy and maculopathy) on image samples taken from the database used here (DIARETDB).











 nueva página del texto (beta)
nueva página del texto (beta)