1 Introduction
In educational environments the course scheduling is an iterative process, where, every period the academic needs must be covered. Due to the number of possible combinations of schedules that can be generated, the number of constraints to be fulfilled, the intrinsic features of needs to be covered, and the limitations of resources, this process is catalogued as a hard work.
This problem has been solved by the expertise of academic departments; during the process, numerous aspects must be taken into consideration: almost a week of human work (for a medium size university) to produce an acceptable course schedule, when the constraints change the majority of work becomes unusable and has to be restarted from scratch, and the generated course schedule generally contains biases to assign resources to needs. The manual approach only considers some of the important conditions, being the process extremely complex to find optimal solutions.
In literature, this problem is known as University Course Timetabling Problem (UCTP). Basically, the UCTP consists of fixing a sequence of meetings between lecturers, classrooms, and schedules to a set of groups and courses in a given period satisfying a set of constraints. The automatic or semi automatic UCTP generators, generally are solved by means of two approaches: the exact and the heuristic approaches. The exact method typically uses a brute-force style and due to its exponential computation cost are not practical to solve complex timetabling problems. Some examples of exact approaches are: branch and bound, dynamic programming, Lagrangian relaxation based method, linear and integer programming, among others 2. On the other hand, the heuristics methods are more efficient to find solutions close to the optimal ones in a very short time. Examples of heuristics methods are: simulated annealing, tabu search, evolutionary algorithms, among others 6, 3, 8.
To tackle the UCTP, this contribution proposed the use of solutions based on Evolutionary Algorithms (EA); the solution uses internally two of the most succesful algorithms that operates on the continuous domain: Genetic Algorithms (GA) and Differential Evolution (DE). It is well known the search power of DE to solve different continuous problems, in this proposal, we decide to use its search advantages in the solution of combinatorial problems 10, and we compare the obtained results against GA 18. In the case of DE naturally operates on continuous domains, and GA as been widely used as a point of comparison between EAs. To test and validate the results, we use three different UCTP instances; the instances are based on Mexican universities, each instance contain different sets and features of resources and needs. The instances are: Instituto Tecnológico de Zitácuaro, Instituto Tecnológico del Valle de Morelia, and Instituto Tecnológico de Tuxtla Gutiérrez.
Formally the UCTP is an optimization problem, where the aim is the minimization of an objective function, subject to a number of constraints. The constraints are categorized in two types:
- Hard Constraints. These constraints must be fulfilled necessarily.
- Soft Constraints. These constraints are desirable but not necessary.
The heart of this work is a procedure (timetabling generator) based on EA to generate optimal solutions for a given UCTP instance; the solutions are represented by combinations of lecturer, classroom, and hours per week, and needs are the courses offered by the university in a period. The performance of algorithms is related with the weighted sum of soft and hard constraints.
The timetabling generator is based on a greedy-based procedure, to optimize its results, the procedure has an internal EA process: from a pool of courses, the procedure selects the courses to be solved, then the process finds the suitable solution for each one. Some of the properties of this approach are: a) the global solution is close to the global optimum (quasi-optimal solution), b) the short time required to solve the instances, c) the dimensionality of the search space (4-dimensions). In general, the purpose of greedy approaches is to obtain good quasi-optimal solutions in a short period of time. Another important aspect to be considered, is the dimensionality of the problem: the size of chromosome grows, as well as resources to be assigned. For a small UCTP the dimensionality of the problem is not a limitation contrary to instances that have a large set of resources to be assigned.
The main contributions of this proposal are: a) the timetabling generator is based on a greedy approach, and the search process is based on two of the most successful EA: GA and DE, 2) the visualization of the landscape depicted by the fitness function using different input parameter for the algorithms, 3) based on the visualization, the identification of the optimal input parameters for the algorithms, and 4) the performance comparison for the EA using the best input parameters in each case.
This paper is organized as follows: Section 2 presents the related work, Section 3 describes the instances to be compared, Section 4 presents the problem statement and formulation of this proposal, Section 5 presents the solution based on EA, the experimental results are presented in Section 6, Section 7 presents a brief discussion, and Section 8 presents conclusions and further research directions.
2 Related Work
The UCTP has been one of the most studied scheduling problems; the solution approaches range from graph coloring to heuristic algorithms, including mathematical programming models and metaheuristics as well. Among metaheuristic techniques to solve timetabling problems, GA is of special interest because there a lot of works where GA has been widely used. Colorniet al. 7 propose a direct GA that uses a matrix to represent the timetable. Each element of this matrix is a gene. An alphabet of characters is used to represent attributes of events, an advantage of this method is the use of a filtering algorithm to generate feasible solutions. Sigl et al. 21 propose a GA and use 3D cubes corresponding to rooms, days, and timeslots to model the timetable. In this method, the individual's genes represent courses and each individual represents a timetable, the algorithm starts from unfeasible timetables trying to get feasible ones. The algorithm was tested on small and large instances. Rushil and Nelishia 19 used a two phase method based on GA, in the first phase the algorithm finds feasible solutions based on hard constraints, and, in the second phase the best solutions based on soft constraints are selected. Moreira 16 proposed the use of an automatic exam timetable system based on GA.
In literature there are different methods to solve timetabling problems based on discrete and continuous encodings. Dino Matijaš et al. 9 propose a solution based on ACO (Ant Colony Optimization) which was proved on 5 UCTP instances, the solutions were compared against solutions based on a GRASP approach, the results showed the best performance for the ACO solution. Chen et al. 5 propose a PSO based solution for the solution of UCTP; their proposal is based on a special version of PSO, the standard PSO (SPSO) which is applied to local search, PSO is based on inertia weight and SPSO in constriction, the results show better results for SPSO. Soza et al. 22 proposed the use of cultural algorithms which incorporate knowledge to the algorithm to solve UCTP instances; they compare their proposal against three different heuristics based on EA and simulated annealing, their results showed that the cultural algorithm is competitive regarding performance.
To validate results, in literature is very common to compare the proposed approach against a GA solution. Raghavjee et al. 17 compare the performance of Genetic Programming (GP) and GA to solve different instances of UCTP. The results showed better results for the GP approach, being one of its limitations the computational time to solve the problem. Raghavjee et al. 18 compare the performance of two approaches based in GA to solve timetabling problems, the first approach uses indirect representation while the second uses a direct representation, direct representation means each solution is a possible timetable. The indirect representation obtained the best success rates. Beligiannis et al. 4 developed a EA based solution to solve a set of Greek UCTP instances, and they compare their results against other algorithms, their algorithm obtained the fastest results.
When EA practitioners try to solve complex optimization problems, such as the UCTP, they must compare their outputs against valid results; generally, they use GA approaches, this due to its success to solve diverse type of problems. Despite the success of DE to solve complex real life problems in the continuous domain, in literature exists very few works that use its search power to solve combinatorial problems. Another important point to emphasize is the fact that many approaches use artificial instances; the needs, resources, constraints, etc. are assumed but not correspond to reality. In previous work we proposed the use of a RCGA approach to solve an instance of the UCTP; to do this we proposed the use of different input parameters for the solver and finally use the most accurate ones. The results showed accurate solutions (the solutions do not violated the constraints) to the UCTP.
In literature, very few works use and compare the performance of continuous solvers in the solution of discrete optimization problems such as the UCTP. The establishment of the input parameters for the solvers, many times is not clear or there is no a comparison between the use of different parameters. This contribution incorporates the following improvements with respect to the ones mentioned above and our previous work: 1) we use a GRASP based procedure to perform the search process on the UCTP. The method incorporates two continuous EA as solvers on the continuous domain (GA and DE), the results show promising results, 2) the experimental phase uses 3 UCTP instances, the instances are based on Mexican universities. Each instance contains different characteristics and complexity, 3) to tune the solvers a calibration phase was performed; we launched experiments using different input parameters, we showed the landscape depicted by the fitness function, 4) with the use of the landscape, we select the optimal input parameters, and we use these parameters to compare the performance between the GA and the GE solvers.
3 Study Cases
At universities, the process to schedule the academic activities vary according to its intrinsic variables. The complexity of schedules is related to the number of combinations of resources and needs, e.g. courses are considered as needs, the availability of classrooms, lecturers, and time are considered as resources, then, its combination determines the number of possible assignments. The following are the general steps to construct an academic schedule: a) the quantification of offered courses in a period, the courses correspond to different academic programs, and the courses contain different specifications (lecturer expertise, type of classroom, etc.), b) for each course, a lecturer is assigned considering his/her expertise and his/her hours availability, c) each course/lecturer is assigned to a classroom, taking into consideration the classroom's characteristics (capacity, and its specifications: laboratory or theory), d) for each course/lecturer/classroom must be scheduled in two-time sessions: one session between Monday to Thursday, and in some cases it is necessary an extra session on Friday, and e) each subset of course/lecturer/classroom/times conform groups, and a set of groups conform an academic program.
The following study cases correspond to three different universities in Mexico; in each case the estimated time to construct its academic schedules vary between one week to four weeks, requiring between two to five human resources. The specifications of the study cases are described below.
3.1 Instituto Tecnológico de Zitácuaro
The Instituto Technologic de Zitácuaro (ITZ) is a public university located at the east of the state of Michoacán, México. The ITZ offers 8 academic programs: Civil Eng., Computer Systems Eng., Industrial Eng., Enterprise Management Eng., Electromechanics Eng., Informatics Eng., Public Accounting, and Management.
The total needs to be covered in each period (semester) for the 8 academic programs is a total of 181 courses offered in each period. The sets of available resources to cover the needs are: 69 lecturers, 34 classrooms, and 24 different times, each one with different features and capacities. These yield a total of 181 x 69 x 34 x 24 = 10,191,024 different forms to combine the academic resources.
3.2 Instituto Tecnológico del Valle de Morelia
The Instituto Tecnológico del Valle de Morelia (ITVM) is a public university located at the center of the state of Michoacan, Mexico. The ITVM offers 5 academic programs: Management, Agronomy Eng., Environmental Eng., Forestry Eng., and Sustainable Agricultural Innovation Eng. The total needs to be covered in each period (semester) for the 5 academic programs is a total of 112 courses offered in each period.
The sets of available resources to cover the needs are: 122 lecturers, 38 classrooms, and 24 different times, each one with different features and capacities. These yield a total of 112 x 122 x 38 x 24 = 12,461,568 different forms to combine the academic resources.
3.3 Instituto Tecnológico de Tuxtla Gutierrez
The Instituto Tecnológico de Tuxtla Gutierrez (ITTG) is a public university located in the state of Chiapas, Mexico. The ITTG offers 8 academic programs: Computer Systems Eng., Industrial Eng., Enterprise Management Eng., Electronic Eng., Electric Eng., Biochemistry Eng, Chemistry Eng., and Mechanical Eng.
The total needs to be covered in each period (semester), for the 8 academic programs is a total of 180 courses offered in each period. The sets of available resources to cover the needs are: 218 lecturers, 102 classrooms, and 24 different times, each one with different features and capacities. These yield a total of 180 x 218 x 102 x 24 = 96,059,520 different forms to combine the academic resources.
4 Problem Statement
The UCTP can be defined as follows. Given the following preliminary definitions:
- ℂ a set of NC courses; each course ci ∈ ℂ, i ∈ [1, Nℂ],
- 𝕃 a set of N𝕃 lecturers; each lecturer lj ∈ 𝕃, j ∈ [1, N𝕃],
- ℝ a set of Nℝ classrooms; each classroom rk ∈ ℝ, k ∈ [1, Nℝ],
- 𝕋1 a set of NT1 available times in the week (from Monday to Thursday); each available time αl ∈ 𝕋1, l ∈ [1, NT1],
- 𝕋2 a set of NT2 available times on Friday; each available time bm ∈ 𝕋2, [m ∈ 0, 1, NT2],
- a target matrix 𝓜=[Xl,r,t1,t2]NL×NR×(NT1+NT2).
All the indices start at 1, except the index for 𝕋2 which starts at 0, to simplify the cases when a course does not occur in a given day (i.e., if does not have an assigned time).
To allocate the taks-resources it is necessary to use a 3D matrix called target matrix (𝓜). This matrix is used to find suitable time slots for scheduling tasks 13. 𝓜 is a ||𝕃|| x ||ℝ|| x (||𝕋1|| + ||𝕋2||) matrix, where the dimensions are: times (x-axis), classrooms (y-axis), and lecturers (z-axis). The combination of times (li , rj , t1k, t2l), are represented for two cells of the target matrix: 𝓜l,r,t1and 𝓜l,r,t2, where 1 ≤ t1 ≤ 12 and 13 ≤ t2 ≤ 24, for each (lecturer, classroom, time1, time2) combination.
𝓗(⋅) is a function that returns the Hard Constraints penalization which are represented by:
A classroom cannot be assigned to more than one course in the same time/day.
A lecturer cannot be assigned to more than one course in the same time/day.
𝓢(·) is a function that returns the Soft Constraints penalization which are represented by:
Check the suitable classroom (Theory or Practice).
The lecturer profile must match the course requirement.
Check the times preference/availability by lecturers.
The assigned classrooms must satisfy the needs of course requirements (capacity).
Classrooms must be assigned consecutively (no holes in schedule)
The number of weekly hours assigned to a course must match the course's needs.
The objective is to minimize the penalization of hard constraints (𝓗) and soft constraints (𝓢); the hard constraints must be fulfil and the soft constraints must be minimized 1. A mathematical formulation can be represented by:
Determine an assignment [Xl,r,t1,t2]NL×NR×(NT1+NT2) that minimizes 12:
Subject to
where 𝓗(X) is a function that penalizes the violation of hard constraints, and 𝓢(X) is a function that penalizes the violation of soft constraints; the penalization for the hard constraints are highest than the soft constraints. The function f(X) assesses the total penalization for a given X. Constraint 3 prevents the overlaps between lecturers assignment, classrooms, and times.
The University Course Timetabling Problem (UCTP) consists of a set of tasks and a set of resources to be assigned. The tasks are the set of courses clustered by groups, every cycle (year) there are different fixed courses by period (semester); the scholar year is divided into two semesters, each of which represents a set of available courses for each academic program. The resources are represented by lecturers, classrooms, and available times, these have a constant length, availability, and special features.
5 Solution based on Evolutionary Algorithms
In this proposal we use two of the most successful EA: the Real Coded Genetic Algorithms (RCGA) and Differential Evolution (DE). The chromosome is a vector of real values, each element represents the distinct combination of resources assigned to a task: C = [l, r, t1, t2] where l, r, t1, and t2 are different genes to be mutated (according to section 4). Since UCTP is a discrete optimization problem, the continuous values into the individuals (chromosome values) are discretized through the following operator ⌊⌉, which quantizes their nearest discrete value.
5.1 Real Coded Genetic Algorithms
The real encoding GA solution (RCGA) allows us to solve the problem directly, that is, there is no intermediate step to configure or deconfigure solutions. The RCGA has the ability to recombine, by means of explotation and exploration, the individuals of the population 15. Algorithm 1 shows the basic operation of GA 11.
The three basic operations of GA are: (1) evaluation of individual fitness, (2) formation of a gene pool (intermediate population) through selection mechanism, and (3) recombination through crossover and mutation operators.
5.2 Differential Evolution
Differential Evolution (DE) like GA is an EA specialized to solve continuous optimization problems. There are different variants of DE algorithms: the most common of them called DE/rand/1/bin, where "rand" means individuals are selected at random, "1" is the number of pairs selected, and "bin" means binomial recombination 14. The idea behind DE is that the difference between two vectors yield a difference vector which can be used with a scaling factor to traverse the search space 10. Algorithm 2 shows a basic DE algorithm 10.
The three basic operations of DE are: (1) the initialization and fitness evaluation of individuals, (2) from population, the selection of three mutually different individuals, (3) a process of mutation and recombination.
5.3 Solution based on EA
Algorithm 3 shows the procedure Course-Solutions to solve the UCTP; the procedure has as input parameters, the set of needs and resources. The needs refer to the courses to be covered, and the resources are the set of lecturers, classrooms and times to be assigned.
The procedure output returns the set solutions for the courses. The computational cost of the procedure is in terms of the number of courses to be optimized (assigned resources) multiplied by the intrinsic cost of metaheuristics (in both cases the population size and number of generations are the same): O(n M) where n is the number of courses and M is the cost of each metaheuristic.
The sets C, L, R, T1,T2 (courses, lecturers, classrooms, times 1, and times 2, respectively) are passed as parameters to Course-Solutions. The set course_solutions is initialized (Line 1), the search space Ω is created (Line 2), initialize the iterative process for each course from ℂ (Line 3), initialize the EA process (Line 4), from Ω at time i, the initial population P is generated (Line 5). Each individual from P is evaluated according to Equation (1) (Line 6).
Once the initialization process ends, the iterative process is started and it reseats while the number of generations is not reached (Line 7); time is increased (Line 8). The EA process is performed (Algorithm 1 or Algorithm 2) (Line 9). The best_individuall,r,t1,t2 from the EA process is added to the set courses_solutions (Line 11), the cells 𝓜l,r,t1 and 𝓜l,r,t2 are marked in matrix M as unavailable; the cells correspond to the tuple best_individuall,r,t1,t2 (Line 12).
The process continues until all courses are covered. Finally the set course_solutions is returned (line 14).
6 Experimental Results
The following subsections show the parameter settings used by metaheuristics, a table with the general information about UCTP instances, and the main results obtained from experiments. To get statistically significant results, the experiments were repeated 30 times and the mean was reported.
6.1 Parameter Settings
Table 1 shows the parameter settings used by the metaheuristics.
Table 1 EA parameters settings
| Parameter | RCGA values | DE values |
|---|---|---|
| Population Size | 100 | 100 |
| Precision | 1 x 10-1 | 1 x 10-1 |
| Generations | 500 | 500 |
| Crossover rate | [0, 1] | - |
| Mutation rate | [0, 1] | - |
| Selection | Tournament of size 10 | - |
| DE variant | - | DE/rand/1/bin |
| CR | - | [0,1] |
| F | - | [0,1] |
Table 2 shows the sets of tasks and resources available at each university considering a period.
6.2 Results
The following Figures (1, 2, 3, 4, 5, 6) show its corresponding 3D fitness plot, obtained by the two approaches (GA and DE) varying its input parameters (crossover and mutation for GA, and cr and f for DE) in the solution of the UCTP instances.

Fig. 1 GA fitness, varying the crossover and mutation values for the ITZ instance. The best fitness is in: crossover = 1.0, mutation = 0.0 and fitness = 961.0
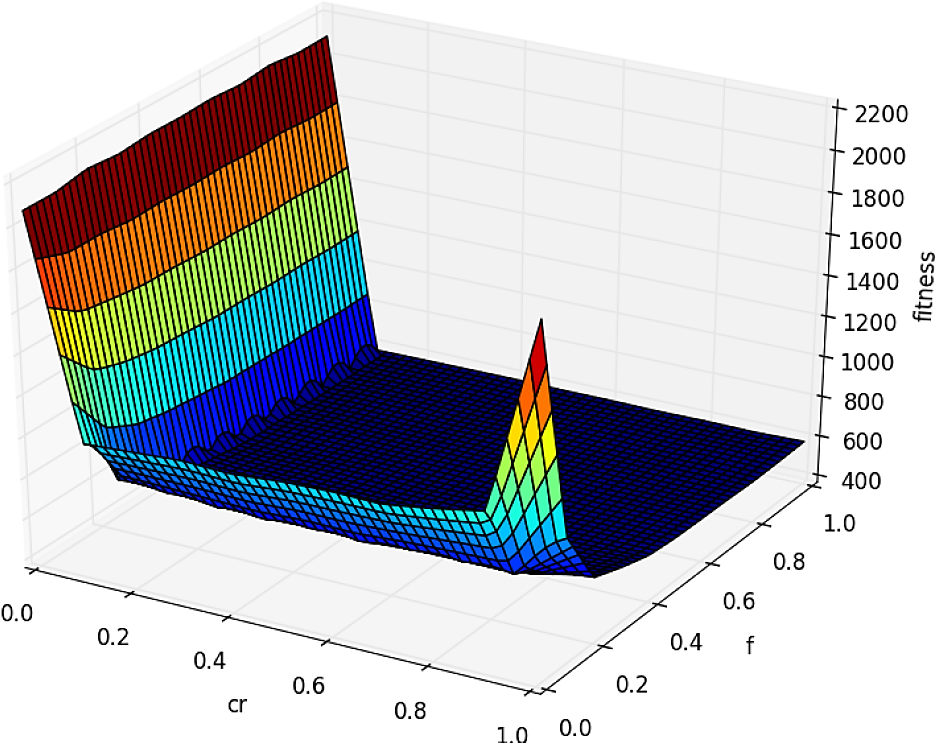
Fig. 2 DE fitness, varying the cr and f values for the ITZ instance. The best fitness is in: cr = 0.1, f = 0.8 and fitness = 564.4
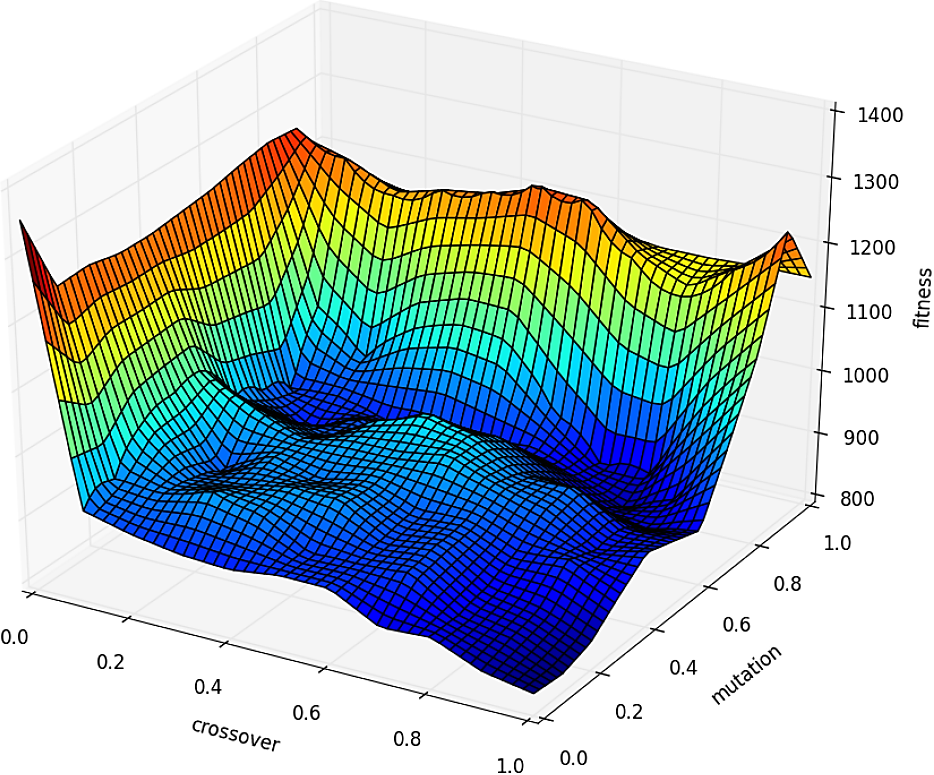
Fig. 3 GA fitness, varying the crossover and mutation values for the ITVM instance. The best fitness is in: crossover = 1.0, mutation = 0.1 and fitness = 817.5
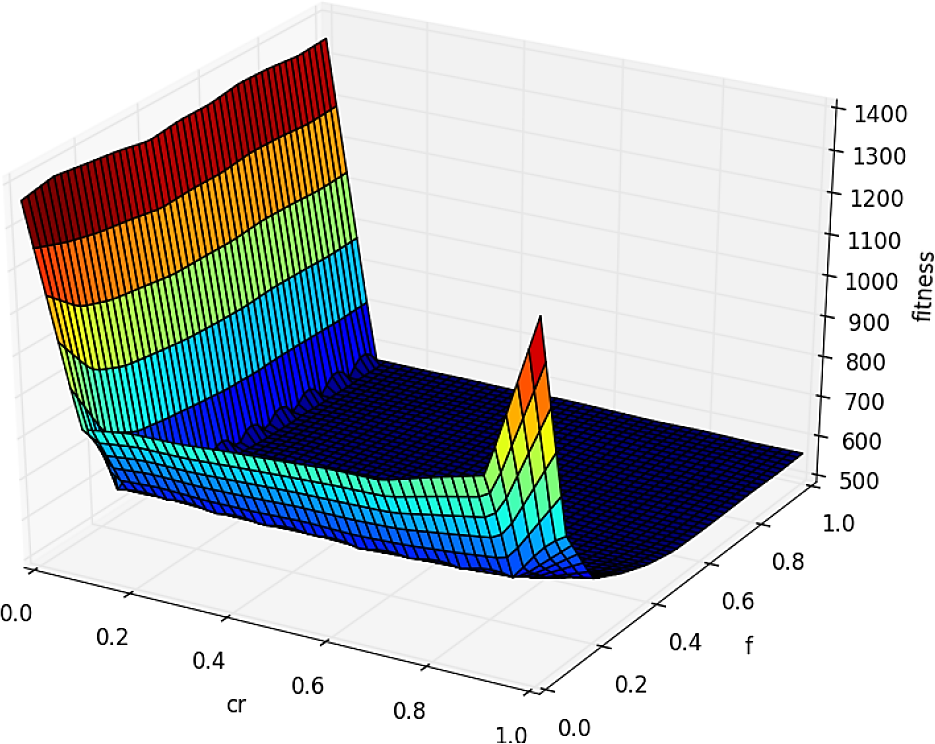
Fig. 4 DE fitness, varying the cr and f values for the ITVM instance. The best fitness is in: cr = 0.6, f = 0.6 and fitness = 555.9
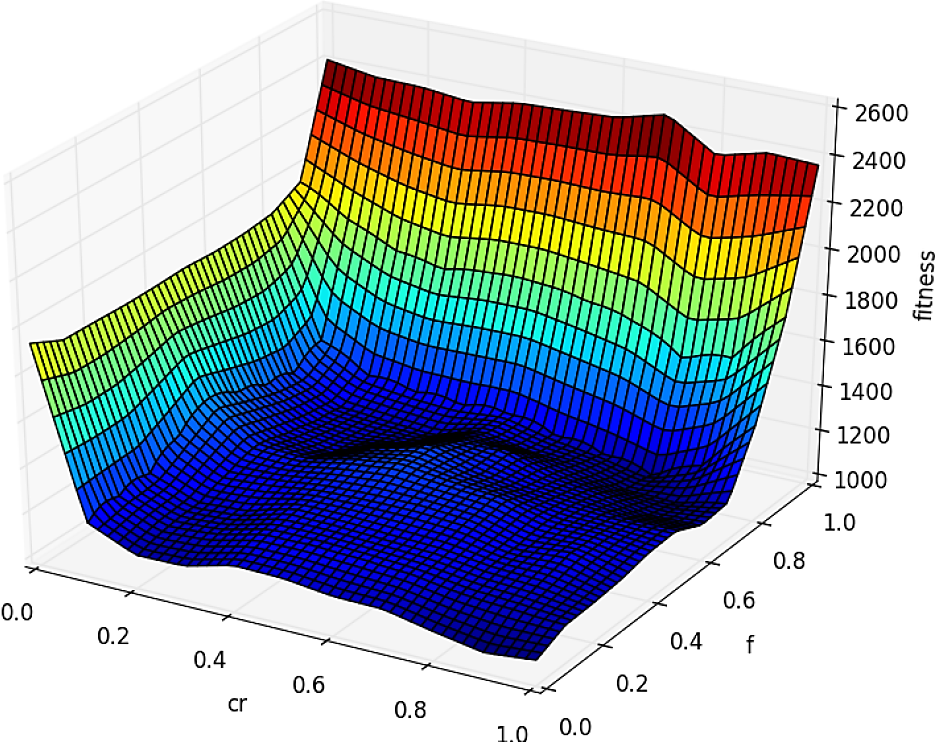
Fig. 5 GA fitness, varying the crossover and mutation values for the ITTG instance. The best fitness is in: crossover = 0.9, mutation = 0.0 and fitness = 1056.9

Fig. 6 DE fitness, varying the cr and f values for the ITTG instance. The best fitness is in: cr = 0.9, f = 0.5 and fitness = 760.8
Considering the last figures, we can establish: a) the fitness pictured by GA are rugged with optimal fitness values in dispersed areas, and b) the fitness pictured by DE has wide neutral areas containing similar optimal values.
To compare the performance of metaheuristics we decided to select some of the optimal parameter setting according to the last figures. The following Table 3 shows the values selected for the input parameters for the metaheuristics:
Table 3 Optimal parameters selected for the metaheuristics
| Parameter | GA values | DE values |
|---|---|---|
| Crossover rate | 1.0 | - |
| Mutation rate | 0.0 | - |
| CR | - | 0.8 |
| F | - | 0.8 |
As we can see in the last Table, in the case of GA its optimal input parameters use high rates of exploitation without no rates of exploration, while DE practically uses the input parameters recommended in literature 23. To perform a most robust comparison between metaheuristics, the following Figure 7 shows the fitness values obtained by the GA and DE to solve the UCTP instances using the optimal parameter settings according to Table 3.
As we can see in all the UCTP instances DE outperforms the performance of GA: for the ITZ instance DE improved in 40% against GA, for the ITVM instance, DE improved 30% against GA, and, for the ITTG instance it improved 27% with respect to GA. Practically the DE results are correlated with the number of possible combinations for the instances (see Section 3), the most difficult one is the ITTG instance, the ITZ and ITVM have very similar number of combinations. To measure the qualification of results, the following Table 4 shows the constraint violations for each of the instances and metaheuristics using the optimal parameter setting.
Table 4 Mean of hard and soft constraint violations
| Constraints | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hard | Soft | |||||||||
| 1 | 2 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| ITZ | GA | μ | 0.0 | 17.4 | 50.5 | 16.1 | 163.4 | 1.5 | 0.4 | 0.0 |
| σ | 0.0 | 3.7 | 4.3 | 3.2 | 0.9 | 0.6 | 0.7 | 0.0 | ||
| DE | μ | 0.0 | 0.0 | 0.8 | 16.7 | 164.0 | 1.0 | 0.4 | 0.0 | |
| σ | 0.0 | 0.0 | 0.9 | 3.3 | 0.0 | 0.0 | 1.0 | 0.0 | ||
| ITVM | GA | μ | 0.0 | 6.6 | 42.9 | 15.4 | 109.1 | 0.2 | 70.4 | 0.0 |
| σ | 0.0 | 2.3 | 5.4 | 2.8 | 0.3 | 0.5 | 2.4 | 0.0 | ||
| DE | μ | 0.0 | 0.0 | 5.7 | 14.3 | 109.0 | 0.0 | 73.6 | 0.0 | |
| σ | 0.0 | 0.0 | 1.7 | 2.8 | 0.0 | 0.0 | 2.3 | 0.0 | ||
| ITTG | GA | μ | 0.0 | 11.7 | 44.4 | 62.9 | 161.5 | 2.3 | 0.0 | 0.0 |
| σ | 0.0 | 2.7 | 4.6 | 3.5 | 0.9 | 1.2 | 0.0 | 0.0 | ||
| DE | μ | 0.0 | 0.0 | 2.2 | 68.8 | 162.0 | 1.0 | 0.0 | 0.0 | |
| σ | 0.0 | 0.0 | 1.6 | 3.8 | 0.0 | 0.0 | 0.0 | 0.0 | ||
The results show how GA violates, for all the instances, all the hard constraints (infeasible solutions), particularly the constraint 2, it is necessary for this approach the implementation of a repair mechanism as in our last work 20.
On the other hand, DE does not violates the hard constraints in all the instances (without the use of a repair mechanism), and, improves the effectiveness regarding the soft constraints in the majority of instances.
7 Discussion
University Course Timetabling Problem (UCTP) has been widely studied around the world; particularly in Mexico there are many works about this topic, but there are no conclusions about the topic. Some reasons are that many works are based on hypothetical cases and the results are in the same sense, or many approaches are based on an unique instance and there is no a comparative scenario. One of our goals, is to develop a useful methodology, that can help implement a UCTP solution easily in many Mexican Universities. The university instances studied here can be considered as an effort to be implemented in other Universities.
GA and DE prove to be efficient tools to solve different instances of UCTP; in the majority of cases, DE obtained the best solutions. To improve the results for the DE and GA approaches, the variation of parameter setting is crucial. In previous work we use a GA approach using different parameter settings for the population size, cross over, and mutation, being the optimal configuration: population size 400, crossover 1.0, and mutation 0.9. This contribution uses a population size 100 and the following parameter settings: for the GA approach crossover rate 1.0, and mutation rate 0.0, in the case of DE approach one of the best parameter settings was cr rate 0.8 and f rate 0.8, the DE parameters are similar to the parameters reported in literature 14. The difference of parameters between the last work and this work, is due that in the last work we used a repair phase to improve the overall performance, whereas in this work we emphasized the comparison between GA and DE performance where the repair phase was not necessary.
It is important to mention that results were verified in terms of qualification, that is, it was verified the correspondence between courses and the allocation of lecturer/classroom/time, e.g., for a particular course it was verified the lecturer profile, the type of classroom and the time slot assigned. The results showed interesting considerations about the performance of DE and GA: the easiest UCTP instance was ITVM and the hardest UCTP was ITTG (according to its performance). In both cases the relation between needs and resources played an important role: the more needs and fitted resources, the harder the problem to solve. Regarding to constraints violations, in all cases, DE obtained the best performance; DE does not violate any hard constraint, moreover, both DE and GA violate soft constraints.
8 Conclusions and Further Research
This contribution presented a procedure to solve the well known University Course Timetabling Problem (UCTP). The procedure was based on Evolutionary Algorithms, particularly Real Coded Genetic Algorithms (RCGA) and Differential Evolution (DE). This approach was tested on three different UCTP instances. DE metaheuristic got the best performance values in the solution of instances, and did not violate any hard constraint. DE and RCGA had similar capacities to avoid soft constraints.
As future work we will address the study of UCTP starting from a partial solution and applying hypermutation. Once a feasible timetabling configuration has been generated, it can be the starting point for a new search. Another interesting topic is the use of hyper heuristics, that is, the use of heuristics to select heuristic to solve the UCTP.











 text new page (beta)
text new page (beta)






