1 Introduction
The automated design process of integrated circuits (IC) based on complementary metal-oxide-semiconductor (CMOS) is carried out by the industry of Electronic Design Automation (EDA), to synthesize amplifiers, voltage followers, current mirrors, among other circuits. EDA is a category of software tools for designing electronic systems, which typically are validated by simulation 4, 15, 17, 26, 33, 35, 25.
EDA tools increase productivity in the design of ICs, even for circuit blocks that are not repetitive. Particularly, analog design automation is more complex compared to digital design automation, because the relationships among their specifications are more complex. Moreover, analog design requires experience, intuition and creativity, primarily because it works with a large number of parameters that usually exhibit complex interactions among them 23.
Enhanced analog signal processing applications are realized thanks to the availability of a plethora of active devices 28. Among the most known active devices we can identify the conventional operational amplifier (opamp), the unity-gain cells (UGCs) 2, 28, the current conveyor (CC) with all its generations and multiple outputs 24, the operational transconductance amplifier (OTA), and the current-feedback operational amplifier (CFOA) 24. These active devices are also useful in the implementation of active filters, sinusoidal oscillators, and chaotic oscillators 4.
In recent years, several researchers have proposed a variety of methods for analog circuit synthesis; such as 4 that focuses on the design of passive circuits or 35 that studies burst-mode circuits. Another example is the work of 5, that employs simmulated annealing as an optimization process to design opamps, comparing favorably with hand-made designs. In general, it possible to define two broad class of automatic design methods for ICs, knowledge-based and optimization-based, as reviewed in 25. The first group of methods used techniques derived from deep domain knowledge and expert experience. As 25 points out, these methods are often quite efficient but usually are very difficult to develop and even more complicated to update as technology evolves. Optimization-based strategies on the other hand are more robust and domain-independent, but can often be complicated to tune or might require long execution times.
Evolutionary algorithms (EA) have proven to be a good choice to generate new circuits, or to optimize previous designs by sizing their topologies 4,15, 26,33. In this work, we focus on finding new topologies that synthesize a current follower (CF) circuit using a binary encoded genetic algorithm (GA) 7. More specifically, a binary genetic encoding of unity gain cells (UGC) is implemented through nullator or norator elements.
EAs are inspired in biological evolution, but a key difference is that artificial evolution is heavily based on an objective function to guide the search, while natural evolution does not follow any objective at all. Natural evolution is an open-ended search process, and as such lacks a predefined purpose. Despite its lack of an objective, an important feature of open-ended search is the continuous emergence of novelty 1. Indeed, this ability has been exploited in open-ended EAs, but mostly been used in specialized domains, such as artificial life 22 and interactive search 8.
One promising open-ended algorithm is Novelty Search (NS) proposed by Lehman and Stanley 10. NS is intended to be a general search paradigm, applicable to those domains where EAs are used. For instance, NS has achieved promising results in various areas of evolutionary robotics 34, such as navigation 10, 31, swarm robotics 6, morphology design 14 and gait control 13. More recently, NS has been applied on machine learning problems, including symbolic regression 16, clustering 18 and classification 19, 20. In general, the best use of NS will be in those areas where a continuous emergence of novelty is sought 27. Such domains will surely include engineering problems, where intuition and creativity are required.
Therefore, in this work we use a GA 7 based on NS to synthesize new topologies for current follower circuits. To the authors knowledge, this is the first work to apply NS in this domain, where unorthodox and unique designs are often sought. Moreover, we apply NS directly in genotype space, unlike previous NS implementations that use a behavior characterization. The experimental results show that NS allows the GA to find different topologies with respect to those found in previous works where a standard objective-based GA was used 2, 28, 29, 30. This work and its results give us insights about the usefulness of NS on electronic circuit synthesis.
The remainder of this paper proceeds as follows. Section 2.1 presents an approach to evolve circuit topologies using a standard GA, based on previously published research, focusing on solution representation and the objective function. Then, Section 3 presents the NS algorithm and our proposal to apply it in this specialized domain. Afterward, Section 4 describes our experimental work and results, highlighting the CF circuts synthesized by GA-NS and comparing the search behavior with that of a standard GA. Finally, we conclude our work in Section 5, discussing the main findings and future work.
2 GA Synthesis and CFs Representation
2.1 Genetic Algorithms
GAs use an abstract model of natural evolution to solve optimization problems, originally introduced by John Holland in the 1960's and 1970's 7. GAs operate on the principle of "survival of the fittest", generating new designs or solutions from a population of existing solutions and discarding those designs that have an inferior performance or fitness. Each member of the population is a solution candidate, referred to as an individual, represented by a chromosome composed by several genes. The genes represent one part or parameter of the solution candidate. In standard GAs, the chromosome is a binary string with a fixed length. New solutions, referred to as offspring, are created by breeding existing solutions, referred to as parents. Parents are randomly selected from the present population, with a bias towards the fittest individuals. Offspring are generated either through mutation (using one parent), but primarily through crossover (using two parents). Mutation involves a random modification of a single gene in the chromosome, while crossover entails merging the chromosomes of two parents. Once the offspring are generated, a survival scheme determines which individuals from the set of parents and offspring will survive and the process is repeated once again, each iteration is referred to as generation. Over successive generations, it is expected that the population "evolves" toward the optimal solution 7.
An important aspect of the basic GA, just like any meta-heuristic, is the role of the objective function. It is mostly assumed that the objective function is equivalent to the fitness function, but a subtle difference should be pointed out. The objective function defines the performance measure from the point of view of the problem, while the fitness function defines performance from the point of view of the search process, in this case the GA. While most works do not differentiate between them, the difference is important because it is not a requirement that both measure be the same.
2.2 Electronic Design with GAs
GAs have been used to design electronic circuits in several works. For instance, an early work on this topic used a GA to generate the topology and the component values of electronic circuits in 4.
Another alternative was proposed by Koza et al. in 9, they use genetic programming (GP) with a variable-length representation containing topology modifying operators, component-creating operators and arithmetic operators. In Koza's approach the operators that modify the circuit topology and select component values are inseparable, and all are under the control of the evolutionary processes operating on the circuit representation.
Circuit synthesis involves both the selection of a suitable topology and the choice of component values, and as Koza has shown 9, these may be optimized simultaneously by the evolutionary process. However, there is no reason why these operations should not be performed separately, with different optimization methods being used, specifically tailored for each task.
The circuit topology can be chosen first, and an appropriate algorithm for this task can be a standard GA. For each circuit topology generated the component values can then be optimized, and the performance of the circuit used as the objective function for the GA. In such cases, circuit fitness can be evaluated using SPICE, a simulation program with IC emphasis. The code for which can be incorporated into the synthesis program.
The component values could also be optimized using a GA, but this is not the best choice for problems involving well-behaved objective functions dependent on a fixed number of variables. It is well established that numerical optimization methods converge much faster and involve fewer objective function evaluations 3. No optimization method guarantees to find the global optimum, but it has been found that numerical optimization of component values achieves results that are close to the global optimum.
This hybrid approach using a GA to select a suitable topology and numerical optimization to choose component values is likely to be more efficient than allowing evolution to perform both tasks concurrently. In this work, however, we will only focus on the first part of the problem, that of finding novel circuit topologies, leaving any further optimization as future work for real-world implementations.
In particular, this work focuses on the synthesis of current follower (CF) circuits. These circuits copy the value of a current to other parts of a circuit. In other words, the CF can maintain a current in less impedance loads, without altering the original source. CFs can be used in various analog circuits, such as filters, oscillators, data transmission, and Current Conveyors (CC) 3, 4, 28, 30.
2.3 Objective Function
The objective function for a synthesized CF circuit K is adapted from 2, and is given by
with θ, λ, and φ defined as
where p=|BW-107|107, and
In Equations 1 to 4, g is the circuit gain, BW is the circuit bandwith, Zin is the input impedance, and Zout is the circuit output impedance. These 4 values are obtained by SPICE.
2.4 Objective-based Fitness Function
Traditionally, EA practitioners use the objective to define fitness, but this is not necessarily the case. A simple but important difference, that will be further discussed in Section 3. The objective function is used to evaluate the CF circuit is given as in Equation 1, posing a minimization problem for the search process. In particular, the parametrization used for Equation 1 is intended to steer the search to find circuits with g = 1, BW = 10MHz, Zin = 100Ω and Zout = 10KΩ, which are standard and good values for CF circuits 24. Hereafter, we refer to the standard GA that uses this fitness function as GA-OS, for objective-based search.
2.5 CFs Representation for a GA
Using nullators and norators, it is possible to describe the behavior of current followers, where for synthesis purposes, a nullator (O) and a norator (P) always must form a joined-pair 2, 28, 29.
The node in the joined terminals of the O-P pair is associated to the source (S) by a MOSFET, the other terminal of the O element is associated to the gate (G), and the other terminal of the P element to the drain (D). Figure 1(a) shows the nullor-based description of a CF, which consists of four P elements (P1-P4), each one joined with an O element.
In this work we use a binary genetic encoding introduced by 29, proposed for the automatic synthesis of analog circuits, particularly to find CF topologies. The O-P pairs can be described by a small-signal gene called SS; the synthesis of each O-P pair are coded by the gene called SMos. Moreover, the current and voltage biases are codified by the gene Bias; and the synthesis of the current biases by the current mirror MOSFET by the gene CM.
The SS gene defines the joined terminals of O-P pairs, using two bits for each O-P pair. The SMos gene can define either a PMOS or NMOS, using one bit for each O-P pair. The Bias gene is three bits for each MOSFET, and the CM gene can define 4 CMs: simple, cascode, Wilson, and modified Wilson; using two bits for each MOSFET. As a result, the genetic representation of the CF consists of a chromosome ChCF of four ordered genes, given by
An example of the CF synthesis for the proposed chromosome is shown in Figure 1(a) is depicted in Figure 1(b) using MOSFETs, where the CF obtained is known. This description has been reported in 2, 24, 29, where CFs were synthesized using a standard GA (Eq. 5). The lenght of the chromosome ChCF is computed by using n as the number of O-P pairs used to define each gene. For instance, gene SS needs 2n O-P pairs, SMos just n, while Bias needs 2n, and CM always requires just 2; therefore, the length is given by
In this work we consider three different topology sizes related with the number of MOSFETs used by the CFs, from 1 to 3. For the topology using just one MOSFET, the chromosome length is 8 bits, when using two MOSFETs 14 bits are used, and for three MOSFETs 20 bits.
3 Novelty Search
NS introduces a new perspective to guide an evolutionary search, inspired by the open-ended nature of biological evolution 27. Lehman and Stanley conjectured that the objective function does not necessarily reward stepping stones in the search space that will ultimately lead to the desired goal, particularly in challenging problems 10. The intuition behind NS is that objective functions for difficult problems, such as design problems where complex and abstract analysis is required, are fundamentally deceptive. In such cases, deceptive functions will lead a search process astray far off the optimal goal and head on towards local optima. Lehman and Stanley argue that this is so because designing explicit analytic expressions that capture the nature of the problem in its entirety lies beyond what is known of many problems, that is precisely why these problems are difficult.
Therefore, instead of the objective function, NS measures progress by focusing on the uniqueness or novelty of each new individual, which is a dynamic measure that depends on the search progress at any given generation.
3.1 Novelty-based Fitness
Instead of designing an objective function that summarizes the performance of each individual, to use NS successfully the concept of uniqueness must be grounded in some way. The uniqueness of a solution must be measured against the rest of the evolved solutions. For instance, solutions can be compared based on their genotype or phenotype, or in the case of many previous works on NS the concept of behavior 10, 16,18, 20. Whichever the chosen characterization, let us assume it is stored in a vector β that describes an individual K in the particular application domain. Lehman and Stanley proposed a measure of sparseness ρ around each individual as
where αi is the ith-nearest neighbor of β with respect to a distance or similarity measure d(· , ·), and the number of neighbors k is an algorithm parameter 10.
Given this definition, when the average distance is large then the individual is located within a sparse region of the search space, and it is located in a dense region if the measure is small, see Figure 2. The original NS proposal considers the current population and an archive of individuals to compute sparseness. An individual is added to the archive if its sparseness satisfies a certain threshold condition ρth, which is the second NS parameter. Several papers 10, 11, 12, 13, 34 have suggested implementing the archive as a FIFO queue of size q, this alleviates the cost of computing sparseness but adds another parameter.
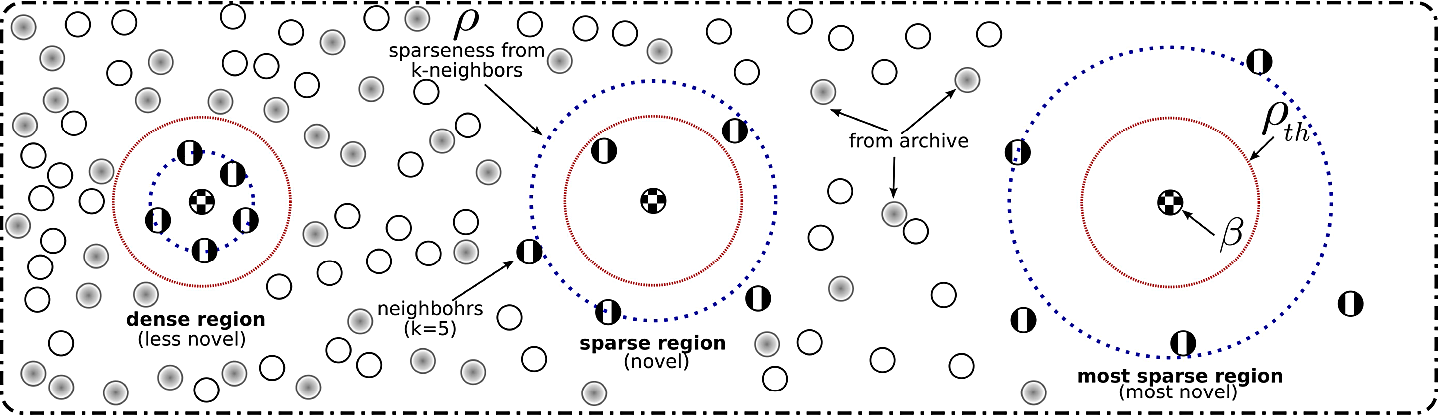
Fig. 2 The original NS proposed in 10 uses a measure of local sparseness ρ around each individual described by β, considering the current population and novel solutions from previous generations based on a threshold ρth. The Figure shows three different scenarios from the most dense region (less novel) to the most sparse (the most novel)
For a minimization problem the inverse of ρ(β) is used to assign fitness during the evolutionary process, since we want to maximize novelty (and thus increment sparseness). Hereafter, we will refer to a GA based on NS as novelty or novelty-based search (GA-NS).
3.2 CF Synthesis with GA-NS
In this work, our main goal is to apply NS in a GA search for automated CF synthesis. In this scenario, we hypothesize that the very nature of circuit design requires an exploratory and unorthodox approach, that promotes uniqueness and creativity. It is precisely in these scenarios, Lehman and Stanley argue, that NS should be able to produce strong results relative to standard objective-based search 27. To apply NS we choose to make β = ChCF , and thus sparseness is computed based on the Hamming distance in genotype space.
The hypothesis in this work is that NS will be able to find new circuit designs, designs that are left unexplored by a standard search process that relies on a fixed objective function. Therefore, in the following experimental section we will focus our work on comparing the performance of the GA-NS with the standard GA-OS approach, highlighting the unique solutions found by GA-NS. It must be stressed that Equation 7 is used to determine fitness in NS, and thus establish the selection pressure for the search. Nonetheless, the final solutions returned by the search are still chosen based on the objective function given in Equation 1. It must be understood that NS changes the manner in which the search progresses, but the underlying goal of the task is still to find the best possible solution based on a domain specific objective. The difference with a standard GA, however, is that the objective function is not used to directly guide the search, it is only used offline to choose the final solution returned by the algorithm.
4 Results and Analysis
The parameters used for both algorithms in all experiments are shown in Table 1, in accordance with previous works 2, 3, 28, 29, 30. The GA-NS parameters are summarized in Table 2, which are also quite standard values in NS-based runs. We do this to highlight the fact that NS can be used "off the shelf", without special tuning, using the same general settings of a standard evolutionary search. All algorithms are executed 10 times and performance is analyzed based on the objective function value of the best solutions found. It is important to note that after each run, the best solution found by the search algorithms are processed and analyzed manually to determine whether the solutions are valid.
Table 1 Shared parameters for the GA and GA-NS
| Parameter | Description |
|---|---|
| population size | 20 |
| Max generations | 200 |
| Stop criteria | 10 generations without |
| the best-fitness changing | |
| Selection | Tournament (size= 3) |
| Crossover | one point |
| Crossover rate | 1.0 |
| mutation | one point |
| Mutation rate | 0.05 |
Table 2 GA-NS parameters
| Parameter | Description |
|---|---|
| k-neighbors | half of pop size |
| ρth | half of chromosome size |
| archive control | FIFO |
| archive size | double of pop size |
Proposing a new topology for an analog IC is not a trivial task, since they rely heavily on the experience of the designer, and as mentioned a 100% automatic tool capable of generating them and validate a design does not exist. For this reason, a relatively small number of runs are performed. It is important to highlight that all of the best solutions found in all 10 runs of both algorithms generated valid and useful circuits, which are further discussed in what follows.
The quality measured by the objective function in Equation 1 is used by GA-NS to choose the best solution at the end of the run, and by GA-OS as the fitness value to guide the search and to choose the best solution. All experiments were carried out on a Workstation with a Xeon 3.50GHz processor with 16GB of RAM.
4.1 CF Topologies
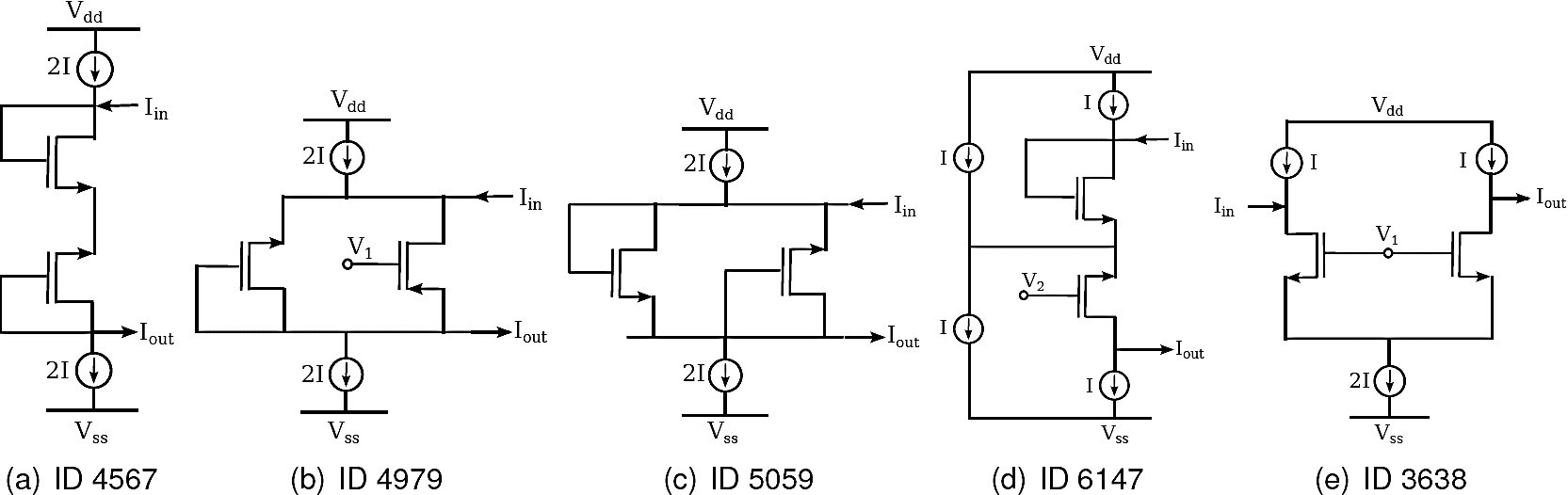
Tables 3 to 5 summarize the most notable topologies found by GA-OS and GA-NS, respectively for the three considered topology sizes (1, 2, and 3 MOSFETs). In these tables, the second column shows the generation where the best CF topology was found, and the third column shows the decimal conversion of the binary chromosome, while the last column shows its performance as given by the objective function. Moreover, Figures 3-5 present the corresponding circuit topologies; i.e., the phenotype of the solutions. For convenience, the legend of each topology in Figures 3-5 provides the corresponding decimal conversion of the genotype (chromosome) of the solution (we will use this number as a reference ID of each circuit).
Table 3 Synthesized CF topologies with one MOSFET
| method | generation | decimal (ID) | score |
| GA-OS | 6 | 143 | 5.4956 |
| GA-NS | 6 | 122 | 5.4522 |
| GA-NS | 4 | 219 | 5.2143 |
Table 4 Synthesized CF topologies with two MOSFET
| method | generation | decimal (ID) | score |
| GA-NS | 8 | 4567 | 5.0003 |
| GA-NS | 6 | 4979 | 5.2450 |
| GA-NS | 95 | 5059 | 5.0003 |
| GA-NS | 27 | 6147 | 4.8482 |
| GA-NS | 91 | 3638 | 4.7058 |
Table 5 Synthesized CF topologies with three MOSFET
| method | generation | decimal (ID) | score |
| GA-NS | 90 | 152195 | 5.2188 |
| GA-NS | 11 | 62399 | 5.2468 |
| GA-NS | 49 | 116851 | 5.2465 |
| GA-NS | 193 | 252746 | 5.3453 |

Fig. 5 Four CF topologies for the synthesis of a CF with the topology size of three MOSFETs found by GA-NS
For the simplest case, considering a single O-P pair, Table 3 and Figure 3 show two topologies found by GA-NS and one by GA-OS. It is important to note that GA-OS consistently found the same topology in all runs. On the other hand, GA-NS found different topologies in several runs. All topologies found have been previously reported and studied in the literature 24; this was expected given the small dimensions of the CF circuit to synthesize, and given that we use a previously proposed representation and fitness function. Nonetheless, both GAs synthesized non trivial circuits with proper behavior and operation. In the case of GA-NS this is important, since the fitness function does not promote any particular type of behavior, only novelty.
For the second series of experiments, considering two O-P pairs (two MOSFETs), Table 4 and Figure 4 present the best topologies found by the GA-NS, since GA-OS converged to previously published results. Topologies 4979 and 5059 can be considered trivial because you can find them manually quite easily. Moreover, topology 36387 shows a known circuit 24; which confirms that the GA-NS is guiding the search to good solutions in the search space. Finally, topologies 4567 and 6147 are novel, and should be considered as new designs of CF circuits. In both topologies gain values are near to one, and even though Zin and Zout are not ideal, these impedance's can be useful for specialized filter designs.
The third set of experiments used three O-P pairs to build circuits with 3 MOSFETs, these results are summarized in Table 5 and Figure 5. Topology 152195 (Figure 5(a)) shows three serial CFs, this a clear example of a modular design where a synthesized CF is built from simpler circuits. Figures 5(b) and 5(c) show more elaborate constructions of CFs found by GA-NS. Finally, topology 252746 in Figure 5(d) shows a novel structure that has not been presented in any related literature. Such a design confirms the ability of the NS paradigm to explore the search space and find unorthodox solutions, even to long-standing and well-known problems.
It bears mentioning that the current sources are ideal for the circuits presented in Figures 3, 4, and 5; the GAs generated a Wilson modified current mirror as the current sources on all the circuits. All topologies behave correctly as CFs, with the typical dimensions of technology, which are: Wn = 6μ, Wp = 4.4, and Ln = Lp = 1.2μ; with Vdd = 1.6V, Vss = 1.6V, and I = 20uA. A deeper analysis of these circuits and their properties is left as future work, as well as use these topologies in a real analog circuit.
4.2 Comparison between GA-OS and GA-NS
Let us now analyze the effect that the NS algorithm has on the search process for circuit synthesis, relative to objective-based search. Figure 6 shows convergence plots of the best solution found by each algorithm, showing the average behavior over all runs. The figure plots the objective function value of the best solution with respect to the number of generations. In particular, we focus on the experiments using two O-P pairs, for circuits with two MOSFETs. Based on this plot, we can see no significant difference between both algorithms. The quality of the solutions found is comparable and the convergence is similar for both algorithms, even though GA-NS reaches a better average performance. However, as stated before, the topologies found by GA-NS do not match those found by GA-OS. Therefore, in terms of the performance of the synthesized circuits both algorithms are more or less equivalent, the difference lies on the actual topologies found by each method. These results should be highlighted, since some have argued that the search carried out by the NS algorithm seems to be random, given its exclusion of the objective function. However, our results support findings in other domains 31, 32, 21, that show that NS is not a random process and that it can at the very least achieve the same level of performance as objective-based search and in many cases outperforms it.

Fig. 6 Convergence plots for GA-NS and GA-OS for the two MOSFET CFs, showing the performance (objective function value) of the best solution found over the initial generations of the search. The lines represent the average over 10 runs of the algorithms
Figure 6 only shows the convergence over the first generations based on the number of generations that GA-OS required to converge. Table 6 presents the average number of generations required by each algorithm to find the best solution for each experiment over 10 runs. It is evident from these results that the GA-OS converges much earlier than GA-NS, much earlier than the maximum number of generations allowed (after the fitness stagnates for 10 generations).
Table 6 Number of generations required by GA-OS and GA-NS to converge for each of the CF circuits: one MOSFET (M1), two MOSFETS (M2) and three MOSFETs (M3). Each row is a different run and the final row shows the average
| Run | GA-OS | GA-NS | ||||
| M1 | M2 | M3 | M1 | M2 | M3 | |
| R1 | 11 | 24 | 20 | 108 | 102 | 140 |
| R2 | 11 | 18 | 11 | 109 | 191 | 201 |
| R3 | 16 | 12 | 13 | 201 | 201 | 97 |
| R4 | 15 | 10 | 21 | 36 | 201 | 97 |
| R5 | 10 | 10 | 22 | 50 | 201 | 113 |
| R6 | 6 | 6 | 6 | 193 | 106 | 176 |
| R7 | 11 | 18 | 11 | 126 | 192 | 70 |
| R8 | 16 | 12 | 13 | 135 | 201 | 201 |
| R9 | 15 | 10 | 21 | 136 | 135 | 201 |
| R10 | 10 | 10 | 22 | 72 | 74 | 201 |
| Aver. | 12.1 | 13.0 | 16.0 | 116.6 | 160.4 | 149.7 |
Since GA-NS fitness is based on novelty, it takes more generations for the search to converge. This behavior highlights the fact that when the search is driven directly by the objective it can become stagnated around local optima. GA-NS certainly finds similar local optima, based on the performance measured by the objective funtion.
However, the search does not stagnate given its ability to promote diversity and explore other regions of the search space, allowing it to find solutions that might become inaccessible to GA-OS. For simplicity, and given the quick convergence of GA-OS, we can take a snapshot of the type of solutions found by each algorithm after the first 10 generations. Figures 7-9 compare the composition of the best solutions found by both GA-OS and GA-NS.
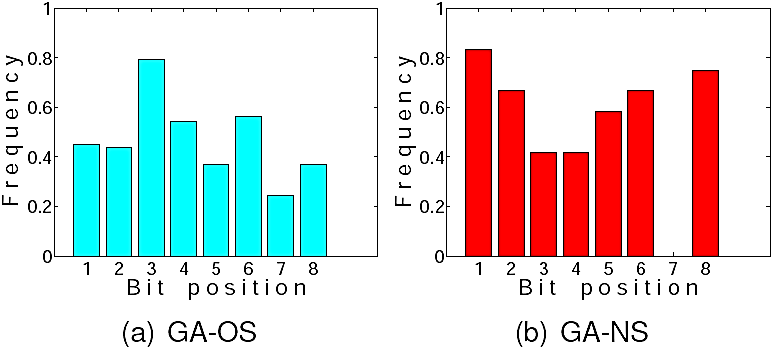
Fig. 7 Histograms showing the average composition of the chromosome of the best solution found by each algorithm after 10 generations, for the single MOSFET circuits

Fig. 8 Histograms showing the average composition of the chromosome of the best solution found by each algorithm after 10 generations, for the two MOSFET circuits
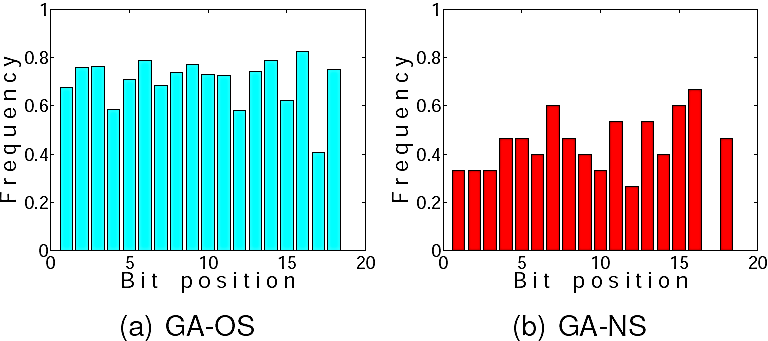
Fig. 9 Histograms showing the average composition of the chromosome of the best solution found by each algorithm after 10 generations, for the three MOSFET circuits
These figures present frequency histograms, where the height of each bar represents the percentage of runs for which a particular bit in the chromosome was set to a 1 value in the best solution found so far. For instance, if a bar reaches a value of 0.5 this means that 50% of the best solutions found after 10 generations have a 1 at that particular position within the chromosome. The plots are divided for each experimental configuration, with Figure 7 showing the results for the single MOSFET CFs, Figure 8 for two MOSFETs and Figure 9 for three MOSFETs.
These figures nicely illustrate our claim, that GA-NS finds solutions that are different from those found by GA-OS. Moreover, that the solutions found, while being different, achieve the same performance based on the objective function. This means that GA-NS explores other areas of the search space, some of which might contain local (or even global) optima that are not accessible to a standard GA-OS.
5 Conclusions
In this work we use an automatic synthesis approach for analog circuit topologies using a GA to generate CF circuits. In particular, this work proposes the use of the NS algorithm for circuit synthesis, the first such work in this field. While standard objective-based search assigns fitness and selective pressure based on the domain-specific objective function, NS guides the search by determining fitness based on the uniqueness, or novelty, of each individual solution. In the proposed GA-NS method, the objective function is only used to select the final solution returned by the algorithm, but the search is carried out based on the concept of solution novelty.
The experimental results showed that NS allows the algorithm to explore the search space in a different way than a standard GA-OS does. While the standard approach converged to expected results, the NS approach was able to discover unique solutions for even this well-known and widely studied circuit design problem.
Moreover, while the GA-NS algorithm found unique circuits, its performance was equivalent to GA-OS, showing that the NS approach can also produce high-performance solutions even when it omits the objective function from the search process.
Future work derived from this research will focus on the following. First, to optimize the evolved topologies of the CF circuits and to subject them to real-world experimental validation. Second, apply the NS paradigm to synthesize other specialized circuits of interest in the field of electronic design automation. Third, we can enhance the NS approach by attempting to force the search away from specific areas of the search space. For example, it should be possible to seed the population with previously known designs that should be avoided by the search, since they are not as interesting. In this way, the NS algorithm could be used to explicitly search for circuits that are unique in electronic literature.











 text new page (beta)
text new page (beta)