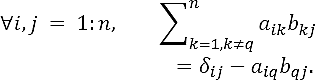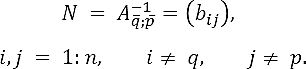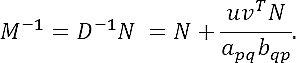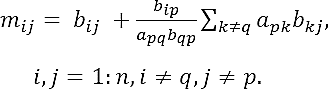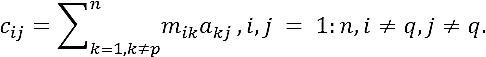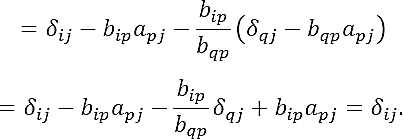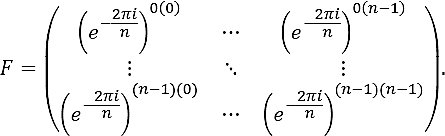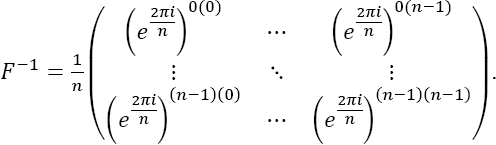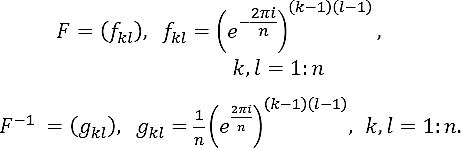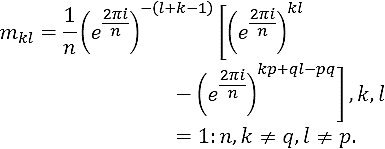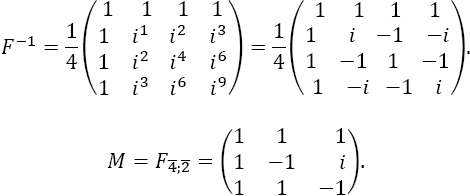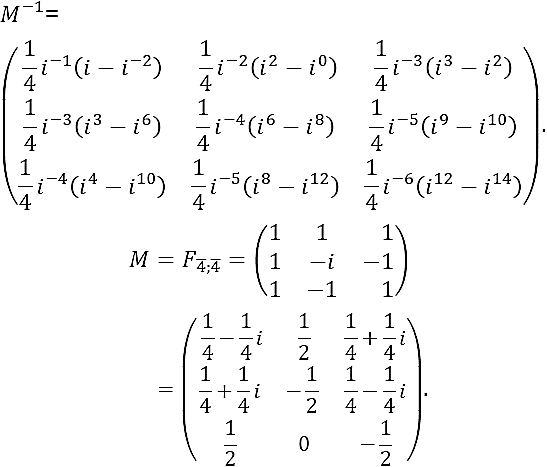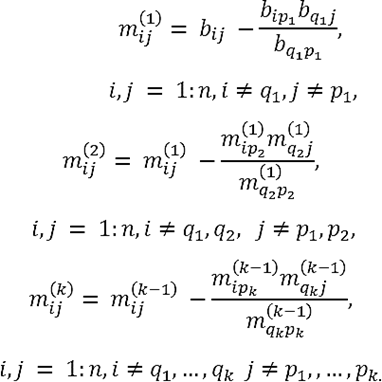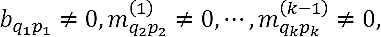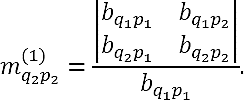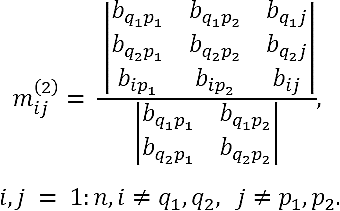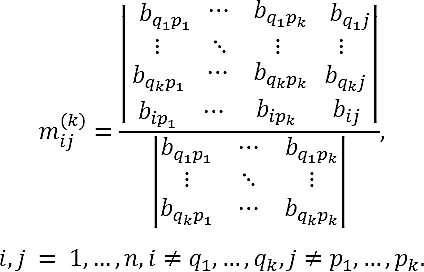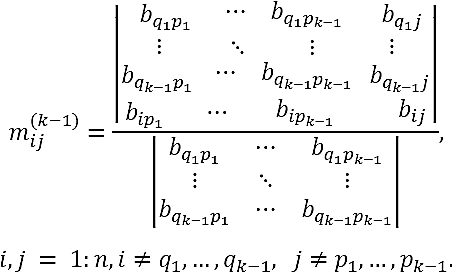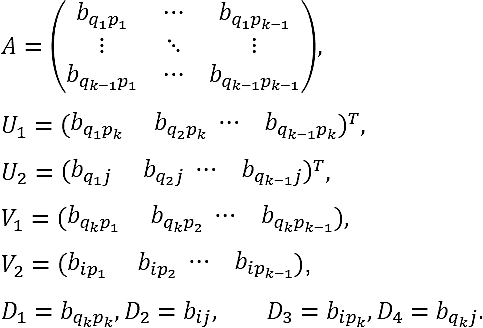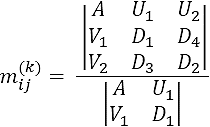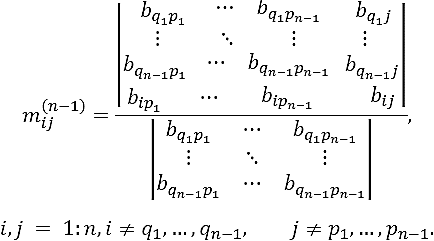1 Introduction
There are a number of situations in which the inverse of a matrix must be computed. For example, in statistics 17, where the inverse can provide important statistical information in certain matrix iterations arising in eigenvalue-related problems.
Direct methods for calculating the inverse of matrices include LU Decomposition, Cholesky Decomposition, and Gaussian Elimination 12, 17.
In Vandermonde matrices
which arise in many approximation and interpolation problems, V is non-singular if scalars 𝛼i , i = 0, ..., n are different. The inverse of V can be calculated explicitly with 6n2 flops (see 17, p. 416). El-Mikkawy 11 provides an explicit expression for the inverse of generalized Vandermonde matrices by using elementary symmetric functions. Fourier matrices obtained from the Discrete Fourier Transform (DFT) are Vandermonde matrices with known inverses 12, 17.
Let A be a non-singular matrix and A-1 be its inverse. Sometimes, it is necessary to determine the inverse of an invertible submatrix of A. This situation is common in applied physics for superconductivity computations 15, photonic crystals 8, 21, metal-dielectric materials 25, and bianisotropic metamaterials 22.
In general, computation of the inverse of a submatrix from a matrix with the known inverse is not direct. Quite recently, Chang 9 provided a recursive method for calculating the inverse of submatrices located at the upper left corner of A.
In this paper, we aim to calculate the inverse of a non-singular submatrix in terms of the elements of the inverse of the original matrix. We compare the number of operations in our method with those of the Sherman-Morrison method and the LU Decomposition.
This problem is directly related to how to calculate the inverse of a perturbed matrix (A + D)-1, where D is a perturbation matrix of A 10, 14, 19, 24. This matrix inverse has been calculated in various disciplines with different applications, derived from the Sherman-Morrison formula 5, 23:
where u, 𝑣 ∈ ℝn are column vectors, from the Sherman-Morrison-Woodbury formula 14, 16:
or from its block-partitioned matrix form 14:
Where
and C = D - VA -1U is the Schur complement of A.
Particularly, formula (2) has been applied by inverting a matrix with the enlargement method 13, which uses the same formula to express the inverse of a leading principal submatrix of order k in terms of a previously calculated submatrix of order (k - 1).
Applications of these formulas have been described in various papers. For example, Hager 14 discusses applications in statistics, networks, structural analysis, asymptotic analysis, optimization, and partial differential equations; Maponi 18 and Bru et al., 7 in solving linear systems of equations; Arsham, Grad, and Jaklic 4 in linear programming; Akgün, Garcelon, and Haftka 1 in structural reanalysis; and Alshehri 3 in the multi-period demand response management problem.
Now, we show a case where the perturbation matrix A - u𝑣T can be used to solve the problem of calculating the inverse of an invertible submatrix of order n - 1 of a known invertible matrix.
Let
The following example illustrates this procedure.
Let A and A-1 be
Let
and
Since A - u𝑣T is invertible, by using the Sherman-Morrison formula we obtain
By eliminating the 3rd row and the 2nd column, we obtain
which is the inverse of the submatrix.
If the number of additions and subtractions (NAS) and the number of multiplications and divisions (NMD) are considered separately, the Sherman-Morrison formula provides a method for calculating the inverse of a submatrix of order n -1, with
where n is the order of the original matrix. The result is obtained by doing a simple sum of each algebraic operation performed on the different steps of the algorithm.
In this paper, we show a simpler, more direct formula with
The paper is organized as follows. In the next section, we show a formula for calculating each element of the inverse of a non-singular submatrix of order n - 1 in terms of the elements of the inverse of the original matrix. An example of the use of the formula is illustrated in Section 3. The formula is implemented computationally in Section 4 on MatLab and Fortran 90 for a Fourier matrix, comparing the formula's runtime with respect to the already implemented algorithms in each programming language that are based on LU decomposition. Then, in Section 5, a general formula for the inverse of any square submatrix of a given n x n matrix is obtained. Finally, in Section 6, the relationship between the inverses of block submatrices and their original matrix, which was used in 8, 22,25, is derived.
2 Submatrices of Order n - 1
In the sequel, we consider the vector space Fnxn of matrices over the real or complex field.
Let A ∈ Fnxn, , A = (aij), i,j = 1,...,n be invertible, and let A-1= (bij), i,j = 1,..., n be its inverse. Then, we obtain
Let
or, in short,
Note that
Next, we derive the formula for the calculation of the inverse of M-1 = (mij).
Theorem 2.1.
Let A = (aij) be a nonsingular
matrix of order n, and let A-1
= (bij) be its inverse. If
apq and bqp are both not null for certain p,
q ∈ {1,...,
n}, then the submatrix
Proof. Since A-1 is the inverse of A and, reciprocally, A-1 A = AA-1 = ln where ln is the identity matrix of order n. Thus,
where δij the Kronecker's delta, being equal to 1 if i = j and to 0 if I ≠ j. These equations can be expressed as
We define D = (dij) ∈ F(n-1)x(n-1) as the matrix
where p and q indicate the number of the row and the column, respectively, which are eliminated from matrix A to obtain the submatrix
Matrix D can be expressed as
where u = (b1p,...,b(q-1)p, b(q+1)p...,bnp)T is the p - th column of A-1 after eliminating its q - th component. Analogously, vector ν = (ap1,…,ap(q -1), ap(q +1)...., apn)T is the p - th row of matrix A after eliminating its q - th component.
The inverse of D in Eq. (10) can be calculated by using the Sherman-Morrison formula (1), which contains the scalar 1 - νTu, and by using Eq. (9) we can see that
Thus, if apqbpq≠0 (i.e., both aqp and bqp are nonzero), D is invertible and, according to Eq. (1), we obtain
On the other hand, D can be expressed as a matrix form by using Eq. (8) such that
where N is the submatrix of A-1 defined as
According to Eq. (11), D-1NM=ln-1. Then,
Substituting u,νT and using matrix N in Eq. (12), the elements mij of matrix M-1 are given by
Finally, using Eq. (9) we obtain the formula
In this theorem, the condition apq ≠ 0 is necessary due to the use of the Sherman-Morrison formula; however, this hypothesis is removed in the theorem below.
Theorem 2.2. Let A be an invertible matrix of order n, and let
A-1
= (bij) be its inverse. If
bqp ≠ 0 for some q, p ∈ {1,
...,n}, then
Proof. It is sufficient to prove that submatrices M and M-1 satisfy the relation M-1M= In-1 (see 6). Since M = (aij), i,j = 1:n, I ± p,j ≠ q and M-1 = (mij), i,j = 1: n , i ≠ q,j ≠ q, the elements of their product M-1M = (cij) are
Substituting mik in Eq. (7),
by Eq. (8)
since j ≠ q, we obtain δqj = 0. ∎
By doing a simple sum of the operations required to obtain the inverse of submatrix
3 Example
Consider the DFT 𝓕 of the sequence of n complex numbers x0, ..., xn-1 into the n complex numbers y0,… ,yn-1 according to the formula:
This linear transformation can be expressed in terms of the n x n Vandermonde matrix F as
where y = (y0, ..., yn-1)T, x = (x0, ..., xn-1)T ∈ ℂn, and F is
The inverse of matrix F corresponds to the Inverse Discrete Fourier Transform
where F-1 is given by
Now, let us apply Theorem 2.2 to calculate the inverses of submatrices of order n - 1 of the matrix F in Eq. (13). To achieve this purpose, it is convenient to express matrices F and F-1 in the form
Note that gqp ≠ 0, for all q, p ∈ {1, ...,n},
then any submatrix
It should be emphasized that Eq. (15) provides the inverse of any submatrix of order n - 1 of matrix F in (13).
For the specific case n = 4, F has the form
or equivalently
And its inverse is given by
i. If
ii. If
4 Computational Implementation
First, we calculate the number of operations of the Sherman-Morrison method, formula in Eq. (7), and the LU algorithm. By using equations (4) and (5), the total number of operations to compute the matrix inverse with the Sherman-Morrison formula in Eq. (1) is 2n(2n - 1) + n(5n + 1) = 9n2 - n = 0(n2); with the formula in Eq. (7), 3(n - 1)2 = 0(n2); and with LU Decomposition, 0(n3) operations are required 2. In the specific case of Vandermonde matrices, we need 6n2 flops.
Although the number of operations with the Sherman-Morrison formula and the formula in Eq. (7) are of the same order, the slopes of the polynomial functions given by the number of operations of each method are 18 and 6, respectively, so we argue that the algorithm provided in this paper is more efficient. With the Vandermonde matrices, the slope of the function given by the number of operations is 12.
In the remaining part of this section, we compare the results of the implementation of formula (7) with LU MatLab algorithm on v.R2008a and Fortran 90 for the specific case of Vandermonde matrices of DFT (see Section 3). The algorithms were executed on a notebook with 2.27 GHz Intel Core i3 processor and a 4 GB RAM memory.
To implement the algorithm, row 4 and column 2 were eliminated in order to obtain the submatrix of order n - 1.
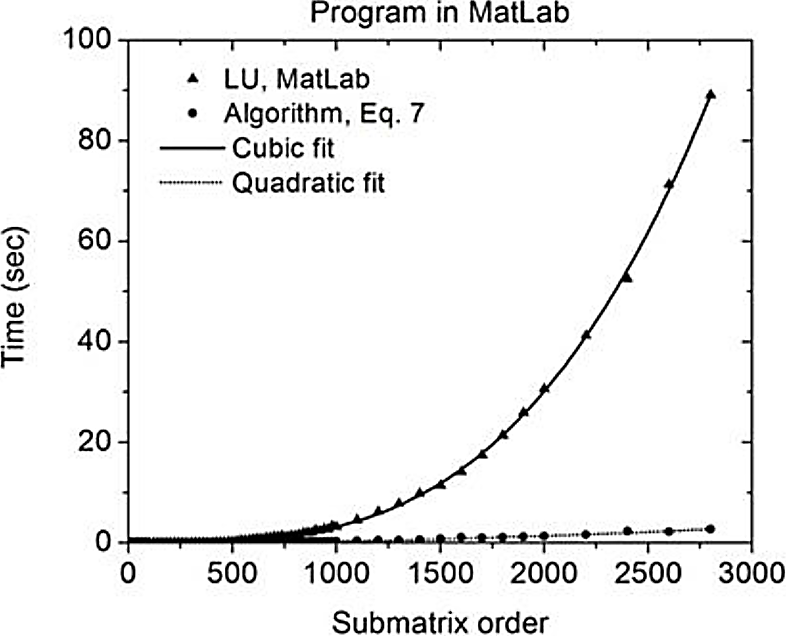
Figure 1 shows the results of comparing the matrix size with runtime on MatLab. For matrices of order 600 approximately, the algorithm performance in Equation (7) is similar to the performance of MatLab's LU algorithm. However, for higher orders, the traditional algorithm requires higher runtimes, whereas formula (7) maintains small values for matrices of order 3 x 103 approximately.
In this case, the runtime is about 3 seconds in comparison to 90 seconds of the LU algorithm.
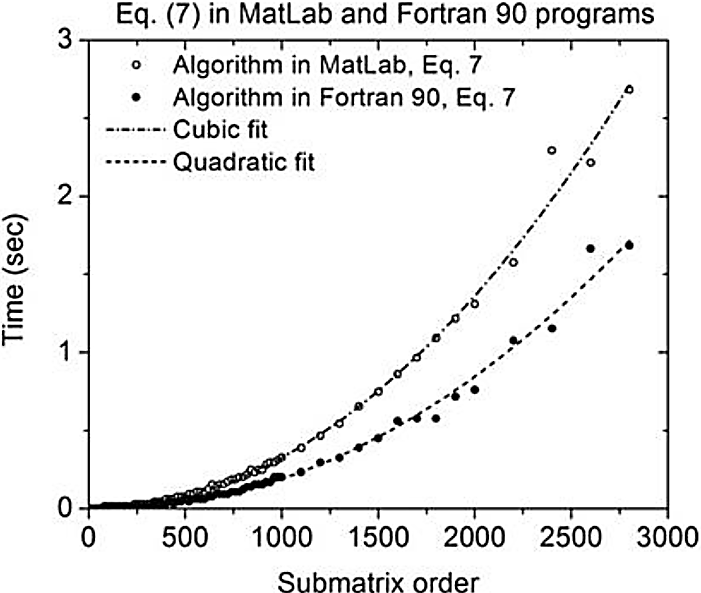
In Figure 2, the implementation results in Fortran 90 are presented. Note that the same pattern with the runtime variant increases significantly. Therefore, for a matrix of order 3 x 103 approximately, the LU algorithm runtime is about 1300 seconds.
Finally, in Figure 3, the performance of Equation (7) in both computational programs is exposed. Note that there is no significant difference on runtime performance, obtaining values of the same order of magnitude. For matrices of order 3 x 103 approximately, the runtime does not exceed three seconds. This is an indicator that algorithm performance does not depend on software.
5 Submatrices of Order n - k
5.1. Iterative Procedure
The derived relation (7) between the inverse of a submatrix
Let
This algorithm is applicable by using Theorem 2.2 if
i.e., all submatrices Ml,(I = 1: k) are invertible.
5.2 General Formula
Let us apply the iterative procedure described above to obtain explicit expressions for the
elements
Case M1. We can express formula (7) for
In particular
Case M2. Consider the invertible submatrix
After simplifying, we obtain
Thus,
In this case, therefore, we have the following theorem.
Theorem 5.1. Let A be a nonsingular matrix of order n ≥ 3, and let A-1 = (bij) be its inverse. If the submatrix of order 2
of A-1
has non-null leading principal minors, for certain
p1, p2,
q1, q2 ∈
{1,2,...,n} with p1 ≠
p2, q1 ≠
q2, then
Proof. The leading principal minors of submatrix (20) are:
If these minors are different from zero, then
Case Mk. The above results obtained for cases M1 and M2 allow us to infer a general formula for Mk, with 1 ≤ k < n.
Theorem 5.2. Let A be a nonsingular matrix of order n, and let A-1 = (bij) be its inverse. Let k ∈ N such that k < n. If the submatrix of order k x k
of A-1
has non-null leading principal minors for certain
p1, …, pk,
q1, …, qk ∈
{1,...,n} satisfying
Proof. Let us demonstrate the theorem by mathematical induction.
Step 1. Let us verify that the proposition of the theorem is true for case M1 . If the 1 x 1 submatrix
of A-1 has non-null leading principal minors, i.e
Step 2. Let us suppose that the proposition is true for case Mk -1. Thus, if the submatrix of A-1 of order k - 1
has non-null leading principal minors, the submatrix
If the conditions in (17) are satisfied, the elements
where we have used the following notation:
Using Eq. (2) for the determinant of a block-partitioned matrix (3), we directly obtain
This result agrees with formula (23). In fact, by expressing (23) as
and using Eq. (2) for the determinant of a block-partitioned matrix (3), we directly obtain
This result agrees with formula (23). In fact, by expressing (23) as
and using Eq. (5), we obtain
Subsequently, this formula is reduced to the expression
which evidently agrees with (26). It implies that this proposition is true for all k values. ∎
Note that in the specific case of k = n - 1 in Theorem 5.2, the submatrix
Then, indexes i and j, respectively, take the remaining value from the integers in {1,...,n}. Permutating the rows and columns of the determinant in the numerator of expression (27), we obtain
By using (6) to calculate the elements of the matrix inverse of A -1((A -1)-1 = A), we obtain the expected result
6 Block Submatrices
We generalize the relationship between the inverses of a matrix and their submatrices, which is derived in Section 2, to the case of block-partitioned matrices having square blocks of the same size.
Theorem 6.1.
Let
A
= (Aij) be a nonsingular block
matrix of order ns, and let
A-1 = (Bij) be its
inverse, where Bij is a s x s
square block matrix, (1 ≤ i; j ≤ n)
. If Bqp is invertible for certain q,
p ∈ {1, ...,n}, then the block-partitioned
submatrix
Proof. The demonstration follows the same procedure as Theorem 2.2.
7 Conclusions
In summary, we have obtained a formula (Eq. (7)) that allows us to calculate the inverse of a submatrix of order (n - 1) in terms of the inverse A-1 of the original n x n matrix A. By applying such a formula iteratively, we have been able to derive an explicit relationship (23) between the inverse of an arbitrary square submatrix and its inverse A-1.
In addition, we have tested the computational efficiency of the formula's runtime when compared with the LU Decomposition for the case of Fourier matrices. We have also generalized formula (5) for the case of inverses of block-partitioned matrices with square blocks of the same size s, see Eq. (28). The relationship in Eq. (28) is particularly useful when the known inverse of the matrix is a very large order (ns » 1), and it is necessary to calculate the inverse of a submatrix of order (n - 1)s.











 nueva página del texto (beta)
nueva página del texto (beta)