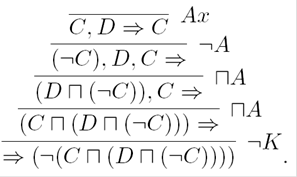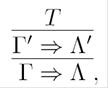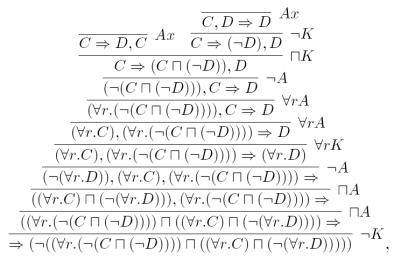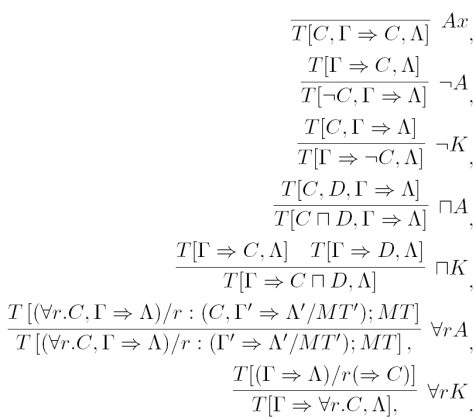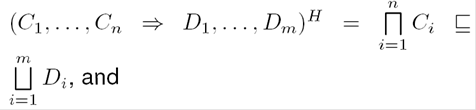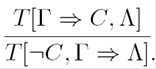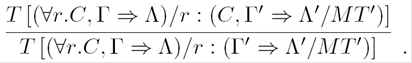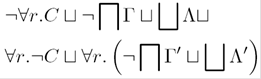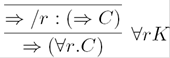1 Introduction
Description logic languages (DL) are nowadays a well-established formalism for knowledge representation 1. Closing the gap between theory and practice is one of the most appreciated features in DL. This is well exemplified by the success of the Web Ontology Language (OWL) and related reasoning technologies in the Semantic Web 11.
On the theoretical side, from the seminal work of Schild 17, a close relationship between modal and description logics is know, namely that basic propositionally closed concept language ALC is a notational variant of the multi-modal logic Km. Other relationships between more expressive logics, such as propositional dynamic logic and ALCreg were later reported in 6. These observations have been very useful in the translation of results, mostly regarding computational complexity, from the modal family to the description one 12. However, mainly due to the semantic tradition of modal logic, there is still an overall perception of unsatisfactory proof theory on description logics 14.
The formal deductive systems of sequents for first order classical and intuitionistic logics were first developed by Gentzen in his search for arithmetic consistency 7. Since then, sequent calculi have been an important tool in the syntactic analysis of proofs and in the automation of reasoning tasks.
More recent generalization of sequents systems such as (tree) hypersequents have lead to important proof theoretic results on large classes of logics, not including description ones 9,14,15. In this paper, we describe a sequent system for ALC with reflexive and transitive roles, that is, the notational variant of the modal logic S4. A complexity analysis of this system is also provided together with an implementation.
Also, a tree hypersequent system for ALC with general roles, i.e., the notational variant of the modal logic K, is also described together with its complexity analysis and implementation.
1.1 Motivations and related work
The proof theory of modal logic is not as well understood as its classical counterpart 15,14. Negri outlines very well in 14 the development and difficulties in the syntactic analysis of proofs for modal logics. In Poggiolesi’s thesis 15, there is a detailed description from the sequent systems perspective. In particular, a tree hypersequent system for the modal logic K is proposed, which is a notational variant from the system proposed in the current work for ALC. We, in addition, provide a complexity analysis of the system and an implementation.
Regarding the proof theory of description logic, we find the works of Rademaker 16, and more recently, Su and Sui 19. In this last work, a sequent system for ALC is prpoposed. However, cut elimination does not hold, and the system is undecidable. In 16, a cut-free sequent system is also proposed for ALC, and counter-models may be extracted from unsuccessful proofs. In the current work, we propose a cut-free deduction system based on tree of hypersequents, which in addition is contraction-free. This allows an implementation of the system, which is also provided.
We also propose a cut and contraction free sequent system for ALC with reflexive and transitive roles, which we name ALCS4 due to its obvious correspondence with the multi-modal logic S4. We also provide an implementation and a complexity analysis of this system.
1.2 Contributions and outline
In Section 2, we describe the basic propositionally closed concept language ALC. Axiomatizations for ALC with general, and reflexive and transitive roles are also provided. A cut and contraction free sequent system for ALC with reflexive and transitive roles is described in Section 3. Also, the system is proven correct and to be in EXPTIME. An implementation of the system is also described. In Section 4, we describe a tree hypersequent system for ALC. The system is also cut and contraction free, which allows to implement it. The implementation is also given in this Section. Correctness and complexity proofs are described.
Finally, in Section 5, we give an outline of the current work together with a discussion of further research perspectives.
2 Description Logics
In this Section, we describe two concept languages, the basic propositionally closed concept language ALC introduced by Schmidt-Schaußand Smolka 18, and a restriction of ALC with reflexive and transitive roles, which we name ALCS4 due to its correspondence to multi-modal logic S4. We define the syntax and semantics of the logics, and we also describe the corresponding axiomatizations, which are used in the completeness proofs of the derivation system proposed in the current paper.
2.1 Syntax and semantics
We assume a fixed alphabet language composed by sets of concept and role names.
Definition 1 (Syntax) Concept descriptions in the basic propositionally closed concept language (ALC) are given by the following grammar:
where A is a concept name and r is a role name.
Concepts names are interpreted on relational structures as node subsets: names A are used as node labels; negation
We also consider the following notation:
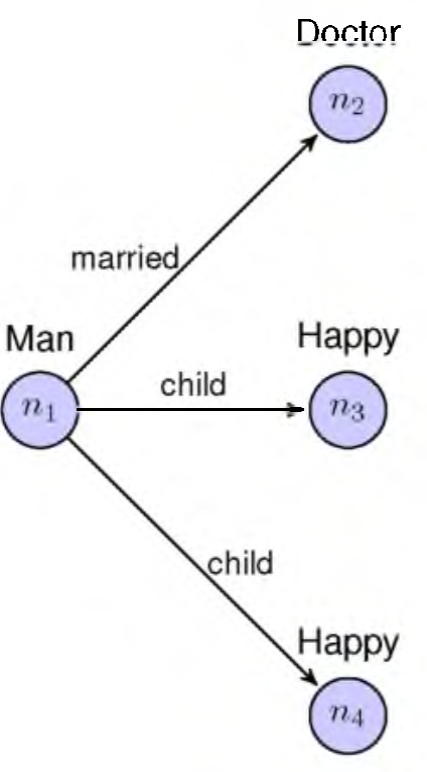
Consider for instance the following concept description 5:
This concept description can be interpreted as men married with a doctor and with happy children only. In Figure 1, a model (as a relational structure) of this concept it is depicted.
Before giving a formal description of ALC semantics we first introduce the notion of interpretation, which is a pair
Definition 2 (Semantics). Given an interpretation
An interpretation I is a model of a concept description C when
2.2 ALC axiomatization
It is well known that ALC is a notational variant of multi-modal logic K 17, hence, an axiomatization for K is also an axiomatization for ALC, which is composed by the axioms of classical logic together with the normality scheme and the rules of Modus Ponens and Necessitation.
We now give an axiomatization of ALC as given in 16.
Definition 3 (ALC axiomatization). Axioms are given as follows.
A1
A2
A3
A4
Inference rules are Modus Ponens (MP) and Necessitation (Nec).
The axioms A1-A3 can be understood as a notational variant of the corresponding axioms in classical propositional calculus, while Axioma A4 corresponds to normality in the multi-modal logic K.
If a concept description C is derivable with the ALC axiomatization, then we write
The correctness of the ALC axiomatization trivially follows.
Theorem 1 5,16. ALC axiomatization is sound and complete, that is, for any ALC concept description C, we have that
2.3 ALCS4
Given a binary relation R over a set S, we say R is reflexive if and only if for all
In the setting of ALC concept descriptions, we say an interpretation
Definition 4 (ALCS4). ALCS4 is the logic of concept descriptions described by the ALC syntax (Definition 1), but whose semantics (Definition 2) considers reflexive and transitive interpretations only.
As expected, the axiom system for ALCS4 corresponds to axiom system of the multi-modal logic S4.
A usual way to study a formal logic consists in defining a set of axioms and inference rules and then, if possible, to obtain an adequate semantic system for it. However, to study DL it is more natural to proceed in the opposite direction, i.e., starting from a semantic interpretation we analyze the valid consequences of the corresponding logic and then, if possible, define a set of axioms and rules for it.
Definition 5 (ALCS4 axiomatization). ALCS4 axiomatization is formed by the axioms and inference rules of the ALC axiomatization (Definition 3) together with the following axioms.
A5
A6
Abusing notation, when clear from context, we also write
The following results present necessary and sufficient conditions to verify axioms A5 and A6.
Proposition 1. An interpretation I is reflexive, if and only if,
it is a model for the concept description
Proof. If
Now, since I is refiexive, then (x,x)
Let x
Proposition 2. An interpretation I is transitive, if and only
if, I is a model for the concept description
Proof. If x ∈(
Now sinse I is transitive then for all z that (y,z) ∈rI, we know that (x,z) ∈rI, hence z ∈ C
I (recall x ∈(
Therefore x ∈(
Now, let x, y, z ∈
If C is such that C
I =
When then conclude that (x,z) ∈ rI.
Theorem 2 ALCS4 axiomatization is sound and complete, that is, for any concept description C and any reflexive and transitive interpretation I, we have that
Proof. We proceed as in the proof of Theorem 1 5,16, with the additional condition that the rules are refiexive and transitive, wich are supported by Propositions 1 and 2.
3 Sequents for ALCS4
We first introduce in this Section a cut and contraction free sequent system for ALCS4. Then we prove its correctness. A complexity analysis of the sequent system together with an implementation are also provided.
3.1 The calculus
The notion of sequent is first described. A sequent is a pair
We denote
A sequent rule is a non empty tuple of sequents
If a sequent rule contains only one sequent, then it is called an initial sequent. The intuitive meaning of a sequent rule is that the first sequent S0 is derived from assumption of the other sequents Si (i >0).
If the rule is an initial sequent, then that sequent can be interpreted as an axiom, because there is no need of assumptions to derive it. A non empty set of sequent rules is called a sequent system.
Before defining a sequent system for ALCS4, we define the following notation:
Definition 6 (ALCS4 sequent system). We define a sequent system for ALCS4 by the following rules.
Intuitively, a proof is defined as a tree of sequents where each step is obtained by a rule of a given sequent system, and where all the branches are finite and begin with initial sequents.
Consider for instance the following proof of axiom A1 in the sequent system ALCS4.
A substitution is a function from the set of names concepts to the set of arbitary concepts which has finite support.
Definition 7 (Proof tree) Given a sequent system, a derivation tree is inductively defined as follows:
- any rule of the sequent system, up to substitution, is a derivation tree;
- the following expression is a derivation tree
provided that Ti (i=1,…,n) are derivation trees, and
is a rule, up to substitution, such that S i
is the corresponding root (lowest sequent) of T i .
A derivation tree is a proof tree, or simply a proof, if all its branches are finite and begin with initial sequents. If there is a proof for a sequent
3.2 Correctness
In order to show ALCS4 is correct, we then show soundness and completeness.
We now state the following lemma required to prove soundness.
Lemma 1. If
Proof. If x ∈ (∀r. C
Now, assume the last. There are two cases, when there is a y, such that (y,x) ∈ rI, and when there is not.
The second case case is straightforward since x ∈(∀r. ∀r. C)I.
In the first case, it is clear that y ∈ (∀r. ∀r. C)I , now, by assumption we know x ∈ DI, and thus y ∈(∀r. D)I.
We are now ready to prove soundness.
Theorem 3 (Soudness). If there is a proof of sequent
Proof. We proceed by induction on the height of the proof tree of
The base case for
If it is now assumed that we have a proof
we then have to show that if there is also proof
Consider the case when the last step in the proof is the following
Then by induction we have that  then
then
It is then not difficult to conclude that if  and
and
We proceed analogously for the cases when the last step of the proof are rules for boolean operators.
Consider now the last proof step is the following:
By induction we thus know that for any reflexive and transitive interpretation I, the following holds:
It is also known that
We consider now the final case:
By induction
Now, we know that
Since all interpretations are transitive, then we also know that
Therefore,
We are going to show completeness by means of ALCS4 axiomatization completeness.
Theorem 4 If a concept description C is derivable in ALCS4 axiomatization, then there is a proof in ALCS4 sequent system, that is,
Proof. We proceed by induction on derivations in ALCS4 axiomatization. The base cases are the axioms and Modus Ponens. A1 has already been shown in an example above. We now show only A4, A5 and A6, which are the representatives axioms of S4.
-A4:
-A5:
-A6:
-Modus Ponens:
Here
For the induction step, we assume we have a proof for a concept description C, then we show the necessitation rule:
We are now ready to show completeness, which is immediate from Theorem 4 and Theorem 2.
Corollary 1 (Completeness) For any reflexive and transitive interpretation
I, if I is a model for a concept
description C, then there is a proof of C in
ALCS4 sequent system, that is,
It is important to state the existence of a hierarchy for the application of the rules. We first apply logical rules, followed by the right quantification rule (if possible) and concluding with the left quantification rule.
3.3 Complexity and implementation
We now show the sequent system for ALCS4 is in EXPTIME. This is mainly due to the fact that proof are binary tree shaped and there is an exponential bound on the number of binary trees.
Theorem 5 (Complexity). ALCS4 sequent system is in EXPTIME.
Proof. First notice that the system satisfies the subformula property, that is, for each rule
It is then clear that the height of the proofs (number of proof steps) is linear with respect to the size of the input sequents.
Now notice that due to the conjunction on the right rule, proofs are binary tree shaped.
The exponential bound comes from the fact that the number of nodes in binary trees are exponentially bounded with respect to height of the tree.
Regarding implementation, we followed a functional approach as in 13, more precisely, the ALCS4 system was implemented in ML 8.
We consider three fundamental data types: concept descriptions, whose alphabet is formed by concept names and roles; sequents, defined as a pair of concept lists; and rules, which can be axioms, and rules with one or two hypothesis. They are depicted in Figure 2.
The code for the implementation of rules described in Definition 6 is depicted in Figure 3.
The entire code for the implementation is in http://aleteya.cs.buap.mx/~iebp/ALCS4_Fin. ML, which was tested in PC with Intel Core i5 1.8 GHz, Windows 8.1, in the Moscow ML version 2.01.
The proof of axiom A5, which is part of the proof of Theorem 4, takes 16.4844 milliseconds in our implementation.
4 Tree Hypersequents for ALC
In this Section, we first introduce the notion of tree hypersequents, which is a generalization of sequents. It is then introduced a tree hypersequent system for ALC, without any restriction to roles. Proofs for correctness and complexity (2EXPTIME) are also given. The corresponding implementation is also described.
4.1 The calculus
Tree hypersequents as their name suggest is tree structure, where each of its nodes is sequent. The following is a more precise definition.
Definition 8 (Tree hypersequents) Tree hypersequents (THS) are inductively defined by the following grammar:
where S is a sequent.
Regarding notation, instead of
As in 10, we now define the zoom for tree hypersequents.
Definition 9 The set of zoom tree hypersequents (ZTHS) is inductively defined an the following way:
-
-If
- If S is a sequent,
- If
-If
-If
Definition 10 (ALC tree hypersequent system) We define a tree hypersequent system for ALC by the following rules.
Notice that the
As example of the use of the tree hypersequent system, consider the following proof of A4:
4.2 Correctness
We now show the ALC tree hypersequent system is correct.
Tree hypersequents are interpreted as a disjunction composed by its branches. More precisely, we inductively define the following interpretation function:
-
Theorem 6 (Soundness). If there is a proof of the tree hypersequent T in the ALC tree hypersequent system, then TH is valid.
Proof. We proceed by induction on the proof height of T.
In the base case, we distinguish two cases: one when
In the first case it is clear that  is valid.
is valid.
In the second case, it is also not difficult to see the validity of  , such that a concept D is satisfied, then ∀rD is also satisfied for any role r, given that
, such that a concept D is satisfied, then ∀rD is also satisfied for any role r, given that
In the induction step we assume a proof of a tree T´, and then we show by cases the rule
Consider now the case when the last proof step is the following:
In this case, we also distinguish two subcases: when
In the first case, we know that  From this, we imply
From this, we imply  and hence
and hence
The other cases when the last proof step involves boolean operators are proven in an analogous manner.
We focus now on the case of the quantification on the left.
We only prove the basic case and when
Then, by De Morgan's laws:
And by normality:
and since
Quantification on the right:
We again only prove the base case when  . Then
. Then  is valid which clearly implies that the root hypersequent is valid under the function H.
is valid which clearly implies that the root hypersequent is valid under the function H.
Completeness is also proven with respect to ALC axiomatization completeness. We then first show the ALC tree hypersequent system is complete with respect to ALC axiomatization.
Theorem 7 If a concept description C is derivable in ALC axiomatization, then there is a proof in ALC tree hypersequent system, that is,
Proof. The proof goes by induction on derivations in ALC axiomatization. In the base case, the only interesting subcase is the proof of axiom A4, which has been given in the example above. For the induction step, we assume we already have a proof of a concept C, then we prove the necessitation rule.
Completeness is now clear from Theorem 7 and Theorem 1.
Corollary 2 (Completeness) For any interpretation I, if
I is a model for a concept description C,
then there is a proof of C in ALC tree hypersequent system,
that is,
4.3 Complexity and Implementation
The complexity of the tree hypersequent system for ALC is in 2EXPTIME. Intuitively, proofs in this system are binary trees where its number of nodes is exponentially bounded by its height, which is itself exponentially bounded by the size of the input concept.
Theorem 8 (Complexity) ALC tree hypersequent system is in 2EXPTIME.
Proof. The first exponential bound comes from the bound on the number of nodes in binary trees with respect to the tree height. Recall from the complexity proof of the ALCS4 sequent system that rules corresponding to boolean connectives produce binary shaped proof trees, due to the subformula property.
We now show the second exponential bound the height of proof trees is exponentially bounded by the size of the input concept.
For this purpose, first recall that each node of the proof tree is a tree hypersequent. We then proceed to show that the number of nodes for each tree hypersequent is exponentially bounded by the concept size.
First, due to the subformula property, it is easy to see that the rank of each tree hypersequent is linearly bounded by the concept size. However, due to the universal quantification on the left rule, there are duplications (nodes in the tree hypersequents).
Now, there is a well-known and straightforward linear reduction of n-ary trees to binary trees2,3,4, such that the height of the binary trees is linearly bounded by the rank of the n-ary trees.
Then, the height of the binary version of the tree hypersequents is also linear.
Recalling again the exponential bound on the number of nodes in binary trees with respect to the height, we obtain that the size of each tree hypersequent (proof node) is exponential with respect to the input concept size.
The implementation of ALC tree hypersequent system is similar as the one described for ALCS4 sequent system in Section 3. However, in the case of the ALC system, the fundamental data structure is composed by tree hypersequents, which is described in Figure 4. In this Figure, a data type for proof trees with tree hypersequents as nodes is also displayed. This data type may have no applicable rule, an axiom, or a rule with one or two hypothesis. The proof of axiom A4, depicted above, takes 19.0497 milliseconds in our implementation. The full code is described in http://aleteya.cs.buap.mx/~iebp/ALC_Fin.ML.
5 Conclusions
In this paper, we introduce the proof theoretic basics for two important description logics (DL). The basic propositionally closed concept language ALC, and its variant with reflexive and transitive roles, which we name ALCS4 due to the straightforward correspondence with the multi-modal logic S4. The system for ALCS4 enjoys of cut elimination, which allows to prove decidability. In addition, this system is also contraction-free. These two features are important requirements for the implementation of sequent-like systems. The implementation is also provided. The system is also proven correct: sound and complete. And the complexity of the system is shown to be in EXPTIME.
We also introduce a proof system for ALC without restrictions on roles. The system is based on tree hypersequents, which is generalization of sequents. This system is also cut and contraction free. Correctness and complexity (2EXPTIME) proofs of the system are also given together with an implementation.
Since both systems described in this work constructively search for candidate proofs, counter-models maybe extracted from unsuccessful proofs. We are currently developing the corresponding algorithms.
We believe the reasoning frameworks provided in the current work will allow further studies in description logics from a proof theoretic perspective. In particular, we are interested in constructive proofs of Craig interpolation in the DL context.
Another immediate research perspective is the study of sequent-like proof system for description logics including terminological (TBoxes) and assertional (ABoxes) reasoning.
Also in this setting, we also plan to study more expressive description logics, including arithmetical (numerical) restrictions, inverse roles and nominals 2,3,4











 nueva página del texto (beta)
nueva página del texto (beta)