1. Introducción

Las aguas de formación altamente mineralizadas pueden causar alteraciones estructurales y composicionales en los materiales que conforman el pozo (^{Gunnlaugsson, 2012}). Adicionalmente, la precipitación de minerales puede obstruir los pozos y ocasionar daños en los equipos de bombeo (^{Diamond y Alt-Epping, 2014}). El modelaje geoquímico cinético puede ser una herramienta de gran utilidad para evaluar y predecir eventos hidrogeoquímicos, como por ejemplo, incrustaciones, corrosión, desgasificación durante la perforación y el funcionamiento de un pozo (^{Bozau et al., 2015}). El modelo presentado en este trabajo es útil para: 1) Predecir la disolución/precipitación de minerales en soluciones acuosas, realizadas como experimentos de laboratorio (^{Rimstidt y Barnes, 1980}; ^{Lin y Clemency, 1981a}, ^1981b; ^{Martínez et al., 2014}); 2) Predecir la precipitación de cuarzo en tuberías de pozos petroleros y/o pozos geotérmicos (^{Mercado et al., 1989}; ^{Lammers et al., 2017}). La precipitación del cuarzo daña las tuberías de producción, las turbinas, etc. y esto afecta la producción, ya sea de petróleo o de energía eléctrica. Conocer la velocidad de precipitación del cuarzo o de otros minerales permitiría estimar el tiempo de vida útil de las tuberías y equipos; 3) Estudiar la interacción roca - fluido en reservorios petroleros donde se está inyectando agua (^{Palandri y Kharaka, 2004}); 4) Predecir las reacciones que ocurren cuando se inyecta CO₂ en reservorios petroleros (^{Gunter et al., 1997}).

Este trabajo presenta los fundamentos matemáticos y los resultados de un desarrollo computacional que resuelve la disolución/precipitación cinética de minerales en fluidos acuosos. Este desarrollo computacional aprovecha las potencialidades del desarrollo de un código de especiación y precipitación termodinámica multifásica llamado SPCALC, Speciation Calculation (^{Pérez et al., 2012}), para predecir la cantidad de mineral disuelto o precipitado cinéticamente en una corriente acuosa, bajo distintas condiciones de presión, temperatura y pH.

2. Especiación termodinámica

SPCALC (^{Pérez et al., 2012}) junto con SOLMINEQ.88 (^{Kharaka et al., 1988}) son códigos particularmente útiles para modelar interacciones agua - roca - gas - hidrocarburo en cuencas sedimentarias profundas y reservorios térmicamente estimulados, donde los líquidos de petróleo juegan un rol muy importante.

El código termodinámico (^{Pérez et al., 2012}) y los algoritmos desarrollados para resolver el problema de disolución/precipitación cinética de minerales en una solución acuosa, usan la base termodinámica generada por SUPCRIT92 (^{Johnson et al., 1992}). El modelo de coeficientes de actividad utilizado es el Ḃ (^{Helgeson et al., 1993}).

Donde aio es el parámetro correspondiente al tamaño del ion; A _DH y B _DH corresponden a coeficientes molales de Debye-Hückel cuyos valores cambian con la temperatura del sistema; Ḃ es la función de desviación; y IS es la fuerza iónica.

Donde z _i corresponde a la carga de cada una de las especies involucradas, m _i . Cuando la carga de la especies es cero, la función Ḃ es distinta y en este trabajo se proponen tres métodos para determinar el valor de la función de desviación (Ḃ). Estos métodos son los siguientes: 1) El valor de Ḃ corresponde a la parametrización obtenida con los datos de ^{Kharaka et al. (1988)}; 2) Para especies no cargadas, el primer término de la ecuación Ḃ se hace igual a cero (0) y el término Ḃ se hace igual a 0.1 (^{Parkhurst y Appelo, 1999}); 3) En este tercer caso, los coeficientes de actividad de especies eléctricamente neutrales o no polares (por ejemplo SiO _2(aq) y H _2(aq) ) son calculados a partir de la fuerza iónica utilizando la siguiente relación (^{Bethke, 2008}):

Donde a, b y c son coeficientes polinomiales que varían con la temperatura y están descritos por las siguientes ecuaciones:

Donde T está en grados Kelvin. La actividad del agua se determina con una ecuación más precisa:

donde φ es el coeficiente osmótico de la solución y m _i es la molalidad de las especies en solución (^{Pitzer, 1973}). A partir del código de especiación termodinámica (^{Pérez et al., 2012}) se obtiene: a) La concentración de todas las especies acuosas, tanto primarias como secundarias, involucradas en el sistema; b) Las reacciones en fase acuosa, las cuales permiten la determinación de las especies secundarias involucradas en la resolución del problema de disolución/precipitación cinética de minerales; c) Las reacciones de los minerales asociados a la disolución, a partir de las cuales se obtienen los coeficientes estequiométricos y las constantes de equilibrio de los minerales que se disuelven/precipitan cinéticamente y las reacciones de todos los minerales asociados que pueden precipitar termodinámicamente; d) Los coeficientes de actividad (γi) de las especies involucradas en el sistema en estudio en el tiempo inicial t ₀ .

El algoritmo desarrollado para resolver el problema de disolución/precipitación cinética de minerales en una solución acuosa trabaja bajo las siguientes premisas: 1) Se considera que las reacciones de los iones y cationes y las reacciones de los minerales asociados a la disolución/precipitación de minerales ocurren en una fase líquida acuosa; 2) La precipitación simultánea de minerales secundarios ocurre termodinámicamente; 3) Para especies no cargadas, se utiliza en todos los casos, un valor de Ḃ igual a 0.1 (^{Parkhurst y Appelo, 1999}).

3. Fundamentos matemáticos del desarrollo computacional de ecuaciones cinéticas

Existen especies primarias y secundarias. Las especies primarias forman parte de la base y las especies secundarias se forman a partir de la combinación de las especies primarias. Por ejemplo, si se estudia la disolución/precipitación cinética de la calcita en una solución acuosa, esta se disuelve o precipita a través de la siguiente reacción química:

En este caso, las especies primarias son: HCO₃ ^- y Ca⁺⁺, pero estas especies pueden combinarse y formar otras especies acuosas, a las que llamaremos especies secundarias, como: CO _2,aq , CaCO _3,aq y Ca(HCO₃)⁺, que se forman según las siguientes reacciones químicas:

La formación de especies secundarias afecta la concentración de las especies primarias en el sistema. Siguiendo la metodología encontrada en la literatura (^{Bethke, 2008}), la base matemática que identifica el sistema en estudio corresponde a un conjunto de especies que cumple con las siguientes características: a) Cada una de las especies secundarias consideradas debe poder formarse a partir de alguna combinación de los componentes de la base; b) El número de componentes de la base es el mínimo necesario para satisfacer la primera regla; c) Los componentes deben ser linealmente independientes entre sí. Para los efectos de este desarrollo se escoge la siguiente base:

donde: A _w , corresponde al agua como solvente; A _i , corresponde a la definición de las especies acuosas primarias de la base, y A _k corresponde a los minerales que se disuelven y/o precipitan.

Las especies secundarias A _j , se definen a partir de la siguiente reacción química:

Donde ʋ representa los coeficientes de reacción: ʋ _wj es el número de moles de agua necesarios para formar A _j , ʋ _ij es el número de moles de las especies primarias necesarias para formar A _j , ʋ _kj y ʋ _mj son el número de moles de minerales y gases para formar un mol de la especie secundaria A _j . Para cada reacción química independiente del tipo (Ecuación 14) se obtiene una constante de equilibrio K _j .

Donde: a _w corresponde a la actividad del agua; a _i actividad de las especies primarias que conforman la base del sistema en el estudio; a _k corresponde a la actividad de los minerales que se disuelven y/o precipita; γj es el coeficiente de actividad de cada una de las especies secundarias; m _j corresponde a la concentración molal de las especies secundarias.

De la Ecuación 15 se despeja m _j para determinar la concentración de las especies primarias en el tiempo t. Simultáneamente se debe formular la velocidad de disolución/precipitación de los minerales denominado rk→, para luego establecer todas las ecuaciones del sistema.

3.2. Solución numérica del problema de disolución/precipitación de minerales

A partir de las Ecuaciones 16 y 17, se puede escribir el cambio instantáneo de los moles de agua con respecto al tiempo, las especies primarias, y los minerales que precipitan o se disuelven cinéticamente involucrados en el sistema:

dMwdt=∑k→vwk→rk→=rk→1 (20)

dMidt=∑k→vik→rk→=rk→ (21)

dMkdt=∑k→vkk→rk→=-rk→ (22)

Los moles del agua (M _w ), de las especies primarias (M _i ) y del mineral que se disuelve/precipita cinéticamente (M _k ) en el tiempo t, se calculan a partir de dichas composiciones en el tiempo inmediatamente anterior t' y las Ecuaciones 20 a la 22. Las ecuaciones resultantes de la resolución del sistema de ecuaciones presentado anteriormente, son las utilizadas para determinar la cinética del sistema (Ecuaciones 23 a la 25).

Mwt=Mwt'+t-t'2rk→t+rk→t' (23)

Mit=Mit'+t-t'2rk→t+rk→t' (24)

Mkt=Mkt'-t-t'2rk→t+rk→t' (25)

Para resolver este sistema químico en t, se utiliza una iteración del tipo Newton-Raphson para minimizar un conjunto de funciones residuales (Ecuaciones 26 y 27).

Rw=nw55.5+∑jvwjmj-Mwt'-t-t'2rk→t+rk→t'=0 (26)

Ri=nwmi+∑jvijmj-Mit'-t-t'2rk→t+rk→t'=0 (27)

El sistema de ecuaciones resultante de evaluar las Ecuaciones 26 y 27 en el tiempo t, se resuelve utilizando un sistema de ecuaciones no lineales como el siguiente:

JΔx=-R (28)

donde:

(29)

Δx=∆nw, ∆m1, ⋅⋅⋅, Δmn (30)

R=Rw, R1, ⋅⋅⋅, Rn (31)

n es el número de especies primarias, n _w es la masa de agua y m _i es la concentración molal de las especies primarias. Para determinar los componentes del Jacobiano, se calculan las derivadas de la Ecuación 17 con respecto a las variables independientes (n _w y m _i ). Para este sistema de ecuaciones se cumplen las siguientes relaciones:

∂mj∂nw=0 (32)

∂mj∂mi=vijmjmi (33)

∂Qk→∂nw=0 (34)

∂Qk→∂mi=vik→Qk→mi (35)

A partir de la definición del producto de las actividades, se puede determinar que drk→∕dnw=0 y que:

drk→dmiAsk+k→1-Qk→Kk→Pk→qk→ddmi∏j→mj→Pj→k→+∏j→mjPj→k→ddmi1-Qk→Kk→Pk→qk→ (36)

La solución de la derivada de la velocidad de reacción con respecto a cada especie primaria (Ecuación 36) se resuelve numéricamente utilizando diferencias finitas hacia adelante. Esto se hizo para optimizar el tiempo de cómputo (Ecuación 37).

drk→dmi=rk→Qmit-rk→Qmit't-t' (37)

En el caso de la Ecuación 37, los valores de las especies primarias que no se encuentran en la derivada (drk→∕dmi), se evalúan en el tiempo inmediatamente anterior (t'). Como se mencionó previamente, los componentes del Jacobiano se determinan derivando las Ecuaciones 26 y 27 con respecto a las variables independientes (n _w y m _i ). Estos elementos se presentan a continuación:

Jww=∂Rw∂nw=55.5+∑jvwjmj (38)

Jwi=∂Rw∂mi=nwmi∑jvwjvijmj-t-t'2∑k→vwk→drk→dmi (39)

Jiw=∂Ri∂nw=mi+∑jvijmj (40)

Jii'=∂Ri∂mi=nwδii'+∑jvijvi'jmj∕mi'-t-t'2∑k→vik→drk→dmi' (41)

donde la función delta de Kronecker (^{Rukmangadachari, 2010}) está definida como:

δii'=1 si i =i'0 si i ≠i' (42)

Es bien sabido que los valores de n _w y m _i deben ser positivos, por tal motivo se utiliza un factor de relajamiento (Ecuación 43).

1δUR=max1, -∆nw12nwt', -∆mi12mit' (43)

Y al resolver el sistema de ecuaciones JΔx=-R, se actualizan los valores correspondientes a n _w y a m _i (Ecuaciones 44 y 45).

nwt=nwt'+δURΔx1 (44)

mit=mit'+δURΔxi+1 (45)

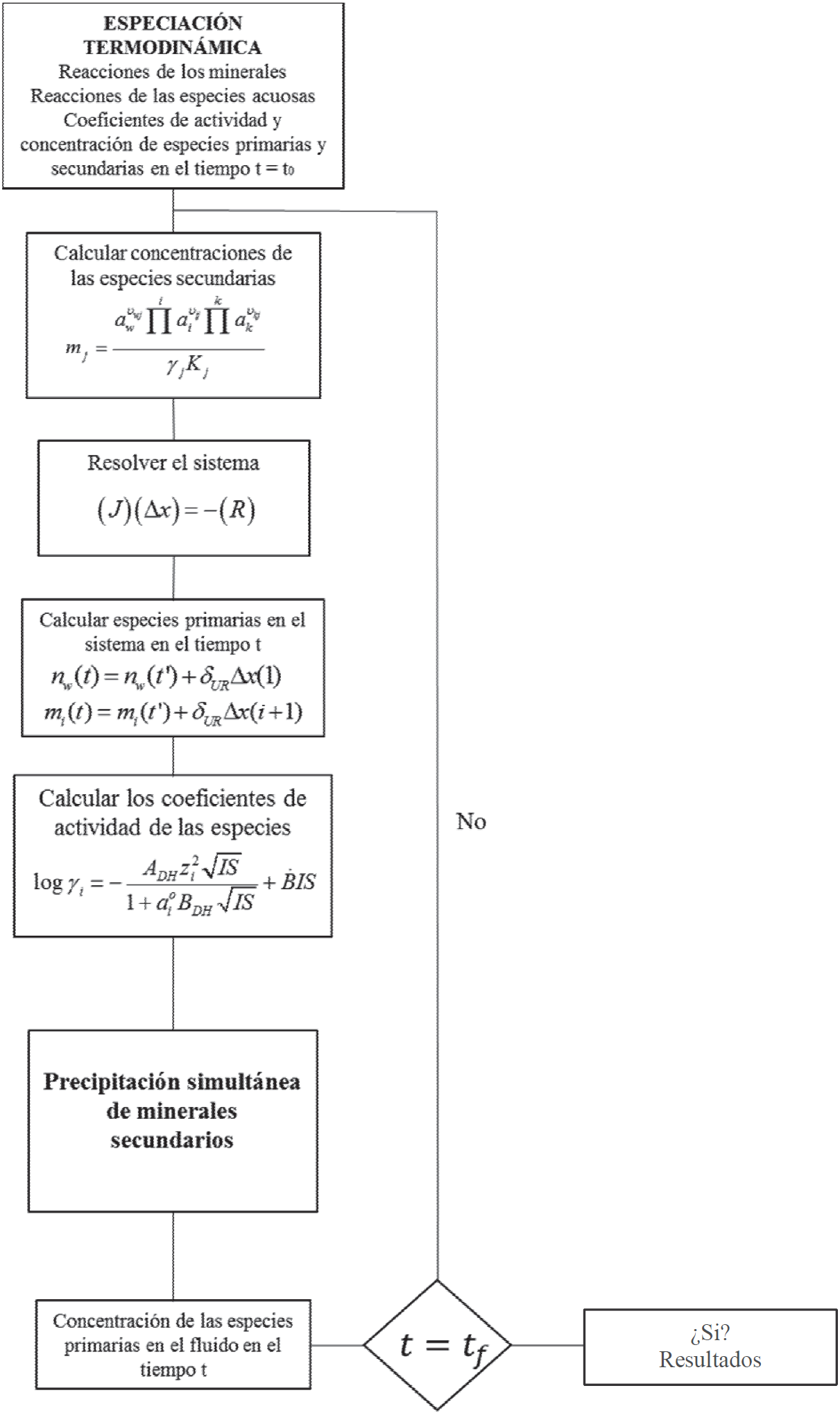
Utilizando el factor de relajamiento, se garantiza que cada variable no será reducida en más de la mitad de su valor, y por lo tanto no se volverá negativa. Este sistema se resuelve desde el tiempo t = t ₀ hasta el tiempo t = t _f (Figura 1). Luego de determinar estos valores se evalúa si hay precipitación simultánea de minerales secundarios.

Figura 1. Diagrama de flujo generalizado para resolver la precipitación/disolución cinética de minerales en soluciones acuosas. 

3.3. Precipitación simultánea de minerales secundarios

Una vez que se calcula la disolución cinética de uno o más minerales en un instante de tiempo ', puede ocurrir precipitación simultánea de otros minerales. Esta precipitación simultánea puede modelarse tanto cinética como termodinámicamente. En el caso que la precipitación simultánea se modele termodinámicamente, se procede a evaluar si dicho mineral se encuentra sobresaturado en el sistema. La sobresaturación de un mineral (A _l ) en una solución acuosa se determina a través del índice de saturación (SI _l ). Un mineral A _l , que no se encuentra en la base del problema a solucionar, se puede definir a través de la siguiente ecuación:

Al=vwlAw+∑ivilAi+∑kakvkl (46)

Quien tiene asociada la constante de equilibrio K _l . Como se mencionó previamente, la saturación del fluido con respecto a un mineral es comúnmente expresado en términos del índice de saturación, el cual es el logaritmo del cociente del producto de las actividades entre la constante de equilibrio del sistema (Ecuación 47).

SIl=log10QlKl (47)

Donde:

Ql=awvwl∏iγimivil∏kakvkl (48)

El índice de saturación dado inicialmente por el código de especiación (Pérez et al., 2012), es una medida termodinámica de la tendencia de precipitación de un mineral. El índice de saturación será negativo si el sistema no está saturado con el mineral, en el punto de saturación el índice será igual a cero (0), y si el sistema está sobresaturado el índice será positivo.

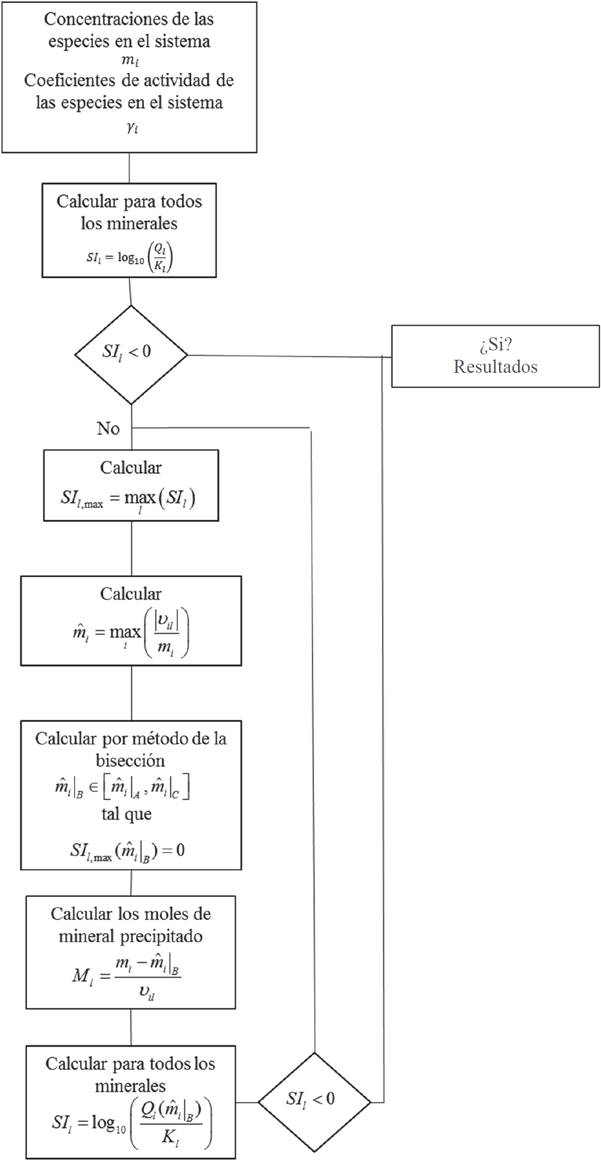
Dado que el problema cinético tiene como variable el tiempo, estas variables se calculan en cada instante de tiempo. Para cada iteración en el tiempo (t), se tienen las concentraciones de las especies en el sistema (n _w , m _i ) y sus respectivos coeficientes de actividad (). Con estos valores y los coeficientes estequiométricos (ʋ _il ) se determinan los índices de saturación de los minerales que se encuentran en el sistema y que son distintos a los minerales cinéticos, utilizando la Ecuación 47. Si los índices de saturación son menores a cero, las concentraciones de las especies en el sistema son iguales a las concentraciones de entrada. Si alguno de los índices de saturación es positivo, se sigue la siguiente metodología:

a) Se identifica el mineral cuyo índice de saturación sea máximo (Ecuación 49)

SIl, max=maxl⁡SIl (49)

b) Se identifica la especie A _i (m^i) que cumpla con la siguiente relación, para el mineral cuyo índice de saturación sea máximo:

m^i=maxi⁡vilmi (50)

c) Se calcula la raíz de la función SI _{l ,max} , utilizando el método de bisección (^{Nakamura, 1997}). Para aplicar el método de bisección, se considera que la función SI _l es una función continua en el intervalo m^iA, m^iC y SIlm^iA⋅SIlm^iC<0. Entonces, existe m^iB ∈m^iA, m^iC tal que SIlm^iB=0.

d) Luego de determinar el valor m^iB, se calculan los moles del mineral que precipitan a partir de la siguiente relación:

Ml=mi-m^iBvil (51)

e) Se evalúan de nuevo los índices de saturación para todos los minerales presentes en el sistema, utilizando la siguiente relación:

SIl=log10Qlm^iBKl (52)

Esta metodología se repite hasta que todos los índices de saturación sean menores a cero. La metodología utilizada para resolver este problema se resume en la Figura 2.

Figura 2. Diagrama de flujo generalizado para la determinación de los moles de minerales precipitados termodinámicamente. 

4. Resultados, comparaciones y ejemplos de cálculo

Los algoritmos desarrollados se comparan con datos obtenidos en experimentos de laboratorio para sistemas cerrados en donde se disuelve o precipita cuarzo (SiO _2(s) ), talco (Mg₃Si₄O₁₀(OH) _2(s) ), forsterita (Mg₂SiO _4(s) ) y muscovita (KAl₃Si₃O₁₀(OH) _2(s) ) (^{Rimstidt y Barnes, 1980}; ^{Lin y Clemency, 1981a}, ^1981b; ^{Martinez et al., 2014}). Se utilizan estos minerales ya que su disolución envuelve la ocurrencia de distintos fenómenos fisicoquímicos. Adicionalmente, el desempeño del cómputo de los algoritmos se compara con las simulaciones obtenidas usando el modelo de ^{Bethke (2008)}. Cuando se realiza la comparación con los datos experimentales, se usan los parámetros cinéticos suministrados por ^{Rimstidt y Barnes (1980)} en el caso del cuarzo; ^{Lin y Clemency (1981a)} en el caso del talco; ^{Martinez et al. (2014)} en el caso de la forsterita; y ^{Lin y Clemency (1981b)} en el caso de la muscovita. En la comparación con las simulaciones obtenidas usando el modelo de ^{Bethke (2008)} se utilizan los parámetros cinéticos compilados por ^{Palandri y Kharaka (2004)}.

4.1. Disolución/precipitación del cuarzo (SiO_2(s))

4.1.1. Comparación con datos experimentales

En este caso, se compara con datos experimentales que corresponden a la disolución y precipitación de cuarzo en una solución electrolítica de 0.5 m de NaOH a 105°C, 10 bar y un pH constante igual a 13 (^{Rimstidt y Barnes, 1980}) en 7 días de reacción. En ambos casos el cuarzo tiene una superficie específica de 920 cm²/g. Las condiciones de reacción de cada una de las experiencias se presentan en la Tabla 3. La disolución/precipitación del cuarzo se modela a través de la siguiente reacción química:

SiO2S=SiO2aq (53)

Tabla 1. Concentración de las especies en una solución acuosa electrolítica similar al agua de mar utilizadas en cada uno de los ejemplos 4.1.2, 4.2.2, 4.3.2 y 4.4.2. 

Iones en solución electrolítica (Especies)	Concentración (molal)
Na+	0.46803
Cl-	0.54584
K+	0.010205
Ca+2	0.010254
HCO3 -	0.0023272a
Mg+2	0.053065
Br-	0.00083855
SiO2(aq )	0.000001
Al+3	0.000001b
SO4 -2	0.028209

^a En el caso de la disolución de forsterita en la solución electrolitica este valor es igual a cero.

^b Este valor en el caso de la disolución cinética de la muscovita, en los demás casos es igual a cero.

Tabla 2. Parámetros cinéticos para la evaluación de la disolución de minerales en una solución acuosa electrolítica. 

Parámetros	a Cuarzo	b Cuarzo pH > 7	a Talco	a Forsterita pH < 7	a Muscovita
A S (cm 2 /g)	1000	920	1000	1000	1000
log k+ (log (mol / cm2∙s))	-13.4	-13.5	-12	-6.85	-11.85
Ak→ (mol / cm2∙s)	0.0333	2.04 x 10-2	2.282 x 10-9	8.382	1.01 x 10-12
Ek→ (J / mol)	90900	67400	42000	67200	22000
Pk→ (adim)	1	1	1	1	1
qk→ (adim)	1	1	1	1	1
Pj→k→ (adim)	0	0	0	0.47	0.37
PM (g / mol)	60.08	60.08	379.27	140.69	398.31

^{a Palandri y Kharaka (2004)};

^b Se usaron como referencia los valores reportados por ^{Rimstidt y Barnes (1980)}.

Tabla 3. Condiciones de reacción de las experiencias de disolución y precipitación del cuarzo. Ejemplo 4.1.1. 

	ASKMkam2g	KMkg	mSiO2aqmolal a t =0
Experiencia 1	2.61 x 10+2	2837	1.06 x 10-3
Experiencia 2	2.65 x 10+2	2880	1.13 x 10-5

^a, KMk masa del mineral que se disuelve/precipita cinéticamente. A_S, superficie específica del cuarzo.

En la Figura 3a se presenta la concentración molal del SiO _2(aq) tanto en la precipitación (Experimento 1), como en la disolución del cuarzo (Experimento 2). En el caso del Experimento 1, la concentración del SiO _2(aq) disminuye de 1.05 x 10^-3 a 9.45 x 10^-4 mol/kg, mientras que en el Experimento 2 esta concentración aumenta de 1.13 x 10^-5 a 7.61 x 10^-4 mol/kg. Si se modela la disolución (Experimento 2) por 50 días se llega a un estado estacionario igual a 9.21 x 10^-4 mol/kg. Ahora, si se modela la precipitación, llega al mismo estado estacionario en el mismo tiempo. En el caso del Experimento 1 (Figura 3b), los moles de cuarzo que precipitan van de 0 a 1.1 x 10^-4. En el caso del Experimento 2 (Figura 3b), los moles de cuarzo que se disuelven van de 0 a 7.5 x 10^-4. Los parámetros cinéticos utilizados son los propuestos por Rimstidt y Barnes (1980; Tabla 2). Para tener un mejor ajuste se modificó el log k ₊ en un 4%, que está dentro del error experimental. Los algoritmos presentados en este trabajo describen correctamente la precipitación y disolución experimental del cuarzo en una solución acuosa.

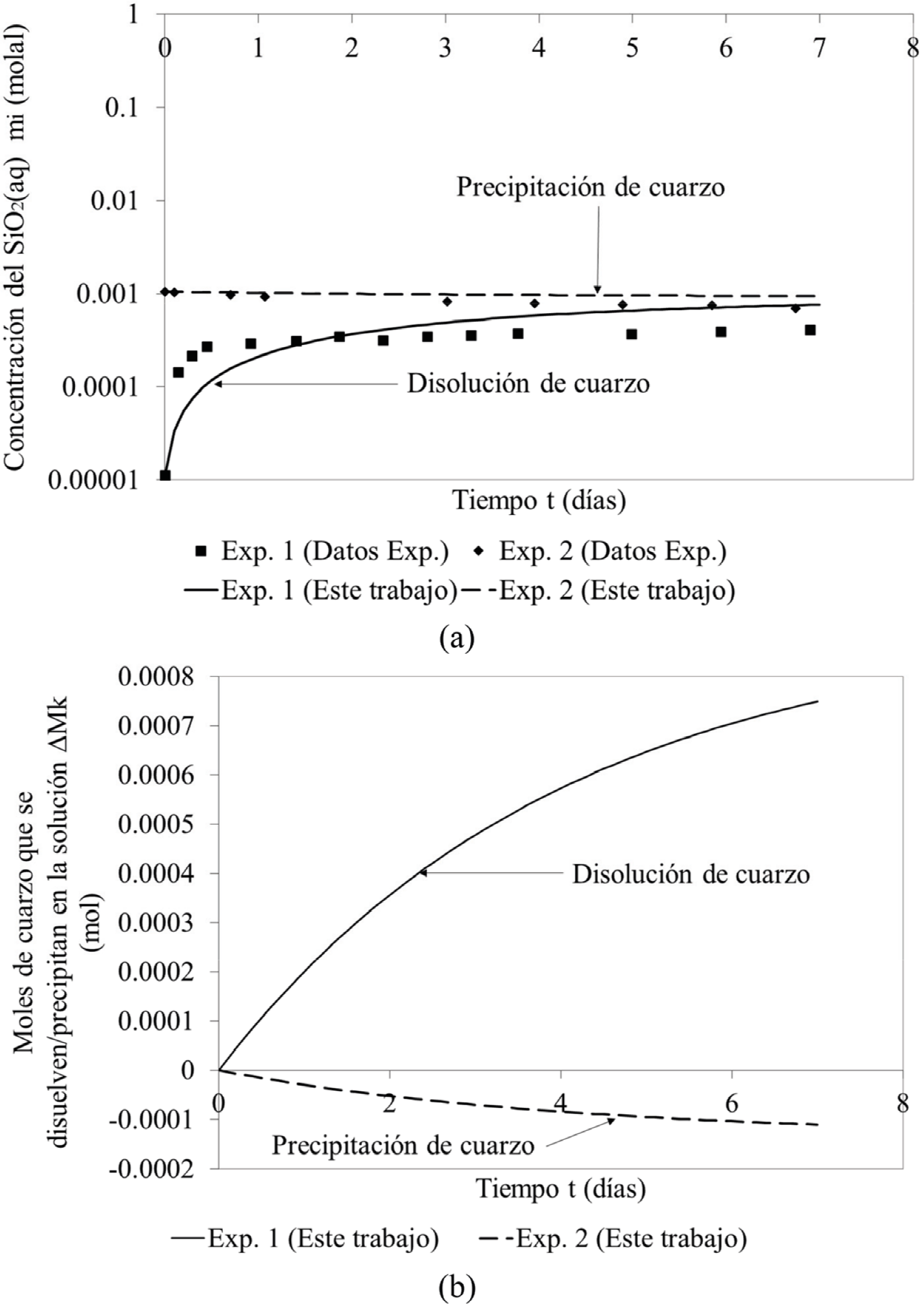
Figura 3. Comparación de la disolución/precipitación de cuarzo en una solución acuosa con una concentración de 0.5 m de NaOH a una temperatura de 105°C. (a) Concentración del SiO_2(aq) en el fluido para los experimentos 1 y 2; (b) Moles de cuarzo que se disuelven (Experimento 1) y precipitan (Experimento 2) en la solución acuosa. 

4.1.2. Comparación con modelo de ^{Bethke (2008)}

En este ejemplo se presenta la disolución de 5000 g de cuarzo en una solución acuosa electrolítica a una temperatura de 25°C y un pH de 7 (Figura 4). La superficie específica del cuarzo es igual a 1000 cm²/g. La concentración del SiO _2(aq) en el fluido aumenta de 1 x 10^-6 a 9 x 10^-6 mol/kg en un tiempo de 5 días, y al compararla con la obtenida con el modelo de ^{Bethke (2008)} se tiene un error relativo promedio de 1.3%. Durante los 5 días la concentración molal del SiO _2(aq) en el sistema y en el fluido (Figura 4a y 4b) aumentó de 1 x 10^-6 a 1 x 10^-5. La dolomita precipita como mineral asociado, en una cantidad de 0.00102 moles de dolomita en cada instante de tiempo (Figura 4d). Las ecuaciones utilizadas para calcular los coeficientes de actividad del SiO _2(aq) reproducen con un error relativo promedio de 0.8% el valor estimado por Bethke (2008). La velocidad de reacción depende fundamentalmente de la concentración de SiO _2(aq) y a medida que esta concentración aumenta, la velocidad de disolución disminuye de forma lineal de 2 x 10^-11 a 1.8 x 10^-11 mol/kg s (Figura 4f). Los cambios en los moles remanentes de cuarzo (Figura 4c) se encuentran por un orden de magnitud de 1 x 10^-6 y debido a la escala utilizada no se pueden apreciar, sin embargo, en la Figura 4g se ve claramente como aumentan los moles de cuarzo disueltos de 0 a 8 x 10^-6 mol en 5 días en la solución acuosa electrolítica. También se presenta los coeficientes de actividad de la especie SiO _2(aq) (Figura 4e). Los errores relativos promedio al comparar la velocidad de reacción, los moles remanentes de cuarzo en la solución y los moles disueltos con los resultados del modelo de Bethke son menores al 5%. Los resultados obtenidos al usar los algoritmos presentados en este trabajo reproducen cualitativa y cuantitativamente los resultados obtenidos por el modelo de ^{Bethke (2008)}.

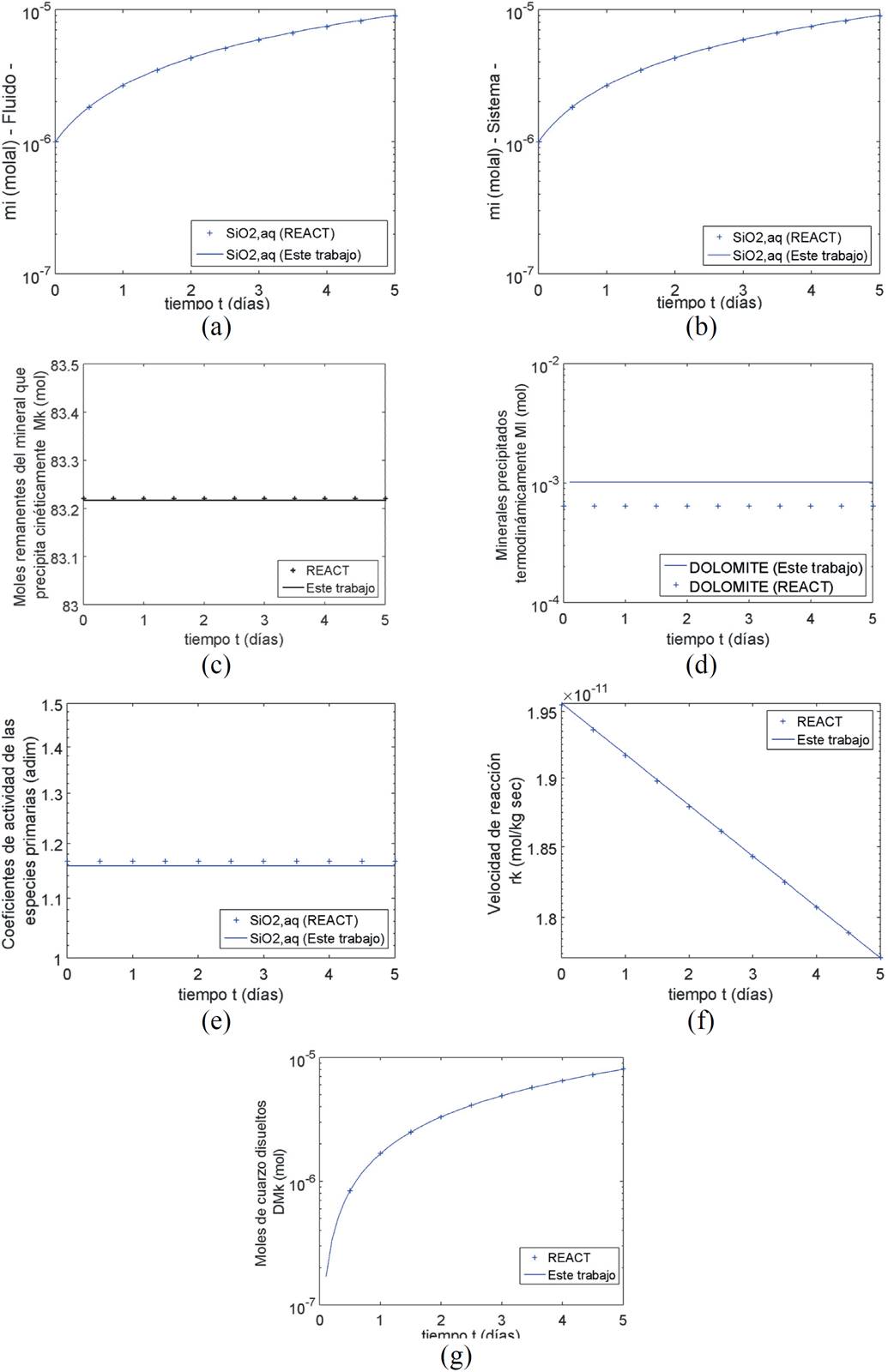
Figura 4. Resultados obtenidos para la disolución de cuarzo en una solución acuosa eléctrolítica a 25°C. (a) Concentración del SiO_2(aq) en el fluido. (b) Concentración del SiO_2(aq) en el sistema. (c) Moles remanentes de cuarzo en la solución. (d) Precipitación termodinámica de dolomita. (e) Coeficiente de actividad del SiO_2(aq). (f) Velocidad de disolución del cuarzo. (g) Moles de cuarzo disueltos. 

4.2. Disolución del talco (Mg₃Si₄O₁₀(OH)_2(s))

4.2.1. Comparación con datos experimentales

Veinticinco gramos de talco (Mg₃Si₄O₁₀(OH) _2(s) ) se disuelven en 1 l de agua destilada a 25°C y 1 atm de presión parcial de CO₂, para mantener un pH constante y cercano a 5 en la solución acuosa (^{Lin y Clemency, 1981a}). El talco se disuelve durante 50 días de acuerdo con la siguiente reacción:

Mg3Si4O10OH2S+6H+=4H2O+3Mg+2+4SiO2aq (54)

En este experimento la superficie específica promedio del talco es de 49000 cm²/g. Los valores del log k ₊ y la energía de activación utilizados para la simulación fueron -12.36 y 40800 J/mol respectivamente (Figura 5). El modelo claramente reproduce la variación de las concentraciones de las especies primarias en solución (Mg⁺² y SiO _2(aq) ) las cuales cambian de 5.1 x 10^-4 a 0.0016 mol/kg y 3.7 x 10^-5 a 1 x 10^-4 mol/kg respectivamente (Figura 5a). Los moles de talco que se disuelven van de 0 a 3.74 x 10^-4 en 50 días de reacción (Figura 5c).

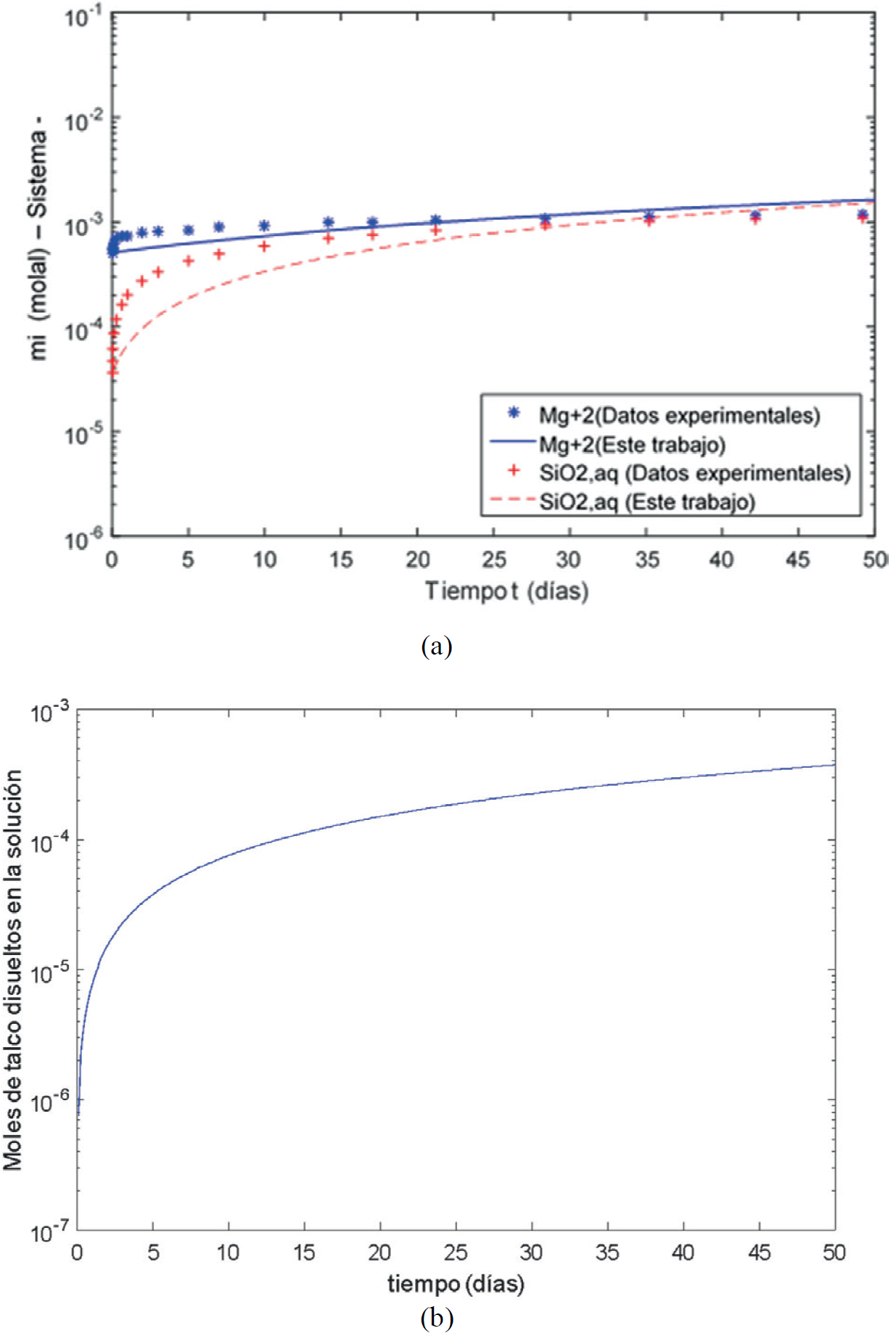
Figura 5. Veinticinco gramos de talco se disuelven en agua destilada a 25°C y una presión parcial de 1 atm de CO₂. (a) Concentración de las especies primarias (Mg⁺², SiO_2(aq)) en el sistema, se compara con los datos experimentales (^{Lin y Clemency, 1981a}). (b) Moles de talco disueltos en la solución, resultado de este trabajo. 

4.2.2. Comparación con el modelo de ^{Bethke (2008)}

En este caso se disuelven cinéticamente 5000 g de talco en una solución acuosa electrolítica durante un período de 5 días (Tabla 1). Durante este tiempo se observan los cambios más significativos en la concentración de SiO _2(aq) en el fluido (Figura 6a); en el sistema (Figura 6b); en los moles de cuarzo que precipitan termodinámicamente (Figura 6c); y en los moles de talco que se disuelven (Figura 6d). La disolución se hace a una temperatura de 25°C y un pH de 7. Al evaluar la disolución de talco en una corriente acuosa (Figura 6) se observa que la concentración de SiO _2(aq) en el sistema (Figura 6b) aumenta de 1 x 10^-6 a 8.7 x 10^-4 mol/kg en 5 días. El error relativo promedio entre los valores reportados por este modelo y los reportados por ^{Bethke (2008)} es 3.4%. Ambos modelos reproducen la disminución de la concentración de SiO _2(aq) en el fluido (Figura 6a) por precipitación de cuarzo y la diferencia entre ambos es despreciable (0.8%). La concentración SiO _2(aq) en el fluido aumenta de 1 x 10^-6 a 8.7 x 10^-7 mol/kg en las primeras 12 h de disolución y luego permanece en un valor constante (8.7 x 10^-7 mol/kg) debido a que la solución se encuentra sobresaturada de cuarzo. Los moles de cuarzo precipitados termodinámicamente (Figura 6c) aumentan de 9.5 x 10^-7 a 7.8 x 10^-4 en 4.5 días. La diferencia promedio con respecto a los valores reportados por Bethke (2008) es de 5.4%; en este caso también hay precipitación termodinámica constante de 0.00102 mol de dolomita durante los 5 días. La concentración de Mg⁺² en el sistema (Figura 6b) y en el fluido (Figura 6a) aumenta de 0.0531 a 0.0537 mol/kg, estos cambios son tan pequeños que visualmente no se observan variaciones significativas en la concentración de esta especie. Los moles de talco que se disuelven (Figura 6d) aumentan de 0 a 2.2 x 10^-4 durante los 5 días de reacción, su variación corresponde a la de un sistema de primer orden con respecto al tiempo y el error relativo promedio con respecto al modelo de Bethke (2008) es de 3.8%.

Figura 6. Resultados obtenidos para la disolución de talco en una solución electrolítica a 25°C. (a) Concentración de las especies primarias (Mg⁺², SiO_2(aq)) en el fluido. (b) Concentración de las especies primarias en el sistema. (c) Precipitación termodinámica del cuarzo y la dolomita. (d) Moles de talco disueltos. 

4.3. Disolución de la forsterita (Mg₂SiO_4(s))

4.3.1. Comparación con datos experimentales

Martínez et al. (2014) disolvió 4 g de forsterita (Mg₂SiO _4(s) ) en un litro de solución electrolítica de 0.01 m de NaNO₃ durante 32 días en un recipiente cerrado. La disolución se hizo a una temperatura constante de 22 ± 1°C y un pH inicial de 9.7. La superficie específica de la forsterita fue igual a 1239 cm²/g. La reacción propuesta fue:

Mg2SiO4S+4H+=2H2O+SiO2aq+2Mg+2 (55)

En el modelado cinético de esta disolución se utiliza un factor pre-exponencial igual a 0.34729 mol/cm²s y la energía de activación fue igual a 79000 J/mol. Los cambios de concentración de las especies primarias en el fluido se presentan en la Figura 7a, en ella se observa que la concentración de Mg⁺² varía de 5.4 x 10^-5 a 1.2 x 10^-4 mol/kg y la concentración de SiO _2(aq) varía de 6.6 x 10^-6 a 4.1 x 10^-5 mol/kg. El error promedio entre los datos experimentales y el modelo propuesto en este trabajo es del 16% y las tendencias de ambas curvas son cualitativa y cuantitativamente correctas. En la Figura 7b se muestran los moles de forsterita disueltos en la solución electrolítica, los cuales tuvieron una variación de 0 a 3.9 x 10^-5 mol en 32 días. En el caso de la forsterita se quiso mostrar también los resultados obtenidos al resolver un ejemplo de cálculo y compararlo con el modelo de ^{Bethke (2008)}.

Figura 7. Forsterita disuelta en un litro de solución electrolítica de 0.01 M de NaNO₃ a 22°C. (a) Comparación de las concentraciones del Mg⁺² y SiO_2(aq) en la solución, obtenidas experimentalmente y con los algoritmos presentados en este trabajo. (b) Moles de forsterita disueltos en la solución. 

4.3.2. Comparación con el modelo de ^{Bethke (2008)}

Se disuelven 5000 g de forsterita (Mg₂SiO _4(s) ) durante 5 días, en una solución electrolítica a una temperatura de 25°C y un pH de 6.8 (Tabla 1). Durante los 5 días de reacción se observan (Figura 8) variaciones importantes en los moles remanentes de forsterita en el sistema (Figura 8b); en el SiO _2(aq) en el sistema (Figura 8a); en el talco precipitado termodinámicamente (Figura 8c); y en los moles de forsterita disueltos cinéticamente (Figura 8e). La disolución de la forsterita ocasiona que las concentraciones de SiO _2(aq) y Mg⁺² en el sistema (Figura 8a) aumenten de 1 x 10^-6 a 0.0710 mol/kg y de 0.0531 a 0.1949 mol/kg respectivamente durante los 5 días que se estudió la disolución. La diferencia al comparar con el modelo de ^{Bethke (2008)} es despreciable (< 1%), y los cambios en la concentración del SiO _2(aq) son más significativos debido a que su concentración inicial es menor que la concentración de Mg⁺². La concentración de SiO _2(aq) en el fluido aumenta de 1 x 10^-6 a 7.6 x 10^-5 mol/kg en el primer instante de tiempo y se mantiene constante en el tiempo, el SiO _2(aq) restante ya que precipita en forma de talco (Figura 8c). Los moles de talco aumentan de 0 a 0.0177 durante 5 días, el error relativo promedio con respecto al modelo de ^{Bethke (2008)} es de 0.3%. Al igual que en los casos anteriores, las ecuaciones utilizadas en este trabajo reproducen los valores de los coeficientes de actividad de las especies primarias (Figura 8d) estimados por ^{Bethke (2008)} con un error relativo promedio de 0.4% para ambas especies primarias. Los moles de forsterita que se disuelven en el sistema aumentan de 0 a 0.0712, tal como lo haría un sistema de primer orden con respecto al tiempo, mientras que los moles remanentes en la solución de la forsterita (Figura 8e) varían linealmente de 35.54 a 35.47 mol en 5 días; la diferencia promedio de estos valores con respecto a lo reportado por Bethke es menor al 0.6%.

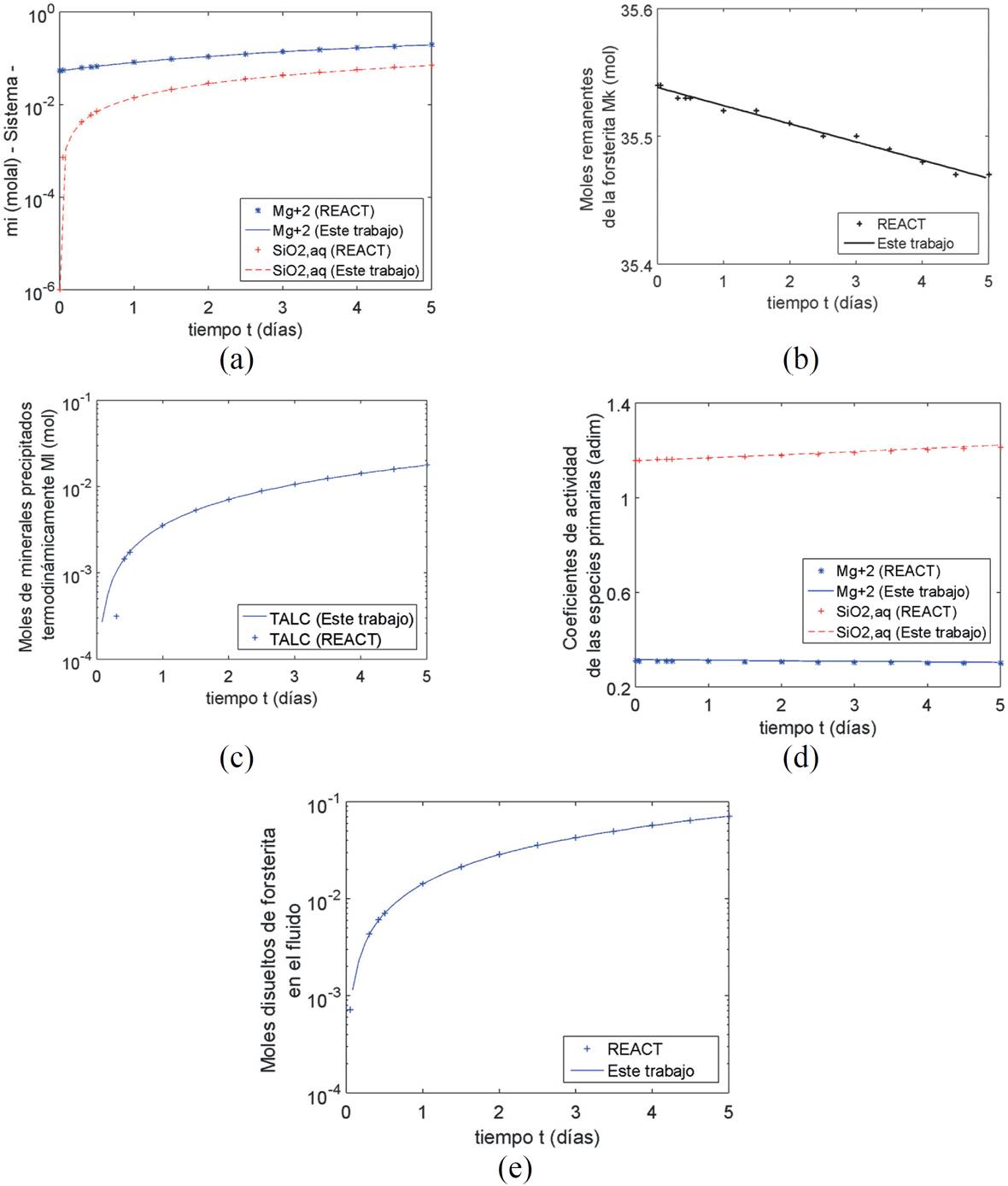
Figura 8. Disolución de forsterita en una solución acuosa a 40°C. (a) Concentración de las especies primarias en el sistema. (b) Moles remanentes de forsterita en la corriente de agua de mar. (c) Precipitación termodinámica del talco. (d) Coeficientes de actividad de las especies primarias. (e) Moles de forsterita disueltos cinéticamente. 

4.4. Disolución de la muscovita (KAl₃Si₃O₁₀(OH)_2(s))

4.4.1. Comparación con datos experimentales

^{Lin y Clemency (1981b)} disolvieron 25 g de muscovita (KAl₃Si₃O₁₀(OH) _2(s) ) en un litro de solución acuosa electrolítica (Tabla 4) a 25°C y un pH de 4.9 durante 50 días. La superficie específica de la muscovita fue 5.84 m²/g. La muscovita se disuelve cinéticamente de acuerdo a la reacción química (Ecuación 56)

Tabla 4. Concentración de las especies en una solución acuosa electrolítica utilizada en la disolución de la muscovita. Ejemplo 4.4.2 (^{Lin y Clemency, 1981b}) 

Iones en solución electrolítica (Especies)	Concentración (molal)
Na+	0.000188
K+	0.00102
Fe+2	3 x 10-6
Mg+2	1.1 x 10-5
SiO 2(aq )	2.4 x 10-5
Al+3	8.3 x 10-6

KAl3Si3O10OH2S+10H+=6H2O+3SiO2aq+K++3Al+3 (56)

Se utilizó un log k ₊ igual a -11.2, una energía de activación igual a 9000 J/mol y el exponente de la especie promotora (Pj→k→) se hizo igual a 0.37. La concentración de las especies en el fluido varía de la siguiente manera: la concentración molal del K⁺ varía de 0.0010 a 0.0014 (Figura 9a); la concentración del SiO _2(aq) varía de 2.5 x 10^-5 a 0.011 mol/kg; y la concentración de Al⁺³ se mantiene prácticamente constante en un valor de 0.8 x 10^-5 mol/kg debido a la precipitación de gibsita. La gibsita precipita termodinámicamente de forma inmediata (^{Hem y Roberson, 1967}) y la constante de equilibrio utilizada para determinar su precipitación fue log K _l = 9.5. Precipitaron 5.5 x 10^-2 moles de gibsita en los 50 días del experimento, este valor fue estimado por los algoritmos presentados en este trabajo. Los moles de muscovita se disuelven de 0 a 3.6 x 10^-4 durante los 50 días del experimento (Figura 9b). Los algoritmos presentados en este trabajo predicen la precipitación de minerales asociados de forma correcta, siguiendo la evidencia experimental y escogiendo acertadamente la especie involucrada en la precipitación termodinámica de dichos minerales.

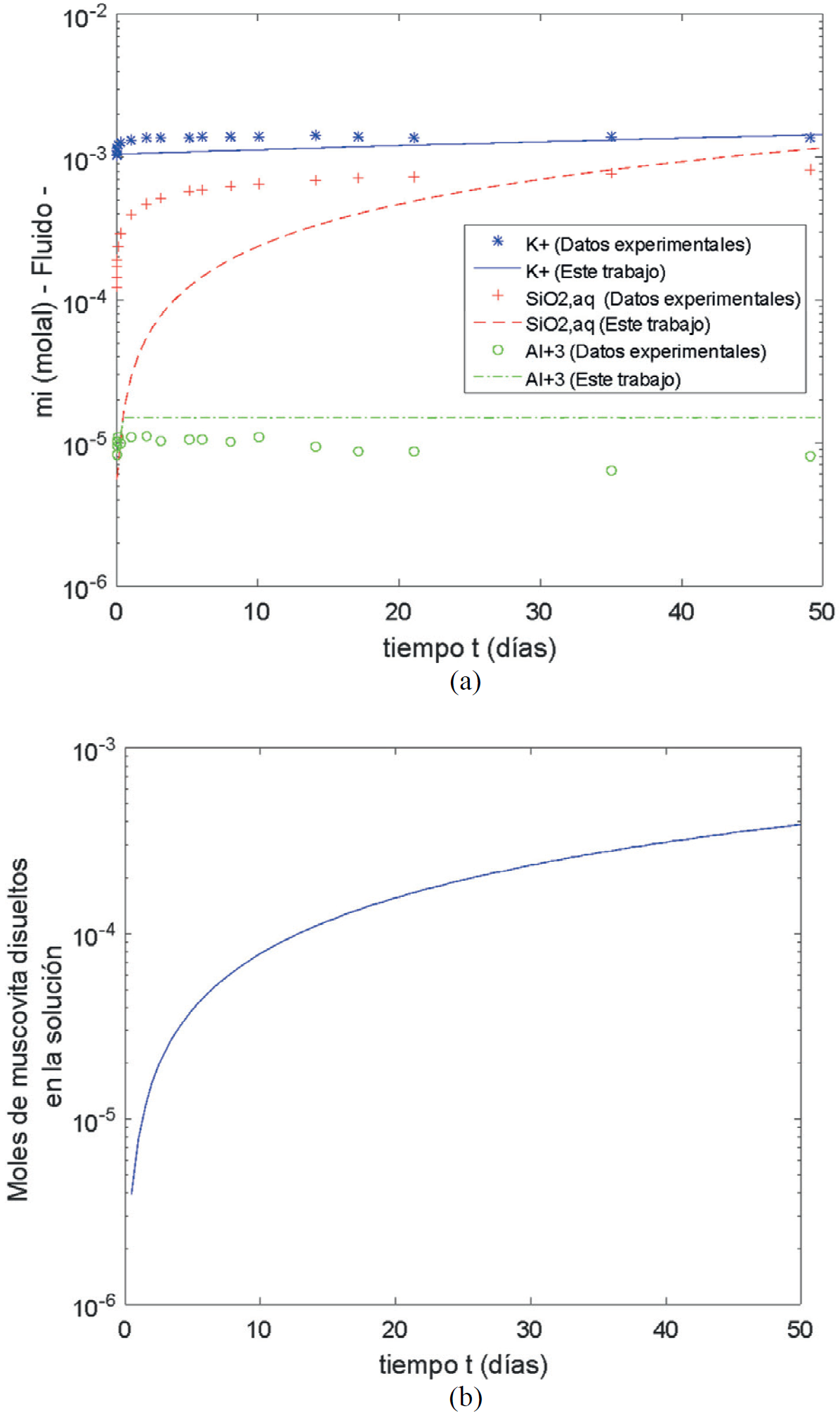
Figura 9. Disolución de la muscovita en una solución acuosa a 25°C. (a) Comparación de las concentraciones de las especies primarias en el fluido obtenidas en este trabajo con las experimentales reportadas por ^{Lin y Clemency (1981b)}. (b) Moles de muscovita que se disuelven en la solución acuosa, resultados del modelo. 

4.4.2. Comparación con el modelo de ^{Bethke (2008)}

En este cómputo se disuelven 5000 g de muscovita (KAl₃Si₃O₁₀(OH) _2(s) ), durante 5 días, en una solución (Tabla 1) a una temperatura de 40°C y un pH de 6.8. A la solución se añade Al⁺³ (Tabla 1). Los resultados de la disolución (Figura 10) muestran que la variación de la concentración del SiO _2(aq) y el Al⁺³ en el sistema (Figura 10b) aumentó de 1 x 10^-6 a 4.2 x 10^-6 mol/kg en 5 días; la concentración de K⁺ se mantiene constante en un valor de 0.0102 mol/kg. En este cómputo precipitan termodinámicamente dos minerales adicionales: dolomita y gibsita (Figura 10c), precipitan 9.8 x 10^-4 mol de dolomita en cada instante de tiempo y la gibsita aumenta de 1 x 10^-6 a 4.2 x 10^-6 mol en 5 días. Para que el índice de saturación de la gibsita sea igual a cero, la concentración de Al⁺³ en el fluido disminuye a un valor de 1.1 x 10^-13 mol/kg (Figura 10a) debido a que la gibsita precipita según la reacción química (Ecuación 57):

AlOH3S+3H+=3H2O+Al+3 (57)

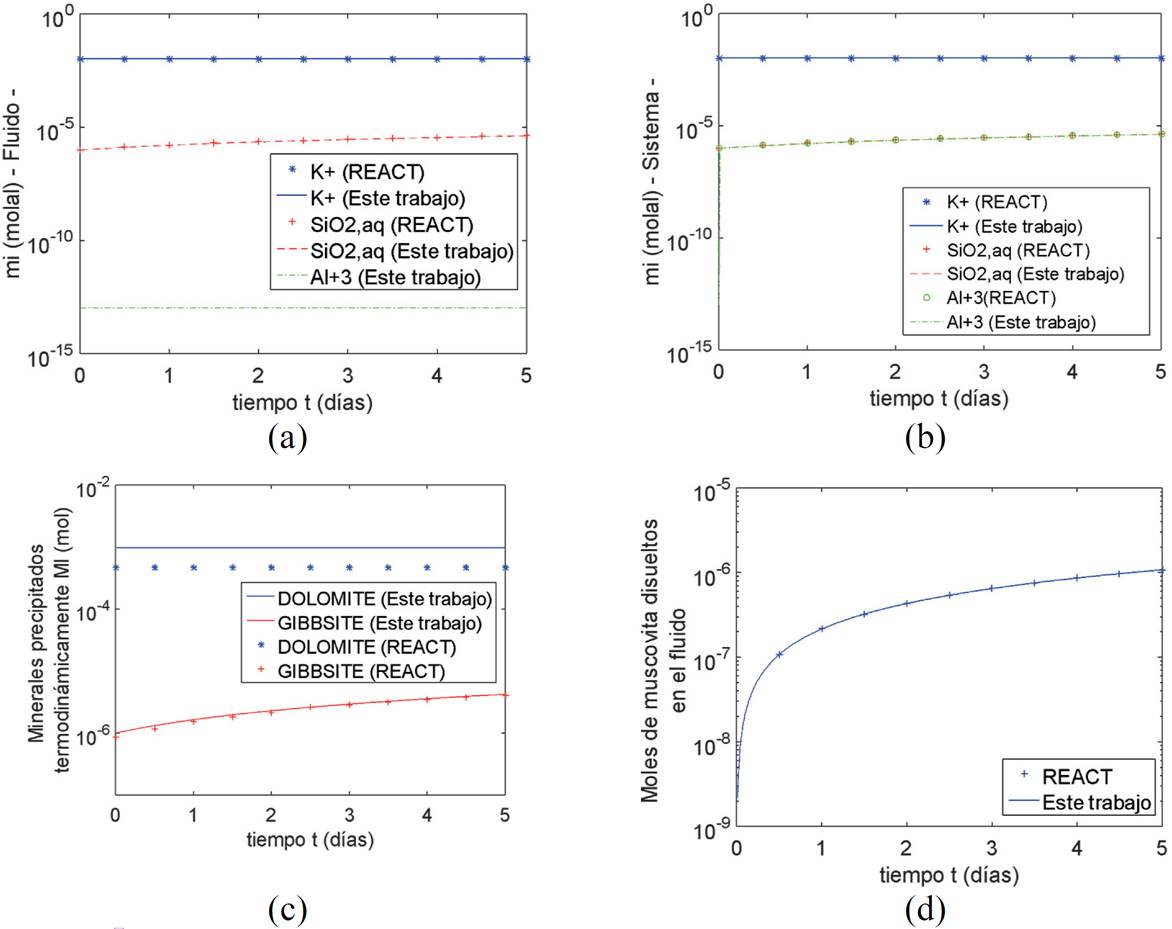
Figura 10. Disolución de la muscovita en una solución a 40°C. (a) Concentración de las especies primarias en el fluido. (b) Concentración de las especies primarias en el sistema. (c) Moles de dolomita y gibsita que precipitan termodinámicamente. (d) Moles de muscovita disueltos cinéticamente. 

La concentración de Al⁺³ en el fluido (Figura 10a) no se puede comparar con los valores obtenidos por ^{Bethke (2008)} porque este no reporta concentraciones de las especies menores a 1 x 10^-8 mol/kg. La concentración molal de SiO _2(aq) y K⁺ en el fluido es igual a la concentración de estas especies en el sistema. Los moles de muscovita disueltos (Figura 10d) en la solución aumentan de 0 a 1.1x10^-6 en 5 días. Al comparar con los resultados de ^{Bethke (2008)}, todos los errores relativos promedios se mantienen por debajo del 7%. Esto nos hace concluir que los algoritmos presentados en este trabajo describen adecuadamente la disolución o precipitación de un mineral en una solución acuosa, considerando la precipitación asociada de otros minerales y el cambio en la concentración de la especie primaria involucrada en la precipitación termodinámica de los minerales sobresaturados.

4.5. Disolución cinética de dos o más minerales simultáneamente

En este ejemplo se determina como se disuelven 5000 g de cuarzo y 250 g de cristobalita alfa en una solución electrolítica (Tabla 1) a una temperatura de 40°C y un pH de 7, durante 5 días. La cristobalita alfa (SiO _2(s) ) y el cuarzo (SiO _2(s) ) se disuelven según la reacción química:

SiO2s=SiO2aq (58)

Ambos minerales tienen la misma fórmula química pero diferente estructura cristalina y por tanto, diferente potencial químico o energía libre de Gibbs. Para ambas reacciones de disolución, la especie primaria es el SiO _2(aq) , cuya concentración es la misma en el sistema (Figura 11b) y en el fluido (Figura 11a) y aumenta de 1 x 10^-6 a 5.82 x 10^-5 mol/kg. Precipita termodinámicamente 0.00108 moles de dolomita en cada instante de tiempo (Figura 11d), pero esto es debido a la presencia en solución del HCO₃ ^-. Las velocidades de reacción de la cristobalita alfa y el cuarzo (Figura 11f) varían de 4.3 x 10^-11 a 3.83 x 10^-11 y de 1.14 x 10^-10 a 7.21 x 10^-11 mol/kg s respectivamente. La cantidad de cristobalita alfa y los moles de cuarzo que se disuelven (Figura 11g) varían de 0 a 1.75 x 10^-5 y de 0 a 5.71 x 10^-5 respectivamente, al igual que para los otros casos estudiados, ambos minerales se disuelven como un sistema de primer orden con respecto al tiempo. Al comparar con el desempeño del modelo de Bethke, el error promedio es igual a 8%. Con los resultados obtenidos en este cálculo, se quiere demostrar que el algoritmo propuesto puede resolver la disolución/precipitación cinética de uno o más minerales que se encuentran en una solución acuosa, permitiendo la precipitación termodinámica de minerales adicionales si alguno de los minerales presentes en el sistema se encuentra sobresaturado.

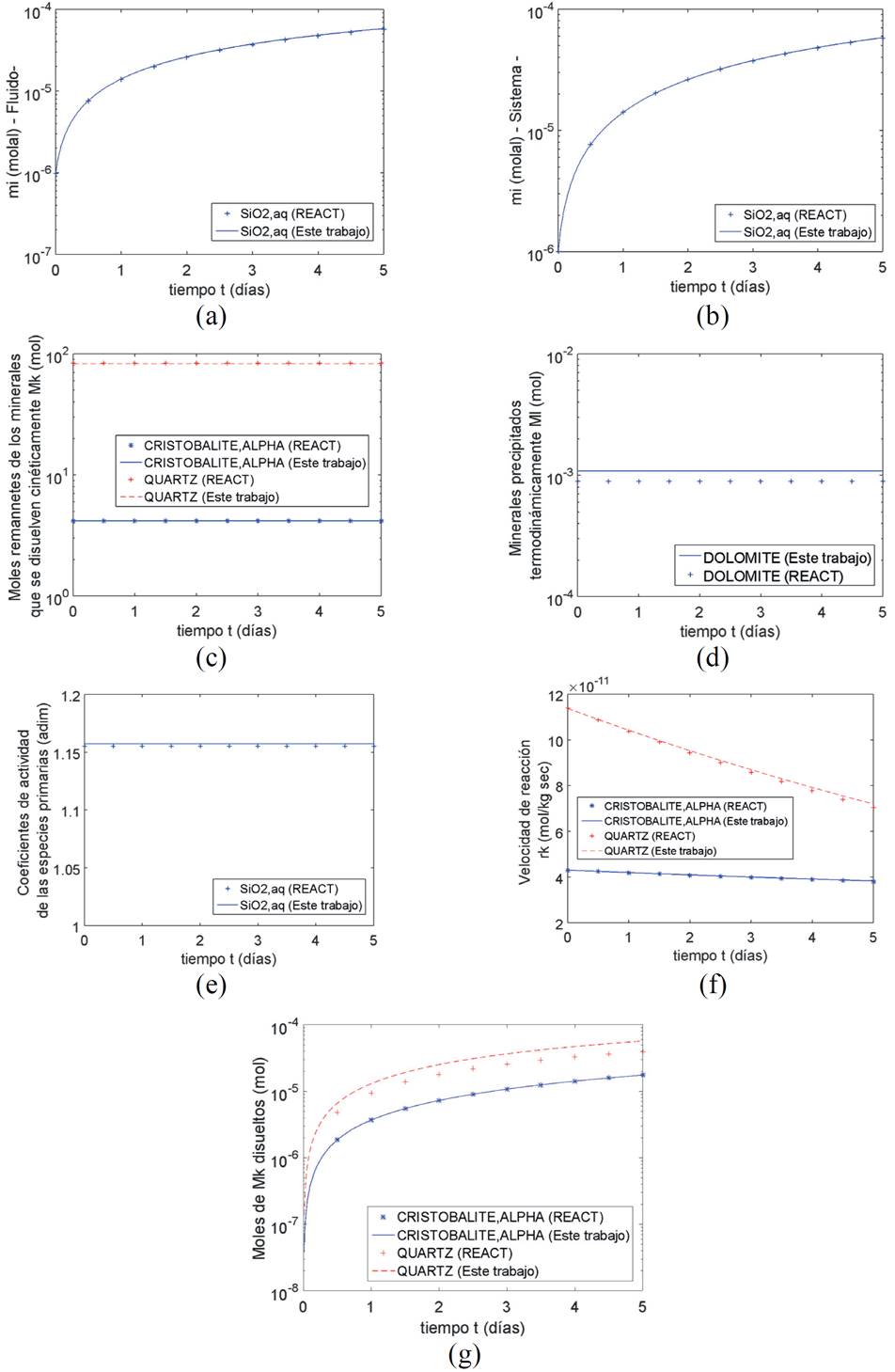
Figura 11. Disolución del cuarzo y la cristobalita alfa en una solución electrolítica similar al agua de mar a 40°C. (a) Concentración del SiO_2(aq) en el fluido. (b) Concentración del SiO_2(aq) en el sistema. (c) Moles remanentes de cuarzo y cristobalita alfa en la corriente de agua de mar. (d) Moles de dolomita que precipita termodinámicamente. (e) Coeficiente de actividad del SiO_2(aq). (f) Velocidades de reacción de la cristobalita alfa y del cuarzo. (g) Moles de cristobalita alfa y cuarzo disueltos en la solución. 

5. Aplicación: Determinación de los moles de cuarzo precipitados cinéticamente, en función del tiempo y la temperatura, en pozos del campo Cerro Prieto

La producción de energía eléctrica a partir de pozos geotérmicos es renovable y sostenible. Sin embargo, la deposición de incrustaciones como silicatos y calcita es uno de los principales problemas que experimentan estos pozos aun desde el inicio de su operación. El Campo geotérmico Cerro Prieto es uno de los cuatro campos geotérmicos que se explotan en México para generar energía eléctrica y se localiza 30 km al suroeste de la Ciudad de Mexicali, Baja California (^{Lira, 2005}); actualmente el campo cuenta con 720 MWe de capacidad instalada. Cerro Prieto es un campo de líquido comprimido de altas temperaturas (> 300°C), en el que los fluidos se han originado probablemente por mezcla de aguas del río Colorado y una salmuera hipersalina de origen marino (^{Truesdell et al., 1995}). Desde su puesta en marcha, los pozos de este campo han tenido problemas de obturación por cuarzo (^{Mercado et al., 1989}), la precipitación de cuarzo en estas tuberías de producción depende básicamente de la composición química de la salmuera y de las condiciones de presión y temperatura del pozo.

Para la óptima operación de dichos pozos es de gran utilidad conocer el tiempo que tardaría en formarse la obturación de la tubería por precipitación de minerales como el cuarzo. En la estimación del tiempo que tarda en formarse una incrustación de cuarzo en una tubería, se utilizan los algoritmos desarrollados en este trabajo para predecir los moles de cuarzo que precipitan cinéticamente en un tiempo determinado a distintas condiciones de presión y temperatura. En esta sección se presenta la variación de los moles de cuarzo precipitados cinéticamente en función de la temperatura y el tiempo de reacción.

Una salmuera que tiene una composición de Na⁺, Cl^-, K⁺, Ca⁺², HCO₃ ^-, Al⁺³, Mg⁺², Zn⁺², SiO _2(aq) y SO₄ ^-2 igual a 0.3214, 0.369, 0.03454, 0.002899, 0.001018, 0.000001, 0.0001011, 0.000001, 0.000001 y 0.0001064 mol/kg respectivamente (^{Mercado et al., 1989}) reacciona con una roca que tiene un 98% de cuarzo a diferentes temperaturas. Dichas temperaturas van de 177°C a 332°C, hasta alcanzar el equilibrio termodinámico. Luego de que las mezclas salmuera-roca se encuentren en equilibrio termodinámico, la temperatura de las mezclas disminuye y el cuarzo precipita de forma cinética, obteniéndose las curvas de esta precipitación de cuarzo en función de la temperatura en 0.5 s, 1 s, 1.5 s y 2 s . En la Figura 12 se observa claramente cómo aumentan los moles precipitados a medida que aumenta la temperatura hasta que alcanza un máximo en 312°C para todos los tiempos de reacción estudiados. Las curvas obtenidas permiten correlacionar los moles de cuarzo precipitados cinéticamente en función del tiempo y la temperatura, para ser incorporados a un modelo que permite predecir el tiempo que tarda en obturarse una tubería debido a la precipitación de cuarzo. Dicho modelo será presentado en un artículo posterior.

Figura 12. Variación de los moles de cuarzo precipitados cinéticamente con cambios en la temperatura del sistema. Aplicación en los pozos del campo geotérmico Cerro Prieto. 

6. Conclusiones

La disolución/precipitación cinética de un mineral en una solución acuosa se predice correctamente resolviendo un sistema no lineal de ecuaciones diferenciales de primer orden, en donde se encuentran involucradas las derivadas parciales de las ecuaciones residuales del agua y las especies primarias con respecto a la masa de agua (n_w) y la concentración molal de las especies primarias (m_i), a través del Jacobiano.

El uso del método numérico de la bisección (^{Nakamura, 1997}) permite determinar la concentración de las especies que se encuentran en el fluido, luego que han precipitado termodinámicamente los minerales asociados al proceso de disolución/precipitación inicial.

El modelo es capaz de reproducir datos experimentales utilizando los parámetros experimentales suministrados por los autores de dichos experimentos.

Este desarrollo predice correctamente las concentraciones en el sistema, antes que ocurra la precipitación de minerales asociados, y en el fluido, luego de la precipitación termodinámica de minerales sobresaturados, de las especies primarias que participan en la disolución/precipitación cinética de uno o más minerales; así como el cálculo de la cantidad de moles remanentes que quedan de uno o más minerales que se disuelven cinéticamente.

Con los algoritmos presentados en este trabajo se realizaron simulaciones de la precipitación cinética del cuarzo en una solución acuosa a temperaturas de hasta 327°C y a la presión de vapor de dicho sistema. Estas simulaciones corroboran la utilidad del modelo a altas presiones y temperaturas.