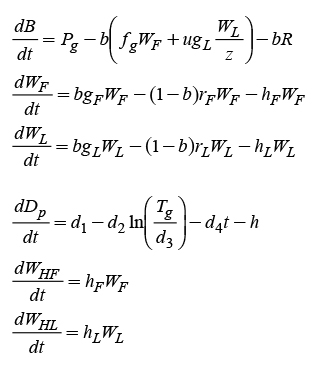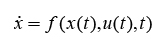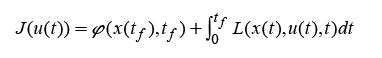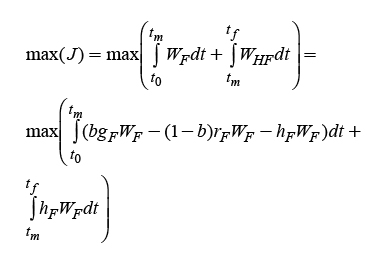Los modelos matemáticos de cultivos en invernadero

Los modelos matemáticos de cultivo simulan algunas características como el crecimiento a través de varios procesos fisiológicos de las plantas tales como la fotosíntesis, respiración, transpiración y desarrollo de cultivo. Los modelos permiten poner a prueba diferentes hipótesis del comportamiento de los cultivos sin la necesidad de realizar experimentos, lo cual implica reducir todos los costos. Por lo tanto, a partir de los modelos matemáticos de los cultivos es posible obtener buenas aproximaciones de la realidad cuando se hace una adecuada calibración y evaluación de estos (^{Bouman et al., 1994}, ^{Wallach et al., 2006}).

Los estudios de aplicación de modelos de cultivos en invernadero se han desarrollado en los Países Bajos, donde también se desarrollaron modelos dinámicos con base en procesos biológicos. Inicialmente todos estos estudios fueron desarrollados en forma numérica usando principios de balances biológicos, posteriormente fueron evaluados con datos experimentales y finalmente se aplicaron en sistemas de cultivo (^{Van Straten et al., 2011}).

Para el cultivo de tomate se han desarrollado varios modelos de crecimiento a lo largo de los años, que van desde algunos muy simples hasta muy complejos. Un modelo determinístico de crecimiento de tomates de invernadero escrito en lenguaje Pascal fue desarrollado basado en un modelo de asimilación de la hoja, más una teoría de respiración y una teoría del rango de fotosíntesis, lo cual es controlado por las condiciones ambientales y los contenidos de carbohidratos en las hojas. El modelo fue aplicado para estimar el efecto del enriquecimiento de CO₂ sobre la producción de frutos de tomate (^{Kano y Van Bavel, 1988}). En cuanto a la distribución de materia seca entre hojas, tallo, raíz y frutos de las plantas ^{Heuvelink y Marcelis (1989)}, desarrollaron un modelo dinámico. Los resultados de simulación de la materia seca entre las hojas, tallos y frutos de tomate correspondieron razonablemente bien con los datos medidos en el experimento.

El modelo TOMGRO para el cultivo de tomate se usó para calcular la fotosíntesis neta del cultivo, el cual integra el modelo Acock para el cálculo de la misma. Los resultados muestran que el modelo es inadecuado para describir el balance de CO₂ del agrosistema del invernadero, sin embargo, se determinó que puede ser usado en un modelo más complejo para describir el crecimiento y el desarrollo del cultivo de tomate (^{Zekki et al., 1999}).

Existen otros modelos para el cultivo de tomate bajo condiciones de invernadero, uno de ellos es el TOMPOUSSE, que predice la producción para los cultivos de tomate (^{Abreu y Meneses, 2000}). Además, ^{Dai et al. (2006)}, desarrollaron un modelo relativamente simple para predecir la producción de biomasa del dosel además de la cosecha de frutos para tres cultivos en invernadero incluido el tomate. Los resultados muestran que el modelo predice satisfactoriamente la producción de biomasa del dosel y la cosecha de los frutos para los tres cultivos. Por otra parte, ^{Dimokas et al. (2008)}, proponen un nuevo modelo modificado del modelo original TOMGRO. El modelo fue evaluado y calibrado en el cultivo de tomate bajo condiciones de invernadero, ya que hubo una buena relación entre los datos medidos y simulados tomando en cuenta el desarrollo del cultivo, la biomasa y la producción de frutos. Tal experimento fue desarrollado para las condiciones del mediterráneo, en el este de Grecia.

El control óptimo en invernaderos

Los métodos de control óptimo permiten la obtención de trayectorias de las condiciones medioambientales dentro del invernadero que permitirán alcanzar los objetivos de producción previamente establecidos. Estos métodos se basan en un modelo dinámico que describe el comportamiento del cultivo que se desea producir y del establecimiento de un criterio de optimización (^{Bryson y Ho, 1975}; ^{Lewis, 1986}). Por esta razón el desarrollo de controles óptimos en invernaderos es un tema que ha sido estudiado de manera muy activa en los últimos años, a continuación se hace una breve descripción de los estudios hechos en este enfoque y que son alternativas al método aquí propuesto.

En los estudios de ^{Boaventura Cunha et al. (1997)} y de ^{Coelho et al. (2005)}, se presenta una técnica general de control predictivo para regular las condiciones medioambientales dentro del invernadero, en la cual se desarrolla una predicción de los futuros estados del sistema cuando se obtiene una trayectoria óptima de control en un horizonte de tiempo fijo, la cual se re-calcula cada horizonte de tiempo. En los estudios de ^{Tap et al. (1996}, ¹⁹⁹⁷⁾ se propone un algoritmo de control óptimo que se aplica en ciertos horizontes de tiempo llamado RHOC (Receding Horizon Optimal Control) por sus siglas en inglés, el cual es evaluado durante las etapas reproductivas en la producción de tomate (Solanum tuberosum L.).

El objetivo de este estudio fue la obtención de una trayectoria subóptima de la temperatura requerida para maximizar la producción de peso fruto (W _F ) y fruto cosechado (W _HF ) de tomate ( Solanum lycopersicum L.) mediante el método de Monte Carlo.

La hipótesis fue que usando simulaciones numéricas es posible determinar la trayectoria subóptima de la temperatura a la que se debe mantener el invernadero durante un período de 120 ddt de tal forma que aumente la producción de tomate.

Modelo dinámico de tomate bajo condiciones de invernadero

Los tipos de modelos matemáticos son los empíricos, los explicativos y los teleonómicos. Los explicativos son del interés del presente estudio, se definen mediante un conjunto de ecuaciones diferenciales ordinarias que describen el comportamiento de las variables de estado del sistema, es decir aquellas variables que representan las propiedades relevantes o atributos del sistema considerado (^{López-Cruz et al., 2005}).

El modelo matemático en el presente estudio fue propuesto por ^{Tap et al. (1996)}, consta de seis ecuaciones dinámicas y por consecuencia seis variables de estado, y se describe aquí:

(1)

B[gm^-2] representa la acumulación de asimilados del peso de la materia seca por unidad de área de la planta, es decir, los recursos metabólicos que le permiten a la planta realizar todos sus procesos biológicos. W _F [gm^-2] y W _L [gm^-2] son el peso seco de los frutos y las hojas que aún están en la planta, respectivamente. D _p [adimensional] es un parámetro que nos indica la etapa de desarrollo de la planta en una escala de cero a uno mientras que W _HF [gm^-2] y W _HL [gm^-2] representan, respectivamente, los frutos y hojas que fueron cosechados, es decir, fueron desprendidos de la planta.

El modelo descrito por ^{Tap et al. (1996)} se evalúo en dos ciclos de cultivo de tomate en un invernadero tipo capilla con cubierta de policarbonato por ^{Juárez-Maldonado et al. (2012)} para las condiciones climáticas de en Saltillo, Coahuila, México (25°25’36” N, 100°59’44” O). Debido al proceso de evaluación y calibración del mismo, los parámetros del modelo en ^{Juárez-Maldonado et al. (2012)} cambiaron en comparación con los de ^{Tap et al. (1996)}. Los parámetros modificados en el presente estudio (Cuadro 1) se usaron en el modelo dinámico (1) y con ello se determinó y se resolvió el problema de maximización de la producción de tomate en condiciones de invernadero, mediante la manipulación de la temperatura.

Cuadro 1 Descripción de los parámetros de (1) obtenidos en ^{Juárez-Maldonado et al. (2012)}. 

Optimización dinámica

El sistema dinámico a estudiar es el siguiente:

(2)

donde x(t) ϵ R ⁿ es el estado, f(x(t), u(t), t) representa un vector de funciones no lineales descritas en el sistema (1), esto es, todas las funciones en forma vectorial al lado derecho de la igualdad yu(t) ϵ R ^m es el vector de entradas de control, las cuales están acotadas como:

(3)

donde α _i (t), β _i (t) son funciones conocidas.

Además tenemos el vector de condiciones iniciales definidos como

(4)

El intervalo de interés es [0, t _f ], donde t _f es el tiempo final ya definido. El problema consiste en encontrar las entradas para el control u(t) en el intervalo de tiempo [0, t _f ] que conduzcan al sistema a la trayectoria x(t), t ϵ [0, t _f ] tal que una función o variable sea maximizada en todo el intervalo de tiempo desde [0, t _f ]. En nuestro caso esa función se conoce como función de costo y está dada de la siguiente forma:

(5)

donde L es el Lagrangiano del sistema que contiene su evolución dinámica expresada en la ecuación (1) (^{Van Straten et al., 2011}) y φ(x(t _f ), t _f ) es una condición final que puede imponerse al sistema.

En el presente estudio se tomó como base el modelo dinámico de crecimiento de tomate en invernadero desarrollado por ^{Tap et al. (1996)}, para calcular una trayectoria subóptima de la temperatura que maximice la producción de fruto (W _F ) y fruto cosechado (W _HF ) de tomate en invernadero. Para resolver este problema se seleccionó el método de solución aleatorio de Monte Carlo, donde se establece un rango de temperatura y lo que se busca es determinar la configuración que garantice un valor máximo en el peso de fruto (W _F ) y fruto cosechado (W _HF ) de tomate. La temperatura se seleccionó como el parámetro para calcular por su efecto mayor en el desarrollo y crecimiento de las plantas y porque es uno de los factores en los que se invierten muchos recursos para su control. Mientras que por otro lado se decidió usar el método de Monte Carlo debido a que es posible obtener aproximaciones de resultados sin conocer el comportamiento del sistema ya que solo es necesario dar entradas de valores y ver cual valor tiene mayor probabilidad de ocurrir y genere el comportamiento deseado en el sistema.

El primer paso es determinar la trayectoria de las entradas de control u(t) a las que se debe mantener el invernadero durante un período de 0 a 120 ddt y durante el desarrollo de tomate para aumentar su producción, utilizando simulaciones numéricas del modelo (1) con los parámetros del Cuadro 1 y con la aplicación del método de Monte Carlo. La suposición es que usando simulaciones numéricas es posible determinar la trayectoria subóptima las entradas de control u(t) que aumenten la producción de tomate. Para lograrlo se plantea maximizar la cantidad de peso de fruto (W _F ) y peso de fruto cosechado (W _HF ) considerando dos funciones de costo descritas a continuación:

En la primera sólo se contempló la maximización del crecimiento de variable W _F en un intervalo de tiempo de [0,120] ddt manipulando las entradas de control u(t), esto es:

(6)

Sujeta a las siguientes restricciones: u ^min ≤u(t)≤u ^max y que se cumplan las ecuaciones dinámicas del sistema (1).

En la segunda se contemplaron la maximización tanto del peso de fruto (W _F ) como del peso del fruto cosechado (W _HF ). En esta forma, del tiempo inicial hasta el tiempo que se alcanza la etapa de cosecha, a partir de 0 a 58 días después del trasplante, se buscó únicamente una mayor productividad de W _F y finalmente desde la etapa de cosecha (59 ddt) hasta el final del período de crecimiento (120 dddt) se incrementó la producción de W _HF , esto es

(7)

Igualmente sujeta a las restricciones del caso anterior, no se buscó obtener un valor máximo sólo de la variable W_HF desde el comienzo de la simulación, ya que esta variable permanece constante con valor cero hasta que se alcanza la etapa de cosecha. Para lograr este objetivo se debe escoger una o diversas entradas del sistema dinámico (1), tales como la temperatura, la radiación PAR o la concentración de CO₂.

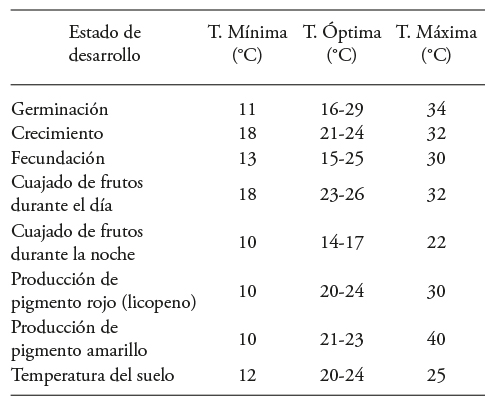
La temperatura es uno de los principales factores climáticos que influye en los estados de desarrollo y procesos fisiológicos de la planta. Esto puede verse en el modelo dinámico (4) como T _g que es una de las entradas al mismo. El desarrollo satisfactorio de las fases de germinación, crecimiento vegetativo, floración, fructificación y maduración de frutos, depende de las temperaturas que se alcanzan en el invernadero en cada etapa de su crecimiento. Además, como el tomate es una planta sensible a cambios extremos de temperaturas y/o humedad relativa, es necesario mantenerlo en un rango óptimo de temperatura para que alcance su máximo desarrollo. Así mismo, cabe agregar que el tomate es una planta termoperiódica, lo cual implica que su crecimiento se ve favorecido por una temperatura variable. Dicha temperatura varía con el estado de desarrollo de la planta, ver Cuadro 2 (^{Jaramillo-Noreña et al., 2013}; ^{Wallach et al., 2006}).

Cuadro 2 Temperaturas mínima, máxima y óptima de las etapas de desarrollo de la planta reportadas en ^{Jaramillo-Noreña et al. (2013)} y ^{Wallach et al. (2006)}. 

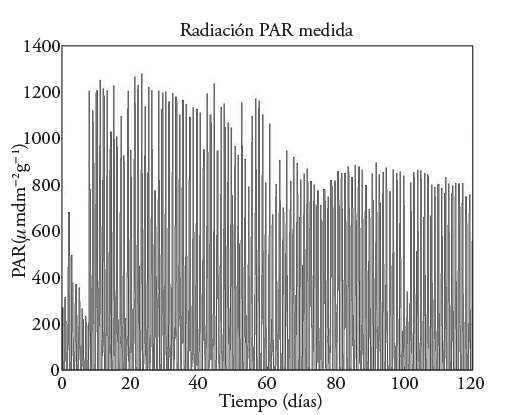
Entonces, para lograr el objetivo de maximización de la producción basándonos en el modelo dinámico (4), se selecciona la temperatura como entrada de control (Cuadro 2) para primero obtener una trayectoria de temperatura que maximice la cantidad de fruto en la planta durante un período de 120 dddt. Posteriormente se elige otra trayectoria de temperatura que maximice la cantidad de fruto en los primeros 58 dddt y del fruto cosechado a partir del día 59 y hasta los 120 d. Es importante aclarar dos puntos: el primero es que a pesar de que existen otras dos entradas en el modelo dinámico (1), las cuales corresponden a la radiación PAR (I) y a la concentración de CO₂, éstas no fueron consideradas en este estudio y se usaron las reportadas en el estudio de ^{Juárez Maldonado et al., 2012} (Figuras 8 y 9); el segundo es que para obtener una trayectoria de temperatura factible en la maximización de la producción de tomate, en cualquiera de los dos problemas aquí planteados, se requiere tener una restricción en la temperatura, que es la entrada manipulada. Por esta razón y considerando los estudios de ^{Pérez et al. (2002)}, ^{Jaramillo-Noreña et al. (2013)} y ^{Wallach et al. (2006)}, se seleccionó un intervalo de restricción de la temperatura de 15 °C≤T _g ≤30 °C. Este rango fue seleccionado de esa manera ya que representa el intervalo medio de temperatura durante el día en la ciudad de Saltillo.

El problema de la maximización de fruto se formula con el sistema de ecuaciones diferenciales (1) que describe la dinámica de crecimiento de las plantas de tomate bajo cultivo: considerando a la entrada de control como u=T _g , la cual está restringida en el intervalo de 15 °C≤u≤30 °C, es decir, u ϵ [15;30] y considerando el vector de estados, x(t)=[B, W _F , W _L , D _p , W _HF , W _HL ], con las condiciones iniciales en el cultivo de x(0)=[0; 0,42; 43,59; 0; 0; 3,95], obtenidas por ^{Juárez-Maldonado et al. (2014)}. Se requiere encontrar la trayectoria de temperatura que generen una mayor cantidad de fruto (W _F ) y fruto cosechado (W _HF ) en el tiempo de crecimiento final t _f =120 días; donde es importante mencionar que cada intervalo de tiempo en el que se calculó una temperatura es de 15 min durante los 120 d de simulación.

Método de Monte Carlo

El método de Monte Carlo consiste en la generación de números aleatorios en base a una distribución de probabilidad dada. De esta manera se exploran configuraciones o entradas accesibles al sistema para posteriormente tomar las de mayor probabilidad en base a los criterios seleccionados.

El algoritmo basado en el Método de Monte Carlo (^{Peña Sánchez de Rivera, 2001}) que se utilizó para obtener la trayectoria de temperatura es:

Se considera que se ha completado un paso de Monte Carlo cuando se cumple todo el proceso descrito anteriormente. La trayectoria subóptima de temperatura se obtiene calculando los promedios de T _g en las iteraciones hechas para graficarlos contra los intervalos de tiempo establecidos usando la ecuación de la media Tg= 1M∑I=1M Tg1 media , donde T _gi es temperatura obtenida en el paso i de la simulación y M es el número total de iteraciones.

El método de Monte Carlo al ser aleatorio y al no estar basado en las condiciones de optimalidad de primer y segundo orden (^{Bryson y Ho, 1975}; ^{Lewis, 1986}) requiere ser evaluado cambiando el número de iteraciones. Es conocido que al aumentar el número de iteraciones este método aproxima mejor su solución, por lo tanto depende de un criterio de finalización al determinar el máximo error que va a ser admitido. Por esta razón, para resolver el problema anterior se realizaron dos simulaciones, una con 500 mil y la segunda con 1 millón de iteraciones con el método de Monte Carlo para los dos casos de maximizar las variables de peso de fruto (W _F ) y peso de fruto cosechado (W _HF ), considerando que los límites de temperatura están entre los 15 y 30 °C.

Primer Caso: maximización de W _F

Las trayectorias subóptimas de temperatura obtenidas después del día 59 para el primer caso de maximización sólo de W _F , en lo que corresponde a un 1 millón de iteraciones, indican que la temperatura se estabiliza alrededor de 15 °C, que corresponde al límite inferior de la restricción impuesta a diferencia de lo que ocurre a 500 mil iteraciones donde no se observa esta estabilidad, así mismo puede observarse que la trayectoria de temperatura subóptima muestra períodos que emulan el día y la noche, alrededor de este mismo intervalo de restricción (Figura 1).

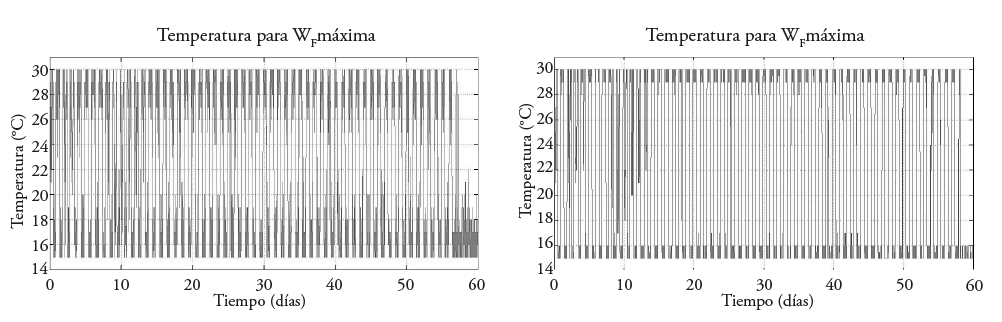
Figura 1 Trayectorias de temperatura subóptima cuando se maximiza W _F . Obtenida con 500 mil iteraciones (izquierda) y con 1 millón de iteraciones (derecha). 

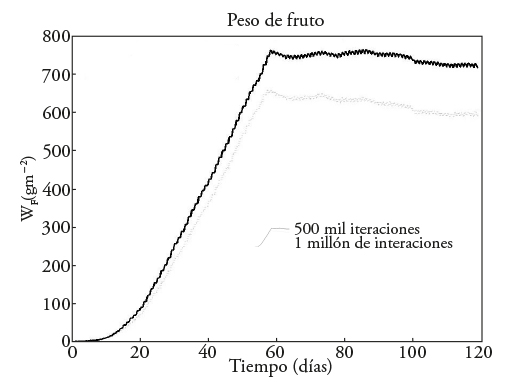
El peso de fruto maximizado (W _F ) con la trayectoria subóptima de temperatura (Figura 1), para 500 mil y 1 millón de iteraciones permite apreciar que el aumento en el número de iteraciones tiene un impacto en la obtención del peso de fruto maximizado y que para 500 mil iteraciones se obtienen alrededor de 650 [gm^-2] de W _F , mientras que para el caso de 1 millón de iteraciones se obtienen 750 [gm^-2] W _F (Figura 2).

Figura 2 W _F [gm^-2] maximizada, obtenida con 500 mil iteraciones y con 1 millón de iteraciones. 

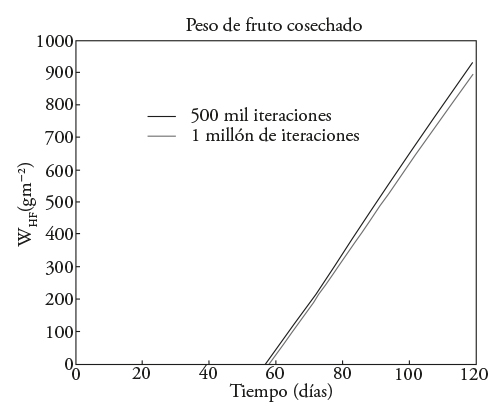
Los resultados del fruto cosechado (W _HF ) para cuando sólo se maximiza el peso de fruto (W _F ), considerando 500 mil y 1 millón de iteraciones señalan que la curva inicia a incrementarse alrededor del día 59, que es cuando el fruto empieza a cosecharse. El peso de fruto cosechado (W _HF ) alcanza un valor aproximado de 900 [gm^-2] tanto para las 500 mil iteraciones y como para un millón de iteraciones (Figura 3).

Figura 3 W _HF [gm^-2] obtenida con 500 mil iteraciones y con 1 millón de iteraciones. 

Segundo caso: maximización de W _F y W _HF

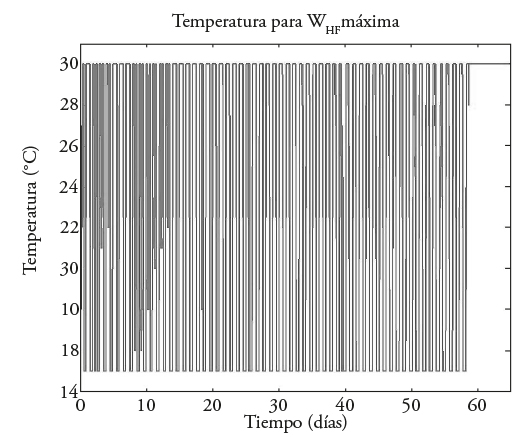
La trayectoria de temperatura subóptima obtenida para la maximización combinada de W _F y W _HF , que es el segundo caso, permite observar una periodicidad tal como cuando se maximiza únicamente el peso de fruta (W _F ). Sin embargo, a partir del día 59 aproximadamente, el cual corresponde a la etapa de la cosecha, la maximización indica que la temperatura debe mantenerse alrededor del intervalo de restricción de temperatura máxima de 30 °C (Figura 4).

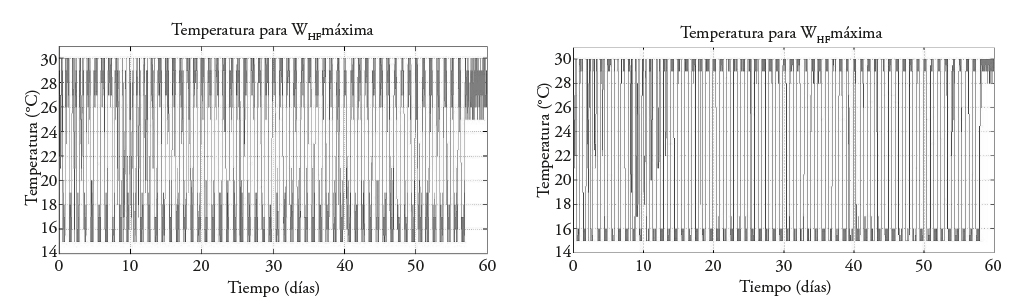
Figura 4 Suboptimal temperature trajectories for maximizing W _F and W _HF . obtained with 500 thousand iterations (left) and with 1 million iterations (right). 

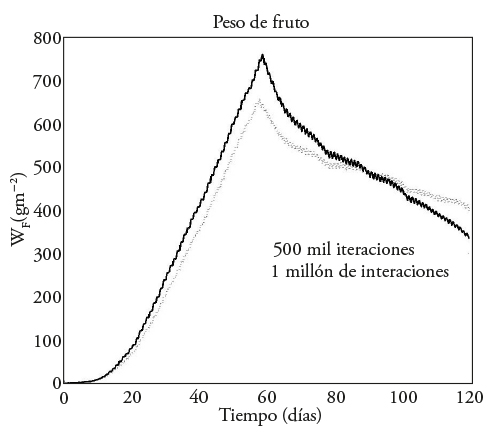
Los resultados del peso de fruta (W _F ) indican valores similares a los del primer caso, en el intervalo de 0-59 d, de 650 [gm^-2] y de 750 [gm^-2] de W _F para 500 mil y un millón de iteraciones, respectivamente. Sin embargo, desde el día 59 en ambas simulaciones el peso de fruto (W _F ) decrece, ya que en esta caso se maximiza sólo el peso de fruto cosechado (W _HF ) (Figura 5).

Figura 5 W _F [gm^-2] maximizada, obtenida con 500 mil iteraciones y con 1 millón de iteraciones. 

En cuanto al peso de fruto cosechado (W _HF ) se observó que éste aumenta considerablemente con respecto al caso donde cuando únicamente se maximiza el peso de fruto (W _F ), es decir, se obtienen aproximadamente 1300 [gm^-2] y 1450 [gm^-2], para 500 mil y un millón de iteraciones, respectivamente; en contraste con los 900 [gm^-2] obtenidos anteriormente (Figura 3).

Resultados de simulación sin optimización reportado por ^{Juárez-Maldonado et al. (2012)}

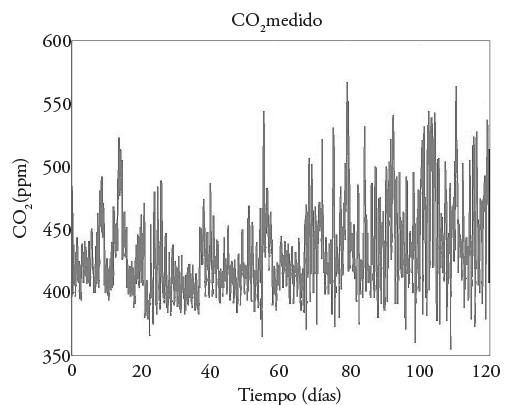
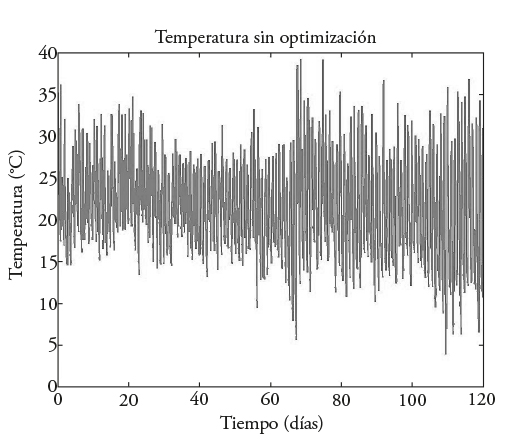
Los resultados del peso de fruto y de peso de fruto cosechado reportados por ^{Juárez-Maldonado et al. (2012)}, reproducidos por simulación y presentados a continuación (Figura 7), no se maximiza W _F ni W _HF y sólo se consideran las trayectorias de temperatura, CO₂ y radiación PAR medidas durante los 120 días ddt dentro del invernadero (Figuras 8-10) sin optimizar. En dichos resultados se observa un aumento del peso de fruto (W _F ) de 600 [gm^-2] sin maximizar a 750 [gm^-2] para cuando se maximiza sólo (W _F ) con 1 millón de iteraciones (Figura 2). En comparación, cuando se maximiza el peso de fruto cosechado (W _HF ) desde el día 59 hay un aumento de 800 [gm⁻²] sin maximizar a 1450 [gm^-2] (Figuras 6 y 7). La temperatura registrada en el estudio de ^{Juárez-Maldonado et al. (2012)} sin optimizar (Figura 8), comparada con las trayectorias subóptimas reportadas en las Figuras 2 y 4, muestra un gran cambio entre ellas. Es necesario un análisis de costo de producción entre el desarrollo del cultivo sin control y con la suboptimización de la trayectoria de temperatura antes de decidir si es posible su aplicación.

Figura 6 W _HF [gm^-2] maximizada, obtenida con 500 mil iteraciones y con 1 millón de iteraciones. 

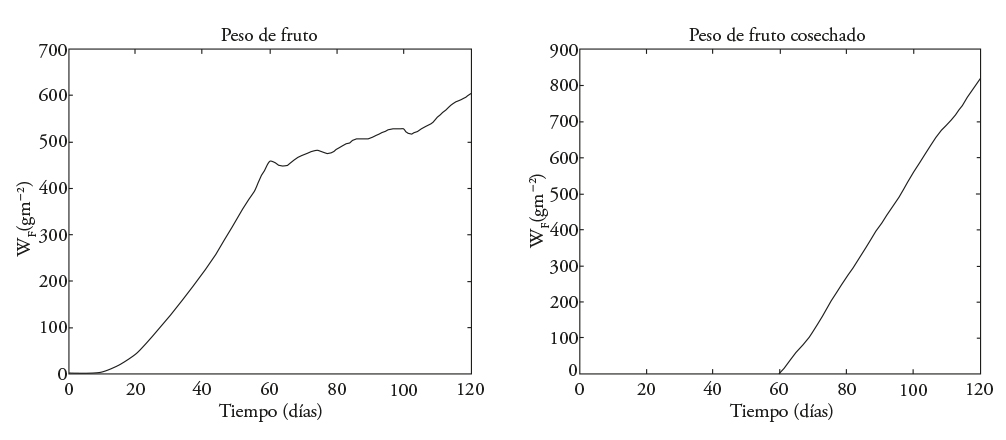
Figura 7 Peso de fruto (izquierda) y de fruto cosechado (derecha) reportado por ^{Juárez-Maldonado et al. (2012)}. 

Figura 8 Radiación PAR reportada por ^{Juárez-Maldonado et al. (2012)}. 

Figura 9 Concentración de CO₂ reportada por ^{Juárez-Maldonado et al. (2012)}. 

Figura 10 Temperatura reportada por ^{Juárez-Maldonado et al. (2012)}. 

Los resultados mostraron dos características importantes. La primera correspondiente a la aproximación de la solución aumentando el número de iteraciones del método de Monte Carlo, de 500 mil a 1 millón. Considerando esta variación de iteraciones se observa (Figuras 1 y 4) una menor oscilación en las gráficas con mayor número de iteraciones lo cual era de esperarse ya que a medida que aumentamos los pasos el sistema tiende a la convergencia de la solución del problema (^{Peña Sánchez de Rivera, 2001}). La segunda es el comportamiento obtenido de la trayectoria de la temperatura para la maximización únicamente del peso de fruto (W _F ) y para la maximización de W _F entre los días 0 y 58, y del peso de fruto cosechado (W _HF ) a partir del día 59 y hasta el final del periodo (120 d). Desde el día 59 que marca el inicio de la cosecha la trayectoria subóptima de temperatura se estabilizó alrededor de 15 °C para la maximización de W _F (Figura 1) y alrededor de 30 °C para la maximización de W _F y W _HF (Figura 4). Este último comportamiento puede explicarse a través de la dinámica de W _F y W _HF (ec. 4): dWFdt= bgFWF-1-brFWF dWHFdt= hFWF ; del cual se observa que ambas están ligadas por el término h _F W _F , y que en el caso de W _F merma su producción, mientras que para W _HF el mismo término permite un incremento del fruto cosechado. Asimismo, se aprecia que la trayectoria de temperatura subóptima para ambos casos muestra períodos que emulan el día y la noche, alrededor de este mismo intervalo de restricción antes del día 59.

Temperatura óptima

Para obtener la trayectoria óptima de temperatura se realizó una comparación entre los métodos de Monte Carlo con 1 millón de iteraciones y la aplicación de control óptimo usando MATLABR11 (^{MathWorks, 2017}) con la herramienta de optimización no lineal y el programa DYNOPT basado en el estudio de ^{Logsdon y Biegler (1989)} y se determina una trayectoria de control óptimo dado un modelo dinámico de un proceso, que está sujeto a restricciones de igualdad y desigualdad. Por brevedad de espacio, sólo mostramos la trayectoria de temperatura óptima en el caso de maximización de W _F y W _HF (Figura 11), en la cual, si se comparamos con la Figura 4, se nota una similitud entre ambas trayectorias. La diferencia radica en que debido a la naturaleza aleatoria del método de Monte Carlo, el comportamiento de la temperatura tiende a oscilar alrededor del valor medio o esperado y esta oscilación está relacionada directamente en el número de pasos de la simulación, mientras que con el método optimización no lineal no existen estas oscilaciones.

Figura 11 Trayectoria óptima de temperatura calculada mediante el programa de control óptimo DYNOPT.